第三章 习题和答案
第三章习题解答

第三章习题解答一、判断下列说法是否正确,凡对的在括号内打“√”,否则打“×”。
(1)现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(2)阻容耦合多级放大电路各级的Q点相互独立,( )它只能放大交流信号。
( )(3)直接耦合多级放大电路各级的Q点相互影响,( )它只能放大直流信号。
( )(4)只有直接耦合放大电路中晶休管的参数才随温度而变化。
( )(5)互补输出级应采用共集或共漏接法。
( )二、现有基本放大电路:A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。
(1)要求输入电阻为1kΩ至2kΩ,电压放大倍数大于3000,第一级应采用,第二级应采用。
(2)要求输入电阻大于10MΩ,电压放大倍数大于300,第一级应采用,第二级应采用。
(3)要求输入电阻为100kΩ~200kΩ,电压放大倍数数值大于100,第一级应采用,第二级应采用。
(4)要求电压放大倍数的数值大于10,输入电阻大于10MΩ,输出电阻小于100Ω,第一级应采用,第二级应采用。
(5)设信号源为内阻很大的电压源,要求将输入电流转换成输出电压,且,输出电阻R o<100,第一级应采用,第二级应采用。
三、选择合适答案填入空内。
(1)直接耦合放大电路存在零点漂移的原因是。
A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定(2)集成放大电路采用直接耦合方式的原因是。
A.便于设计B.放大交流信号C.不易制作大容量电容(3)选用差分放大电路的原因是。
A.克服温漂B. 提高输入电阻C.稳定放入倍数(4)差分放大电路的差模信号是两个输入端信号的,共模信号是两个输入端信号的。
A.差B.和C.平均值(5)用恒流源取代长尾式差分放大电路中的发射极电阻R e,将使电路的。
A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大(6)互补输出级采用共集形式是为了使。
第3章习题及答案

第三章审计的法律责任习题一、单项选择题1、如果被审计单位的财务报表中存在重大错报,则在()情况下很可能在诉讼中被判为重大过失。
A、注册会计师运用常规审计程序通常能够发现该错报B、审计人员确实遵守了审计准则,但却提出错误的审计意见C、注册会计师明知道存在重大错报但却虚伪的陈述,出具无保留意见的审计报告D、注册会计师基本上遵循了审计准则的相关要求2、审计人员对被审单位的应收账款进行了大量的函证,仅发现一封回函声称与被审单位记录不同:该企业表示,其仅向被审计单位发出过定货单,但随即就收回了订货要求。
对此封回函,注册会计师只看了一半,因为接一个电话而没有看完,接完电话后误以为这是一封已看完的回函,便认可了该笔应收账款的存在性。
但后来查清,该笔应收账款是被审计单位虚构的。
你认为审计人员的这种作法属于()。
A、欺诈B、普通过失C、重大过失D、没有过失3、由于Q会计师事务所下属的各个分所均可以Q事务所的名义独立承揽业务,导致某分所为P公司出具虚假审计报告而Q所尚不知晓,给Q所带来严重影响。
为避免类似情况的再次发生,Q会计师事务所应采取的针对性措施是()。
A、严格遵循职业道德、专业标准的要求B、建立健全会计师事务所的质量控制制度C、与委托人签订审计业务约定书D、提取风险基金或购买责任保险4、在注册会计师为避免法律诉讼而采取的以下具体措施中,()既可以起到防患于未然的作用,又可能在出现法律纠纷后作为减轻法律责任的抗诉理由。
A、建立、健全会计师事务所的质量控制制度B、审慎地选择被审计单位C、深入了解被审计单位的业务D、严格遵循职业道德和专业标准的要求5、注册会计师在认定了以下4个账户的情况后,由于各种原因而未能作进一步的审查,致相应于该账户的财务报表项目中存在重大问题而未被发现。
其中,最有可能被判定为欺诈的是()。
A、营业外支出账户金额不大,与以前5年情况基本一致B、应收账款账户余额异乎寻常地高,被审计单位不能加以合理解释C、累计折旧大幅度增加,但被审计单位的有关内部控制健全而有效D、实收资本大量增加,而被审计单位已出示了验资报告6、注册会计师在对ABC股份有限公司2006年度会计报表进行审计时,按照函证具体准则对有关应收账款进行了函证,并实施了其他必要的审计程序,但最终仍有应收账款业务中的错报未能查出。
数据结构第三章栈和队列习题及答案

习题三栈和队列一单项选择题1. 在作进栈运算时,应先判别栈是否(① ),在作退栈运算时应先判别栈是否(② )。
当栈中元素为n个,作进栈运算时发生上溢,则说明该栈的最大容量为(③ )。
①, ②: A. 空 B. 满 C. 上溢 D. 下溢③: A. n-1 B. n C. n+1 D. n/22.若已知一个栈的进栈序列是1,2,3,…,n,其输出序列为p1,p2,p3,...,pn,若p1=3,则p2为( )。
A 可能是2B 一定是2C 可能是1D 一定是13. 有六个元素6,5,4,3,2,1 的顺序进栈,问下列哪一个不是合法的出栈序列?()A. 5 4 3 6 1 2B. 4 5 3 1 2 6C. 3 4 6 5 2 1D. 2 3 4 1 5 64.设有一顺序栈S,元素s1,s2,s3,s4,s5,s6依次进栈,如果6个元素出栈的顺序是s2,s3,s4, s6, s5,s1,则栈的容量至少应该是()A.2B. 3C. 5D.65. 若栈采用顺序存储方式存储,现两栈共享空间V[1..m],top[i]代表第i个栈( i =1,2)栈顶,栈1的底在v[1],栈2的底在V[m],则栈满的条件是()。
A. |top[2]-top[1]|=0B. top[1]+1=top[2]C. top[1]+top[2]=mD. top[1]=top[2]6. 执行完下列语句段后,i值为:()int f(int x){ return ((x>0) ? x* f(x-1):2);}int i ;i =f(f(1));A.2 B. 4 C. 8 D. 无限递归7. 表达式3* 2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和算符栈为(),其中^为乘幂。
A. 3,2,4,1,1;(*^(+*-B. 3,2,8;(*^-C. 3,2,4,2,2;(*^(-D. 3,2,8;(*^(-8. 用链接方式存储的队列,在进行删除运算时()。
会计课后习题答案(第三章)

19 企业计提当年盈余公积的基数,不包括年初未分配利润。
答案: 正确
20 年度终了,“利润分配”账户所属的各明细账户中,除“未分配利润”明细账户可能有余额外,其他明细账户均无余额。
答案: 正确
21 得利与损失是与企业日常活动直接关联的经济利益总流入或总流出。
答案: 错误
8 下列支出不得列入成本费用的是 。
A: 支付给金融机构的手续费
答案: 制造费用
10 “应付职工薪酬”账户可设置 、 、 、 、 和“非货币性福利”等明细分类账户。
答案: 工资 社会保险费 职工福利 工会经费 职工教育经费
11 .直接生产工人的薪酬费用应计入 账户,车间技术及管理人员薪酬费用应计入 账户,销售机构人员的薪酬费用计入 账户,行政管理人员薪酬费用计入 账户。
答案: 正确
15 企业按职工工资总额一定比例计提的工会经费及职工教育经费应记入管理费用。
答案: 错误
16 企业专设销售机构的固定资产修理费用应计入销售费用。
答案: 正确
17 “生产成本”账户若有余额应在借方,反映期末自制半成品的实际生产成本。
答案: 错误
18 企业当年可供分配的利润包括当年实现的净利润和年初未分配利润。
B: 制造费用
C: 本年利润
D: 管理费用
E: 利润分配
答案: B, D
5 工业企业以下收入中应记入其他业务收入的有 。
A: 销售产品
B: 销售材料
C: 固定资产盘盈
D: 固定资产出租收入
E: 处置固定资产净收益
答案: B, D
6 工业企业以下各项应记入营业外支出的是 。
第三章_投入产出核算习题_答案)

6. 目前我国公布的投入产出表是_A__。
A. 产品部门×产品部门 C. 产业部门×产品部门
B.产品部门×产业部门 B.产业部门×产业部门.
7.B(I A )1 被称为列昂惕夫逆矩阵,它蕴含着丰富的经济意义。下列关于列 昂惕夫逆矩阵说法错误的是__D_。 A. 列昂惕 第Ⅲ象限的行标题包括 ABCD。 A. 固定资产折旧 C. 生产税净额 B. D. 劳动者报酬 营业盈余 E. 存货增加
新疆财经大学
国民经济核算
2.投入产出表的基本平衡关系有 ACE A. 中间投入+最初投入=总投入 B. 中间使用+最终使用+进口=总产出 C. 中间使用+最终使用=总产出 D. 总投入=总产出+进口 E. 总投入=总产出 3. A. B. C. D. E. 关于投入产出表的第Ⅰ象限,下列说法正确的是 ABCE 行标题是中间投入 列标题是中间投入 其含义可以从行向和列向两个方向解读 反映的是最终产品的规模和结构 反映国民经济各产业部门之间的技术经济联系
B. b 表示j部门增加一个单位最终使用时,对i 部门的完全需求量 ij C. 列昂惕夫逆矩阵和完全消耗系数的关系是 B BI
D. 以上说法至少有一个是错误的
新疆财经大学
国民经济核算
8. 在一个三产业投入产出表中,直接消耗系数a 的数值为0.2864, 21 则它所代表的含义是_A__. A. 第一产业生产1单位总产出对第二产业的消耗量 B. 第二产业生产1单位总产出对第一产业的消耗量 C. 第一产业产品分配给第二产业使用部分所占的比例 D. 第二产业产品分配给第一产业使用部分所占的比例
B. 前者只包括主要生产活动也包括次要生产活动,而后者仅包括 一种生产活动 C. 后者既包括主要生产活动也包括次要生产活动,而前者仅包括 一种生产活动
第三章习题解答

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
第3章习题参考答案
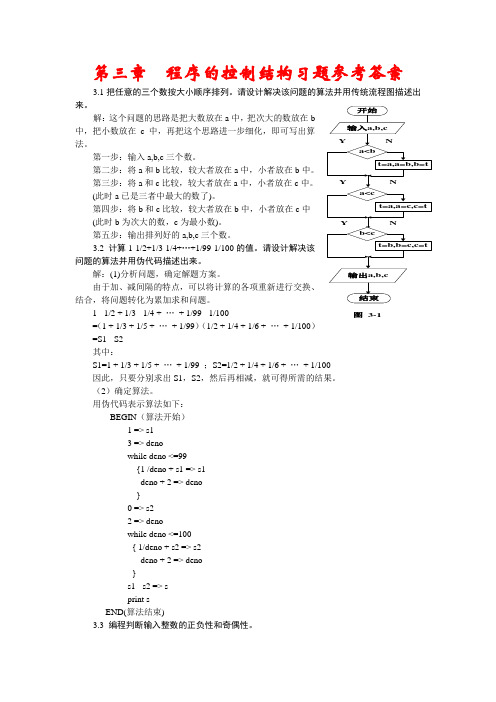
第三章 程序的控制结构习题参考答案3.1把任意的三个数按大小顺序排列。
请设计解决该问题的算法并用传统流程图描述出来。
解:这个问题的思路是把大数放在a 中,把次大的数放在b中,把小数放在c 中,再把这个思路进一步细化,即可写出算法。
第一步:输入a,b,c 三个数。
第二步:将a 和b 比较,较大者放在a 中,小者放在b 中。
第三步:将a 和c 比较,较大者放在a 中,小者放在c 中。
(此时a 已是三者中最大的数了)。
第四步:将b 和c 比较,较大者放在b 中,小者放在c 中(此时b 为次大的数,c 为最小数)。
第五步:输出排列好的a,b,c 三个数。
3.2 计算1-1/2+1/3-1/4+…+1/99-1/100的值。
请设计解决该问题的算法并用伪代码描述出来。
解:(1)分析问题,确定解题方案。
由于加、减间隔的特点,可以将计算的各项重新进行交换、结合,将问题转化为累加求和问题。
1 - 1/2 + 1/3 - 1/4 + … + 1/99 - 1/100 =(1 + 1/3 + 1/5 + … + 1/99)-(1/2 + 1/4 + 1/6 + … + 1/100)=S1 - S2其中:S1=1 + 1/3 + 1/5 + … + 1/99 ;S2=1/2 + 1/4 + 1/6 + … + 1/100因此,只要分别求出S1,S2,然后再相减,就可得所需的结果。
(2)确定算法。
用伪代码表示算法如下:BEGIN (算法开始)1 => s13 => denowhile deno <=99{1 /deno + s1 => s1deno + 2 => deno}0 => s22 => denowhile deno <=100{ 1/deno + s2 => s2deno + 2 => deno}s1 - s2 => sprint sEND(算法结束)3.3 编程判断输入整数的正负性和奇偶性。
第三章习题(含答案)

第三章会计等式与复式记账一、单项选择题1、总分类账户与明细分类账户平行登记四要点中的“依据相同”是指()。
A.总分类账要根据明细分类账进行登记B.明细分类账要根据总分类账进行登记C.根据同一会计凭证登记D.由同一人员进行登记2、某企业原材料总分类科目的本期借方发生额为25 000元,贷方发生额为24 000元,其所属的三个明细分类账中;甲材料本期借方发生额为8 000元,贷方发生额为6 000;乙材料借方发生额为13 000元,贷方发生额为16 000元;则丙材料的本期借、贷方发生额分别为()。
A.借方发生额为12 000元,贷方发生额为2 000元B.借方发生额为4 000元,贷方发生额为2 000元C.借方发生额为4 000元,贷方发生额为10 000元D.借方发生额为6 000元,贷方发生额为8 000元3、甲公司月末编制的试算平衡表中,全部科目的本月贷方发生额合计为120万元,除银行存款外的本月借方发生额合计104万元,则银行存款科目()。
A.本月借方余额为16万元B.本月贷方余额为16万元C.本月贷方发生额为16万元D.本月借方发生额为16万元4、下列记账错误中,不能通过试算平衡检查发现的是()。
A.将某一分录的借方发生额600元,误写成6 000元B.某一分录的借贷方向写反C.借方的金额误记到贷方D.漏记了借方的发生额5、下列关于试算平衡法的说法,正确的是()。
A.漏记某项经济业务影响试算平衡B.包括发生额试算平衡法和余额试算平衡法C.试算平衡了,账户记录一定正确D.发生额试算平衡法理论的依据是会计等式6、企业购入原材料10 000元,已开出支票支付6 000元,另4 000元暂欠。
下列会计分录正确的是()。
A.借:原材料10 000贷:银行存款10 000B.借:原材料10 000贷:应付账款10 000C.借:原材料10 000贷:银行存款6 000应付账款4 000D.借:原材料10 000贷:应付票据6 000应付账款4 0007、企业计算应交所得税时,正确的会计分录是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 0 2 −1 求得: [ M ] m = = 0 1 , [ K ] k −1 1
x x 系统运动微分方程可写为: [ M ] 1 + [ K ] 1 = 0 ………… (a) x2 x2 设系统固有振动的解为:
系统的动能和势能分别为 1 1 12 + mx 22 = ET mx 2 2 1 2 1 U = kx1 + k(x1 − x2 )2 + mg(x1 + x2 ) 2 2
解得: ω1,2 2 = 所以: ω1 =
(3 ± 5) k 2 m (3 − 5) k (3 + 5) k < ω2 = 2 m 2 m ………… (c)
得到频率方程: (ω 2 ) =
2 4 即: (ω 2 )= 3m2 ω − 14k2 m2ω 2 + 7 k2 2= 0
解得: ω1,2
所以: ω1 =
将(c)代入(b)可得: (7 ± 2 7) k2 − k2 2k2 − 3m2 3 m2 u1 = 0 u2 (7 ± 2 7) k2 4k 2 − − k2 m2 3 m2 解得: u11 2 7 + 5 u12 5 − 2 7 ; = − = u21 3 u22 3
………… (c)
令 u2 = 1 ,得到系统的振型为 :
1
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
1 0.09 -3.430
3.3 如图所示弹簧质量系统,写出系统的频率方程并求出固 有频率和振型,画出振型图。 解:以静平衡位置为原点,设 m1 , m2 的位移 x1 , x2 为广义坐标,
求图所示系统的固有频率和振型,并画出振型图。设杆质量分布均匀。
求图所示系统当左边质量有初始位移 A 而其余初始条件均为零时的响
3.7
如图 T—3.7 所示由弹簧耦合的双摆,杆长为 L。 1.写出系统的刚度矩阵、质量矩阵和频率方程; 2.求出固有频率和振型; 3.讨论是值改变对固有频率的影响。
解:
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
得到频率方程: = (ω 2 )
2 4 即: (ω 2 = ) 2I2 ω − 4kt1 I 2ω 2 + kt12 = 0
解得: ω1,2
所以: ω1 =
将(c)代入(b)可得: (2 ± 2) kt1 − kt 1 2kt1 − 2I 2 2 I2 u1 = 0 (2 ± 2) kt1 u2 − kt 1 kt 1 − I 2 2 I 2 解得: u11 u 2 2 ; 12 = = − u21 2 u22 2
3.1
如图所示扭转系统。设 = I1 2= I 2 ; kt 1 kt 2 1.写出系统的刚度矩阵和质量矩阵; 2.写出系统的频率方程并求出 I1 , I 2 的转角 θ1 , θ 2 为广义坐标,画出 I1 , I 2 隔 离体,根据牛顿第二定律得到运动微分方程: + k θ + k (θ − θ ) = + (k + k )θ − k θ = 0 0 I1θ I1θ 1 t1 1 t2 1 2 1 t1 t2 1 t2 2 ,即: 0 0 I 2θ 2 + kt 2 (θ 2 − θ1 ) = I 2θ 2 − kt 2θ1 + kt 2θ 2 = k + k I1 0 所以: [ M ] = = , [ K ] t1 t 2 0 I2 − kt 2 − kt 2 kt 2
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
2 −1 2 0 由于 , [ K ] kt 1 = I1 2= I 2 ; kt1 kt= I= 2 ,所以 [ M ] 2 0 1 −1 1 θ u 2)设系统固有振动的解为: 1 = 1 cos ωt ,代入(a)可得: θ 2 u2 u1 ([ K ] − ω 2 [ M ]) = 0 u2 ………… (b)
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
− k2 k 2 + k3
3 0 2 −1 由于 = = m = , [ K ] k2 m1 3m2 ;= k3 3= k2 3k 1 ,所以 [ M ] 2 0 1 −1 4 x u 2)设系统固有振动的解为: 1 = 1 cos ωt ,代入(a)可得: x2 u2 u1 ([ K ] − ω 2 [ M ]) = 0 u2 ………… (b)
k + k m1 0 所以: [ M ] = = ,[ K ] 1 2 0 m2 − k2
x x 系统运动微分方程可写为: [ M ] 1 + [ K ] 1 = 0 ………… (a) x2 x2 或者采用能量法:系统的动能和势能分别为 1 1 12 + m2x 22 = ET m1x 2 2 1 1 1 U= k1x12 + k2(x1 − x2 )2 + k3x22 2 2 2 求偏导也可以得到 [ M ] , [ K ]
2k − ω 2 m −k 得到频率方程: = (ω ) = 0 −k k − ω 2m
2 2 ) m 2ω 4 − 3kmω 2 + k = 0 即: (ω 2=
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
x1 u1 = cos ωt ,代入(a)可得: x2 u2 ………… (b) u ([ K ] − ω 2 [ M ]) 1 = 0 u2
型图。
解: 1)以静平衡位置为原点, 设 m1 , m2 的位移 x1 , x2 为广义坐标, 画出 m1 , m2 隔 离体,根据牛顿第二定律得到运动微分方程: 0 x1 + k1 x1 + k2 ( x1 − x2 ) = m1 x2 + k2 ( x2 − x1 ) + k3 x2 = 0 m2
1 1 -2.736
3.4 如图 T—3.4 所示,由一弹簧是连接两个质量 m1,m2 构成的系统以速 度 v 撞击制动器 k1, 求传到基础上的力的最大值。 设 v 为常数且弹簧无初始 变形,并设 m1=m2 与 k1=2k。
3.5
3.6 应
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
将(c)代入(b)可得:
解得:
令 u2 = 1 ,得到系统的振型为:
1.736
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
(3 ± 5) k m −k 2k − u 2 m 1= 0 (3 ± 5) k u2 k− m −k 2 m u11 5 − 1 u12 1+ 5 ; = = − u21 2 u22 2
(2 − 2) kt1 (2 + 2) kt1 < ω2 = 2 2 I2 I2
………… (c)
令 u2 = 1 ,得到系统的振型为:
1 0.707 1
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
-0.707
3.2
求图所示系统的固有频率和振型。设 = m1 3m2 ;= k3 3= k2 3k1 。并画出振
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
−k2 2k2 − 3ω 2 m2 = 0 −k2 4k2 − ω 2 m2
2 2 14k2 m2 ± (14k2 m2 ) 2 − 4 × 3m2 × 7 k2 2 (7 ± 2 7) k2 = 2 6m2 3 m2
(7 − 2 7) k2 (7 + 2 7) k2 < ω2 = 3 m2 3 m2
θ θ 系统运动微分方程可写为: [ M ] 1 + [ K ] 1 = 0 ………… (a) θ θ 2 2 或者采用能量法:系统的动能和势能分别为 1 2 1 2 = ET I 1θ1 + I 2θ2 2 2 1 1 1 1 U = kt 1θ12 + kt 2(θ1 − θ2 )2 = (kt 1 + kt 2 )θ12 + kt 2θ22 − kt 1θ1θ2 2 2 2 2 求偏导也可以得到 [ M ] , [ K ]
爱 ww 答 w. 案 ai 学 da 习 an 资 .c 源 n 网
2kt1 − 2ω 2 I 2 − kt 1 = 0 − kt 1 kt 1 − ω 2 I 2
2 2 4kt1 I 2 ± (4kt1 I 2 ) 2 − 4 × 2 I 2 × kt12 (2 ± 2) kt1 = 2 4I2 2 I2
