理论力学期末复习
理论力学期末复习题

理论力学期末复习题一、填空题1. 在介质中上抛一质量为m 理论力学期末复习题v k R;若选择坐标轴x 铅直向上;则小球的运动微分方程为理论力学期末复习题_。
2. 质点在运动过程中;在下列条件下;各作何种运动?①0 t a ;0 n a (答): ;②0 t a ;0 n a (答): ;③0 t a ;0 n a (答): ;④0 t a ;0 n a (答): 。
3. 质量为kg 10的质点;受水平力F的作用;在光滑水平面上运动;设t F 43 (t 以s 计;F 以N 计);初瞬间(0 t )质点位于坐标原点;且其初速度为零。
则s t 3 时;质点的位移等于_______________;速度等于_______________。
4. 在平面极坐标系中;质点的径向加速度为__________;横向加速度为_______。
5. 哈密顿正则方程用泊松括号表示为 ; 。
6. 质量kg m 2 的重物M ;挂在长m l 5.0 的细绳下端;重物受到水平冲击后获得了速度105 s m v ;则此时绳子的拉力等于 。
7. 平面自然坐标系中的切向加速度为 ;法向加速度为 。
8. 如果V F;则力所作的功与 无关;只与 的位置有关。
9. 在南半球地面附近自南向北的气流有朝 的偏向;而北半球的河流岸冲刷较为严重。
10. 已知力的表达式为axy F x ;2az F y ;2ax F z 。
则该力做功与路径_ (填“有关”或“无关”);该力_ 保守力(填“是”或“不是”)。
11. 一质量组由质量分别为0m 、20m 、30m 的三个质点组成;某时刻它们的位矢和速度分别为j i r 1、i v21 、k j r 2、i v 2、k r 3、k j i v3。
则该时刻质点组相对于坐标原点的动量等于 ;相对于坐标原点的动量矩等于_ 。
12. 一光滑水平直管中有一质量为m 的小球;直管以恒定角速度 绕通过管子一端的竖直轴转动;若某一时刻;小球到达距O 点的距离为a 的P 点;取x 轴沿管;y 轴竖直向上;Ox yz P v ma并垂直于管;z 轴水平向前;并于管面垂直;如图所示;此时小球相对于管子的速度为v;则惯性离心力大小为 ;方向为 ;科里奥利力大小为 ;方向为 。
《理论力学》期末复习资料

a
L
T k(2b cos b a)
L
L F k(2b x b a)
b
2L L
x
a
FL2 k b2
例16、试用牛顿方法和拉氏方法证明单摆的运动微分方程 g sin 0
l
其中为摆线与铅直线之间的夹角,l为摆线长度。
解: (1)用牛顿法:
l
ml mg sin
T
g sin 0
l
mg
3
3
33
v2 x2 y 2 an
v2
2 2m
9
11
例4、一质点受有心力 轨道的微分方程。
F
km r2
作用,列出求解其
解:
h2u
2
(
d 2u
d 2
u)
F (r) m
F km kmu2 r2
d 2u u k
d 2
h2
例5、如下图所示,船长为L=2a,质量为M的小船,在船头上站一质量为m的人,
cos3 d
L
o
x
mg
y
18
例12、如下图所示的机构,已知各杆长为L,弹簧的原长L,弹性系数 k,若忽略各处摩擦不计,各杆的重量忽略不计。试用虚功原理求平衡
时p的大小与角度之间的关系。
y
TT
解: 2TxD pyA 0
xD L cos xD L sin yA 2L sin yA 2L cos
x
(2TLsin 2 pLcos ) 0
o
2TLsin 2 pLcos 0
p T tan k(2L cos L) tan kL(2sin tan )
19
例13、如下图所示的机构,已知各杆长为L,弹簧的原长也L,弹性系数为 k,若忽略各处摩擦不计,各杆的重量也忽略不计。试用虚功原理求平衡时
理论力学 期末复习知识点

第一章静力学公理与物体的受力分析§1.1 静力学公理✧公理1 二力平衡公理(条件)作用在刚体上的两个力,使刚体保持平衡的充分必要条件是:这两个力大小相等,方向相反,且在同一直线上。
✧公理2 加减平衡力系原理在已知力系上加上或减去任意的平衡力系,不改变原力系对刚体的作用。
(效应不变)✧公理3 力的平行四边形法则作用在物体上的同一点的两个力,可以合成为一个合力。
合力作用点也是该点,合力的大小和方向,由这两个力为边构成的平行四边形的对角线确定。
✧公理4 作用和反作用定律作用力与反作用力总是同时存在,两力的大小相等、方向相反、沿着同一直线,分别作用在两个相互作用的物体上。
✧公理5 刚化原理变形体在某一力系作用下处于平衡,如将此变形体刚化为刚体,其平衡状态保持不变。
✓推论1 力的可传性作用于刚体上某点的力,可以沿着它的作用线移到刚体内任意一点,并不改变该力对刚体的作用。
✓推理2 三力平衡汇交定理作用于刚体上三个相互平衡的力,若其中两个力的作用线汇交于一点,则此三力必在同一平面内,且第三力的作用线通过汇交点。
§1.2 约束和约束力一、约束的概念•自由体:位移不受限制的物体。
•非自由体:位移受限制的物体。
•约束:对非自由体的某些位移起限制作用的周围物体。
二、约束反力(约束力)•约束力:约束对物体作用的力。
•在静力学中,约束力和物体受到的其它已知力(主动力)组成平衡力系,可用平衡条件求出未知的约束力。
三、工程常见约束•光滑平面约束•柔索约束•光滑铰链约束•固定铰链支座•止推轴承径向轴承•平面固定端约束§1.3 物体的受力分析和受力图受力分析:确定构件受了几个外力,每个力的作用位置和方向的分析过程。
•步骤:1.取研究对象(画分离体:按原方位画出简图)。
2.画主动力:主动力照搬。
3.画约束反力:根据约束性质确定。
第二章 平面汇交力系与平面力偶系§2–1 平面汇交力系平面汇交力系:各力的作用线都在同一平面内且汇交于一点的力系。
成人教育专升本《理论力学》期末考试复习题及参考答案

专升本理论力学一单选1、力对刚体的作用效果决定于()。
A、力的大小和力的方向B、力的方向和力的作用点C、力的大小、力的方向、力的作用点D、力的大小、力的作用点2、物体的平衡是指物体相对于地球处于()状态。
A、静止B、静止或匀速直线运动C、加速运动D、减速运动3、作用力与反作用力是()。
A、作用在一个物体上B、分别作用在两个物体上C、作用在第三各物体上D、作用在任意物体4、力系合力在某坐标轴上的投影等于该力系中 ( )。
A、各分力在该坐标轴上投影的代数和B、各分力的矢量和C、合力的大小D、合力在该坐标轴方向的分力5、固定铰链支座其约束反力一般用()分量来表示。
A、三个B、平行C、一个D、两个正交6、在任一力系中加上或减去一个(),不会影响原力系对刚体的作用效果。
A、空间力系B、任意力系C、平面力系D、平衡力系7、力在坐标轴上的投影等于力的大小乘以与坐标轴正向间夹角()。
A、正弦B、余弦C、正切D、余切8、平面汇交力系平衡的几何条件是()。
A、力多边形自行封闭B、力多边形成圆形C、力多边形成正方形D、力多边形成三角形9、平面任意力系平衡的必要和充分条件是()。
A、主矢等于零B、主矩等于零C、主矢和主矩同时等于零D、以上都不是10、同一个平面内的两个力偶的等效条件是()。
A、力偶矩大小相等B、力偶转向相同C、力偶矩大小相等且力偶转向相同D、以上都不是11、作用于物体同一点的两个力可以合成一个力,合力的大小等于两个力的()和。
A、代数B、矢量C、投影D、力矩12、一动点沿一曲线作匀加速运动,则该点的切向加速度一定()。
A、指向该曲线的曲率中心B、与速度的方向无关C、与速度异号D、与速度同号13、直角坐标表示的动点的运动方程为x=2t,y=2t2,由此可知该动点的轨迹为()。
A、直线B、圆弧C、抛物线D、椭圆14、切向加速度反映了()。
A、速度大小的变化率B、速度方向的变化率C、速度大小和方向的变化率D、以上答案都不是15、描述刚体绕定轴转动快慢的物理量是()。
(完整版)理论力学复习总结(知识点)

第一篇静力学第1 章静力学公理与物体的受力分析1.1 静力学公理公理 1 二力平衡公理:作用于刚体上的两个力,使刚体保持平衡的必要和充分条件是:这两个力大小相等、方向相反且作用于同一直线上。
F=-F’工程上常遇到只受两个力作用而平衡的构件,称为二力构件或二力杆。
公理 2 加减平衡力系公理:在作用于刚体的任意力系上添加或取去任意平衡力系,不改变原力系对刚体的效应。
推论力的可传递性原理:作用于刚体上某点的力,可沿其作用线移至刚体内任意一点,而不改变该力对刚体的作用。
公理 3 力的平行四边形法则:作用于物体上某点的两个力的合力,也作用于同一点上,其大小和方向可由这两个力所组成的平行四边形的对角线来表示。
推论三力平衡汇交定理:作用于刚体上三个相互平衡的力,若其中两个力的作用线汇交于一点,则此三个力必在同一平面内,且第三个力的作用线通过汇交点。
公理4作用与反作用定律:两物体间相互作用的力总是同时存在,且其大小相等、方向相反,沿着同一直线,分别作用在两个物体上。
公理5 钢化原理:变形体在某一力系作用下平衡,若将它钢化成刚体,其平衡状态保持不变。
对处于平衡状态的变形体,总可以把它视为刚体来研究。
1.2 约束及其约束力1.柔性体约束2.光滑接触面约束3.光滑铰链约束第2章平面汇交力系与平面力偶系1.平面汇交力系合成的结果是一个合力,合力的作用线通过各力作用线的汇交点,其大小和方向可由失多边形的封闭边来表示,即等于个力失的矢量和,即FR=F1+F2+…..+Fn=∑F2.矢量投影定理:合矢量在某轴上的投影,等于其分矢量在同一轴上的投影的代数和。
3.力对刚体的作用效应分为移动和转动。
力对刚体的移动效应用力失来度量;力对刚体的转动效应用力矩来度量,即力矩是度量力使刚体绕某点或某轴转动的强弱程度的物理量。
(Mo(F)=±Fh)4.把作用在同一物体上大小相等、方向相反、作用线不重合的两个平行力所组成的力系称为力偶,记为(F,F’)。
理论力学期末复习题
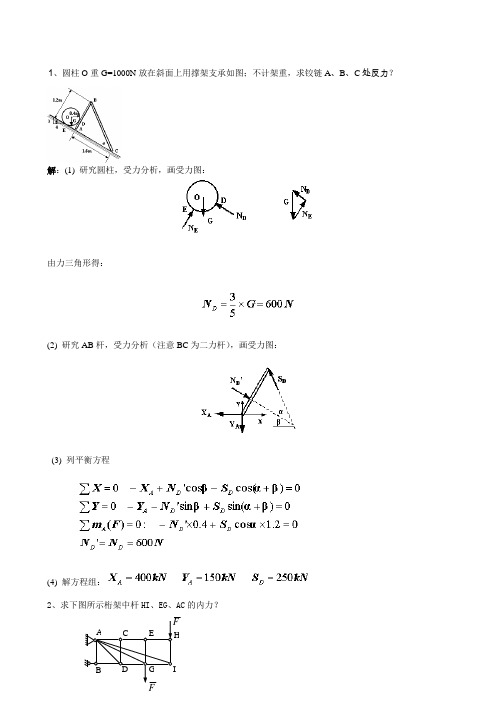
1、圆柱O 重G=1000N 放在斜面上用撑架支承如图;不计架重,求铰链A 、B 、C 处反力?解:(1) 研究圆柱,受力分析,画受力图:由力三角形得:(2) 研究AB 杆,受力分析(注意BC 为二力杆),画受力图:(3) 列平衡方程(4) 解方程组:2、求下图所示桁架中杆HI 、EG 、AC 的内力?FHC A E答:F F F F HI AC EG -===003、重物悬挂如图,已知G=1.8kN ,其他重量不计;求铰链A 的约束反力和杆BC 所受的力?解:(1) 研究整体,受力分析(BC 是二力杆),画受力图:(2)列平衡方程:(3)解方程组:X A =2.4KN; Y A =1.2KN; S=0,848KN4、三铰门式刚架受集中荷载F P 作用,不计架重,求支座A 、B 的约束力。
答:F A =F B =0。
707F P5、求梁的支座约束力,长度单位为m 。
解:∑M A(F)=0 F B×4-2×Sin450×6-1.5=O∑M B(F)=0 -F AY×4-2×Sin450×2-1.5=O∑F X=0 F AX+2×coS450=O解得: F AX=-1.41KN,F AY=-1.1KN,F B=2.50KN6、求刚架的支座约束力。
解得:F AX=0 F AY=17KN F B=33KN。
M7、四连杆机构OABO1在图示位置平衡,已知OA=40㎝,O1B=60㎝,作用在曲柄OA上的力偶矩大小为M1=1N.m,求力偶矩M2的大小及连杆AB所受的力(各杆的重量不计)?解:(1)先取0A杆为研究对象,∑M=0 F AB×OAsin300-M1=0解得:F AB=5N(2)取O1B杆研究。
F′AB= F AB=5N∑M=0 M2- F′AB×O1B=0解得:M2= F′AB×O1B=3N.m飞轮加速转动时,其轮缘上一点M的运动规律为s=0.02 t3(单位为m、s),飞轮的半径R=0.4m。
理论力学期末考试纲要

a n
=
=
ρ
24
=
2
t = 1s时
π ϕ=
4
a τ
= 6π
v = 6π
3π 2
a n
=
2
解法 2 直角坐标法(坐标建立如图)
应用力的平移定理,将力系向一点简化的方法是力系简化的普遍方法。
4.平面力系向平面内一点简化
力系向任一点 O(称简化中心)简化,得到通过简化中心的一个力及一个力偶。力的大小、方 向决定于力系的主矢量,力偶的矩决定于力系对简化中心的主矩。
力系中各力的矢量和称为力系的主矢量(简称主矢)。即
FR′ = ∑ F
小为 3P / 3,此力系向 O 点简化的主矩大小为( 3Pa / 3)。
B
1.基本概念
第 5 章摩擦
C
D
3
v P
v P
3
动滑动摩擦、静滑动摩擦
O
A
当物体处于临界平衡状态时,静摩擦力的大小 F 与相互接触物体之间的正压力大小与正比。
2.基本计算
动滑动摩擦、静滑动摩擦的计算
【例】物 A 重 100KN,物 B 重 25KN,A 物与地面
2
主矢量与简化中心位置无关。 力系中各力对简化中心之矩的代数和称为力系对简化中心的主矩。即
∑ M O = M O (F )
主矩与简化中心位置有关。
5.主矢和主矩的解析式
如以简化中心为原点,建立直角坐标系 Oxy 则主矢与主矩的解析表达式分别为
FR′ = ∑ Xi + ∑Yj
∑ ∑ MO = MO (F ) = (xiYi − yi X i )
3.力对点之矩
力对点之矩是力使物体绕该点转动效果的度量,是定位矢量。表为
理论力学期末复习

讨论三种可能发生
FD f D FND 0.4 300N 120N, 的运动情况 FE f E FNE 0.2 643N 128.6N
Fx 0, FT1 FD FE 0
FT1 FD FE 248.6N
线圈架沿AB梁滚动而无滑动
FD f D FND , FE f E FNE =128.6 N
解:解除约束,画整体受力图
列平衡方程
M A F 0
•
FNB AB FT AD r FT DE r 0
FNB FT AD DE 120 2 1.5 kN 105 kN AB 4
FAy FNB FT 0
•
Fy 0
2-4-2 物系平衡问题解法
受力分析
① 首先从二力构件入手,可使受力图比较简单,易于求解。
② 解除约束时,要严格地按照约束的性质,画出相应的约 束力,切忌凭主观想象。对于一个销钉连接三个或三个以上物 体时,要明确所选对象中是否包括该销钉?解除了哪些约束? 然后正确画出相应的约束力。
③ 画受力图时,关键在于正确画出铰链约束力,除二力构
d FR
MO FR
FR 0 M O 0
FR 0
MO 0
合力 力螺旋
FR 0 M O 0 FR // MO
FR 0 M O 0 ( FR , MO )= 力螺旋
1-3-3 力系的最简形式
1.图示力系沿正方体棱边作用,F1=F2=F3=F,
三 点的复合运动
3-1 运动学基础(填空题) 3-2 点的复合运动概念 3-3 点的运动合成定理(注意科氏加速度) 3-4 点的复合运动问题(计算题2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图所示,构架中各杆件自重不计, 为铰链,尺寸如图所示。已知:轮重,
物重,,。试求处的约束反力 (图中长度单位)
A
G
q
B
K
C
20
D FH
E
20
15
15
20
20
QR
M PΒιβλιοθήκη 运动学❖ 一、刚体的基本运动
❖ ①平动—运动特征、运动参数的关系 ❖ ②定轴转动—运动特征、运动参数的计算
❖ 二、点的合成运动 ❖ 1、主要概念 ❖ ①动点、动系,三种运动、速度、加速度,尤
A C
B
O
动力学
❖ 一、动量定理
❖ ①动量的概念,质点系动量(矢量和),质心动量 =质系动量
❖ ②冲量的概念 ❖ ③动量定理、质心运动定理 ❖ ④动量守恒、质心坐标守恒、质心动量守恒
❖ ③两矩式,三矩式应满足的条件
❖ ④物体系统平衡问题,最简方法的要 求—最少研究对象、最少方程数
❖ ⑤两个主要技巧—投影方向选择、取矩 点选择
❖ ⑥桁架;节点法,截面法;零杆判断
❖ 4、空间力系 ❖ ①空间力矩、力偶用矢量表示 ❖ ②空间力对点、对轴取矩 ❖ ③六个独立平衡方程 ❖ 5、摩擦 ❖ ①静滑动摩擦力的平衡范围 ❖ ②库仑定律 ❖ ③摩擦角 ❖ ④滚动摩擦
考试安排
❖ 一月十六号上午8.30-10.30 ❖ 机11-1;11-2;11-3:逸夫楼505 ❖ 机11-4:逸夫楼502 ❖ 机11-5;11-6:逸夫楼506 ❖ 机11-7;11-8:逸夫楼504 ❖ 重修生:逸夫楼503
静力学
❖ 一、主要概念
❖ 1、受力分析、受力图 ❖ ①约束性质及相应约束反力 ❖ ②分离体图 ❖ ③二力杆 ❖ ④三力汇交 ❖ ⑤均布力画法 ❖ ⑥作用反作用关系
O1C
A C
O
B
试用符合运动法求图所示凸轮机构挺杆AB沿铅垂导槽运动之 速度及加速度。已知偏心轮半径为R,偏心距,偏心轮绕轴 转动的角速度等于常量.
❖ 在图示平面机构中,已知OA=CD=1m,AB=DE=2m, 铰链C为AB杆中点。图示瞬时 ,OA水平AB铅直,OA 杆角速度ω=4rad/s,角加速度ε=0。求此瞬时DE杆的角 速度与角加速度。
❖
V
A
B
C
O
F D
E
平面机构如图所示。已知:滚子沿水平面纯滚动,半径r=1
0cm, h =60cm,BD=80cm,C为BD杆中点,
在 图 示 位 置 时 , φ= 3 0 ° , O A 杆 的 角 速 度 0 = 2
rad/s,角加速度α0=0。试求该瞬时滚子的角速度和角加
速度。
D
r
E F
h
其是牵连运动、牵连速度、牵连加速度 ❖ ②动点、动系选取的原则,合成运动三种类型 ❖ ③速度合成定理、加速度合成定理 ❖ ④速度图、加速度图 ❖ ⑤科氏加速度的概念,大小计算,方向判断 ❖ ⑥求加速度的投影式 ❖ 2、解题步骤 ❖ ㈠、求速度量 ❖ ①动点、动系选择
❖ ②三种运动分析
❖ ③速度合成定理、已知未知量判断、速 度图
二、解题步骤
❖ ①取—研究对象 ❖ ②画—受力图 ❖ ③列—方程 ❖ ④解—方程(答案)
图示结构如图所示。已知:重物, 滑轮半径,,,不计各杆及滑轮、绳 自重,试求A、E铰支座的约束反力
及AB杆在铰链D处所受的力。
C E
H
A
D
B
❖ 平面结构如图,A、B为固定铰支座,已知:,,在铰链C 处作用一铅直载荷Q=1 KN,在AD杆的中点作用一水平 载荷P =0.4 KN,各构件自重不计,试求支座A、B的反
力及杆BD,杆CD的内力。
Q
D
C
a
30o
P
a
A
B
❖ 如图七结构,尺寸及载荷均标出,求的约束反力。
q MA
XA
A
YA
P
D B
C M
图(d)
60o E
XE
YE
AD, BC,CD, EG,CFH
❖ 如图所示结构由
五部分组成,载荷及尺寸如图,
各杆自重不计,求处的约束反力。
Bd
d
d
C
2d
D
A
E
Gq
F
H
2d
❖
Ow
A D
j C
j
E
B
A
a0 w0
O
O1
C
B
f R
D
❖ 曲柄OA和O1B长度均为r,连杆AB长2r。当曲柄OA以角 速度ω0绕O轴转动时,带动连杆CD沿水平轨道滑动,图 示位置,OA水平O1B铅直,C点位于AB中点,求此时CD 杆的绝对速度。
O w0
A 60o
C
D
30o
B
O1
❖ 平面机构如图所示,穿过套筒E的AD杆在A端铰接两杆, 在C处铰接的滑块C可沿铅垂导轨滑动,一直AB=EF=r, AC=2r,OA=。在图示位置时,AB与EF水平,OA铅垂 ,B、C、F三点在同一铅垂线上,滑块B点速度为匀速V ,试求该瞬时EF杆的角速度和角加速度。
❖ ④根据三角关系求出所有速度量,包括 求加速度所需速度量
❖ ㈡、求加速度量
❖ ①加速度合成定理、已知未知量判断、 加速度图
❖ ②投影式求解
❖ 三、刚体的平面运动 ❖ 1、主要概念 ❖ ①基点,动点动系的特殊选取,牵连运动—随基点
的平动,相对运动—刚体上的点绕基点的圆周运动 ❖ ②速度合成关系(基点法) ❖ ③瞬心的概念,确定瞬心的方法、瞬时平动 ❖ ④速度投影定理 ❖ ⑤加速度合成定理(基点法,无科氏加速度) ❖ ⑥速度图、加速度图 ❖ 2、解题步骤 ❖ ㈠、求速度量
❖ 2、平面汇交力系 ❖ ①合力投影定理 ❖ ②两个独立的平衡方程∑X=0,∑Y=0 ❖ 可求两个未知数 ❖ 3、平面力偶系 ❖ ①力矩、力偶 ❖ ②合力矩定理 ❖ ③∑m=0,力偶平衡
❖ 3、平面任意力系
❖ ①力线平移定理
❖ ②三个独立平衡方程可解三个未知数, 每个研究对象最多可列三个有效平衡方 程,多列无效
❖ 1、瞬心法 ❖ ①确定瞬心、作图、文字说明 ❖ ②画速度图 ❖ ③计算已知速度(A)点到瞬心的距离和待求速度
(B)点到瞬心的距离(AK=?,BK=?)
❖ ④ω=VA/AK,VB=ω×BK
❖ 2、投影法 ❖ ①文字说明投影法 ❖ ②写出投影式、求解 ❖ ㈡求加速度量(基点法) ❖ ①画加速度图
❖ ②加速度合成定理(基点法) ❖ ③投影式、解答
❖ 四、五种题型
❖ ⒈简单基本题(平面运动的两次基点法) ❖ ⒉基本综合题 ❖ ⒊两次动点、动系 ❖ ⒋套筒问题(速度问题) ❖ ⒌必须用基点法求速度的问题
❖ 图示结构中,滑块B带动摇杆O1C绕轴O1转动,设曲 柄OA的角速度ω为一常量,OA=AB=r,,此瞬时φ =60o,求此瞬时摇杆O1C的角速度ω1与角加速度
