冲激偶函数
冲激信号是偶函数,冲激偶信号是奇函数

冲激信号是偶函数,冲激偶信号是奇函数
冲激函数既不是偶函数也不是奇函数.是一个非正常函数,某种极限函数。
冲激偶函数是奇函数,关于原点对称,在全时域对其积分为零,即正、负两个冲激的面积相互抵消。
所以说冲激函数是偶函数,冲激偶就是奇函数
信号的分解,可以分解为冲激函数和阶跃函数的卷积,只不过对于阶跃函数而言会有一个初值的问题,这个初值产生原因就在于其对信号分解可以看成冲激函数与信号卷积的微分和积分(微分分配给f,积分分配给冲激函数),无论是先微分或者先积分,都会存在一个常数是无法确切表示的,需要有初值条件,从频域分析时,是因为存在微分性质使用时要保证是没有直流分量
在频域分析时,同样我们可以的得到一个有趣的结论,可以将任意信号分解为该信号的基函数的幅频特性曲线必没有0点,进一步拓展,一个有限长的信号,一定不能作为基函数表示任意信号(在时域来看这是显然的)。
冲激偶函数和函数进行卷积

冲激偶函数和函数进行卷积哎呀,今天咱们聊聊冲激偶函数和卷积这个话题,听起来好像有点高深,其实不然,咱们就像喝茶聊天一样,轻松一下。
先说说冲激偶函数,嘿,这东西可有趣了。
想象一下,你在一条安静的小路上走,突然之间,旁边的草丛里蹦出一只小兔子,那一瞬间的感觉就像是冲激偶函数发出来的信号,突然之间,给你来个“咣”!这可不是普通的兔子,而是个既甜美又令人意外的声音,瞬间吸引了你的注意力。
什么是冲激偶函数呢?简单来说,它就是在某一点上值很大,其他地方都很小的函数。
就像那只小兔子,只在一个瞬间出现,之后又悄无声息地消失了。
这种函数在信号处理中可是个好帮手,它就像是无声无息的超人,帮助我们捕捉那些瞬息万变的信息。
你可能会想,这有什么用呢?哈哈,别急,咱们慢慢说。
再说说卷积,卷积就像是把两种口味的冰淇淋混在一起,形成一个新口味,哦,真的是太美妙了。
咱们想象一下,一个浓郁的巧克力冰淇淋,搭配上清新的薄荷味,咔嚓一口,瞬间就被那种冰凉的感觉包围。
卷积就是把一个函数“涂抹”到另一个函数上,这样每个点都能感受到来自对方的“味道”。
这可是个神奇的过程,感觉就像是在厨房里忙碌的厨师,不断试验新的配方,最终得出了一个绝妙的味道。
当冲激偶函数和其他函数卷积在一起的时候,嘿,这就是一场美味的碰撞!我们可以把冲激偶函数看作是一种“撒娇”的方法,随时准备给你带来惊喜。
想象一下,假设你有一个普通的函数,比如说,一个平滑的波浪。
然后,加入冲激偶函数,这一下子就像是在波浪上加了个大大的泡泡,瞬间让你的波浪变得生动有趣。
这种卷积的效果,让你的信号不再单调,活力四射。
这里面其实有个小秘密,冲激偶函数本身就是一种“记忆”,它能把过去的信息保留在卷积的结果中。
就像老一辈总是说的,记得要常回家看看,过去的回忆永远会影响我们的现在和未来。
卷积之后的新函数中,冲激偶函数的影响一直存在,就像是心里那段刻骨铭心的回忆,时刻提醒着你,不要忘了那些重要的时刻。
冲激信号δ(t)的三种定义与有关性质的简单讨论

冲激信号δ(t)的三种定义与相关性质的简单讨论信息科学与工程学院1132班 樊列龙 学号:0909113224有一些物理现象,如理学中的爆炸、冲击、碰撞··,电学中的放电、闪电雷击等,它们都有共同特点: ① 持续时间短. ② 取值极大.冲击函数(或冲击信号)就是对这些物理现象的科学抽象与描述。
通常用δ(t)表示冲激信号,它是一个具有有限面积的窄而高的尖峰信号,它也可以被称作δ函数或狄拉克(Dirac )函数,在信号领域中占有非常重要的地位. 由于冲激函数的特殊性,现给出其两种不严格的定义如下:定义一:用脉冲函数极限定义冲激信号. 如图1-1(a)的矩形脉冲,宽为τ,高为τ1,其面积为A.当A=1称之为单位冲激信号. 现保持脉冲面积不变,逐渐减小τ,则脉冲的幅度逐渐增大,当0→τ时,矩形脉冲的极限成为单位冲激函数,即:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+=→221lim )(0τετετδτt t t (1-1)冲击信号的波形就如1-1(b)所示.δ(t)只表示在t=0点有“冲激”,在t=0点以外的各处函数值图1-2均为0,其冲激强度(冲激面积)为1,若为A 则表示一个冲击强度为E 倍单位值得函数δ,描述为A=E δ(t),图形表示时,在箭头旁边注上E 。
也可以用抽样函数的极限来定义δ(t)。
有⎥⎦⎤⎢⎣⎡=∞→)(lim )(kt Sa kt k πδ (1-2)对式(1-2)作如下说明:Sa(t)是抽样信号,表达式为ttt a sin )(S = (1-3) 其波形如图1-2所示,Sa(t)∝1/t, 1/t 随t 的增大而减小,sint 是周 期振荡的,因而Sa(t)呈衰减振荡; 并且是一个偶函数,当t=±π,±2π, ·,sint=0,从而Sa(t)=0,是其(a)τ逐渐减小的脉冲函数(b)冲激信号图1-1图 1-3零点. 把原点两侧两个第一个零点之间的曲线部分称为“主瓣”, 其余的衰减部分称为“旁瓣”。
信号与系统1-2冲激函数课件
f (t) (t) dt f (0)
f (t) (t t0 ) dt f (t0 )
是冲激函数的 严格的数学定义。
2
冲激函数的性质
单位冲激函数为偶函数 (t) (t)
缩放性质
(at) 1 (t)
a
(at t0 )
1 a
(t t0 )
a
这里 a 和 t0为常数,且a0。
冲激偶的采样性质
f (t) (t)dt f (0)
f (t) (t t0 )dt f (t0 )
冲激偶’(t)是 t 的奇函数
(t) (t)
任何偶函数的导数为奇函数。
5
例1.8 阶跃函数和冲激函数的关系
(t) d (t)
dt
t
(t) ( )d
f1(t)
2 1
折叠信号的平移
已知 f (t)f求(-ft)f(的-(t--波1t-)1=形)f向[-(左t+移1)动]将1。
f (t)
反折 1
f (t)
平移
f (t 1)
0
1t
平移
1 0
f (t 1)
1
t
2 1 0 t
反折
0
12 t
12
信号的平移与折叠
折叠信号的平移
已知 f (t)f求(-ft)(f的-(t+-波t1+)形=1)向f [-右(t-移1)动]将1。
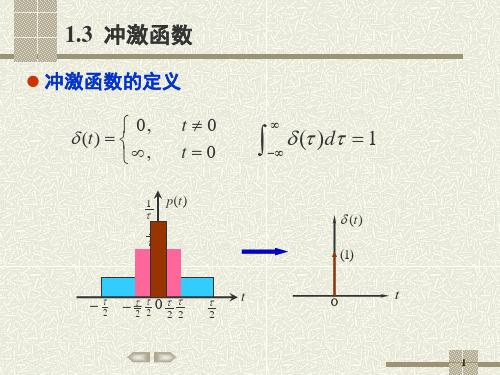
1.3 冲激函数
冲激函数的定义
(t)
0, ,
t0 t 0
( )d 1
1 p(t)
1
1
2
2
2
0
2
2
2
t
(t) (1)
冲激偶函数的拉普拉斯变换

冲激偶函数的拉普拉斯变换拉普拉斯变换是数学中一种非常重要的变换方法,它在信号与系统、控制理论、电路分析等领域广泛应用。
冲激偶函数是一种特殊的函数形式,在拉普拉斯变换中有着重要的作用。
本文将以冲激偶函数的拉普拉斯变换为主题,介绍其定义、性质以及在实际应用中的意义。
我们来了解一下什么是冲激偶函数。
冲激偶函数是一种理想化的函数形式,它在时间t=0时取无穷大,在其他时间上取0。
冲激偶函数的数学表示形式为δ(t),其中δ表示冲激函数,t表示时间。
冲激偶函数在信号与系统分析中扮演着重要的角色,它可以用来描述信号的幅度、频率特性等。
接下来,我们来介绍冲激偶函数的拉普拉斯变换。
拉普拉斯变换是一种对函数进行变换的方法,它将一个函数f(t)变换为另一个函数F(s)。
冲激偶函数的拉普拉斯变换可以表示为L{δ(t)}=1。
这个变换表明,冲激偶函数在拉普拉斯域中的变换结果为常数1。
冲激偶函数的拉普拉斯变换具有一些重要的性质。
首先,拉普拉斯变换具有线性性质,即对于任意常数a和b,有L{af(t)+bg(t)}=aF(s)+bG(s),其中F(s)和G(s)分别是f(t)和g(t)的拉普拉斯变换。
其次,拉普拉斯变换具有时移性质,即L{f(t-t0)}=e^(-st0)F(s),其中F(s)是f(t)的拉普拉斯变换。
此外,拉普拉斯变换还具有尺度变换性质、频移性质等。
冲激偶函数的拉普拉斯变换在实际应用中具有重要的意义。
首先,它可以用来求解微分方程。
通过将微分方程转化为拉普拉斯域中的代数方程,可以得到方程的解析解。
其次,冲激偶函数的拉普拉斯变换可以用来描述系统的频率特性。
通过对系统的冲激响应进行拉普拉斯变换,可以得到系统在不同频率下的响应特性,从而对系统进行分析和设计。
此外,在信号处理中,冲激偶函数的拉普拉斯变换还可以用来进行信号滤波、频谱分析等。
冲激偶函数的拉普拉斯变换是一种重要的数学工具,在信号与系统、控制理论、电路分析等领域具有广泛的应用。
冲激偶函数的积分

冲激偶函数的积分冲激偶函数是一种用于描述冲击和突变的数学函数,经常在物理学、工程学和信号处理中用到。
冲激偶函数通常记作δ(t),其定义为在t = 0时刻取极限,且满足单位面积条件。
在数学上,冲激偶函数可以用多种方式表示和描述,下面将介绍一些常见的表示和相关参考内容。
1. 冲激偶函数的直观表示:冲激偶函数可以通过图形的方式来表示。
通常,冲激偶函数在t = 0时刻取正无穷大,其他时刻取零,形成单位面积的尖峰。
这个图形可以用来描述瞬时的力、电流、电压等冲击现象。
2. 冲激偶函数的数学定义:冲激偶函数的数学定义可以通过极限来表达。
定义如下:δ(t) = lim (Δt→0) 1/Δt, 当-∞<t<∞时,否则为零。
其中,Δt表示一个趋近于零的小区间。
3. 冲激偶函数的性质:冲激偶函数具有一些重要的性质,如单位面积、奇对称性、不可积性等。
这些性质使得冲激偶函数在数学分析和应用中具有重要的作用。
4. 冲激偶函数的傅里叶变换:冲激偶函数在频域中的表示可以通过傅里叶变换来得到。
冲激偶函数的傅里叶变换结果是一个常数函数,即在所有频率上恒为1。
这表示冲激偶函数是频域中的均匀分布。
5. 冲激偶函数与卷积运算:冲激偶函数与其他函数进行卷积运算时,类似于乘法的“单位元”。
即,冲激偶函数与函数f(t)进行卷积运算得到f(t)本身。
6. 冲激偶函数在信号处理中的应用:冲激偶函数在信号处理中被广泛应用。
例如,在脉冲响应函数中,冲激响应函数可以通过冲激偶函数和系统的传递函数进行卷积来得到。
此外,冲激偶函数还可以用于信号重构、滤波器设计等方面。
7. 冲激偶函数在物理学中的应用:冲激偶函数在物理学中也有重要的应用。
例如,冲激偶函数可以用来描述物体的冲击力、电荷的突然变化、粒子的碰撞等等。
通过应用冲激偶函数,可以研究这些冲击和突变现象的影响。
综上所述,冲激偶函数是一种用于描述冲击和突变的数学函数,在物理学、工程学和信号处理中有广泛的应用。
冲激偶函数的性质.

冲激偶函数的性质.
冲激函数的性质有:1、筛选性质。
2、取样性质。
3、导数性质。
4、尺度变换性质。
冲激函数是个奇异函数,它是对强度极大、作用时间极短暂且积分有限的一类理想化数学
模型。
冲激函数可用于对连续信号进行线性表达,也可用于求解线性非时变系统的零状态
响应。
冲激函数求导可得到冲激偶函数,单位冲激偶是这样的一种函数:当 t从负值趋于0时,它是一个强度为无限大的正的冲激函数,当t从正值趋于0时,它是一个强度为无限
大的负的冲激函数。
应用领域:
冲激函数可用于信号处理,通过冲激函数来表示复杂的信号,可以简化对复杂信号的
一些特性的研究。
冲激函数及其延时冲激函数的线性组合去则表示或迫近,再利用系统的vary原理,
可以通过直观的信号例如单位冲激函数的频谱,以及频域特性去探讨比较复杂信号的频谱。
从而增加排序繁杂信号频谱的难度。
冲激偶函数的积分

冲激偶函数的积分冲激偶函数,也称为狄拉克δ函数,是数学中的一种特殊函数。
它在物理学、工程学和其他领域中经常被用来描述瞬时电流、电荷分布以及信号传输等现象。
本文将介绍冲激偶函数的积分。
冲激偶函数在数学表示上通常用符号δ(x)表示,其中x为自变量。
δ(x)在x=0处取无穷大,其它位置取值为零,并满足积分为1的性质,即∫δ(x)dx=1。
我们首先来分析冲激偶函数的积分在定义域内的性质。
由于冲激偶函数在除x=0处都为零,我们只需关注x=0的附近。
为了方便计算,我们可以使用一个趋于无穷小的宽度ε来近似表示冲激偶函数。
具体表达式可以写作δε(x)。
那么冲激偶函数的积分可以近似表示为∫δε(x)dx。
对于这个积分,我们可以采用定积分的定义来计算。
首先,我们需要确定积分的上下限。
由于δε(x)只在x=0的附近有显著值,我们可以将积分的上下限分别设为[-ε,ε]。
这样,我们可以将δε(x)在[-ε,ε]内的值视为常数k,即δε(x)=k。
根据定积分的定义,我们可以将∫δε(x)dx转化为求区间[-ε,ε]上δε(x)的面积。
因为δε(x)只在x=0的附近有显著值,所以这个面积近似等于一个矩形的面积,即k*2ε。
由于δ(x)是随着ε趋于零的函数,所以k*2ε在ε趋近于零的情况下会等于1。
因此,我们可以得出结论,∫δε(x)dx在ε趋近于零时等于1。
进一步地,我们可以得出∫δ(x)dx=lim(ε→0)∫δε(x)dx=1的结论。
即冲激偶函数的积分等于1。
通过以上分析,我们可以得出冲激偶函数在定义域[-∞,∞]上的积分结果为1。
这个结论在数学和物理学的研究中有着重要的应用。
例如,在物理学中,根据冲激偶函数的性质,我们可以利用积分等于1的特性来求解复杂的物理问题。
总结起来,冲激偶函数的积分在定义域[-∞,∞]上等于1。
这一结论通过分析冲激偶函数的性质,使用定积分的定义进行推导得出。
冲激偶函数在物理学、工程学和其他领域中广泛应用,其积分性质的研究对于解决实际问题具有重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、单位冲激偶信号
冲激函数)(t δ的导数定义为(单位)冲激偶函数,用)(t δ'或)()1(t δ表示。
t t t d )
(d )(δδ=
' (1.3-16)
式(1.3-16)可从极限的角度理解,)(ˆlim )(0t t δδτ'='→,由图1.3-6,)(ˆ
t δ的导数)(ˆt δ'如图1.3-11(a)所示,用公式表示为
)2(1)2(1)(ˆτδττδτδ--+='t t t
当0→τ时,)(ˆ
t δ'由两个在时间上无限靠近,而强度趋于无限大的冲激构成。
故称它为冲激偶函数,用图1.3-11(b)表示。
(a ) (b )
图1.3-11 冲激偶函数
设)(t x 为常规函数,其导数)(t x '在0t t =处连续,则积分
()
()t t t t x t t t t x t t t x t t t x t t t t x d )()(d )()()(d )(d )()(00000-'-=-'-
-=-=-'⎰⎰⎰⎰∞
∞-∞∞-∞∞-∞
∞-∞
∞-δδδδδ
利用冲激函数的抽样性质,从上式得
)(d )()(00t x t t t t x '-=-'⎰∞
∞-δ
(1.3-17)
该式称为)(t δ'的抽样性质。
采用对)()(t t x δ分步求导的方法,或利用式(1.3-17),还可得
)()0()()0()()(t x t x t t x δδδ'-'=' (1.3-18)
注意)()0()()(t x t t x δδ'≠' 。
再来考虑)(t δ'的对称性。
t ττt -==-'τδδd )
(d )(
由于)(t δ为偶对称函数,则有
)(d )(d )(t t t t δδδ'-=-=-' (1.3-19)
可见,)(t δ'为奇对称函数。
故
⎰∞
∞-='0d )(t t δ
当然,令式(1.3-17)中的1)(=t x ,也可得上式结果 。
函数)(t δ的各阶导数统称为高阶冲激。
特别指出,在同一时刻出现的单
位冲激函数、高阶冲激函数间的乘积,如)(2t δ,)()(t t δδ'等没有意义。
