您的位置：360文档中心› 中考数学中考数学压轴题 复习专题强化试卷检测试卷

中考数学中考数学压轴题 复习专题强化试卷检测试卷

合集下载

初中数学中考试卷压轴题

初中数学中考试卷压轴题

一、填空题（每空2分，共10分）1. 已知等差数列{an}的首项a1=3，公差d=2，求第10项a10的值。

2. 在直角坐标系中，点A（2，3），点B（4，1），点C（x，y）在直线y=2x+1上，求三角形ABC的面积。

3. 已知正方形的边长为a，求正方形内切圆的半径。

4. 若一个等比数列的前三项分别为2，6，18，求该数列的公比。

5. 在平面直角坐标系中，点P（2，3），点Q（4，-1），点R（x，y）在直线y=-x+6上，求三角形PQR的周长。

二、选择题（每题3分，共15分）6. 下列数列中，不是等差数列的是（）A. 1，4，7，10，13B. 2，4，8，16，32C. 1，3，5，7，9D. 1，1/2，1/4，1/8，1/167. 已知等差数列{an}的首项a1=5，公差d=3，求第n项an的值。

A. 5nB. 5n-4C. 3n+2D. 3n-48. 在平面直角坐标系中，点A（1，2），点B（3，4），点C（5，6），求三角形ABC的面积。

A. 3B. 6C. 9D. 129. 已知等比数列的前三项分别为2，6，18，求该数列的公比。

A. 2B. 3C. 6D. 910. 在平面直角坐标系中，点P（2，3），点Q（4，-1），点R（x，y）在直线y=-x+6上，求三角形PQR的周长。

A. 5B. 10C. 15D. 20三、解答题（每题10分，共30分）11. 已知等差数列{an}的首项a1=1，公差d=3，求前n项和Sn。

12. 在平面直角坐标系中，点A（1，2），点B（3，4），点C（5，6），求三角形ABC的面积。

13. 已知等比数列的前三项分别为2，6，18，求该数列的公比和前n项和。

四、附加题（10分）14. 在平面直角坐标系中，点P（2，3），点Q（4，-1），点R（x，y）在直线y=-x+6上，求三角形PQR的面积。

解答：一、填空题1. a10 = a1 + (n-1)d = 3 + (10-1)×2 = 212. S△ABC = 1/2 × |x1(y2-y3) + x2(y3-y1) + x3(y1-y2)| = 1/2 × |2(1-6) + 3(6-2) + 5(2-1)| = 93. 正方形内切圆的半径 = a/24. 公比q = a2/a1 = 6/2 = 35. 周长 = PQ + QR + RP = √[(2-4)² + (3+1)²] + √[(x-4)² + (y+1)²] +√[(2-x)² + (3-y)²]二、选择题6. D7. A8. B9. B10. B三、解答题11. Sn = n/2 × (a1 + an) = n/2 × (1 + 1 + (n-1)×3) = n/2 × (2 + 3n - 3) = 3n²/212. S△ABC = 1/2 × |1(4-6) + 3(6-2) + 5(2-4)| = 613. 公比q = a2/a1 = 6/2 = 3，前n项和Sn = a1(1 - q^n)/(1 - q) = 2(1 - 3^n)/(1 - 3)四、附加题14. S△PQR = 1/2 × |2(-1-y) + 4(y-3) + x(3+1)| = 1/2 × |2(-1-y) + 4(y-3) + x(4)| = 1/2 × |2(-1-y) + 4y - 12 + 4x|。

中考压轴数学试卷及答案

中考压轴数学试卷及答案

1. 已知函数f(x) = 2x - 3，若对于任意实数x，都有f(x + 1) = 2f(x) - 5，则f(2)的值为（）A. 1B. 3C. 5D. 72. 在直角坐标系中，点A(1, 2)，点B(4, 6)在直线y = kx + b上，则k和b的值分别为（）A. 1, 1B. 1, 3C. 2, 1D. 2, 33. 若等比数列{an}的首项a1 = 2，公比q = 3，则第n项an的值为（）A. 2 × 3^(n-1)B. 6 × 3^(n-2)C. 6 × 3^(n-1)D. 18 × 3^(n-2)4. 在△ABC中，∠A = 60°，∠B = 45°，则sinC的值为（）A. √3/2B. √6/4C. √2/2D. 15. 若复数z = a + bi（a，b∈R）满足|z| = 1，则z的共轭复数是（）A. a - biB. -a - biC. a + biD. -a + bi6. 已知数列{an}的前n项和为Sn，若an = 2n - 1，则S10的值为（）A. 55B. 100C. 105D. 1107. 在平面直角坐标系中，点P(2, 3)关于直线y = x的对称点为Q，则Q的坐标为（）A. (2, 3)B. (3, 2)C. (-2, -3)D. (-3, -2)8. 若等差数列{an}的前n项和为Sn，若a1 = 3，公差d = 2，则S10的值为（）A. 100B. 105C. 110D. 1159. 在△ABC中，∠A = 90°，∠B = 30°，则sinC的值为（）A. 1/2B. √3/2C. 1D. √310. 若复数z = a + bi（a，b∈R）满足|z| = 1，则z的模是（）A. a^2 + b^2 = 1B. a^2 - b^2 = 1C. a^2 + b^2 = 0D. a^2 - b^2 = 011. 函数f(x) = x^2 - 4x + 3的零点为______。

2024中考数学(人教版)押题卷 (564)

2024中考数学(人教版)押题卷 (564)

一、单选题1. 若关于，的方程组的解满足，则的值为（）A．B．1C．D．-12. 如图，的顶点B在反比例函数的图象上，边在x轴上，已知，，，则图中阴影部分的面积是（）A．12B．C．D．3. 点关于轴对称的点的坐标是（）A．B．C．D．4. 下列图形属于轴对称图形的是（）A．B．C．D．5. -3的相反数是（）A．B．3C．D．06. 二次函数在范围内的最大值为（）A．25B．30C．36D．407. 抛物线的部分图象如上图所示，若，则的取值范围是( )A．B．C．或D．或8. 如图，为的直径，半径的垂直平分线交于点，，交于点，若，则的长为（）A．B．6C．D．89. 某种药品售价为每盒300元，经过医保局连续两次“灵魂砍价”，药品企业同意降价若干进入国家医保用药目录．如果每次降价的百分率都是x，则两次降价后的价格y（元）与每次降价的百分率x之间的函数关系式是（）A．B．C．D．二、多选题10. 如图是一个数值转换机，若输入，则输出的结果是（）A．B ．0C．D ．111. 下列函数中为二次函数的是（ ）A ．y ＝3x ﹣1B．C ．yD．12. 学校有n 位师生乘坐m 辆客车外出参观，若每辆车坐人，则还有人没上车，若每客车坐50人，则空出一辆客车，并且有一辆还可以坐12人．则下列等式成立的是（ ）A．B．C．D．13. 下列说法中不正确的是（ ）A ．-6和-4之间的数都是有理数B ．数轴上表示-a 的点一定在原点左边C ．在数轴上离开原点越远的点表示的数越大D ．-1和0之间有无数个负数14. 下列运算中，正确的是（ ）A．B．C．D．15. 如图，若二次函数y ＝ax 2+bx +c （a ≠0）的图象的对称轴是直线x ＝﹣1，则下列四个结论中，错误的是（ ）A ．abc ＞0B ．2a ﹣b ≠0C ．4ac ﹣b 2＜0D ．4a +c ＜2b16. 在下列图形中，属于中心对称图形的有（ ）A ．菱形B ．梯形C ．矩形D ．等边三角形17. 如图所示，是四边形ABCD 的对称轴，AD ∥BC ，现给出下列结论，其中正确的有（）A ．AB ∥CD ；B ．AB=BC ；C ．AB ⊥BC ；D ．AO=OC18. 下列选项中，能利用图形的面积关系解释平方差公式的是（ ）三、填空题A．B．C．D．19. 如图是抛物线y 1=ax 2+bx +c （a ≠0）图象的一部分，抛物线的顶点坐标A （1，3），与x 轴的一个交点B （4，0），直线y 2=mx +n （m ≠0）与抛物线交于A ，B 两点，下列结论中正确的是（　　）A ．2a +b =0B ．abc ＞0C ．方程ax 2+bx +c =3有两个相等的实数根D ．抛物线与x 轴的另一个交点是（﹣1，0）E ．当1＜x ＜4时，有y 2＜y 120. 黄金分割在生活中的应用十分广泛，例如大多数窗户的宽和长的比是黄金比，已知某扇窗户的长为1.8米，则宽约为______米．（结果精确到0.1）21.若是关于的一元二次方程的一个根，则方程的另一个根为______．22.如图，已知直线，直线m 、n 分别与直线、、分别交于点A 、B 、C 、D 、E 、F，若，，则的值为____．23. 已知，则________．24. 如图，E ，F 是正方形ABCD 的边AD 上两个动点，满足AE ＝DF ．连接CF 交BD 于G ，连接BE 交AG 于点H ．若正方形的边长为2，则线段DH长度的最小值是__________．25. 化简：______26. 如图，∠B 的同位角是__________.四、解答题五、解答题27. 已知一组数据有50个，把它分成六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.2，则第六组的频数是_________．28.不等式组 的解集为 ．29. 如图，已知OA ＝OB ，点C 在OA 上，点D 在OB 上，OC ＝OD ，AD 与BC 相交于点E ，那么图中全等的三角形共有___________对．30. 化简：（1）（2）31. 计算：(1)；(2)；(3)；(4)．32. 先化简，再求值：，其中，．33. 已知某经济开发区有一块四边形空地ABCD ，如图所示，现计划在该空地上种植草皮，经测量∠B =90°，AB =400m ，AD =1300m ，CD =1200m ，BC =300m，请计算种植草皮的面积．34. 计算：(1)；(2)；(3)．35. 某市教育局组织了汉字听写大赛，从1000名参赛选手中随机抽取200参赛选手的成绩进行整理（注：成绩在30-40含起点值30，不含终点值40，依次类推），得到其频数及频率如下表：数据段频数频率30-40100.0540-5036c 50-60a 0.3960-70b d 70-80200.10总计2001（1）表中a 、b 、c 、d 的值分别为：a = ； b = ； c = ； d = ．（2）补全频数分布直方图；（3）如果成绩不低于60即为优秀，则这次参赛选手中总共有 名同学获得优秀．36. 对于平面直角坐标系xOy 中的任意点，如果满足(x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点中，满足此条件的特征点为__________________；②⊙W的圆心为，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数，请利用特征点求出该函数的最小值．37. 如图，在每个小正方形边长为1的方格纸中，△ABC 的顶点都在方格纸格点上，将△ABC 向左平移2格，再向上平移3格，得到△A ′B ′C ′．（1）请在图中画出平移后的△A ′B ′C ′；（2）求△A ′B ′C ′的面积．38. 已知四边形，画出以顶点为对称中心的对称四边形．六、解答题39. 我市某校为了让学生的课余生活丰富多彩，开展了以下课外活动：代号活动类型A 经典诵读与写作B 数学兴趣与培优C 英语阅读与写作D 艺体类E其他为了解学生的选择情况，现从该校随机抽取了部分学生进行问卷调查（参与问卷调查的每名学生只能选择其中一项），并根据调查得到的数据绘制了如图所示的两幅不完整的统计图．请根据统计图提供的信息回答下列问题（要求写出简要的解答过程）．（1）此次共调查了 名学生．（2）将条形统计图补充完整．（3）“数学兴趣与培优”所在扇形的圆心角的度数为 ．（4）若该校共有2000名学生，请估计该校喜欢A 、B 、C 三类活动的学生共有多少人？（5）学校将从喜欢“A ”类活动的学生中选取4位同学（其中女生2名，男生2名）参加校园“金话筒”朗诵初赛，并最终确定两名同学参加决赛，请用列表或画树状图的方法，求出刚好一男一女参加决赛的概率．40. 某运动会期间，甲、乙、丙三位同学参加乒乓球单打比赛，用抽签的方式确定第一场比赛的人选．（1）若已确定甲参加第一次比赛，求另一位选手恰好是乙同学的概率；（2）用画树状图或列表的方法，写出参加第一场比赛选手的所有可能，并求选中乙、丙两位同学参加第一场比赛的概率．41. “读书，使人思想活跃，聪颖智慧；使人增长见识，谈吐不凡；使人目光远大，志存高远”．某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆384人次，进馆人次逐月增加，到第三个月末累计进馆1824人次，若进馆人次的月平均增长率相同．(1)求进馆人次的月平均增长率；(2)因条件限制，学校图书馆每月接纳能力不超过1350人次，在进馆人次的月平均增长率不变的条件下，校图书馆能否接纳第四个月的进馆人次，并说明理由．42. 从社会效益和经济效益出发，某地制定了三年规划，投入资金进行生态环境建设，并以此发展旅游产业．根据规划，第一年度投入资金800万元，第二年度比第一年度减少，第三年度比第二年度减少．第一年度当地旅游业收入估计为400万元，要使三年内的投入资金与旅游业总收入持平，旅游业收入的年增长率应是多少？（以下数据供选用：=1.414，=3.606 计算结果精确到百分位）43. 某校七（1）班有56人参加过“数学兴趣小组”的学习活动，其中上学期有25名男生，15名女生参加过学习，下学期有27名男生，25名女生七、解答题参加过学习，有23名男生从上学期到下学期一直没有间断过学习，那么只在上学期参加过学习的女生有多少名？44. 2023年元旦期间，某超市打出促销广告，如下表所示：一次性所购物品的原价优惠办法不超过200元没有优惠超过200元，但不超过600元全部按九折优惠超过600元其中600元仍按九折优惠，超过600元部分按8折优惠(1)小张一次性购买物品的原价为400元，则实际付款为 元；(2)小王购物时一次性付款588元，则所购物品的原价是多少元？(3)小赵和小李分别前往该超市购物，两人各自所购物品的原价之和为1200元，且小李所购物品的原价高于小赵，两人实际付款共1074元，则小赵和小李各自所购物品的原价分别是多少元？45. 如图，在ΔABC 中，AD 是高，CE 是中线，点G 是CE 的中点，DG ⊥CE ，垂足为G．(1)求证：CD =AB ；(2)若∠AEC =66°，求∠BCE 的度数．46.如图，四边形是菱形，对角线相交于点O ．过点C 作，交的延长线于点E．(1)求证：．(2)，，则菱形的面积为______．47.如图，是的外接圆，AB 是的直径，D 是AB 延长线上的一点，连接DC ，，于点E．(1)求证：DC 是的切线；(2)若，，求DC 的长；(3)在（2）的条件下，若点P是上一点，连接CP 交线段OA 于点F ，若，求BF 的长．48. 如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，DE ⊥AC ，BF ⊥AC ，垂足分别为E 、F ．延长BF 至G ，使FG ＝BF ，连结DG ．（1）求证：GF ＝DE ．（2）当OF ∶BF ＝1∶2时，判断四边形DEFG 是什么特殊四边形？并说明理由．八、解答题九、判断题49.如图，，，的直径为6．求证：直线是的切线．50. 用白铁皮做水桶，每张铁皮能做1个桶身或8个桶底，而1个桶身和1个桶底正好配套做1个水桶，现在有63张这样的铁皮，则多少张做桶身、多少张做桶底正好配套？(请依题意列二元一次方程组解答本题)51. 实验发现，某种金属丝当温度每上升时伸长，当温度每下降时缩短．现将这种金属丝先从加热到，再冷却至时，请问，在这个过程中金属丝与原来相比经历了什么样的变化？请说明理由（假设伸长为正，缩短为负）52. 如图，已知在原点为O 的数轴上三个点A 、B 、C ，，动点P 从点O出发向右以每秒的速度匀速运动；同时，动点Q 从点C 出发向左以每秒的速度匀速运动．设运动时间为t秒．(1)当点P 从点O 运动到点C 时，求t 的值；(2)若，那么经过多长时间P ，Q 两点相距？(3)当，时，求a 的值．53. 已知关于x 的方程的解为负数，试求k 的取值范围．54. 阿静家在新建的楼房旁围成一个矩形花圃，花圃的一边利用20米长的院墙，另三边用总长为32米的离笆恰好围成．如图，设AB 边的长为x 米，矩形ABCD 的面积为S 平方米．（1）求S 与x 之间的函数关系式，并写出自变量x 的取值范围．（2）当x 为何值时，S有最大值？并求出最大值．55. 两直线平行，一组同位角的角平分线互相平行．（____）（填“√”“×”）56. ；______（判断对错）57. 用含字母的式子可以表示数量关系．( )58. （1）小英语文、数学、英语、物理四科的成绩分别是92分、98分、95分、91分，则她四科的平均成绩是94分．( )（2）3个4，2个5，1个3的平均数是4．( )59. 长方形、正方形、平行四边形和圆都是轴对称图形．( )。

中考数学 中考数学压轴题测试试题及答案

中考数学 中考数学压轴题测试试题及答案

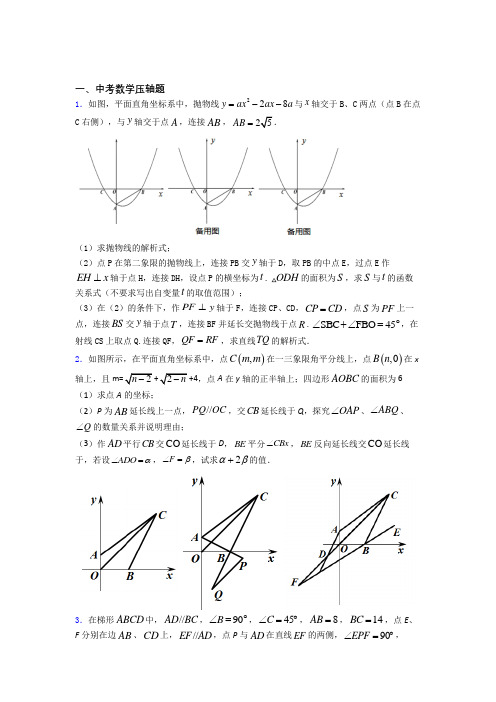
一、中考数学压轴题1．如图，平面直角坐标系中，抛物线228y ax ax a =--与x 轴交于B 、C 两点（点B 在点C 右侧），与y 轴交于点A ，连接AB ，25AB =．（1）求抛物线的解析式；（2）点P 在第二象限的抛物线上，连接PB 交y 轴于D ，取PB 的中点E ，过点E 作EH x ⊥轴于点H ，连接DH ，设点P 的横坐标为t .ODH 的面积为S ，求S 与t 的函数关系式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，作PF y ⊥轴于F ，连接CP 、CD ，CP CD =，点S 为PF 上一点，连接BS 交y 轴于点T ，连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒，在射线CS 上取点Q.连接QF ，QF RF =，求直线TQ 的解析式．2．如图所示，在平面直角坐标系中，点(),C m m 在一三象限角平分线上，点(),0B n 在x 轴上，且m=2n -+2n -+4，点A 在y 轴的正半轴上；四边形AOBC 的面积为6 （1）求点A 的坐标；（2）P 为AB 延长线上一点，//PQ OC ，交CB 延长线于Q ，探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由；（3）作AD 平行CB 交CO 延长线于D ，BE 平分CBx ∠，BE 反向延长线交CO 延长线于，若设ADO α∠=，F β∠=，试求2αβ+的值．3．在梯形ABCD 中，//AD BC ，90B ∠=︒，45C ∠=︒，8AB =，14BC =，点E 、F 分别在边AB 、CD 上，//EF AD ，点P 与AD 在直线EF 的两侧，90EPF ∠=︒，PE PF =，射线EP 、FP 与边BC 分别相交于点M 、N ，设AE x =，MN y =．（1）求边AD 的长；（2）如图，当点P 在梯形ABCD 内部时，求关于x 的函数解析式，并写出定义域； （3）如果MN 的长为2，求梯形AEFD 的面积．4．如图，90EOF ∠=︒，矩形ABCD 的边BA 、BC 分别在OF 、OE 上，4AB =，3BC =，矩形ABCD 沿射线OD 方向，以每秒1个单位长度的速度运动．同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动，当点P 到达点C 时，矩形ABCD 也停止运动，设点P 的运动时间为()t s ，PDO △的面积为S ． （1）分别写出点B 到OF 、OE 的距离（用含t 的代数式表示）；（2）当点P 不与矩形ABCD 的顶点重合时，求S 与t 之间的函数关系式；（3）设点P 到BD 的距离为h ，当15h OD =时，求t 的值； （4）若在点P 出发的同时，点Q 从点B 以每秒43个单位长度的速度向终点A 运动，当点Q 停止运动时，点P 与矩形ABCD 也停止运动，设点A 关于PQ 的对称点为E ，当PQE 的一边与CDB △的一边平行时，直接写出线段OD 的长．5．如图，在ABC ∆中，14AB =，45B ∠=︒，4tan 3A =，点D 为AB 中点．动点P 从点D 出发，沿DA 方向以每秒1个单位长度的速度向终点A 运动，点P 关于点D 对称点为点Q ，以PQ 为边向上作正方形PQMN ．设点P 的运动时间为t 秒．（1）当t =_______秒时，点N 落在AC 边上．（2）设正方形PQMN 与ABC ∆重叠部分面积为S ，当点N 在ABC ∆内部时，求S 关于t 的函数关系式．（3）当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时，直接写出t 的值．6．如图，在平面直角坐标系xoy 中，直线122y x =-+与x 轴交于点B ，与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点．（1）求抛物线的解析式；（2）点M 为抛物线对称轴上一动点，当BM CM -的值最小时，请你求出点M 的坐标；（3）抛物线上是否存在点N ，过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似？若存在，请直接写出点N 的坐标；若不存在，请说明理由．7．小明研究了这样一道几何题：如图1，在ABC 中，把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB '，把AC 绕点A 逆时针旋转β得到AC '，连接B C ''．当180a β+=︒时，请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：（1）①如图2，当ABC 为等边三角形时，猜想AD 与BC 的数量关系为AD =_______BC ；②如图3，当90BAC ∠=︒，8BC =时，则AD 长为________． 猜想论证：（2）在图1中，当ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用：（3）如图4，在四边形ABCD ，90C ∠=︒，120A B ∠+∠=︒，123BC =，6CD =，63DA =，在四边形内部是否存在点P ，使PDC △与PAB △之间满足小明探究的问题中的边角关系？若存在，请画出点P 的位置（保留作图痕迹，不需要说明）并直接写出PDC △的边DC 上的中线PQ 的长度；若不存在，说明理由．8．在平面直角坐标系中，点O 为坐标原点，抛物线(2)()y a x x m =++与x 轴交于点A C 、（点A 在点C 的左侧），与y 轴正半轴交于点B ，24OC OB ==．（1）如图1，求a m 、的值；（2）如图2，抛物线的顶点坐标是M ，点D 是第一象限抛物线上的一点，连接AD 交抛物线的对称轴于点N ，设点D 的横坐标是t ，线段MN 的长为d ，求d 与t 的函数关系式；（3）如图3，在（2）的条件下，当154d =时，过点D 作DE x 轴交抛物线于点E ，点P 是x 轴下方抛物线上的一个动点，连接PE 交x 轴于点F ，直线211y x b =+经过点D 交EF 于点G ，连接CG ，过点E 作EH CG 交DG 于点H ，若3CFG EGH S S =△△，求点P 的坐标．9．（1）如图1，A 是⊙O 上一动点，P 是⊙O 外一点，在图中作出PA 最小时的点A ． （2）如图2，Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，以点C 为圆心的⊙C 的半径是3.6，Q 是⊙C 上一动点，在线段AB 上确定点P 的位置，使PQ 的长最小，并求出其最小值． （3）如图3，矩形ABCD 中，AB ＝6，BC ＝9，以D 为圆心，3为半径作⊙D ，E 为⊙D 上一动点，连接AE ，以AE 为直角边作Rt △AEF ，∠EAF ＝90°，tan ∠AEF ＝13，试探究四边形ADCF 的面积是否有最大或最小值，如果有，请求出最大或最小值，否则，请说明理由．10．如图，正方形ABCD 的边长为8，M 是AB 的中点，P 是BC 边上的动点，连结PM ，以点P 为圆心，PM 长为半径作⊙P ．（1）当BP ＝ 时，△MBP ～△DCP ；（2）当⊙P 与正方形ABCD 的边相切时，求BP 的长；（3）设⊙P 的半径为x ，请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围．11．如图，在平面直角坐标系中，Rt ABC △的斜边在AB 在x 轴上，点C 在y 轴上90ACB ∠=︒，OC 、OB 的长分别是一元二次方程2680x x -+=的两个根，且OC OB <．（1）求点A 的坐标；（2）D 是线段AB 上的一个动点（点D 不与点A ，B 重合），过点D 的直线l 与y 轴平行，直线l 交边AC 或边BC 于点P ，设点D 的横坐标为t ，线段DP 的长为d ，求d 关于t 的函数解析式；（3）在（2）的条件下，当12d =时，请你直接写出点P 的坐标．12．已知：如图①，在等腰直角ABC ∆中，斜边2AC =．（1）请你在图①的AC 边上求作一点P ，使得90APB ∠=︒；（2）如图②，在（1）问的条件下，将AC 边沿BC 方向平移，使得点A 、P 、C 对应点分别为E 、Q 、D ，连接AQ ，BQ ．若平移的距离为1，求AQB ∠的大小及此时四边形ABDE 的面积；（3）将AC 边沿BC 方向平移m 个单位至ED ，是否存在这样的m ，使得在直线DE 上有一点M ，满足30AMB ∠=︒，且此时四边形ABDE 的面积最大？若存在，求出四边形ABDE 面积的最大值及平移距离m 的值；若不存在，请说明理由．13．已知：AB 为⊙O 的直径，点C 为弧AB 的中点，点D 为⊙O 上一点，连接CD ，交AB 于点M ，AE 为∠DAM 的平分线，交CD 于点E ．（1）如图1，连接BE ，若∠ACD=22°，求∠MBE 的度数；（2） 如图2，连接DO 并延长，交⊙O 于点F ，连接AF ，交CD 于点N ．①求证：DM 2+CN 2=CM 2；②如图3，当AD=1，AB=10时，请直接写出．．．．线段ME 的长． 14．如图①，在△ABC 中，∠ACB =90°，∠B =30°，AC =1，D 为AB 的中点，EF 为△ACD 的中位线，四边形EFGH 为△ACD 的内接矩形（矩形的四个顶点均在△ACD 的边上）． （1）计算矩形EFGH 的面积；（2）将矩形EFGH 沿AB 向右平移，F 落在BC 上时停止移动．在平移过程中，当矩形与△CBD 重叠部分的面积为3时，求矩形平移的距离； （3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形1111E F G H ，将矩形1111E F G H 绕1G 点按顺时针方向旋转，当1H 落在CD 上时停止转动，旋转后的矩形记为矩形2212E F G H ，设旋转角为α，求cos α的值．15．如图，已知ABF 为等腰直角三角形，90BAF ∠=︒，D 、C 为直线AF 上两点，且满足DF AC =，连接BD 、BC ，过点A 作AE BD ⊥于点E ，交BF 于点H ，连接CH ．（1）若30BAE ∠=︒，1BE =，求DE 的长；（2）若点M 是线段BF 上的动点，连AM 并延长交BD 于N ，当M 在线段BF 的什么位置上时，AH BN =？请说明理由；（3）在（2）的结论下，判断线段CH 、AH 、BD 的数量关系．请说明理由．16．已知抛物线2y ax bx c =++过点(6,0)A -，(2,0)B ，(0,3)C -．（1）求此抛物线的解析式；（2）若点H 是该抛物线第三象限的任意一点，求四边形OCHA 的最大面积；（3）若点Q 在y 轴上，点G 为该抛物线的顶点，且45GQA ∠=︒，求点Q 的坐标．17．定义：将函数l 的图象绕点P （m ，0）旋转180°，得到新的函数l '的图象，我们称函数l '是函数关于点P 的相关函数．例如：当m ＝1时，函数y ＝（x +1）2+5关于点P （1，0）的相关函数为y ＝﹣（x ﹣3）2﹣5．（1）当m ＝0时①一次函数y ＝x ﹣1关于点P 的相关函数为 ； ②点（12，﹣98）在二次函数y ＝﹣ax 2﹣ax +1（a ≠0）关于点P 的相关函数的图象上，求a 的值．（2）函数y ＝（x ﹣1）2+2关于点P 的相关函数y ＝﹣（x +3）2﹣2，则m ＝ ； （3）当m ﹣1≤x ≤m +2时，函数y ＝x 2﹣mx ﹣12m 2关于点P （m ，0）的相关函数的最大值为6，求m 的值．18．已知四边形ABCD 为矩形，对角线AC 、BD 相交于点O ，AD ＝AO ．点E 、F 为矩形边上的两个动点，且∠EOF ＝60°．（1）如图1，当点E 、F 分别位于AB 、AD 边上时，若∠OEB ＝75°，求证：DF ＝AE ； （2）如图2，当点E 、F 同时位于AB 边上时，若∠OFB ＝75°，试说明AF 与BE 的数量关系；（3）如图3，当点E 、F 同时在AB 边上运动时，将△OEF 沿OE 所在直线翻折至△OEP ，取线段CB 的中点Q ．连接PQ ，若AD ＝2a （a ＞0），则当PQ 最短时，求PF 之长．19．如图，在矩形ABCD中，点E为BC的中点，连接AE，过点D作DF AE⊥于点F，过点C作CN DF⊥于点N，延长CN交AD于点M．（1）求证：AM MD=（2）连接CF，并延长CF交AB于G①若2AB=，求CF的长度；②探究当ABAD为何值时，点G恰好为AB的中点．20．已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC．（1）如图1，当BM=1时，求PC的长；（2）如图2，设AM与BD交于点E，当∠PCM=45°时，求证：BEDE=33+；（3）如图3，取PC的中点Q，连接MQ，AQ．①请探究AQ和MQ之间的数量关系，并写出探究过程；②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由．21．在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A 顺时针旋转90°，得到线段AE，连接DE．（1）如图1，点E落在BA的延长线上时，∠EDC= （度）直接填空．（2）如图2，点D在运动过程中，DE⊥AC时，AB=4 ，求DE的值．（3）如图3，点F为线段DE中点，AB=2a，求出动点D从B运动到C，点F经过的路径长度．22．在一次数学课上，李老师让同学们独立完成课本第23页第七题选择题（2）如图 1，如果 AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝（）A．180° B．270° C．360° D．540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB∥EF，请直接写出∠BAD，∠ADE，∠DEF之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示），当AD，ED分别平分∠BAC，∠CEF时，∠ACE与∠ADE之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB∥EF，当∠ACD=90°时，∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系？请你直接写出结果，不需要证明．23．发现来源于探究．小亮进行数学探究活动，作边长为a的正方形ABCD和边长为b的正方形AEFG（a>b），开始时，点E在AB上，如图1．将正方形AEFG绕点A逆时针方向旋转．（1）如图2，小亮将正方形AEFG绕点A逆时针方向旋转，连接BE、DG，当点G恰好落在线段BE上时，小亮发现DG⊥BE，请你帮他说明理由．当a=3，b=2时，请你帮他求此时DG 的长．（2）如图3，小亮旋转正方形AEFG ，点E 在DA 的延长线上，连接BF 、DF ．当FG 平分∠BFD 时，请你帮他求a ：b 及∠FBG 的度数．（3）如图4，BE 的延长线与直线DG 相交于点P ，a=2b ．当正方形AEFG 绕点A 从图1开始，逆时针方向旋转一周时，请你帮小亮求点P 运动的路线长（用含b 的代数式表示）．24．已知，抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ，B ，且B 点的坐标为()2,0．（1）求该抛物线的解析式．（2）如图1，若点P 是线段AB 上的一动点，过点P 作//PE AC ，交BC 于E ，连接CP ，求PCE ∆面积的最大值．（3）如图2，若直线y x m =+与线段AC 交于点M ，与线段BC 交于点N ，是否存在M ，N ，使得OMN ∆为直角三角形，若存在，请求出m 的值；若不存在，请说明理由．25．如图，在平面直角坐标系中，矩形ABCD 的顶点,A D 在坐标轴上，两点的坐标分别是点()0,,A m 点(),0,D m 且m 满足：322m m -+62=边AB 与x 轴交于点,E 点F 是边AD 上一动点，连接FB ，分别与x 轴，y 轴交于点,P 点,H 且FD BE =．（1）求m 的值；（2）若45,APF ∠=︒求证：AHF HFA ∠=∠；（3）若点F 的纵坐标为,n 则线段HF 的长为 ．(用含n 的代数式表示)【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．H解析：（1）211242y x x =--；（2）213S 242t t =---；（3）7433y x =-+ 【解析】【分析】(1)先把B 、C 两点坐标求解出来，再根据待定系数法即可把函数解析式求解出来；(2) 过点P 作PK x ⊥轴于点K ，PF y ⊥轴于点F ，把OH 、OD 的长度用t 表示出来，再根据ODH ∆的面积为S ，即可表示出S 与t 的函数关系式；(3)先证明PKC COD ∆≅∆，再过点R 作RN x ⊥轴，设211m,242R m m ⎛⎫-- ⎪⎝⎭，连接RC 、RO ，作CL RO ⊥于L ，求出Q 点的坐标，再利用待定系数法即可把直线TQ 的解析式求解出来；【详解】（1）∵228y ax ax a =--与x 轴交于B 、C 两点∴令0y =，即2280ax ax a --=解得14x =，22x =-由题意得，∴B(4,0)，C(2,0)-在Rt OAB 中，4OB =，25AB =.∴22OA 2AB OB =-=∴()0,2A -∴82a -=-∴14a = ∴抛物线的解析式为211242y x x =-- （2）过点P 作PK x ⊥轴于点K ，PF y ⊥轴于点F∴PKO PFO 90∠=∠=︒，FOK 90∠=︒∴四边形FPKO 为矩形∴FO PK =∵E 为PB 的中点∴PE BE =∵EH BK ⊥∴PKB EHB 90∠=∠=︒∴PK //EH ∴BH BM HK PM= ∴BH HK = ∵211,242P t t t ⎛⎫-- ⎪⎝⎭ ∴211PK OF 242t t ==--，OK PF t ==- ∴BK 4t =- ∴1t BH BK 222==- ∴t t OH 42222⎛⎫=--=+ ⎪⎝⎭ ∵OD PK tan DBO OB BK ∠==， 即21441422t t OD t--=- ∴OD t 2=-- ∴211t 13S OD OH (t 2)2222242t t ⎛⎫=⋅=--+=--- ⎪⎝⎭， （3）∵OK t =-，OC 2=，∴CK OD t 2==--，∵CP CD =，PKC COD 90∠=∠=︒，∴PKC COD ∆≅∆，∴PK OC 2==，∴2OF = ∴OF 1tan FBO OB 2∠== 过点R 作RN x ⊥轴，如图设211m,242R m m ⎛⎫-- ⎪⎝⎭∴RN 1tan FBO BN 2∠==， ∴211214242m m m --=- 解得4m =-或4m =（舍去），∴R(4,4)- ∴CN 1tan CRN RN 2∠== ∴CRN FBO ∠=∠连接RC 、RO ，作CL RO ⊥于L ，如上图∵RN ON =∴45NRO RON NRC CRO ∠=∠=∠+∠=︒，∴LC LO =，RO 42=， ∴CL OL 2==， ∴CL 1tan CRO RL 3∠=， ∵SBC FBO 45∠+∠=︒， ∴OT 1tan TBO OB 3∠==， ∴4OT 3=，2TF 3=， ∴4T 0,3⎛⎫ ⎪⎝⎭∵//PF OB ，∴2FT 13tan FST FS 3FS ∠=== ∴2FS =，∴FS CO OF 2===，∴QC BC ⊥∵QF FB =，QSF BOF 90∠=∠=︒，∴QFS BFO ∆≅∆∴QS OB 4==∴(2,6)Q -设直线TQ 的解析式为y kx b =+ ∴2643k b b -+=⎧⎪⎨=⎪⎩ 解得7343k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线TQ 的解析式为7433y x =-+． 【点睛】本题主要考查了二次函数的综合应用，涉及到用待定系数法求解函数解析式、一次函数、全等三角形、图形的面积计算、矩形的性质、解直角三角形等相关知识，灵活运用所学知识是解题的关键． 2．A解析：（1）A （0，1）（2）结论：∠ABQ +∠OAB ﹣∠Q ＝135°.（3）α+2β＝45°．【解析】【分析】（1）利用二次根式的性质求出m 、n 的值，求出B 、C 两点坐标，由S 四边形AOBC ＝S △OBC +S △AOC ，推出12×2×4+12×OA ×4＝6，求出OA 即可； （2）如图2中，结论：∠ABQ +∠OAB ﹣∠Q ＝135°．根据三角形内角和定理，三角形的外角的性质即可解决问题；（3）由AD ∥BC ，推出∠ADC ＝∠DCB ＝α，由BE 平分∠CBx ，推出∠CBE ＝∠EBx ，由∠CBE ＝∠F +∠OCB ＝α+β，推出∠OBF ＝∠EBx ＝α+β，由OC 平分∠AOB ，可得∠COB ＝45°＝∠F +∠OBF ＝α+（α+β），由此即可解决问题；【详解】解：（1）由题意2020n n -≥⎧⎨-≥⎩，，得，解得n ＝2，∴m＝4，B（2，0），C（4，4）．如图：∵S四边形AOBC＝S△OBC+S△AOC，∴12×2×4+12×OA×4＝6，∴OA＝1，∴A（0，1）．（2）结论：∠ABQ+∠OAB﹣∠Q＝135°．如图：理由如下：∵OC∥PQ，∴∠Q＝∠OCB，∵∠ABQ＝∠1+∠OCB＝∠1+∠Q，∠1＝180°﹣∠OAB﹣∠AOC＝180°﹣∠OAB﹣45°＝135°﹣∠OAB，∴∠ABQ＝∠Q+135°﹣∠OAB，∴∠ABQ+∠OAB﹣∠Q＝135°．（3）如图：∵AD∥BC，∴∠ADC＝∠DCB＝α，∵BE平分∠CBx，∴∠CBE＝∠EBx，∵∠CBE＝∠F+∠OCB＝α+β，∴∠OBF＝∠EBx＝α+β，∵C（4，4），∴OC平分∠AOB，∴∠COB＝45°＝∠F+∠OBF＝α+（α+β），∴α+2β＝45°．【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识，解题的关键是灵活运用所学知识解决问题，属于压轴题．3．D解析：（1）6；（2）y=－3x+10(1≤x＜103)；（2）1769或32【解析】【分析】（1）如下图，利用等腰直角三角形DHC可得到HC的长度，从而得出HB的长，进而得出AD的长；（2）如下图，利用等腰直角三角形的性质，可得PQ、PR的长，然后利用EB=PQ+PR得去x、y的函数关系，最后根据图形特点得出取值范围；（3）存在2种情况，一种是点P在梯形内，一种是在梯形外，分别根y的值求出x的值，然后根据梯形面积求解即可．【详解】（1）如下图，过点D作BC的垂线，交BC于点H∵∠C=45°，DH ⊥BC∴△DHC 是等腰直角三角形∵四边形ABCD 是梯形，∠B=90°∴四边形ABHD 是矩形，∴DH=AB=8∴HC=8∴BH=BC －HC=6∴AD=6（2）如下图，过点P 作EF 的垂线，交EF 于点Q ，反向延长交BC 于点R ，DH 与EF 交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理，PR=12y ∵AB=8，∴EB=8－x∵EB=QR∴8－x=()11622x y ++ 化简得：y=－3x+10 ∵y ＞0，∴x ＜103 当点N 与点B 重合时，x 可取得最小值则BC=NM+MC=NM+EF=－3x+10+614x +=，解得x=1∴1≤x ＜103（3）情况一：点P 在梯形ABCD 内，即（2）中的图形 ∵MN=2，即y=2，代入（2）中的关系式可得：x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二：点P 在梯形ABCD 外，图形如下：与（2）相同，可得y=3x －10则当y=2时，x=4，即AE=4∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质，难点在于第（2）问中确定x 的取值范围，需要一定的空间想象能力． 4．B解析：（1）35t ，45t ；（2）当0＜t ＜3时，224655S t t =--+；当3＜t ＜7时，23391052S t t =+-；（3）75；（4）132，7713，477 【解析】【分析】（1）过点B 作x 轴垂线，利用相似三角形可求得； （2）分2种情况，一种是点P 在AD 上，另一种是点P 在CD 上，然后利用三角形面积公式可求得；（3）直接令15h OD =即可求出； （4）存在3种情况，第一种是：QP ∥BD ，第二种是EP ∥CD 或EQ ∥CB ，第三种是QE ∥BD ，分别按照几何性质分析求解．【详解】（1）如下图，过点B 作x 轴垂线，垂足为点M根据平移的特点，可得∠BOM=∠DBA∵∠BMO=∠DAB=90°，∴△BMO ∽△DAB∵AB=4，AD=BC=3∴BD=5∵BM OM BO DA BA BD==，OB=t ∴BM=35t ，OM=45t （2）情况一：当0＜t ＜3时，图形如下，过点P 作OD 的垂线，交OD 于点N∵∠NDP=∠BDA ，∠PND=∠BAD ，∴△PND ∽△BAD∵AP=t ，∴PD=3－t∵PN BA PD BD =，∴PN=()435t - 图中，OD=5+t ∴()()243124562555OBD t S t t t -=+=--+ 情况二：当3＜t ＜7时，图形如下，过点P 作OD 的垂线，交OD 于点N图中，PD=t －3，OD=5+t同理，△PND ∽△BCD ，可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- （3）情况一：当0＜t ＜3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得：t=75情况二：当3＜t ＜7时则h=PN=()335t - ∵15h OD =∴()33555t t -+= 解得：t=7(舍)（4）情况一：QP ∥BD ，图形如下由题意可得：BQ=43t ，AP=t ，则QA=4－43t ，DP=3－t ∵BD ∥QP∴QA PA QB PD= 代入得：4()2243t t =-解得：t=32∴OD=5+t=132 情况二：如下图，EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点∴EP=PA ，EQ=QA ，QP=QP∴△APQ ≌△EPQ∵EP ∥CD ，CD ⊥AD∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形，AQ=PA∴4－43t t = 解得：t=127∴OD=5+t=477 情况三：如下图，QE ∥BD ，延长QE 交DA 于点N∵△APQ ≌△EPQ ，∴∠QEP=∠QAP=90°∴△ENP 是等腰直角三角形∵QN ∥BD ，∴∠NQA=∠DBA ，∠A=∠A∴△QNA ∽△BDA∵BQ=43t ，AP=t ，QA=4－43t ，DP=3－t ∴QN QA AN BD BA AD== ∴QN=5－43t ，NA=3－t ∴EN=QN －QE=QN －QA=1－3t ，NP=NA －AP=3－2t ，EP=PA=t ∴在Rt △ENP 中，()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得：t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题，解题关键是利用相似将图形中各边用t 表示出来．5．A解析：（1）145；（2）2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩；（3）t 的值为477或727．【解析】【分析】（1）如下图，根据4tan 3A =，可得出PN 与AP 的关系，从而求出t 的值； （2）如下图，存在2种情况，一种是点M 在△ABC 内，另一种是点M 在△ABC 外部，分别根据正方形和三角形求面积的公式可求解；（3）如下图，存在2种情况，一种是PM 所在的直线将△ABC 的面积平分，另一种是QN 所在的直线将△ABC 的面积平分．【详解】（1）如图1，点N 在AC 上图1由题意可知：PD=DQ=t ，AP=7－t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =，即2473t t =- 解得：t=145 （2）①如图2，图2四边形PQMN 是正方形，90BQM ∴∠=︒，45B ∠=︒，BQ MQ ∴=，即72t t -=解得73t =， 故当0t <≤73时，22(2)4S t t ==； ②如图3，图390BQF ∠=︒，45B ∠=︒，7BQ FQ t ∴==-，45BFQ MFE ∠=∠=︒，则37MF MQ QF t =-=-，90M ∠=︒，37ME MF t ∴==-， 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭； 综上，2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩． （3）如下图，过点C 作AB 的垂线，交AB 于点G图4∵4tan 3A = ∴设CG=4x ，则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14，解得：x=2∴1148562ABC S== ∴1282ABCS = 情况一：PM 所在的直线平分△ABC 的面积，如下图，PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形，∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB－PA=14－(7－t)=7+t∴7+t=47t=477-情况二：如下图，QN所在线段平分△ABC的面积，QF交AC于点F，过点F作AB的垂线，交AB于点H图6同理，28AFQS=∵四边形PQMN是正方形，∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y，则AH=3y，HQ=FH=4y，∴AQ=7y∴174282AFQS y y==，解得：2∵AQ=AB－QB=14－(7－t)=7+t ∴2解得：7∴综上得：t 的值为7或7．【点睛】本题考查动点问题，解题关键是根据动点的变化情况，适当划分为几种不同的形式分别分析求解．6．B解析：（1）213222y x x =-++；（2）3(,0)2；（3）存在；(0,2)N 或(3,2)N 或(2,3)--N 或(5,18)--N【解析】【分析】（1）由直线122y x =-+可得B 、C 两点的坐标，根据二次函数的对称轴求得A 点坐标，可设抛物线的解析式为(1)(4)y a x x =+-，将C 点坐标代入可求得a ，即可得抛物线的解析式；（2）根据绝对值的性质得出BM CM -的值最小时，点M 为BC 的垂直平分线与直线32x =的交点，求得BC 垂直平分线的解析式，联立直线32x =即可求得点M ； （3）分四种情况进行讨论，设出N 的坐标，根据相似三角形的对应边成比例的性质，求得N 的横坐标与纵坐标的关系，然后联立抛物线解析式即可求解．【详解】 解：∵直线122y x =-+与x 轴交于点B ，与y 轴交于点C ， ∴当y =0时，即1022x =-+，解得：x =4，则点B 的坐标为(4,0)， 当x =0时，10222=-⨯+=y ，则点C 的坐标为(0,2)，由二次函数的对称性可知：点A 与点B 关于直线32x =对称， ∴点A 的坐标为(1,0)-，∵抛物线与x 轴的交点为点(1,0),(4,0)A B -，∴可设抛物线的解析式为(1)(4)y a x x =+-，又∵抛物线过点(0,2)C ，∴2(01)(04)a =+-，解得：12a =-， ∴2113(1)(4)2222y x x x x =-+-=-++∴抛物线的解析式为213222y x x =-++； （2）如图1，连结CM 、BM ，作线段BC 的垂直平分线l 分别交BC 、直线32x =于点'、N M ，则N 为BC 中点；由绝对值的性质可得：0≥-BM CM ，∴当BM CM -的值最小时，即0=-BM CM ，则此时CM BM =， ∴点M 为l 与直线32x =的交点，此时M 与'M 重合， 设l 的解析式为：y kx b =+，∵直线BC 的解析式为：122y x =-+，BC l ⊥ ∴112-⋅=-k ，解得：2k =，则l 的解析式可化为：2y x b =+， 由(4,0),(0,2)B C 得点N 的坐标为(2,1)，将(2,1)N 代入2y x b =+得： 14b =+，解得：3b =-，∴23y x =-，将32x =代入23y x =-，得323=02=⨯-y ，即3'(,0)2M ， ∴当BM CM -的值最小时，点M 的坐标为3(,0)2，（3）抛物线上存在点N ，使得以点、、B N H 为顶点的三角形与ABC 相似； ∵(1,0),(4,0),(0,2)-A B C∴1,4==OA OB ，2OC =，5AB =， ∴2222125=+=+=AC OA OC 22224225BC OB OC =+=+=， ∵22252025+=+==AC BC AB ，∴ABC 为直角三角形，90ACB ∠=︒，∵NH x ⊥轴，∴90∠=︒NHB ，则90∠=∠=︒NHB ACB ，如图2所示，分四种情况，点N 的坐标分别为1234、、、N N N N ，设点N 的坐标为(,)m n ，①当点1N 在x 轴的上方，要使11N BH ABC ，则11∠=∠N BH ABC ，则此时点1N 与点C 重合，则此时点1H 与点O 重合，则11≅N BH ABC ，满足题意，∴此时点1N 的坐标为(0,2)；②当点2N 在x 轴的上方，要使22BN H ABC ，则2222==N H BC BH AC ， ∴24=-n m，即28n m =-+，代入抛物线的解析式得： 21328222mm m ，化简得：27120m m ， 解得：13m =，24m =（不符合题意，故舍去），将3m =代入抛物线解析式得：2n =，∴此时点2N 的坐标为(3,2)；③当点3N 在x 轴的下方，要使33N BH ABC ，则3332==BH BC N H AC ， ∴42-=-m n ，即42-=m n ，代入抛物线的解析式得：24132222m m m ，化简得：2280m m --=，解得：12m =-，24m =（不符合题意，故舍去），将2m =-代入抛物线解析式得：3n =-，∴此时点3N 的坐标为(2,3)--；④当点4N 在x 轴的下方，要使44BN H ABC ，则4442==N H BC BH AC ， ∴24-=-n m，即28=-n m ，代入抛物线的解析式得： 21328222m m m ，化简得：2200m m ， 解得：15m =-，24m =（不符合题意，故舍去），将5m =-代入抛物线解析式得：18n =-，∴此时点4N 的坐标为(5,18)--；综上所述，抛物线存在点N 的坐标为(0,2)或(3,2)或(2,3)--或(5,18)--使得以点、、B N H 为顶点的三角形与ABC 相似．【点睛】本题主要考查了一次函数与二次函数的性质、相似三角形的性质，运用数形结合与分类讨论的方法是解题的关键．7．（1）①12；②4，（2）12AD BC =；理由见解析，（3）存在； 【解析】 【分析】 （1）①首先证明ADB '∆是含有30的直角三角形，可得1122AD AB BC '==，即可解决问题；②首先证明BAC B AC ''∆∆≌，根据直角三角形斜边中线定理即可解决问题． （2）AD 与BC 的数量关系为12AD BC =，如图5，延长AD 到M ，使AD DM =，连接B M '、C M '，先证四边形AC MB ''是平行四边形，再证明BAC AB M '∆∆≌，即可解决问题．（3）存在，如图6，延长AD 交BC 的延长线于M ，作BE AD ⊥于E ，做直线BC 的垂直平分线交BE 于P ，交BC 于F ，连接PA 、PD 、PC ，作PDC ∆的中线PQ ，连接DF 交PC 于O ，先证明PA PD =，PB PC =，再证明+180APD BPC ∠∠=︒，即可得出结论，再在Rt PDQ ∆中，根据勾股定理，即可求出PQ 的长．【详解】（1）①如图2，∵ABC ∆是等边三角形，把AB 绕点A 顺时针旋转α得到AB '，把AC 绕点A 逆时针旋转β得到AC '，∴===AB AC BC AB AC ''=，又∵AD 是AB C ''△边B C ''上的中线，∴=DB DC ''，∴AD B C ''⊥，即90ADB '∠=︒，∵60BAC ∠=︒，180BAC B AC ''∠+∠=︒，∴120B AC ''∠=︒，∴=30B C ''∠∠=︒，∴在ADB '∆中，90ADB '∠=︒，30B '∠=︒， ∴1122AD AB BC '==． 故答案为：12． ②如图3，∵90BAC ∠=︒，+=180BAC B AC ''∠∠︒，∴==90BAC B AC ''∠∠︒，即ABC ∆和AB C ''∆为直角三角形，∵把AB 绕点A 顺时针旋转α得到AB '，把AC 绕点A 逆时针旋转β得到AC '， ∴=AB AB '，=AC AC '，∴在ABC ∆和AB C ''∆中，===AB AB BAC B AC AC AC '''∠'⎧⎪∠⎨⎪⎩∴BAC B AC ''∆∆≌，∴=BC B C ''，∵AD 是AB C ''△边B C ''上的中线，AB C ''∆为直角三角形，∴1122AD B B C C ''==， 又∵8BC =， ∴11=8=422AD BC =⨯． 故答案为：4． （2）12AD BC =， 如图5，延长AD 到M ，使AD DM =，连接B M '、C M '，图5∵=B D DC ''，AD DM =，∴四边形AC MB ''是平行四边形，∴AC B M AC ''==，∵+=180BAC B AC ''∠∠︒，+=180B AC AB M '''∠∠︒，∴=BAC AB M '∠∠，∵=AB AB '，∴在BAC ∆和AB M '∆中，==AC B M BAC AB M AB AB ''=⎧'⎪∠∠⎨⎪⎩∴BAC AB M '∆∆≌，∴BC AM =， ∴12AD BC =． （3）存在，如图6，延长AD 交BC 的延长线于M ，作BE AD ⊥于E ，作直线BC 的垂直平分线交BE 于P ，交BC 于F ，连接PA 、PD 、PC ，作PDC ∆的中线PQ ，连接DF 交PC 于O ，图6∵+=120A B ∠∠︒，∴=180=60M A B ∠︒-∠-∠︒， ∵=90C ∠︒，∴=180=30MDC M MCD ∠︒-∠-∠︒，在Rt DCM ∆中，∵=6CD ，=90DCM ∠︒，=30MDC ∠︒， ∴=23CM =43DM =60M ∠︒， 在Rt BEM ∆中，∵=90BEM ∠︒，143BM BC CM =+==30MDC ∠︒，∴1732EM BM ==， ∴33DE EM DM =-=，∵=63AD =AE DE ，∵BE AD ⊥，∴PA PD =，PB PC =，在Rt CDF ∆中，∵=6CD ，CF∴tan CDF ∠=∴60CDF CPF =︒=∠∠，∴FCP CFD ∆∆≌，∴CD PF =，∵//CD PF ，∴四边形CDPF 是矩形，∴=90CDP ∠︒，∴=60ADP ADC CDP ∠∠-∠=︒，∴ADP ∆是等边三角形，∴=PA PD AD =∵=60BPF CPF ∠∠=︒，∴120BPC ∠=︒，∴+180APD BPC ∠∠=︒，∴PDC ∆与PAB ∆之间满足小明探究的问题中的边角关系，在Rt PDQ ∆中，∵=90PDQ ∠︒，PD PA AD ===132DQ CD ==，∴PQ ==【点睛】本题考查了三角形的综合问题．掌握全等三角形的性质以及判定定理、直角三角形斜边中线定理、解直角三角形、勾股定理、中线的性质是解题的关键．在处理三角形的边旋转问题时，旋转前后边长不变，根据已知角度变化，求得线段之间关系．在证明某点是否存在问题时，先假设这点存在，能求出相关线段或坐标，即证实存在性． 8．B解析：（1）14a =，4m =-；（2）3344d t =-；（3）220,39P ⎛⎫- ⎪⎝⎭． 【解析】【分析】（1）根据24OC OB ==得出B,C 的坐标，令(2)()0y a x x m =++=即可求出m 的值，将B 的坐标代入抛物线的解析式中即可求出a 的值；（2）过点D 作DI AC ⊥于点I ，设MN 与x 轴的交点为J ，先利用抛物线的解析式求出M 的坐标，然后利用平行线分线段成比例有AF NF AE DE =，代入相应的值计算即可得出答案； （3）先根据154d =求出此时D,E 的坐标，然后将点D 的坐标代入211y x b =+中求出直线的解析式，设G 点的坐标为232(,)1111m m +，利用待定系数法求出直线GE 的解析式，进而求出F 的坐标及CFG S ，然后利用待定系数法求出GC,EH 的解析式，进而求出H 点的坐标，然后表示出EGH S，然后利用3CFG EGH S S =△△求出ｍ的值，进而求出直线GE 的解析式，通过直线GE 的解析式与抛物线解析式联立即可求出P 点的坐标． 【详解】（1）24OC OB ==(0,2),(4,0)B C ∴- ．令(2)()0y a x x m =++=，解得2,x x m =-=-，4m ∴-= ，4m ∴=- ，∴抛物线的解析式为(2)(4)y a x x =+- ，将点(0,2)B -代入得，82a -=-，解得14a = ； （2）如图，过点D 作DI AC ⊥于点I ，设MN 与x 轴的交点为J ，∵1,44a m ==- ， 2119(2)(4)(1)444y x x x ∴=+-=--， 9(1,)4M ∴- ． ∵点D 的横坐标是t ，∴211(,2)42D t t t --， 211242DI t t ∴=--． MN x ⊥轴，DI x ⊥轴，//NM DI ∴ ，AJ NJAI DI∴=．NM d=，291(2)4112242dt t t---∴=+--，解得3344d t=-；（3）如图，当154d=时，3315444d t=-=，解得6t=，此时D的坐标为(6,4)．//DE x轴，∴点E的纵坐标也是4，令1(2)(4)44y x x=+-=，解得4x=-或6x=，∴(4,4)E-．∵直线211y x b=+经过点D，∴26411b⨯+=，解得3211b=，∴2321111y x=+．设点G的坐标为232(,)1111m m+，设直线EG的解析式为y kx b=+，将232(4,4),(,)1111E G m m -+代入解析式中得 442321111k b mk b m -+=⎧⎪⎨+=+⎪⎩ 解得2121144521281144m k m m b m -⎧=⎪⎪+⎨+⎪=⎪+⎩∴直线EG 解析式为2125212811441144m m y x m m -+=+++ ， 令0y = ，即21252128011441144m m x m m -++=++，解得26646m x m+=- ， 2664(,0)6m F m+∴- ， ∴26643040466m m CF m m ++=-=--， 113040232(3040)(16)()226111111(6)CFG G m m m S CF y m m m +++∴=⋅=⨯⨯+=-- ． 设直线GC 的解析式为y ax c =+ ， 将232(4,0),(,)1111C G m m +代入解析式中得 402321111a c ma c m +=⎧⎪⎨+=+⎪⎩ 解得232114481281144m a m m c m +⎧=⎪⎪-⎨+⎪=-⎪-⎩∴直线GC 解析式为232812811441144m m y x m m ++=--- ． ∵EH CG ， ∴设直线EH 解析式为2321144m y x n m +=+-， 将点(4,4)E -代入得232(4)41144m n m +⨯-+=-， 解得52481144m n m -=- ， ∴直线EH 解析式为232524811441144m m y x m m +-=+--． 将直线GD 的解析式与直线EH 的解析式联立，23211232524811441144y x x m m y x m m ⎧=+⎪⎪⎨+-⎪=+⎪--⎩解得422811m x m y +⎧=-⎪⎪⎨-⎪=⎪⎩∴428(,)211m m H +--， 11341520()10()221111EGH EDG EDH H G m m S S S ED y y ++∴=-=⋅-=⨯⨯-=- ． ∵3CFG EGH S S =△△，∴(3040)(16)11(6)m m m ++-15203()11m +=⨯-， 解得154m =-或43m =-． 当154m =-时，GE 的解析式为4433y x =--， 将直线GE 的解析式与抛物线的解析式联立， 2443311242y x y x x ⎧=--⎪⎪⎨⎪=--⎪⎩解得23209x y ⎧=⎪⎪⎨⎪=-⎪⎩或44x y =-⎧⎨=⎩（点E 的坐标，舍去）， ∴220(,)39P -； 当43m =-时，GE 的解析式为122y x =-+， 将直线GE 的解析式与抛物线的解析式联立212211242y x y x x ⎧=-+⎪⎪⎨⎪=--⎪⎩解得40x y =⎧⎨=⎩(点C 的坐标，舍去) 或44x y =-⎧⎨=⎩（点E 的坐标，舍去）， ∴综上所述，点P的坐标为220(,)39P- ． 【点睛】本题主要考查二次函数，一次函数与几何综合，难度较大，尤其是计算量太大，容易出错，掌握待定系数法，平行线分线段成比例，合理的设出点的坐标并准确的计算是解题的关键． 9．A解析：（1）作图见解析；（2）PQ 长最短是1.2；（3）四边形ADCF 面积最大值是812+，最小值是812- 【解析】【分析】（1）连接线段OP 交⊙C 于A ，点A 即为所求；（2）过C 作CP ⊥AB 于Q ，P ，交⊙C 于Q ，这时PQ 最短，根据勾股定理以及三角形的面积公式即可求出其最小值；（3）△ACF的面积有最大和最小值，取AB的中点G，连接FG，DE，证明△FAG～△EAD，进而证明点F在以G为圆心1为半径的圆上运动，过G作GH⊥AC于H，交⊙G于F1，GH 反向延长线交⊙G于F2，①当F在F1时，△ACF面积最小，分别求出△ACD的面积和△ACF 的面积的最小值即可得出四边形ADCF的面积的最小值；②当F在F2时，四边形ADCF的面积有最大值，在⊙G上任取异于点F2的点P，作PM⊥AC于M，作GN⊥PM于N，利用矩形的判定与性质以及三角形的面积公式即可得出得出四边形ADCF的面积的最大值．【详解】解：（1）连接线段OP交⊙C于A，点A即为所求，如图1所示；（2）过C作CP⊥AB于Q，P，交⊙C于Q，这时PQ最短．理由：分别在线段AB，⊙C上任取点P'，点Q'，连接P'，Q'，CQ'，如图2，由于CP⊥AB，根据垂线段最短，CP≤CQ'+P'Q'，∴CO+PQ≤CQ'+P'Q'，又∵CQ＝CQ'，∴PQ＜P'Q'，即PQ最短．在Rt△ABC中22228610AB AC BC=+=+=，1122ABCS AC BC AB CP∆=•=•，∴684.810AC BCCPAB•⨯===，∴PQ＝CP﹣CQ＝6.8﹣3.6＝1.2，∴22226 4.8 3.6BP BC CP-=-=．当P在点B左侧3.6米处时，PQ长最短是1.2．（3）△ACF的面积有最大和最小值．如图3，取AB的中点G，连接FG，DE．∵∠EAF＝90°，1 tan3AEF∠=，∴13 AF AE=。

2024年中考考前押题密卷数学(全国卷)(全解全析)

2024年中考考前押题密卷数学(全国卷)(全解全析)

2024年中考考前押题密卷（全国卷）数学·全解全析第Ⅰ卷一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）1．下列各数中，相反数是它本身的数是（）A ．2-B ．1-C ．0D ．11.C【分析】根据相反数的意义，只有符号不同的数为相反数．【解析】相反数等于本身的数是0．故选：C ．【点睛】本题考查了相反数的意义．注意掌握只有符号不同的数为相反数，0的相反数是0．2．如图所示的几何体是由7个相同的小正方体组合成的，则这个几何体的左视图是（）A ．B ．C ．D ．2.D【分析】根据观察几何体，从左边看，底层有2个正方体，上层有一个正方体，即可得到答案．【解析】从左边看，底层有2个正方体，上层有一个正方体，∴几何体的左视图为：，故选：D ．【点睛】本题考查三视图的知识，解题的关键是学会找几何体的三视图．3．据国家统计局预测，截止2024年底，我国GDP 将突破23万亿美元，23万亿用科学记数法表示为（）A ．132.310⨯B ．142.310⨯C ．140.2310⨯D ．122310⨯3.A【分析】本题考查科学记数法的表示方法．科学记数法的表示形式为10n a ⨯的形式，其中110a ≤<，n 为整数，表示时关键要正确确定a 的值以及n 的值．【解析】23万亿23000000000000=元132.310=⨯元．故选：A ．4．下列运算中，正确的是（）A ．326326x x x ⋅=B ．4482x x x +=C ．633x x x ÷=D ．()32528x x =4.C【分析】分别利用单项式乘单项式、合并同类项、同底数幂的除法和积的乘方运算法则化简求出即可．【解析】A 、3x 3•2x 2=6x 5，故此选项错误；B 、x 4+x 4=2x 4，故此选项错误；C 、x 6÷x 3=x 3，故此选项正确；D 、（2x 2）3=8x 6，故此选项错误．故选：C ．【点睛】此题主要考查了单项式乘单项式、合并同类项、同底数幂的除法和积的乘方等知识，熟练掌握相关运算法则是解题关键．5．如图，在平面直角坐标系中，点P 坐标为()1,2，以点O 为圆心，以OP 的长为半径画弧，交x 轴的正半轴于点A ，则点A 的横坐标介于（）A ．1和2之间B ．2和3之间C ．3和4之间D ．4和5之间5.B【分析】先根据勾股定理计算出OP 的长度，OP OA =可以知道A 点的横坐标，再利用估算无理数的方法得出答案．【解析】22125OP =+=，则A 点横坐标为5，459<<，即253<<，∴A 的横坐标介于2和3之间，故选B ．【点睛】本题主要考查了估算无理数的大小和勾股定理，正确估计5最接近的整数是解题的关键．6．某居民小区开展节约用电活动，对该小区30户家庭的节电量情况进行了统计，五月份与四月份相比，节电情况如下表：节电量（度）10203040户数215103则五月份这30户家庭节电量的众数与中位数分别为（）A ．20，20B ．20，25C ．30，25D ．40，206.A【分析】根据表格中的数据可以得到这组数据的众数和中位数，本题得以解决．【解析】由表格中的数据可得，五月份这30户家庭节电量的众数是：20，中位数是20，故选：A ．【点睛】本题考查众数、统计表、中位数，解题的关键是明确它们各自的含义，会找一组数据的众数和中位数．7．如图，Rt ABC △中，90ACB ∠=︒，30B ∠=︒，2AC =，23BC =，将ABC 绕点C 逆时针旋转至A B C ''△，使得点A '恰好落在AB 上，A B ''与BC 交于点D ，则A CD '△的面积为（）A ．32B ．53C ．5D ．237.A【分析】由已知结合旋转的性质可知CA CA '=，60A CA B ''∠=∠=︒，可证得ACA ' 是等边三角形，可得2A C A B ''==，30A CB B '∠=∠=︒，进而可知A D BC '⊥，由等腰三角形的性质和含30度的直角三角形的性质可知112A D A C ''==，132CD BC ==，进而利用面积公式即可求解．【解析】在Rt ABC △中，90ACB ∠=︒，2AC =，30B ∠=︒，∴9060A B ∠=︒-∠=︒，24AB AC ==，由旋转可知，CA CA '=，60A CA B ''∠=∠=︒，∴ACA ' 是等边三角形，∴2AA AC A C ''===，∴2A C A B ''==，∴30A CB B '∠=∠=︒，∵60CA B ∠=''︒，∴18090CDA A CD CA D '''∠=︒-∠-∠=︒，则A D BC '⊥，∴112A D A C ''==，132CD BC ==，∴131322A CD S '=⨯⨯=△．故选：A ．【点睛】本题考查直角三角形30度角的性质、勾股定理、等边三角形的判定和性质、旋转的性质等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．8．小明骑自行车上学，开始以正常速度匀速行驶，但行至途中自行车出了故障，只好停下来修车，车修好后，因怕耽误上课，加快了骑车速度．下面是小明距离学校的路程s 关于行驶时间t 的函数图象，那么符合小明行驶情况的图象大致是（）A ．B ．C ．D ．8.D【分析】根据函数图象与因变量和自变量的关系判断选项即可．【解析】根据题意，小明距离学校的路程s 关于行驶时间t 的函数图象应该分为三段：第一段随着时间的增加，路程s 逐渐减小；第二段小明停下修车，路程s 随着时间的增加没有发生变化；第三段小明加速行驶，随着时间的增加，路程s 减小的更快，所以只有D 选项符合题意，故选：D ．【点睛】本题考查函数的图象，熟练掌握函数的图象与因变量和自变量的变化关系是解答的关键．9．如图，AB 为O 的直径．弦CD AB ⊥于点E ，5OC cm =，8CD cm =，则BE 的值为（）A ．2cmB ．3cmC ．5cmD ．8cm9.A【分析】根据垂径定理得出4CE DE ==cm ，根据勾股定理得出222OC CE OE =+，代入求出答案即可．【解析】AB 是O 的直径，5OB OC ∴==（厘米），弦CD AB ⊥，4CE DE ∴==（厘米），在Rt OCE ∆中，5OC =（厘米），22543OE ∴=-=（厘米），532BE OB OE ∴=-=-=（厘米）．故选：A ．【点睛】本题考查了勾股定理和垂径定理，能熟记垂直于弦的直径平分这条弦是解此题的关键．10．如图，在正方形ABCD 中，O 是对角线AC ，BD 的交点．过点O 作OE OF ⊥，分别交AB ，BC 于点E ，F ．若3AE =，1CF =，则EF =（）A ．2B 10C ．4D ．2210.B【分析】本题考查正方形的性质，证明()ASA BOE COF ≌，得到1BE CF ==，继而得到3BF AE ==，最后在Rt BEF △中，利用勾股定理可得EF 的值．掌握正方形的性质及勾股定理是解题的关键．【解析】∵四边形ABCD 是正方形，3AE =，1CF =，∴AB BC =，OB OC =，90BOC ∠=︒，90ABC ∠=︒，45OBE OCF ∠=∠=︒，∵OE OF ⊥，∴90EOF BOC ∠=︒=∠，∴EOB FOC ∠=∠，在BOE △和COF 中，OBE OCF OB OCEOB FOC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA BOE COF ≌，∴1BE CF ==，∴3BF BC CF AB BE AE =-=-==，在Rt BEF △中，3BF =，1BE =，∴22221310EF BE BF =+=+=．故选：B ．第Ⅱ卷二、填空题（本大题共6个小题，每小题3分，共18分）11．因式分解：236m m -=．11.()32m m -【分析】提取公因式3m 即可．【解析】()23632.m m m m -=-故答案为：()32m m -【点睛】本题考查的是利用提公因式分解因式，掌握“公因式的确定”是解本题的关键．12．有一个圆形飞镖盘，上面画有五个圆，半径由小到大依次为2cm 4cm 6cm 、、、8cm 10cm 、，如图所示，投中镖盘时，飞镖落在阴影部分的概率为．12.35/0.6【分析】本题考查了概率，掌握相关知识并熟练使用是解题的关键．根据概率的定义，分别求出阴影部分的面积和大圆的面积，它们的比值就是所求．【解析】∵()2224cm S ππ=⨯=小阴影，()()2226420cm S ππ=⨯-=中阴影，()()22210836cm S ππ=⨯-=大阴影，()2210100cm S ππ=⨯=大圆，∴飞镖落在阴影部分的概率4203631005ππππ++==．故答案为：35．13．如图，直线4y x =-+与双曲线=y x交于A B ，两点，若AOB △的面积为4，则k 的值为．13.3【分析】根据直线4y x =-+与双曲线=ky x关于直线=y x 对称，得出AOC BOD ≌，求得2AOC S = ，根据三角形面积求得点A 的坐标，代入一次函数求得纵坐标，即可求解．【解析】如图，设4y x =-+与y 轴交于点C ，与x 轴交于点D ，∵直线4y x =-+与双曲线=ky x关于直线=y x 对称，∴AOC BOD ≌，由4y x =-+，令=0x ，得=4y ，令=0y 得=4x ，∴(0,4),(4,0)C D ,∴14482COD S ∆=⨯⨯=，∵AOB △的面积是4，∴()18422AOC S =-= ，∴1422A x ⨯⨯=，解得1A x =，代入4y x =-+得，43y x =-+=，∴(1,3)A ，∴133k =⨯=，∴k 的值为3，故答案为：3．【点睛】本题是反比例函数与一次函数的交点问题，考查了函数的对称性，三角形的面积，一次函数图象上点的坐标特征，求得A 的坐标是解题的关键．14．将一张长方形纸条ABCD 沿EF 折叠，点B ，A 分别落在B '，A '位置上，FB '与AD 的交点为G ．若∠DGF =110°，则∠FEG 的度数为．14.55°/55度【分析】根据平行的性质可知∠DGF=∠GFB，再根据翻折的性质可知∠BFE=∠EFG，即可求解．【解析】∵四边形ABCD是长方形，∴AD BC∥，∴∠GFB=∠DGF，∵∠DGF=110°，∴∠GFB=∠DGF=110°，∵根据翻折的性质有∠BFE=∠EFG，∴∠BFE=∠EFG=12∠GFB，∴∠FEG=1110552⨯=o o，故答案为：55°．【点睛】本题考查了平行的性质、矩形的性质以及翻折的性质，掌握平行的性质是解答本题的关键．15．如图，MN是半圆O的直径，K是MN延长线上一点，直线KP交半圆于点Q，P．若20K∠=︒，40PMQ∠=︒，则MQP∠=．15.35°【分析】连接PO、QO，根据圆周角定理，得∠POQ=2∠PMQ=80°，则∠OPQ=∠OQP=50°，则∠POM=70°，再根据圆周角定理即可求解．【解析】连接PO、QO．根据圆周角定理，得∠POQ=2∠PMQ=80°，又OP =OQ ，则∠OPQ =∠OQP =50°，则∠POM =∠K +∠OPK =70°，所以∠PQM =12∠POM =35°．故答案为：35°．【点睛】此题综合运用了圆周角定理，等腰三角形的性质，三角形的外角的性质，难度适中．16．如图，ABC ∆的顶点都在正方形网格纸的格点上，则sin C =．16.31010【分析】连接AD ，利用勾股定理的逆定理先证明ACD ∆是直角三角形，从而可得90ADC ∠=︒，然后在Rt ACD ∆中，利用锐角三角函数的定义进行计算即可解答．【解析】如图：连接AD ，由题意得：2221750AC =+=，222125CD =+=，2226345AD =+=，∴222AD CD AC +=，∴ACD ∆是直角三角形，∴90ADC ∠=︒，在Rt ACD ∆中，35AD =，52AC =，∴35310sin 1052AD C AC ===，故答案为：31010．【点睛】本题考查了解直角三角形，勾股定理的逆定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．三、解答题（本大题共8个小题，共52分．解答应写出文字说明，证明过程或演算步骤）17．（4分）计算：2023221(1)|13()231--+--．【解析】2023221(1)|13|()231--+-----=()131314-+--+-=131314-+----=7-【点睛】本题主要考查了实数的运算，熟练掌握运算法则是解答本题的关键．18．（5分）为提高病人免疫力，某医院精选甲、乙两种食物为确诊病人配制营养餐，两种食物中的蛋白质含量和铁质含量如表．如果病人每餐需要35单位蛋白质和40单位铁质，那么每份营养餐中，甲、乙两种食物各需多少克？每克甲种食物每克乙种食物其中所含蛋白质0.5单位0.7单位其中所含铁质1单位0.4单位【解析】设甲、乙两种食物各需x 克、y 克，则0.50.7350.440x y x y +=⎧⎨+=⎩，解得2830x y =⎧⎨=⎩.答：每份营养餐中，甲、乙两种食物分别要28，30克．【点睛】本题考查了二元一次方程组的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．19．（6分）如图，AM BN ∥，AC 平分BAM ∠，交BN 于点C ，过点B 作BD AC ⊥，交AM 于点D ，垂足为O ，连接CD ，求证：四边形ABCD是菱形．【解析】证明：∵AC 平分BAM ∠，AM BN ∥，∴12∠=∠，23∠∠=．∴13∠=∠．∴BA BC =．又∵BD AC ⊥于点O ，∴OA OC =．在AOD △和COB △中，23OA OC AOD COB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()AOD COB ASA ≌．∴OD OB =．∴四边形ABCD 是平行四边形．又∵BA BC =，∴平行四边形ABCD 是菱形．【点睛】本题主要考查了菱形的判定，涉及平行四边形的判定和性质，全等三角形的判定和性质，角平分线的性质，平行线的性质等知识，熟练掌握菱形的判定方法是解题的关键．20．（6分）某校九年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B 、E 两组发言的人数比为10:3，请结合图中相关数据回答下列问题：（1）A组有人，C组有人，E组有人，并补全直方图；（2）该年级共有学生600人，请估计全年级在这天发言次数不少于20的人数；（3）已知A组发言的学生中恰有一位女生，E组发言的学生中恰有两位男生，现从A组与E组中分别抽一位学生写报告，求所抽的两位学生至多有一位男生的概率．【解析】试题分析：（1）根据B、E两组发言的人数比为10:3，即可求得B组发言人数的百分比，从而可以求得抽取的总人数，即可求得结果；（2）先求得发言次数不少于20的人数所占的百分比，再乘以600即可得到结果；（3）先列树状图表示出所有等可能的情况，再根据概率公式求解即可.（1）∵B、E两组发言的人数比为10:3，E组发言人数的百分比为6%∴B组发言人数的百分比为20%∴B组发言的人数=10÷20%=50人∴A组有50×4%=2人，C组有50×40%=20人，E组有50×6%=3人（2）由题意得（人）答：全年级在这天发言次数不少于20的人数为60人；（3）列树状图：共有6六种等可能情况，符合至多有一位男生的情况有4种因此P （至多有一位男生）4263==.21．（6分）电力公司在高山上建设如图1所示的输电铁塔，其示意图如图2所示，铁塔A 沿着坡面到山脚的距离200m AC =，铁塔B 沿着坡面到山脚的距离60m BD =，坡面AC 与山脚水平线CD 的夹角140ACD ∠=︒，坡面BD 与山脚水平线CD 的夹角120BDC ∠=︒．(1)求铁塔A 到山脚水平线CD 的距离；(2)若从铁塔A 看铁塔B 的俯角为10°，求铁塔A 与铁塔B 的距离AB 的长（结果精确到1m ）．（参考数据：sin 400.643︒≈，cos 400.766︒≈，tan 400.839︒≈，sin100.174︒≈，cos100.985︒≈，tan100.176︒≈，3 1.732≈）【解析】（1）解：如下图，过A 作AE CD ⊥交DC 延长线于E ，90AEC ∴∠=︒，140ACD ∠=︒，18014040ACE ∴∠=︒-︒=︒，200m AC =Q ．∴在Rt ACE 中，sin AE ACE AC∠=，sin 200sin 402000.643128.6m AE AC ACE ∴=⋅∠=︒≈⨯=．答：铁塔A 到山脚水平线CD 的距离约为128.6m ．（2）如上图，过B 作BF CD ⊥交CD 的延长线于F ，过A 作AH CD ∥交FB 的延长线于H ，则90AEC BFE H ∠=∠=∠=︒，∴四边形AEFH 为矩形，128.6m HF AE ∴==．120BDC ∠=︒ ，60BDF ∴∠=︒；60m BD = ，∴在Rt BDF △中，sin BF BDF BD∠=，3sin 60sin 606030330 1.73251.96m 2BF BD BDF ∴=⋅∠=⨯≈︒=⨯=⨯=，128.651.9676.64m BH HF BF ∴=-=-=．在Rt ABH △中，sin BH BAH AB ∠=，76.6476.64440m sin sin100.174BH BA AB H ∴==≈≈∠︒．答：铁塔A 到铁塔B 的距离AB 的长约为440m ．22．（7分）如图，直线MN 交⊙O 于A ，B 两点，AC 是直径，AD 平分∠CAM 交⊙O 于D ，过点D 作DE ⊥MN 于点E ．(1)求证：DE 是⊙O 的切线；(2)若DE ＝4cm ，AE ＝3cm ，求⊙O 的半径．【解析】（1）证明：连接OD ，∵OA＝OD，∴∠1＝∠2，∵AD平分∠CAM，∴∠2＝∠3，∴∠1＝∠3，∴MN∥OD，∵DE⊥MN，∴DE⊥OD，∴DE是⊙O的切线；（2）解：连接CD，∵AC是⊙O的直径，∴∠ADC＝90°，43+＝5，∴AD＝22+＝22DE AE∵DE⊥MN，∴∠AED＝90°，∴∠ADC＝∠AED，又∵∠2＝∠3，∴△ADC ∽△AED ，∴AC AD AD AE =，即553AC =，∴AC ＝253，∴OA ＝12AC ＝256，即⊙O 的半径为256cm ．【点睛】本题考查了切线的判定、等腰三角形的性质、平行线的判定与性质、相似三角形的判定与性质、勾股定理等知识；本题综合性强，有一定难度．23．（8分）如图，已知抛物线22y ax bx =++()0a <与y 轴交于点C ，与x 轴交于()1,0A -，()2,0B 两点．(1)求抛物线的函数表达式；(2)若点D 是第二象限抛物线上的动点，DE x 轴，交直线BC 于点E ，点G 在x 轴上，点F 在坐标平面内，是否存在点D ，使以D ，E ，F ，G 为顶点的四边形是正方形？若存在，求点D 的坐标；若不存在，请说明理由．【解析】（1）将()1,0A -，()2,0B 代入22y ax bx =++()0a <中，得204220a b a b -+=⎧⎨++=⎩，解得：11a b =-⎧⎨=⎩∴抛物线的函数表达式为22y x x =-++．（2）由题意和22y x x =-++可得()0,2C ，()2,0B ，可设直线BC 的函数表达式为：2y kx =+，将()2,0B 代入得：220k +=，∴1k =-，∴直线BC 的函数表达式为2y x =-+.设()2,2D t t t -++（0t <），分两种情况：①当DE 为边时，如图1，四边形DEFG 是正方形（点G 、F 可互换位置）.则22DG D t E t ==-++，故E 的纵坐标与D 的纵坐标相等为22t t -++，将22y t t =-++代入2y x =-+中，可得E 的横坐标为2t t -，则点E 的坐标为()22,2t t t t --++，2t t tDE =--∴DE EF =，即222t t t t t --=-++，解得2t =（0t <，要舍）或12t =-，∴点D 的坐标为15,24⎛⎫- ⎪⎝⎭．②当DE 为对角线时，如图2，连接FG ，过点D 作DH x ⊥轴于点H ，DE HG ∥，DH FG ∥，易得2DE FG DH ==，则()2222224DE t t t t =-++=-++，则E 的纵坐标为2224t t t -+++，∴点E 的坐标为()22224,2t t t t t -+++-++．点E 在直线2y x =-+上，∴2222342t t t t -++=--+，解得23t =-或2（0t <，要舍），∴点D 的坐标为28,39⎛⎫- ⎪⎝⎭．综上可得：存在点D ，使以D ，E ，F ，G 为顶点的四边形是正方形，点D 的坐标为15,24⎛⎫- ⎪⎝⎭或28,39⎛⎫- ⎪⎝⎭．24．（10分）如图1，在正方形ABCD 中，E ，F 分别在边AB BC ，上，且CE DF ⊥于点O ．(1)试猜想线段CE 与DF 的数量关系为______；(2)数学小组的同学在此基础上进行了深入的探究：①如图2，在正方形ABCD 中，若点E ，F ，G ，H 分别在边AB BC CD DA ，，，上，且EG FH ⊥于点O ，求证：EG FH =；②如图3，将①中的条件“在正方形ABCD 中”改为“在矩形ABCD 中，AB a =，2BC a =”，其他条件不变，试推理线段EG 与FH 的数量关系；③如图4，在四边形ABCD 中，90ABC ∠=︒，60BCD ∠=︒，6AB BC CD ===，点M 为AB 的三等分点，连接CM ，过点D 作DN CM ⊥，垂足为点O ，直接写出线段DN 的长．【解析】（1）证明：∵四边形ABCD 是正方形，90,B DCF BC CD ︒∴∠=∠==，90BCE DCE ∴∠+∠=︒，CE DF ⊥ ，90CPD ︒∴∠=，90CDF DCE ∴∠+∠=︒，BCE CDF ∴∠=∠，()CBE DCF ASA ∴ ≌，CE DF ∴=．（2）①证明：过点H 作HN BC ⊥交于N ，过点G 作GM BA ⊥交于M ，∵四边形ABCD 是正方形，BC CD∴= 四边形BCGM 为矩形，四边形CDHN 为矩形，MG BC ∴=,HN CD=∴MG HN =，∵HF EG ⊥，∴90MGE OPG NHF OPG ∠+∠=∠+∠=︒，∴MGE NHF ∠=∠，∴()HFN GEM ASA ≌，∴HF EG =；②解：2EG FH =；理由：过点H 作HQ BC ⊥交于Q ，过点G 作GP ⊥AB 交于P ，由①可得，QHF PGE ∠=∠，QHF PGE ∴V V ∽，HF HQ GE PG∴=，,2AB a BC a ==Q ，2,PG a HQ a ∴==，122HF a GE a ∴==，2EG FH ∴=；③解：如图3，过点D 作DS BC ⊥于S ，90DSN DSC B ∴∠=∠=∠=︒，60,6DCS CD ∠=︒=Q ，3sin 60332DS CD CD ∴=⋅︒==， 点M 是AB 的三等分点，6AB =，2BM ∴=或4BM =，6BC = ，22210CM BC BM ∴=+=或213，DN CM ⊥Q ，BM DS ∴∥，BMC DJM ∴∠=∠，90DJM NDS NDS DNS ∠+∠=∠+∠=︒Q ，DNS DJM ∴∠=∠，BMC DJM DNS ∴∠=∠=∠，∴BCM SDN ∽，CM BC DN SD ∴=，210633DN ∴=，或213633DN =，解得30DN 或39．【点睛】本题考查了四边形的综合题，正方形的性质，矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，正确地作出辅助线是解题的关键．。

中考数学压轴题专项训练十套(含答案)

中考数学压轴题专项训练十套(含答案)

中考数学压轴题专项训练十套(含答案)中考数学压轴题专项训练（一）做题时间：_______至_______ 家长签字：_____________ 共__________分钟日期：_____月_____日三、解答题23.（11分）如图，在直角梯形 $OABC$ 中，$AB\parallel OC$，$BC\perp x$ 轴于点 $C$，$A(1,1)$，$B(3,1)$．动点$P$ 从点 $O$ 出发，沿 $x$ 轴正方向以每秒 $1$ 个单位长度的速度移动．过点 $P$ 作 $PQ\perp OA$，垂足为 $Q$．设点$P$ 移动的时间为 $t$ 秒（$0<t<4$），$\triangle OPQ$ 与直角梯形 $OABC$ 重叠部分的面积为 $S$．1）求经过 $O$，$A$，$B$ 三点的抛物线解析式．2）求 $S$ 与 $t$ 的函数关系式．3）将 $\triangle OPQ$ 绕着点 $P$ 顺时针旋转$90^{\circ}$，是否存在 $t$，使得 $\triangle OPQ$ 的顶点$O$ 或 $Q$ 在抛物线上？若存在，直接写出 $t$ 的值；若不存在，请说明理由．解析：1）由题意可知，经过 $O$，$A$，$B$ 三点的抛物线为$y=ax^{2}+bx+c$，代入三点的坐标可得：begin{cases}a+b+c=1\\4a+2b+c=1\\9a+3b+c=1end{cases}$解得 $a=-\dfrac{1}{4}$，$b=\dfrac{5}{4}$，$c=\dfrac{1}{2}$，即经过 $O$，$A$，$B$ 三点的抛物线解析式为 $y=-\dfrac{1}{4}x^{2}+\dfrac{5}{4}x+\dfrac{1}{2}$．2）设 $\triangle OPQ$ 的高为 $h$，则 $\triangle OPQ$ 的面积为 $\dfrac{1}{2}xh$，其中 $x=OP=t$．由于 $\triangle OPQ$ 与直角梯形 $OABC$ 重叠部分的面积为 $S$，所以$S=\dfrac{1}{2}(AB+BC)h=\dfrac{1}{2}(3+2t)h$．又因为 $P$ 沿 $x$ 轴正方向以每秒 $1$ 个单位长度的速度移动，所以 $h$ 的变化率为$\dfrac{\mathrm{d}h}{\mathrm{d}t}=-1$，即 $h=-t+4$．综上所述，$S=\dfrac{1}{2}(3+2t)(-t+4)=-t^{2}+5t-6$，即$S$ 与 $t$ 的函数关系式为 $S=-t^{2}+5t-6$．3）将 $\triangle OPQ$ 绕着点 $P$ 顺时针旋转$90^{\circ}$，则 $\triangle OPQ$ 变为 $\triangle OP'Q'$，其中$P'$，$Q'$ 分别为 $P$，$Q$ 绕着点 $P$ 顺时针旋转$90^{\circ}$ 后的点．易知 $\triangle OP'Q'$ 的顶点为 $O'$，坐标为 $(1+t,1)$．将 $O'$ 的坐标代入抛物线的解析式中，得到 $y=-\dfrac{1}{4}(1+t)^{2}+\dfrac{5}{4}(1+t)+\dfrac{1}{2}$．令 $y=0$，解得 $t=2\pm\sqrt{3}$．由于 $0<t<4$，所以 $t=2+\sqrt{3}$，即存在 $t$，使得$\triangle OPQ$ 的顶点 $O$ 在抛物线上．答案：（1）$y=-\dfrac{1}{4}x^{2}+\dfrac{5}{4}x+\dfrac{1}{2}$；（2）$S=-t^{2}+5t-6$；（3）$t=2+\sqrt{3}$．2）正方形以每秒5个单位长度的速度沿射线AB下滑，直至顶点D落在x轴上时停止。

2024中考数学(人教版)押题卷 (470)

2024中考数学(人教版)押题卷 (470)

一、单选题1. 如图，已知直线PQ⊥MN于点O，点A，B分别在MN，PQ上，OA=1，OB=2，在直线MN或直线PQ上找一点C，使△ABC是等腰三角形，则这样的C点有（）A．3 个B．4 个C．7 个D．8 个2. 如图，已知点A（3，4），点B为直线x＝﹣2上的动点，点C（x，0）且﹣2＜x＜3，BC⊥AC垂足为点C，连接AB．若AB与y轴正半轴的所夹锐角为α，当tanα的值最大时x的值为（ ）A．B．C．1D．3. 元旦前夕，某商店购进某种特色商品100件，按进价每件加价30%作为定价，可是总卖不出去，后来每件按定价降价20%，以每件104元出售，终于在元旦前全部售出，则这批商品在销售过程中的盈亏情况是（）A．亏40元B．赚400元C．亏400元D．不亏不赚4. 小明调查了涟水县1月份一周的最低气温（单位：℃），分别是：，0，3，，，0，2，其中0℃以上（不含0℃）出现的频数是（）A．2B．3C．4D．55. 三地位于同一条笔直的直线上，B在之间，甲、乙两人分别从两地同时出发赶往C地，甲、乙两人距C地的距离s（单位：m）与甲运动的时间t（单位：s）之间的关系如图所示．根据图象判断下列说法错误的是（）A．两地之间的距离为B．甲的速度比乙快C．甲、乙两人相遇的时间为D．时，甲、乙两人之间的距离为6. 如图是一个正方体展开图，把展开图折叠成正方体后，“你”字一面相对面上的字是（）A．我B．中C．国D．梦二、多选题7. 估计的值应在（ ）A ．4和5之间B ．3和4之间C ．2和3之间D ．1和2之间8. 如图是一圆锥的侧面展开图，其弧长为，则该圆锥的全面积为A ．60πB ．85πC ．95πD ．169π9. 如图，△ABC 是等腰直角三角形，AC=BC=2，以斜边AB 上的点O 为圆心的圆分别与AC 、BC 相切于点D 、E ，与AB 分别相交于点G 、H ，且DG 的延长线与CB 的延长线交于点F ，分析下列四个结论：①HG=2；②BG=BF ；③AH=BG=；④CF=.其中正确的结论个数有( )A ．1个B ．2个C ．3个D ．4个10. 关于x 的方程无解，则a 的值为（ ）A ．1B ．3C ．1或D ．1或311. 在下列图形中，只是中心对称图形不是轴对称图形的是（ ）A．B．C．D．12. 下列说法中，正确的是（ ）A ．若，则B ．A 、B 、C 三点在数轴上对应的数分别是、6、x，若相邻两点的距离相等，则C ．若代数式的值与x 无关，则该代数式值为2021D ．若，则的值为13. 已知直线l 外一点P 到直线l 上两点A ，B 的距离分别为6和7，则点P 到直线l 的距离可能为（ ）A ．4B ．5C ．6D ．714. 有这样一列数：1，1，2，3，5，8，13，21，…即第一项，第二项，第三项，第四项，…可以发现从第三项开始，每一项都是它前面两项的和，该数列称为斐波那契数列．则下列关于斐波那契数列说法正确的是A．B．是偶数C．D．15. 表中所列、的7对值是二次函数图象上的点所对应的坐标，其中611116根据表中提供约信息，以下4个判断中正确的是（ ）三、填空题A．B．C ．当时，的值是D．16. 在某市举办的端午节龙舟比赛中，甲、乙两队在比赛时的路程与时间之间的函数关系图象如图所示，根据图象得到下列结论，你认为正确的是（）A．这次比赛的全程是B ．经过乙队追上了甲队C ．甲队速度大于乙队速度D．两队相遇时乙队速度是17. △ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，如果a 2+b 2=c 2，那么下列结论不正确的是（ ）A ．bcosB =cB ．csinA =aC ．atanA =bD ．tanB =18. 下列说法不正确的是（ ）A ．相切两圆的连心线经过切点B ．长度相等的两条弧是等弧C ．平分弦的直径垂直于弦D ．相等的圆心角所对的弦相等19. 下列尺规作图能得到平行线的是（ ）A．B．C．D．20.若，则________．21. 如图，已知网格中每个小正方形的边长为1，则菱形ABCD 的面积为_____．22.计算的结果等于______．23. 的小数部分是_________．24.如图，四边形为平行四边形，延长至，使，连接，，，若添加一个条件后，使四边形成为矩形，则添加的条件是_____．2024中考数学(人教版)押题卷四、解答题五、解答题25.已知如图：中，，以为直径的圆交于，若，则阴影部分的面积为__________．26. 如图，已知圆的半径为R ，正方形的边长为a ．（1）表示出阴影部分的面积________；（2）当，阴影部分面积________．27.在中，，，则此三角形外接圆半径为________．28. 中国古代数学家杨辉的《田亩比数乘除减法》中记载：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步？翻译成数学问题是：一块矩形田地的面积为864平方步，它的宽比长少12步，问它的长与宽各多少步？利用方程思想，设宽为x 步，则依题意列方程为____________．29. 已知，则的值_____．30.计算：31. 计算：|﹣2|+（π﹣1）0×（﹣1）2012+（）﹣3．32. 计算：（﹣1）11﹣8÷（﹣2）＋4×|﹣5|．33. 婷婷对“化简：”的解答过程如下：解：原式．试问婷婷的解答过程是否正确？若正确，请再写出一种解答过程：若有错误，请写出正确的解答过程．34. ①计算：；②解方程：．35. 王老师对试卷讲评课中学生参与的深度与广度进行评价调查，每位学生最终评价结果为主动质疑、独立思考、专注听讲、讲解题目四项中的一项评价组随机抽取了若干名学生的参与情况，绘制成如图所示的统计图（均不完整），请根据图中所给信息解答下列问题：（1）在这次评价中，一共抽查了 名学生；（2）在扇形统计图中，项目“主动质疑”所在扇形的圆心角度数为 度；（3）请将条形图补充完整；（4）如果全校学生有2800名，那么在试卷讲评课中，“独立思考”的学生约有多少人？36. 如图，在平面直角坐标系中，，，．(1)画出关于x轴的对称图形；(2)在坐标系中，找出一点，使与关于直线对称，直接写出点的坐标．37. 如图，在中，．（1）尺规作图：按要求完成下列作图，不写做法，保留作图痕迹，并标明字母．作的平分线交于点F，连接、；（2）在（1）的条件下，若，求的度数．38. 如图，在平面直角坐标系中，的顶点坐标分别为，，．将绕点O逆时针旋转得到，点A旋转后的对应点为．(1)画出旋转后的图形，并写出的坐标；(2)在（1）的条件下，求点B经过的路径长（结果保留）．六、解答题七、解答题39. 如图：在平面直角坐标系中，三角形ABC 的顶点坐标分别是A(1，1)；B(2，﹣1)；C(4，3)，将三角形ABC 向左平移2个单位长度，再向上平移3个单位长度后得三角形A 1B 1C 1．（1）画出三角形A 1B 1C 1；（2）分别写出A 1、B 1、C 1的坐标；（3）求三角形A 1B 1C 1的面积．40. 某超市用500元购进了甲、乙两种商品，其中甲种商品购进14件，乙种商品购进18件，已知乙种商品每件进价比甲种商品每件进价多10元．(1)求甲、乙两种商品每件进价；(2)若甲种商品售价为15元/件，乙种商品售价为35元/件．求该超市甲、乙两种商品全部销售完后的利润（注：利润售价进价）．41. 某商场经销A 玩具，购进时的单价是60元．根据市场调查，销售单价定为80元时，每天可以卖出200件，而销售单价每降低1元，每天就可多售出20件．求销售单价定为多少时，顾客得到优惠，且该商场每天销售A 玩具可以获利4000元．42. 如图，在一条水平的码头上有两处灯塔A 和B ，在灯塔处测得某一渔船位于北偏西方向的处，当渔船沿着正北方向前进到达处时，在灯塔处测得处位于西北方向．已知，求处到码头的距离．43. 某工厂1月份的产值是25万元，计划3月份的产值达到36万元，那么这家工厂2月、3月这两个月产值的月平均的增长率是多少？44. 我国古代数学家赵爽利用影子对物体进行测量的方法，至今仍有借鉴意义．如图，身高1.5米的小王晚上在路灯灯柱下散步，他想通过测量自己的影长来估计路灯灯泡的高度，具体做法如下：先从路灯底部沿方向走20步到处，发现自己的影子端点落在点处，作好记号后，从点沿方向走4步恰好到达点处，此时他影子的端点在点处，已知在同一水平线上，路灯的灯泡在上，，小王的步间距保持一致．(1)请在图中画出灯泡和影子端点的位置；(2)估计灯泡的高，并求出影长的步数．45. 如图，直线EF 分别与直线AB ，CD 交于点E ，F ．EM 平分∠BEF ，FN 平分∠CFE ，且EM FN．求证：．请在下面的证明过程中的横线处填写正确的结论或理由．证明：∵EM∥FN （已知），∴∠FEM=∠EFN ( )．∵EM平分∠BEF（已知），∴∠FEM= ∠FEB（角平分线定义）．又∵FN平分∠CFE（已知），∴∠EFN= （角平分线定义）．∴∠FEB =（等量代换），∴AB CD ( )46. 如图，在四边形ABCD中，AD⊥CD，CD=BC，AB=AC．求证：∠1=∠BAC．47. 在正方形中，点，，分别在边，，上（点，，不与正方形的顶点重合），，相交于点，且．（1）猜想与的数量关系并证明：（2）证明：；（3）若，，请直接写出点到直线的距离．48. 如图，四边形木架．(1)加上木条后，木架不易变形，其中蕴含的数学道理是____________；(2)如，平分，求证：．49. 【感受与猜想】(1)如图，四边形和四边形均为正方形，点正好落在对角线上．试猜想与的数量关系：__．八、解答题【探究与证明】(2)如图，四边形和四边形均为正方形，正方形绕点顺时针旋转角()，连结，．()中的结论是否还成立，若成立，请给出证明．【拓展与延伸】(3)如图3，在平面直角坐标系中，直线分别交轴，轴于，两点，点为线段上一点，以为底边向下作等腰直角三角形．①若，求点的坐标．②若点落在边的中点处，与交于点，已知，求的长．50. 如图，点A 在第一象限内，轴于点B ，反比例函数的图象分别交于点C ，D ．已知点C 的坐标为．(1)求k 的值及点D 的坐标．(2)已知点P 在该反比例函数图象上，且在的内部（包括边界），直接写出点P 的横坐标x 的取值范围．51. 已知a 、b 为有理数，现规定一种新运算※，满足，例如：．(1)求的值：(2)求的值．52. 如图，直线AB 是某天然气公司的主输气管道，点C 、D 是在AB 异侧的两个小区，现在主输气管道上寻找支管道连接点，铺设管道向两个小区输气．有以下两个方案：方案一：只取一个连接点P ，使得向两个小区铺设的支管道总长度最短；方案二：取两个连接点M 和N ，使得点M 到C 小区铺设的支管道最短，使得点N 到D 小区铺设的管道最短．（1）在图中标出点P 、M 、N 的位置，保留画图痕迹；（2）设方案一中铺设的支管道总长度为l 1，方案二中铺设的支管道总长度为l 2，则l 1 与l 2的大小关系为：l 1 l 2（填“＞”，“＜”或“＝”）．53. +cos30°54. 已知 是直线l 和双曲线的交点．九、判断题(1)求m 的值．(2)若直线l 分别和x 轴、y 轴交于E 、F 两点，且点A 是的中点，试确定直线l 的解析式．(3)在双曲线上另取一点B ，过B 作轴于K ．问：在y 轴上是否存在点P ，使得？若存在，请求出点P 的坐标；若不存在，请说明理由．55.一个几何体，从正面和左面看都是 ，这个几何体至少有4个小正方体．( )56. 中心对称是指一个图形之间的关系． ( )57. 平行四边形有2条对称轴． _____（判断对错）58. 所有的负数和0一定都比正数小．( )59. 一个等腰三角形的两条边的长度分别为厘米和厘米，则这个三角形的周长为厘米． _____（判断对错）。

2024年浙江中考数学最后一卷终极押题卷及答案

2024年浙江中考数学最后一卷终极押题卷及答案

2024年浙江中考最后一卷数学注意事项：1．本试卷共有三个大题，分为单项选择题、填空题、解答题，满分120分，考试时间100分钟。

2．本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上，答在试卷上的答案无效。

一、单选题（本大题共有10小题，每小题3分，共30分）1．下列各数中最大的数是（）A．5−B．0 C．1−D2．下面计算正确的是（）A．3a﹣2a＝1 B．2a2+4a2＝6a4C．（x3）2＝x5D．x8÷x2＝x63．今年春节电影《热辣滚烫》《飞驰人生2》《熊出没•逆转时空》《第二十条》在网络上持续引发热议，根据国家电影局2月18日发布数据，我国2024年春节档电影票房达80.16亿元，创造了新的春节档票房纪录．其中数据80.16亿用科学记数法表示为（）A．8×80.16108.01610×B．9C．10×80.1610×D．100.8016104．下列立体图形中，主视图是三角形的是（）A．B．C．D．5．在数轴上表示不等式x﹣2≤0的解集，正确的是（）A．B．C ．D ．6．随着自动驾驶技术的不断发展，某知名汽车制造公司近期对研发的自动驾驶汽车进行了一次大规模的路测，有45辆自动驾驶汽车参与了这次测试．测试结束后，技术部门对每辆汽车的性能进行评估（车辆的自动驾驶技术、安全性、反应速度等综合表现），得分如下：得分（分） 75 80 85 90车辆（辆） 5 16 14 10得分的中位数和众数分别是（ ）A ．80，80B ．82.5，80C ．80，85D ．85，807．如图，线段CD 是O 的直径，CD AB ⊥于点E ，若8AB =，3OE =，则CE 的长是（ ）A ．8B ．7C ．6D ．58．《九章算术》中曾记载：“今有牛五羊二，直金十两；牛二羊五，直金八两．问牛、羊各直金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？若设每头牛值金x 两，每只羊值金y 两，则可列方程组为（ ）A ．5210258x y x y += +=B ．2510528x y x y += +=C ．51058x y x y += +=D ．21028x y x y += +=9．二次函数2y =的图象如图所示，点O 为坐标原点，点A 在y 轴的正半轴上，点B ，C 在函数图象上，四边形OBAC 为菱形，且120ABO ∠=°，则点C 的坐标为（ ）A ．14 −B ．14 −C ． −D ．(− 10．如图，四边形ABCD 是一张矩形纸片．折叠该矩形纸片，使AB 边落在AD 边上，点B 的对应点为点F ，折痕为AE ，展平后连接EF ；继续折叠该纸片，使FD 落在FE 上，点D 的对应点为点H ，折痕为FG ，展平后连接HG ．若矩形HECG ∽矩形ABCD ，1AD =，则CD 的长为（ ）．A ．0.5B 1−C D二、填空题（本大题共有6小题，每小题4分，共24分）11．因式分解： 34t t −=12．实现中国梦，必须弘扬中国精神．在如图所示除正面图案不同外，其余无差别的四张不透明卡片上分别写有“红船精神”、“长征精神”、“延安精神”、“特区精神”，将卡片置于暗箱摇匀后随机抽取一张，则所抽取卡片为“特区精神”的概率为 ．13x 的值可以是 ．（写出一个即可） 14．如图，《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕塑，掷铁饼者张开的双臂与肩宽可以近似看像一张拉满弦的弓，若弧长为2π3米，“弓”所在圆的半径1．2米，则“弓”所对的圆心角θ的度数为 ．15．如图，点A 为反比例函数(0,0)k y k x x=<<的图象上一点，AB x ⊥轴于点B ，点C 是y 轴正半轴上一点，连接BC ，AD BC ∥交y 轴于点D ，若0.5ABCD S =四边形，则k 的值为 ．16．如图，正方形ABCD 的边长为2，以AB 边上的动点O 为圆心，OB 为半径作圆，将AOD △沿OD 翻折至A OD ′ ，若O 过A OD ′ 一边上的中点，则O 的半径为 ．三、解答题（本大题共有8小题，共66分）（共66分）17．（本题6分）计算或化简：(1)()201253π− +−−+−； (2)()()()2m n n m m n +−−−．18．（本题6分）如图，在平面直角坐标系中，ABC 的顶点坐标分别为()2,4A ，()3,1B ，()5,3C ．(1)作ABC 关于y 轴对称的111A B C △；(2)将ABC 绕原点O 顺时针旋转90°，得到222A B C △，作出222A B C △并求点C 旋转到点2C 所经过的路径长．19．（本题6分）2023年全国教育工作会议提出要把开展读书活动作为一件大事来抓．引导学生爱该书．读好书，善读书，贵阳市某校为了推进这项工作，对全校学生一周内平均读书时间进行抽样调查．将调查结果的数据分成A 、B 、C 、D 、E 五个等级并绘制成表格和扇形统计图如下．等级 周平均读书时间t （单位：小时） 人数A01t ≤< 4 B12t ≤< a C23t ≤< 20 D34t ≤< 15 E 4t ≥5 每个等级人数扇形统计图(1)求统计图表中=a ______，m =______．(2)已知该校共有2800名学生，试估计该校每周读书时间至少3小时的人数为______．(3)请写出一条你对读书的建议．20．（本题8分）我国是世界上最早发明历法的国家之一，《周礼》中记载：垒土为圭，立木为表，测日影，正地中，定四时，如图1，圭是地面上一根水平标尺，指向正北，表是一根垂直于地面的杆，正午，表的日影（即表影）落在圭上，根据表影的长度可以测定节气．在一次数学活动课上，要制作一个圭表模型，如图2，地面上放置一根长2米的杆AB ，向正北方向画一条射线BC ，在BC 上取点D ，测得 1.5m BD =， 2.5m AD =．(1)判断：这个模型中AB 与BC 是否垂直．答：______（填“是”或“否”）；你的理由是：______．(2)利用这个圭表模型，测定某市冬至正午阳光与日影夹角30°，夏至正午阳光与日影夹角为60°，请求出这个模型中该市冬至与夏至的日影的长度差（结果保留根号）．21．（本题8分）如图，在矩形ABCD 中，沿EF 将矩形折叠，使A 、C 重合，AC 与EF 交于点H ．(1)求证：AE ＝AF ；(2)若AB ＝4，BC ＝8，求△ABE 的面积．22．（本题10分）我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售．按计划，20辆车都要装运，每辆汽车只能装运同一种脐橙．且必须装满，根据下表组织的信息，解答以下问题．脐橙品种A B C 每辆汽车运载量（吨） 6 5 4每吨脐橙获利（元） 1200 1600 1000(1)设转运A 种脐橙的车辆数为x ，转运B 种脐橙的车辆数为y ，求y 与x 的函数表达式；(2)如果转运每种脐橙的车辆数都不少于4，那么车辆的安排方案有几种？(3)若要使此次销售获利最大，应采用哪种安排方案？并求出此时最大利润的值．23．（本题10分）定义：平面直角坐标系xOy 中，当点N 在图形M 的内部，或在图形M 上，且点N 的横坐标和纵坐标相等时，则称点N 为图形M 的“梦之点”．(1)如图①，矩形ABCD 的顶点坐标分别是(1,2)A −，(1,1)B −−，(3,1)C −，(3,2)D ，在点1(2,2)P −−，2(0,0)P ，3(1,1)P ，4(2,2)P 中，是矩形ABCD “梦之点”的是________；(2)如图②，已知A 、B 是抛物线21922y x x =−++上的“梦之点”，点C 是抛物线的顶点： ①求出AC ，AB ，BC 三条线段的长度；②判断ABC 的形状，并说明理由．24．（本题12分）如图，ABC 内接于圆O ，AD 是ABC 的高线，9AD =，12CD =，tan 3ABD ∠=，连接OC ．(1)求证：ABC 是等腰三角形；(2)求证：BCO BAD ∠=∠；(3)若点E 是OC 上一动点，EF AB ∥交BC 于点F ．①若OEF 与ABD △相似，求EF 的长；②当OEF 的面积与CEF △的面积差最大时，直接写出此时CF 的长．2024年浙江中考最后一卷数学解析及参考答案一、单选题1．D【分析】此题考查了实数的大小比较法则：正数大于零，零大于负数，两个负数绝对值大的反而小，据此判断．【详解】∵510−<−<<故选：D ．2．D【分析】根据各个选项中的式子可以计算出正确的结果，本题得以解决．【详解】解：∵3a ﹣2a ＝a ，故选项A 错误；∵2a 2+4a 2＝6a 2，故选项B 错误；∵（x 3）2＝x 6，故选项C 错误；∵x 8÷x 2＝x 6，故选项D 正确；故选D ．【点睛】本题考查整式的混合运算，解答本题的关键是明确整式混合运算的计算方法．3．B【分析】此题考查科学记数法的表示方法．科学记数法的表示形式为10n a ×的形式，其中110a ≤<，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值10≥时，n 是正数；当原数的绝对值1<时，n 是负数．【详解】解：80.16亿98.01610×，故选：B ．4．B【分析】本题考查立体几何的三视图．根据题意，逐项判断即可．【详解】解：A.主视图为长方形，此项不符合题意；B.主视图为三角形，此项符合题意；C.主视图为圆，此项不符合题意；D.主视图为长方形，此项不符合题意．故选：B ．5．C【分析】先解不等式，求出解集，然后在数轴上表示出来．【详解】解：不等式x ﹣2≤0，得：2x ≤ ，把不等式的解集在数轴上表示出来为：．故选：C【点睛】本题主要考查了解不等式，并在数轴上表示解集，解题的关键是熟练掌握解不等式的步骤，不等式的解集在数轴表示时空心圈不包含该点，实心圈包含该点．6．D【分析】本题为统计题，考查众数与中位数的意义，根据众数的定义，找到该组数据中出现次数最多的数即为众数；根据中位数定义，将该组数据按从小到大依次排列，处于中间位置的两个数的平均数即为中位数．【详解】有45辆自动驾驶汽车参与了这次测试，45个分数，按大小顺序排列最中间的数据是第23个数：85，故得分的中位数是85（分），得80分的人数最多，有16人，故众数为80，故选D ．7．A【分析】本题考查了垂径定理和勾股定理的应用，根据垂径定理求出AE 的长是解此题的关键．连接OA ，根据垂径定理求出AE ，再根据勾股定理求出OA ，最后根据线段的和差求解即可．【详解】解：如图，连接OA ，线段CD 是O 的直径，CD AB ⊥于点E ，∴12AE AB =，8AB =， ∴4AE =，3OE =，∴5OA ，∴5OC OA ==，∴8CE OC OE =+=，故选：A ．8．A【分析】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是设每头牛、每只羊分别值金x 两、y 两，根据“5头牛，2只羊，值金10两；2头牛，5只羊，值金8两”列出方程组即可得答案．【详解】解：设每头牛值金x 两，每只羊值金y 两，则可列方程组为5210258x y x y += +=， 故选A ．9．B【分析】本题考查了菱形的性质、二次函数图象上点的坐标特征，根据二次函数图象上点的坐标性质得出BD 的长是解题关键．连接BC 交OA 于D ，如图，根据菱形的性质得BC OA ⊥，60OBD ∠=°，利用含30度的直角三角形三边的关系得OD =，设BD t =，则OD =，()B t ，利用二次函数图象上点的坐标特征得2=，得出14BD =，OD =C 点坐标． 【详解】解：连接BC 交OA 于D ，如图，四边形OBAC 为菱形，BC OA ，120ABO ∠=° ，60OBD ∴∠=°，OD ∴，设BD t =，则OD =，()B t ∴，把()B t 代入2y =,得2=，解得10t =（舍去）， 214t =，14BD ∴=，OD =故C 点坐标为：14 − ．故答案为：B ．10．C【分析】本题考查的是矩形的性质、翻折的性质及相似多边形性质，熟练应用矩形和相似多边形性质是解题关键，设CD x =，则()1,1EC x CG x x =-=--，根据两矩形相似求出即可．【详解】解：在矩形ABCD 中，设CD x =，则ABCD x ==，1AD BC ==， 由翻折得,90AB AF x AFE B BAF ==∠=∠=∠=︒，∴四边形ABEF 是正方形，同理，四边形DFHG 是正方形，,1BE AB x DF DG x ∴====-，()1,121CE x CG x x x ∴=-=--=-，矩形HECG ∽矩形ABCD ，EC CG BC CD∴=，即1211x x x --=，解得：x =，经检验，xCD ∴ 故选：C ．二、填空题11．()()22t t t +−【分析】本题考查了因式分解，先提取公因式，再利用公式法即可求解，熟练掌握提公因式法及公式法分解因式是解题的关键．【详解】解：()()()324422t t t t t t t −=−=+−，故答案为：()()22t t t +−．12．14/0.25 【分析】本题考查了概率公式的应用，用到的知识点为：概率所求情况数与总情况数之比．全部情况的总数是四种，符合条件的情况的是一种，二者的比值就是其发生的概率．【详解】由于概率为所求情况数与总情况数之比，而抽取卡片为“特区精神”的情况数只有一种，从暗箱随机抽取一张的情况数为四种，故抽取卡片为“特区精神”的概率为14， 故答案为14． 13．0（答案不唯一）【分析】本题主要考查了二次根式有意义的条件，分式有意义的条件，根据二次根式有意义的条件的条件是被开方数大于等于0，分式有意义的条件是分母不为0进行求解即可．∴10x −>，解得1x <．∴x 的值可以是0，故答案为：0（答案不唯一）．14．100°/100度【分析】本题考查的是已知弧长与半径求解弧所对的圆心角，熟记弧长公式是解本题的关键．直接利用弧长公式计算即可．【详解】解： 设“弓”所在的圆的弧长圆心角度数是n °， 则1.2π2π1803n =， 解得：100n =，故答案为：100°．15．0.5−【分析】本题考查了反比例函数k 值的几何意义，熟练掌握k 值的几何意义是解答本题的关键.根据反比例函数k 值的几何意义进行解答即可.【详解】AB x ⊥ 轴于点B ，CD x ⊥轴，∴AB CD ，又 AD BC ，∴四边形ABCD 是平行四边形，过点作AM y ⊥轴，则四边形ABOM 是矩形， ∴0.5,ABOMABCD S S k ===矩形平行四边形∵反比例函数图象在第二象限，0.5k ∴=−，故答案为：0.5−.16．23、54【分析】本题考查了折叠的性质，正方形的性质，勾股定理，圆的定义；分三种情况讨论，设O 的半径为r ，分别根据勾股定理，即可求解．【详解】设O 的半径为r ，当O 经过A O ′的中点，即经过AO 的中点， ∴1233r AB =，当O 经过OD 的中点，则12r OB OD ==， ∴2OD r =，2AO AB OB r =−=−， 在Rt AOD 中，222AD AO OD +=∴()()222222r r +−=解得：r = 当O 经过A D ′的中点，即经过AD 的中点，设AD 的中点为M ，∴2,1,AO r AM OM r =−== ∴()22221r r −+= 解得：54r =综上所述，半径为23、54故答案为：23、54 三、解答题17．(1)5(2)222m mn −+【分析】此题考查了实数的运算以及整式的混合运算，熟练掌握运算法则是解本题的关键．（1）原式利用零指数幂、绝对值的代数意义以及负整数指数幂法则计算即可求出值；（2）根据平方差公式和完全平方公式化简，再合并同类项即可．【详解】（1）解：原式159=-+5=；（2）原式()22222n m m mn n =−−−+22222n m m mn n =−−+−222m mn =−+18．(1)图见解析(2)【分析】本题考查作图-轴对称变换，旋转变换，以及求弧长，熟练掌握相关作图方法是解题关键； （1）根据点关于y 轴对称的性质分别找到对应的点1A ，1B ，1C ，然后进一步连接即可；（2）利用旋转变换的性质分别作出A ，B ，C 的对应点2A ，2B ，2C ，再顺次连接即可，利用弧长公式求得点C 经过的路径长．【详解】（1）解：如图，111A B C △即为所求；（2）如图，222A B C △即为所求，由题意可知，OC∴点C 旋转到点2C =． 19．(1)6，40(2)1120(3)全校学生一周内平均读书时间23t ≤<(答案不唯一)【分析】本题考查了扇形统计图，样本估计总体等知识．（1）由等级得到学生总数，即可得出a ，再求C 等级的占比即可；（2）用样本估计总体即可得出结果；（3）根据表格可题建议合理即可．【详解】（1）解：由等级D 得到学生总数1530%50÷=人， ∴504201556a −−−−，()%2050100%40%m =÷×=，40m =，故答案为：6，40．（2）1552800112050+×=人， 故该校2800名学生每周读书时间至少3小时的人数为1120人．故答案为：1120．（3）根据表格可建议：全校学生一周内平均读书时间23t ≤<．20．(1)是；222AB BD AD +=，由勾股定理的逆定理可知AB BC ⊥．(2)．【分析】本题考查的勾股定理的逆定理的应用，解直角三角形的应用，理解题意是解本题的关键． （1）利用勾股定理的逆定理判断即可；（2）先画图，利用三角函数再计算BE=BF =，从而可得答案． 【详解】（1）解：是， 理由：由测量结果可知得 1.5m BD =， 2.5m AD =，而2m AB =，∴2226.25AB BD AD +==，∴90ABD ，∴AB BC ⊥．故答案是：是；222AB BD AD +=，由勾股定理的逆定理可知AB BC ⊥．（2）如图，由题意可得：90ABC ∠=°，2AB =，30AFB ∠=°，60AEB ∠=°，∴tan tan 60AB AEB BE∠=°=，∴BE =， 同理：tan tan 30AB AFBBF ∠=°=，∴BF =，∴FE BF BE =−==． 21．(1)证明见解析(2)6【分析】（1）依据平行线的性质以及矩形的性质，即可得到∠AFE =∠AEF ，进而得出AE =AF ．（2）设BE =x ，则AE =EC =8-x ，在Rt △ABE 中，根据勾股定理可得方程，即可得到BE 的长，再根据三角形面积计算公式求解．【详解】（1）证明：∵四边形ABCD 矩形，∴AD ∥BC ，∴∠AFE =∠FEC ，由折叠的性质得：∠AEF =∠FEC ，∴∠AFE =∠AEF ，∴AE =AF ．（2）解：根据折叠的性质可得AE =EC ，设BE =x ，则AE =EC =8-x ，在Rt △ABE 中，根据勾股定理可得：222AB BE AE +=，即()22248x x +=−，解得：x =3，∴BE =3，∴ABE S = 12AB •BE =12×4×3=6． 【点睛】本题主要考查了折叠问题以及矩形的性质的运用，解题的方法是设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．22．(1)220y x =−+ (2)5种(3)当转运A 种脐橙的车4辆，转运B 种脐橙的车12辆，转运C 种脐橙的车4辆时，利润最大为140800元【分析】（1）根据题意列式：()20651040x x y y −−=++，整理后即可得到220y x =−+； （2）根据装运每种水果的车辆数都不少于4辆，4x ≥，2204x −+≥，解不等式组即可；（3）设利润为W 元，则()480016000048W x x =−+≤≤，根据一次函数的增减性求解即可． 【详解】（1）根据题意，装运A 种水果的车辆数为x ，装运B 种水果的车辆数为y ，∴装运C 种水果的车辆数为()20x y −−，∴()20651040x x y y −−=++， 整理得220y x =−+． （2）由（1）知，装运A ，B ，C 三种水果的车辆数分别为x ，220x −+，x ，由题意得2204x −+≥，解得8x ≤，∵4x ≥，∴48x ≤≤．∵x 为整数，∴x 的值为4，5，6，7，8，∴安排方案共有5种．（3）设利润为W 元，∴()612005220160041000W x x x =×+−+×+× 4800160000x =−+，因为48000−<，且x 的值为4，5，6，7，8，∴W 的值随x 的增大而减小，∴当4x =时，销售利润最大．当装运A 种水果4车，B 种水果12车，C 种水果4车，销售获利最大．最大利润48004160000140800W =−×+=（元）．【点睛】主要考查利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义求解．注意要根据自变量的实际范围确定函数的最值．23．(1)2(0,0)P ，3(1,1)P ，4(2,2)P(2)①AC =BC =AB =ABC 是直角三角形，理由见解析【分析】本题考查了二次函数的图象与性质、勾股定理以及勾股定理逆定理：（1）根据“梦之点”的定义判断这几个点是否在矩形的内部或者边上即可得到答案；（2）①根据“梦之点”的定义求出A ，B 的坐标，再求出顶点的坐标，计算出AC ，AB ，BC 的长； ②根据勾股定理逆定理，即可求解．【详解】（1）解：∵矩形ABCD 的顶点坐标分别是(1,2)A −，(1,1)B −−，(3,1)C −，(3,2)D ，∴矩形ABCD 的“梦之点”(),x y 满足2,131x y −−≤≤≤≤，∴点2(0,0)P ，3(1,1)P ，4(2,2)P 是矩形ABCD 的“梦之点”，1(2,2)P −−不是矩形的“梦之点”．故答案为：2(0,0)P ，3(1,1)P ，4(2,2)P（2）解：①A 、B 是抛物线21922y x x =−++上的“梦之点”， ∴21922x x x =−++， 解得：123,3x x ==−，当3x =时，3y =，当3x =−时，=3y −，∴()()3,3,3,3A B −−， ∵()2219115222y x x x =−++=−−+， ∴顶点坐标为()1,5C ，∴AC =BC =AB =； ②ABC 是直角三角形，理由如下：∵AC =BC =AB =∴((2222280AB AC BC +=+==，∴ABC 是直角三角形．24．(1)证明见解析(2)证明见解析(3)①EF =253CF =【分析】本题考查了圆的性质，等腰三角形的判定与性质，相似三角形的判定与性质，锐角三角函数等知识，掌握相关知识是解题的关键．（1）利用勾股和锐角三角函数求得AC BC =即可证明；（2）连接,OA OB ，延长CO 交AD 于点M ，交AB 于点N ，先证明CO 是ACB ∠的角平分线，再证明ANM CDM ∽即可得出结论；（3）①过O 点作OH BC ⊥交BC 于点H ，点E 是OC 上一动点，EF AB ∥交BC 于点F ，先证明CHO CFB ∽，设EF x =3x =即可求解，②要使OEF 的面积与CEF △的面积差最大，必须使EF 和()CE OE −最大，当E 点与O 点重合时，EF 最大，CE OE OC −=最大，先求得EF =即可求出CF ． 【详解】（1）证明：∵AD 是ABC 的高线，∴90ADC ADB ∠=∠=°， ∵9AD =，12CD =，∴15AC ===，∵tan 3ABD ∠=， ∴tan 3AD ABD BD∠==， ∴3BD =，∴31215BC BD CD =+=+=， ∴AC BC =，∴ABC 是等腰三角形．（2）证明：连接,OA OB ，延长CO 交AD 于点M ，交AB 于点N ，如图：∵AC BC =，∴CAB CBA ∠=∠， ∵OA OB =，∴OAB OBA ∠=∠， ∴CAO CBO ∠=∠， ∵OA OC =，∴CAO ACO ∠=∠， ∵OB OC =，∴BCO CBO ∠=∠， ∴ACO BCO ∠=∠， ∴CO 是ACB ∠的角平分线， 又∵ AC BC =，∴CN AB ⊥，∴90ANC BNC ∠=∠=°， ∴90MDC ANE ∠=∠=°， 又∵AMN CMD ∠=∠， ∴ANM CDM ∽，∴DCM NAM ∠=∠， ∴BCO BAD ∠=∠． （3）解：①过O 点作OH BC ⊥交BC 于点H ，点E 是OC 上一动点，EF AB ∥交BC 于点F ，如图：∵,,15OB OC OH BC BC =⊥=， ∴17.52CH BC ==，90CHO CFB ∠=∠=°， ∴CHO CFB ∽，∴COH CBF ∠=∠， ∵tan 3ABD ∠=， ∴tan tan 3CH COH CBF OH∠=∠==， ∴ 2.5OH =，∴OC =， ∵EF AB ∥，90BNC ∠=°， ∴CEF CNB ∽，∴90CEF CNB ∠=∠=°， 设EF x =，∴tan tan 3CE CE CFE CBN EF x∠=∠===， ∴3CE x =，∵OEF ADB ∽，∴OE EF AD BD=， ∵OEOC CE =−， 3x =， 解得：x =∴EF ②∵90CEF ∠=°，即EF OC ⊥， ∴12CEF S CE EF =⋅ ，12OEF S OE EF =⋅ ， ∴()111222CEF OEF S S CE EF OE EF EF CE OE −=⋅−⋅=⋅− ， 由题知，要使OEF 的面积与CEF △的面积差最大，必须使EF 和()CE OE −最大，∴当E 点与O 点重合时，EF 最大，CE OE OC −=最大，如图：∵EF AB ∥，∴CEF CNB ∽，∴CFE CBN ∠=∠，CE OC ==，∴tan tan 3CE CFE CBN EF ∠=∠==，∴EF∴253CF =．。

2024年山东省中考数学模拟押题预测卷及答案

2024年山东省中考数学模拟押题预测卷及答案

2024年初中学生学业水平考试数学押题预测试卷注意事项:1.本试题分为第1卷和第Ⅱ卷两部分。

第1卷为选择题，30分;第Ⅱ卷为非选择题，90分;共120分。

考试时间为120分钟。

2.答卷前务必将试题密封线内及答题卡上面的项目填涂清楚。

所有答案都必须涂、写在答题卡相应位置，答在本试卷上一律无效。

第Ⅰ卷(选择题 30分)一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.计算82024×(−0.125)2023的结果为( )A. −8B. 8C. −2D. −0.1252.剪纸是中国优秀的传统文化.如图剪纸图案中，是中心对称图形的是( )A. B. C. D.3.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4600000000人，这个数用科学记数法表示为( )A. 46×108B. 4.6×108C. 4.6×109D. 4.6×10104.如图是一个玻璃烧杯，图2是玻璃烧杯抽象的几何体，以箭头所指的方向为主视图方向，则它的俯视图为( )A. B. C. D.5.下列计算正确的是( )A. aa2+aa4=aa6B. (−aa3)2=aa6C. 2aa+3bb=5aabbD. aa6÷aa3=aa26.如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=30°，则∠2的度数是( )A. 45°B. 55°C. 65°D. 75°7.乘坐高铁现在是人们非常方便快捷的一种出行方式，甲、乙两城市之间的铁路距离约2800kkkk，乘坐高铁列车比普通快车能提前8ℎ到达，已知高铁列车的平均行驶速度是普通快车的2倍.设普通快车的平均行驶速度为xx kkkk/ℎ，根据题意所列出的方程为( )A. 2800xx=2800×2xx+8B. 2800×2xx=2800xx+8C. 28002xx−2800xx=8D. 2800xx−28002xx=88.如图，点AA，BB分别在反比例函数yy=12xx和yy=kk xx的图象上，分别过AA，BB两点向xx轴，yy轴作垂线，形成的阴影部分的面积为7，则kk的值为( )A. 6B. 7C. 5D. 89.某品牌20寸的行李箱拉杆拉开后放置如图所示，经测量该行李箱从轮子底部到箱子上沿的高度AABB与从轮子底部到拉杆顶部的高度CCCC之比是黄金比.已知CCCC=80cckk，则AABB的长度是( )A. (20√ 5−20)cckkB. (80−40√ 5)cckkC. (40√ 5−40)cckkD. (120−40√ 5)cckk10.如图，在平面直角坐标系xxxxyy中，四边形xxAABBCC的顶点xx在原点上，xxAA边在xx轴的正半轴上，AABB⊥xx轴，AABB=CCBB=2，xxAA=xxCC，∠AAxxCC=60°，将四边形xxAABBCC绕点xx逆时针旋转，每次旋转90°，则第2024次旋转结束时，点CC的坐标为( )A. (√ 3,3)B. (3,−√ 3)C. (−√ 3,1)D. (1,−√ 3)第Ⅱ卷(非选择题 90分)二、填空题：本题共6小题，每小题3分，共18分。

中考数学压轴题 复习专题强化试卷检测试题

中考数学压轴题 复习专题强化试卷检测试题

一、中考数学压轴题1．如图，四边形AOBC 是正方形，点C 的坐标是(82,0)．（1）正方形AOBC 的边长为 ，点A 的坐标是 ；（2）将正方形AOBC 绕点O 顺时针旋转45︒，点A ，B ，C 旋转后的对应点为A '，B '，C '，求点A '的坐标及旋转后的正方形与原正方形的重叠部分的面积；（3）动点P 从点O 出发，沿折线OACB 方向以1个单位/秒的速度匀速运动，同时，另一动点Q 从点O 出发，沿折线OBCA 方向以2个单位/秒的速度匀速运动，运动时间为t 秒，当它们相遇时同时停止运动，当OPQ △为等腰三角形时，求出t 的值（直接写出结果即可）．2．定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（概念感知）（1）如图1，在ABC 中，12AC =，10BC =，30ACB ∠=︒，试判断ABC 是否是“准黄金”三角形，请说明理由．（问题探究）（2）如图2，ABC 是“准黄金”三角形，BC 是“金底”，把ABC 沿BC 翻折得到DBC △，连AB 接AD 交BC 的延长线于点E ，若点C 恰好是ABD △的重心，求AB BC的值．（拓展提升） （3）如图3，12l l //，且直线1l 与2l 之间的距离为3，“准黄金”ABC 的“金底”BC 在直线2l 上，点A 在直线1l 上．10AB BC =，若ABC ∠是钝角，将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C ''，线段A C '交1l 于点D ．①当30α=︒时，则CD =_________；②如图4，当点B 落在直线1l 上时，求AD CD 的值．3．（1）阅读理解：如图①，在ABC 中，若8AB =，5AC =，求BC 边上的中线AD 的取值范围． 可以用如下方法：将ACD 绕着点D 逆时针旋转180︒得到EBD △，在ABE △中，利用三角形三边的关系即可判断中线AD 的取值范围是______；（2）问题解决：如图②，在ABC 中，D 是BC 边上的中点，DE DF ⊥于点D ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，求证：BE CF EF +>；（3）问题拓展：如图③，在四边形ABCD 中，180B D ∠+∠=︒，CB CD =，100BCD ∠=︒，以C 为顶点作一个50︒的角，角的两边分别交AB 、AD 于E 、F 两点，连接EF ，探索线段BE ，DF ，EF 之间的数量关系，并说明理由．4．如图，已知正方形ABCD 中，4,BC AC BD =、相交于点O ，过点A 作射线AM AC ⊥，点E 是射线AM 上一动点，连接OE 交AB 于点F ，以OE 为一边，作正方形OEGH ，且点A 在正方形OEGH 的内部，连接DH ．（1）求证：EDO EAO ∆≅∆；（2）设BF x =，正方形OEGH 的边长为y ，求y 关于x 的函数关系式，并写出定义域；（3）连接AG ，当AEG ∆是等腰三角形时，求BF 的长．5．问题提出（1）如图①，在ABC 中，42,6,135AB AC BAC ==∠=，求ABC 的面积．问题探究（2）如图②，半圆O 的直径10AB =，C 是半圆AB 的中点，点D 在BC 上，且2CD BD =，点P 是AB 上的动点，试求PC PD +的最小值．问题解决（3）如图③，扇形AOB 的半径为20,45AOB ∠=在AB 选点P ，在边OA 上选点E ，在边OB 上选点F ，求PE EF FP ++的长度的最小值．6．如图，直线y ＝12x ﹣2与x 轴交于点B ，与y 轴交于点A ，抛物线y ＝ax 2﹣32x+c 经过A ，B 两点，与x 轴的另一交点为C ．（1）求抛物线的解析式；（2）M 为抛物线上一点，直线AM 与x 轴交于点N ，当32MN AN =时，求点M 的坐标； （3）P 为抛物线上的动点，连接AP ，当∠PAB 与△AOB 的一个内角相等时，直接写出点P 的坐标．7．如图，在平面直角坐标系xoy 中，直线122y x =-+与x 轴交于点B ，与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点．（1）求抛物线的解析式；（2）点M 为抛物线对称轴上一动点，当BM CM -的值最小时，请你求出点M 的坐标；（3）抛物线上是否存在点N ，过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似？若存在，请直接写出点N 的坐标；若不存在，请说明理由．8．小明研究了这样一道几何题：如图1，在ABC 中，把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB '，把AC 绕点A 逆时针旋转β得到AC '，连接B C ''．当180a β+=︒时，请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么？以下是他的研究过程：特例验证：（1）①如图2，当ABC 为等边三角形时，猜想AD 与BC 的数量关系为AD =_______BC ；②如图3，当90BAC ∠=︒，8BC =时，则AD 长为________． 猜想论证：（2）在图1中，当ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用：（3）如图4，在四边形ABCD ，90C ∠=︒，120A B ∠+∠=︒，123BC =，6CD =，63DA =，在四边形内部是否存在点P ，使PDC △与PAB △之间满足小明探究的问题中的边角关系？若存在，请画出点P 的位置（保留作图痕迹，不需要说明）并直接写出PDC △的边DC 上的中线PQ 的长度；若不存在，说明理由．9．如图，直线y ＝﹣x+4与抛物线y ＝﹣12x 2+bx+c 交于A ，B 两点，点A 在y 轴上，点B 在x 轴上．（1）求抛物线的解析式；（2）在x 轴下方的抛物线上存在一点P ，使得∠ABP ＝90°，求出点P 坐标；（3）点E 是抛物线对称轴上一点，点F 是抛物线上一点，是否存在点E 和点F 使得以点E ，F ，B ，O 为顶点的四边形是平行四边形？若存在，求出点F 的坐标；若不存在，请说明理由．10．（1）如图1，A 是⊙O 上一动点，P 是⊙O 外一点，在图中作出PA 最小时的点A ． （2）如图2，Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，以点C 为圆心的⊙C 的半径是3.6，Q 是⊙C 上一动点，在线段AB 上确定点P 的位置，使PQ 的长最小，并求出其最小值． （3）如图3，矩形ABCD 中，AB ＝6，BC ＝9，以D 为圆心，3为半径作⊙D ，E 为⊙D 上一动点，连接AE ，以AE 为直角边作Rt △AEF ，∠EAF ＝90°，tan ∠AEF ＝13，试探究四边形ADCF 的面积是否有最大或最小值，如果有，请求出最大或最小值，否则，请说明理由．11．在菱形ABCD 中，P 为直线DA 上的点，Q 为直线CD 上的点，分别连接PC ，PQ ，且PC PQ =．（1）若60B ∠=︒，点P 在线段DA 上，点Q 在线段CD 的延长线上，如图①，易证：DQ PD AB +=（不需证明）；（2）如图②，若∠B ＝120°，点P 在线段DA 上，点Q 在线段CD 的延长线上，如图③，猜想线段DQ ，PD 和AB 之间有怎样的数量关系？请直接写出对图②，图③的猜想，并选择其中一种情况给予证明．12．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．13．将一个直角三角形纸片ABO ，放置在平面直角坐标系中，点0(3)A ，，点()0, 3B ，点(0,0)O(I)过边OB 上的动点D (点D 不与点B ，O 重合)作DE OB ⊥交AB 于点E ，沿着DE 折叠该纸片，点B 落在射线BO 上的点F 处．①如图，当D 为OB 中点时，求E 点的坐标；②连接AF ，当AEF ∆为直角三角形时，求E 点坐标：(Ⅱ) P 是AB 边上的动点(点 P 不与点B 重合)，将AOP ∆沿OP 所在的直线折叠，得到'A OP ∆，连接'BA ，当'BA 取得最小值时，求P 点坐标(直接写出结果即可)．14．在ABC ∆中，若存在一个内角角度，是另外一个内角角度的n 倍（n 为大于1的正整数），则称ABC ∆为n 倍角三角形．例如，在ABC ∆中，80A ∠=︒，75B ∠=︒，25C ∠=︒，可知3∠=∠B C ，所以ABC ∆为3倍角三角形．（1）在ABC ∆中，55A ∠=︒，25B ∠=︒，则ABC ∆为________倍角三角形；（2）若DEF ∆是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的13，求DEF ∆的最小内角． （3）若MNP ∆是2倍角三角形，且90M N P ∠<∠<∠<︒，请直接写出MNP ∆的最小内角的取值范围．15．如图，在▱ABCD 中，对角线AC ⊥BC ，∠BAC ＝30°，BC ＝23，在AB 边的下方作射线AG ，使得∠BAG ＝30°，E 为线段DC 上一个动点，在射线AG 上取一点P ，连接BP ，使得∠EBP ＝60°，连接EP 交AC 于点F ，在点E 的运动过程中，当∠BPE ＝60°时，则AF ＝_____．16．如图，在矩形ABCD 中，点E 为BC 的中点，连接AE ，过点D 作DF AE ⊥于点F ，过点C 作CN DF ⊥于点N ，延长CN 交AD 于点M ．（1）求证：AM MD =（2）连接CF ，并延长CF 交AB 于G①若2AB =，求CF 的长度；②探究当AB AD为何值时，点G 恰好为AB 的中点．17．如图1，以AB 为直径作⊙O ，点C 是直径AB 上方半圆上的一点，连结AC ，BC ，过点C 作∠ACB 的平分线交⊙O 于点D ，过点D 作AB 的平行线交CB 的延长线于点E ．（1）如图1，连结AD ，求证：∠ADC ＝∠DEC ．（2）若⊙O 的半径为5，求CA •CE 的最大值．（3）如图2，连结AE ，设tan ∠ABC ＝x ，tan ∠AEC ＝y ，①求y 关于x 的函数解析式； ②若CB BE ＝45，求y 的值． 18．如图1，Rt △ABC 中，点D ，E 分别为直角边AC ，BC 上的点，若满足AD 2+BE 2＝DE 2，则称DE 为R △ABC 的“完美分割线”．显然，当DE 为△ABC 的中位线时，DE 是△ABC 的一条完美分割线．（1）如图1，AB ＝10，cos A ＝45，AD ＝3，若DE 为完美分割线，则BE 的长是 ． （2）如图2，对AC 边上的点D ，在Rt △ABC 中的斜边AB 上取点P ，使得DP ＝DA ，过点P 画PE ⊥PD 交BC 于点E ，连结DE ，求证：DE 是直角△ABC 的完美分割线．（3）如图3，在Rt △ABC 中，AC ＝10，BC ＝5，DE 是其完美分割线，点P 是斜边AB 的中点，连结PD 、PE ，求cos ∠PDE 的值．19．问题探究（1）如图1．在ABC 中，8BC =，D 为BC 上一点，6AD =．则ABC 面积的最大值是_______．（2）如图2，在ABC 中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC 的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值：若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．20．已知，抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ，B ，且B 点的坐标为()2,0． （1）求该抛物线的解析式．（2）如图1，若点P 是线段AB 上的一动点，过点P 作//PE AC ，交BC 于E ，连接CP ，求PCE ∆面积的最大值．（3）如图2，若直线y x m =+与线段AC 交于点M ，与线段BC 交于点N ，是否存在M ，N ，使得OMN ∆为直角三角形，若存在，请求出m 的值；若不存在，请说明理由．21．在综合与实践课上老师将直尺摆放在三角板上，使直尺与三角板的边分别交于点P 、M 、N 、Q ，（1）如图①所示．当∠CNG ＝42°，求∠HMC 的度数．（写出证明过程）（2）将直尺向下平移至图 2 位置，使直尺的边缘通过点 C ，交 AB 于点 P ，直尺另一侧与三角形交于 N 、Q 两点。

中考数学压轴题 复习专题强化试卷检测试卷

中考数学压轴题 复习专题强化试卷检测试卷

一、中考数学压轴题1．在Rt ABC ∆中，6AB =，90B ∠=︒，8BC =，点P 从A 出发沿AC 方向在运动速度为3个单位/秒，点Q 从C 出发向点B 运动，速度为1个单位/秒，P 、Q 同时出发，点Q 到点B 时两点同时停止运动．（1）点P 在线段AC 上运动，过P 作DP PQ ⊥交边AB 于D ，2t =时，求PD PQ的值； （2）运动t 秒后，90BPQ ∠=︒，求此时t 的值；（3）t =________时，AQ QP =． 2．如图，已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点，与y 轴交于C 点，直线BD 交抛物线于点D ，并且()D 2,3，()B 4,0-．（1）求抛物线的解析式；（2）已知点M 为抛物线上一动点，且在第三象限，顺次连接点B 、M 、C ，求BMC 面积的最大值；（3）在（2）中BMC 面积最大的条件下，过点M 作直线平行于y 轴，在这条直线上是否存在一个以Q 点为圆心，OQ 为半径且与直线AC 相切的圆？若存在，求出圆心Q 的坐标；若不存在，请说明理由．3．综合与实践4A 纸是我们学习工作最常用的纸张之一， 2，我们定义：长宽之比是2的矩形纸片称为“标准纸”．操作判断：()1如图1所示，矩形纸片2=是一张“标准纸”，将纸片折叠一次，使点ABCD AD AB()AB=求CF的B与D重合，再展开，折痕EF交AD边于点,E交BC边于点F，若1,长，()2如图2，在()1的基础上，连接,BE判断四边形BD折痕EF交BD于点O，连接,BFDE的形状，并说明理由．探究发现：()3如图3所示，在(1)和(2)的基础上，展开纸片后，将纸片再折叠一次，使点A与点C重合，再展开，痕MN交AD边于点M，BC交边于点,N交BD也是点O.然后将四边形ENFM剪下，探究纸片ENFM是否为“标准纸”，说明理由．∆的三个顶点坐标分别为4．如图，在平面直角坐标中，点O为坐标原点，ABC(),C n O，5-，(),，()B m OA O m,∠=∠，其中m，n满足AC=且OBA OAB725m n m n +=⎧⎨-=⎩．（1）求点A ，C 的坐标；（2）点P 从点A 出发，以每秒1个单位长度的速度沿y 轴负方向运动，设点P 的运动时间为t 秒.连接BP 、CP ，用含有t 的式子表示BPC ∆的面积为S （直接写出t 的取值范围）；（3）在（2）的条件下，是否存在t 的值，使得ΔΔ32PAB POC S S =，若存在，请求出t 的值，并直接写出BP 中点Q 的坐标；若不存，请说明理由．5．问题提出（1）如图①，在ABC 中，2,6,135AB AC BAC ==∠=，求ABC 的面积．问题探究（2）如图②，半圆O 的直径10AB =，C 是半圆AB 的中点，点D 在BC 上，且2CD BD =，点P 是AB 上的动点，试求PC PD +的最小值．问题解决（3）如图③，扇形AOB 的半径为20,45AOB ∠=在AB 选点P ，在边OA 上选点E ，在边OB 上选点F ，求PE EF FP ++的长度的最小值．6．如图，平面上存在点P、点M与线段AB．若线段AB上存在一点Q，使得点M在以PQ 为直径的圆上，则称点M为点P与线段AB的共圆点．已知点P（0，1），点A（﹣2，﹣1），点B（2，﹣1）．（1）在点O（0，0），C（﹣2，1），D（3，0）中，可以成为点P与线段AB的共圆点的是；（2）点K为x轴上一点，若点K为点P与线段AB的共圆点，请求出点K横坐标x K的取值范围；（3）已知点M（m，﹣1），若直线y＝12x+3上存在点P与线段AM的共圆点，请直接写出m的取值范围．7．如图1，△ABC内接于⊙O，直径AD交BC于点E，延长AD至点F，使DF＝2OD，连接FC并延长交过点A的切线于点G，且满足AG∥BC，连接OC，若cos∠BAC＝13，BC＝8．（1）求证：CF是⊙O的切线；（2）求⊙O的半径OC；（3）如图2，⊙O的弦AH经过半径OC的中点F，连结BH交弦CD于点M，连结FM，试求出FM的长和△AOF的面积．8．附加题：在平面直角坐标系中，抛物线21y axa=-与y轴交于点A，点A关于x轴的对称点为点B ，（1）求抛物线的对称轴；（2）求点B 坐标（用含a 的式子表示）；（3）已知点11,P a ⎛⎫ ⎪⎝⎭，(3,0)Q ，若抛物线与线段PQ 恰有一个公共点，结合函数图像，求a 的取值范围． 9．已知四边形ABCD 是正方形，点P 在直线BC 上，点G 在直线AD 上（P ，G 不与正方形顶点重合，且在CD 的同侧），PD =PG ，DF ⊥PG 于点H ，交直线AB 于点F ，将线段PG 绕点P 逆时针旋转90°得到线段PE ，连结EF ．（1）如图1，当点P 与点G 分别在线段BC 与线段AD 上时．①求证：DF =PG ；②若AB =3，PC =1，求四边形PEFD 的面积；（2）如图2，当点P 与点G 分别在线段BC 与线段AD 的延长线上时，请猜想四边形PEFD 是怎样的特殊四边形，并证明你的猜想．10．如图，抛物线214y x bx c =++与x 轴交于点A （-2，0），交y 轴于点B （0，52-）．直线32y kx =+过点A 与y 轴交于点C ，与抛物线的另一个交点是D ．(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式； (2)点P 是抛物线上A 、D 间的一个动点，过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ，问是否存在P 点使得四边形PMEC 为平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由;②作PN ⊥AD 于点N ，设△PMN 的周长为m ，点P 的横坐标为x ，求m 关于x 的函数关系式，并求出m 的最大值．11．如图，正方形ABCD 的边长为8，M 是AB 的中点，P 是BC 边上的动点，连结PM ，以点P 为圆心，PM 长为半径作⊙P ．（1）当BP ＝ 时，△MBP ～△DCP ；（2）当⊙P 与正方形ABCD 的边相切时，求BP 的长；（3）设⊙P 的半径为x ，请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围．12．如图1，平面直角坐标系xoy 中，A (－4，3)，反比例函数(0)k y k x=<的图象分别交矩形ABOC 的两边AC ，BC 于E ，F （E ，F 不与A 重合），沿着EF 将矩形ABOC 折叠使A ，D 重合．（1）①如图2，当点D 恰好在矩形ABOC 的对角线BC 上时，求CE 的长；②若折叠后点D 落在矩形ABOC 内（不包括边界），求线段CE 长度的取值范围． （2）若折叠后，△ABD 是等腰三角形，请直接写出此时点D 的坐标．13．已知抛物线y=﹣x 2﹣2x+3交x 轴于点A 、C （点A 在点C 左侧），交y 轴于点B ．（1）求A ，B ，C 三点坐标；（2）如图1，点D 为AC 中点，点E 在线段BD 上，且BE=2DE ，连接CE 并延长交抛物线于点M ，求点M 坐标；（3）如图2，将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ，连接CG ，点P 为△ACG 内一点，连接PA 、PC 、PG ，分别以AP 、AG 为边，在它们的左侧作等边△APR 和等边△AGQ ，求PA+PC+PG 的最小值，并求当PA+PC+PG 取得最小值时点P 的坐标（直接写出结果即可）．14．在平面直角坐标系xOy 中，点A 为x 轴上的动点，点B 为x 轴上方的动点，连接OA ，OB ，AB ．（1）如图1，当点B 在y 轴上，且满足OAB ∠的角平分线与OBA ∠的角平分线交于点P ，请直接写出P ∠的度数；（2）如图2，当点B 在y 轴上，OAB ∠的角平分线与OBA ∠的角平分线交于点P ，点C 在BP 的延长线上，且满足45AOC ∠=︒，求OAB OCB∠∠；（3）如图3，当点B 在第一象限内，点P 是AOB ∆内一点，点M ，N 分别是线段OA ，OB 上一点，满足：1902APB AOB ∠=︒+∠，PM PN =，180ONP OMP ∠+∠=︒．以下结论：①OM ON =；②AP 平分OAB ∠；③BP 平分OBA ∠；④AM BN AB +=．正确的是：________．（请填写正确结论序号，并选择一个正确的结论证明，简写证明过程）．15．已知：AB 为⊙O 的直径，点C 为弧AB 的中点，点D 为⊙O 上一点，连接CD ，交AB 于点M ，AE 为∠DAM 的平分线，交CD 于点E ．（1）如图1，连接BE ，若∠ACD=22°，求∠MBE 的度数；（2） 如图2，连接DO 并延长，交⊙O 于点F ，连接AF ，交CD 于点N ．①求证：DM 2+CN 2=CM 2；②如图3，当AD=1，AB=10时，请直接写出．．．．线段ME 的长． 16．如图，平面直角坐标系中，抛物线228y ax ax a =--与x 轴交于B 、C 两点（点B 在点C 右侧），与y 轴交于点A ，连接AB ，25AB =．（1）求抛物线的解析式；（2）点P 在第二象限的抛物线上，连接PB 交y 轴于D ，取PB 的中点E ，过点E 作EH x ⊥轴于点H ，连接DH ，设点P 的横坐标为t .ODH 的面积为S ，求S 与t 的函数关系式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，作PF y ⊥轴于F ，连接CP 、CD ，CP CD =，点S 为PF 上一点，连接BS 交y 轴于点T ，连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒，在射线CS 上取点Q.连接QF ，QF RF =，求直线TQ 的解析式．17．ABC 内接于O ，AB BC =，连接BO ；（1）如图1，连接CO 并延长交O 于点M ，连接AM ，求证：//AM BO ；（2）如图2，延长BO 交AC 于点H ，点F 为BH 上一点，连接AF ，若AH HF AB BF =，求证：BAF HAF ∠=∠；（3）在（2）的条件下，如图3，点E 为AB 上一点，点D 为O 上一点，连接ED 、OE ，若CBD 3ABH 90∠+∠=︒，若OF 3=，FH 4=，13623EBD S ∆=，连接OE ，求线段OE 的长．18．如图，已知ABF 为等腰直角三角形，90BAF ∠=︒，D 、C 为直线AF 上两点，且满足DF AC =，连接BD 、BC ，过点A 作AE BD ⊥于点E ，交BF 于点H ，连接CH ．（1）若30BAE ∠=︒，1BE =，求DE 的长；（2）若点M 是线段BF 上的动点，连AM 并延长交BD 于N ，当M 在线段BF 的什么位置上时，AH BN =？请说明理由；（3）在（2）的结论下，判断线段CH 、AH 、BD 的数量关系．请说明理由．19．已知抛物线2y ax bx c =++过点(6,0)A -，(2,0)B ，(0,3)C -．（1）求此抛物线的解析式；（2）若点H 是该抛物线第三象限的任意一点，求四边形OCHA 的最大面积；（3）若点Q 在y 轴上，点G 为该抛物线的顶点，且45GQA ∠=︒，求点Q 的坐标．20．如图1，Rt △ABC 中，点D ，E 分别为直角边AC ，BC 上的点，若满足AD 2+BE 2＝DE 2，则称DE 为R △ABC 的“完美分割线”．显然，当DE 为△ABC 的中位线时，DE 是△ABC 的一条完美分割线．（1）如图1，AB ＝10，cos A ＝45，AD ＝3，若DE 为完美分割线，则BE 的长是 ． （2）如图2，对AC 边上的点D ，在Rt △ABC 中的斜边AB 上取点P ，使得DP ＝DA ，过点P 画PE ⊥PD 交BC 于点E ，连结DE ，求证：DE 是直角△ABC 的完美分割线．（3）如图3，在Rt △ABC 中，AC ＝10，BC ＝5，DE 是其完美分割线，点P 是斜边AB 的中点，连结PD 、PE ，求cos ∠PDE 的值．21．（操作发现）如图1，ABC ∆为等腰直角三角形，90ACB ∠=︒，先将三角板的90︒角与ACB ∠重合，再将三角板绕点C 按顺时针方向旋转（旋转角大于0︒且小于45︒），旋转后三角板的一直角边与AB 交于点D ．在三角板另一直角边上取一点F ，使CF CD =，线段AB 上取点E ，使45DCE ∠=︒，连接AF ，EF ．（1）请求出EAF ∠的度数？（2）DE 与EF 相等吗？请说明理由；（类比探究）如图2，ABC ∆为等边三角形，先将三角板中的60︒角与ACB ∠重合，再将三角板绕点C 按顺时针方向旋转（旋转角大于0︒且小于30）.旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ，使CF CD =，线段AB 上取点E ，使30DCE ∠=︒，连接AF ，EF .（3）直接写出EAF ∠=_________度；（4）若1AE =，2BD =，求线段DE 的长度.22．如图，平行四边形ABCD 中，AB ⊥AC ，AB =2，AC =4．对角线AC 、BD 相交于点O ，将直线AC 绕点O 顺时针旋转α°（0°＜α＜180°），分别交直线BC 、AD 于点E 、F ．（1）当α=_____°时，四边形ABEF 是平行四边形；（2）在旋转的过程中，从A 、B 、C 、D 、E 、F 中任意4个点为顶点构造四边形， ①当α=_______°时，构造的四边形是菱形； ②若构造的四边形是矩形，求该矩形的两边长．23．（问题探究）课堂上老师提出了这样的问题：“如图①，在ABC 中，108BAC ∠=︒，点D 是BC 边上的一点，7224BAD BD CD AD ∠=︒==，，，求AC 的长”．某同学做了如下的思考：如图②，过点C 作CE AB ∥，交AD 的延长线于点E ，进而求解，请回答下列问题： （1）ACE ∠=___________度； （2）求AC 的长．（拓展应用）如图③，在四边形ABCD 中，12075BAD ADC ∠=︒∠=︒，，对角线AC BD 、相交于点E ，且AC AB ⊥，22EB ED AE ==，，则BC 的长为_____________．24．（1）（发现）如图1，在ABC 中，//DE BC 分别交AB 于D ，交AC 于E ．已知CD BE ⊥，3CD =，5BE =，求BC DE +的值．思考发现，过点E 作//EF DC ，交BC 延长线于点F ，构造BEF ，经过推理和计算能够使问题得到解决（如图2）．请回答：BC DE +的值为______．（2）（应用）如图3，在四边形ABCD 中，//AB CD ，AD 与BC 不平行且AD BC =，对角线AC BD ⊥，垂足为O ．若3CD =，5AB =，DAB CBA ∠=∠，求AC 的长．（3）（拓展）如图4，已知平行四边形ABCD 和矩形ABEF ，AC 与DF 交于点G ，FD FB =，且30BFD ∠=︒，60EBF ∠=︒，判断AC 与DF 的数量关系并证明． 25．如图，在矩形ABCD 中，6AB cm =，8AD cm =，连接BD ，将ABD △绕B 点作顺时针方向旋转得到A B D '''△（B ′与B 重合），且点D '刚好落在BC 的延长上，A D ''与CD 相交于点E ．（1）求矩形ABCD 与A B D '''△重叠部分（如图1中阴影部分A B CE ''）的面积； （2）将A B D '''△以每秒2cm 的速度沿直线BC 向右平移，如图2，当B ′移动到C 点时停止移动．设矩形ABCD 与A B D '''△重叠部分的面积为y ，移动的时间为x ，请你直接写出y 关于x 的函数关系式，并指出自变量x 的取值范围；（3）在（2）的平移过程中，是否存在这样的时间x ，使得AA B ''△成为等腰三角形？若存在，请你直接写出对应的x 的值，若不存在，请你说明理由．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题 1．A解析：（1）2；（2）2t =或3019；（3）10023【解析】 【分析】（1）如图1中，作PE AB ⊥于E ，PF BC ⊥于F ，利用勾股定理求出AC=10，根据//PE BC ，得到PA PE AEAC BC AB==，求出 4.8PE =， 3.6AE =， 2.4BE =，证明四边形EBFP 是矩形，得到 2.4PF BE ==，证明PED PFQ ∆∆∽，得到4.822.4PD PE PQ PF ===； （2）作PE AB ⊥于E ，根据//PE BC ，得到PE AP AE BC AC AB ==，求出125PE t =，95AE t =，965EB t =-，再证明PEB BPQ ∆∆∽，得到PE PB PB BQ =，即可求出2t =或3019； （3）如图3中作QF AC ⊥于F ，证明QFC ABC ∆∆∽，求出35QF t =，利用AQ QP =得到32AF FP t ==，根据22222AQ AB BQ QF AF =+=+即可列式求出t.【详解】（1）如图1中，作PE AB ⊥于E ，PF BC ⊥于F ，∵6AB =，90B ∠=︒，8BC =， ∴AC=10， ∵2t =，∴6AP =，2CQ =， ∵//PE BC ，∴PA PE AEAC BC AB ==， ∴61086PE AE ==， ∴ 4.8PE =， 3.6AE =， 2.4BE =，∵90PEB EBF PFB ∠=∠=∠=︒， ∴四边形EBFP 是矩形， ∴ 2.4PF BE ==， ∵90EPF QPD ∠=∠=︒， ∴EPD FPQ ∠=∠， ∴PED PFQ ∆∆∽， ∴4.822.4PD PE PQ PF ===．（2）如图2中，作PE AB ⊥于E ， ∵//PE BC ，∴PE AP AEBC AC AB==，∴125PE t =，95AE t =，965EB t =-， ∵EPB PBQ ∠=∠，90PEB BPQ ∠=∠=︒，∴PEB BPQ ∆∆∽， ∴PE PBPB BQ=， ∴2212129(8)6555t t t t ⎛⎫⎛⎫⋅-=+- ⎪ ⎪⎝⎭⎝⎭， ∴2t =或3019．（3）如图3中作QF AC ⊥于F ， ∵QCF ACB ∠=∠，QFC ABC ∠=∠， ∴QFC ABC ∆∆∽，∴QF QCAB AC=， ∴35QF t =，∵AQ QP =，∴32AF FP t ==， ∵22222AQ AB BQ QF AF =+=+，∴2222336(8)52t t t ⎛⎫⎛⎫+-=+ ⎪ ⎪⎝⎭⎝⎭， 整理得：21611600100000t t +-=，解得10023t =（或1007-舍弃）． 故答案为：10023．【点睛】此题考查勾股定理，相似三角形的判定及性质，矩形的判定及性质，三角形与动点问题，是一道比较综合的三角形题.2．B解析：（1）213y x x 222=+-；（2）4；（3）存在，Q 的坐标为()2,4-或()2,1-- 【解析】 【分析】()1根据题意将()D 2,3、()B 4,0-的坐标代入抛物线表达式，即可求解；()2由题意设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭，则点1K x,x 22⎛⎫-- ⎪⎝⎭，BMC1SMK OB 2=⋅⋅，即可求解； ()3由题意和如图所示可知，1tan QHN 2∠=，在RtQNH 中，QH m 6=+，222QN OQ (2)m m 4==-+=+2QN m 4sin QHN QHm 65∠+===+，进行分析计算即可求解． 【详解】解：()1将()D 2,3、()B 4,0-的坐标代入抛物线表达式得：422316420a b a b +-=⎧⎨--=⎩，解得：1232a b ⎧=⎪⎪⎨⎪=⎪⎩， 则抛物线的解析式为：213y x x 222=+-； ()2过点M 作y 轴的平行线，交直线BC 于点K ，将点B 、C 的坐标代入一次函数表达式：y k'x b'=+得：04'''2k b b =-+⎧⎨=-⎩，解得：1'2'2k b ⎧=-⎪⎨⎪=-⎩， 则直线BC 的表达式为：1y x 22=--， 设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭，则点1K x,x 22⎛⎫-- ⎪⎝⎭， 22BMC1113SMK OB 2x 2x x 2x 4x 2222⎛⎫=⋅⋅=----+=-- ⎪⎝⎭， a 10=-<，BMC S∴有最大值，当bx 22a=-=-时， BMCS最大值为4，点M 的坐标为()2,3--；()3如图所示，存在一个以Q 点为圆心，OQ 为半径且与直线AC 相切的圆，切点为N ，过点M 作直线平行于y 轴，交直线AC 于点H ，点M 坐标为()2,3--，设：点Q 坐标为()2,m -， 点A 、C 的坐标为()1,0、()0,2-，OA 1tan OCA OC 2∠==， QH //y 轴， QHN OCA ∠∠∴=， 1tan QHN2∠∴=，则sin QHN ∠= 将点A 、C 的坐标代入一次函数表达式：y mx n =+得：02m n n +=⎧⎨=-⎩，则直线AC 的表达式为：y 2x 2=-， 则点()H 2,6--，在Rt QNH 中，QH m 6=+，QN OQ ===QN sin QHNQHm 6∠===+， 解得：m 4=或1-，即点Q 的坐标为()2,4-或()2,1--． 【点睛】本题考查的是二次函数知识的综合运用，涉及到解直角三角形、圆的基本知识，本题难点是()3，核心是通过画图确定圆的位置，本题综合性较强．3．(1) CF 长为4；(2) 四边形BFDE 是菱形，理由见解析；(3) 纸片ENFM 是“标准纸"，理由见解析 【解析】 【分析】（1）1AB =，则AD =ABCD 是矩形，得到1,CD AB BC AD ==-=FB FD =，设CF x =，则FB FD x ==，在Rt DCF △中，222+=CD CF DF ，可得)2221x x +=即可求解．（2）当顶点B 与点D 重合时，折痕EF 垂直平分BD ，可得OB OD =，90BOF DOE ∠=∠=，在矩形ABCD 中，//AD BC ，得到OBF ODE ∠=∠，在BOF 和DOE △中，,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,，可得BOF DOE ≅，OE OF =，再根据OB OD =，可得四边形BFDE 是平行四边形，最后根据EF BD ⊥，即可求证平行四边形BFDE 是菱形．（3）由()2可知，OE OF =，同理可知，OM ON =，可得四边形ENFM 是平行四边形，根据90DOE DAB ∠=∠=︒，得到DOEDAB ，再根据2AD AB =，可得222OE AB OD AD ===，进而得到22OE OD =，22EF BD =，同理可得，22MN AC =，根据四边形ABCD 是矩形，可得AC BD =，EF MN =，四边形ENFM 是矩形，90EMF ∠=，2MF ODtan FEM ME OE∠===，2MF ME =，即可求证纸片ENFM 是“标准纸"． 【详解】 解：()11,AB =则2,2AD AB ==四边形ABCD 是矩形1,2CD AB BC AD ∴==-=由折叠得FB FD = 设CFx =，则2FB FD x ==- 在Rt DCF △中，222+=CD CF DF()22212x x +=-24x =答：CF 长为24()2四边形BFDE 是菱形.理由：当顶点B 与点D 重合时，折痕EF 垂直平分,BDOB OD ∴=，90BOF DOE ∠=∠=在矩形ABCD 中，//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中，,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,BOF DOE ∴≅ OE OF ∴= OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下：由()2可知，,OE OF =同理可知，,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒DOE DAB ∴2AD =222OE AB OD AD ∴===22OE OD ∴=2EF BD ∴=同理可得，2MN AC =四边形ABCD 是矩形，AC BD ∴=， EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.2,MF ODtan FEM ME OE∴∠=== 2MF ME ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数，灵活运用判定和性质是解题关键．4．A解析：（1）A （0，4），C （3，0）；（2）S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩；（3）存在，满足条件的t 的值为3617或36，点Q 的坐标为162,17⎛⎫- ⎪⎝⎭或()2,16--．【解析】 【分析】（1）解方程组求出m ，n 即可解决问题．（2）分两种情形：如图1中，当0＜t ＜4时，如图2中，当t ＞4时，根据S=12•BC•OP 求解即可．（3）分两种情形分别构建方程求解即可． 【详解】解：（1）由725m n m n +=⎧⎨-=⎩，解得：43m n =⎧⎨=⎩， ∴A （0，4），C （3，0）； （2）如图1中，当0＜t ＜4时，S=12•BC•OP=12×5×（4-t ）=-52t+10． 如图2中，当t ＞4时，S=12•BC•OP=12×5×（t-4）=52t-10． 综上所述，S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩，（3）当04t <<时，由题意，1314(4)3222t t ⨯⨯=⨯⨯-⨯，解得3617t =， 此时，363241717OP =-=， 32(0,)17P ∴， (4,0)B -，BQ ∴的中点Q 的坐标为162,17⎛⎫- ⎪⎝⎭，当4t >时，由题意，1314(4)3222t t ⨯⨯=⨯⨯-⨯，解得36t =， 此时36432OP =-=， (0,32)P ∴-， (4,0)B -，BP ∴的中点Q 的坐标为(2,16)--．综上所述，满足条件的t 的值为3617或36．点Q 的坐标为16(2,)17-或(2,16)--．【点睛】本题属于三角形综合题，考查了解方程组，三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．5．B解析：（1）12；（2）533）202 【解析】【分析】（1）如图1中，过点B 作BD CA ⊥，交CA 延长线于点D ，通过构造直角三角形，求出BD 利用三角形面积公式求解即可.（2）如图示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ，确定点P 的位置，利用勾股定理与矩形的性质求出CQ 的长度即为答案.（3）解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、，通过轴对称性质的转化，最终确定最小值转化为SN 的长. 【详解】（1）如解图1所示，过点B 作BD CA ⊥，交CA 延长线于点D ，135BAC ∠=，180********BAD BAC ∴∠=-∠=-=，BD CA ⊥，交CA 延长线于点D ，BAD ∴为等腰直角三角形，且90BDA ∠=，BD AD ∴=，在BAD 中，,90BD AD BDA =∠=，222BD AD AB ∴+=，即222BD AB =，42AB =，2222(42)32BD AB ∴===，解得：4BD =，6AC =，11641222ABCSAC BD ∴=⋅=⨯⨯=．（2）如解图2所示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ，D 关于AB 的对称点Q ，CQ 交AB 于点P ，PD PQ ∴=，PC PD PC PQ CQ ∴+=+=，点P 为AB 上的动点，PC PD CQ ∴+≥，∴当点P 处于解图2中的位置，PC PD +取最小值，且最小值为CQ 的长度，点C 为半圆AB 的中点，90COB ∴∠=，90BOD COD COB ∠+∠=∠=， 11903033BOD COB ∴∠=∠=⨯=，10AB =，1110522OD AB ∴==⨯=， 在Rt ODH △中，由作图知，90OHD ∠=，且30HOD BOD ∠=∠=，155,222DH OD QH DH ∴==∴==， 222255352OH OD DH ⎛⎫∴=-=-=⎪⎝⎭， 由作图知，四边形OMQH 为矩形，553,22OM QH MQ OH ∴====， 515522CM OM OC ∴=+=+=， 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭， PC PD ∴+的最小值为53．（3）如解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、， 点P 关于OA 的对称点S ，点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，PE SE ∴=，FP FN =，SOA POA ∠=∠，,NOB POB OS OP ON ∠=∠==，．PE EF FP SE EF FN SN ∴++=++=，SOA NOB POA POB ∠+∠=∠+∠， E 为OA 上的点，F 为OB 上的点 PE EF FP SN ∴++≥，∴当点E F 、处于解图3的位置时，PE EF FP ++的长度取最小值，最小值为SN 的长度，45POA POB AOB ∠+∠=∠=，45SOA NOB ∴∠+∠=，454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=．扇形AOB 的半径为20，20OS ON OP ∴===，在Rt SON 中，90SON ∠=，20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202．【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容，理解题意，作出辅助线是做题的关键.6．C解析：（1）C ；（2）﹣12≤x k 22﹣1≤x k 2；（3）m≤3﹣10或m≥3+210． 【解析】 【分析】（1）由题意可知当Q 与A 重合时，点C 在以AP 为直径的圆上，所以可以成为点P 与线段AB 的共圆点的是C ；（2）根据题意由两点的距离公式可得AP=BP=22，分别画以AP 和BP 为直径的圆交x 轴于4个点：K 1、K 2、K 3、K 4，结合图形2可得4个点的坐标，从而得结论； （3）由题意先根据直线y=12x+3，当x=0和y=0计算与x 轴和y 轴的交点坐标，分两种情况：M 在A 的左侧和右侧，先计算圆E 与直线y=12x+3相切时m 的值，从而根据图形可得结论． 【详解】解：（1）如图1，可以成为点P 与线段AB 的共圆点的是C ，故答案为：C ；（2）∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）． ∴AP ＝BP ＝22(20)(11)--+--＝22，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP ＝OG ＝1，OE ∥AB ， ∴PE ＝AE 2， ∴OE ＝12AG ＝1， ∴K 1（﹣12，0），k 2（120），k 32﹣1，0），k 4（2，0），∵点K 为点P 与线段AB 的共圆点， ∴﹣1﹣2≤x k ≤1﹣2或2﹣1≤x k ≤1+2； （3）分两种情况：①如图3，当M 在点A 的左侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，当x ＝0时，y ＝3，当y ＝0时，y ＝12x+3＝0，x ＝﹣6， ∴ON ＝3，OH ＝6， ∵tan ∠EHF ＝ON EF OH FH =＝36＝12， 设EF ＝a ，则FH ＝2a ，EH 5， ∴OE ＝65，Rt △OEP 中，OP ＝1，EP ＝a ， 由勾股定理得：EP 2＝OP 2+OE 2， ∴2221(65)a a =+， 解得：a 3522+3522-， ∴QG ＝2OE ＝2（65）＝﹣10， ∴m≤3﹣10②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG＝10，∴10综上，m的取值范围是m≤3﹣10或10．【点睛】本题属于圆和一次函数综合题，考查一次函数的应用，新定义：M为点P与线段AB的共圆点，圆的切线的性质等知识，解题的关键是理解题意，学会利用图象法解决问题，学会利用特殊点解决取值范围问题.7．D解析：（1）见解析；（2）32332232【解析】【分析】（1）由DF=2OD，得到OF=3OD=3OC，求得13OE OCOC OF==，推出△COE∽△FOE，根据相似三角形的性质得到∠OCF=∠DEC=90°，于是得到CF是⊙O的切线；（2）利用三角函数值，设OE=x，OC=3x，得到CE=3，根据勾股定理即可得到答案；（3）连接BD，根据圆周角定理得到角相等，然后证明△AOF∽△BDM，由相似三角形的性质，得到FM为中位线，即可求出FM的长度，由相似三角形的性质，以及中线分三角形的面积为两半，即可求出面积.【详解】解：（1）∵DF＝2OD，∴OF＝3OD＝3OC，∴13 OE OCOC OF==，∵∠COE＝∠FOC，∴△COE∽△FOE，∴∠OCF＝∠DEC＝90°，∴CF是⊙O的切线；（2）∵∠COD＝∠BAC，∴cos ∠BAC ＝cos ∠COE ＝13OE OC =， ∴设OE ＝x ，OC ＝3x ， ∵BC ＝8， ∴CE ＝4， ∵CE ⊥AD ， ∴OE 2+CE 2＝OC 2， ∴x 2+42＝9x 2，∴x ＝2（负值已舍去）， ∴OC ＝3x ＝32， ∴⊙O 的半径OC 为32； （3）如图，连结BD ，由圆周角定理，则∠OAF=∠DBM ，2AOF ADC ∠=∠， ∵BC ⊥AD ， ∴AC AB =， ∴∠ADC=∠ADB ，∴2AOF ADC BDM ∠=∠=∠， ∴△AOF ∽△BDM ； ∵点F 是OC 的中点， ∴AO ：OF=BD ：DM=2， 又∵BD=DC ， ∴DM=CM ， ∴FM 为中位线， ∴322， ∴S △AOF : S △BDM =(326 2 34=； ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯= ∴S △AOF =3424=32【点睛】本题考查了圆的综合问题，圆周角定理，切线的判定和性质，相似三角形的判定和性质，利用勾股定理求边长，以及三角形中线的性质，解题的关键是熟练掌握所学的定理和性质，运用属性结合的思想进行解题.8．B解析：（1）直线x=0；（2）B （0，1a ）；（3）≤a ≤13-或13≤a 【解析】 【分析】（1）根据抛物线的表达式直接得出对称轴即可；（2）根据题意得出点A 的坐标，再利用关于x 轴对称的点的坐标规律得出点B 坐标； （3）分a ＞0和a ＜0两种情况分别讨论，画图图像，求出a 的范围. 【详解】解：（1）在抛物线21y ax a=-中， 002a-=， ∴对称轴为直线x=0，即y 轴； （2）∵抛物线与y 轴交于点A ，∴A （0，1a-）， ∵点A 关于x 轴的对称点为点B ，∴B （0，1a）； （3）当a ＞0时，点A （0，1a-）在y 轴负半轴上， 当点P 恰好在抛物线上时，代入得：11a a a -=，解得：a =（舍），当点Q 恰好在抛物线上时，代入得：190a a-=， 解得：13a =或13-（舍），∴当13≤a 时，抛物线与线段PQ 恰有一个公共点；当a＜0时，点A（0，1a-）在y轴正半轴上，同理可知：当点P恰好在抛物线上时，代入得：11aa a -=，解得：2a=（舍）或2-，当点Q恰好在抛物线上时，代入得：190 aa-=，解得：13a=（舍）或13-，∴当2-≤a≤13-时，抛物线与线段PQ只有一个公共点；综上：若抛物线与线段PQ恰有一个公共点，a的取值范围是2-≤a≤13 -或13≤a2.【点睛】本题是一道二次函数的综合题目，主要考查二次函数的性质、二次函数图象上点的坐标特征，解答本题的关键是明确题意，画出相应的函数图象，利用分类讨论的方法和数形结合的思想解答．9．E解析：（1）①详见解析；②8；（2）（2）四边形PEFD是菱形，证明详见解析【解析】【分析】（1）①根据四边形ABCD为正方形得AD=CD ，然后证明△ADF≌△CDP，则DF=DP，得到DF=PG；②先判断四边形PEFD是菱形，然后求出PG=DP=223110+=，过点P作PM⊥AD于点M，则四边形CDMP是矩形，则△DHG∽△PMG，根据相似三角形的性质，即可求出答案；（2）根据四边形ABCD为正方形得AD=AB，由四边形ABPM为矩形得AB=PM，则AD=PM，再利用等角的余角相等得到∠GDH=∠MPG，于是可根据“ASA”证明△ADF≌△MPG，得到DF=PG，加上PD=PG，得到DF=PD，然后利用旋转的性质得∠EPG=90°，PE=PG，所以PE=PD=DF，再利用DF⊥PG得到DF∥PE，于是可判断四边形PEFD为平行四边形，加上DF=PD，则可判断四边形PEFD为菱形．【详解】解：（1）①证明∵四边形ABCD是正方形，∴AD=CD ，∠A= ∠C=∠ADC=90°，∵DF⊥PG，∴∠DHG=90°，∴∠HGD+∠ADF=90°，∠CDP+∠PDG=90°，∵ PD=PG ，∴∠PGD=∠PDG，∴∠ADF=∠CDP，∴△ADF≌△CDP（ASA），∴DF=DP，∵ PD=PG，∴DF=PG；②∵线段PG绕点P逆时针旋转90°得到线段PE∴∠GPE=∠DHG=90°， PG=PE=DF= PD∴PE∥DF∴四边形PEFD是菱形在Rt△DCP中，AD=AB=3，PC=1，PG=DP=22+=3110过点P作PM⊥AD于点M，则四边形CDMP是矩形∴DM=MG=PC=1，DG=2DM=2，∠PMG=∠DHG=90°，∠DGH=∠PGM ∴△DHG∽△PMG∴DG GH PG MG=即=110GH∴GH=10， PH=PG-GH=410由（1）DF=DP=10∴四边形PEFD的面积是DF PH⋅=10×410=8 ；（2）四边形PEFD是菱形；作PM⊥DG于M，如图2，∵四边形ABCD为正方形，∴AD=AB，∵四边形ABPM为矩形，∴AB=PM，∴AD=PM，∵DF⊥PG，∴∠DHG=90°，∴∠GDH+∠DGH=90°，∵∠MGP+∠MPG=90°，∴∠GDH=∠MPG，在△ADF和△MPG中FAD PMGAD MPADF MPG∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADF≌△MPG（ASA），∴DF=PG，而PD=PG，∴DF=PD，∵线段PG绕点P逆时针旋转90°得到线段PE，∴∠EPG=90°，PE=PG，∴PE=PD=DF而DF⊥PG，∴DF ∥PE ，且DF =PE ，∴四边形PEFD 为平行四边形，∵DF=PD ，∴四边形PEFD 为菱形．【点睛】本题考查了四边形的综合题：熟练掌握平行四边形、矩形、菱形和正方形的判定与性质是解题的关键；同时会运用等腰三角形的性质和旋转的性质；会利用三角形全等解决线段相等的问题．10．A解析：（1）2135442y x x =--，33y x 42=+ ；（2）① 存在，点P 的坐标是（2，-3）和（4，32-）；②231848555m x x =-++ ， m 的最大值是15． 【解析】【分析】 （1）将点A 和点B 的坐标代入抛物线的解析式可求得b 、c 的值，然后可求得抛物线的解析式，将点A 的坐标代入直线的解析式可求得k 的值，从而可求得直线的解析式； （2）①将2135442y x x =--与33y x 42=+联立，可求得点158,2D ⎛⎫ ⎪⎝⎭，然后再求得点30,2C ⎛⎫ ⎪⎝⎭则6CE =，设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭，则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭．然后可得到PM 的长与x 的函数关系式，然后依据PM CE =，可求得x 的值，从而可得到点P 的坐标；②在Rt CDE ∆中，依据勾股定理可知：10DC =，则CDE ∆的周长是24，接下来，证明PMN CDE ∆∆∽，依据相似三角形的周长比等于相似比可得到m 与x 的函数关系式，最后利用配方法可求得m 的最大值．【详解】解：（1）214y x bx c =++经过点A 和点B ， ∴12052b c c -+=⎧⎪⎨=⎪⎩， 解得3452b c ⎧=-⎪⎪⎨⎪=-⎪⎩， ∴抛物线的解析式为2135442y x x =--， 直线32y kx =+经过点(2,0)A -，3202k ∴-+=，解得：34k =． ∴直线的解析式为33y x 42=+； （2）①将2135442y x x =--与33y x 42=+联立，解得2x =-或8x =， 将8x =代入33y x 42=+得：152y =， 158,2D ⎛⎫∴ ⎪⎝⎭， 将0x =代入33y x 42=+得：32y =， 30,2C ⎛⎫∴ ⎪⎝⎭， 6CE ∴=，设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭，则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭， 点P 在直线AD 的下方，22331351344244242PM x x x x x ⎛⎫⎛⎫∴=+---=-++ ⎪ ⎪⎝⎭⎝⎭， 四边形PMEC 为平行四边形，PM CE ∴=，2134642x x ∴-++=，解得2x =或4x =， 当2x =时，3y =-，当4x =时，32y =-， ∴当点P 的坐标为()2,3-或34,2⎛⎫- ⎪⎝⎭时，四边形PMEC 为平行四边形； ②在Rt CDE ∆中，8DE =，6CE =，依据勾股定理可知：10DC =， CDE ∴∆的周长是24，//PM y 轴，PMN DCE ∴∠=∠，又90PNM DEC ∠=∠=︒，PMN CDE ∴∆∆∽， ∴PMN CDE l PM l DC ∆∆=，即2134422410x x m -++=， 化简整理得：231848555m x x =-++，配方得：23(3)155m x =--+， ∴当3x =时，m 有最大值，m 的最大是15．【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数、一次函数的解析式，平行四边形的性质、相似三角形的性质和判定，依据相似三角形的周长比等于相似比列出m 与x 的函数关系式是解题的关键．11．B解析：（1）83；（2）3或43；（3）565x ≤＜ 【解析】【分析】（1）设BP=a ，则PC=8-a ，由△MBP ～△DCP 知MB BP DC CP=，代入计算可得； （2）分别求出⊙P 与边CD 相切时和⊙P 与边AD 相切时BP 的长即可得；（3）①当PM=5时，⊙P 经过点M ，点C ；②当⊙P 经过点M 、点D 时，由PC 2+DC 2=BM 2+PB 2，可求得BP=7，继而知227465PM=+=．据此可得答案． 【详解】（1）设BP=a ，则PC=8-a ，∵AB=8，M 是AB 中点，∴AM=BM=4，∵△MBP ～△DCP ，∴MB BP DC CP =，即488a a=-， 解得83a =， 故答案为：83． （2）如图1，当⊙P 与边CD 相切时，设PC=PM=x ，在Rt △PBM 中，∵PM 2=BM 2+PB 2，∴x 2=42+（8-x ）2，∴x=5，∴PC=5，BP=BC-PC=8-5=3．如图2，当⊙P 与边AD 相切时，设切点为K ，连接PK ，则PK ⊥AD ，四边形PKDC 是矩形．∴PM=PK=CD=2BM ，∴BM=4，PM=8，在Rt △PBM 中，228443PB -=＝．综上所述，BP 的长为3或43．（3）如图1，当PM=5时，⊙P 经过点M ，点C ；如图3，当⊙P 经过点M 、点D 时，∵PC 2+DC 2=BM 2+PB 2，∴42+BP 2=（8-BP ）2+82，∴BP=7，∴227465PM =+=综上，565x ≤＜【点睛】本题是圆的综合问题，主要考查切线的性质、正方形的性质、勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题．12．E。

2024中考数学(人教版)押题卷 (794)

2024中考数学(人教版)押题卷 (794)

一、单选题1. 一张薄纸，一双巧手，在一剪一刻间幻化出千姿百态的美丽图案，令人叹为观止，这就是剪纸艺术．佛山剪纸，流传于广东省佛山市的传统美术，是国家级第一批非物质文化遗产之一．剪纸作品形式多样，以下剪纸作品中不是轴对称图形的是（）A．B．C．D．2. 若关于x的不等式组的整数解只有3个，则a的取值范围是( )A．6≤a＜7B．5≤a＜6C．4＜a≤5D．5＜a≤63. 市运会举行射击比赛，校射击队从甲，乙、丙、丁四人中选拔一人参赛．在选拔赛中，每人射击10次，计算他们10发成绩的平均数（环）及方差如表．甲乙丙丁平均数8.28.08.08.2方差 2.1 1.8 1.6 1.4根据表中数据选一人参加比赛，最合适的人选是（ ）A．甲B．乙C．丙D．丁4. 下列各式：2，，，，，其中多项式的个数是（ ）A．2B．3C．4D．55. 1999年11月1日起，国家对个人在银行的存款利息征收利息税，税率为20%（即存款到期后利息的20%），储户取款时由银行代扣代收，小杨于2006年1月9日存入期限为1年的人民币24000元，年利率为2.25%，到期时小杨拿回本息和为（ ）A．24540元B．24432元C．24506元D．24423元6. 不等式组的解集是（）A．－1≤＜2B．－1＜≤2C．－1≤≤2D．－1＜＜27. 下面四个选项中的美术字体，可以看做轴对称图形的是（）A．B．C．D．8. 以下调查中，最适合采用抽样调查的是（）A．调查某班学生的视力情况B．了解一沓钞票中有没有假钞C．了解某批次汽车的抗撞击能力D．检查神舟飞船的设备零件的质量情况9. 小颖随机抽样调查本校20名女同学所穿运动鞋尺码，并统计如表：尺码/cm21.522.022.523.023.5人数24383二、多选题学校附近的商店经理根据统计表决定本月多进尺码为23.0cm 的女式运动鞋，商店经理的这一决定应用的统计量是（ ）A ．平均数B ．加权平均数C ．众数D ．中位数10. 下列关于x 的一元二次方程中，没有实数根的是（ ）A．B．C．D．11. 依据“双减”政策要求，初中学生书面作业每天完成时间不超过90分钟．某中学为了解学生作业管理情况，抽查了七年级（一）班全体同学某天完成作业时长情况，绘制出如图所示的频数直方图：（数据分成3组：，，）．则下列说法正确的是（）A ．该班有40名学生B ．该班学生当天完成作业时长在分钟的人数最多C ．该班学生当天完成作业时长在分钟的频数是5D．该班学生当天完成作业时长在分钟的人数占全班人数的12.如图，，，平分，平分，关于下列结论：①，②，③平分，④，正确的有（）A ．①B ．②C ．③D ．④13. 如图，点P 在直线m 上移动，A ，B 是直线n上的两个定点，且直线．对于下列各值，不会随点P 的移动而变化的是（）A ．点P 到直线n 的距离B ．的周长C ．的面积D ．的大小14. 下列各式符合代数式书写规范的是（ ）A．B ．5aC．D ．（2n +m ）元15. 下列计算中，不正确的有（ ）A ．（ab 2）3＝ab 6B ．（3xy 2）3＝9x 3y 6C ．（﹣2x 3）2＝﹣4x 6D ．（﹣a 2m ）3＝a 6m三、填空题16. 下列运算错误的是（ ）A．B．C．D．17. 已知＜，则下列不等式中正确的是（ ）A ．4＜4B ．+4＜+4C ．－4＜－4D ．－4＜－418. 已知2a ＝3，2b ＝6，2c ＝12，则a ，b ，c 的关系如下，其中正确的有（ ）A ．b ＝a ＋1B ．c ＝a ＋2C ．a ＋c ＝2bD ．b ＋c ＝2a ＋3，19. （多选）小明进行投篮游戏，第一个没进，已知投篮20次，命中了17个，其中20次投篮的命中概率为，则下列哪个数一定会在中出现？（ ）A ．0.5B ．0.6C ．0.7D ．0.820. 如图，在⊙O 中，CD 是直径，弦AB ⊥CD ，垂足为E ，连接BC ，若AB=，∠BCD=30°，则⊙O 的半径是________．21. 如图，在每个小正方形的边长为1的网格中，的顶点，，均落在格点上，点为线段的中点．（Ⅰ）线段的长等于______；（Ⅱ）在线段上有两个动点，（点靠近点），满足．当取得最小值时，请用无刻度的直尺，在如图所示的网格中，画出点，点，并简要说明点，点的位置是如何找到的（不要求证明）________________________________________．22.若，则______．23. 分解因式：4x 2y 2+xy -1=___________________．24. 如图，圆柱高底面直径，高，一只蚂蚁从点出发，沿圆柱的侧面爬到点处，则蚂蚁爬行的最短路程为 _______（）．25. 如图，在矩形ABCD 中，E ，F 分别是AD ，BC 边上的点，AE ＝CF ，∠EFB ＝45°，若AB ＝5，BC ＝13，则AE 的长为_____．四、解答题五、解答题26. 为了了解某校800名初一学生的睡眠时间，从中抽取80名学生进行调查，在这个问题中样本容量是 ___．27. 如图，利用标杆BE 测量建筑物的高度，标杆BE 高1.5m ，测得AB=2m ，BC=14cm ，则楼高CD 为_______m．28. a是的整数部分，b 的立方根为-2，则a+b 的值为________．29. 如图，矩形ABCD 中，AB ＝2，BC ＝4，AE 为∠BAD 的角平分线，F 为AE 上一动点，M 为DF 的中点，连接BM ，则BM 的最小值是_____．30. 计算：．31. 化简分式并求值：，其中．32.计算：33. 计算：（1）；（2）．34. 计算(1)(2)35. 如图，已知平面内有四个点A ，B ，C ，D，按下列要求尺规作图（不写作法，保留作图痕迹）并解答．(1)画射线，直线，连接；(2)在线段的延长线上作；(3)在直线上确定一点P ，使得的值最小，并说明作图依据．六、解答题36. 如图，已知等边△ABC ，射线AM ，请用尺规作图法，在射线AM 上找一点D，使得．（保留作图痕迹，不写作法）37. 如图，在由边长为个单位长度的小正方形组成的的网格中，已知的顶点均为网格线的交点．在给定的网格中，画出关于直线对称的．将绕着点旋转后能与重合，请在网格中画出点的位置．在给定的网格中，画出以点为位似中心，将放大为原来的倍后得到的．38. 如图，方格纸中的每个小方格都是边长为个单位长度的正方形，建立平面直角坐标系后的顶点均在格点上．（1）作出关于轴对称的（2）写出顶点的坐标分别是，，（3）求39. 如图，在中，点为边的中点，请用尺规作图法在边上求作一点，使得．（保留作图痕迹，不写作法）40. 甲、乙、丙、丁四名同学进行一次乒乓球单打比赛，要从中选两位同学打第一场比赛．（1）请用树状图或列表法求恰好选中甲、乙两位同学的概率；（2）请利用若干个除颜色外其余都相同的乒乓球，设计一个摸球的实验（至少摸两次），并根据该实验写出一个发生概率与（1）所求概率相同的事件．41. 某公司设计了一款工艺品，每件的成本是40元，为了合力定价，投放市场进行试销：据市场调查，销售单价是50元时，每天的销售量是100件，而销售单价每提高1元，每天就减少售出2件，但要求销售单价不得超过65元．七、解答题（1）若销售单价为每件60元，求每天的销售利润；（2）要使每天销售这种工艺品盈利1350元，那么每件工艺品售价应为多少元？42. 去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为万元，第七天的营业额是前六天总营业额的．(1)求该商店去年“十一黄金周”这七天的总营业额；(2)去年，该商店月份的营业额为375万元，，月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与月份的营业额相等．求该商店去年，月份营业额的月增长率．43. 某商场经销-种进价为每千克50元的水产品，据市场分析，每千克售价为60元时，月销售量为，销售单价每涨1元时，月销售量就减少，针对这种情况，请解答以下问题：（1）当销售单价定为65元时，计算销售量和月销售利润；（2）若想在月销售成本不超过12000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？44. 某校七年级有象棋、足球、演讲、美术共四个社团，参加象棋社团的有人，参加足球社团的人数比象棋社团的人数的两倍少人，参加演讲社团的人数是足球社团人数的一半，每个学生都限报一项，参加社团的学生共有人．(1)足球社团有_________人，演讲社团有________人．（用含，的式子表示）(2)若，，求参加美术社团的人数．45. 如图，在中，，以FB 为直径作，与直角边AC 相切，切点为E．(1)求证：；(2)若，求的长．46. 对于一个三位正整数，如果十位上的数字是其百位上的数字与个位数字之和，那么我们称这个三位正整数为“十和数”．比如：三位正整数297，因为9＝2+7，所以297是“十和数”．已知一个三位正整数的个位，十位，百位上的数字分别为a ，b ，c ．(1)若某个三位正整数是“十和数”，请证明个三位正整数能被11整除；(2)已知某个三位正整数的各位上的数字之和是一个正整数的立方，且这个三位正整数是“十和数”，求满足条件的所有三位正整数．47. 【模型发现】某校七年级数学兴趣小组的同学在活动中发现：如图1的几何图形，很像小猪的猪蹄，于是大家就把这个图形形象的称为“猪踣模型”，“猪蹄模型”中蕴含着角的数量关系．(1)如图1，，是、之间的一点，连接，，则有．请你证明这个结论；【运用】(2)如图2，，、是、之间的两点，且，请你利用（1）中“猪蹄模型”的结论，找出、、三者之间的数量关系，并说明理由；【延伸】(3)如图3，，点、分别在、上，、分别平分和，且．如果，那么八、解答题等于多少？（用含的代数式表示，请直接写出结论，无需证明）48. 如图，在中，是的垂直平分线，与边交于点，点在直线上，且，连接．(1)求证：．(2)延长与交于点，若．①求证：是的中点；②连接，若，则与的数量关系是 49. 如图，点E 是∠AOB 的平分线上一点，EC ⊥OA ，ED ⊥OB ，垂足分别为C 、D．(1)求证：∠ECD =∠EDC ；(2)若∠AOB =60°，OE=8，试求EF 的长．50. 如图，⊙O 的半径为7，是的弦，点P 在弦上，若，，求的长．51. 如图，已知点P 、Q分别在的边上，按下列要求画图：(1)画射线；(2)过点P画垂直于射线的线段，垂足为点C ；(3)过点Q画直线平行于射线．52. 已知2b+3的平方根是±3，3a+2b+1的算术平方根为4，求3a+6b 的立方根；九、判断题53. 已知梯形上底的长是，下底的长是，高是，梯形的面积记为．(1)求梯形的面积与上底长之间的关系式；(2)请将下面的表格补充完整，并说明当每增加时，如何变化；(3)当时，的值表示的含义是什么？54. 已知A －B=7a 2－7ab ，且B=－4a 2＋5ab ＋8．求A 等于多少．55. 一个整数省略“万”后面尾数后约等于20万，这个数最大是199999( )56. 请判断下面说法正确与否：与的交点在第一象限或第四象限_____．57. 在同一平面图上，数对和数对所表示的位置相同．( )58. 六（1）班同学的平均体重是，如果把平均体重记作，红红同学记作，聪聪同学记作．( )59. 妈妈花450元买了一条裙子，是按照先打八折，再打九五折优惠的，这条裙子的标价是600元．( )。

中考数学压轴题测试综合卷检测试卷

中考数学压轴题测试综合卷检测试卷

一、中考数学压轴题1．AB 是O 直径，,C D 分别是上下半圆上一点，且弧BC =弧BD ，连接,AC BC ，连接CD 交AB 于E ，（1）如图(1)求证：90AEC ∠=︒；（2）如图(2)F 是弧AD 一点，点,M N 分别是弧AC 和弧FD 的中点，连接FD ，连接MN 分别交AC ，FD 于,P Q 两点，求证：MPC NQD ∠=∠（3）如图(3)在(2)问条件下，MN 交AB 于G ，交BF 于L ，过点G 作GH MN ⊥交AF 于H ，连接BH ，若,6,BG HF AG ABH ==∆的面积等于8，求线段MN 的长度2．已知：如图①，在等腰直角ABC ∆中，斜边2AC =．（1）请你在图①的AC 边上求作一点P ，使得90APB ∠=︒；（2）如图②，在（1）问的条件下，将AC 边沿BC 方向平移，使得点A 、P 、C 对应点分别为E 、Q 、D ，连接AQ ，BQ ．若平移的距离为1，求AQB ∠的大小及此时四边形ABDE 的面积；（3）将AC 边沿BC 方向平移m 个单位至ED ，是否存在这样的m ，使得在直线DE 上有一点M ，满足30AMB ∠=︒，且此时四边形ABDE 的面积最大？若存在，求出四边形ABDE 面积的最大值及平移距离m 的值；若不存在，请说明理由．3．如图，已知抛物线y ＝2ax bx c ++与x 轴交于A 3,0-（），B 33,0（）两点，与y 轴交于点C 0,3（）．（1）求抛物线的解析式及顶点M 坐标；（2）在抛物线的对称轴上找到点P ，使得PAC 的周长最小，并求出点P 的坐标； （3）在（2）的条件下，若点D 是线段OC 上的一个动点（不与点O 、C 重合）．过点D 作DE //PC 交x 轴于点E ．设CD 的长为m ，问当m 取何值时，PDE ABMC 1S S 9=四边形． 4．如图所示，在平面直角坐标系中，点(),C m m 在一三象限角平分线上，点(),0B n 在x 轴上，且m=2n -+2n -+4，点A 在y 轴的正半轴上；四边形AOBC 的面积为6 （1）求点A 的坐标；（2）P 为AB 延长线上一点，//PQ OC ，交CB 延长线于Q ，探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由；（3）作AD 平行CB 交CO 延长线于D ，BE 平分CBx ∠，BE 反向延长线交CO 延长线于，若设ADO α∠=，F β∠=，试求2αβ+的值．5．“阅读素养的培养是构建核心素养的重要基础，重庆十一中学校以‘大阅读’特色课程实施为突破口，着力提升学生的核心素养．”全校师生积极响应和配合，开展各种活动丰富其课余生活．在数学兴趣小组中，同学们从书上认识了很多有趣的数．其中有一个“和平数”引起了同学们的兴趣．描述如下：一个四位数，记千位上和百位上的数字之和为x ，十位上和个位上的数字之和为y ，如果x y =，那么称这个四位数为“和平数”． 例如：1423，14x =+，23y =+，因为x y =，所以1423是“和平数”．（1）直接写出：最小的“和平数”是________，最大的“和平数”是__________；（2）求同时满足下列条件的所有“和平数”：①个位上的数字是千位上的数字的两倍；②百位上的数字与十位上的数字之和是12的倍数；（3）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后这两个“和平数”为“相关和平数”．例如：1423于4132为“相关和平数”求证：任意的两个“相关和平数”之和是1111的倍数．6．一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，第一颗弹珠弹出后其速度1y （米/分钟）与时间x （分钟）前2分钟满足二次函数21y ax =，后3分钟满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟．（1）求第一颗弹珠的速度1y （米/分钟）与时间x （分钟）之间的函数关系式；（2）第一颗弹珠弹出1分钟后，弹出第二颗弹珠，第二颗弹珠的运行情况与第一颗相同，直接写出第二颗弹珠的速度2y （米/分钟）与弹出第一颗弹珠后的时间x （分钟）之间的函数关系式；（3）当两颗弹珠同时在轨道上时，第____分钟末两颗弹珠的速度相差最大，最大相差______；（4）判断当两颗弹珠同时在轨道上时，是否存在某时刻速度相同？请说明理由，并指出可以通过解哪个方程求出这一时刻．7．在平面直角坐标系xOy 中，对于点A 和图形M ，若图形M 上存在两点P ，Q ，使得3AP AQ =，则称点A 是图形M 的“倍增点”．（1）若图形M 为线段BC ，其中点()2,0B -，点()2,0C ，则下列三个点()1,2D -，()1,1E -，()0,2F 是线段BC 的倍增点的是_____________；（2）若O 的半径为4，直线l ：2y x =-+，求直线l 上O 倍增点的横坐标的取值范围；（3）设直线1y x =-+与两坐标轴分别交于G ，H ，OT 的半径为4，圆心T 是x 轴上的动点，若线段GH 上存在T 的倍增点，直接写出圆心T 的横坐标的取值范围．8．如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2+bx+c 的图象与x 轴交于A （﹣3，0）、B （2，0）两点，与y 轴交于点C （0，3）．（1）求抛物线的解析式；（2）点E （m ，2）是直线AC 上方的抛物线上一点，连接EA 、EB 、EC ，EB 与y 轴交于D ．①点F 是x 轴上一动点，连接EF ，当以A 、E 、F 为顶点的三角形与△BOD 相似时，求出线段EF 的长；②点G 为y 轴左侧抛物线上一点，过点G 作直线CE 的垂线，垂足为H ，若∠GCH ＝∠EBA ，请直接写出点H 的坐标．9．对于平面内的点M 和点N ，给出如下定义：点P 为平面内的一点，若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形，则称点P 是点M 关于点N 的锐角等腰点P ．如图，点P 是点M 关于点N 的锐角等腰点．在平面直角坐标系xOy 中，点O 是坐标原点．（1）已知点(2,0)A ，在点123(0,2),(1,3),(1,3)P P P -，4(2,2)P -中，是点O 关于点A 的锐角等腰点的是___________．（2）已知点(3,0)A ，点C 在直线2y x b =+上，若点C 是点O 关于点A 的锐角等腰点，求实数b 的取值范围．（3）点D 是x 轴上的动点，(,0),(2,0)D t E t -，点(,)F m n 是以D 为圆心，2为半径的圆上一个动点，且满足0n ≥．直线24y x =-+与x 轴和y 轴分别交于点H K ，，若线段HK 上存在点E 关于点F 的锐角等腰点，请直接写出t 的取值范围．10．（1）如图①，在Rt ABC 中，90C ∠=︒，13AB =，5BC =，则tan A 的值是_______．（2）如图②，在正方形ABCD 中，5AB =，点E 是平面上一动点，且2BE =，连接CE ，在CE 上方作正方形EFGC ，求线段CF 的最大值．问题解决：（3）如图③，O 半径为6，在Rt ABC 中，90B ∠=︒，点, A B 在O 上，点C 在O 内，且3tan 4A =．当点A 在圆上运动时，求线段OC 的最小值．11．已知：菱形 ABCD ，点 E 在线段 BC 上，连接 DE ，点 F 在线段 AB 上，连接 CF 、DF ， CF 与 DE 交于点 G ，将菱形 ABCD 沿 DF 翻折，点 A 恰好落在点 G 上．（1）求证：CD=CF ；（2）设∠CED = x ，∠DCF = y ，求 y 与 x 的函数关系式；（不要求写出自变量的取值范围） （3）在（2）的条件下，当 x =45°时，以 CD 为底边作等腰△CDK ，顶角顶点 K 在菱形 ABCD 的内部，连接 GK ，若 GK ∥CD ，CD =4 时，求线段 KG 的长．12．如图1，在O 中，弦AB ⊥弦CD ，垂足为点E ，连接AD 、BC 、AO ，AD AB =．（1）求证：2CAO CDB ∠=∠（2）如图2，过点O 作OH AD ⊥，垂足为点H ，求证：2OH CE DE +=（3）如图3，在（2）的条件下，延长DB 、AC 交于点F ，过点D 作DM AC ⊥，垂足为M ，交AB 于N ，若12BC =，3AF BF =，求MN 的长．13．如图，正方形ABCD 的边长为8，M 是AB 的中点，P 是BC 边上的动点，连结PM ，以点P 为圆心，PM 长为半径作⊙P ．（1）当BP ＝ 时，△MBP ～△DCP ；（2）当⊙P 与正方形ABCD 的边相切时，求BP 的长；（3）设⊙P 的半径为x ，请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围．14．在平面直角坐标系xOy 中，点A 为x 轴上的动点，点B 为x 轴上方的动点，连接OA ，OB ，AB ．（1）如图1，当点B 在y 轴上，且满足OAB ∠的角平分线与OBA ∠的角平分线交于点P ，请直接写出P ∠的度数；（2）如图2，当点B 在y 轴上，OAB ∠的角平分线与OBA ∠的角平分线交于点P ，点C 在BP 的延长线上，且满足45AOC ∠=︒，求OAB OCB∠∠；（3）如图3，当点B 在第一象限内，点P 是AOB ∆内一点，点M ，N 分别是线段OA ，OB 上一点，满足：1902APB AOB ∠=︒+∠，PM PN =，180ONP OMP ∠+∠=︒．以下结论：①OM ON =；②AP 平分OAB ∠；③BP 平分OBA ∠；④AM BN AB +=．正确的是：________．（请填写正确结论序号，并选择一个正确的结论证明，简写证明过程）．15．如图，在矩形ABCD 中，6AB cm =，8AD cm =，连接BD ，将ABD △绕B 点作顺时针方向旋转得到A B D '''△（B ′与B 重合），且点D '刚好落在BC 的延长上，A D ''与CD 相交于点E ．（1）求矩形ABCD 与A B D '''△重叠部分（如图1中阴影部分A B CE ''）的面积； （2）将A B D '''△以每秒2cm 的速度沿直线BC 向右平移，如图2，当B ′移动到C 点时停止移动．设矩形ABCD 与A B D '''△重叠部分的面积为y ，移动的时间为x ，请你直接写出y 关于x 的函数关系式，并指出自变量x 的取值范围；（3）在（2）的平移过程中，是否存在这样的时间x ，使得AA B ''△成为等腰三角形？若存在，请你直接写出对应的x 的值，若不存在，请你说明理由．16．在Rt ABC ∆中，6AB =，90B ∠=︒，8BC =，点P 从A 出发沿AC 方向在运动速度为3个单位/秒，点Q 从C 出发向点B 运动，速度为1个单位/秒，P 、Q 同时出发，点Q 到点B 时两点同时停止运动．（1）点P 在线段AC 上运动，过P 作DP PQ ⊥交边AB 于D ，2t =时，求PD PQ 的值； （2）运动t 秒后，90BPQ ∠=︒，求此时t 的值；（3）t =________时，AQ QP =． 17．已知：AB 为⊙O 的直径，点C 为弧AB 的中点，点D 为⊙O 上一点，连接CD ，交AB 于点M ，AE 为∠DAM 的平分线，交CD 于点E ．（1）如图1，连接BE ，若∠ACD=22°，求∠MBE 的度数；（2） 如图2，连接DO 并延长，交⊙O 于点F ，连接AF ，交CD 于点N ．①求证：DM 2+CN 2=CM 2；②如图3，当AD=1，10时，请直接写出．．．．线段ME 的长． 18．已知抛物线2y ax bx c =++过点(6,0)A -，(2,0)B ，(0,3)C -．（1）求此抛物线的解析式；（2）若点H 是该抛物线第三象限的任意一点，求四边形OCHA 的最大面积；（3）若点Q 在y 轴上，点G 为该抛物线的顶点，且45GQA ∠=︒，求点Q 的坐标．19．问题提出（1）如图1，已知三角形ABC ，请在BC 边上确定一点D ，使得AD 的值最小． 问题探究（2）如图2，在等腰ABC 中，AB AC =，点P 是AC 边上一动点，分别过点A ，点C 作线段BP 所在直线的垂线，垂足为点,D E ，若5,6AB BC ==，求线段BP 的取值范围，并求AD CE +的最大值．问题解决（3）如图3，正方形ABCD 是一块蔬菜种植基地，边长为3千米，四个顶点处都建有一个蔬菜采购点，根据运输需要，经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道，其余三个采购点都修建垂直于快速通道的蔬菜输送轨道，分别为BB '、CC '、DD '．若你是此次项目设计的负责人，要使三条运输轨道的距离之和()BB CC DD '''++最小，你能不能按照要求进行规划，请通过计算说明．20．在综合与实践课上老师将直尺摆放在三角板上，使直尺与三角板的边分别交于点P 、M 、N 、Q ，（1）如图①所示．当∠CNG ＝42°，求∠HMC 的度数．（写出证明过程）（2）将直尺向下平移至图 2 位置，使直尺的边缘通过点 C ，交 AB 于点 P ，直尺另一侧与三角形交于 N 、Q 两点。

中考数学数学中考数学压轴题的专项培优易错试卷练习题含答案

中考数学数学中考数学压轴题的专项培优易错试卷练习题含答案

一、中考数学压轴题1．在菱形ABCD 中，P 为直线DA 上的点，Q 为直线CD 上的点，分别连接PC ，PQ ，且PC PQ =．（1）若60B ∠=︒，点P 在线段DA 上，点Q 在线段CD 的延长线上，如图①，易证：DQ PD AB +=（不需证明）；（2）如图②，若∠B ＝120°，点P 在线段DA 上，点Q 在线段CD 的延长线上，如图③，猜想线段DQ ，PD 和AB 之间有怎样的数量关系？请直接写出对图②，图③的猜想，并选择其中一种情况给予证明．2．如图所示，在平面直角坐标系中，点(),C m m 在一三象限角平分线上，点(),0B n 在x 轴上，且m=2n -+2n -+4，点A 在y 轴的正半轴上；四边形AOBC 的面积为6 （1）求点A 的坐标；（2）P 为AB 延长线上一点，//PQ OC ，交CB 延长线于Q ，探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由；（3）作AD 平行CB 交CO 延长线于D ，BE 平分CBx ∠，BE 反向延长线交CO 延长线于，若设ADO α∠=，F β∠=，试求2αβ+的值．3．已知：如图，AB 为O 的直径，弦CD AB ⊥垂足为E ，点H 为弧AC 上一点．连接DH 交AB 于点F ，连接HA 、BD ，点G 为DH 上一点，连接AG ，HAG BDC ∠=∠． （1）如图1，求证：AG HD ⊥；（2）如图2，连接HC ，若HC HF =，求证：HC HA =；（3）如图3，连接HO 交AG 于点K ，若点F 为DG 的中点，HC 2HG =，求KG AK的值．4．我们知道，平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系，如果两条数轴不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么这两条数轴构成的是平面斜坐标系，两条数轴称为斜坐标系的坐标轴，公共原点称为斜坐标系的原点，如图1，经过平面内一点P 作坐标轴的平行线PM 和PN ，分别交x 轴和y 轴于点M ，N ．点M 、N 在x 轴和y 轴上所对应的数分别叫做P 点的x 坐标和y 坐标，有序实数对（x ，y ）称为点P 的斜坐标，记为P （x ，y ）（1）如图2，ω＝45°，矩形OABC 中的一边OA 在x 轴上，BC 与y 轴交于点D ， OA ＝2，OC ＝1．①点A 、B 、C 在此斜坐标系内的坐标分别为A ，B ，C ．②设点P （x ，y ）在经过O 、B 两点的直线上，则y 与x 之间满足的关系为 ． ③设点Q （x ，y ）在经过A 、D 两点的直线上，则y 与x 之间满足的关系为 ． （2）若ω＝120°，O 为坐标原点．①如图3，圆M 与y 轴相切原点O ，被x 轴截得的弦长OA ＝3，求圆M 的半径及圆心M 的斜坐标．②如图4，圆M 的圆心斜坐标为M （33y 轴的距离为1，则圆M 的半径r 的取值范围是 ．5．已知抛物线217222y x mx m 的顶点为点C ． （1）求证：不论m 为何实数，该抛物线与x 轴总有两个不同的交点；（2）若抛物线的对称轴为直线3x ，求m 的值和C 点坐标；（3）如图，直线1y x =-与（2）中的抛物线并于A B 、两点，并与它的对称轴交于点D ，直线x k =交直线AB 于点M ，交抛物线于点N ．求当k 为何值时，以C D M N 、、、为顶点的四边形为平行四边形．6．如图，在四边形ABCD 中，∠B=90°，AD//BC ，AD=16，BC=21，CD=13．（1）求直线AD 和BC 之间的距离；（2）动点P 从点B 出发，沿射线BC 以每秒2个单位长度的速度运动，动点Q 从点A 出发，在线段AD 上以每秒1个单位长度的速度运动，点P 、Q 同时出发，当点Q 运动到点D 时，两点同时停止运动，设运动时间为t 秒．试求当t 为何值时，以P 、Q 、D 、C 为顶点的四边形为平行四边形？（3）在（2）的条件下，是否存在点P ，使△PQD 为等腰三角形？若存在，请直接写出相应的t 值，若不存在，请说明理由．7．如图，90EOF ∠=︒，矩形ABCD 的边BA 、BC 分别在OF 、OE 上，4AB =，3BC =，矩形ABCD 沿射线OD 方向，以每秒1个单位长度的速度运动．同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动，当点P 到达点C 时，矩形ABCD 也停止运动，设点P 的运动时间为()t s ，PDO △的面积为S ．（1）分别写出点B 到OF 、OE 的距离（用含t 的代数式表示）；（2）当点P 不与矩形ABCD 的顶点重合时，求S 与t 之间的函数关系式；（3）设点P 到BD 的距离为h ，当15h OD =时，求t 的值； （4）若在点P 出发的同时，点Q 从点B 以每秒43个单位长度的速度向终点A 运动，当点Q 停止运动时，点P 与矩形ABCD 也停止运动，设点A 关于PQ 的对称点为E ，当PQE 的一边与CDB △的一边平行时，直接写出线段OD 的长．8．对于平面直角坐标系xOy 中的任意点()P x y ，，如果满足x y a += (x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点(1,2),(1,3),(2.5,0)A B C 中，满足此条件的特征点为__________________；②⊙W 的圆心为(,0)W m ，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数()10Z x x x=+>，请利用特征点求出该函数的最小值．9．如图1，抛物线23y ax bx =++与x 轴交于点(1,0)A -、点B ，与y 轴交于点C ，顶点D 的横坐标为1，对称轴交x 轴交于点E ，交BC 与点F .（1）求顶点D 的坐标；（2）如图2所示，过点C 的直线交直线BD 于点M ，交抛物线于点N .①若直线CM 将BCD ∆分成的两部分面积之比为2:1，求点M 的坐标；②若NCB DBC ∠=∠，求点N 的坐标．10．如图，在正方形ABCD 中，DC=8，现将四边形BEGC 沿折痕EG(G ，E 分别在DC ，AB 边上)折叠，其顶点B ，C 分别落在边AD 上和边DC 的上部，其对应点设为F ，N 点，且FN 交DC 于M ．特例体验：(1)当FD=AF 时，△FDM 的周长是多少?类比探究：(2)当FD≠AF≠0时，△FDM 的周长会发生变化吗?请证明你的猜想．拓展延伸：(3)同样在FD≠AF≠0的条件下，设AF 为x ，被折起部分(即：四边形FEGN)的面积为S ，试用含x 的代数式表示S ，并问：当x 为何值时，S=26?11．定义：两个相似等腰三角形，如果它们的底角有一个公共的顶点，那么把这两个三角形称为“关联等腰三角形”．如图，在ABC ∆与AED ∆中，,BA BC EA ED == ，且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”，设它们的顶角为α，连接,EB DC ，则称DC EB 会为“关联比"． 下面是小颖探究“关联比”与α之间的关系的思维过程，请阅读后，解答下列问题：[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”，且90α︒=时， ①在图1中，若点E 落在AB 上，则“关联比”DC EB=②在图2中，探究ABE ∆与ACD ∆的关系，并求出“关联比”DC EB的值．[类比探究]()2如图3，①当ABC ∆与AED ∆为“关联等腰三角形”，且120a ︒=时，“关联比”DC EB = ②猜想：当ABC ∆与AED ∆为“关联等腰三角形”，且n α=︒时，“关联比”DC EB= (直接写出结果，用含n 的式子表示)[迁移运用] ()3如图4， ABC ∆与AED ∆为“关联等腰三角形”．若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点，且1PA =，点E 为PB 上一动点，求点E 自点B 运动至点P 时，点D 所经过的路径长．12．如图，已知抛物线y ＝2ax bx c ++与x 轴交于A 3,0-（），B 33,0（）两点，与y 轴交于点C 0,3（）．（1）求抛物线的解析式及顶点M 坐标；（2）在抛物线的对称轴上找到点P ，使得PAC 的周长最小，并求出点P 的坐标； （3）在（2）的条件下，若点D 是线段OC 上的一个动点（不与点O 、C 重合）．过点D 作DE //PC 交x 轴于点E ．设CD 的长为m ，问当m 取何值时，PDE ABMC 1S S 9=四边形． 13．如图，直线y ＝﹣x+4与抛物线y ＝﹣12x 2+bx+c 交于A ，B 两点，点A 在y 轴上，点B 在x 轴上．（1）求抛物线的解析式；（2）在x 轴下方的抛物线上存在一点P ，使得∠ABP ＝90°，求出点P 坐标；（3）点E 是抛物线对称轴上一点，点F 是抛物线上一点，是否存在点E 和点F 使得以点E ，F ，B ，O 为顶点的四边形是平行四边形？若存在，求出点F 的坐标；若不存在，请说明理由．14．新定义，若关于x ，y 的二元一次方程组①111222a x b y c a x b y c +=⎧⎨+=⎩的解是00x x y y =⎧⎨=⎩，关于x ，y 的二元一次方程组②111222e x f y d e x f y d +=⎧⎨+=⎩的解是11x x y y =⎧⎨=⎩，且满足1000.1x x x -≤，1000.1y y y -≤，则称方程组②的解是方程组①的模糊解．关于x ，y 的二元一次方程组222104x y m x y m +=+⎧⎨-=+⎩的解是方程组10310x y x y +=⎧⎨+=-⎩的模糊解，则m 的取值范围是________． 15．如图，在平面直角坐标系中，矩形ABCD 的顶点,A D 在坐标轴上，两点的坐标分别是点()0,,A m 点(),0,D m 且m 满足：322m m -+62=边AB 与x 轴交于点,E 点F 是边AD 上一动点，连接FB ，分别与x 轴，y 轴交于点,P 点,H 且FD BE =．（1）求m 的值；（2）若45,APF ∠=︒求证：AHF HFA ∠=∠；（3）若点F 的纵坐标为,n 则线段HF 的长为 ．(用含n 的代数式表示)16．在Rt ABC ∆中，6AB =，90B ∠=︒，8BC =，点P 从A 出发沿AC 方向在运动速度为3个单位/秒，点Q 从C 出发向点B 运动，速度为1个单位/秒，P 、Q 同时出发，点Q 到点B 时两点同时停止运动．（1）点P 在线段AC 上运动，过P 作DP PQ ⊥交边AB 于D ，2t =时，求PD PQ的值； （2）运动t 秒后，90BPQ ∠=︒，求此时t 的值；（3）t =________时，AQ QP =．17．如图，四边形AOBC 是正方形，点C 的坐标是(82,0)．（1）正方形AOBC 的边长为 ，点A 的坐标是 ；（2）将正方形AOBC 绕点O 顺时针旋转45︒，点A ，B ，C 旋转后的对应点为A '，B '，C '，求点A '的坐标及旋转后的正方形与原正方形的重叠部分的面积；（3）动点P 从点O 出发，沿折线OACB 方向以1个单位/秒的速度匀速运动，同时，另一动点Q 从点O 出发，沿折线OBCA 方向以2个单位/秒的速度匀速运动，运动时间为t秒，当它们相遇时同时停止运动，当OPQ △为等腰三角形时，求出t 的值（直接写出结果即可）．18．已知四边形ABCD 为矩形，对角线AC 、BD 相交于点O ，AD ＝AO ．点E 、F 为矩形边上的两个动点，且∠EOF ＝60°．（1）如图1，当点E 、F 分别位于AB 、AD 边上时，若∠OEB ＝75°，求证：DF ＝AE ； （2）如图2，当点E 、F 同时位于AB 边上时，若∠OFB ＝75°，试说明AF 与BE 的数量关系；（3）如图3，当点E 、F 同时在AB 边上运动时，将△OEF 沿OE 所在直线翻折至△OEP ，取线段CB 的中点Q ．连接PQ ，若AD ＝2a （a ＞0），则当PQ 最短时，求PF 之长．19．如图，直角梯形ABCD 中，1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠＝＝＝＝的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动，2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动，1O 半径为22,cm O 的半径为4cm ，若12,O O 分别从点A 、点B 同时出发，运动的时间为ts（1）请求出2O 与腰CD 相切时t 的值；（2）在03s t s ≤＜范围内，当t 为何值时，1O 与2O 外切？20．如图，在等腰Rt △ABC 中，∠ACB=90°，AC=BC=8，点D 在△ABC 外，连接AD 、BD ，且∠ADB=90°，AB 、CD 相交于点E ，AB 、CD 的中点分别是点F 、G ，连接FG ．（1）求AB 的长；（2）求证：2CD ；（3）若BD=6，求FG 的值．21．如图1，在平面直角坐标系中，O 是坐标原点，矩形OACB 的顶点A 、B 分别在x 轴和y 轴上，已知OA=5，OB=3，点D 的坐标是（0，1），点P 从点B 出发以每秒1个单位的速度沿折线BCA 的方向运动，当点P 与点A 重合时，运动停止，设运动的时间为t 秒．（1）点P 运动到与点C 重合时，求直线DP 的函数解析式；（2）求△OPD 的面积S 关于t 的函数解析式，并写出对应t 的取值范围；（3）点P 在运动过程中，是否存在某些位置使△ADP 是不以DP 为底边的等腰三角形，若存在，请求出点P 的坐标；若不存在，请说明理由．22．在平面直角坐标系xOy 中，点A 、B 为反比例函数()4x 0x y =>的图像上两点，A 点的横坐标与B 点的纵坐标均为1，将()4x 0x y =>的图像绕原点O 顺时针旋转90°，A 点的对应点为A’，B 点的对应点为B’．（1）点A’的坐标是 ，点B’的坐标是 ；（2）在x 轴上取一点P ，使得PA+PB 的值最小，直接写出点P 的坐标． 此时在反比例函数()4x 0xy =>的图像上是否存在一点Q ，使△A’B’Q 的面积与△PAB 的面积相等，若存在，求出点Q 的横坐标；若不存在，请说明理由；（3）连接AB’，动点M 从A 点出发沿线段AB’以每秒1个单位长度的速度向终点B’运动；动点N 同时从B’点出发沿线段B’A’以每秒1个单位长度的速度向终点A’运动．当其中一个点停止运动时，另一个点也随之停止运动．设运动的时间为t 秒，试探究：是否存在使△MNB’为等腰直角三角形的t 值．若存在，求出t 的值；若不存在，说明理由．23．发现来源于探究．小亮进行数学探究活动，作边长为a 的正方形ABCD 和边长为b 的正方形AEFG （a>b ），开始时，点E 在AB 上，如图1．将正方形AEFG 绕点A 逆时针方向旋转．（1）如图2，小亮将正方形AEFG 绕点A 逆时针方向旋转，连接BE 、DG ，当点G 恰好落在线段BE 上时，小亮发现DG ⊥BE ，请你帮他说明理由．当a=3，b=2时，请你帮他求此时DG 的长．（2）如图3，小亮旋转正方形AEFG ，点E 在DA 的延长线上，连接BF 、DF ．当FG 平分∠BFD 时，请你帮他求a ：b 及∠FBG 的度数．（3）如图4，BE 的延长线与直线DG 相交于点P ，a=2b ．当正方形AEFG 绕点A 从图1开始，逆时针方向旋转一周时，请你帮小亮求点P 运动的路线长（用含b 的代数式表示）．24．（1）探究发现数学活动课上，小明说“若直线21y x =-向左平移3个单位，你能求平移后所得直线所对应函数表达式吗？”经过一番讨论，小组成员展示了他们的解答过程：在直线21y x =-上任取点()01A -，， 向左平移3个单位得到点()31，'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+．因为2y x n =+过点()31，'--A ， 所以61n -+=-，所以5n =，填空：所以平移后所得直线所对应函数表达式为（2）类比运用已知直线21y x =-，求它关于x 轴对称的直线所对应的函数表达式；（3）拓展运用将直线21y x =-绕原点顺时针旋转90°，请直接写出：旋转后所得直线所对应的函数表达式 ．25．如图，抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点，与y 轴交于点B ．()1求这条抛物线的顶点坐标；()2已知AD AB =(点D 在线段AC 上)，有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动：同时另一个点Q 以某一速度从点B 沿线段BC 移动，经过()t s 的移动，线段PQ 被BD 垂直平分，求t 的值；()3在()2的情况下，抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在，请求出点M 的坐标：若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．A解析：（1）见解析；（2）②结论：PD DQ AB -=；③结论：DQ PD AB -=，证明见解析【解析】【分析】（1）连接AC ，过P 作PE ∥CD 交AC 于E ，由四边形ABCD 是菱形，∠B=60°，得出△ACD 是等边三角形，∠PDQ=120°，由PE ∥CD ，得出△APE 是等边三角形，∠PEC=120°，由AAS 证得△PCE ≌△PQD ，得出PE=DQ ，AP=DQ ，即可得出结论；（2）①结论：PD DQ AB -=．如图②中，延长CA 到M ，使得AM AP =，连接PM ．只要证明PAM ∆是等边三角形，PCM PQD ∆≅∆即可解决问题； ②结论：DQ PD AB -=．如图③中，在DQ 上截取DM DP =，连接PM ．只要证明PDM ∆是等边三角形，PCM PQD ∆≅∆即可解决问题；【详解】解：（1）证明：连接AC ，过P 作PE ∥CD 交AC 于E ，如图①所示：∵四边形ABCD 是菱形，∴AD=CD=AB ，∠ADC=∠B=60°，∴△ACD 是等边三角形，∠PDQ=120°，∴AC=AD ，∠DAC=∠ACD=60°，∵PE ∥CD ，∴∠AEP=∠ACD=60°，∠APE=∠ADC=60°，∴△APE 是等边三角形，∠PEC=120°，∴AE=PE=AP ，∵PC=PQ ，∴∠PCQ=∠Q ，∵∠ACD=∠ECP+∠PCQ ，∠ADC=∠DPQ+∠Q ，∴∠ECP=∠DPQ ，在△PCE 和△PQD 中，120PEC PDQ ECP DPQPC PQ ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩， ∴△PCE ≌△PQD （AAS ），∴PE=DQ ，∴AP=DQ ，∴DQ+PD=AP+PD=AD=AB ；（2）②结论：PD DQ AB -=．理由：如图②中，延长CA 到M ，使得AM AP =，连接PM ．四边形ABCD 是菱形，60B ∠=︒，ABC ∆∴，ACD ∆都是等边三角形，60CAD PAM ∴∠=∠=︒，PAM ∴∆是等边三角形，AM PM ∴=，60M ACD ∠=∠=︒，//PM CD ∴，180PCD CPM ∴∠+∠=︒，PC PQ =，PCQ PQC ∴∠=∠，180PQC PQD ∠+∠=︒，CPM PQD ∴∠=∠，PCM PQD ∴∆≅∆，CM PD ∴=，PM QD AM ==，CM AC AM AB QD =+=+，PD DQ AB ∴-=；③结论：DQ PD AB -=．理由：如图③中，在DQ 上截取DM DP =，连接PM ．120B ADC ∠=∠=︒，60PDM ∴∠=︒，DP DM =，PDM ∴∆是等边三角形，PD PM ∴=，60PMC PDQ ∠=∠=︒，PC PQ =，PCM Q ∴∠=∠，PCM PQD ∴∆≅∆，CM DQ ∴=，CD DM DQ ∴+=，AB PD DQ ∴+=，DQ PD AB ∴-=．【点睛】本题考查四边形综合题、菱形的性质、等边三角形的性质和判定、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．2．A解析：（1）A （0，1）（2）结论：∠ABQ +∠OAB ﹣∠Q ＝135°.（3）α+2β＝45°．【解析】【分析】（1）利用二次根式的性质求出m 、n 的值，求出B 、C 两点坐标，由S 四边形AOBC ＝S △OBC +S △AOC ，推出12×2×4+12×OA ×4＝6，求出OA 即可； （2）如图2中，结论：∠ABQ +∠OAB ﹣∠Q ＝135°．根据三角形内角和定理，三角形的外角的性质即可解决问题；（3）由AD∥BC，推出∠ADC＝∠DCB＝α，由BE平分∠CBx，推出∠CBE＝∠EBx，由∠CBE＝∠F+∠OCB＝α+β，推出∠OBF＝∠EBx＝α+β，由OC平分∠AOB，可得∠COB＝45°＝∠F+∠OBF＝α+（α+β），由此即可解决问题；【详解】解：（1）由题意2020nn-≥⎧⎨-≥⎩，，得，解得n＝2，∴m＝4，B（2，0），C（4，4）．如图：∵S四边形AOBC＝S△OBC+S△AOC，∴12×2×4+12×OA×4＝6，∴OA＝1，∴A（0，1）．（2）结论：∠ABQ+∠OAB﹣∠Q＝135°．如图：理由如下：∵OC∥PQ，∴∠Q＝∠OCB，∵∠ABQ＝∠1+∠OCB＝∠1+∠Q，∠1＝180°﹣∠OAB﹣∠AOC＝180°﹣∠OAB﹣45°＝135°﹣∠OAB，∴∠ABQ＝∠Q+135°﹣∠OAB，∴∠ABQ+∠OAB﹣∠Q＝135°．（3）如图：∵AD ∥BC ，∴∠ADC ＝∠DCB ＝α，∵BE 平分∠CBx ，∴∠CBE ＝∠EBx ，∵∠CBE ＝∠F +∠OCB ＝α+β，∴∠OBF ＝∠EBx ＝α+β，∵C （4，4），∴OC 平分∠AOB ，∴∠COB ＝45°＝∠F +∠OBF ＝α+（α+β），∴α+2β＝45°．【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识，解题的关键是灵活运用所学知识解决问题，属于压轴题．3．A解析：（1）详见解析；（2）详见解析；（3）15KG AK = 【解析】【分析】（1）根据同弧所对的圆周角相等，进行角度计算，得90AHG HAG ∠+∠=︒，进而得到90AGH ∠=︒，即可证明AG HD ⊥；（2）连接AC 、AD 、CF ，根据同弧所对的圆周角相等，进行角度计算，得HFA HAF ∠=∠，进而得到HF HA =，再根据已知HC HF =，得到HC HA =； （3）在DH 上截取DT HC =，过点C 作CM HD ⊥于点M ，通过证明AHC ≌ATD 得到AH AT =，进而得到HG CH GD +=，再根据F 为DG 中点，得到GF DF =，通过勾股定理逆用，证明90HCF ∠=︒，再通过解ACE △得1tan 3CAB ∠=，解△CDH 得1tan 2CDF ∠=，求得OF 、OH ，逆用勾股定理证明90HOF ∠=︒，易求1tan 2KHG ∠=，1tan 3HAG ∠=，最后求得KG AK 的值． 【详解】（1）证明：如图，设HAG ∠为α，∵HAG BDC ∠=∠，∴HAG BDC α∠=∠=，∵CD AB ⊥，∴90BDC DBE ∠+∠=︒∴90DBE α∠=︒-，∵AHG ∠与ABD ∠为同对弧AD 所对的圆周角，∴90AHG ABD α∠=∠=︒-，∴90AHG HAG ∠+∠=︒，∴18090AGH AHG HAG ∠=︒-∠-∠=︒∴AG HD ⊥（2）如图，连接AC 、AD 、CF ，∵AB 为直径，AB CD ⊥，∴CE DE =，∴AB 垂直平分CD ，∴AC AD =，FC FD =，∴ACD ADC ∠=∠，FCD FDC ∠=∠，∴ACD FCD ADC FDC ∠-∠=∠-∠，即ACF ADF ∠=∠，设FCD FDC α∠=∠=，ACF ADF β∠=∠=，∵ADH ∠与ACH ∠为同对弧AH 所对的圆周角，∴ADH ACH β∠=∠=，∴2HCF HCA ACF β∠=∠+∠=，∵HFC FCD FDC ∠=∠+∠，∴2HFC α∠=，∵HC HF =，∴HCF HFC ∠=∠，∴22αβ=，∴αβ=，∵AB 为直径，∴90ADB ∠=︒，∴90HDB β∠=︒-，∵HAB ∠与为HDB ∠同对弧BH 所对的圆周角，∴90HAB HDB β∠=∠=︒-，∵AB CD ⊥，∴9090BFD αβ∠=︒-=︒-，∵9090HFA BFD αβ∠=∠=︒-=︒-，∴HFA HAF ∠=∠，∴HF HA =，∴HC HA =；（3）如图，在DH 上截取DT HC =，∵ADH ∠与ACH ∠同对弧AH 所对的圆周角，∴ADH ACH ∠=∠，∵AB 为直径，且AB CD ⊥∴AC =AD ，∴AC AD =，∴AHC ≌ATD ，∴AH AT =，∵AG HT ⊥，∴HG TG =，∴HG CH GT DT GD +=+=，设2HG k =，则4CH k =，GD 6k =，∵F 为DG 中点，∴3GF DF k ==，∴5HF HG GF k =+=，FD =CF =3k ，在HCF 中，由勾股定理逆定理得90HCF ∠=︒，过点C 作CM HD ⊥于点M ，由△HCF 面积，可求CM =125k ，∴95MF k =， ∴1tan 2CM CM CDF MD MF FD ∠===+， 解ACE △得1tan 3CAB ∠=， 易求OF ，OH ，由勾股定理逆定理得90HOF ∠=︒， 易求1tan 2KHG ∠=，1tan 3HAG ∠=， ∴15KG AK =． 【点睛】本题考查圆与三角形综合，主要考查知识点有同弧所对的圆周角相等，垂径定理，三角形全等的判定与性质，勾股定理的逆用，解直角三角形，锐角三角函数等，知识点跨度大，计算量多；熟练掌握圆的性质和三角形相关知识是解决本题的关键．4．B解析：（1）①（2，0），（1），（﹣1y x ；③y ＝﹣x ；（2）①半径为2，M 2＜r ＜4 【解析】【分析】（1）①如图2−1中，作BE ∥OD 交OA 于E ，CF ∥OD 交x 轴于F ．求出OE 、OF 、CF 、OD 、BE 即可解决问题；②如图2−2中，作BE ∥OD 交OA 于E ，作PM ∥OD 交OA 于M ．利用平行线分线段成比例定理即可解决问题；③如图3−3中，作QM ∥OA 交OD 于M ．利用平行线分线段成比例定理即可解决问题； （2）①如图3中，作MF ⊥OA 于F ，作MN ∥y 轴交OA 于N ．解直角三角形即可解决问题；②如图4中，连接OM ，作MK ∥x 轴交y 轴于K ，作MN ⊥OK 于N 交⊙M 于E 、F ．求出FN ＝NE ＝1时，⊙M 的半径即可解决问题；【详解】解：（1）①如图2﹣1中，作BE ∥OD 交OA 于E ，CF ∥OD 交x 轴于F ．由题意OC ＝CD ＝1，OA ＝BC ＝2，∴BD ＝OE ＝1，OD ＝CF ＝BE＝2， ∴A(2,0)，B(1,2)，C(﹣1,2)，故答案为：A(2,0)，B(1,2)，C(﹣1,2)．②如图2﹣2中，作BE ∥OD 交OA 于E ，作PM ∥OD 交OA 于M ．∵OD ∥BE ，OD ∥PM ，∴BE ∥PM ，∴BE OE PM OM=， ∴21y x=， ∴y ＝2x ．故答案为：y ＝2x ．③如图2﹣3中，作QM ∥OA 交OD 于M ．222MQ DM OA DOx ∴=∴=∴222y x=-+故答案为：y＝﹣22x+2．（2）①如图3中，作MF⊥OA于F，作MN∥y轴交OA于N．∵ω＝120°，OM⊥y轴，∴∠MOA＝30°，∵MF⊥OA，OA＝23，∴OF＝FA＝3，∴FM＝1，OM＝2FM＝2，∴圆M的半径为2∵MN∥y轴，∴MN⊥OM，∴MN＝233，ON＝2MN＝433，∴M4323,⎛⎫⎪ ⎪⎝⎭．②如图4中，连接OM，作MK∥x轴交y轴于K，作MN⊥OK于N交⊙M于E、F．∵MK∥x轴，ω＝120°，∴∠MKO＝60°，∵MK＝OK＝3∴△MKO是等边三角形，∴MN ＝3，当FN ＝1时，MF ＝3﹣1=2， 当EN ＝1时，ME ＝3+1=4，观察图象可知当⊙M 的半径r 的取值范围为2＜r ＜4． 故答案为：2＜r ＜4． 【点睛】本题考查圆综合题、平行线分线段成比例定理、等边三角形的判定和性质、平面斜坐标系等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考压轴题． 5．（1）详见解析；（2）3m =，点C 坐标为(3,2)-；（3）5k =或417k 或417k时，可使得C D M N 、、、为顶点的四边形是平行四边形．【解析】 【分析】 （1）从2172022x mxm的判别式出发，判别式总大于等于3，而证得；（2）根据抛物线的对称轴32b xa来求m 的值；然后利用配方法把抛物线解析式转化为顶点式，由此可以写出点C 的坐标；（3）根据平行四边形的性质得到：215|1(3)|422MN k k kCD ． 需要分类讨论：①当四边形CDMN 是平行四边形，2151(3)422MN k k k，通过解该方程可以求得k 的值；②当四边形CDNM 是平行四边形，2153(1)422NM k kk ，通过解该方程可以求得k 的值． 【详解】 解：（1）2217()4(2)(2)322m m m， ∵不论m 为何实数，总有2(2)0m -≥，2(2)30m ，∴无论m 为何实数，关于x 的一元二次方程2172022x mxm总有两个不相等的实数根，∴无论m 为何实数，抛物线217222y x mxm与x 轴总有两个不同的交点． （2）抛物线的对称轴为直线3x =，3122m ，即3m =，此时，抛物线的解析式为221513(3)2222yx xx ，∴顶点C 坐标为(3,2)-；（3）//,CD MN C D M N 、、、为顶点的四边形是平行四边形，∴四边形CDMN 是平行四边形（直线在抛物线的上方）或四边形CDMN （直线在抛物线的下方），如图所示，由已知215(3,2),(,1),(3)22D M k k N k k k，， (3,2)C ，4CD ∴=，2151(3)422MNk k kCD，①当四边形CDMN 是平行四边形，2151(3)422MNk k k，整理得，28150k k -+=，解得13k =（不合题意，舍去），25k =； ②当四边形CDNM 是平行四边形，2153(1)422NMk kk ，整理得2810k k ， 解得，12417417k k ，，综上，5k =或417k或417k时，可使得C D M N 、、、为顶点的四边形是平行四边形． 【点睛】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求二次函数解析式，抛物线的顶点公式和平行四边形的判定与性质．在求有关动点问题时要注意分析题意分情况讨论结果．6．A解析：（1）12；（2）5s 或373s ；（3）163s 或685s 或72s 【解析】 【分析】（1）AD 与BC 之间的距离即AB 的长，如下图，过点D 作BC 的垂线，交BC 于点E ，在RtDEC中可求得DE的长，即AB的长，即AD与BC间的距离；（2）四边形QDCP为平行四边形，只需QD=CP即可；（3）存在3大类情况，情况一：QP=PD，情况二：PD=QD，情况三：QP=QD，而每大类中，点P存在2种情况，一种为点P还未到达点C，另一种为点P从点C处返回．【详解】（1）如下图，过点D作BC的垂线，交BC于点E∵∠B=90°，AD∥BC∴AB⊥BC，AB⊥AD∴AB的长即为AD与BC之间的距离∵AD=16，BC=21，∴EC=5∵DC=13∴在Rt DEC中，DE=12同理，DE的长也是AD与BC之间的距离∴AD与BC之间的距离为12（2）∵AD∥BC∴只需QD=PC，则四边形QDCP是平行四边形QD=16－t，PC=21－2t或PC=2t－21∴16－t=21－2t或16－t=2t－21解得：t=5s或t=37 3s（3）情况一：QP=PD图形如下，过点P作AD的垂线，交AD于点F∵PQ=PD，PF⊥QD，∴QF=FD∵AF∥BP，AB∥FP，∠B=90°∴四边形ABPF是矩形，∴AF=BP由题意得：AQ=t ，则QD=16－t ，QF=8－2t ，AF=8+2t BP=2t 或BP=21－(2t －21)=42－2t ∵AF=BP ∴8+2t =2t 或8+2t=42－2t 解得：t=163或t=685情况二：PD=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理QD=16－t ，PF=AB=12 BP=2t 或21－(2t －21)=42－2t则FD=AD －AF=AD －BP=16－2t 或FD=16－(42－2t)=2t －26∴在Rt PFD 中，()22212162PD t =+-或()22212226PD t =+- ∵PD=QD ， ∴22PD QD =∴()()22216t 12162t =+-－或()()22216t 12226t =+-－ 解得：2个方程都无解情况三：QP=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理：QD=16－t ，FP=12 BP=2t 或BP=42－2tQF=AF －AQ=BP －AQ=2t －t=t 或QF=42－2t －t=42－3t在Rt QFP 中，22212PQ t =+或()22212423PQ t =+-∵PQ=QD ， ∴22PQ QD =∴()22216t 12t =+－或()()22216t 12423t =+-－第一个方程解得：t=72，第二个方程解得：无解 综上得：t=163或685或72 【点睛】本题考查四边形中的动点问题，用到了勾股定理、平行四边形的性质、矩形的性质，解题关键是根据点Q 运动的轨迹，得出BP 的长度．7．B解析：（1）35t ，45t ；（2）当0＜t ＜3时，224655S t t =--+；当3＜t ＜7时，23391052S t t =+-；（3）75；（4）132，7713，477【解析】 【分析】（1）过点B 作x 轴垂线，利用相似三角形可求得；（2）分2种情况，一种是点P 在AD 上，另一种是点P 在CD 上，然后利用三角形面积公式可求得； （3）直接令15h OD =即可求出； （4）存在3种情况，第一种是：QP ∥BD ，第二种是EP ∥CD 或EQ ∥CB ，第三种是QE ∥BD ，分别按照几何性质分析求解． 【详解】（1）如下图，过点B 作x 轴垂线，垂足为点M根据平移的特点，可得∠BOM=∠DBA ∵∠BMO=∠DAB=90°，∴△BMO ∽△DAB ∵AB=4，AD=BC=3 ∴BD=5 ∵BM OM BODA BA BD==，OB=t ∴BM=35t ，OM=45t （2）情况一：当0＜t ＜3时，图形如下，过点P 作OD 的垂线，交OD 于点N∵∠NDP=∠BDA ，∠PND=∠BAD ，∴△PND ∽△BAD ∵AP=t ，∴PD=3－t ∵PN BAPD BD =，∴PN=()435t - 图中，OD=5+t ∴()()243124562555OBDt St t t -=+=--+情况二：当3＜t ＜7时，图形如下，过点P 作OD 的垂线，交OD 于点N图中，PD=t －3，OD=5+t 同理，△PND ∽△BCD ，可得PN=()335t -∴()()23313395251052OBDt St t t -=+=-+- （3）情况一：当0＜t ＜3时 则h=PN=()435t -∵15h OD = ∴()43555t t-+= 解得：t=75情况二：当3＜t ＜7时则h=PN=()335t -∵15h OD = ∴()33555t t-+=解得：t=7(舍)（4）情况一：QP ∥BD ，图形如下由题意可得：BQ=43t ，AP=t ，则QA=4－43t，DP=3－t ∵BD ∥QP ∴QA PAQB PD= 代入得：4()2243t t =- 解得：t=32 ∴OD=5+t=132情况二：如下图，EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点 ∴EP=PA ，EQ=QA ，QP=QP ∴△APQ ≌△EPQ ∵EP ∥CD ，CD ⊥AD ∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形，AQ=PA ∴4－43tt = 解得：t=127 ∴OD=5+t=477情况三：如下图，QE ∥BD ，延长QE 交DA 于点N∵△APQ ≌△EPQ ，∴∠QEP=∠QAP=90° ∴△ENP 是等腰直角三角形∵QN ∥BD ，∴∠NQA=∠DBA ，∠A=∠A ∴△QNA ∽△BDA ∵BQ=43t ，AP=t ，QA=4－43t，DP=3－t ∴QN QA AN BD BA AD== ∴QN=5－43t，NA=3－t ∴EN=QN －QE=QN －QA=1－3t，NP=NA －AP=3－2t ，EP=PA=t ∴在Rt △ENP 中，()2223213t t t ⎛⎫-+-= ⎪⎝⎭解得：t=1213或t=3(舍) ∴OD=5+t=7713【点睛】本题考查动点问题，解题关键是利用相似将图形中各边用t 表示出来．8．A解析：（1）①(1,2),(2.5,0)A C ；②2232m ≤；（2）最小值为2． 【解析】【分析】（1）①根据“特征点”的定义判断即可；②如图2中，当⊙W 1与直线y =−x +2相切时，1(22,0)W -，当⊙W 2与直线y =−x +3相切时，2(32,0)W +，结合图象，⊙W 与图中阴影部分有交点时，⊙W 上存在满足条件的特征点．（2）特征点的图象是由原点向外扩大，当与反比例函数的图象第一次有交点时，1x x+的值最小（如图3中）． 【详解】解：（1）①∵1+2=3，1+3=4，2.5+0=2.5， 又∵2≤a ≤3， ∴A ，C 是特征点，故答案为：(1,2),(2.5,0)A C ； ②如图1，∵2≤a ≤3，∴直线y =−x +2和直线y =−x +3之间的区域（包括两直线）上的点都为“特征点”， 直线y =−x +2和直线y =−x +3分别与x 轴的交点为(2,0)P ，(3,0)Q ，当⊙W 1与直线y =−x +2相切时，设切点为M ，此时2OP =，1MW MP ⊥，145MPW ∠=︒，则1MPW 为等腰直角三角形， ∵⊙W 1半径为1，即11MW =，∴12PW =1122OW OP PW =-=- ∴1(22,0)W ，当⊙W 2与直线y =−x +3相切时，设切点为N ，此时3OQ =，2NW NQ ⊥，245NQW ∠=︒，则2NQW 为等腰直角三角形， 同理得：22QW =，则2232OW OQ QW =+=+， ∴2(32,0)W +，观察图象可知满足条件的m 取值范围为：2232m ≤（2）根据0x >，在第一象限画出1y x=的图象， ∴在此坐标系中图象上的点就是1x x ⎛⎫⎪⎝⎭，，∵特征点满足x y a +=（x ≥0，a 为常数）， ∴在此图象上对应的就是1x a x+=， ∴将特征点的图象由原点向外扩大，当与反比例函数1y x =的图象第一次有交点时，1x x+出现最小值， 如图2，由x >0可将1x a x+=整理得：210x ax -+=， ∴2()40a ∆=--=，解得：12a =，22a =-（舍去），∴2a =， ∴12Z x x =+=，即()10Z x x x=+>的最小值为2．【点睛】本题属于反比例函数综合题，考查了直线与圆的位置关系，反比例函数的性质等知识，解题的关键是理解题意，学会利用图象法解决问题，属于中考压轴题．9．A解析：（1）(1,4)D ；（2）158(,)33M ，274(,)33M ；（3）N 的坐标为57(,)24． 【解析】 【分析】（1）将点A 坐标代入函数关系式可得a 与b 的方程，再根据顶点D 的横坐标为1可得另一个关于a 和b 的方程，联立方程组求解即可得到a 和b 的值，进而求得抛物线的函数关系式，再将顶点D 的横坐标代入即可求得点D 坐标；（2）①如图，取DB 得三等分点12,M M ，过点12,M M 分别作x 轴，y 轴的平行线分别交DE 、x 轴于点G 、H 、P 、Q ，通过证相似三角形可得点M 的横纵坐标与点B 、D 的横纵坐标之间的数量关系，进而得解；（3）取线段BC 的中点G ，连接GM ，由中点坐标可得33(,)22G ，根据等腰三角形的三线合一可得GM ⊥BC ，在根据两条直线互相垂直可求得:GM l y x =，与:26BD l y x =-+联立方程组可求得点M 的坐标，再由(2,2),(0,3)M C 利用待定系数法可得1:32CM l y x =-+，最后将132y x =-+与2y x 2x 3=-++联立方程组即可求得点N 的坐标． 【详解】解：（1）将(1,0)A -代入23y ax bx =++可得03a b =-+①∵顶点D 的横坐标为1，∴12ba-=，即2b a =-② 联立①②解得1,2a b =-=∴2y x 2x 3=-++ 当1x =时，4y =(1,4)D ∴（2）由（1）得2y x 2x 3=-++ 当y=0时，x 1=-1，x 2=3， ∴B （3,0），即BO=3，如图，取DB 的三等分点12,M M ，过点12,M M 分别作x 轴，y 轴的平行线分别交DE 、x 轴于点G 、H 、P 、Q ，则可得△DGM 1∽△DHM 2∽△DEB ，△BQM 2∽△BPM 1∽△BED ，且相似比为1:2:3， ∴12833M D y y == 115()33M D B D x x x x =+-=158(,)33M ∴同理可得：274(,)33M∴点M 的坐标为：158(,)33M ，274(,)33M（3）NCB DBC ∠=∠CM MB ∴=取线段BC 的中点G ，作直线GM ，∵点B （3,0），点C （0，3） ∴中点G 的坐标为33(,)22∵CM MB =，点G 为线段BC 的中点， ∴GM ⊥BC ， ∴设直线GM 为y=x+m 将33(,)22G 代入得m=0， ∴:GM l y x =① 设直线BD 为y=kx+n将,B D 坐标代入得k=-2，n=6， ∴:26BD l y x =-+② 联立①②可得22x y =⎧⎨=⎩∴(2,2)M 设直线MC 为y=k 2x+n 2将(2,2),(0,3)M C 坐标代入得k 2=12-，n 2=3， ∴1:32CM l y x =-+③ 联立③与2y x 2x 3=-++可得5274x y ⎧=⎪⎪⎨⎪=⎪⎩∴57(,)24N 故N 的坐标为57(,)24. 【点睛】本题考查了一次函数与二次函数的综合应用以及相似三角形的判定及性质的应用，能够根据题意做出正确的辅助线，利用数形结合思想进行转化是解决本题的关键．10．F解析：（1）16；（2）不变，证明见解析；（3）214322S x x =-+，当x=2或6时，四边形FEGN 的面积为26． 【解析】 【分析】（1）如图1中，在△AEF 中，设AE=x ，则EF=8-x ，AF=4，∠A=90°，理由勾股定理构建方程求出x ，再根据△AEF ∽△DFM ，可得3124FDMAE DF C ∆==，由此即可解决问题； （2）△FDM 的周长与（1）中结论相同．证明方法与（1）类似；（3）作GK ⊥AB 于K ．连接BF 交GE 于P ．由△AFB ≌△KEG ，可得FB=GE ，由（2）可知：AE=21416x -，设AF=EK=x ，AK=AE+EK=AF+AE=21416x x -+，根据S=82AE DG+⨯，构建二次函数即可解决问题； 【详解】解：（1）在△AEF 中，设AE=x ，则EF=8-x ，AF=4，∠A=90°， 由勾股定理，得：42﹢x 2=(8-x)2， ∴x=3， ∴AE=3，EF=5． ∴△AEF 的周长为12， 如图，。

中考数学中考数学压轴题达标提高题检测试卷

中考数学中考数学压轴题达标提高题检测试卷

一、中考数学压轴题1．在平面直角坐标系中，直线4(0)3y x b b =-+>交x 轴于点A ，交y 轴于点B ，10AB =．（1）如图1，求b 的值；（2）如图2，经过点B 的直线(4)(40)y n x b n =++-<<与直线y nx =交于点C ，与x 轴交于点R ，//CD OA ，交AB 于点D ，设线段CD 长为d ，求d 与n 的函数关系式； （3）如图3，在（2）的条件下，点F 在第四象限，CF 交OA 于点E ，45AEF ∠=︒,点P 在第一象限，PH OA ⊥，点N 在x 轴上，点M 在PH 上，MN 交PE 于点G ，PH EN =，过点E 作EQ CF ⊥，交PH 于点Q ， 32==EQ EF PM ，∠=∠OBR HNM ，BC CR =，点G 的坐标为1927,55⎛⎫ ⎪⎝⎭，连接FN ，求EFN 的面积．2．在平面直角坐标系中，抛物线24y mx mx n =-+（m >0）与x 轴交于A ，B 两点，点B 在点A 的右侧，顶点为C ，抛物线与y 轴交于点D ，直线CA 交y 轴于E ，且:3:4∆∆=ABC BCE S S ．（1）求点A ，点B 的坐标；（2）将△BCO 绕点C 逆时针旋转一定角度后，点B 与点A 重合，点O 恰好落在y 轴上，①求直线CE 的解析式；②求抛物线的解析式．3．已知抛物线217222y x mx m 的顶点为点C ． （1）求证：不论m 为何实数，该抛物线与x 轴总有两个不同的交点；（2）若抛物线的对称轴为直线3x =，求m 的值和C 点坐标；（3）如图，直线1y x =-与（2）中的抛物线并于A B 、两点，并与它的对称轴交于点D ，直线x k =交直线AB 于点M ，交抛物线于点N ．求当k 为何值时，以C D M N 、、、为顶点的四边形为平行四边形．4．如图1，正方形CEFG 绕正方形ABCD 的顶点C 旋转，连接AF ，点M 是AF 中点． （1）当点G 在BC 上时，如图2，连接BM 、MG ，求证：BM =MG ；（2）在旋转过程中，当点B 、G 、F 三点在同一直线上，若AB =5，CE =3，则MF = ；（3）在旋转过程中，当点G 在对角线AC 上时，连接DG 、MG ，请你画出图形，探究DG 、MG 的数量关系，并说明理由．5．如图，在等边ABC ∆中，延长AB 至点D ，延长AC 交BD 的中垂线于点E ，连接BE ，DE ．（1）如图1，若310DE =，23BC =CE 的长；（2）如图2，连接CD 交BE 于点M ，在CE 上取一点F ，连接DF 交BE 于点N ，且DF CD =，求证：12AB EF =；（3）在（2）的条件下，若45AED ∠=︒直接写出线段BD ，EF ，ED 的等量关系6．如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根，且其中一个根为另一个根的一半，则称这样的方程为“半等分根方程”．（1）①方程2280x x --= 半等分根方程（填“是”或“不是”）；②若(1)()0x mx n -+=是半等分根方程，则代数式2252m mn n ++= ； （2）若点(,)p q 在反比例函数8x y =的图象上，则关于x 的方程260px x q -+=是半等分根方程吗？并说明理由； （3）如果方程20ax bx c ++=是半等分根方程，且相异两点(1,)M t s +，(4,)N t s -都在抛物线2y ax bx c =++上，试说明方程20ax bx c ++=的一个根为53． 7．已知：如图，二次函数213222y x x =-++的图象交x 轴于A 点和B 点（A 点在B 点左则），交y 轴于E 点，作直线,EB D 是直线EB 上方抛物线上的一个动点．过D 点作 直线l 平行于直线.EB M 是直线 EB 上的任意点，N 是直线l 上的任意点，连接,MO NO ，始终保持MON ∠为90︒，以MO 和ON 边，作矩形MONC ．（1）在D 点移动过程中，求出当DEB ∆的面积最大时点D 的坐标；在DEB ∆的面积最大 时，求矩形MONC 的面积的最小值．（2）在DEB ∆的面积最大时，线段ON 交直线EB 于点G ，当点,,,D N G B 四个点组成平行 四边形时，求此时线段ON 与抛物线的交点坐标．8．问题提出（1）如图①，在ABC 中，42,6,135AB AC BAC ==∠=，求ABC 的面积．问题探究（2）如图②，半圆O 的直径10AB =，C 是半圆AB 的中点，点D 在BC 上，且2CD BD =，点P 是AB 上的动点，试求PC PD +的最小值．问题解决（3）如图③，扇形AOB 的半径为20,45AOB ∠=在AB 选点P ，在边OA 上选点E ，在边OB 上选点F ，求PE EF FP ++的长度的最小值．9．如图1，△ABC 内接于⊙O ，直径AD 交BC 于点E ，延长AD 至点F ，使DF ＝2OD ，连接FC 并延长交过点A 的切线于点G ，且满足AG ∥BC ，连接OC ，若cos ∠BAC ＝13，BC ＝8． （1）求证：CF 是⊙O 的切线；（2）求⊙O 的半径OC ；（3）如图2，⊙O 的弦AH 经过半径OC 的中点F ，连结BH 交弦CD 于点M ，连结FM ，试求出FM 的长和△AOF 的面积．10．如图，在正方形ABCD 中，DC=8，现将四边形BEGC 沿折痕EG(G ，E 分别在DC ，AB 边上)折叠，其顶点B ，C 分别落在边AD 上和边DC 的上部，其对应点设为F ，N 点，且FN 交DC 于M ．特例体验：(1)当FD=AF 时，△FDM 的周长是多少?类比探究：(2)当FD≠AF≠0时，△FDM 的周长会发生变化吗?请证明你的猜想．拓展延伸：(3)同样在FD≠AF≠0的条件下，设AF 为x ，被折起部分(即：四边形FEGN)的面积为S ，试用含x 的代数式表示S ，并问：当x 为何值时，S=26?11．平面直角坐标系中，点A 、B 分别在x 轴正半轴、y 轴正半轴上，AO =BO ，△ABO 的面积为8.（1）求点A 的坐标；（2）点C 、D 分别在x 轴负半轴、y 轴正半轴上（D 在B 点上方），AB ⊥CD 于E ，设点D 纵坐标为t ，△BCE 的面积为S ，求S 与t 的函数关系；（3）在（2）的条件下，点F 为BE 中点，连接OF 交BC 于G ，当∠FOB +∠DAE =45°时，求点E 坐标.12．已知：如图①，在等腰直角ABC ∆中，斜边2AC =．（1）请你在图①的AC 边上求作一点P ，使得90APB ∠=︒；（2）如图②，在（1）问的条件下，将AC 边沿BC 方向平移，使得点A 、P 、C 对应点分别为E 、Q 、D ，连接AQ ，BQ ．若平移的距离为1，求AQB ∠的大小及此时四边形ABDE 的面积；（3）将AC 边沿BC 方向平移m 个单位至ED ，是否存在这样的m ，使得在直线DE 上有一点M ，满足30AMB ∠=︒，且此时四边形ABDE 的面积最大？若存在，求出四边形ABDE 面积的最大值及平移距离m 的值；若不存在，请说明理由．13．在平行四边形ABCD 中，60B ∠=︒，点E ，F 分别在边AB ，AD 上，且60ECF ∠=︒．（1）如图1，若AB BC =，求证：AE AF BC +=；（2）如图2，若4AB BC ==，且点E 为AB 的中点，连接BF 交CE 于点M ，求FM ；（3）如图3，若AB kBC =，探究线段BE 、DF 、BC 三之间的数量关系，说明理由．14．已知，抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ，B ，且B 点的坐标为()2,0．（1）求该抛物线的解析式．（2）如图1，若点P 是线段AB 上的一动点，过点P 作//PE AC ，交BC 于E ，连接CP ，求PCE ∆面积的最大值．=+与线段AC交于点M，与线段BC交于点N，是否存在（3）如图2，若直线y x m∆为直角三角形，若存在，请求出m的值；若不存在，请说明理M，N，使得OMN由．15．如图，四边形AOBC是正方形，点C的坐标是(82,0)．（1）正方形AOBC的边长为，点A的坐标是；（2）将正方形AOBC绕点O顺时针旋转45︒，点A，B，C旋转后的对应点为A'，B'，C'，求点A'的坐标及旋转后的正方形与原正方形的重叠部分的面积；（3）动点P从点O出发，沿折线OACB方向以1个单位/秒的速度匀速运动，同时，另一动点Q从点O出发，沿折线OBCA方向以2个单位/秒的速度匀速运动，运动时间为t 秒，当它们相遇时同时停止运动，当OPQ△为等腰三角形时，求出t的值（直接写出结果即可）．16．如图，在⊙O中，直径AB＝10，tanA＝33．（1）求弦AC的长；（2）D是AB延长线上一点，且AB＝kBD，连接CD，若CD与⊙O相切，求k的值；（3）若动点P以3cm/s的速度从A点出发，沿AB方向运动，同时动点Q以32cm/s的速度从B点出发沿BC方向运动，设运动时间为t （0＜t＜103），连结PQ．当t为何值时，△BPQ为Rt△？17．已知四边形ABCD为矩形，对角线AC、BD相交于点O，AD＝AO．点E、F为矩形边上的两个动点，且∠EOF＝60°．（1）如图1，当点E、F分别位于AB、AD边上时，若∠OEB＝75°，求证：DF＝AE；（2）如图2，当点E、F同时位于AB边上时，若∠OFB＝75°，试说明AF与BE的数量关系；（3）如图3，当点E、F同时在AB边上运动时，将△OEF沿OE所在直线翻折至△OEP，取线段CB的中点Q．连接PQ，若AD＝2a（a＞0），则当PQ最短时，求PF之长．18．已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC．（1）如图1，当BM=1时，求PC的长；（2）如图2，设AM与BD交于点E，当∠PCM=45°时，求证：BEDE=33；（3）如图3，取PC的中点Q，连接MQ，AQ．①请探究AQ和MQ之间的数量关系，并写出探究过程；②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由．19．在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A 顺时针旋转90°，得到线段AE，连接DE．（1）如图1，点E落在BA的延长线上时，∠EDC= （度）直接填空．（2）如图2，点D在运动过程中，DE⊥AC时，AB=4 ，求DE的值．（3）如图3，点F为线段DE中点，2a，求出动点D从B运动到C，点F经过的路径长度．20．在一次数学课上，李老师让同学们独立完成课本第23页第七题选择题（2）如图 1，如果 AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝（）A．180° B．270° C．360° D．540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB∥EF，请直接写出∠BAD，∠ADE，∠DEF之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示），当AD，ED分别平分∠BAC，∠CEF时，∠ACE与∠ADE之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB∥EF，当∠ACD=90°时，∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系？请你直接写出结果，不需要证明．21．阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”：如图1．在△ABC中，如果AB＞AC，那么∠ACB＞∠ABC．证明如下：将AB沿△ABC的角平分线AD翻折（如图2），因为AB＞AC，所以点B落在AC的延长线上的点B'处．于是，由∠ACB＞∠B'，∠ABC=∠B'，可得∠ACB＞∠ABC．（1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”：如图3．在△ABC中，如果∠ACB＞∠ABC，那么AB＞AC．小明的思路是：沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程．（2）拓展延伸：请运用上述方法或结论解决如下问题：如图4，已知M为正方形ABCD的边CD上一点（不含端点），连接AM并延长，交BC的延长线于点N．求证：AM＋AN＞2BD．22．如图1，以AB为直径作⊙O，点C是直径AB上方半圆上的一点，连结AC，BC，过点C作∠ACB的平分线交⊙O于点D，过点D作AB的平行线交CB的延长线于点E．（1）如图1，连结AD ，求证：∠ADC ＝∠DEC ． （2）若⊙O 的半径为5，求CA •CE 的最大值． （3）如图2，连结AE ，设tan ∠ABC ＝x ，tan ∠AEC ＝y ， ①求y 关于x 的函数解析式； ②若CB BE ＝45，求y 的值． 23．如图1，在ABC 中，BD 平分ABC ∠，CD 平分ACB ∠． (1)若80A ∠=︒，则BDC ∠的度数为______； (2)若A α∠=，直线MN 经过点D ．①如图2，若//MN AB ，求NDC MDB ∠-∠的度数(用含α的代数式表示)； ②如图3，若MN 绕点D 旋转，分别交线段,BC AC 于点,M N ，试问在旋转过程中NDC MDB ∠-∠的度数是否会发生改变?若不变，求出NDC MDB ∠-∠的度数(用含α的代数式表示)，若改变，请说明理由：③如图4，继续旋转直线MN ，与线段AC 交于点N ，与CB 的延长线交于点M ，请直接写出NDC ∠与MDB ∠的关系(用含α的代数式表示)．24．在△ABC 中，∠BAC ＝90°，点D 是BC 上一点，将△ABD 沿AD 翻折后得到△AED ，边AE 交BC 于点F ．(1)如图①，当AE ⊥BC 时，写出图中所有与∠B 相等的角： ；所有与∠C 相等的角： ．(2)若∠C －∠B ＝50°，∠BAD ＝x °(0＜x ≤45) ． ① 求∠B 的度数；②是否存在这样的x 的值，使得△DEF 中有两个角相等．若存在，并求x 的值；若不存在，请说明理由．25．如图，在ABC 中，90ABC ∠=︒，AB BC <，O 为AC 中点，点D 在BO 延长线上，CD BC =，AE BC ∥，CE CA =，AE 交BD 于点G ． （1）若28DCE ∠=︒，求AOB ∠的度数； （2）求证：AG GE =； （3）设DC 交GE 于点M ．①若3AB =，4BC =，求::AG GM ME 的值；②连结DE ，分别记ABG ，DGM ，DME 的面积为1S ，2S ，3S ，当AC DE 时，123::S S S = ．（直接写出答案）【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题 1．B解析：（1）8b =；（2）382d n =+；（3）92EFN S =△【解析】 【分析】（1）先用b 表示出点B 和点A 的坐标，然后利用勾股定理列出方程即可求出b 的值； （2）联立直线BC 的解析式和直线AB 的解析式即可用n 表示出点C 的坐标，从而求出点D 的坐标，从而求出d 与n 的函数关系式；（3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I ，根据相似三角形判定可得△RSC ∽△ROB ，列出比例式即可求出OR 和CS ，然后根据等角的锐角三角函数相等求出ON ，再根据等腰直角三角形的性质求出NE ，然后结合已知条件和等角的锐角三角函数相等求出TF ，即可求出结论． 【详解】解：（1）当x=0时，y=b ；当y=0时，x=34b∴点B 的坐标为（0，b ），点A 的坐标为（34b ，0） ∴OB=b ，OA=34b 根据勾股定理OB 2＋OA 2=AB 2 b 2＋（34b ）2=102 解得：b=8或-8（不符合已知条件，舍去） ∴b=8（2）直线BC 的解析式为(4)8=++y n x ，直线AB 的解析式为483y x =-+ 联立(4)8y n x y nx =++⎧⎨=⎩解得：22x y n =-⎧⎨=-⎩∴点C 的坐标为（-2，-2n ） ∵//CD OA ∴点D 的纵坐标为-2n 将y=-2n 代入483y x =-+中，解得：x=362+n∴点D 的坐标为36,22⎛⎫+- ⎪⎝⎭n n∴线段CD 长d =362+n －（-2）=382+n （3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I ∴OD=275，GD=195由（2）知点C 坐标为（-2，-2n ）∴CS=-2n ，OS=2 ∵BC CR =，CS ∥y 轴 ∴RB=2RC ，△RSC ∽△ROB ∴12===CS RS RC OB OR RB 即22182--==n OR OR 解得：n=-2，OR=4 ∴CS=4∵∠=∠OBR HNM ，GD ∥x 轴 ∴∠=∠OBR HNM =∠DGI∴tan tan ∠=∠OBR HNM =tan ∠DGI∴==OR OI IDOB ON GD即48927515-==IDID ON解得：1910,7==ID ON ∵45AEF ∠=︒∴∠CES=∠AEF=45°，∠QEH=∠QEF －∠AEF=45° ∴△CES 、△EFT 和△EHQ 都是等腰直角三角形 ∴CS=SE=4，ET=TF=2EF ， EH=HQ ，设EH=HQ=a ，则∴EN=ON ＋OE=ON ＋SE －OS=9∵3==EQ EF ，PH EN =∴，PM=a ，PH=9， ∴NH=EN ＋EH=9＋a ，MH=PH －PM=9－a ∴tan ∠HNM =12==MH OI NH ON ∴9192-=+a a 解得：a=3 ∴EF=33⨯=∴TF=12=∴S △EFN =12EN ·TF=12×9×1=92【点睛】此题考查的是一次函数与几何图形的综合题型，此题难度较大，掌握勾股定理、联立方程求交点坐标、锐角三角函数的性质、勾股定理、等腰直角三角形的性质和相似三角形的判定及性质是解决此题的关键．2．A解析：（1） A （12,0） B （72,0）；(2) ①233y x =-+，②24316373y x x =-+． 【解析】 【分析】（1）根据抛物线的解析式可得对称轴为x =2，利用:3:4∆∆=ABC BCE S S 得出CA :CE =3:4，由△AOE ∽△AGC 可得13=AO AG ，进而求得OA 、OB 的长，即可求得点A 、点B 的坐标； （2）根据旋转的性质求出C 点坐标，利用C 点坐标和△AOE ∽△AGC 可求得E 点坐标，，分别利用待定系数法即可求得直线CE 和抛物线的解析式． 【详解】解：（1）∵抛物线的解析式为24(0)=-+>y mx mx n m ，∴对称轴为直线422-=-=mx m， 如图，设对称轴与x 轴交于G ，则//CG y 轴，2OG =，∴△AOE ∽△AGC ， ∴=AO AEAG AC， ∵:3:4ABCBCES S=，∴CA :CE =3:4 ，则31AE AC =， ∴13==AO AE AG AC ， ∴1142==OA OG ，3342==AG OG ， 则23==AB AG ，72=+=OB OA AB ， ∴A (12,0)， B (72,0)； （2）如图，设O 旋转后落在点Q 处，过点C 作CP y ⊥轴于点P ，由旋转的性质得：△BCO ≌△ACQ ， ∴BO =AQ =72，CO =CQ ， ∴OQ =222271()()2322=-=-=AQ AO∵CP y ⊥轴， ∴132==OP OQ ∴点C 的坐标为(2,3)-，则3CG =由（1）得△AOE ∽△AGC ，13==OE AE CG AC ， ∴3OE =E 的坐标为3，①设CE 的解析式为y kx b =+，分别代入C (2,，E (0,3得：23k b b ⎧+=⎪⎨=⎪⎩，解得：k b ⎧=⎪⎪⎨⎪=⎪⎩， ∴CE的解析式为y =； ②将A (12,0)，C (2,分别代入24y mx mx n =-+得：120448m m n m m n ⎧-+=⎪⎨⎪-+=⎩，解得：m n ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线解析式为2999y x x =-+． 【点睛】本题考查了二次函数的综合、旋转的性质、相似三角形的性质和求一次函数的解析式，正确的理解题意，熟练运算“数形结合思想”是解题的关键．3．（1）详见解析；（2）3m =，点C 坐标为(3,2)-；（3）5k =或417k 或417k时，可使得C D M N 、、、为顶点的四边形是平行四边形．【解析】 【分析】 （1）从2172022x mxm的判别式出发，判别式总大于等于3，而证得；（2）根据抛物线的对称轴32b xa来求m 的值；然后利用配方法把抛物线解析式转化为顶点式，由此可以写出点C 的坐标；（3）根据平行四边形的性质得到：215|1(3)|422MN k k kCD ． 需要分类讨论：①当四边形CDMN 是平行四边形，2151(3)422MN k k k，通过解该方程可以求得k 的值；②当四边形CDNM 是平行四边形，2153(1)422NM k kk ，通过解该方程可以求得k 的值． 【详解】 解：（1）2217()4(2)(2)322m m m，∵不论m 为何实数，总有2(2)0m -≥，2(2)30m ，∴无论m 为何实数，关于x 的一元二次方程2172022xmxm总有两个不相等的实数根，∴无论m 为何实数，抛物线217222y x mxm与x 轴总有两个不同的交点． （2）抛物线的对称轴为直线3x =，3122m ，即3m =，此时，抛物线的解析式为221513(3)2222y x xx ，∴顶点C 坐标为(3,2)-；（3）//,CD MN C D M N 、、、为顶点的四边形是平行四边形，∴四边形CDMN 是平行四边形（直线在抛物线的上方）或四边形CDMN （直线在抛物线的下方），如图所示，由已知215(3,2),(,1),(3)22D M k k N k k k，， (3,2)C ，4CD ∴=，2151(3)422MNk k kCD，①当四边形CDMN 是平行四边形，2151(3)422MNk k k，整理得，28150k k -+=，解得13k =（不合题意，舍去），25k =； ②当四边形CDNM 是平行四边形，2153(1)422NMk kk ，整理得2810k k ， 解得，12417417k k ，，综上，5k =或417k或417k时，可使得C D M N 、、、为顶点的四边形是平行四边形． 【点睛】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求二次函数解析式，抛物线的顶点公式和平行四边形的判定与性质．在求有关动点问题时要注意分析题意分情况讨论结果．4．D解析：（1）证明见解析；（2）29或5；（3）DG =2MG ，理由见解析． 【解析】 【分析】(1)连接MG 并延长交AB 于N 点，证明△ANM ≌△FGM 后得到MG=MN ，AN=CG ，进而得到BN=BG ，得到△ANG 为等腰直角三角形，即可证明MG=MB. (2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.(3)先画出图形，然后证明△ADG ≌△ABG ，得到DG=BG ，又△BMG 为等腰直角三角形，故而得到DG=BG=2MG. 【详解】解：(1) 连接MG 并延长交AB 于N 点，如下图所示：∵GF ∥AN ， ∴∠NAM=∠GFM 在△ANM 和△FGM 中∠∠=⎧⎪=⎨⎪∠=∠⎩BAM GFM AM FMNMA GMF ，∴△ANM ≌△FGM(ASA) ∴MG=MN ，CG=GF=AN ∴AB-AN=BC-CG ∴NB=GB∴△NBG 为等腰直角三角形 又M 是NG 的中点∴由直角三角形斜边上的中线等于斜边的一半知：故有：MG=MB. (2)分类讨论：情况一：当B 、G 、F 三点在正方形ABCD 外同一直线上时延长MG 到N 点，并使得MG=MN ，连接AN ，BN∴∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ，∴△AMN ≌△FMG(SAS) ∴AN=GF=GC ，∠NAM=∠GFM ∴AN ∥GF∴∠NAB+∠ABG=180° 又∠ABC=90° ∴∠NAB+∠CBG=90°又在△BCG 中，∠BCG+∠CBG=90° ∴∠NAB=∠BCG∴在△ABN 中和△CBG 中：∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ，∴△ABN ≌△CBG(SAS)∴BN=BG ，∠ABN=∠CBG ∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形，且∠BGN=45° 在Rt △BCG 中，2222=534--=BG BC CG 过M 点作MH ⊥BG 于H 点，∴△MHB 为等腰直角三角形 ∴MH=BH=HG=12BG=2 在Rt △MFH 中，2222MF=2529+=+=MH HF 情况二：当B 、G 、F 三点在正方形ABCD 内同一直线上时如下图所示，延长MG 到MN ，并使得MG=MN ，连接NA 、NB ，同情况一中证明思路，∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ，△AMN ≌△FMG(SAS)∴AN=GF=GC ，∠NAM=∠GFM∴AN ∥GF∴∠NAB=∠ABG又∠ABG+∠GBC=90°∠GBC+∠BIF=90°∴∠BIF=∠ABG又∠BIF=∠BCG ，∠ABC=∠NAB∴∠NAB=∠GCB∴在△ABN 中和△CBG 中：∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ，∴△ABN ≌△CBG(SAS)∴BN=BG ，∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形，且∠BGN=45°在△BCG 中，2222=534-=-=BG BC CG过M 点作MH ⊥BG 于H 点，∴△MHB 为等腰直角三角形∴MH=BH=HG=12BG=2 ∴HF=HG-GF=2-1=1在Rt △MFH 中，2222MF=215+=+=MH HF 29 5.(3)由题意作出图形如下所示：DG 、MG 的数量关系为：2，理由如下：∵G 点在AC 上∴∠DAG=∠BAG=45°在△ADG 和△ABG 中：∠∠=⎧⎪=⎨⎪=⎩AD AB DAG BAG AG AG ，∴△ADG ≌△BAG(SAS)∴DG=BG又由(2)中的证明过程可知：△MBG 为等腰直角三角形∴2MG∴2MG故答案为：2MG.【点睛】本题考查了正方形的旋转、三角形的全等、勾股定理等知识，难度很大，关键是要能正确做出图形，利用数形结合的思想，熟练的使用正方形的性质是解题的关键.5．B解析：（1）93CE =-2）详见解析；（3）612BD EF =- 【解析】【分析】（1）过点B 作BH AC ⊥于点H ，分别求出BH ，BE ，根据勾股定理问题得解； （2）如图在FE 上取一点G ，使FG AC =，连接DG ，先证明()ACD GFD SAS ∆∆≌，再证明()ECB DGE AAS ∆∆≌，问题得证；（3）过点D 作AE 的垂线，构造出一个30，60︒，90︒的三角形和一个等腰直角三角形,借助（2）的结论，设222EF AB AC x ===，2ED =，通过解两个直角三角形，代换x 和y 的关系，得出结论．【详解】解：（1）如图，过点B 作BH AC ⊥于点H ，在等边ABC ∆中∵23BC =∴3AH HC ==，223BH BC CH =-=, ∵点E 在BD 的垂直平分线上， ∴310BE DE == ，在Rt BHE ∆中229EH BE BH =-=∴93CE EH HC =-=-（2）如图在FE 上取一点G ，使FG AC =，连接DG∵DF CD =∴FCD CFD ∠=∠∴ACD EFD ∠=∠在ACD ∆和GFD ∆中，DF CD ACD EFD FG AC =⎧⎪∠=∠⎨⎪=⎩∴()ACD GFD SAS ∆∆≌∴AD DG =∴60A DGA ∠=∠=︒∴60A DGA ADG ∠=∠=∠=︒设EBD EDB α∠=∠=∴120CBE α∠=︒-在ADE ∆中∴18060120AED αα∠=︒-︒-=︒-∴120AED CBE α∠=∠=︒-在ECB ∆和DGE ∆中120AED CBE ECB ECD EB DE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()ECB DGE AAS ∆∆≌∴BC GE =∴AB AC BC GE FG ====12AB EF = （3）如图，设222EF AB AC x ===，DP=y ，过点DP ⊥AE ，垂足为P ，∵∠AED=45°, ∠A=60°,∴2sin sin 45DP y ED y AED ===∠︒，23sin sin 603DP y y AD A ===∠︒， ∴2=y DE , ∴BD=AD-AB =2323216122y x DE EF DE EF -=-=-， 故答案为：612BD DE EF =-． 【点睛】本题涉及知识点较多，设计新颖，综合性强，难度较大，根据题意添加适当辅助线，构造直角三角形或构造全等是解题关键．6．（1）①不是；②0；（2）若点(,)p q 在反比例函数8y x=的图象上，则关于x 的方程260px x q -+=是半等分根方程，理由详见解析；（3）详见解析【解析】【分析】（1）①解方程2280x x --=，根据“半等分根方程”定义作出判断即可；②解方程(1)()0x mx n -+=得11x =，2n x m =-，所以12n m -=或2n m -=，即：n =-2m 或m =-2n ，分别代入代数式2252m mn n ++=结果均为0 （2）根据点(,)p q 在反比例函数8y x =的图象上，得到8q p =，代入260px x q -+=，得到关于x 的方程2860px x p-+=，解方程，用含p 的式子表示x ，根据“半等分根方程”定义判断即可；（3）根据两点(1,)M t s +，(4,)N t s -都在抛物线上，且纵坐标相等，可以求出对称轴为52x =，根据方程20ax bx c ++=是半等分根方程，得到两根关系，根据抛物线对称轴为 12522x x +=，即可求出两个根，问题得证． 【详解】解：（1）①解方程2280x x --=得124,2x x ==-，不符合“半等分根方程”定义， 故答案为：不是；②解方程(1)()0x mx n -+=得11x =，2n x m =-，所以12n m -=或2n m-=，即：n =-2m 或m =-2n ， 当n =-2m 时，()()22225522022m mn n m m n m ++=+-+-=； 当m =-2n 时，()()22225522022m mn n n n n n ++=-+-+=； 故答案为：0； （2）若点(,)p q 在反比例函数8y x=的图象上，则关于x 的方程260px x q -+=是半等分根方程 理由：∵点(,)p q 在反比例函数8y x =的图象上∴8q p=代入方程260px x q -+=得： 2860px x p -+= 解得：12x p =，24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程（3）∵相异两点(1,)M t s +，(4,)N t s -都在抛物线2y ax bx c =++上， ∴抛物线的对称轴为：(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有：12522x x += 所以153x =，2103x = 所以方程20ax bx c ++=的一个根为53得证． 【点睛】本题为“新定义问题”，考查了学生自主学习的能力，解决此题关键是理解新定义概念，并结合所学数学知识进行解答．7．D解析：（1）D 点坐标为()2,3，矩形MONC 的最小值为645；（2）交点坐标为（），（3），（1），（）． 【解析】【分析】（1）当△DEB 的面积最大时，直线DN 与抛物线相切，可求出直线DN 的解析式和点D 的坐标，当矩形面积最小时，MG 最小，求出MG 的最小值即可．（2）分两种情况讨论，以DB 为边和以DB 为对角线，分别求出此时ON 的解析式，联立求出交点坐标即可．【详解】解：（1）如图1所示，过点D 作y 轴的平行线交MB 于点H ，过点O 作OQ 垂直MB 于点Q，令y＝0，解得x1＝﹣1，x2＝4，∴A（﹣1，0），B（4，0），令x＝0，y＝2，∴E（0，2），设直线BE的解析式为y＝kx+b，则2, 40,bk b=⎧⎨+=⎩解得122kb⎧=-⎪⎨⎪=⎩，∴直线BE的解析式为y＝﹣12x+2，∵DN∥BE，∴设直线DN的解析式为y＝﹣12x+b1，S△DEB＝DH12⨯•（x B﹣x E），∴当△DEB面积最大时，即是DH最大的时候，∴﹣12x+b1＝﹣12x2+32x+2，△＝b2﹣4ac＝0，即16﹣4（2b1﹣4）＝0，解得b1＝4，点D（2，3），S矩＝2S△MOG+S平形四边形，∴矩形面积最小时就是MG最小，设QG＝m，MQ＝n，∴MG＝m+n，∵m+n≥mn∵△QOG∽△MQO，∴OQ 2＝m •n ，∵△OEQ ∽△EOB ，∴OQ ＝5，∴m •n ＝165，∴m +n 的最小值为5．∴MG ，∴S 矩＝2S △MOG +S 平形四边形＝645．（2）分两种情况讨论，情况一：当GN ∥DB 时，直线DB 的解析式为：y ＝﹣32x +6，则直线NG 的解析式为y ＝﹣32x ， ∴﹣32x ＝﹣12x 2+32x +2，解得x 1＝x 2＝3∴交点坐标为（92+），（392-），情况二：DB 为对角线时，此时NG 必过DB 的中点（3，32），设直线ON 的解析式为y ＝k 1x ，则k 1＝12，∴直线OD 的解析式为y ＝12x ，12＝﹣12x 2+32x +2，解得x 1＝1x 2＝∴交点坐标为（112），（12），综上所述：交点坐标为（92+），（392-），（1﹣12），（12）． 【点睛】此题考查了二次函数的性质以及二次函数与几何相结合的问题，转化矩形面积最小和三角形面积最大为某条线段的最值为解题关键．8．B解析：（1）12；（2）3）【解析】【分析】（1）如图1中，过点B 作BD CA ⊥，交CA 延长线于点D ，通过构造直角三角形，求出BD 利用三角形面积公式求解即可.（2）如图示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ，确定点P 的位置，利用勾股定理与矩形的性质求出CQ 的长度即为答案.（3）解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、，通过轴对称性质的转化，最终确定最小值转化为SN 的长.【详解】（1）如解图1所示，过点B 作BD CA ⊥，交CA 延长线于点D ，135BAC ∠=，180********BAD BAC ∴∠=-∠=-=，BD CA ⊥，交CA 延长线于点D ，BAD ∴为等腰直角三角形，且90BDA ∠=，BD AD ∴=，在BAD 中，,90BD AD BDA =∠=，222BD AD AB ∴+=，即222BD AB =，4AB =222232BD AB ∴===，解得：4BD =，6AC =，11641222ABC S AC BD ∴=⋅=⨯⨯=．（2）如解图2所示，作点D 关于AB 的对称点Q ，交AB 于点H ，连接CQ ，交AB 于点P ，连接PD 、OD 、OC ，过点Q 作QM CO ⊥，交CO 延长线于点M ， D 关于AB 的对称点Q ，CQ 交AB 于点P ，PD PQ ∴=，PC PD PC PQ CQ ∴+=+=，点P 为AB 上的动点，PC PD CQ ∴+≥，∴当点P 处于解图2中的位置，PC PD +取最小值，且最小值为CQ 的长度， 点C 为半圆AB 的中点，90COB ∴∠=，90BOD COD COB ∠+∠=∠=，11903033BOD COB ∴∠=∠=⨯=， 10AB =，1110522OD AB ∴==⨯=， 在Rt ODH △中，由作图知，90OHD ∠=，且30HOD BOD ∠=∠=， 155,222DH OD QH DH ∴==∴==， 222255352OH OD DH ⎛⎫∴=-=-= ⎪⎝⎭， 由作图知，四边形OMQH 为矩形，553,2OM QH MQ OH ∴==== 515522CM OM OC ∴=+=+=， 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，PC PD ∴+的最小值为53．（3）如解图3所示，在AB 上这一点作点P 关于OA 的对称点S ，作点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，连接OS ON OP EP FP 、、、、， 点P 关于OA 的对称点S ，点P 关于OB 的对称点N ，连接SN ，交OA 于点E ，交OB 于点F ，PE SE ∴=，FP FN =，SOA POA ∠=∠，,NOB POB OS OP ON ∠=∠==，．PE EF FP SE EF FN SN ∴++=++=，SOA NOB POA POB ∠+∠=∠+∠，E 为OA 上的点，F 为OB 上的点PE EF FP SN ∴++≥，∴当点E F 、处于解图3的位置时，PE EF FP ++的长度取最小值，最小值为SN 的长度，45POA POB AOB ∠+∠=∠=，45SOA NOB ∴∠+∠=，454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=．扇形AOB 的半径为20，20OS ON OP ∴===，在Rt SON 中，90SON ∠=，20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容，理解题意，作出辅助线是做题的关键.9．D解析：（1）见解析；（2）32332232【解析】【分析】（1）由DF=2OD，得到OF=3OD=3OC，求得13OE OCOC OF==，推出△COE∽△FOE，根据相似三角形的性质得到∠OCF=∠DEC=90°，于是得到CF是⊙O的切线；（2）利用三角函数值，设OE=x，OC=3x，得到CE=3，根据勾股定理即可得到答案；（3）连接BD，根据圆周角定理得到角相等，然后证明△AOF∽△BDM，由相似三角形的性质，得到FM为中位线，即可求出FM的长度，由相似三角形的性质，以及中线分三角形的面积为两半，即可求出面积.【详解】解：（1）∵DF＝2OD，∴OF＝3OD＝3OC，∴13 OE OCOC OF==，∵∠COE＝∠FOC，∴△COE∽△FOE，∴∠OCF＝∠DEC＝90°，∴CF 是⊙O 的切线；（2）∵∠COD ＝∠BAC ，∴cos ∠BAC ＝cos ∠COE ＝13OE OC =， ∴设OE ＝x ，OC ＝3x ，∵BC ＝8，∴CE ＝4，∵CE ⊥AD ，∴OE 2+CE 2＝OC 2，∴x 2+42＝9x 2，∴x ＝2（负值已舍去），∴OC ＝3x ＝32，∴⊙O 的半径OC 为32；（3）如图，连结BD ，由圆周角定理，则∠OAF=∠DBM ，2AOF ADC ∠=∠， ∵BC ⊥AD ，∴AC AB =，∴∠ADC=∠ADB ，∴2AOF ADC BDM ∠=∠=∠，∴△AOF ∽△BDM ；∵点F 是OC 的中点，∴AO ：OF=BD ：DM=2，又∵BD=DC ，∴DM=CM ，∴FM 为中位线，∴322， ∴S △AOF : S △BDM =(326 2 34=； ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯=∴S△AOF=3 424⨯=32；【点睛】本题考查了圆的综合问题，圆周角定理，切线的判定和性质，相似三角形的判定和性质，利用勾股定理求边长，以及三角形中线的性质，解题的关键是熟练掌握所学的定理和性质，运用属性结合的思想进行解题.10．F解析：（1）16；（2）不变，证明见解析；（3）214322S x x=-+，当x=2或6时，四边形FEGN的面积为26．【解析】【分析】（1）如图1中，在△AEF中，设AE=x，则EF=8-x，AF=4，∠A=90°，理由勾股定理构建方程求出x，再根据△AEF∽△DFM，可得3124FDMAEDF C∆==，由此即可解决问题；（2）△FDM的周长与（1）中结论相同．证明方法与（1）类似；（3）作GK⊥AB于K．连接BF交GE于P．由△AFB≌△KEG，可得FB=GE，由（2）可知：AE=21416x-，设AF=EK=x，AK=AE+EK=AF+AE=21416x x-+，根据S=82AE DG+⨯，构建二次函数即可解决问题；【详解】解：（1）在△AEF中，设AE=x，则EF=8-x，AF=4，∠A=90°，由勾股定理，得：42﹢x2=(8-x)2，∴x=3，∴AE=3，EF=5．∴△AEF的周长为12，如图，∵∠MFE=90°，∴∠DFM+∠AFE=90°又∵∠A=∠D=90，∠AFE=∠DMF，∴△AEF∽△DFM，∴AEDF=34=12FDMC，∴△FDM的周长为16；（2）△FDM的周长不会发生变化；理由：如下图，设AF=x，EF=8-AE，x2+AE2=（8-AE）2，∴AE=21416x-，∵△AEF∽△DFM，∴8FDMAE xDF C∆+=，∴△FMD的周长：2(8)(8)161416FDMx xCx∆-+==-．（3）如图，作GK⊥AB于K．连接BF交GE于P．∵B、F关于GE对称，∴BF⊥EG，∴∠FBE=∠KGE，在正方形ABCD中，GK=BC=AB，∠A=∠EKG=90°，∴△AFB≌△KEG，∴FB=GE，由（2）可知：AE=21416x-，∴AF=EK=x，AK=AE+EK=AF+AE=21416x x-+，∴梯形AEGD 的面积为：22211184(44)432216162AE DG x x x x x +⨯=⨯-+-+=-++， ∴221188(432)43222S x x x x =⨯--++=-+， 当S=26时，有 21432262x x -+=， 解得：x=2或x=6，∴当x=2或6时，四边形FEGN 的面积为26．【点睛】本题考查四边形综合题、正方形的性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理、二次函数的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会构建二次函数，理由方程解决问题，属于中考压轴题．11．A解析：（1）A （4，0）；（2）2144S t =-；（3）(4,8)E - 【解析】【分析】（1）利用三角形的面积公式构建方程即可解决问题．（2）证明△CEA 和△COD 是等腰直角三角形，由EN ⊥AC ，推出42t CN NE NA +===，AC=4+t ，根据S=S △AEC -S △ABC 计算即可．（3）过点F 作FM ⊥AC 于点M ，由（2）求出点F 的坐标为(1,3)44t t -+，从而得到 1144t t OM =-=-，34t FM =+，由∠ABO=∠BDA+∠BAD=45°，∠FOB +∠DAE =45°，得出∠FOB=∠BDA ，进而得出∠MFO=∠ODA ，tan ∠MFO =tan ∠ODA ，故而OA OM OD MF =， 即14434t t t -=+，解出t 的值，再求点E 的坐标即可. 【详解】（1）由题意可得：211•••822AOB S OA OB OA ==＝， ∴OA 2=16，∵OA ＞0，∴OA=OB=4，。

中考数学中考数学压轴题 复习测试卷(1)

中考数学中考数学压轴题 复习测试卷(1)

一、中考数学压轴题1．在平面直角坐标系中，直线4(0)3y x b b =-+>交x 轴于点A ，交y 轴于点B ，10AB =．（1）如图1，求b 的值；（2）如图2，经过点B 的直线(4)(40)y n x b n =++-<<与直线y nx =交于点C ，与x 轴交于点R ，//CD OA ，交AB 于点D ，设线段CD 长为d ，求d 与n 的函数关系式； （3）如图3，在（2）的条件下，点F 在第四象限，CF 交OA 于点E ，45AEF ∠=︒,点P 在第一象限，PH OA ⊥，点N 在x 轴上，点M 在PH 上，MN 交PE 于点G ，PH EN =，过点E 作EQ CF ⊥，交PH 于点Q ， 32==EQ EF PM ，∠=∠OBR HNM ，BC CR =，点G 的坐标为1927,55⎛⎫ ⎪⎝⎭，连接FN ，求EFN 的面积．2．“阅读素养的培养是构建核心素养的重要基础，重庆十一中学校以‘大阅读’特色课程实施为突破口，着力提升学生的核心素养．”全校师生积极响应和配合，开展各种活动丰富其课余生活．在数学兴趣小组中，同学们从书上认识了很多有趣的数．其中有一个“和平数”引起了同学们的兴趣．描述如下：一个四位数，记千位上和百位上的数字之和为x ，十位上和个位上的数字之和为y ，如果x y =，那么称这个四位数为“和平数”．例如：1423，14x =+，23y =+，因为x y =，所以1423是“和平数”．（1）直接写出：最小的“和平数”是________，最大的“和平数”是__________； （2）求同时满足下列条件的所有“和平数”：①个位上的数字是千位上的数字的两倍；②百位上的数字与十位上的数字之和是12的倍数；（3）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后这两个“和平数”为“相关和平数”．例如：1423于4132为“相关和平数”求证：任意的两个“相关和平数”之和是1111的倍数．3．已知．在Rt △OAB 中，∠OAB=90°，∠BOA=30°，OA=23，若以O 为坐标原点，OA 所在直线为x 轴，建立如图所示的平面直角坐标系，点B 在第一象限内，将Rt △OAB 沿OB 折叠后，点A 落在第一象限内的点C 处．（1）求经过点O ，C ，A 三点的抛物线的解析式．（2）若点M 是抛物线上一点，且位于线段OC 的上方，连接MO 、MC ，问：点M 位于何处时三角形MOC 的面积最大？并求出三角形MOC 的最大面积．（3）抛物线上是否存在一点P ，使∠OAP=∠BOC ？若存在，请求出此时点P 的坐标；若不存在，请说明理由．4．一种实验用轨道弹珠，在轨道上行驶5分钟后离开轨道，第一颗弹珠弹出后其速度1y （米/分钟）与时间x （分钟）前2分钟满足二次函数21y ax =，后3分钟满足反比例函数关系，如图，轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟．（1）求第一颗弹珠的速度1y （米/分钟）与时间x （分钟）之间的函数关系式；（2）第一颗弹珠弹出1分钟后，弹出第二颗弹珠，第二颗弹珠的运行情况与第一颗相同，直接写出第二颗弹珠的速度2y （米/分钟）与弹出第一颗弹珠后的时间x （分钟）之间的函数关系式；（3）当两颗弹珠同时在轨道上时，第____分钟末两颗弹珠的速度相差最大，最大相差______；（4）判断当两颗弹珠同时在轨道上时，是否存在某时刻速度相同？请说明理由，并指出可以通过解哪个方程求出这一时刻．5．综合与实践A纸是我们学习工作最常用的纸张之一，其长宽之比是2:1，我们定义：长宽之比是42:1的矩形纸片称为“标准纸”．操作判断：()1如图1所示，矩形纸片2=是一张“标准纸”，将纸片折叠一次，使点ABCD AD AB()AB=求CF的B与D重合，再展开，折痕EF交AD边于点,E交BC边于点F，若1,长，()2如图2，在()1的基础上，连接,BE判断四边形BD折痕EF交BD于点O，连接,BFDE的形状，并说明理由．探究发现：()3如图3所示，在(1)和(2)的基础上，展开纸片后，将纸片再折叠一次，使点A 与点C 重合，再展开，痕MN 交AD 边于点M ，BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下，探究纸片ENFM 是否为“标准纸”，说明理由．6．如图，90EOF ∠=︒，矩形ABCD 的边BA 、BC 分别在OF 、OE 上，4AB =，3BC =，矩形ABCD 沿射线OD 方向，以每秒1个单位长度的速度运动．同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动，当点P 到达点C 时，矩形ABCD 也停止运动，设点P 的运动时间为()t s ，PDO △的面积为S ． （1）分别写出点B 到OF 、OE 的距离（用含t 的代数式表示）；（2）当点P 不与矩形ABCD 的顶点重合时，求S 与t 之间的函数关系式；（3）设点P 到BD 的距离为h ，当15h OD =时，求t 的值； （4）若在点P 出发的同时，点Q 从点B 以每秒43个单位长度的速度向终点A 运动，当点Q 停止运动时，点P 与矩形ABCD 也停止运动，设点A 关于PQ 的对称点为E ，当PQE 的一边与CDB △的一边平行时，直接写出线段OD 的长．7．如图①，四边形ABCD 中，//,90AB CD ADC ∠=︒．（1）动点M 从A 出发，以每秒1个单位的速度沿路线A B C D →→→运动到点D 停止，设运动时间为a ，AMD ∆的面积为,S S 关于a 的函数图象如图②所示，求AD CD 、的长．（2）如图③动点P 从点A 出发，以每秒2个单位的速度沿路线A D C →→运动到点C 停止，同时，动点Q 从点C 出发，以每秒5个单位的速度沿路线C D A →→运动到点A 停止，设运动时间为t ，当Q 点运动到AD 边上时，连接CP CQ PQ 、、，当CPQ ∆的面积为8时，求t 的值．8．如图1，抛物线2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于C 点，连接AC 、BC ，已知点A 、C 的坐标为()2,0A -、()0,6C -．（1）求抛物线的表达式；（2）点P 是线段BC 下方抛物线上的一动点，如果在x 轴上存在点Q ，使得以点B 、C 、P 、Q 为顶点的四边形为平行四边形，求点Q 的坐标；（3）如图2，若点M 是AOC △内一动点，且满足AM AO =，过点M 作MN OA ⊥，垂足为N ，设AMN 的内心为I ，试求CI 的最小值．9．∠MON=90°，点A ，B 分别在OM 、ON 上运动（不与点O 重合）．（1）如图①，AE、BE分别是∠BAO和∠ABO的平分线，随着点A、点B的运动，∠AEB=°（2）如图②，若BC是∠ABN的平分线，BC的反向延长线与∠OAB的平分线交于点D①若∠BAO=60°，则∠D=°．②随着点A，B的运动，∠D的大小会变吗？如果不会，求∠D的度数；如果会，请说明理由．（3）如图③，延长MO至Q，延长BA至G，已知∠BAO，∠OAG的平分线与∠BOQ的平分线及其延长线相交于点E、F，在△AEF中，如果有一个角是另一个角的3倍，求∠ABO 的度数．10．如图，平面上存在点P、点M与线段AB．若线段AB上存在一点Q，使得点M在以PQ为直径的圆上，则称点M为点P与线段AB的共圆点．已知点P（0，1），点A（﹣2，﹣1），点B（2，﹣1）．（1）在点O（0，0），C（﹣2，1），D（3，0）中，可以成为点P与线段AB的共圆点的是；（2）点K为x轴上一点，若点K为点P与线段AB的共圆点，请求出点K横坐标x K的取值范围；（3）已知点M（m，﹣1），若直线y＝12x+3上存在点P与线段AM的共圆点，请直接写出m的取值范围．11．如图一，矩形ABCD 中，AB=m ，BC=n ，将此矩形绕点B 顺时针方向旋转θ（0°＜θ＜90°）得到矩形A 1BC 1D 1，点A 1在边CD 上．（1）若m=2，n=1，求在旋转过程中，点D 到点D 1所经过路径的长度；（2）将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2，点D 2在BC 的延长线上，设边A 2B 与CD 交于点E ，若161A E EC =-，求n m 的值． （3）如图二，在（2）的条件下，直线AB 上有一点P ，BP=2，点E 是直线DC 上一动点，在BE 左侧作矩形BEFG 且始终保持BE n BG m =，设AB=33，试探究点E 移动过程中，PF 是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．12．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．13．平面直角坐标系中，点A 、B 分别在x 轴正半轴、y 轴正半轴上，AO =BO ，△ABO 的面积为8.（1）求点A 的坐标；（2）点C 、D 分别在x 轴负半轴、y 轴正半轴上（D 在B 点上方），AB ⊥CD 于E ，设点D 纵坐标为t ，△BCE 的面积为S ，求S 与t 的函数关系；（3）在（2）的条件下，点F 为BE 中点，连接OF 交BC 于G ，当∠FOB +∠DAE =45°时，求点E 坐标.14．已知，在四边形ABCD 中，AD ∥BC ，AB ∥DC ，点E 在BC 延长线上，连接DE ，∠A ＋∠E ＝180°．（1）如图1，求证：CD=DE ；（2）如图2，过点C 作BE 的垂线，交AD 于点F ，请直接写出BE 、AF 、DF 之间的数量关系_______________________；（3）如图3，在（2）的条件下，∠ABC 的平分线，交CD 于G ，交CF 于H ，连接FG ，若∠FGH=45°，DF=8，CH=9，求BE 的长．15．AB 是O 直径，,C D 分别是上下半圆上一点，且弧BC =弧BD ，连接,AC BC ，连接CD 交AB 于E ，（1）如图(1)求证：90AEC ∠=︒；（2）如图(2)F 是弧AD 一点，点,M N 分别是弧AC 和弧FD 的中点，连接FD ，连接MN 分别交AC ，FD 于,P Q 两点，求证：MPC NQD ∠=∠（3）如图(3)在(2)问条件下，MN 交AB 于G ，交BF 于L ，过点G 作GH MN ⊥交AF 于H ，连接BH ，若,6,BG HF AG ABH ==∆的面积等于8，求线段MN 的长度16．如图，在平面直角坐标系中，Rt ABC △的斜边在AB 在x 轴上，点C 在y 轴上90ACB ∠=︒，OC 、OB 的长分别是一元二次方程2680x x -+=的两个根，且OC OB <．（1）求点A 的坐标；（2）D 是线段AB 上的一个动点（点D 不与点A ，B 重合），过点D 的直线l 与y 轴平行，直线l 交边AC 或边BC 于点P ，设点D 的横坐标为t ，线段DP 的长为d ，求d 关于t 的函数解析式；（3）在（2）的条件下，当12d =时，请你直接写出点P 的坐标．17．如图，在平面直角坐标系中，点O 为坐标原点，直线y =-x + m 交 y 轴的正半轴于点A ，交x 轴的正半轴于点B ，过点A 的直线AF 交x 轴的负半轴于点F ，∠AFO=45°． （1）求∠FAB 的度数；（2）点 P 是线段OB 上一点，过点P 作 PQ ⊥OB 交直线 FA 于点Q ，连接 BQ ，取 BQ 的中点C ，连接AP 、AC 、CP ，过点C 作 CR ⊥AP 于点R ，设 BQ 的长为d ，CR 的长为h ，求d 与 h 的函数关系式（不要求写出自变量h 的取值范围）；（3）在（2）的条件下，过点 C 作 CE ⊥OB 于点E ，CE 交 AB 于点D ，连接 AE ，∠AEC=2∠DAP ，EP=2，作线段 CD 关于直线AB 的对称线段DS ，求直线PS 与直线 AF 的交点K 的坐标．18．在Rt ABC ∆中，6AB =，90B ∠=︒，8BC =，点P 从A 出发沿AC 方向在运动速度为3个单位/秒，点Q 从C 出发向点B 运动，速度为1个单位/秒，P 、Q 同时出发，点Q 到点B 时两点同时停止运动．（1）点P 在线段AC 上运动，过P 作DP PQ ⊥交边AB 于D ，2t =时，求PD PQ的值；（2）运动t 秒后，90BPQ ∠=︒，求此时t 的值；（3）t =________时，AQ QP =．19．如图，四边形AOBC 是正方形，点C 的坐标是(82,0)．（1）正方形AOBC 的边长为 ，点A 的坐标是 ；（2）将正方形AOBC 绕点O 顺时针旋转45︒，点A ，B ，C 旋转后的对应点为A '，B '，C '，求点A '的坐标及旋转后的正方形与原正方形的重叠部分的面积；（3）动点P 从点O 出发，沿折线OACB 方向以1个单位/秒的速度匀速运动，同时，另一动点Q 从点O 出发，沿折线OBCA 方向以2个单位/秒的速度匀速运动，运动时间为t秒，当它们相遇时同时停止运动，当OPQ △为等腰三角形时，求出t 的值（直接写出结果即可）．20．如图，在长方形ABCD 中，AB ＝4cm ，BE ＝5cm ，点E 是AD 边上的一点，AE 、DE 分别长acm ．bcm ，满足(a －3)2＋|2a ＋b －9|＝0．动点P 从B 点出发，以2cm/s 的速度沿B→C→D 运动，最终到达点D ，设运动时间为t s ．（1）a ＝______cm ，b ＝______cm ；（2）t 为何值时，EP 把四边形BCDE 的周长平分？（3）另有一点Q 从点E 出发，按照E→D→C 的路径运动，且速度为1cm/s ，若P 、Q 两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t 为何值时，△BPQ 的面积等于6cm 2．21．如图所示，在直角梯形ABCD 中，AD ∥BC ，∠A=90°，AB=12，BC=21，AD=16．动点P 从点B 出发，沿射线BC 的方向以每秒2个单位长的速度运动，动点Q 同时从点A 出发，在线段AD 上以每秒1个单位长的速度向点D 运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t （秒）．（1）设△DPQ 的面积为S ，求S 与t 之间的关系式；（2）当t 为何值时，四边形PCDQ 是平行四边形？（3）分别求出当t 为何值时，①PD=PQ ；②DQ=PQ ．22．在一次数学课上，李老师让同学们独立完成课本第23页第七题选择题（2）如图 1，如果 AB ∥CD ∥EF ，那么∠BAC+∠ACE+∠CEF ＝（ ）A ．180°B ．270°C ．360°D ．540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB ∥EF ，请直接写出∠BAD ，∠ADE ，∠DEF 之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示），当AD ，ED 分别平分∠BAC ，∠CEF 时，∠ACE 与∠ADE 之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB ∥EF ，当∠ACD=90°时，∠BAC 、∠CDE 和∠DEF 之间又有怎样的数量关系？请你直接写出结果，不需要证明．23．如图1，Rt △ABC 中，点D ，E 分别为直角边AC ，BC 上的点，若满足AD 2+BE 2＝DE 2，则称DE 为R △ABC 的“完美分割线”．显然，当DE 为△ABC 的中位线时，DE 是△ABC 的一条完美分割线．（1）如图1，AB ＝10，cos A ＝45，AD ＝3，若DE 为完美分割线，则BE 的长是 ． （2）如图2，对AC 边上的点D ，在Rt △ABC 中的斜边AB 上取点P ，使得DP ＝DA ，过点P 画PE ⊥PD 交BC 于点E ，连结DE ，求证：DE 是直角△ABC 的完美分割线．（3）如图3，在Rt △ABC 中，AC ＝10，BC ＝5，DE 是其完美分割线，点P 是斜边AB 的中点，连结PD 、PE ，求cos ∠PDE 的值．24．综合与探究：如图1，抛物线24832999y x x =-++与x 轴交于,A B 两点（点A 在点B 的左侧），顶点为D ，P 为对称轴右侧抛物线的一个动点，直线AD 与y 轴于点C ，过点P 作//PF AD ，交x 轴于点F ．（1）求直线AD 的函数表达式及点C 的坐标；（2）如图2，当//PC x 轴时，将AOC ∆以每秒1个单位长度的速度沿x 轴的正方向平移，当点C 与点P 重合时停止平移．设平移t 秒时，在平移过程中AOC ∆与四边形AFPC 重叠部分的面积为S ，求S 关于t 的函数关系式，并写出自变量t 的取值范围； （3）如图3，过点P 作x 轴的平行线，交直线AD 于点E ，直线DF 与PE 交于点M ，设点P 的横坐标为m ．①当3DM MF =时，求m 的值；②试探究点P 在运动过程中，是否存在值m ，使四边形AFPE 是菱形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．25．如图1，抛物线23y ax bx =++与x 轴交于点(1,0)A -、点B ，与y 轴交于点C ，顶点D 的横坐标为1，对称轴交x 轴交于点E ，交BC 与点F .（1）求顶点D 的坐标；（2）如图2所示，过点C 的直线交直线BD 于点M ，交抛物线于点N .①若直线CM 将BCD ∆分成的两部分面积之比为2:1，求点M 的坐标；②若NCB DBC ∠=∠，求点N 的坐标．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．B解析：（1）8b =；（2）382d n =+；（3）92EFN S =△ 【解析】【分析】（1）先用b 表示出点B 和点A 的坐标，然后利用勾股定理列出方程即可求出b 的值； （2）联立直线BC 的解析式和直线AB 的解析式即可用n 表示出点C 的坐标，从而求出点D 的坐标，从而求出d 与n 的函数关系式；（3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I ，根据相似三角形判定可得△RSC ∽△ROB ，列出比例式即可求出OR 和CS ，然后根据等角的锐角三角函数相等求出ON ，再根据等腰直角三角形的性质求出NE ，然后结合已知条件和等角的锐角三角函数相等求出TF ，即可求出结论．【详解】解：（1）当x=0时，y=b ；当y=0时，x=34b ∴点B 的坐标为（0，b ），点A 的坐标为（34b ，0） ∴OB=b ，OA=34b 根据勾股定理OB 2＋OA 2=AB 2b 2＋（34b ）2=102 解得：b=8或-8（不符合已知条件，舍去）∴b=8（2）直线BC 的解析式为(4)8=++y n x ，直线AB 的解析式为483y x =-+ 联立(4)8y n x y nx =++⎧⎨=⎩解得：22x y n =-⎧⎨=-⎩∴点C 的坐标为（-2，-2n ）∵//CD OA∴点D 的纵坐标为-2n将y=-2n 代入483y x =-+中，解得：x=362+n ∴点D 的坐标为36,22⎛⎫+-⎪⎝⎭n n ∴线段CD 长d =362+n －（-2）=382+n（3）过点C 作CS ⊥x 轴于S ，过点F 作FT ⊥x 轴于T ，过点G 作GD ⊥y 轴于D ，MN 与y 轴交于点I∴OD=275，GD=195由（2）知点C 坐标为（-2，-2n ）∴CS=-2n ，OS=2∵BC CR =，CS ∥y 轴 ∴RB=2RC ，△RSC ∽△ROB∴12===CS RS RC OB OR RB 即22182--==n OR OR 解得：n=-2，OR=4∴CS=4∵∠=∠OBR HNM ，GD ∥x 轴∴∠=∠OBR HNM =∠DGI∴tan tan ∠=∠OBR HNM =tan ∠DGI∴==OR OI ID OB ON GD即48927515-==ID ID ON解得：1910,7==ID ON ∵45AEF ∠=︒∴∠CES=∠AEF=45°，∠QEH=∠QEF －∠AEF=45°∴△CES 、△EFT 和△EHQ 都是等腰直角三角形 ∴CS=SE=4，ET=TF=22EF ， EH=HQ ，设EH=HQ=a ，则2a∴EN=ON ＋OE=ON ＋SE －OS=9∵3==EQ EF ，PH EN =∴，PM=a ，PH=9， ∴NH=EN ＋EH=9＋a ，MH=PH －PM=9－a ∴tan ∠HNM =12==MH OI NH ON ∴9192-=+a a 解得：a=3∴EF=33⨯=∴TF=12= ∴S △EFN =12EN ·TF=12×9×1=92【点睛】此题考查的是一次函数与几何图形的综合题型，此题难度较大，掌握勾股定理、联立方程求交点坐标、锐角三角函数的性质、勾股定理、等腰直角三角形的性质和相似三角形的判定及性质是解决此题的关键．2．（1）1001；9999；（2）2754和4848；（3）见解析【解析】【分析】（1）根据“和平数”的定义可直接得出最小的“和平数”是1001，最大的“和平数”是9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤，则个位数字是2a ，又由029a ≤≤得到a 的可能取值为1，2，3，4；根据百位上的数字与十位上的数字之和是12的倍数，可知m +n =12，得到122a m +=，由a 的可能取值可得m 的取值，即可求得符合条件的“和平数”；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ，计算它们的和，根据“和平数”的定义可知a+b=c+d ，因式分解可得原式= 1111(a+b )，即可证明．【详解】解：（1）根据“和平数”的定义可得：最小的“和平数”1001，最大的“和平数”9999，故答案为1001；9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤，则个位数字是2a ，又∵029a ≤≤，∴a 的可能取值为1，2，3，4；∵百位上的数字与十位上的数字之和是12的倍数，∴m+n =0或m+n =12，∵“和平数”中a+m =n+2a ，当m+n =0时，即m=n =0，则此时a =0，不符合题意，∴m+n =12，∴a+m =12−m +2a ，解得：122a m +=， ∵a 的可能取值为1，2，3，4；且m 为正整数，∴m 的可能取值为7，8；当a =2时，m =7，这个“和平数”是2754；当a =4时，m =8，这个“和平数”是4848；综上所述，满足条件的“和平数”是2754和4848；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ， ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知：a+b =c+d ，∴原式1100()11()a b a b =+++1111()a b =+，∵a ，b 为正整数，则1111()a b +能被1111整除，即(100010010)(100010010)a b c d b a d c +++++++能被1111整除，∴任意的两个“相关和平数”之和是1111的倍数．【点睛】本题考查新定义运算、因式分解的应用；能够读懂题意，根据数的特点，确定数的取值范围，进行正确的因式分解是解题关键．3．C解析：（1）y=﹣x 2；（2）⎝⎭3）存在，53)或(﹣73) 【解析】【分析】（1）根据折叠的性质可得OC=OA ，∠BOC=∠BAO=30°，过点C 作CD ⊥OA 于D ，求出OD 、CD ，然后写出点C 的坐标，再利用待定系数法求二次函数解析式解答；（2）求出直线OC 的解析式，根据点M 到OC 的最大距离时，面积最大；平行于OC 的直线与抛物线只有一个交点，利用根的判别式求出m 的值，利用锐角三角函数的定义求解即可；（3）分两种情况求出直线AP 与y 轴的交点坐标，然后求出直线AP 的解析式，与抛物线解析式联立求解即可得到点P 的坐标．【详解】解：（1）∵Rt △OAB 沿OB 折叠后，点A 落在第一象限内的点C 处，∴OC=OA=23，∠BOC=∠BAO=30°，∴∠AOC=30°+30°=60°，过点C 作CD ⊥OA 于D ，则OD=1233 33， 所以，顶点C 33），设过点O ，C ，A 抛物线的解析式为为y=ax 2+bx ，则223)33(23)230a b a b ⎧=⎪⎨+=⎪⎩， 解得：123a b =-⎧⎪⎨=⎪⎩ ∴抛物线的解析式为y=﹣x 23；（2）∵C 33），∴直线OC 的解析式为：3y x =，设点M 到OC 的最大距离时，平行于OC 的直线解析式为3y x m =+，联立2y x ⎨=-+⎪⎩， 消掉未知数y并整理得，20x m +=，△=（2-4m=0，解得：m=34．∴2304x +=，∴x =； ∴点M 到OC 的最大距离=34×sin30°=313428⨯=；∵OC ==∴1328MOC S ∆=⨯⨯= 此时，M ⎝⎭（3）∵∠OAP=∠BOC=∠BOA =30°，∴2=， ∴直线AP 与y 轴的交点坐标为（0，2）或（0，﹣2）， 当直线AP经过点（0）、（0，2）时，解析式为2y x =+，联立22y x y x ⎧=-+⎪⎨=+⎪⎩，解得110x y ⎧=⎪⎨=⎪⎩2253x y ⎧=⎪⎪⎨⎪=⎪⎩． 所以点P53）， 当直线AP经过点（0）、（0，﹣2）时，解析式为23y x =-，联立2y x ⎪⎨=-⎪⎩解得110x y ⎧=⎪⎨=⎪⎩2273x y ⎧=⎪⎪⎨⎪=-⎪⎩； 所以点P的坐标为（3-73-）． 综上所述，存在一点P，5373），使∠OAP=∠BOA ． 【点睛】本题是二次函数综合题型，主要利用了折叠的性质，待定系数法求二次函数解析式，联立两函数解析式求交点的方法，（2）判断出点M 到OC 的距离最大是，平行于OC 的直线与抛物线只有一个交点是解题的关键，（3）确定出直线AP 的解析式是解题的关键．4．（1）212(02)16(25)x x y x x ⎧≤≤⎪=⎨≤≤⎪⎩；（2）220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩；（3）第2分钟末两颗弹珠速度相差最大，最大相差6米/分钟；（4）存在，理由详见解析【解析】【分析】（1）将（1，2）代入21y ax =，得2a =，从而得到212y x =，再代入2x =求出18y =，即可得到反比例函数解析式，即可得解；（2）当01x ≤≤时，第二颗弹珠未弹出，故第二颗弹珠的解析式为20y =；再分别根据（1）中的结论，即可求出当13x <≤和36x <≤时第二颗弹珠的解析式；（3）由图可知看出，前2分钟，弹珠的速度逐渐增大，则第2分钟末两颗弹珠速度相差最大，分别求出第2分钟末时两颗弹珠的速度，再相减即可的解；（4）第2分钟末到第3分钟末，第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟，第二颗弹珠的速度由2米/分逐步上升到8米/分，故在此期间必定存在一时刻，两颗弹珠的速度相同．可以根据速度相等时列方程求得时刻．【详解】（1）当02x ≤≤时，将（1，2）代入21y ax =，得2a =，212y x ∴=，∵当2x =时，18y =，∴当25x ≤≤时，116y x=， 1y ∴与x 的函数关系式为212(02)16(25)x x y x x⎧≤≤⎪=⎨≤≤⎪⎩；（2）当01x ≤≤时，第二颗弹珠未弹出，∴第二颗弹珠的解析式为20y =；当13x <≤时，第二颗弹珠的解析式为222(1)y x =-；当36x <≤时，第二颗弹珠的解析式为2161y x =-； ∴2y 与x 的函数关系式为220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩；（3）由图可知看出，前2分钟，弹珠的速度逐渐增大，∴第2分钟末两颗弹珠速度相差最大，∵第一颗弹珠的速度为2218222y x =⨯==米/分钟，第二颗弹珠的速度为2122(1)212y x =⨯==-米/分钟，∴两颗弹珠的速度最大相差8-2=6米/分钟；（4）存在，理由如下：第2分钟末到第3分钟末，第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟， 第二颗弹珠的速度由2米/分逐步上升到8米/分，故在此期间必定存在一时刻，两颗弹珠的速度相同． 这个时刻可以通过解方程2162(1)x x =-求得． 【点睛】本题考查了反比例函数和二次函数的应用．解题的关键是从图中得到关键性的信息，明确自变量的取值范围和图象所经过的点的坐标．5．(1) CF长为4 ；(2) 四边形BFDE 是菱形，理由见解析；(3) 纸片ENFM 是“标准纸"，理由见解析【解析】【分析】（1）1AB =，则AD =ABCD是矩形，得到1,CD AB BC AD ==-=FB FD =，设CF x =，则FB FD x ==，在Rt DCF △中，222+=CD CF DF ，可得)2221x x +=即可求解．（2）当顶点B 与点D 重合时，折痕EF 垂直平分BD ，可得OB OD =，90BOF DOE ∠=∠=，在矩形ABCD 中，//AD BC ，得到OBF ODE ∠=∠，在BOF 和DOE △中，,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,，可得BOF DOE ≅，OE OF =，再根据OB OD =，可得四边形BFDE 是平行四边形，最后根据EF BD ⊥，即可求证平行四边形BFDE 是菱形．（3）由()2可知，OE OF =，同理可知，OM ON =，可得四边形ENFM 是平行四边形，根据90DOE DAB ∠=∠=︒，得到DOE DAB ，再根据AD =，可得2OE AB OD AD ===，进而得到2OE OD =，2EF BD =，同理可得，2MN AC =，根据四边形ABCD 是矩形，可得AC BD =，EF MN =，四边形ENFM 是矩形，90EMF ∠=，MF OD tan FEM ME OE ∠===MF =，即可求证纸片ENFM 是“标准纸"．【详解】解：()11,AB =则AD AB ==四边形ABCD 是矩形1,CD AB BC AD ∴==-=由折叠得FB FD =设CF x =，则FB FD x ==在Rt DCF △中，222+=CD CF DF)2221x x +=4x =答：CF 长为4()2四边形BFDE 是菱形.理由：当顶点B 与点D 重合时，折痕EF 垂直平分,BDOB OD ∴=，90BOF DOE ∠=∠=在矩形ABCD 中，//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中，,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,BOF DOE ∴≅OE OF ∴=OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下：由()2可知，,OE OF =同理可知，,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒DOE DAB ∴ 2AD =222OE AB OD AD ∴=== 22OE OD ∴=2EF BD ∴=同理可得，2MN AC = 四边形ABCD 是矩形，AC BD ∴=，EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.MF OD tan FEM ME OE∴∠===MF ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数，灵活运用判定和性质是解题关键．6．B解析：（1）35t ，45t ；（2）当0＜t ＜3时，224655S t t =--+；当3＜t ＜7时，23391052S t t =+-；（3）75；（4）132，7713，477 【解析】【分析】（1）过点B 作x 轴垂线，利用相似三角形可求得； （2）分2种情况，一种是点P 在AD 上，另一种是点P 在CD 上，然后利用三角形面积公式可求得；（3）直接令15h OD =即可求出； （4）存在3种情况，第一种是：QP ∥BD ，第二种是EP ∥CD 或EQ ∥CB ，第三种是QE ∥BD ，分别按照几何性质分析求解．【详解】（1）如下图，过点B 作x 轴垂线，垂足为点M根据平移的特点，可得∠BOM=∠DBA∵∠BMO=∠DAB=90°，∴△BMO ∽△DAB∵AB=4，AD=BC=3∴BD=5 ∵BM OM BO DA BA BD ==，OB=t ∴BM=35t ，OM=45t （2）情况一：当0＜t ＜3时，图形如下，过点P 作OD 的垂线，交OD 于点N∵∠NDP=∠BDA ，∠PND=∠BAD ，∴△PND ∽△BAD∵AP=t ，∴PD=3－t∵PN BA PD BD =，∴PN=()435t - 图中，OD=5+t ∴()()243124562555OBD t S t t t -=+=--+ 情况二：当3＜t ＜7时，图形如下，过点P 作OD 的垂线，交OD 于点N图中，PD=t －3，OD=5+t同理，△PND ∽△BCD ，可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- （3）情况一：当0＜t ＜3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得：t=75情况二：当3＜t ＜7时则h=PN=()335t - ∵15h OD =∴()33555t t -+= 解得：t=7(舍)（4）情况一：QP ∥BD ，图形如下由题意可得：BQ=43t ，AP=t ，则QA=4－43t ，DP=3－t ∵BD ∥QP∴QA PA QB PD= 代入得：4()2243t t =-解得：t=32∴OD=5+t=13 2情况二：如下图，EP∥CD(或EQ∥CB)∵点E是点A关于QP对称的点∴EP=PA，EQ=QA，QP=QP∴△APQ≌△EPQ∵EP∥CD，CD⊥AD∴EP⊥AD∴∠APQ=∠EPQ=45°∴△AQP是等腰直角三角形，AQ=PA∴4－43 tt=解得：t=12 7∴OD=5+t=47 7情况三：如下图，QE∥BD，延长QE交DA于点N∵△APQ≌△EPQ，∴∠QEP=∠QAP=90°∴△ENP是等腰直角三角形∵QN∥BD，∴∠NQA=∠DBA，∠A=∠A∴△QNA∽△BDA∵BQ=43t，AP=t，QA=4－43t，DP=3－t∴QN QA AN BD BA AD==∴QN=5－43t ，NA=3－t ∴EN=QN －QE=QN －QA=1－3t ，NP=NA －AP=3－2t ，EP=PA=t ∴在Rt △ENP 中，()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得：t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题，解题关键是利用相似将图形中各边用t 表示出来．7．C解析：（1）12,16AD CD ==；（2）277和297. 【解析】【分析】（1）根据题意由函数图象可知动点M 从A 出发，以每秒1个单位的速度从C 到D 耗时16秒求出CD ，再利用三角形面积公式求得AD 即可；（2）由题意可知只能有P 和Q 点都在AD 边上，此时分当P 在Q 上方时以及当P 在Q 下方时两种情况运用数形结合思维进行分析得出答案.【详解】解：（1）由函数图象可知动点M 从A 出发，以每秒1个单位的速度从C 到D 耗时36-20=16秒，即CD=16，而此时AMD ∆的面积为96，又因为90ADC ∠=︒， 即有11169622CD AD AD =⨯=,解得12AD =. 所以12,16AD CD ==. （2）由题意可知Q 运动到点A 停止的时间为285，而P 运动到点D 停止的时间为6， 所以只能有P 和Q 点都在AD 边上，此时以PQ 为底边，CD 为高，设运动时间为t ，则AP=2t ，QD=5t-16，（162855t ≤<）， ①当P 在Q 上方时，则有PQ=AD-AP-QD= 122516287t t t --+=-， 可知CPQ ∆的面积为8时即11(287)16822PQ CD t =⨯-⨯=，解得277t =（满足条件）；②当P 在Q 下方时，则有PQ=QD-（AD-AP ）= 516(122)728t t t ---=-，可知CPQ ∆的面积为8时即11(728)16822PQ CD t =⨯-⨯=，解得297t =（满足条件）. 所以当CPQ ∆的面积为8时，t 的值为277和297. 【点睛】本题考查四边形动点问题和一次函数结合，熟练掌握四边形动点问题的解决办法和一次函数图象的相关性质，运用数形结合思维分析是解题的关键.8．C解析：（1）26y x x =--；（2）Q 的坐标为()2,0或()4,0；（3）CI 的最小值为【解析】【分析】（1）待定系数法求解析式；（2）根据//CP BQ 即点C 坐标，可以求出P 点坐标，算出CP 长，即可写出Q 点坐标; （3）利用AIM AIO ≌△△可判断出I 的运动轨迹是圆弧，设I 运动轨迹所在的圆心为G 计算出圆心G 的坐标及半径为，当G 、I 、C 三点共线时候CI 最短.【详解】（1）由题意得：A 点坐标为()2,0-，C 点坐标为()0,6-带入2y x bx c =++中得：4206b c c -+=⎧⎨=-⎩， 解得：16b c =-⎧⎨=-⎩∴抛物线的解析式为26y x x =--．（2）∵点Q 在x 轴上，又点B 、C 、P 、Q 为顶点的四边形是平行四边形∴//CP BQ ，由对称性可知，P 点的坐标为()1,6-∴1PC =，∴1BQ =．∴Q 的坐标为()2,0或()4,0．（3）连接AI ，MI ，OI。

中考数学压轴题测试综合卷检测试题

中考数学压轴题测试综合卷检测试题

一、中考数学压轴题1．如图，在▱ABCD 中，对角线AC ⊥BC ，∠BAC ＝30°，BC ＝23，在AB 边的下方作射线AG ，使得∠BAG ＝30°，E 为线段DC 上一个动点，在射线AG 上取一点P ，连接BP ，使得∠EBP ＝60°，连接EP 交AC 于点F ，在点E 的运动过程中，当∠BPE ＝60°时，则AF ＝_____．2．如图，已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点，与y 轴交于C 点，直线BD 交抛物线于点D ，并且()D 2,3，()B 4,0-． （1）求抛物线的解析式；（2）已知点M 为抛物线上一动点，且在第三象限，顺次连接点B 、M 、C ，求BMC 面积的最大值；（3）在（2）中BMC 面积最大的条件下，过点M 作直线平行于y 轴，在这条直线上是否存在一个以Q 点为圆心，OQ 为半径且与直线AC 相切的圆？若存在，求出圆心Q 的坐标；若不存在，请说明理由．3．如图，在梯形ABCD 中，AD//BC ，AB=CD=AD=5，cos 45B =，点O 是边BC 上的动点，以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ，联结AM ，作∠CMN=∠BAM ，射线MN 与边AD 、射线CD 分别交于点F 、N ．（1）当点E 为边AB 的中点时，求DF 的长；（2）分别联结AN 、MD ，当AN//MD 时，求MN 的长；（3）将O 绕着点M 旋转180°得到'O ，如果以点N 为圆心的N 与'O 都内切，求O 的半径长．4．定义：如果一个三角形一条边上的高与这条边的比值是3：5，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．（概念感知）（1）如图1，在ABC 中，12AC =，10BC =，30ACB ∠=︒，试判断ABC 是否是“准黄金”三角形，请说明理由．（问题探究）（2）如图2，ABC 是“准黄金”三角形，BC 是“金底”，把ABC 沿BC 翻折得到DBC △，连AB 接AD 交BC 的延长线于点E ，若点C 恰好是ABD △的重心，求AB BC的值．（拓展提升） （3）如图3，12l l //，且直线1l 与2l 之间的距离为3，“准黄金”ABC 的“金底”BC 在直线2l 上，点A 在直线1l 上．10AB BC =，若ABC ∠是钝角，将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C ''，线段A C '交1l 于点D ．①当30α=︒时，则CD =_________；②如图4，当点B 落在直线1l 上时，求AD CD 的值．5．如图，在ABC ∆中，14AB =，45B ∠=︒，4tan 3A =，点D 为AB 中点．动点P 从点D 出发，沿DA 方向以每秒1个单位长度的速度向终点A 运动，点P 关于点D 对称点为点Q ，以PQ 为边向上作正方形PQMN ．设点P 的运动时间为t 秒．（1）当t =_______秒时，点N 落在AC 边上．（2）设正方形PQMN 与ABC ∆重叠部分面积为S ，当点N 在ABC ∆内部时，求S 关于t 的函数关系式．（3）当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时，直接写出t 的值． 6．∠MON=90°，点A ，B 分别在OM 、ON 上运动（不与点O 重合）．（1）如图①，AE 、BE 分别是∠BAO 和∠ABO 的平分线，随着点A 、点B 的运动，∠AEB= °（2）如图②，若BC 是∠ABN 的平分线，BC 的反向延长线与∠OAB 的平分线交于点D ①若∠BAO=60°，则∠D= °．②随着点A ，B 的运动，∠D 的大小会变吗？如果不会，求∠D 的度数；如果会，请说明理由．（3）如图③，延长MO 至Q ，延长BA 至G ，已知∠BAO ，∠OAG 的平分线与∠BOQ 的平分线及其延长线相交于点E 、F ，在△AEF 中，如果有一个角是另一个角的3倍，求∠ABO 的度数．7．对于平面直角坐标系xOy 中的任意点()P x y ，，如果满足x y a += (x ≥0，a 为常数)，那么我们称这样的点叫做“特征点”．（1）当2≤a ≤3时，①在点(1,2),(1,3),(2.5,0)A B C 中，满足此条件的特征点为__________________；②⊙W 的圆心为(,0)W m ，半径为1，如果⊙W 上始终存在满足条件的特征点，请画出示意图，并直接写出m 的取值范围；（2）已知函数()10Z x x x=+>，请利用特征点求出该函数的最小值．8．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是 ；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．9．如图，在ABC 中，90ABC ∠=︒，AB BC <，O 为AC 中点，点D 在BO 延长线上，CD BC =，AE BC ∥，CE CA =，AE 交BD 于点G ．（1）若28DCE ∠=︒，求AOB ∠的度数；（2）求证：AG GE =；（3）设DC 交GE 于点M ．①若3AB =，4BC =，求::AG GM ME 的值；②连结DE ，分别记ABG ，DGM ，DME 的面积为1S ，2S ，3S ，当AC DE 时，123::S S S = ．（直接写出答案）10．已知：如图，在平面直角坐标系中，点 A 的坐标为（6，0），2，点 P 从点 O 出发沿线段 OA 向终点 A 运动，点 P 的运动速度是每秒 2 个单位长度，点 D 是线段 OA 的中点．（1）求点 B 的坐标；（2）设点 P 的运动时间为点 t 秒，△BDP 的面积为 S ，求 S 与 t 的函数关系式；（3）当点 P 与点 D 重合时，连接 BP ，点 E 在线段 AB 上，连接 PE ，当∠BPE =2∠OBP 时， 求点 E 的坐标．11．如图，在平面直角坐标系中，Rt ABC△的斜边在AB在x轴上，点C在y轴上90ACB∠=︒，OC、OB的长分别是一元二次方程2680x x-+=的两个根，且OC OB<．（1）求点A的坐标；（2）D是线段AB上的一个动点（点D不与点A，B重合），过点D的直线l与y轴平行，直线l交边AC或边BC于点P，设点D的横坐标为t，线段DP的长为d，求d关于t的函数解析式；（3）在（2）的条件下，当12d=时，请你直接写出点P的坐标．12．如图1，在O中，弦AB⊥弦CD，垂足为点E，连接AD、BC、AO，AD AB=．（1）求证：2CAO CDB ∠=∠（2）如图2，过点O 作OH AD ⊥，垂足为点H ，求证：2OH CE DE +=（3）如图3，在（2）的条件下，延长DB 、AC 交于点F ，过点D 作DM AC ⊥，垂足为M ，交AB 于N ，若12BC =，3AF BF =，求MN 的长．13．我们知道，在等腰直角三角形中，底边与一边腰长比为2:1．如图1，90A ∠=︒，AB AC =，则2BC AB=．知识应用：(1)如图2，ADE ∆和ABC ∆均为等腰直角三角形，90DAE BAC ∠=∠=︒，D ，E ，C 三点共线，若2AD =2BD =，求CD 的长． 知识外延：(2)如图3，正方形ABCD 中，BE 和BC 关于BG 对称，C 点的对应点为E 点，AE 交BG 的延长线于F 点，连接CF ．①求证：GF EC =；②若2AE =，2CE =BF 的长．14．（问题探究）课堂上老师提出了这样的问题：“如图①，在ABC 中，108BAC ∠=︒，点D 是BC 边上的一点，7224BAD BD CD AD ∠=︒==，，，求AC 的长”．某同学做了如下的思考：如图②，过点C 作CE AB ∥，交AD 的延长线于点E ，进而求解，请回答下列问题：（1）ACE ∠=___________度；（2）求AC 的长．（拓展应用）如图③，在四边形ABCD 中，12075BAD ADC ∠=︒∠=︒，，对角线AC BD 、相交于点E ，且AC AB ⊥，22EB ED AE ==，，则BC 的长为_____________．15．已知四边形ABCD为矩形，对角线AC、BD相交于点O，AD＝AO．点E、F为矩形边上的两个动点，且∠EOF＝60°．（1）如图1，当点E、F分别位于AB、AD边上时，若∠OEB＝75°，求证：DF＝AE；（2）如图2，当点E、F同时位于AB边上时，若∠OFB＝75°，试说明AF与BE的数量关系；（3）如图3，当点E、F同时在AB边上运动时，将△OEF沿OE所在直线翻折至△OEP，取线段CB的中点Q．连接PQ，若AD＝2a（a＞0），则当PQ最短时，求PF之长．16．如图，在矩形ABCD中，点E为BC的中点，连接AE，过点D作DF AE⊥于点F，过点C作CN DF⊥于点N，延长CN交AD于点M．（1）求证：AM MD=（2）连接CF，并延长CF交AB于G①若2AB=，求CF的长度；②探究当ABAD为何值时，点G恰好为AB的中点．17．在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A 顺时针旋转90°，得到线段AE，连接DE．（1）如图1，点E落在BA的延长线上时，∠EDC= （度）直接填空．（2）如图2，点D在运动过程中，DE⊥AC时，AB=4 ，求DE的值．（3）如图3，点F为线段DE中点，AB=2a，求出动点D从B运动到C，点F经过的路径长度．18．阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”：如图1．在△ABC中，如果AB＞AC，那么∠ACB＞∠ABC．证明如下：将AB沿△ABC的角平分线AD翻折（如图2），因为AB＞AC，所以点B落在AC的延长线上的点B'处．于是，由∠ACB＞∠B'，∠ABC=∠B'，可得∠ACB＞∠ABC．（1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”：如图3．在△ABC中，如果∠ACB＞∠ABC，那么AB＞AC．小明的思路是：沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程．（2）拓展延伸：请运用上述方法或结论解决如下问题：如图4，已知M为正方形ABCD的边CD上一点（不含端点），连接AM并延长，交BC的延长线于点N．求证：AM＋AN＞2BD．19．如图1，Rt△ABC中，点D，E分别为直角边AC，BC上的点，若满足AD2+BE2＝DE2，则称DE为R△ABC的“完美分割线”．显然，当DE为△ABC的中位线时，DE是△ABC的一条完美分割线．（1）如图1，AB ＝10，cos A ＝45，AD ＝3，若DE 为完美分割线，则BE 的长是 ． （2）如图2，对AC 边上的点D ，在Rt △ABC 中的斜边AB 上取点P ，使得DP ＝DA ，过点P 画PE ⊥PD 交BC 于点E ，连结DE ，求证：DE 是直角△ABC 的完美分割线．（3）如图3，在Rt △ABC 中，AC ＝10，BC ＝5，DE 是其完美分割线，点P 是斜边AB 的中点，连结PD 、PE ，求cos ∠PDE 的值．20．如图，二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ，另一个交点为A ，且与y 轴相交于C 点（1）则m =_________；C 点坐标为___________；（2）在直线BC 上方的抛物线上是否存在一点M ，使得它与B ，C 两点构成的三角形面积最大，若存在，求出此时M 点坐标；若不存在，请简要说明理由．（3）P 为抛物线上一点，它关于直线BC 的对称点为Q①当四边形PBQC 为菱形时，求点P 的坐标；②点P 的横坐标为(04)t t <<，当t =________时，四边形PBQC 的面积最大．21．问题探究（1）如图1．在ABC 中，8BC =，D 为BC 上一点，6AD =．则ABC 面积的最大值是_______．（2）如图2，在ABC 中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC 的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值：若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由． 22．在综合与实践课上老师将直尺摆放在三角板上，使直尺与三角板的边分别交于点P 、M 、N 、Q ，（1）如图①所示．当∠CNG ＝42°，求∠HMC 的度数．（写出证明过程）（2）将直尺向下平移至图 2 位置，使直尺的边缘通过点 C ，交 AB 于点 P ，直尺另一侧与三角形交于 N 、Q 两点。

中考数学中考数学压轴题 易错题难题测试综合卷检测试卷

中考数学中考数学压轴题 易错题难题测试综合卷检测试卷

一、中考数学压轴题1．如图，在等边△ABC中，AB=BC=AC=6cm，点P从点B出发，沿B→C方向以1．5cm/s 的速度运动到点C停止，同时点Q从点A出发，沿A→B方向以1cm/s的速度运动，当点P停止运动时，点Q也随之停止运动，连接PQ，过点P作BC的垂线，过点Q作BC的平行线，两直线相交于点M．设点P的运动时间为x（s），△MPQ与△ABC重叠部分的面积为y（cm2）（规定：线段是面积为0的图形）．（1）当x= （s）时，PQ⊥BC；（2）当点M落在AC边上时，x= （s）；（3）求y关于x的函数解析式，并写出自变量x的取值范围．2．我们知道，平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系，如果两条数轴不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么这两条数轴构成的是平面斜坐标系，两条数轴称为斜坐标系的坐标轴，公共原点称为斜坐标系的原点，如图1，经过平面内一点P作坐标轴的平行线PM和PN，分别交x轴和y轴于点M，N．点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标，有序实数对（x，y）称为点P的斜坐标，记为P（x，y）（1）如图2，ω＝45°，矩形OABC中的一边OA在x轴上，BC与y轴交于点D，OA＝2，OC＝1．①点A、B、C在此斜坐标系内的坐标分别为A，B，C．②设点P（x，y）在经过O、B两点的直线上，则y与x之间满足的关系为．③设点Q（x，y）在经过A、D两点的直线上，则y与x之间满足的关系为．（2）若ω＝120°，O为坐标原点．①如图3，圆M 与y 轴相切原点O ，被x 轴截得的弦长OA ＝23，求圆M 的半径及圆心M 的斜坐标．②如图4，圆M 的圆心斜坐标为M （23，23），若圆上恰有两个点到y 轴的距离为1，则圆M 的半径r 的取值范围是 ．3．如图1，抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，点E 是BD 上方抛物线上的一点，连接AE 交DB 于点F ，若AF=2EF ，求出点E 的坐标．（3）如图3，点M 的坐标为（32，0），点P 是对称轴左侧抛物线上的一点，连接MP ，将MP 沿MD 折叠，若点P 恰好落在抛物线的对称轴CE 上，请求出点P 的横坐标．4．在学习了轴对称知识之后，数学兴趣小组的同学们对课本习题进行了深入研究，请你跟随兴趣小组的同学，一起完成下列问题．(1)（课本习题）如图①，△ABC 是等边三角形，BD 是中线，延长BC 至E ，使CE=CD ． 求证：DB=DE(2)（尝试变式）如图②，△ABC 是等边三角形，D 是AC 边上任意一点，延长BC 至E ，使CE=AD ．求证：DB=DE ．(3)（拓展延伸）如图③，△ABC 是等边三角形，D 是AC 延长线上任意一点，延长BC 至E ，使CE=AD 请问DB 与DE 是否相等? 并证明你的结论．5．如图，已知正方形ABCD 中，4,BC AC BD =、相交于点O ，过点A 作射线AM AC ⊥，点E 是射线AM 上一动点，连接OE 交AB 于点F ，以OE 为一边，作正方形OEGH ，且点A 在正方形OEGH 的内部，连接DH ．（1）求证：EDO EAO ∆≅∆；（2）设BF x =，正方形OEGH 的边长为y ，求y 关于x 的函数关系式，并写出定义域；（3）连接AG ，当AEG ∆是等腰三角形时，求BF 的长．6．在平面直角坐标系xOy 中，对于点A 和图形M ，若图形M 上存在两点P ，Q ，使得3AP AQ =，则称点A 是图形M 的“倍增点”．（1）若图形M 为线段BC ，其中点()2,0B -，点()2,0C ，则下列三个点()1,2D -，()1,1E -，()0,2F 是线段BC 的倍增点的是_____________；（2）若O 的半径为4，直线l ：2y x =-+，求直线l 上O 倍增点的横坐标的取值范围；（3）设直线1y x =-+与两坐标轴分别交于G ，H ，OT 的半径为4，圆心T 是x 轴上的动点，若线段GH 上存在T 的倍增点，直接写出圆心T 的横坐标的取值范围．7．如图1，△ABC 内接于⊙O ，直径AD 交BC 于点E ，延长AD 至点F ，使DF ＝2OD ，连接FC 并延长交过点A 的切线于点G ，且满足AG ∥BC ，连接OC ，若cos ∠BAC ＝13，BC ＝8． （1）求证：CF 是⊙O 的切线；（2）求⊙O 的半径OC ；（3）如图2，⊙O 的弦AH 经过半径OC 的中点F ，连结BH 交弦CD 于点M ，连结FM ，试求出FM 的长和△AOF 的面积．8．如图，直角三角形ABC ∆中，90460ACB AC A ∠︒=∠︒＝，，＝，O 为BC 中点，将ABC ∆绕O 点旋转180︒得到DCB ∆．一动点P 从A 出发，以每秒1的速度沿A B D →→的路线匀速运动，过点P 作直线PM ，使PM AC ⊥．（1）当点P 运动2秒时，另一动点Q 也从A 出发沿A B D →→的路线运动，且在AB 上以每秒1的速度匀速运动，在BD 上以每秒2的速度匀速运动，过Q 作直线QN 使//QN PM ，设点Q 的运动时间为t 秒，(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ，求S 关于t 的函数关系式，并求出S 的最大值．（2）当点P 开始运动的同时，另一动点R 从B 处出发沿B C D →→的路线运动，且在BC 上以每秒3的速度匀速运动，在CD 上以每秒2的速度匀度运动，是否存在这样的P R 、，使BPR ∆为等腰三角形？若存在，直接写出点P 运动的时间m 的值，若不存在请说明理由． 9．如图，在平面直角坐标系xoy 中，直线122y x =-+与x 轴交于点B ，与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点．（1）求抛物线的解析式；（2）点M 为抛物线对称轴上一动点，当BM CM -的值最小时，请你求出点M 的坐标；（3）抛物线上是否存在点N ，过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似？若存在，请直接写出点N 的坐标；若不存在，请说明理由．10．如图1，抛物线23y ax bx =++与x 轴交于点(1,0)A -、点B ，与y 轴交于点C ，顶点D 的横坐标为1，对称轴交x 轴交于点E ，交BC 与点F .（1）求顶点D 的坐标；（2）如图2所示，过点C 的直线交直线BD 于点M ，交抛物线于点N .①若直线CM 将BCD ∆分成的两部分面积之比为2:1，求点M 的坐标；②若NCB DBC ∠=∠，求点N 的坐标．11．如图，在正方形ABCD 中，DC=8，现将四边形BEGC 沿折痕EG(G ，E 分别在DC ，AB 边上)折叠，其顶点B ，C 分别落在边AD 上和边DC 的上部，其对应点设为F ，N 点，且FN 交DC 于M ．特例体验：(1)当FD=AF 时，△FDM 的周长是多少?类比探究：(2)当FD≠AF≠0时，△FDM 的周长会发生变化吗?请证明你的猜想．拓展延伸：(3)同样在FD≠AF≠0的条件下，设AF 为x ，被折起部分(即：四边形FEGN)的面积为S ，试用含x 的代数式表示S ，并问：当x 为何值时，S=26?12．在平面直角坐标系中，抛物线24y mx mx n =-+（m >0）与x 轴交于A ，B 两点，点B 在点A 的右侧，顶点为C ，抛物线与y 轴交于点D ，直线CA 交y 轴于E ，且:3:4∆∆=ABC BCE S S ．（1）求点A ，点B 的坐标；（2）将△BCO 绕点C 逆时针旋转一定角度后，点B 与点A 重合，点O 恰好落在y 轴上， ①求直线CE 的解析式；②求抛物线的解析式．13．已知：如图，在平面直角坐标系中，点 A 的坐标为（6，0），2，点 P 从点 O 出发沿线段 OA 向终点 A 运动，点 P 的运动速度是每秒 2 个单位长度，点 D 是线段 OA 的中点．（1）求点 B 的坐标；（2）设点 P 的运动时间为点 t 秒，△BDP 的面积为 S ，求 S 与 t 的函数关系式；（3）当点 P 与点 D 重合时，连接 BP ，点 E 在线段 AB 上，连接 PE ，当∠BPE =2∠OBP 时， 求点 E 的坐标．14．如图①，在△ABC 中，∠ACB =90°，∠B =30°，AC =1，D 为AB 的中点，EF 为△ACD 的中位线，四边形EFGH 为△ACD 的内接矩形（矩形的四个顶点均在△ACD 的边上）． （1）计算矩形EFGH 的面积；（2）将矩形EFGH 沿AB 向右平移，F 落在BC 上时停止移动．在平移过程中，当矩形与△CBD 3 （3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形1111E F G H ，将矩形1111E F G H 绕1G 点按顺时针方向旋转，当1H 落在CD 上时停止转动，旋转后的矩形记为矩形2212E F G H ，设旋转角为α，求cos α的值．15．如图，直线y ＝﹣x+4与抛物线y ＝﹣12x 2+bx+c 交于A ，B 两点，点A 在y 轴上，点B 在x 轴上．（1）求抛物线的解析式； （2）在x 轴下方的抛物线上存在一点P ，使得∠ABP ＝90°，求出点P 坐标；（3）点E 是抛物线对称轴上一点，点F 是抛物线上一点，是否存在点E 和点F 使得以点E ，F ，B ，O 为顶点的四边形是平行四边形？若存在，求出点F 的坐标；若不存在，请说明理由．16．如图，在矩形ABCD 中，6AB cm =，8AD cm =，连接BD ，将ABD △绕B 点作顺时针方向旋转得到A B D '''△（B ′与B 重合），且点D '刚好落在BC 的延长上，A D ''与CD 相交于点E ．（1）求矩形ABCD 与A B D '''△重叠部分（如图1中阴影部分A B CE ''）的面积； （2）将A B D '''△以每秒2cm 的速度沿直线BC 向右平移，如图2，当B ′移动到C 点时停止移动．设矩形ABCD 与A B D '''△重叠部分的面积为y ，移动的时间为x ，请你直接写出y 关于x 的函数关系式，并指出自变量x 的取值范围；（3）在（2）的平移过程中，是否存在这样的时间x ，使得AA B ''△成为等腰三角形？若存在，请你直接写出对应的x 的值，若不存在，请你说明理由．17．如图，在平面直角坐标系中，Rt ABC△的斜边在AB在x轴上，点C在y轴上90ACB∠=︒，OC、OB的长分别是一元二次方程2680x x-+=的两个根，且OC OB<．（1）求点A的坐标；（2）D是线段AB上的一个动点（点D不与点A，B重合），过点D的直线l与y轴平行，直线l交边AC或边BC于点P，设点D的横坐标为t，线段DP的长为d，求d关于t的函数解析式；（3）在（2）的条件下，当12d=时，请你直接写出点P的坐标．18．如图，在长方形ABCD中，AB＝4cm，BE＝5cm，点E是AD边上的一点，AE、DE分别长acm．bcm，满足(a－3)2＋|2a＋b－9|＝0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D，设运动时间为t s．（1）a＝______cm，b＝______cm；（2）t为何值时，EP把四边形BCDE的周长平分？（3）另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．19．如图，在⊙O中，直径AB＝10，tanA3（1）求弦AC的长；（2）D是AB延长线上一点，且AB＝kBD，连接CD，若CD与⊙O相切，求k的值；（3）若动点P以3cm/s的速度从A点出发，沿AB方向运动，同时动点Q以32cm/s的速度从B点出发沿BC方向运动，设运动时间为t （0＜t＜103），连结PQ．当t为何值时，△BPQ为Rt△？20．如图，在矩形ABCD中，点E为BC的中点，连接AE，过点D作DF AE⊥于点F，过点C作CN DF⊥于点N，延长CN交AD于点M．（1）求证：AM MD=（2）连接CF，并延长CF交AB于G①若2AB=，求CF的长度；②探究当ABAD为何值时，点G恰好为AB的中点．21．已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC．（1）如图1，当BM=1时，求PC的长；（2）如图2，设AM与BD交于点E，当∠PCM=45°时，求证：BEDE=33+；（3）如图3，取PC的中点Q，连接MQ，AQ．①请探究AQ和MQ之间的数量关系，并写出探究过程；②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由．22．在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A 顺时针旋转90°，得到线段AE，连接DE．（1）如图1，点E 落在BA 的延长线上时，∠EDC= （度）直接填空．（2）如图2，点D 在运动过程中，DE ⊥AC 时，AB=4 ，求DE 的值．（3）如图3，点F 为线段DE 中点，AB=2a ，求出动点D 从B 运动到C ，点F 经过的路径长度．23．如图，直角梯形ABCD 中，1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠＝＝＝＝的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动，2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动，1O 半径为22,cm O 的半径为4cm ，若12,O O 分别从点A 、点B 同时出发，运动的时间为ts（1）请求出2O 与腰CD 相切时t 的值；（2）在03s t s ≤＜范围内，当t 为何值时，1O 与2O 外切？24．在平面直角坐标系xOy 中，点A 为x 轴上的动点，点B 为x 轴上方的动点，连接OA ，OB ，AB ．（1）如图1，当点B 在y 轴上，且满足OAB ∠的角平分线与OBA ∠的角平分线交于点P ，请直接写出P ∠的度数；（2）如图2，当点B 在y 轴上，OAB ∠的角平分线与OBA ∠的角平分线交于点P ，点C 在BP 的延长线上，且满足45AOC ∠=︒，求OAB OCB∠∠；（3）如图3，当点B 在第一象限内，点P 是AOB ∆内一点，点M ，N 分别是线段OA ，OB 上一点，满足：1902APB AOB ∠=︒+∠，PM PN =，180ONP OMP ∠+∠=︒．以下结论：①OM ON =；②AP 平分OAB ∠；③BP 平分OBA ∠；④AM BN AB +=．正确的是：________．（请填写正确结论序号，并选择一个正确的结论证明，简写证明过程）．25．定义：两个相似等腰三角形，如果它们的底角有一个公共的顶点，那么把这两个三角形称为“关联等腰三角形”．如图，在ABC ∆与AED ∆中，,BA BC EA ED == ，且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”，设它们的顶角为α，连接,EB DC ，则称DC EB 会为“关联比"． 下面是小颖探究“关联比”与α之间的关系的思维过程，请阅读后，解答下列问题：[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”，且90α︒=时， ①在图1中，若点E 落在AB 上，则“关联比”DC EB=②在图2中，探究ABE ∆与ACD ∆的关系，并求出“关联比”DC EB的值．[类比探究]()2如图3，①当ABC ∆与AED ∆为“关联等腰三角形”，且120a ︒=时，“关联比”DC EB= ②猜想：当ABC ∆与AED ∆为“关联等腰三角形”，且n α=︒时，“关联比”DC EB = (直接写出结果，用含n 的式子表示)[迁移运用]()3如图4， ABC ∆与AED ∆为“关联等腰三角形”．若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点，且1PA =，点E 为PB 上一动点，求点E 自点B 运动至点P 时，点D所经过的路径长．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．B解析：（1）1.5；（2）3；（3）()())222422423.0 1.51534x xy xxxxxx⎧-⎪⎪⎪⎪=-+-⎨⎪⎪-⎪⎪⎩≤≤≤≤＜＜【解析】【分析】（1）令PQ⊥BC，表示出BP和BQ的长，利用余弦的定义得出方程，求解即可；（2）根据△ABC是等边三角形得出BQ=CM，表示出PC的长，结合余弦的定义得出方程，求解即可；（3）根据（1）和（2）中结论，分0≤x＜1.5时，1.5≤x≤3时，3＜x≤4时三种情况画出图形，求出相应边长，可得函数解析式.【详解】解：（1）当PQ⊥BC时，BP=1.5x，BQ=6-x，∴BQ=1.5cos cos60BP xABC=∠︒，即6-x=1.512x，∴6-x=3x，解得：x=1.5，∴当x=1.5时，PQ⊥BC；（2）∵△ABC是等边三角形，QM∥BC，∴AQ=AM，BQ=CM，PC=6-1.5x，CM=6 1.51231cos602PC xx-==-︒，∴BQ=12-3x，AQ=x，∴12-3x+x=6，解得x=3，∴当点M落在AC上时，x=3（s）；（3）当0≤x ＜1.5时，过Q 作QE ⊥BC 于E ，∵BQ=6-x ，∴QE=BQsin ∠B=BQsin60°，而DP=BPtan ∠B=BPtan60°，y=S △BPQ -S △BPD =1122BP QE BP DP ⋅-⋅ =()()11sin 60tan 6022BP BQ BP BP ︒-︒ =29333x x -；当1.5≤x≤3时，过点Q 作QD ⊥BC 于D ，可知：四边形QDPM 为矩形， ∴QM=DP=BP-BD=BP-BQ·cos60°， PM=MC·sin60°=BQ·sin60°，则y=S △PQM=12QM PM ⋅ =()1cos60sin 602BP BQ BQ -⋅︒⋅⋅︒ =2315393x x +；当3＜x≤4时，如图所示，过点Q 作QE ⊥BC 于点E ，可知四边形QEPM 为矩形，∴QM=EP=BP-BE=BP-BQ·tan ∠B=1.5x-12（6-x ）=2x-3， ∵QM ∥BC ，∴△AQO 为等边三角形，∠MON=∠C=60°，∴AQ=OQ=AO=x ，∴OM=QM-OQ=2x-3-x=x-3，∵PC=6-1.5x ，∠C=60°， ∴NP=PC·tan ∠C= PC·tan60°=3632x ⎛⎫-⨯ ⎪⎝⎭， ∴MN=MP-NP=QE-NP=BQ·sin ∠B-NP=（6-x ）·sin60°-3632x ⎛⎫-⨯ ⎪⎝⎭=333x -，y=S △PQM -S △NOM=1122MQ PM OM MN ⋅-⋅ =2315393x x +-12（x-3333x -） =23334x x +-故y关于x的函数解析式为()()()2229333423153932422733.30 1.5153493x xy xxxxxx x⎧-⎪⎪⎪⎪=-+-⎨⎪⎪-+-⎪⎪⎩≤≤≤≤＜＜.【点睛】本题考查了等边三角形的判定和性质，解直角三角形，二次函数的应用—几何问题，难度较大，解题的关键是根据图形的运动情况分情况求解.2．B解析：（1）①（2，0），（1，2），（﹣1，2）；②y＝2x；③y＝﹣22x+2；（2）①半径为2，M（4323,）；②2＜r＜4【解析】【分析】（1）①如图2−1中，作BE∥OD交OA于E，CF∥OD交x轴于F．求出OE、OF、CF、OD、BE即可解决问题；②如图2−2中，作BE∥OD交OA于E，作PM∥OD交OA于M．利用平行线分线段成比例定理即可解决问题；③如图3−3中，作QM∥OA交OD于M．利用平行线分线段成比例定理即可解决问题；（2）①如图3中，作MF⊥OA于F，作MN∥y轴交OA于N．解直角三角形即可解决问题；②如图4中，连接OM，作MK∥x轴交y轴于K，作MN⊥OK于N交⊙M于E、F．求出FN＝NE＝1时，⊙M的半径即可解决问题；【详解】解：（1）①如图2﹣1中，作BE∥OD交OA于E，CF∥OD交x轴于F．由题意OC＝CD＝1，OA＝BC＝2，∴BD＝OE＝1，OD＝CF＝BE2，∴A(2,0)，2)，C(﹣2，故答案为：A(2,0)，2)，C(﹣2)．②如图2﹣2中，作BE∥OD交OA于E，作PM∥OD交OA于M．∵OD∥BE，OD∥PM，∴BE∥PM，∴BE OEPM OM=，∴21y x=，∴y＝2x．故答案为：y＝2x．③如图2﹣3中，作QM∥OA交OD于M．222MQ DMOA DOx y∴=-∴=∴222y x=-+故答案为：y＝﹣22x+2．（2）①如图3中，作MF⊥OA于F，作MN∥y轴交OA于N．∵ω＝120°，OM⊥y轴，∴∠MOA ＝30°，∵MF ⊥OA ，OA ＝23， ∴OF ＝FA ＝3，∴FM ＝1，OM ＝2FM ＝2，∴圆M 的半径为2∵MN ∥y 轴，∴MN ⊥OM ，∴MN ＝233，ON ＝2MN ＝433， ∴M 4323,⎛⎫ ⎪ ⎪⎝⎭． ②如图4中，连接OM ，作MK ∥x 轴交y 轴于K ，作MN ⊥OK 于N 交⊙M 于E 、F ．∵MK ∥x 轴，ω＝120°，∴∠MKO ＝60°，∵MK ＝OK ＝3∴△MKO 是等边三角形，∴MN ＝3，当FN ＝1时，MF ＝3﹣1=2，当EN ＝1时，ME ＝3+1=4，观察图象可知当⊙M 的半径r 的取值范围为2＜r ＜4．故答案为：2＜r ＜4．【点睛】本题考查圆综合题、平行线分线段成比例定理、等边三角形的判定和性质、平面斜坐标系等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考压轴题．3．E解析：（1）2y x 2x 3=-++；（2）E （2，3）或（1，4）；（3）P 点横坐标为112018【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），设抛物线的解析式为2(1)4y a x =-+，由抛物线过点B,（3，0），即可求出a 的值，即可求得解析式； （2）过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x xx -++，求出A 、D 点的坐标，得到OM=x ，则AM=x+1，由AF=2EF 得到22(1)33x AN AM +==，从而推出点F 的坐标21210(,)3333x x --+，由23FN EM =，列出关于x 的方程求解即可；（3）先根据待定系数法求出直线DM 的解析式为y=-2x+3，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.证明△FGP ≌△FHQ ，得到FG=FH ，PT=45GH.设点P （m ，-m²+2m+3），则T （m ，-2m+3），则PT=m²-4m ，GH=1-m ， 可得m²-4m=45（1-m ），解方程即可. 【详解】（1）∵抛物线的顶点为C （1，4），∴设抛物线的解析式为2(1)4y a x =-+，∵抛物线过点B,（3，0），∴20(31)4a =-+，解得a=-1，∴设抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++；（2）如图，过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x x x -++，∵抛物线的解析式为2y x 2x 3=-++，当y=0时，2023x x =-++，解得x=-1或x=3，∴A （-1.0），∴点D （0,3），∴过点BD 的直线解析式为3y x =-+，点F 在直线BD 上，则OM=x ，AM=x+1， ∴22(1)33x AN AM +==， ∴2(1)2111333x x ON AN +=-=-=-， ∴21210(,)3333x x F --+， ∴2210332233FN EM x x x +--++==， 解得x=1或x=2， ∴点E 的坐标为（2，3）或（1，4）；（3）设直线DM 的解析式为y=kx+b ，过点D （0,3），M （32，0）， 可得，3023k b b ⎧+=⎪⎨⎪=⎩，解得k=-2，b=3，∴直线DM 的解析式为y=-2x+3，∴32OM =，3OD =， ∴tan ∠DMO=2， 如图，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.∵PQ ⊥MT ，∴∠TFG=∠TPF ，∴TG=2GF ，GF=2PG ，∴PT=25 GF，∵PF=QF，∴△FGP≌△FHQ，∴FG=FH，∴PT=45 GH.设点P（m，-m²+2m+3），则T（m，-2m+3），∴PT=m²-4m，GH=1-m，∴m²-4m=45（1-m），解得：1118m-=，或2118m+=（不合题意，舍去），∴点P的横坐标为118-.【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识，解题的关键是学会用转化的思想思考问题，学会用数形结合的思想解决问题，有一定难度.4．D解析：（1）见详解；（2）见详解；（3）DB=DE成立，证明见详解【解析】【分析】（1）由等边三角形的性质，得到∠CBD=30°，∠ACB=60°，由CD=CE，则∠E=∠CDE=30°，得到∠E=∠CBD=30°，即可得到DB=DE；（2）过点D作DG∥AB，交BC于点G，证明△BDC≌△EDG，根据全等三角形的性质证明结论；（3）过点D作DF∥AB交BE于F，由“SAS”可证△BCD≌△EFD，可得DB=DE．【详解】证明：（1）∵△ABC是等边三角形∴∠ABC=∠BCA=60°，∵点D为线段AC的中点，∴BD平分∠ABC，AD=CD，∴∠CBD=30°，∵CD=CE，∴∠CDE=∠CED，又∵∠CDE+∠CED=∠BCD，∴2∠CED=60°，∴∠CED=30°=∠CBD，∴DB=DE；（2）过点D 作DG ∥AB ，交BC 于点G ，如图，∴∠DGC=∠ABC=60°，又∠DCG=60°，∴△DGC 为等边三角形，∴DG=GC=CD ，∴BC-GC=AC-CD ，即AD=BG ，∵AD=CE ，∴BG=CE ，∴BC=GE ，在△BDC 和△EDG 中，60DC DG BCD EGD BC EG =⎧⎪∠=∠=︒⎨⎪=⎩，∴△BDC ≌△EDG （SAS ）∴BD=DE ；（3）DB=DE 成立，理由如下：过点D 作DF ∥AB 交BE 于F ，∴∠CDF=∠A ，∠CFD=∠ABC ，∵△ABC 是等边三角形∴∠ABC=∠BCA=∠A=60°，BC=AC=AB ，∴∠CDF=∠CFD=60°=∠ACB=∠DCF ，∴△CDF 为等边三角形∴CD=DF=CF ，又AD=CE ，∴AD-CD=CE-CF ，∴BC=AC=EF ，∵∠BCD=∠CFD+∠CDF=120°，∠DFE=∠FCD+∠FDC=120°，∴∠BCD=∠DFE ，且BC=EF ，CD=DF ，∴△BCD ≌△EFD （SAS ）∴DB=DE ．【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，以及平行线的性质，正确添加恰当辅助线构造全等三角形是本题的关键．5．A解析：（1）详见解析；（2）y x=（04x <<）；（3）当AEG ∆是等腰三角形时，2BF =或43【解析】【分析】 （1）根据正方形的性质得到∠AOD=90°，AO=OD ，∠EOH=90°，OE=OH ，由全等三角形的性质即可得到结论；（2）如图1，过O 作ON ⊥AB 于N ，根据等腰直角三角形的性质得到122AN BN ON AB ====，根据勾股定理得到OF ===线段成比例定理即可得到结论；（3）①当AE=EG 时，△AEG 是等腰三角形，②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP ⊥EG 于P ③当GE=AG 时，△AEG 是等腰三角形，如图3，过G 作GQ ⊥AE 于Q ，根据相似三角形的性质或全等三角形的性质健即可得到结论．【详解】（1）∵四边形ABCD 是正方形，,OA OD AC BD ∴=⊥，90AOD ∴∠=︒，∵四边形OEGH 是正方形，,90OE OH EOH ∴=∠=︒，AOD EOH ∴∠=∠，AOD AOH EOH AOH ∴∠-∠=∠-∠，即HOD EOA ∠=∠，HDO EAO ∴∆≅∆．（2）如图1，过O 作ON⊥AB 于N ，则122AN BN ON AB ====， ∵BF=x，∴AF=4-x ，∴FN=2-x ，∴()222222248OF FN ON x x x =+=-+=-+，∴248EF y x x =--+，∵AM⊥AC，∴AE∥OB，∴BF OF AF EF＝， ∴2248448x x x x y x x -+=---+， ∴()244804x x y x -+≤＝＜； （3）①当AE=EG 时，△AEG 是等腰三角形，则AE=OE ，∵∠EAO=90°，∴这种情况不存在；②当AE=AG 时，△AEG 是等腰三角形，如图2，过A 作AP⊥EG 于P ，则AP∥OE，∴∠PAE=∠AEO，∴△APE∽△EAO，∴PE AE OA OE=，∵AE=AG，∴24148 2x xPE y-+==，()22248xAE yx-=-=，∴()22222224448448xx xxx xx---+=+，解得：x=2，②当GE=AG时，△AEG是等腰三角形，如图3，过G作GQ⊥AE于Q，∴∠GQE=∠EAO=90°，∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°，∴∠EGQ=∠AEO，∵GE=OE，∴△EGQ≌△OEA（AAS），∴22EQ AO==∴24242()xAE ExQ-===，∴43x=，∴BF=2或43．【点睛】本题考查了四边形的综合题，正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质，勾股定理，正确的作出辅助线构造全等三角形是解题的关键．6．A解析：（1）()1,1E-；（2）1312m-≤≤-或0131m≤≤3）639t≤≤.【解析】【分析】（1）首先要理解点A 是图形M 的“倍增点”的定义，将三个点逐一代入验证即可； （2）分两种情况:①点"倍增点”在O 的外部，分别求得“倍增点”横坐标的最大值和最小值，②点"倍增点"在O 的内部，依次求得“倍增点"横坐标的最大值和最小值，即可确定“倍增点”横坐标的范围；（3）分别求得线段GH 两端点为T "倍增点”时横坐标的最大值和最小值即可．【详解】（1）()1,2D -到线段BC 的距离为2， 22(12)(20)1332DC =--+-=<⨯∴()1,2D -不是线段BC 的倍增点；()1,1E -到线段BC 的距离为1，22(12)(10)103EC =--+-=>,∴在线段BC 上必存在一点P 使EP=3，∴()1,1E -是线段BC 的倍增点；()0,2F 到线段BC 的距离为2，22(02)(20)2232FC =-+-=<⨯∴()0,2F 不是线段BC 的倍增点；综上，()1,1E -是线段BC 的倍增点；（2）设直线l 上“倍增点”的横坐标为m ，当点在O 外时，222(2)8,m m +-+≤解方程222(2)8m m +-+=，得1131m =+，2131m =-当点在O 内部时，22224(2)3(44(2))m m m m ++-+≥--+-+解得：m≥0或m≤-2∴直线l 上“倍增点”的橫坐标的取值范围为1312m -≤≤-或0131m ≤≤+；（3）如图所示，当点G(1,0)为T "倍增点"时，T(9,0)，此时T 的横坐标为最大值，当点H(0,1)为T “倍增点”时，则T(，此时T 的横坐标为最小值；∴圆心T(t, 0)的横坐标的取值范围为：9t ≤≤．【点睛】在正确理解点A 是图形M 的“倍增点”定义的基础上，利用（1）判断是否是倍增点的不等关系式，即可列不等式组求解范围．7．D解析：（1）见解析；（2）3【解析】【分析】（1）由DF=2OD ，得到OF=3OD=3OC ，求得13OE OC OC OF ==，推出△COE ∽△FOE ，根据相似三角形的性质得到∠OCF=∠DEC=90°，于是得到CF 是⊙O 的切线；（2）利用三角函数值，设OE=x ，OC=3x ，得到CE=3，根据勾股定理即可得到答案；（3）连接BD ，根据圆周角定理得到角相等，然后证明△AOF ∽△BDM ，由相似三角形的性质，得到FM 为中位线，即可求出FM 的长度，由相似三角形的性质，以及中线分三角形的面积为两半，即可求出面积.【详解】解：（1） ∵DF ＝2OD ，∴OF ＝3OD ＝3OC ， ∴13OE OC OC OF ==， ∵∠COE ＝∠FOC ，∴△COE ∽△FOE ，∴∠OCF ＝∠DEC ＝90°，∴CF 是⊙O 的切线；（2）∵∠COD ＝∠BAC ，∴cos ∠BAC ＝cos ∠COE ＝13OE OC =， ∴设OE ＝x ，OC ＝3x ，∵BC ＝8，∴CE ＝4，∵CE ⊥AD ，∴OE 2+CE 2＝OC 2，∴x 2+42＝9x 2，∴x ＝2（负值已舍去），∴OC ＝3x ＝32，∴⊙O 的半径OC 为32；（3）如图，连结BD ，由圆周角定理，则∠OAF=∠DBM ，2AOF ADC ∠=∠，∵BC ⊥AD ，∴AC AB =，∴∠ADC=∠ADB ，∴2AOF ADC BDM ∠=∠=∠，∴△AOF ∽△BDM ；∵点F 是OC 的中点，∴AO ：OF=BD ：DM=2，又∵BD=DC ，∴DM=CM ，∴FM 为中位线， ∴322， ∴S △AOF : S △BDM =(326 2 34=； ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯= ∴S △AOF =3424=32 【点睛】本题考查了圆的综合问题，圆周角定理，切线的判定和性质，相似三角形的判定和性质，利用勾股定理求边长，以及三角形中线的性质，解题的关键是熟练掌握所学的定理和性质，运用属性结合的思想进行解题.8．C解析：（1）2233(06)53103343(68)333031503(810)2t t S t t t t t t ⎧+⎪⎪⎪⎪=-+-<⎨⎪⎪-+<⎪⎪⎩，S 的最大值为63；（2）存在，m 的值为165或32163-或163或1423-. 【解析】【分析】（1）分06t 、68t 和810t 三种情况分别表示出有关线段求得两个变量之间的函数关系即可．（2）分两种情形：①如图31-中，由题意点P 在AB 上运动的时间与点R 在BC 上运动的时间相等，即8m =．当RP BR =时，当PB BR =时，当PR PB =时，分别构建方程求解即可．②如图32-中，作RH BC ⊥于H ．首先证明90BPR ∠=︒，根据BP PR =构建方程即可解决问题．【详解】解：（1）如图21-中，当06t 时，点P 与点Q 都在AB 上运动，PM AC ⊥，//NQ PM ，90ANQ AMP ∴∠=∠=︒，AQ t =，2AP t =+，60A ∠=︒，1122AN AQ t ∴==，33QN ==，112AM t =+，33PM ． ∴此时两平行线截平行四边形ABCD 的面积为33S +． 如图22-中，当68t 时，点P 在BD 上运动，点Q 仍在AB 上运动．则AQ t =，12AN t =，142CN t =-，3QN t =，6BP t =-，10DP t =-，3(10)PM t =-，而43BC =，故此时两平行线截平行四边形ABCD 的面积为： BCNQ BCMP S S S =+四边形四边形()()3111434433106222t t t t ⎛⎫⎛⎫⎡⎤=+⋅-++-⋅- ⎪ ⎪⎣⎦ ⎪⎝⎭⎝ 253103343t t =-+-， 如图23-中，当810t 时，点P 和点Q 都在BD 上运动．则202DQ t =-，(202)3QN t =-，10DP t =-，(10)3PM t =-．∴此时两平行线截平行四边形ABCD 的面积为2333031503S t =-+故S 关于t 的函数关系式为2233(06)53103343(68)3331503(810)t S t t t t ⎪⎪⎪=+-<⎨-+<⎪⎩， 当06t 时，S 随t 增大而增大， 当68t <时，S 随t 增大而增大， 当810t <时，S 随t 增大而减小， ∴当t=8时，S 最大，代入可得S=63（2）如图31-中，由题意点P 在AB 上运动的时间与点R 在BC 上运动的时间相等，8m =． 当RP BR =时，3PB BR =，则有383m m -=⋅，解得165m =， 当PB BR =时，则有38m m -=，解得32163m =-， 当PR PB =时，3BR PB =，则有33(8)m m =-，解得163m =． 如图32-中，作RH BC ⊥于H ．在Rt △CHR 中，2(8)CR m =-，30RCH ∠=︒， 182RH CR m ∴==-，8BP m =-，RH BP ∴=， HR BP ∥，∴四边形RHBP 是平行四边形，90RHB ∠=︒，∴四边形RHBP 是矩形，90BPR ∴∠=︒，当BP PR =时，则有83(12)m m -=-，解得1423m =- 综上所述，满足条件的m 的值为165或32163-163或1423-． 【点睛】本题属于四边形综合题，考查了平行四边形的性质，多边形的面积，等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考压轴题．9．B解析：（1）213222y x x =-++；（2）3(,0)2；（3）存在；(0,2)N 或(3,2)N 或(2,3)--N 或(5,18)--N【解析】 【分析】（1）由直线122y x =-+可得B 、C 两点的坐标，根据二次函数的对称轴求得A 点坐标，可设抛物线的解析式为(1)(4)y a x x =+-，将C 点坐标代入可求得a ，即可得抛物线的解析式；（2）根据绝对值的性质得出BM CM -的值最小时，点M 为BC 的垂直平分线与直线32x =的交点，求得BC 垂直平分线的解析式，联立直线32x =即可求得点M ； （3）分四种情况进行讨论，设出N 的坐标，根据相似三角形的对应边成比例的性质，求得N 的横坐标与纵坐标的关系，然后联立抛物线解析式即可求解． 【详解】 解：∵直线122y x =-+与x 轴交于点B ，与y 轴交于点C ， ∴当y =0时，即1022x =-+，解得：x =4，则点B 的坐标为(4,0)， 当x =0时，10222=-⨯+=y ，则点C 的坐标为(0,2)， 由二次函数的对称性可知：点A 与点B 关于直线32x =对称， ∴点A 的坐标为(1,0)-，∵抛物线与x 轴的交点为点(1,0),(4,0)A B -， ∴可设抛物线的解析式为(1)(4)y a x x =+-， 又∵抛物线过点(0,2)C ， ∴2(01)(04)a =+-，解得：12a =-， ∴2113(1)(4)2222y x x x x =-+-=-++ ∴抛物线的解析式为213222y x x =-++；（2）如图1，连结CM 、BM ，作线段BC 的垂直平分线l 分别交BC 、直线32x =于点'、N M ，则N 为BC 中点；由绝对值的性质可得：0≥-BM CM ，∴当BM CM -的值最小时，即0=-BM CM ，则此时CM BM =， ∴点M 为l 与直线32x =的交点，此时M 与'M 重合， 设l 的解析式为：y kx b =+， ∵直线BC 的解析式为：122y x =-+，BC l ⊥ ∴112-⋅=-k ，解得：2k =，则l 的解析式可化为：2y x b =+， 由(4,0),(0,2)B C 得点N 的坐标为(2,1)，将(2,1)N 代入2y x b =+得： 14b =+，解得：3b =-，∴23y x =-， 将32x =代入23y x =-，得323=02=⨯-y ，即3'(,0)2M ， ∴当BM CM -的值最小时，点M 的坐标为3(,0)2，（3）抛物线上存在点N ，使得以点、、B N H 为顶点的三角形与ABC 相似； ∵(1,0),(4,0),(0,2)-A B C∴1,4==OA OB ，2OC =，5AB =，∴2222125=+=+=AC OA OC 22224225BC OB OC =+=+=， ∵22252025+=+==AC BC AB ， ∴ABC 为直角三角形，90ACB ∠=︒， ∵NH x ⊥轴，∴90∠=︒NHB ，则90∠=∠=︒NHB ACB ，如图2所示，分四种情况，点N 的坐标分别为1234、、、N N N N ，设点N 的坐标为(,)m n ，①当点1N 在x 轴的上方，要使11N BH ABC ，则11∠=∠N BH ABC ，则此时点1N 与点C 重合，则此时点1H 与点O 重合， 则11≅N BH ABC ，满足题意， ∴此时点1N 的坐标为(0,2)； ②当点2N 在x 轴的上方，要使22BN H ABC ，则2222==N H BCBH AC， ∴24=-nm，即28n m =-+，代入抛物线的解析式得： 21328222mm m ，化简得：27120m m ，解得：13m =，24m =（不符合题意，故舍去）， 将3m =代入抛物线解析式得：2n =， ∴此时点2N 的坐标为(3,2)； ③当点3N 在x 轴的下方，要使33N BH ABC ，则3332==BH BCN H AC， ∴42-=-m n ，即42-=m n ，代入抛物线的解析式得： 24132222m m m ，化简得：2280m m --=，解得：12m =-，24m =（不符合题意，故舍去）， 将2m =-代入抛物线解析式得：3n =-，∴此时点3N 的坐标为(2,3)--； ④当点4N 在x 轴的下方，要使44BN H ABC ，则4442==N H BCBH AC， ∴24-=-nm，即28=-n m ，代入抛物线的解析式得： 21328222m m m ，化简得：2200m m，解得：15m =-，24m =（不符合题意，故舍去）， 将5m =-代入抛物线解析式得：18n =-， ∴此时点4N 的坐标为(5,18)--；综上所述，抛物线存在点N 的坐标为(0,2)或(3,2)或(2,3)--或(5,18)--使得以点、、B N H 为顶点的三角形与ABC 相似． 【点睛】本题主要考查了一次函数与二次函数的性质、相似三角形的性质，运用数形结合与分类讨论的方法是解题的关键．10．A解析：（1）(1,4)D ；（2）158(,)33M ，274(,)33M ；（3）N 的坐标为57(,)24． 【解析】 【分析】（1）将点A 坐标代入函数关系式可得a 与b 的方程，再根据顶点D 的横坐标为1可得另一个关于a 和b 的方程，联立方程组求解即可得到a 和b 的值，进而求得抛物线的函数关系式，再将顶点D 的横坐标代入即可求得点D 坐标；（2）①如图，取DB 得三等分点12,M M ，过点12,M M 分别作x 轴，y 轴的平行线分别交DE 、x 轴于点G 、H 、P 、Q ，通过证相似三角形可得点M 的横纵坐标与点B 、D 的横纵坐标之间的数量关系，进而得解；（3）取线段BC 的中点G ，连接GM ，由中点坐标可得33(,)22G ，根据等腰三角形的三线合一可得GM ⊥BC ，在根据两条直线互相垂直可求得:GM l y x =，与:26BD l y x =-+联立方程组可求得点M 的坐标，再由(2,2),(0,3)M C 利用待定系数法可得1:32CM l y x =-+，最后将132y x =-+与2y x 2x 3=-++联立方程组即可求得点N 的坐标． 【详解】解：（1）将(1,0)A -代入23y ax bx =++可得03a b =-+①∵顶点D 的横坐标为1，。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、中考数学压轴题1．如图，等腰△ABC ，AB ＝CB ，边AC 落在x 轴上，点B 落在y 轴上，将△ABC 沿y 轴翻折，得到△ADC（1）直接写出四边形ABCD 的形状：______；（2）在x 轴上取一点E ，使OE ＝OB ，连结BE ，作AF ⊥BC 交BE 于点F ．①直接写出AF 与AD 的关系：____（如果后面的问题需要，可以直接使用，不需要再证明）；②取BF 的中点G ，连接OG ，判断OG 与AD 的数量关系，并说明理由；（3）若四边形ABCD 的周长为8，直接写出GE 2＋GF 2＝____．2．在平面直角坐标系中，抛物线24y mx mx n =-+（m >0）与x 轴交于A ，B 两点，点B 在点A 的右侧，顶点为C ，抛物线与y 轴交于点D ，直线CA 交y 轴于E ，且:3:4∆∆=ABC BCE S S ．（1）求点A ，点B 的坐标；（2）将△BCO 绕点C 逆时针旋转一定角度后，点B 与点A 重合，点O 恰好落在y 轴上， ①求直线CE 的解析式；②求抛物线的解析式．3．已知：如图，在平面直角坐标系中，点O 为坐标原点，()2,0C ．直线26y x =+与x 轴交于点A ，交y 轴于点B ．过C 点作直线AB 的垂线，垂足为E ，交y 轴于点D ． （1）求直线CD 的解析式；（2）点G 为y 轴负半轴上一点，连接EG ，过点E 作EH EG ⊥交x 轴于点H ．设点G 的坐标为()0,t ，线段AH 的长为d ．求d 与t 之间的函数关系式（不要求写出自变量的取值范围）（3）过点C 作x 轴的垂线，过点G 作y 轴的垂线，两线交于点M ，过点H 作HN GM ⊥于点N ，交直线CD 于点K ，连接MK ，若MK 平分NMB ∠，求t 的值．4．如图1，抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）．（1）求抛物线的解析式；（2）如图2，点E 是BD 上方抛物线上的一点，连接AE 交DB 于点F ，若AF=2EF ，求出点E 的坐标．（3）如图3，点M 的坐标为（32，0），点P 是对称轴左侧抛物线上的一点，连接MP ，将MP 沿MD 折叠，若点P 恰好落在抛物线的对称轴CE 上，请求出点P 的横坐标．5．已知抛物线217222y x mx m 的顶点为点C ． （1）求证：不论m 为何实数，该抛物线与x 轴总有两个不同的交点；（2）若抛物线的对称轴为直线3x =，求m 的值和C 点坐标；（3）如图，直线1y x =-与（2）中的抛物线并于A B 、两点，并与它的对称轴交于点D ，直线x k =交直线AB 于点M ，交抛物线于点N ．求当k 为何值时，以C D M N 、、、为顶点的四边形为平行四边形．6．如图，在四边形ABCD 中，∠B=90°，AD//BC ，AD=16，BC=21，CD=13．（1）求直线AD 和BC 之间的距离；（2）动点P 从点B 出发，沿射线BC 以每秒2个单位长度的速度运动，动点Q 从点A 出发，在线段AD 上以每秒1个单位长度的速度运动，点P 、Q 同时出发，当点Q 运动到点D 时，两点同时停止运动，设运动时间为t 秒．试求当t 为何值时，以P 、Q 、D 、C 为顶点的四边形为平行四边形？（3）在（2）的条件下，是否存在点P ，使△PQD 为等腰三角形？若存在，请直接写出相应的t 值，若不存在，请说明理由．7．“阅读素养的培养是构建核心素养的重要基础，重庆十一中学校以‘大阅读’特色课程实施为突破口，着力提升学生的核心素养．”全校师生积极响应和配合，开展各种活动丰富其课余生活．在数学兴趣小组中，同学们从书上认识了很多有趣的数．其中有一个“和平数”引起了同学们的兴趣．描述如下：一个四位数，记千位上和百位上的数字之和为x ，十位上和个位上的数字之和为y ，如果x y =，那么称这个四位数为“和平数”． 例如：1423，14x =+，23y =+，因为x y =，所以1423是“和平数”．（1）直接写出：最小的“和平数”是________，最大的“和平数”是__________； （2）求同时满足下列条件的所有“和平数”：①个位上的数字是千位上的数字的两倍；②百位上的数字与十位上的数字之和是12的倍数；（3）将一个“和平数”的个位上与十位上的数字交换位置，同时，将百位上与千位上的数字交换位置，称交换前后这两个“和平数”为“相关和平数”．例如：1423于4132为“相关和平数”求证：任意的两个“相关和平数”之和是1111的倍数．8．已知，在Rt △ABC 和Rt △DEF 中，∠ACB=∠EDF=90°，∠A=30°，∠E=45°，AB =EF =6，如图1，D 是斜边AB 的中点，将等腰Rt △DEF 绕点D 顺时针方向旋转角α（0°<α<90°），在旋转过程中，直线DE ，AC 相交于点M ，直线DF ，BC 相交于点N ．（1）如图1，当α=60°时，求证：DM =BN ；（2）在上述旋转过程中，DN DM 的值是一个定值吗？请在图2中画出图形并加以证明； （3）如图3，在上述旋转过程中，当点C 落在斜边EF 上时，求两个三角形重合部分四边形CMDN 的面积．9．如图，在平面直角坐标中，点O 为坐标原点，ABC ∆的三个顶点坐标分别为()A O m ,，(),B m O -，(),C n O ，5AC =且OBA OAB ∠=∠，其中m ，n 满足725m n m n +=⎧⎨-=⎩．（1）求点A ，C 的坐标；（2）点P 从点A 出发，以每秒1个单位长度的速度沿y 轴负方向运动，设点P 的运动时间为t 秒.连接BP 、CP ，用含有t 的式子表示BPC ∆的面积为S （直接写出t 的取值范围）；（3）在（2）的条件下，是否存在t 的值，使得ΔΔ32PAB POC S S =，若存在，请求出t 的值，并直接写出BP 中点Q 的坐标；若不存，请说明理由．10．问题背景：如图，四边形ABCD 中，AD BC ∥，8BC =，17AD =+，32AB =，45ABC ∠=︒，P 为边AD 上一动点，连接BP 、CP ．问题探究（1）如图1，若30PBC ∠=︒，则AP 的长为__________．（2）如图2，请求出BPC △周长的最小值；（3）如图3，过点P 作PE BC ⊥于点E ，过点E 分别作EM PB ⊥于M ，EN PC ⊥于点N ，连接MN①是否存在点P ，使得PMN 的面积最大？若存在，求出PMN 面积的最大值，若不存在，请说明理由；②请直接写出PMN 面积的最小值．11．如图，抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点，与y 轴交于点B ．()1求这条抛物线的顶点坐标；()2已知AD AB =(点D 在线段AC 上)，有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动：同时另一个点Q 以某一速度从点B 沿线段BC 移动，经过()t s 的移动，线段PQ 被BD 垂直平分，求t 的值；()3在()2的情况下，抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在，请求出点M 的坐标：若不存在，请说明理由．12．如图1，在O 中，弦AB ⊥弦CD ，垂足为点E ，连接AD 、BC 、AO ，AD AB =．（1）求证：2CAO CDB ∠=∠（2）如图2，过点O 作OH AD ⊥，垂足为点H ，求证：2OH CE DE +=（3）如图3，在（2）的条件下，延长DB 、AC 交于点F ，过点D 作DM AC ⊥，垂足为M ，交AB 于N ，若12BC =，3AF BF =，求MN 的长．13．如图1，已知点B （0，9），点C 为x 轴上一动点，连接BC ，△ODC 和△EBC 都是等边三角形．（1）求证：DE ＝BO ；（2）如图2，当点D 恰好落在BC 上时．①求点E 的坐标；②在x 轴上是否存在点P ，使△PEC 为等腰三角形？若存在，写出点P 的坐标；若不存在，说明理由；③如图3，点M 是线段BC 上的动点（点B ，点C 除外），过点M 作MG ⊥BE 于点G ，MH ⊥CE 于点H ，当点M 运动时，MH ＋MG 的值是否发生变化？若不会变化，直接写出MH ＋MG 的值；若会变化，简要说明理由．14．问题一：如图①，已知AC ＝160km ，甲，乙两人分别从相距30km 的A ，B 两地同时出发到C 地．若甲的速度为80km /h ，乙的速度为60km /h ，设乙行驶时间为x （h ），两车之间距离为y （km ）．（1）当甲追上乙时，x ＝ ．（2）请用x 的代数式表示y ．问题二：如图②，若将上述线段AC 弯曲后视作钟表外围的一部分，线段AB 正好对应钟表上的弧AB （1小时的间隔），易知∠AOB ＝30°．（3）分针OD 指向圆周上的点的速度为每分钟转动 km ，时针OE 指向圆周上的点的速度为每分钟转动 °；（4）若从2：00起计时，求几分钟后分针与时针第一次重合？15．如图，正方形ABCD 的边长为8，M 是AB 的中点，P 是BC 边上的动点，连结PM ，以点P 为圆心，PM 长为半径作⊙P ．（1）当BP ＝ 时，△MBP ～△DCP ；（2）当⊙P 与正方形ABCD 的边相切时，求BP 的长；（3）设⊙P 的半径为x ，请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围．16．如图，在矩形ABCD 中，6AB cm =，8AD cm =，连接BD ，将ABD △绕B 点作顺时针方向旋转得到A B D '''△（B ′与B 重合），且点D '刚好落在BC 的延长上，A D ''与CD 相交于点E ．（1）求矩形ABCD 与A B D '''△重叠部分（如图1中阴影部分A B CE ''）的面积； （2）将A B D '''△以每秒2cm 的速度沿直线BC 向右平移，如图2，当B ′移动到C 点时停止移动．设矩形ABCD 与A B D '''△重叠部分的面积为y ，移动的时间为x ，请你直接写出y 关于x 的函数关系式，并指出自变量x 的取值范围；（3）在（2）的平移过程中，是否存在这样的时间x ，使得AA B ''△成为等腰三角形？若存在，请你直接写出对应的x 的值，若不存在，请你说明理由．17．如图，已知ABF 为等腰直角三角形，90BAF ∠=︒，D 、C 为直线AF 上两点，且满足DF AC =，连接BD 、BC ，过点A 作AE BD ⊥于点E ，交BF 于点H ，连接CH ．（1）若30BAE ∠=︒，1BE =，求DE 的长；（2）若点M 是线段BF 上的动点，连AM 并延长交BD 于N ，当M 在线段BF 的什么位置上时，AH BN =？请说明理由；（3）在（2）的结论下，判断线段CH 、AH 、BD 的数量关系．请说明理由．18．如图①，△ABC 是等腰直角三角形，在两腰AB 、AC 外侧作两个等边三角形ABD 和ACE ，AM 和AN 分别是等边三角形ABD 和ACE 的角平分线，连接CM 、BN ，CM 与AB 交于点P ．（1）求证：CM ＝BN ；（2）如图②，点F 为角平分线AN 上一点，且∠CPF ＝30°，求证：△APF ∽△AMC ； （3）在（2）的条件下，求PF BN的值． 19．定义：将函数l 的图象绕点P （m ，0）旋转180°，得到新的函数l '的图象，我们称函数l '是函数关于点P 的相关函数．例如：当m＝1时，函数y＝（x+1）2+5关于点P（1，0）的相关函数为y＝﹣（x﹣3）2﹣5．（1）当m＝0时①一次函数y＝x﹣1关于点P的相关函数为；②点（12，﹣98）在二次函数y＝﹣ax2﹣ax+1（a≠0）关于点P的相关函数的图象上，求a的值．（2）函数y＝（x﹣1）2+2关于点P的相关函数y＝﹣（x+3）2﹣2，则m＝；（3）当m﹣1≤x≤m+2时，函数y＝x2﹣mx﹣12m2关于点P（m，0）的相关函数的最大值为6，求m的值．20．如图，在长方形ABCD中，AB＝4cm，BE＝5cm，点E是AD边上的一点，AE、DE分别长acm．bcm，满足(a－3)2＋|2a＋b－9|＝0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D，设运动时间为t s．（1）a＝______cm，b＝______cm；（2）t为何值时，EP把四边形BCDE的周长平分？（3）另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．21．已知菱形ABCD中，∠ABC=60°，AB=4，点M在BC边上，过点M作PM∥AB交对角线BD于点P，连接PC．（1）如图1，当BM=1时，求PC的长；（2）如图2，设AM与BD交于点E，当∠PCM=45°时，求证：BEDE=33；（3）如图3，取PC的中点Q，连接MQ，AQ．①请探究AQ和MQ之间的数量关系，并写出探究过程；②△AMQ的面积有最小值吗？如果有，请直接写出这个最小值；如果没有，请说明理由．22．如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．（1）设△DPQ的面积为S，求S与t之间的关系式；（2）当t为何值时，四边形PCDQ是平行四边形？（3）分别求出当t为何值时，①PD=PQ；②DQ=PQ．23．如图，在等腰Rt△ABC中，∠ACB=90°，AC=BC=8，点D在△ABC外，连接AD、BD，且∠ADB=90°，AB、CD相交于点E，AB、CD的中点分别是点F、G，连接FG．（1）求AB的长；（2）求证：AD+BD=2CD；（3）若BD=6，求FG的值．24．在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交BC于点F．(1)如图①，当AE⊥BC时，写出图中所有与∠B相等的角：；所有与∠C相等的角：．(2)若∠C－∠B＝50°，∠BAD＝x°(0＜x≤45) ．①求∠B的度数；②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．25．如图，抛物线214y x bx c =++与x 轴交于点A （-2，0），交y 轴于点B （0，52-）．直线32y kx =+过点A 与y 轴交于点C ，与抛物线的另一个交点是D ．(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式； (2)点P 是抛物线上A 、D 间的一个动点，过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ，问是否存在P 点使得四边形PMEC 为平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由;②作PN ⊥AD 于点N ，设△PMN 的周长为m ，点P 的横坐标为x ，求m 关于x 的函数关系式，并求出m 的最大值．【参考答案】***试卷处理标记，请不要删除一、中考数学压轴题1．A解析：（1）菱形；（2）①AF =ADAF ⊥AD ；②2AD OG =，理由见解析；（3）4【解析】【分析】（1）由折叠的性质可得AB=AD=BC=CD ，可得四边形ABCD 是菱形；（2）①由菱形的性质可得AD ∥BC ，且AF ⊥BC ，可得AD ⊥AF ，由等腰三角形的性质和外角的性质可求∠OBE=∠OEB=45°，∠ABE=∠AFB ，可得AF=AB ；②取AB 中点M ，由三角形中位线定理可得MO ∥AD ，AD=2MO ，AF ∥MG ，AF=2MG ，且AF=AD ，AD ⊥AF ，可得MO=MG ，MG ⊥MO ，可得2OM ，即可得OG 与AD 的数量关系；（3）连接AG ，由等腰三角形的性质可得AG ⊥BF ，且∠BEO=45°，可得AG=GE ，由勾股定理可求解．【详解】解：（1）∵将△ABC沿y轴翻折∴AB=AD，BC=CD又∵AB=CB∴AB=AD=BC=CD∴四边形ABCD是菱形故答案为：菱形；（2）①∵四边形ABCD是菱形∴AD∥BC，且AF⊥BC∴AD⊥AF，∴∠FAC+∠CAD=90°，且∠CAD+∠ADO=90°，∴∠FAC=∠ADO，∵AB=AD∴∠ABD=∠ADB，∴∠ABD=∠FAC∵OE=OB∴∠OBE=∠OEB=45°∴∠ABD+∠OBE=∠FAC+∠OEB∴∠ABE=∠AFB∴AF=AB∴AF=AD，故答案为：AF=AD，AD⊥AF；②AD=2OG；如图，取AB中点M，∵点M是AB的中点，点G是BF的中点，点O是AC的中点，∴MO∥AD，AD=2MO，AF∥MG，AF=2MG，且AF=AD，AD⊥AF ∴MO=MG，MG⊥MO∴2OM∵2GO；（3）∵四边形ABCD的周长为8，∴AB=BC=CD=AD=2=AF如图，连接AG，∵AB=AF ，点G 是BF 的中点，∴AG ⊥BF ，且∠BEO=45°∴∠GAE=∠BEO=45°∴AG=GE ，∵AG 2+GF 2=AF 2=4，∴GE 2+GF 2=4，故答案为：4；【点睛】本题是四边形综合题，考查了菱形的判定和性质，等腰直角三角形的性质，三角形中位线定理，折叠的性质，添加恰当辅助线是本题的关键．2．A解析：（1） A （12,0） B （72,0）；(2) ①23333y x =-+，②24316373999y x x =-+ 【解析】【分析】（1）根据抛物线的解析式可得对称轴为x =2，利用:3:4∆∆=ABC BCE S S 得出CA :CE =3:4，由△AOE ∽△AGC 可得13=AO AG ，进而求得OA 、OB 的长，即可求得点A 、点B 的坐标； （2）根据旋转的性质求出C 点坐标，利用C 点坐标和△AOE ∽△AGC 可求得E 点坐标，，分别利用待定系数法即可求得直线CE 和抛物线的解析式．【详解】解：（1）∵抛物线的解析式为24(0)=-+>y mx mx n m ， ∴对称轴为直线422-=-=m x m， 如图，设对称轴与x 轴交于G ，则//CG y 轴，2OG =，∴△AOE ∽△AGC ， ∴=AO AE AG AC ， ∵:3:4ABC BCE S S =，∴CA :CE =3:4 ，则31AE AC =， ∴13==AO AE AG AC ， ∴1142==OA OG ，3342==AG OG ， 则23==AB AG ，72=+=OB OA AB ， ∴A (12,0)， B (72,0)； （2）如图，设O 旋转后落在点Q 处，过点C 作CP y ⊥轴于点P ，由旋转的性质得：△BCO ≌△ACQ ，∴BO =AQ =72，CO =CQ ， ∴OQ==== ∵CP y ⊥轴，∴12==OP OQ ∴点C的坐标为(2,，则CG =由（1）得△AOE ∽△AGC ，13==OE AE CG AC ，∴3OE =，即点E的坐标为(0,3， ①设CE 的解析式为y kx b =+，分别代入C (2,，E 得：23k b b ⎧+=⎪⎨=⎪⎩，解得：k b ⎧=⎪⎪⎨⎪=⎪⎩， ∴CE的解析式为33y x =-+； ②将A (12,0)，C (2,分别代入24y mx mx n =-+得：120448m m n m m n ⎧-+=⎪⎨⎪-+=⎩，解得：99m n ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线解析式为2999y x x =-+． 【点睛】本题考查了二次函数的综合、旋转的性质、相似三角形的性质和求一次函数的解析式，正确的理解题意，熟练运算“数形结合思想”是解题的关键． 3．C解析：（1）112y x =-+；（2）1d t =-+；（3）65t -= 【解析】【分析】（1）根据互相垂直两直线斜率积为-1，设出直线CE 的解析式，再将点C 坐标代入即可求解；（2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，通过解直角三角形可证EDM ≌EAN ，ENH ≌EMG ，得到AN =DM ，HN =GM ，进而得到AH DG =，再根据CE 解析式求出D 点坐标，即可找出d 与t 之间的函数关系式；（3）过点B 作BT CM ⊥于点T ，在直线BT 上截取TL NK =，证四边形BGMT 与四边形HNMC 均为矩形，得MN MT =，再进一步证明ENH ≌EMG ，利用全等三角形的性质通过角度计算，得出△BML 为等腰三角形且BM BL =，再用含有t 的代数式表示BM ，最后在Rt △BMG 中利用勾股定理建立等式，求出t 的值．【详解】解：（1）∵CE ⊥AB ，∴设直线CE 的解析式为：12y x c =-+， 把点C （2，0）代入上述解析式，得1c =，∴直线CD 的解析式为：112y x =-+； （2）过点E 作EM ⊥y 轴于点M ，过点E 作EN x ⊥轴于点N ，令26112y x y x =+⎧⎪⎨=-+⎪⎩， 解得22x y =-⎧⎨=⎩， ∴()2,2E -，易证EDM ≌EAN ，ENH ≌EMG ，∴AN =DM ，HN =GM ，∴AH DG =，由直线CE 的解析式112y x =-+，可求点D （0，1） ∴DG =1—t ，∴1d t =-+；（3）过点B 作BT CM ⊥于点T ，在直线BT 上截取TL NK =，易证四边形BGMT 与四边形HNMC 均为矩形，由（2）问可知1t AH GD ==-，则6t HC =-∴6t BG MT ==-，∴MN MT =，∵90KNM LTM ∠=∠=︒，∴ENH ≌EMG ，∴L NKM ∠=∠，设KMN α∠=，则KMB KMN α∠=∠=，∴90NKM α∠=︒-，∴90NKM L α∠=∠=︒-，∵//BL MN ，∴2MBL BMN α∠=∠=，∴18090BML MBL L α∠=︒-∠-∠=︒-，∴BM BL =， ∵1tan 2KCH ∠=， ∴11322KH CH t ==-， ∴133322KN KH HN t t t TL =+=--=-=， ∴352BL BT TL t BM =+=-=， 在Rt BMG △中， 222BM BG GM =+， 解得64215t +=（不合题意舍去）或64215t -= 故，6215t -=． 【点睛】本题一次函数综合题，考查了待定系数法求解析式，一次函数的性质，全等三角形的判定与性质，角平分线的性质，勾股定理等，利用已知条件求相等交，相等线段是解决本题的关键．4．E解析：（1）2y x 2x 3=-++；（2）E （2，3）或（1，4）；（3）P 点横坐标为118【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C （1，4），设抛物线的解析式为2(1)4y a x =-+，由抛物线过点B,（3，0），即可求出a 的值，即可求得解析式； （2）过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x xx -++，求出A 、D 点的坐标，得到OM=x ，则AM=x+1，由AF=2EF 得到22(1)33x AN AM +==，从而推出点F 的坐标21210(,)3333x x --+，由23FN EM =，列出关于x 的方程求解即可；（3）先根据待定系数法求出直线DM 的解析式为y=-2x+3，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.证明△FGP ≌△FHQ ，得到FG=FH ，PT=45GH.设点P （m ，-m²+2m+3），则T （m ，-2m+3），则PT=m²-4m ，GH=1-m ， 可得m²-4m=45（1-m ），解方程即可. 【详解】（1）∵抛物线的顶点为C （1，4），∴设抛物线的解析式为2(1)4y a x =-+，∵抛物线过点B,（3，0），∴20(31)4a =-+，解得a=-1，∴设抛物线的解析式为2(1)4y x =--+，即2y x 2x 3=-++；（2）如图，过点E 、F 分别作x 轴的垂线，交x 轴于点M 、N ，设点E 的坐标为()2,23x x x -++，∵抛物线的解析式为2y x 2x 3=-++，当y=0时，2023x x =-++，解得x=-1或x=3，∴A （-1.0），∴点D （0,3），∴过点BD 的直线解析式为3y x =-+，点F 在直线BD 上，则OM=x ，AM=x+1， ∴22(1)33x AN AM +==， ∴2(1)2111333x x ON AN +=-=-=-， ∴21210(,)3333x x F --+， ∴2210332233FN EM x x x +--++==， 解得x=1或x=2， ∴点E 的坐标为（2，3）或（1，4）；（3）设直线DM 的解析式为y=kx+b ，过点D （0,3），M （32，0）， 可得，3023k b b ⎧+=⎪⎨⎪=⎩，解得k=-2，b=3，∴直线DM 的解析式为y=-2x+3， ∴32OM =，3OD =， ∴tan ∠DMO=2， 如图，过点P 作PT ∥y 轴交直线DM 于点T ，过点F 作直线GH ⊥y 轴交PT 于点G ，交直线CE 于点H.∵PQ ⊥MT ，∴∠TFG=∠TPF ，∴TG=2GF ，GF=2PG ，∴PT=25GF ， ∵PF=QF ，∴△FGP ≌△FHQ ，∴FG=FH ，∴PT=45GH. 设点P （m ，-m²+2m+3），则T （m ，-2m+3），∴PT=m²-4m ，GH=1-m ，∴m²-4m=45（1-m ）， 解得：111201m -=211201m +=（不合题意，舍去）， ∴点P 11201- 【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识，解题的关键是学会用转化的思想思考问题，学会用数形结合的思想解决问题，有一定难度.5．（1）详见解析；（2）3m =，点C 坐标为(3,2)-；（3）5k =或417k 或417k 时，可使得C D M N 、、、为顶点的四边形是平行四边形． 【解析】【分析】（1）从2172022x mx m 的判别式出发，判别式总大于等于3，而证得；（2）根据抛物线的对称轴32bx a 来求m 的值；然后利用配方法把抛物线解析式转化为顶点式，由此可以写出点C 的坐标；（3）根据平行四边形的性质得到：215|1(3)|422MN k k kCD ． 需要分类讨论：①当四边形CDMN 是平行四边形，2151(3)422MN k k k，通过解该方程可以求得k 的值；②当四边形CDNM 是平行四边形，2153(1)422NM k kk ，通过解该方程可以求得k 的值． 【详解】 解：（1）2217()4(2)(2)322m m m， ∵不论m 为何实数，总有2(2)0m -≥，2(2)30m ，∴无论m 为何实数，关于x 的一元二次方程2172022x mxm总有两个不相等的实数根，∴无论m 为何实数，抛物线217222y x mxm与x 轴总有两个不同的交点． （2）抛物线的对称轴为直线3x =，3122m ，即3m =，此时，抛物线的解析式为221513(3)2222y x xx ，∴顶点C 坐标为(3,2)-；（3）//,CD MN C D M N 、、、为顶点的四边形是平行四边形，∴四边形CDMN 是平行四边形（直线在抛物线的上方）或四边形CDMN （直线在抛物线的下方），如图所示，由已知215(3,2),(,1),(3)22D M k k N k k k，， (3,2)C ，4CD ∴=，2151(3)422MNk k kCD，①当四边形CDMN 是平行四边形，2151(3)422MNk k k，整理得，28150k k -+=，解得13k =（不合题意，舍去），25k =； ②当四边形CDNM 是平行四边形，2153(1)422NMk kk ，整理得2810k k ， 解得，12417417k k ，，综上，5k =或417k或417k时，可使得C D M N 、、、为顶点的四边形是平行四边形． 【点睛】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求二次函数解析式，抛物线的顶点公式和平行四边形的判定与性质．在求有关动点问题时要注意分析题意分情况讨论结果．6．A解析：（1）12；（2）5s 或373s ；（3）163s 或685s 或72s 【解析】 【分析】（1）AD 与BC 之间的距离即AB 的长，如下图，过点D 作BC 的垂线，交BC 于点E ，在RtDEC 中可求得DE 的长，即AB 的长，即AD 与BC 间的距离； （2）四边形QDCP 为平行四边形，只需QD=CP 即可；（3）存在3大类情况，情况一：QP=PD ，情况二：PD=QD ，情况三：QP=QD ，而每大类中，点P 存在2种情况，一种为点P 还未到达点C ，另一种为点P 从点C 处返回． 【详解】（1）如下图，过点D 作BC 的垂线，交BC 于点E∵∠B=90°，AD ∥BC ∴AB ⊥BC ，AB ⊥AD∴AB 的长即为AD 与BC 之间的距离 ∵AD=16，BC=21， ∴EC=5 ∵DC=13∴在Rt DEC 中，DE=12同理，DE 的长也是AD 与BC 之间的距离 ∴AD 与BC 之间的距离为12 （2）∵AD ∥BC∴只需QD=PC ，则四边形QDCP 是平行四边形 QD=16－t ，PC=21－2t 或PC=2t －21 ∴16－t=21－2t 或16－t=2t －21 解得：t=5s 或t=373s （3）情况一：QP=PD图形如下，过点P 作AD 的垂线，交AD 于点F∵PQ=PD ，PF ⊥QD ， ∴QF=FD∵AF ∥BP ，AB ∥FP ，∠B=90° ∴四边形ABPF 是矩形， ∴AF=BP由题意得：AQ=t ，则QD=16－t ，QF=8－2t ，AF=8+2t BP=2t 或BP=21－(2t －21)=42－2t ∵AF=BP ∴8+2t =2t 或8+2t=42－2t 解得：t=163或t=685情况二：PD=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理QD=16－t ，PF=AB=12 BP=2t 或21－(2t －21)=42－2t则FD=AD －AF=AD －BP=16－2t 或FD=16－(42－2t)=2t －26∴在Rt PFD 中，()22212162PD t =+-或()22212226PD t =+- ∵PD=QD ， ∴22PD QD =∴()()22216t 12162t =+-－或()()22216t 12226t =+-－ 解得：2个方程都无解情况三：QP=QD ，图形如下，过点P 作AD 的垂线，交AD 于点F同理：QD=16－t ，FP=12 BP=2t 或BP=42－2tQF=AF －AQ=BP －AQ=2t －t=t 或QF=42－2t －t=42－3t在Rt QFP 中，22212PQ t =+或()22212423PQ t =+-∵PQ=QD ， ∴22PQ QD =∴()22216t 12t =+－或()()22216t 12423t =+-－ 第一个方程解得：t=72，第二个方程解得：无解 综上得：t=163或685或72 【点睛】本题考查四边形中的动点问题，用到了勾股定理、平行四边形的性质、矩形的性质，解题关键是根据点Q 运动的轨迹，得出BP 的长度． 7．（1）1001；9999；（2）2754和4848；（3）见解析 【解析】 【分析】（1）根据“和平数”的定义可直接得出最小的“和平数”是1001，最大的“和平数”是9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤，则个位数字是2a ，又由029a ≤≤得到a 的可能取值为1，2，3，4；根据百位上的数字与十位上的数字之和是12的倍数，可知m +n =12，得到122a m +=，由a 的可能取值可得m 的取值，即可求得符合条件的“和平数”；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ，计算它们的和，根据“和平数”的定义可知a+b=c+d ，因式分解可得原式= 1111(a+b )，即可证明． 【详解】解：（1）根据“和平数”的定义可得： 最小的“和平数”1001，最大的“和平数”9999， 故答案为1001；9999；（2）设这个“和平数”的千位数字是a ，百位数字是m ，十位数字是n ，其中a ，m ，n 均是正整数且19a ≤≤，09m ≤≤，09n ≤≤， 则个位数字是2a ， 又∵029a ≤≤，∴a 的可能取值为1，2，3，4；∵百位上的数字与十位上的数字之和是12的倍数， ∴m+n =0或m+n =12， ∵“和平数”中a+m =n+2a ，当m+n =0时，即m=n =0，则此时a =0，不符合题意， ∴m+n =12，∴a+m =12−m +2a ，解得：122a m +=， ∵a 的可能取值为1，2，3，4；且m 为正整数， ∴m 的可能取值为7，8；当a =2时，m =7，这个“和平数”是2754； 当a =4时，m =8，这个“和平数”是4848； 综上所述，满足条件的“和平数”是2754和4848；（3）设任意一个“和平数”千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，则它的“相关和平数”千位数字为b ，百位数字为a ，十位数字为d ，个位数字为c ， ∴(100010010)(100010010)a b c d b a d c +++++++ 110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知：a+b =c+d ， ∴原式1100()11()a b a b =+++ 1111()a b =+，∵a ，b 为正整数，则1111()a b +能被1111整除，即(100010010)(100010010)a b c d b a d c +++++++能被1111整除， ∴任意的两个“相关和平数”之和是1111的倍数． 【点睛】本题考查新定义运算、因式分解的应用；能够读懂题意，根据数的特点，确定数的取值范围，进行正确的因式分解是解题关键．8．A解析：（1）详见解析；（2）3DNDM =，是一个定值；（3）92【解析】 【分析】（1）利用ASA 证ADM DBN △≌△，从而得出DM BN =； （2）如下图，先证NDQ MDP △∽△，得出DN DQDM DP=，然后在Rt BDQ △，利用tan ∠B 得出DQ BQ 的值，最后得出DNDM的值； （3）如下图，先证点C 是EF 的中点，然后利用CD 平分EDF ∠可推导出四边形CGDH 为正方形，从而得出CHN CGM △≌△，进而得出面积． 【详解】解：（1）由题意，∵60α=︒，90EDF ∠=︒，∴30BDN ∠=︒，∴BDN A ∠=∠，B EDA ∠=∠， ∵点D 是斜边AB 的中点，∴AD BD =， ∴ADM DBN △≌△，∴DM BN =． （2）3DNDM=，是一个定值． 证明：如图1，作DP AC ⊥于点P ，DQ BC ⊥于点Q ，∴90NQD MPD ∠=∠=︒，又∵90MDN PDQ ∠=∠=︒，∴NDQ MDP ∠=∠， ∴NDQ MDP △∽△，∴DN DQDM DP=， 在Rt BDQ △中，60B ∠=︒，∴tan ∠B 3DQBQ==又由（1）可知：DP BQ =，∴3DQDP =， ∴3DNDM= （3）连接CD ，作CG DE ⊥于点G ，CH DF ⊥于点H ，在Rt ABC 中，点D 是AB 的中点，∴132CD AB ==， ∵AB EF =，∴12CD EF =，∵90EDF ∠=︒，∴C 是EF 中点， ∴CD 平分EDF ∠，45CDE ∠=︒， ∵CG DE ⊥，CH DF ⊥，∴CG CH =， ∵90CGD CHD EDF ∠=∠=∠=︒， ∴四边形CGDH 为正方形，90GCH ∠=︒， ∴GCM HCN ∠=∠，∴CHN CGM △≌△， ∴S 四边形CMDN S =正方形21922CGDH CD ==． 【点睛】本题综合考查了全等三角形和相似三角形的证明和性质，解题关键是找出两个全等(相似)三角形，根据三角形全等(相似)的性质推出结论．9．A解析：（1）A （0，4），C （3，0）；（2）S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩；（3）存在，满足条件的t 的值为3617或36，点Q 的坐标为162,17⎛⎫- ⎪⎝⎭或()2,16--．【解析】 【分析】（1）解方程组求出m ，n 即可解决问题．（2）分两种情形：如图1中，当0＜t ＜4时，如图2中，当t ＞4时，根据S=12•BC•OP 求解即可．（3）分两种情形分别构建方程求解即可． 【详解】解：（1）由725m n m n +=⎧⎨-=⎩，解得：43m n =⎧⎨=⎩，∴A （0，4），C （3，0）； （2）如图1中，当0＜t ＜4时，S=12•BC•OP=12×5×（4-t ）=-52t+10． 如图2中，当t ＞4时，S=12•BC•OP=12×5×（t-4）=52t-10． 综上所述，S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩，（3）当04t <<时，由题意，1314(4)3222t t ⨯⨯=⨯⨯-⨯，解得3617t =， 此时，363241717OP =-=， 32(0,)17P ∴， (4,0)B -，BQ ∴的中点Q 的坐标为162,17⎛⎫- ⎪⎝⎭，当4t >时，由题意，1314(4)3222t t ⨯⨯=⨯⨯-⨯，解得36t =，此时36432OP =-=， (0,32)P ∴-， (4,0)B -，BP ∴的中点Q 的坐标为(2,16)--．综上所述，满足条件的t 的值为3617或36．点Q 的坐标为16(2,)17-或(2,16)--．【点睛】本题属于三角形综合题，考查了解方程组，三角形的面积等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．10．B解析：（1）333-；（2）18；（3）①2716；②972625【解析】 【分析】（1）过点B 作BF ⊥AD ，交DA 的延长线于点F ，利用等腰直角三角形ABF 求得AF 和BF 的长，再利用Rt △PBF 求得PF 的长，进而得解；（2）作点B 关于直线AD 的对称点B'，连接B'C ，交AD 于点P'，连接BP'，根据两点之间线段最短可知当B'，P ，C 三点共线时，BPC △周长取得最小值，再利用勾股定理计算即可；（3）①②根据EM PB ⊥，EN PC ⊥可得点E 、M 、P 、N 在以PE 为直径的圆上，利用圆周角定理和直角三角形两锐角互余可证得△MPN ∽△CPB ，进而可知当MN 最大时，PMN 面积的最大，当MN 最小时，PMN 面积的最小，由圆的性质可知当MN 为直径时MN 最大，当MN ⊥PE 时，MN 最小，最后利用勾股定理、等积法和相似三角形的性质求解即可． 【详解】解：（1）如图，过点B 作BF ⊥AD ，交DA 的延长线于点F ，∵AD ∥BC ，∠ABC ＝45°， ∴∠FAB ＝∠ABC ＝45°， ∵BF ⊥AD ，∴在Rt △ABF 中，AF 2+BF 2＝AB 2， ∵32AB =∴AF ＝BF 22323=， ∵AD ∥BC ，∠PBC ＝30°， ∴∠FPB ＝∠PBC ＝30°，∵在Rt △PBF 中，tan ∠FPB＝BFPF∴tan30°＝333PF =， ∴33PF=∴333AP PF AF =-=-；（2）如图，作点B 关于直线AD 的对称点B'，连接B'C ，交AD 于点P'，连接BP'，∵点B 与点B'关于直线AD 对称， ∴AD 垂直平分BB'，BF ＝B'F ＝3， ∴P'B ＝P'B'，BB'＝6，∴当点P 在点P'时，PB+PC 取得最小值，最小值为B'C 的长，此时△BPC 的周长最小， 在Rt △BB'C 中，B'C ＝22226810'BB BC +=+=， ∴△BPC 的周长最小值为B'C +BC ＝10+8＝18； （3）①∵EM PB ⊥，EN PC ⊥， ∴∠EMP ＝∠ENP ＝90°，∴点E 、M 、P 、N 在以PE 为直径的圆上，如图所示，则∠PMN ＝∠PEN ， ∵PE BC ⊥，EN PC ⊥， ∴∠PEC ＝∠ENC ＝90°，∴∠PEN+∠NEC ＝∠NEC+∠PCB ＝90°， ∴∠PEN ＝∠PCB ， ∴∠PMN ＝∠PCB ， 又∵∠MPN ＝∠CPB ， ∴△MPN ∽△CPB ，∴2PMN PCB S MN S BC ⎛⎫= ⎪⎝⎭∵PE BC ⊥， ∴PE ＝3，∴118312 22PCBS BC PE==⨯⨯=∴2 128PMNS MN⎛⎫= ⎪⎝⎭∴当MN取得最大值时，PMN的面积取得最大值，当MN＝PE＝3时，23128PMNS⎛⎫= ⎪⎝⎭解得2716PMNS=即当MN＝PE＝3时，PMN的面积最大，最大值为27 16；②由①可知，2 128PMNS MN⎛⎫= ⎪⎝⎭，∴当MN取得最小值时，PMN的面积取得最小值，由垂径定理可知，当MN⊥PE时，MN取得最小值，如图，当MN⊥PE时，则弧ME＝弧NE∴∠MPE＝∠NPE，∵PE BC⊥，∴∠PEB＝∠PEC＝90°，∴△PEB≌△PEC，∴EB＝EC＝12BC＝4，在Rt△BEP中，BP2222435BE PE+=+=,∵1122BEPS BE PE BP ME ==∴1143522ME ⨯⨯=⨯∴125 ME=,在Rt△PME中，PM2222129355 PE ME⎛⎫-=-=⎪⎝⎭∵1122PMES PM ME PE MH ==∴191213 2552MH ⨯⨯=⨯∴3625MH =, ∴72225MN MH ==, ∴227292512825PMN S ⎛⎫ ⎪⎛⎫== ⎪ ⎪⎝⎭⎪⎝⎭, 解得972625PMN S =， ∴PMN 面积的最小值为972625． 【点睛】本题考查了等腰直角三角形、特殊角的三角函数、相似三角形的判定及性质、勾股定理、垂径定理和圆周角定理等相关知识，有点难度，属中考压轴题，能够将第（3）问转化为利用圆的相关知识和相似三角形的性质解决是解决本题的关键．11．A解析：(1) 149,212⎛⎫⎪⎝⎭；(2) 257t =；(3)存在，见解析 【解析】 【分析】（1）已知抛物线的2点，代入可直接求解；（2）根据A 、B 的坐标，得出AD 、AB 的长，通过推导可证ABCQDB ∆∆，利用相似得到的比例线段即可求得DQ 、PD 的长，从而得出t ；（3）根据轴对称的最短路径先作C 关于对称轴的对称点，即点A ，连接AO 与对称轴的交点即为点M ．【详解】（1）抛物线()240y ax bx a =++≠与x 轴交于()()3,0,4,0A C -两点 164409340a b a b ++=⎧∴⎨-+=⎩ 解这个方程组，得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩ ∴抛物线的解析式为211433y x x =-++ 221111494333212y x x x ⎛⎫=-++=--+ ⎪⎝⎭。

相关文档
最新文档