神经网络短期负荷预测的输入变量选择研究
基于模糊神经网络的电力系统短期负荷预测研究
应 的 电力系 统 短期 负荷 预 测 研 究
孙 伟
( 疆 乌 鲁 木 齐 电 业 局 营 销 部 ,新 疆 乌 鲁木 齐 8 0 1 新 3 0 1)
摘 要 电力系统短 期负荷受 到多方面 因素 的影响 ,具有 明显 的多元 非线性动 态变化特性 ,很难准确 的用 单一的线性数学模 型进行建模 预 测分析 。为获得具有模糊 自适应 调节 预测功能 的负荷预测模型 ,将模糊控制 与B 神经 网络相结合 ,形 成一个具有模糊 自推理的负荷预测模 P
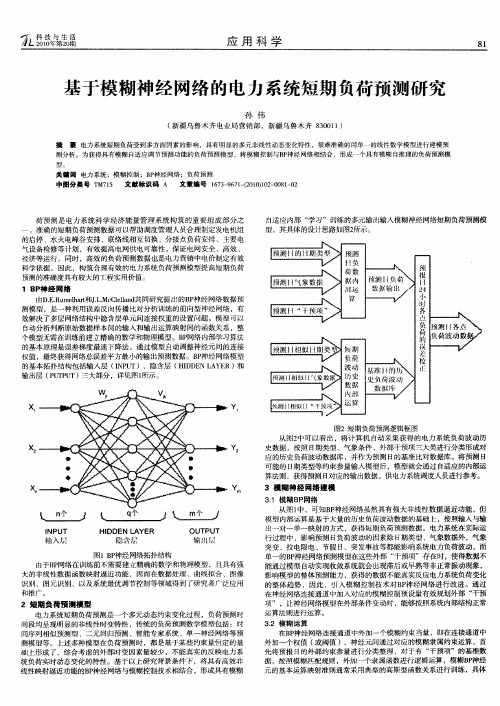
颓 I 豫 数 I
颓测 负 赫 数 獭 内 预测 负荷 赧 运 数 挺 输 出 算
鳓测 “ 预项 ”
测 褥 点 便 衙 波动 数
自 动分析判断原始数据样本 间的输入和输 出运算映射间的函数关系 , 整 个模型无需在训练前建立精确的数学和物理模 型。B 网络内部学习算法 P 的基本原理是误差梯度最速下 降法 ,通过模 型自动调整神经元间的连接 权值 ,最终获得网络总误差平方最小 的输出预测数据 B 神经 网络模型 P 的基本拓扑结构包括输入层 (NP T)、隐含层 ( I D N L Y R)和 I U H D E A E 输出层 ( L 1 T)三大部分 ,详见 图1 P 兀P u 所示 。
图1B 神经网络拓扑结构 P 由于B 网络在训练前不需要建立精确 的数学和物理模型 ,且具有强 P 大的非线性数据函数映射逼近功能 ,因而在数据处理 、曲线拟合 、图像 识别、图元识别 、以及系统最优调节控制等领域得 到了研究者广泛应用 和推广 。
单一的B 神经网络预测模 型在这些外部 “ P 干预项 ”存在时,使得数据不 能通过模型 自动实现收敛系统就会 出现滞后或早熟等非正常振动现象 ,
一
短期负荷预测研究开题报告

短期负荷预测研究开题报告短期负荷预测研究开题报告一、研究背景与意义电力是现代社会发展的重要基础设施之一,而负荷预测作为电力系统运行的重要组成部分,对于保障电力供应的稳定性和经济性具有重要意义。
短期负荷预测是指对未来一段时间内电力系统负荷变化进行预测,通常时间范围为数小时到数天。
准确的短期负荷预测可以帮助电力公司合理调度发电设备,提高电力系统的运行效率,降低供电成本,同时也有助于优化电力资源配置,提高电力供应的可靠性。
目前,随着电力系统规模的不断扩大和电力需求的不断增长,短期负荷预测的准确性和稳定性对电力系统运行的影响越来越大。
因此,对短期负荷预测进行深入研究,提高预测准确性和可靠性,对于实现电力系统的可持续发展具有重要意义。
二、研究目标与内容本研究旨在通过对历史负荷数据的分析和建模,结合影响负荷变化的各种因素,开展短期负荷预测的研究。
具体研究内容包括以下几个方面:1. 数据采集与处理:收集历史负荷数据,并对数据进行预处理,包括数据清洗、异常值处理等,以保证数据的准确性和可靠性。
2. 特征提取与选择:通过对历史负荷数据的分析,提取出影响负荷变化的主要特征,并进行特征选择,以减少模型复杂度和提高预测准确性。
3. 模型建立与优化:基于历史负荷数据和选取的特征,建立合适的负荷预测模型,包括传统的统计模型和机器学习模型。
同时,通过参数调整和模型优化,提高模型的预测准确性和稳定性。
4. 预测结果评估与应用:对研究所得的负荷预测模型进行评估,包括预测误差、稳定性等指标。
并将预测结果应用于实际电力系统中,验证模型的实际效果和可行性。
三、研究方法与技术路线本研究将采用数据驱动的方法进行短期负荷预测。
具体的技术路线如下:1. 数据采集与处理:通过电力公司提供的历史负荷数据,利用数据挖掘技术进行数据清洗和异常值处理,以获得准确可靠的数据集。
2. 特征提取与选择:基于历史负荷数据,使用统计分析和特征工程技术,提取出影响负荷变化的主要特征,并使用相关性分析和特征选择算法,选择出最具代表性的特征。
基于BP神经网络数学模型的短期负荷预测研究

时控 制 中更是不 可缺 少 的 。首先 ,准确 的短期 负荷 预测 可 以帮助调 度人员 经 济合理 地安 排发 电机组 的 启动 、停机 ,合 理安排 好备 用设 备 ,使 系统 在安 全 运行 范 围内发 电成本最 小 。其 次 ,在 不 同系统 间能 量交 换 以及进 行合 理 的负荷 分配 也必 须 以准确 的短
维普资讯
第3 O卷第 2期
20 07年 6月
长春理 工大学 学报
J u n l fCh n c u ie st fS in e a d T c n l g o r a a g h n Un v r i o c e c n e h o o y o y
基本的 B P算法 采 用 有监 督 学 习方 式 ,基 于梯 度 下降算 法 ,极小化 误 差 函数 。其 主要 思想是 将学 习过程分 为信 号正 向传播 过程 和误差 后 向传播过 程
两个 阶段 。 , v为输 人样 本 的个数 。 表示 网络权 向量 。 误 差 函数 : ( E W)=g 厂 W, , )) E称 为 (( , 误差 ( 测度 )函数 。 用误 差 函数来 判别 网络 的实 际输 ・ 设 ( , )表示 输人 样 本 , ∈ { , … , v , P l 2, ,}
期负荷 预测 为前提 。
出向量 与教师信号向量 的误差。 常采用二乘误
差 函数加 以判 别 ( 为输 出 向量 的维 数 ) m :
负荷预 测是 电力 系统 一项非 常重要 的工 作 ,它
用转移 函数 进行 处理 。第一 隐层 的输 出传递 给下 一 隐层 ,各个 隐层依 次类 推 ,最后 一个 隐层 的输 出作
为输 出层 的 输 人 ,输 出层 给 出 输 人 样 本 的 网络 预
基于PSO-Elman神经网络的电力系统短期负荷预测模型研究

1 El n神 经 网 络 模 型 构 造 ma
1 1 El n NN 的 动 态 递 归 原 理 . ma -
E ma — l nNN模 型 的结构 如 图 1 示 , 步负 荷预 测 的输 出节 点为 一个 。从 图 中可 见 , l nNN 由输 入 所 单 E ma — 层、 隐含层 、 关联 层 和输 出层所 组成 , 每一 个 隐含层 节点 都 有 一个对 应 的关 联 层 节点 与之连 接 。输 入层 节 点 与 隐含层节 点 、 隐含层 节 点与输 出层 节点 以及 关联 层节 点与 隐含层 节点 均 由可调权 值相 连接 。
保证 负荷 预测 的精度 。采 用粒 子群 优化算 法对 Ema l n神 经 网络进 行 学 习训 练 , 可充 分 利 用 粒 子群优 化算 法 的全 局 寻优 性 能 , 服 常 规学 习算 法 易 于 陷入 局 部 最 优解 、 克 收敛 速 度 慢 、 程复 杂等 缺陷 。通过 对地 区 电网负 荷 系统 的实例仿 真证 实 了所 提 出方法 的有 效性 , 编
中图分 类号 : TM 7 5 1 文献标 识 码 : A . .
电力 系统 短 期 负荷 预 测 (h r— r la oea t g S L ) 准确 性 将 直 接影 响 电力 系统 的运 行 性 s ot em dfrcsi , T F 的 t o n
能 。负荷预 测精度 越 高 , 有利 于提 高发 电设备 的利 用 率 和经 济调 度 的有 效性 。特别 是 电力 市 场竞 争 机 制 越
获 得 了较满 意 的预测精 度 , 均 绝对 误 差 和 最 大相 对误 差 分 别达 到 19 8 和 4 63 。 平 . 8 . 7 为 该 模 型 用 于 实 际 工 程 取 得 了有 效 的 进 展 。
基于人工免疫算法的神经网络电力系统短期负荷预测

排电网设备调度及检修计划 , 还能提高电力系统运行 的稳定性 , 减少 电网的发 电成本【 2 】 . 本研究 构造 了基 于人工免疫算法 的神经 网络电力系统短期负荷预测 方法 , 并通过仿真实验对方法进行 了验证 .
模型 的神经网络规模相对较小 , 过度训 练的现象不 容易 出现 , 预测速度 比较快 . 多输出模型可 以一次性 得到预测 E l 的负荷数据 , 有较好的通用性 , 缺点是网 络模型比较大, 该网络可能需要数千个 网络权值 、 阈 值等参数 , 耗费较长的训练时间【 4 】 . 本研究对预测 日
・
1 6 0・
成都 大 学学报 ( 自然科 学版 )
1 . 3 层 . 依据 K o 1 .
m o g o r o v 定理 , 3层前 向 网络 可 以满 意再 现任 意 连 续
函数 , 如果有合理 的结构和适当的权值[ 6 】 . 绝大多数
使用人工神经 网络短期负荷研究都是基于单个隐含 层的 . 对 3层前 向层 网 络 的 结构 分 析 主 要 是针 对 隐
到 电力系统 的安全运行 和经 济调 度 , 便 于更合 理 地安
电力市场的负荷数据进行负荷 的频谱分析 , 采用快
速傅里叶变换 ( F a s t F o u r i e r T r a n s f o r m , F F T ) 对历史负 荷数据进行频谱 分析 . F F I | 的输人是所有小时负荷 数据构成的数据序列 , 从 中分析出隐含于负荷数据 中的周 期特 性 . 分析 结果 显示 , 负荷 数据 中存在 8个
基于小波-LMBP神经网络短期电力负荷预测研究

3 . 2 . 3构建 c 3 、 d 3 、 d 2 、 d 1 分量合适的预测模 型。 根据各分量 的特点构建各 自的神经 网络结构 。由于 c 3分量与 原 始数 据 序 列 形 状 相 似 , 应 考 虑 系 统 实 际 负 荷 的特 点 , 加 入 气 象 因 子数据作为输入变量 。预测第 d天 t 时刻 c 分量负荷值 , 输入参数 为t 时刻前 1 2点 ,第 d - 1 、d - 2 、d - 7 天t 时刻前后三点的 c 3分量 值, 以及 对 应 日期 的天 气 数 据 ( 降雨 量 R、 日最 高气 温 T m a x 、 日最 低 气温 T a r i n ) 和 日期 类 型共 3 4个 输人 数 据 。由于 d 3 、 d 2 在 整个 负 荷 中 所 占 比例 较小 , 并 且 受 天 气 因 素影 响 较 小 , 因此 , 预 测 第 d天 t 时刻 d 3 、 d 2分量负荷值 , 神经 网络 的输入数据为 t 时刻前 1 2点 , 第d - 1 、 d 一 2及 d 一 7 天t 时刻 周 围 三 点对 应 的 d 3 、 d 2 分量 , 各为 2 2个 输 入数 据 。 隐含 层节 点 数 采用 试 凑法 , 因此 , 对单点( 每小 时 ) 负荷的 c 3 分 量采用 L MB P神经网络结构为: 3 4 — 7 — 1 , d 3 、 d 2分量 L MB P神经网络 结构为 : 2 2 — 6 — 1 。由于 d 1 分 量 呈 现很 强 的 随机 性且 在 整个 负 荷 中 的 占的比例很小 , 使用加权平均法对其进行近似预测。 4将 c 3和 d 3 、 d 2 、 d l 预测分量结果进行重构 ( 调用 w a v e r e c函 数) 得到 2 0 1 2年 8月 2 7日 2 4小 时 的 负 荷 预 测值 , 并 与 实 际 负 荷 比较得到误差 曲线 , 仿真结果见图 1 , 图2 为单独使用 L M B P神经 网 络进行预测得到的预测值与误差 曲线。
《2024年短期电力负荷预测关键问题与方法的研究》范文

《短期电力负荷预测关键问题与方法的研究》篇一一、引言随着社会经济的快速发展和人民生活水平的不断提高,电力需求日益增长,电力负荷预测成为了电力系统管理和运行中不可或缺的一环。
短期电力负荷预测作为其中一项关键技术,其准确性直接关系到电力系统的安全、稳定、经济运行。
本文将重点探讨短期电力负荷预测的关键问题及其解决的方法。
二、短期电力负荷预测的关键问题1. 数据质量问题数据是短期电力负荷预测的基础,数据质量直接影响到预测的准确性。
数据质量问题主要包括数据缺失、数据异常、数据不准确等。
这些问题的存在会使得预测模型无法准确捕捉到电力负荷的变化规律,从而影响预测的准确性。
2. 模型选择问题选择合适的预测模型是短期电力负荷预测的关键。
不同的预测模型有不同的适用范围和预测效果,如何根据实际数据特点选择合适的预测模型是一个需要解决的问题。
此外,预测模型的复杂度和计算效率也需要考虑,以保证预测的实时性和可行性。
3. 影响因素问题电力负荷受到多种因素的影响,如气温、节假日、经济状况等。
如何准确地考虑这些影响因素,并将其纳入预测模型中,是提高短期电力负荷预测准确性的关键。
三、短期电力负荷预测的方法1. 传统统计方法传统统计方法是短期电力负荷预测的常用方法,如回归分析、时间序列分析等。
这些方法通过对历史数据进行统计分析,建立数学模型,从而进行短期电力负荷预测。
这些方法的优点是简单易行,但需要考虑的因素较为有限,且对于复杂的数据变化规律可能无法准确捕捉。
2. 机器学习方法机器学习方法在短期电力负荷预测中得到了广泛应用,如支持向量机、神经网络、集成学习等。
这些方法可以通过学习历史数据的特征和规律,建立复杂的非线性模型,从而更准确地预测电力负荷。
机器学习方法的优点是可以处理多种影响因素和复杂的数据变化规律,但需要大量的训练数据和计算资源。
3. 深度学习方法深度学习是近年来兴起的一种机器学习方法,其在短期电力负荷预测中也取得了较好的效果。
基于BP神经网络短期电力负荷预测论文

基于BP神经网络的短期电力负荷预测摘要:本论文首先对短期电力负荷预测进行了概述,在详细分析bp神经网络原理的基础上,通过对某市历史负荷数据的分析,应用bp神经网络,建立了短期负荷预测模型,应用matlab 6.5软件进行实际建模仿真。
关键词:电力负荷bp神经网络预测建模仿真1.引言由于电力的生产与使用具有特殊性,即电能是不能储存的,这样就要求系统发电出力随时紧跟系统负荷的变化动态平衡,否则,就会影响供用电的质量,重则危及系统的安全与稳定。
随着电力系统的商品化和市场化,电力负荷预测的准确性对电力系统安全经济运行和国民经济发展具有重要意义。
正确地预测电力负荷,既是为了保证供应国民经济各部门及人民生活以充足的电力需要,也是电力工业自身发展的需要。
2.输入层和输出层的设计在预测日的前一天中,每1个小时对电力负荷进行一次测量,这样一来,一天共测得24组负荷数据。
由于负荷值曲线相邻的点之间不会发生突变,因此后一时刻的值必然和前一时刻的值有关,除非出现重大事故等特殊情况。
所以这里将前一天的实时负荷数据作为网络的样本数据。
此外,由于电力负荷还与环境因素有关,如最高和最低温度等。
因此,还需要通过天气预报等手段获得预测日的最高和最低温度。
这里将电力负荷预测日当日的气象特征数据作为网络的输入变量。
因此,输入变量就是一个26维的向量。
显而易见,目标向量就是预测日当天的24个负荷值,即一天中每个整点的电力负荷。
这样一来,输出变量就成为一个24维的向量。
获得输入和输出变量后,要对其进行归一化处理,将数据处理为区间[0,1]之间的数据。
归一化方法有许多种形式,本文采用如下公式:在样本中,输入向量为预测日前天的电力实际负荷数据,目标向量是预测日当天的电力负荷。
由于这都是实际的测量值,因此,这些数据可以对网络进行有效的训练。
如果从提高网络精度的角度出发,一方面可以增加网络训练样本的数目,另一方面还可以增加输入向量的维数。
目前,训练样本数目的确定没有通用的方法,一般认为样本过少可能使得网络的表达不够充分,从而导致网络外推能力不够;而样本过多可能会出现样本冗长现象,既增加了网络的训练负担,也可能出现信息量过剩使得网络出现过拟合现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 3期
2004 年 9 月
电子测量与仪器学报 JOURNAL OF ELECTRONIC MEASUREMENT AND INSTRUMENT
Vol 18
No 3
∀ 13 ∀
神经网络短期负荷预测的输入变量选择研究
杨奎河1, 2 王宝树1 赵玲玲2
( 1 西安电子科技大学计算机学院 , 西安 710071; 2 河北科技大学信息科学与工程 学院 , 石家庄 050054) 摘要 短期负荷预测中输入变量的选择直接关系到神 经网络的预 测性能。本 文将自 相关函 数的概 念应用 于神经网络短期负荷预测中的输入变量集选择 , 对输入变量集的选择提出了一种比较科学系统的方 法。通过采 用 FFT 来实现对自相关函数的快速计算 , 增加 了该方法的可操作性 , 并通过具体的实例验证了该方 法的有效性。 关键词 : 神经网络 输入变量 短期负荷 预测
2N - 1 1 2N - 1 - j m % x 2N ( n ) % x 2N ( n + m) e ( 7) m = - ( N - 1) N n= 0 令 l = n + m, 由于 x 2 N ( n + m) = x 2N ( l ) 的取值区间是 0~ 2N - 1, 所以 l 的变化范围是 0~
1 引
言
影响负荷预测的因素非常多, 如何从大量的影响因素中选择出对期望输出影响最大的一些 因素 , 组成一个有效输入变量集, 成为神经网络预测方法首先要面对的问题。现在对神经网络输 入变量的选择尚未提出一种比较系统的方法 , 一般都根据设计者的经验选取 。 [ 3] 用相空间嵌入法 来确定神经网络的输入变量, 只能在负荷序列中寻找对预报时刻影响最 大的负荷点 , 直接将选择结果用于预测时效果比较差。OLS 法 [ 4] 对输入变量进行正交变化 , 可求 出天气等输入变量的单独贡献 , 但该方法不适合处理随时间连续变化的负荷序列, 而且计算较复 杂。本文将自相关函数的概念应用于神经网络短期负荷预测中的输入变量选择, 从影响因素集 中选择与期望输出相关度较大的负荷点作为输入变量, 并通过采用 FFT 来实现对负荷自相关函 数的快速计算, 增加了该方法的可操作性, 取得了较为理想的结果。
Study on Input Variables Selection of Short- term Load Forecasting Based on Neural Network Yang Kuihe1, 2 Wang Baoshu1 Zhao Lingling2 ( 1 College of Computer Science and Engineering, Xidian University, Xi! an 710071 2 College of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang 050054 ) Abstract: The input variables selection for short- term load forecasting is relevant to the performance of neural network forecasting. In this paper, by using the autocorrelat ion function on input variables sets se lection for neural network short - term load forecasting, a systemic and scientific method for input variables sets selection is put forward. FFT is adopted to accomplish the speediness calculation, which enhances the maneuverability of this approach. A load forecasting example is given, whole result indicates that the method is effect ive. Keywords: Neural network, input variables, short- term load forecasting.
[ 5]
( 5)
对于一个固定的延迟 | m | , 当 N 足够大时 , R ^ ( m) 是 R( m ) 的一致估计 。在利用式( 5) 估 计R ^ ( m ) 时 , 如果 N 和 m 都比较大, 则需要的乘法次数太多, 因而其应用受到了限制。采用快速 傅里叶变换( FFT ) 可实现对 R ^ ( m ) 的快速计算。 2 2 用 FFT 对自相关函数的快速计算 通过式( 4) 对 R ^ ( m ) 作傅里叶变换 , 得 : % R ^ ( m) e m= - ( N - 1)
N- 1
j m
N- 1 N- 1 = 1 m= -% % xN ( n) x N ( n + m ) e ( N - 1) n= 0 N
j m
N- 1 N- 1 = 1 n% x % xN ( n + m ) e N ( n) m= - ( N - 1) N =0
j m
( 6) 两个长度为 N 的序列的线性卷积 , 其结果是一长度为 ( 2N - 1) 的序列。为了能用离散傅里 叶变换( DTF) 来计算线性卷积, 需要把这两个序列的长度扩充到( 2N - 1) 。利用 DTF 来计算线性 相关时 , 同样也是如此。为此, 现把 xN ( n) 补 N 个零, 得到 x 2N ( n) , 即 : 当 0 & n & N - 1 时, x 2N ( n) = xN ( n) ; 当 N & n & 2N - 1 时 , x 2N ( n) = 0。记 x 2N ( n ) 的傅里叶变换是 X 2 N ( ej ) , 则 :
3 负荷数据的相关曲线
设负荷序列为 x ( i ) ( = 0, 1, . . . , N - 1) , 下面结合石家庄地区电网的实际数据来计算 x ( i ) 的自相关函数 R ^ ( m) , 并由此得出与当前负荷点关系最密切的历史负荷点。在计算过程中 , 为了 使求出的相关系数更具有可比性, 把 R ^ ( m) 按下式作归一化处理 : ^ ( m)= R ^ ( m)/ R ^ ( 0) 取石家庄地区电网 2000 年 7 月 6 日至 8 月 5 日各小时整点负荷值 , 共 24 ∋ 31= 744 个数据 , 因此公式中 的 N = 744, 用 FFT 估算 R ^ ( m ) , 并按 式( 10) 作归一化处理, 算出 8 月 5 日 24 点与它前面 8 天 24 ∋ 8= 192 个时 段的自相关函数曲线 , 如图 1 所示。 同样, 再计算 2000 年 8 月 5 日 其他 23 个时段与其前面 8 天各点的 自相关 函数, 也可以得 到相似的 曲 线。因此图 1 的自相关函数曲线对 图 1 负荷的自相关函数曲线 ( 10)
% R ^ ( m) e m = - ( N - 1)
N- 1
- j m
=
2N - 1, 这样 ,
N- 1 m=
% R ^ ( m) e - ( N - 1)
j m
=
1 2N - 1 % x ( n) eN n= 0 2N
j n
2N - 1 l= 0
% x 2N ( l ) e -
j l
( 8)
第3 期 即:
负荷各个时段具有代表性。 若假设当前时刻为 t , 记当前负荷值为 x ( t ) , 记 x ( t - k ) 表示在 t 时刻之前 k 个时段的负荷 值, 且记 ( t - k ) 表示负荷 x ( t ) 与 x ( t - k ) 的相关系数 , 则从图 1 可以得出结论 : 在负荷序列 中, 当前负荷与以前其他各个时段负荷的相关程度是不同的。图 1 中负荷 x ( t ) 与 x ( t - k ) 相关 系数大于 0 760 的点分别为 ( t - 1 ) = 0 911、 ( t - 2 ) = 0 823、 ( t - 22 ) = 0 795、 ( t - 23) = 0 889、 ( t - 24) = 0 912、 ( t - 25 ) = 0 887、 ( t - 26) = 0 786、 ( t - 47 ) = 0 803、 ( t - 48 ) = 0 819、 ( t - 49) = 0 799、 ( t - 72) = 0 768。因此 , 当前负荷点与上述历史负荷点相关性较大, 完 全可以通过相关系数的显著性校验。
x ( n) 只能假设为零。现在的任务是如何由这 N 个观察值来估计出 x ( n) 的自相关函数 R ( m ) 。 在式 ( 3) 中, 由于观察值的点数 N 为有限值, 则用下式可求 R ( m) 的估计值 R ^ ( m) : 1 N- 1 % x ( n) x N ( n + m) ( 4) N n= 0 N 由于 x ( n) 只有 N 个观察值 , 因此 , 对每一个固定的延迟| m | , 可以利用的数据只有 N - 1R ^ ( m) = | m | 个 , 且在 0~ N - 1 的范围内, xN ( n) = x ( n) , 所以在实际计算 R ^ ( m ) 时 , 式( 4) 变为 : N- 1- | m | 1 R ^ ( m)= % x ( n) x ( n + m) N n= 0
神经网络短期负荷预测的输入变量选择研究
N- 1
∀ 15 ∀
1 | X ( ej ) | 2 ( 9) N 2N 式( 9) 中 | X 2N ( ej ) | 2 是有限长信号 x 2N ( n) 的能量谱, 除以 N 后即为其功率谱。这说明自相
