电子科技大学-图论第二次作业-杨春
电子科技大学图论作业

图论作业3一、填空题1. 完全图K2n共有个不同的完美匹配。
2. 超方体Q6的最小覆盖包含的点数为。
3. 图K m,n (m≤n)的最小覆盖包含的点数为。
4. 完全图K60能分解为个边不重的一因子之并。
5. 完全图K61能分解为个边不重的二因子之并。
6. 假设G是具有n个点、m条边、k个连通分支的无圈图,则G的荫度为。
7. 图G是由3个连通分支K1, K2, K4组成的平面图,则其共有个面。
8. 设图G与K5同胚,则至少从G中删掉条边才可能使其成为可平面图。
9. 设连通平面图G具有5个顶点,9条边,则其面数为。
10. 若图G是10阶极大平面图,则其面数等于。
11. 若图G是10阶极大外平面图,其内部面共有个。
二、不定项选择题1. 关于非平凡树T,下面说法错误的是( )(A) T至少包含一个完美匹配;(B) T至多包含一个完美匹配;(C) T的荫度大于1;(D) T是只有一个面的平面图;(E) T的对偶图是简单图。
2. 下列说法正确的是( )(A) 三正则的偶图存在完美匹配;(B) 无割边的三正则图一定存在完美匹配;(C) 有割边的三正则图一定没有完美匹配;(D) 有完美匹配的三正则图一定没有割边;(E) 三正则哈密尔顿图存在完美匹配。
3. 下列说法正确的是( )(A) 在偶图中,最大匹配包含的边数等于最小覆盖包含的点数;(B) 任一非平凡正则偶图包含完美匹配;(C) 任一非平凡正则偶图可以1-因子分解;(D) 偶度正则偶图可以2-因子分解;(E) 非平凡偶图的最大匹配是唯一的。
4. 下列说法中错误的是( )(A) 完全图K101包含1-因子;(B) 完全图K101包含2-因子;(C) 完全图K102包含1-因子;(D) 完全图K102包含2-因子;(E) 图G的一个完美匹配实际上就是它的一个1因子;(F) 图G的一个2-因子实际上就是它的一个哈密尔顿圈。
5. 下列说法正确的是( )(A) 方体Q n可以1-因子分解;(B) 非平凡树可以1-因子分解;(C) 无割边的3正则图可以1-因子分解;(D) 有割边的3正则图一定不可以1-因子分解;(E) 可1-因子分解的3正则图一定是哈密尔顿图。
图论电子科大ppt2

1 (d2 1, d3 1, , dd11 1, dd12 , , dn )
是图序列。
证明:" "
设G是Π对应的简单图,d (vi)=di
情形1:点v1与点v2,v3,…,vd1+1邻接,则G-v1的度序列正好 为Π1
15
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
n
dn , di 2m i 1
r
n
di r(r 1) minr, di,1 r n 1
i 1
ir 1
该定理证明很难!
上世纪60年代以来,人们又研究所谓的唯一图序列问题。
例5就是一个唯一图序列!
19
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
9
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
0.6 0.4 x 0.2
奇数度的顶点称为奇点,偶数度的顶点称偶点。
设G = (V, E)为简单图,如果对所有 v V ,有 d (v) = k,称图G为k-正则图
定理: 图G= (V, E)中所有顶点的度的和等于边数 m的2倍,即:
证明 : 设G是k-正则图,若k为奇数,则由推论1知 正则图G的点数必为偶数
例4 Δ与δ是简单图G的最大度与最小度,求证: 2m
n
11
H G 1
0.5 n 0
0.5
1 2 1.5 t1
0.5
00
1 0.8
电子科技大学-图论第二次作业

习题四:3. (1)画一个有Euler闭迹和Hamilton圈的图;(2) 画一个有Euler闭迹但没有Hamilton圈的图;(3) 画一个有Hamilton圈但没有Euler闭迹的图;(4) 画一个即没有Hamilton圈也没有Euler闭迹的图;解:找到的图如下:(1)一个有Euler闭迹和Hamilton圈的图;(2)—个有Euler闭迹但没有Hamilton圈的图;⑶一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.4. 设n阶无向简单图G有m条边,证明:若2 ) * ',则G是血加此"图。
证明:G是H图。
若不然,因为G是无向简单图,则n芝3,由定理%若G是n芝3的非单图,则G、一 ...C …度弱丁某个阵".于是有:- - 1 2 E(G)| E(C m,n ) - m (n 2m)(n m 1) m(m 1)1.这与条件矛盾!所以G 是H 图若G 有个奇点,则存在k 条边不重的迹Q1・Q 矿心,使得 E(G) = E(Q 】)U E(Q J U E(Q 3) U …U E(Q k ) 证明:不失一般性,只就 G 是连通图进行证明。
设 G=(n, m)是连通图。
令 虬 V 2,…,v,V k+1,…,v 是G 的所有奇度点。
在V i与v i+k 问连新边e i 得图G* (1三隹k). 则G*是欧拉图,因此,由Fleury 算法得欧拉环游C 在C 中删去e i (1m M k).得 k 条边不重的迹Qi (1 MiMk):E(G) E(Q1^E(Q2^^E(Qk)10. 证明:若:(1) G 不是二连通图,或者(2) G 是具有二分类|(X,Y)的偶图,这里|X” |Y|则G 是非Hamilton 图。
证明:(1) G|不是二连通图,则G 不连通或者存在割点v ,俨任-v) >2 ,由丁课本 上的相关定理:若G 是Hamilton 图,则对丁*勇)的任意非空顶点集S,有: w(G- S) <|S|,则该定理的逆否命题也成立,所以可以得出:若不是二连通图, 则G 是非Hamilton 图(2)因为是具有二分类(XI)的偶图,乂因为|X|丰1丫1,在这里假设|X| < |Y|,则有 w(G-X) = |Y|>|X|,也就是说:对北(G)|的非空顶点集S,有:w(G-S)>||S|成 立,则可以得出则G 是非Hamilton 图。
图论及其应用 杨春 课件 全 电子科技大学

图可以用图形表示:V中的元素用平面上一个黑点表示,E 中的元素用一条连接V中相应点对的任意形状的线表示。
例1、设图G=<V,E>。这里V={v1,v2,v3,v4} E={e1,e2,e3,e4,e5,e6},
e1=(v1,v2),e2=(v1,v3),e3=(v1,v4), e4=(v2,v3),e5=(v3,v2),e6=(v3,v3)。
定理:若n阶图G是自补图( G G ),则有:
n0,1(mod4)
证明:n阶图G是自补图,则有:
H G
m (G ) m (G )m (K n)1 2n (n 1 ) 所以: m(G) 1 n(n1)
4
由于n是正整数,所以:n0,1(mod4)
自补图是很有意义的图类。它在对角型拉姆齐数 方面的研究、关于图的香农容量的研究、强完美图 方面的研究等都有重要作用。
H G
图G 的“拓扑不变量”是指与图G有关的一个 数
或数组(向量)。它对于与图G同构的所有图来说, 不会发生改变。
一个图G可以对应很多拓扑不变量。如果某组不 变量可完全决定一个图,称它为不变量的完全集。
定理:非负整数组(d1,d2,…., d n)是图的度序列的 充分必要条件是:n d i 为偶数。
H G
推论1 在任何图中,奇点个数为偶数。
证明:设V1,V2分别是G中奇点集和偶点集.则由 握手定理有:
dv dv dv
v V 1
v V 2
v V
是偶数,由于
vV 2
d
v
是偶数, 所以 d v vV1
是
偶数,于是 V 1 是偶数。
推论2 正则图的阶数和度数不同时为奇数 。
证明 : 设G是k-正则图,若k为奇数,则由推论1知 正则图G的点数必为偶数 例4 Δ与δ是简单图G的最大度与最小度,求证:
图论作业电子科大 杨春
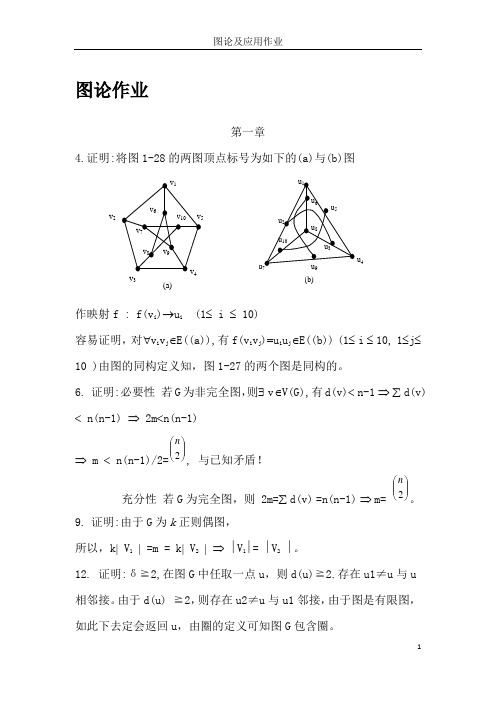
图论作业第一章4.证明:将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明,对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 )由图的同构定义知,图1-27的两个图是同构的。
6. 证明:必要性 若G 为非完全图,则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾!充分性 若G 为完全图,则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。
9. 证明:由于G 为k 正则偶图,所以,k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。
12. 证明:δ≧2,在图G 中任取一点u ,则d(u)≧2.存在u1≠u 与u 相邻接。
由于d(u) ≧2,则存在u2≠u 与u1邻接,由于图是有限图,如此下去定会返回u ,由圈的定义可知图G 包含圈。
(a)v 2 3u 4u (b)17.证明:设u、v是G的任意两个顶点。
若u和v在G中不邻接,则在中他们邻接。
若u和v在G中邻接,他们属于G的同一分支。
在另一个分支中有一点w,在中u和v均与w邻接,即uwv是一条通路,故是连通图。
第二章2.证明:由题意可知如果一棵树恰有两个1度的顶点,则其他顶点的度必为2(如果树其他顶点至少有一个大于2,则该树度为1的顶点树必然大于2),连通的无圈图称为树,一棵树恰有两个1度的顶点而且其他顶点的度数为2,显然这样的树均是路。
16.对于(1)和(2)都可以用Kruskal算法。
具体用法是:对(1)有两种方法:<1>把Kruskal算法中的“小”字换为“大”字。
<2>重新规定图的权为:W’(e)=1/w(e) 当w(e)≠0M(充分大)当w(e)=0这样就可直接用Kruskal算法。
电子科大图论-第二次作业

图论及其应用第二次作业要求:1、交电子档给助教【助教给每个班设置邮箱,助教设置提交回复】;2、第7章授课结束前均可以提交;3、希望能够独立完成。
1.判断图4-43所示的四个图是否可以一笔画。
上面四个图都是连通图,看是否能一笔画成问题本质上看图是否存在欧拉迹;连通图有欧垃迹当且仅当G 最多有两个奇点。
(a )不可以 有4个奇点(b )可以 一个奇点(c )可以 两个奇点(d )可以 没有奇点2.(1)画一个有欧拉闭迹和哈密尔顿圈的图;(2)画一个有欧拉闭迹但没有哈密尔顿圈的图;(3) 画一个有哈密尔顿圈但没有欧拉闭迹的图;(4)画一个既没有欧拉闭迹也没有哈密尔顿圈的图。
3. 设n 阶无向简单图G 有m 条边。
证明:若m ≥⎪⎪⎭⎫ ⎝⎛-21n +2,则G 是哈密尔顿图。
(b) (c) (d ) 图4-43证明:G 是H 图。
若不然,因为G 是无向简单图,则n ≥3,由定理1:若G 是n ≥3的非单图,则G 度弱于C m,n 。
于是有:2,1()()(2)(1)(1)21111(1)(2)(1)(21) 1.222m n E G E C m n m n m m n n n m m m n m ⎡⎤≤=+---+-⎣⎦--⎛⎫⎛⎫=+-------≤+ ⎪ ⎪⎝⎭⎝⎭ 这与条件矛盾!所以G 是H 图。
4. 在图4-45中,哪些图是哈密尔顿图?哪些图中有哈密尔顿路?(a)非哈密尔顿图,没有哈密尔顿路(b)哈密尔顿图 (abcdejhfiga)(c)哈密尔顿图 (kjdhbagciefk)(d)非哈密尔顿图 有哈密尔顿路(hjaidebcgf)(e)不是哈密尔顿图,因为有割点a ,有哈密尔顿路(jaibcedkgfh )5. 证明:若G 没有奇点,则存在边不重的圈C 1, C 2,…, C m ,使得,E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。
证明:将G 中孤立点除去后的图记为G 1,则G 1也没有奇点,且δ(G 1),则G 1含圈C 1,在去掉()11G E C -的孤立点后,得图G 2,显然G 2仍无奇度点,且δ(G 2)≥ 2,从而G 2含圈C 1,如此重复下去,直到圈C m ,且G m -E (C m )全为孤立点为止,于是得到E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。
图论第二次作业 电子科技大学
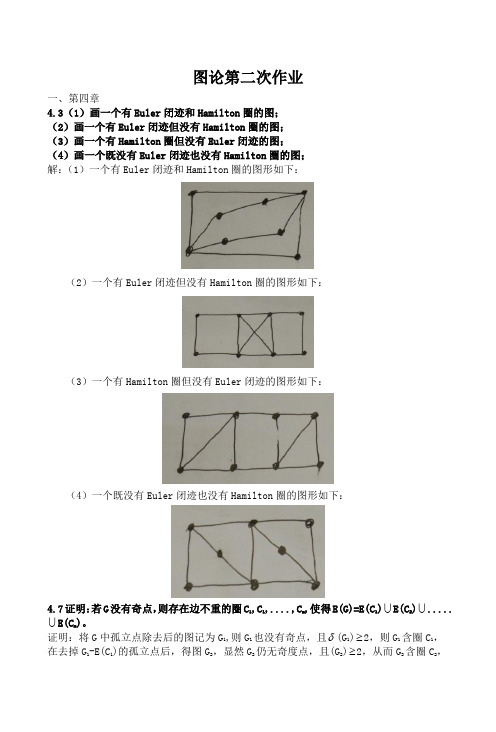
图论第二次作业一、第四章4.3(1)画一个有Euler 闭迹和Hamilton 圈的图; (2)画一个有Euler 闭迹但没有Hamilton 圈的图; (3)画一个有Hamilton 圈但没有Euler 闭迹的图; (4)画一个既没有Euler 闭迹也没有Hamilton 圈的图; 解:(1)一个有Euler 闭迹和Hamilton 圈的图形如下:(2)一个有Euler 闭迹但没有Hamilton 圈的图形如下:(3)一个有Hamilton 圈但没有Euler 闭迹的图形如下:(4)一个既没有Euler 闭迹也没有Hamilton 圈的图形如下:4.7证明:若G 没有奇点,则存在边不重的圈C 1,C 1,....,C m ,使得E(G)=E(C 1) E(C 2) ..... E(C m )。
证明:将G 中孤立点除去后的图记为G 1,则G 1也没有奇点,且δ(G 1)≥2,则G 1含圈C 1,在去掉G 1-E(C 1)的孤立点后,得图G 2,显然G 2仍无奇度点,且(G 2)≥2,从而G 2含圈C 2,如此重复下去,直到圈C m ,且G m -E(C m )全为孤立点为止,于是得到E(G) E(C 1) E(C 2) ... E(C m )。
4.10证明:若(1)G 不是二连通图,或者(2)G 是具有二分类(X,Y)的偶图,这里|X|≠|Y|, 则G 是非Hamilton 图。
证明:(1)因为G 不是二连通图,则G 不连通或者存在割点V ,有w(GV)2,由相关定理得:若G 是Hamilton 图,则对于V(G)的任意非空顶点集S ,有:w(GS)S ,则该定理得逆否命题也成立,所以可得:若G 不是二连通图,则G 是非Hamilton 图。
(2)因为G 是具有二分类(X,Y)的偶图,又因为|X|≠|Y|,在这里假设|X|≠|Y|,则有w(G-X)=Y>X ,也就是说:对于V(G)的非空顶点集S ,有:w(G-S)>S 成立,则可以得出G 是非Hamilton 图。
电子行业图论25电子科大杨春

电子行业图论25电子科大杨春引言电子行业是指以电子技术为核心的一类产业,包括电子元器件制造、电子设备制造、电子信息服务等。
其中,电子科大(University of Electronic Science and Technology of China,简称电子科大)是中国著名的电子工科高校之一。
本文将介绍电子行业图论,并聚焦于电子科大杨春教授的研究成果。
电子行业图论简介图论是数学中的一个分支,研究的是图的性质和图的应用。
在电子行业中,图论被广泛应用在网络通信、电路设计等方面。
图是由顶点(节点)和边(连接线)构成的数据结构。
顶点表示对象,边表示对象之间的关系。
在电子行业中,顶点可以表示电子元器件、电子设备、节点等,边可以表示电子元器件之间的连接关系、电子设备之间的通信路径,以及节点之间的数据传输等。
图论通过研究图的性质和算法,为电子行业提供了很多解决方案。
例如,在网络通信中,图论可以用于路由算法的设计,以在复杂网络中寻找最短路径或者负载均衡;在电路设计中,图论可以用于布线算法的优化,以提高电子装置的性能和可靠性。
电子科大杨春教授的研究成果杨春教授是电子科大的杰出学者,他在电子行业图论方面的研究取得了很多重要成果。
以下将介绍杨春教授的两个主要研究成果。
成果一:基于图论的网络通信优化算法杨春教授在网络通信方面的研究中,提出了一种基于图论的优化算法,用于解决复杂网络中的路由问题。
该算法通过构建网络拓扑图,并基于图的特性,设计出高效的路由方案,可以同时考虑网络的负载均衡和数据传输的可靠性。
杨教授的算法在实际网络中进行了验证,取得了较好的效果,优化了网络通信的性能。
成果二:图论在电路设计中的应用杨春教授的另一个研究方向是图论在电路设计中的应用。
他提出了一种基于图论的布线算法,用于解决大规模电路的布线问题。
该算法通过将电路抽象为图,利用图的性质和算法进行布线优化,可以降低电路的时延、功耗等指标。
杨教授的算法在实际电路中得到了验证,对提高电子设备的工作效率和可靠性有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2) 若 ek 不在 Ck 中,令 Gk-1=Gk-ek, Ck-1=Ck; 否则转 3);
பைடு நூலகம்
6
3) 设 ek=u0v0 ∈Ck, 令 Gk-1=Gk-ek; 求 Ck 中两个相邻点 u 与 v 使得 u0,v0,u,v 依序 排列在 Ck 上,且有:uu0,vv0 ∈E(Gk-1),令:
Ck1 Ck u0v0,uvuu0,vv0
电子科技大学-图论第二次 作业-杨春
-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
习题四:
3.(1)画一个有 Euler 闭迹和 Hamilton 圈的图; (2)画一个有 Euler 闭迹但没有 Hamilton 圈的图; (3)画一个有 Hamilton 圈但没有 Euler 闭迹的图;
1)(m
2)
(m
1)(n
2m
1)
n
1
2
1.
这与条件矛盾!所以 G 是 H 图。
8.证明:若 G 有
个奇点,则存在 条边不重的迹 .
,使得
证明:不失一般性,只就 G 是连通图进行证明。设 G=(n, m)是连通图。令 vl, v2,…,vk,vk+1,…,v2k 是 G 的所有奇度点。在 vi 与 vi+k 间连新边 ei 得图 G*(1≦i ≦k).则 G*是欧拉图,因此,由 Fleury 算法得欧拉环游 C.在 C 中删去 ei (1≦i ≦k).得 k 条边不重的迹 Qi (1≦i≦k):
4.设 n 阶无向简单图 G 有 m 条边,证明:若 证明: G 是 H 图。
,则 是
图。
若不然,因为 G 是无向简单图,则 ,由定理 1:若 G 是 的非单图,则
G 度弱于某个 .于是有:
2
E(G)
E(Cm,n )
1 2
m2
(n 2m)(n m 1) m(m 1)
n
1
2
1
1 2
(m
(C S) S
所以,有:(G S) (C S) S ,则必然有:
.
12. 设 G 是度序列为(d1,d2,…,dn)的非平凡单图,且 d1≦d2≦…≦dn。证明:若 G
不存在小于(n+1)/2 的正整数 m,使得:dm<m 且 dn-m+1<n-m,则 G 有 H 路。
证明:在 G 之外加上一个新点 v,把它和 G 的其余各点连接得图 G1
≦(n-1)-r < n-r, 这样与 u0,v0 在 Gk 中度和大于等于 n 矛盾!
上面结论表明:可以从 Ck+1 中去掉 由此,我们设计算法如下:
而得到新的 H 圈,实现 H 圈的边交换。
1)在闭包构造中,将加入的边依加入次序记为 ei (1≦i≦N),这里,N=n(n-1)/2-
m(G).在 GN 中任意取出一个 H 圈 CN,令 k=N;
G1 的度序列为: (d1+1,d2+1,…,dn+1, n) ,由条件:不存在小于(n+1)/2 的正整数 m,使得 dm+1≦m,且 dn-m+1+1<n-m+1=(n+1)-m。于是由度序列判定定理知:G1 是 H 图,得 G 有 H 路。
15. 写出下列问题的一个好算法: (1) 构作一个图的闭包; (2) 若某图的闭包是完全图,求该图的 H 圈。
图,则 是非 Hamilton 图
3
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则
有
,也就是说:对于
的非空顶点集 ,有:
成立,则可以得出则 是非 Hamilton 图。
11.证明:若 有 Hamilton 路,则对于 V 的每个真子集 S,有
.
证明:G 是 H 图,设 C 是 G 的 H 圈。则对 V(G)的任意非空子集 S, 容易知道:
10.证明:若:
E(G) E(Q1) E(Q2 )
E(Qk )
(1) 不是二连通图,或者
(2) 是具有二分类 的偶图,这里
,
则 是非 Hamilton 图。
证明:(1) 不是二连通图,则 不连通或者存在割点 ,有
,由于课
本上的相关定理:若 是 Hamilton 图,则对于
的任意非空顶点集 ,有:
,则该定理的逆否命题也成立,所以可以得出:若 不是二连通
3) 如果
dGk (u0 ) dGk (v0 ) n 则转 4);否则,停止,
此时得到 G 的闭包;
4) 令
,
,转 2).
复杂性分析:在第 k 次循环里,找到点 u0 与 v0,要做如下运算: (a) 找出所
有不邻接点对----需要 n(n-1)/2 次比较运算;(b) 计算不邻接点对度和----需要做
该方法是基于如下一个事实:
在闭包算法中,
, 与 在 中不邻接,且度和大于等于 n.
如果在 中有 H 圈 如下:
5
Ck1 (u0 , v0 , v1,..., vn2 , u0 )
我们有如下断言: 在Ck1上,vi , vi1, 使得u0vi , v0vi1 E(Gk )
若不然,设
那么在 Gk 中,至少有 r 个顶点与 v0 不邻接,则
(4)画一个即没有 Hamilton 圈也没有 Euler 闭迹的图; 解:找到的图如下: (1) 一个有 Euler 闭迹和 Hamilton 圈的图;
(2) 一个有 Euler 闭迹但没有 Hamilton 圈的图;
(3) 一个有 Hamilton 圈但没有 Euler 闭迹的图;
(4)一个即没有 Hamilton 圈也没有 Euler 闭迹的图.
4
解:(1) 构作一个图的闭包: 根据图的闭包定义,构作一个图的闭包,可以通过不断在度和大于等于 n 的非 邻接顶点对间添边得到。据此设计算法如下:
图的闭包算法: 1) 令 =G ,k=0; 2) 在 中求顶点 与 ,使得:
dGk (u0 ) dGk (v0 ) max dGk (u) dGk (v) uv E(Gk )
n(n-1)/2-m(G)次加法运算;(c ),选出度和最大的不邻接点对----需要 n(n-1)/2-m(G)
次比较运算。所以,总运算量为:
1 2
n(n
1)
2
1 2
n(n
1)
m(G
)
O(n
2
)
所以,上面的闭包算法是好算法。
(2) 若某图的闭包是完全图,求该图的 H 圈。
方法:采用边交换技术把闭包中的一个 H 圈逐步转化为 G 的一个 H 圈。
4) 若 k=1,转 5);否则,令 k=k-1,转 2); 5) 停止。C0 为 G 的 H 圈。 复杂性分析: 一共进行 N 次循环,每次循环运算量主要在 3),找满足要求的邻接顶点 u 与 v, 至多 n-3 次判断。所以总运算量:N(n-3),属于好算法。
