揭秘Σ-Δ ADC的工作原理
(σ-δ) adc工作原理

(σ-δ) adc工作原理
(σ-δ) ADC是一种模数转换器,全称为Sigma-Delta模数转换器。
它的工作原理是通过对输入信号进行高速取样,并利用高速数字信号处理技术,将模拟信号转换为数字信号。
Sigma-Delta ADC 的工作原理可以从以下几个方面来解释:
1. 模拟信号输入,首先,模拟信号被输入到Sigma-Delta ADC 的输入端。
这个模拟信号可以是来自传感器、放大器、滤波器等外部电路的输出信号。
2. 量化和采样,Sigma-Delta ADC对输入信号进行高速取样和量化。
它以高速的采样率对输入信号进行采样,并将采样值转换为数字形式。
3. Sigma-Delta调制,接下来,ADC使用Sigma-Delta调制技术,将采样到的模拟信号转换为高速的1比特数据流。
这个过程涉及将模拟信号与一个高频时钟信号进行比较,生成一个1比特的数据流。
4. 数字滤波,接着,ADC使用数字滤波器对1比特数据流进行
处理,以减小高频噪声和提高信噪比。
这个数字滤波器通常是一个低通滤波器,用于去除高频噪声,并将1比特数据流转换为更高精度的数字输出。
5. 数字输出,最后,经过数字滤波器处理后的数据被输出为高精度的数字信号,代表了原始模拟信号的数值。
这个数字输出可以被用于后续的数字信号处理、存储或传输。
总的来说,Sigma-Delta ADC通过高速取样、Sigma-Delta调制和数字滤波等技术,实现了对模拟信号的高精度数字化转换。
它在音频处理、传感器接口、通信系统等领域有着广泛的应用。
sigmadeltaadc的工作原理

sigmadeltaadc的工作原理Sigma-Delta ADC,全称为Sigma-Delta Analog-to-Digital Converter,是一种高精度的模数转换器。
它的工作原理基于Sigma-Delta调制技术,通过对输入信号进行高速采样和数字化处理,实现对模拟信号的准确量化和转换。
Sigma-Delta ADC的核心部件是一个差分运算放大器和一个数字滤波器。
首先,输入信号经过差分运算放大器进行放大,并与一个参考电压进行比较。
差分运算放大器会将输入信号转换为差分信号,并将其与参考电压进行比较,产生一个差分输出信号。
这个差分输出信号包含了输入信号与参考电压之间的差异。
接下来,差分输出信号经过一个积分器,将其进行积分运算。
积分器的作用是将输入信号中的高频成分滤除,只保留低频成分。
积分后的信号再经过一个比较器,将其与一个数字信号进行比较。
比较器会产生一个数字输出信号,表示差分输出信号与数字信号之间的差异。
然后,数字输出信号通过一个反馈回路送回到差分运算放大器的输入端,起到调节放大器增益的作用。
通过不断调节放大器增益,使得差分输出信号与数字信号之间的差异尽可能小。
这个反馈回路的作用类似于一个控制系统,通过自动调节放大器增益,使系统的稳定性和精度得到保证。
Sigma-Delta ADC的工作原理可以用一个简单的例子来说明。
假设我们要将一个模拟信号转换为一个8位的数字信号。
首先,输入信号经过差分运算放大器进行放大,并与一个参考电压进行比较。
差分运算放大器会将输入信号转换为差分信号,并将其与参考电压进行比较,产生一个差分输出信号。
如果差分输出信号大于参考电压,则比较器输出1;如果差分输出信号小于参考电压,则比较器输出0。
接下来,差分输出信号经过积分器进行积分运算。
积分器会将差分输出信号进行积分,得到一个积分后的信号。
然后,积分后的信号再经过比较器进行比较,产生一个数字输出信号。
如果积分后的信号大于数字信号,则比较器输出1;如果积分后的信号小于数字信号,则比较器输出0。
Sigma-DeltaADC讲稿

反馈系数用于控制比较器的输出电压的大小和 方向,从而控制模拟信号的调整程度。
噪声整形技术
噪声整形技术是sigma-delta ADC的关键技术之一,它通过将噪声从高频区域转移至低 频区域,从而提高ADC的信噪比和线性度。
Part
05
sigma-delta ADC的挑战与 未来发展
面临的挑战
噪声抑制
sigma-delta ADC在转换过程中 容易受到噪声干扰,如何有效抑 制噪声是亟待解决的问题。
动态范围
随着技术的发展,对sigma-delta ADC的动态范围要求也越来越高, 如何提高动态范围是当前面临的 重要挑战。
动态范围与信噪比
动态范围
动态范围是指ADC能够处理的信号的最大值与最小值之间的比值。动态范围越大,ADC能够处理的信号范围越宽。
信噪比
信噪比是指信号功率与噪声功率之间的比值。信噪比越高,ADC的抗干扰能力越强,输出的数字信号质量越好。
采样率与带宽
采样率
采样率是指ADC每秒钟采样的次数 。采样率越高,ADC能够捕捉到的 信号细节越多,但同时也会增加电路 复杂度和功耗。
它通常由比较器和计数器组成,比较器将模拟信 号与参考电压进行比较,产生一个二进制码,然 后计数器根据二进制码的长度进行计数,得到数 字输出。
量化器的非线性误差会影响ADC的线性度,因此 需要采取措施减小非线性误差。
数字滤波器
1
数字滤波器用于对sigma-delta ADC的输出进行 滤波,以减小噪声和消除量化误差。
功耗与性能平衡
在便携式设备中,功耗是一个关 键因素,如何在保证性能的同时 降低功耗是一个具有挑战性的问 题。
Σ-Δ模数转换器基本原理及应用
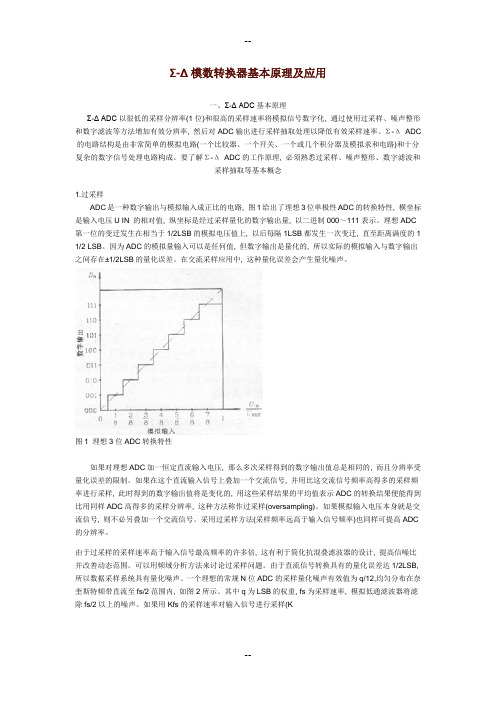
Σ-Δ模数转换器基本原理及应用一、Σ-Δ ADC基本原理Σ-Δ ADC以很低的采样分辨率(1位)和很高的采样速率将模拟信号数字化, 通过使用过采样、噪声整形和数字滤波等方法增加有效分辨率, 然后对ADC输出进行采样抽取处理以降低有效采样速率。
Σ-ΔADC 的电路结构是由非常简单的模拟电路(一个比较器、一个开关、一个或几个积分器及模拟求和电路)和十分复杂的数字信号处理电路构成。
要了解Σ-ΔADC的工作原理, 必须熟悉过采样、噪声整形、数字滤波和采样抽取等基本概念1.过采样ADC是一种数字输出与模拟输入成正比的电路, 图1给出了理想3位单极性ADC的转换特性, 横坐标是输入电压U IN 的相对值, 纵坐标是经过采样量化的数字输出量, 以二进制000~111表示。
理想ADC 第一位的变迁发生在相当于1/2LSB的模拟电压值上, 以后每隔1LSB都发生一次变迁, 直至距离满度的1 1/2 LSB。
因为ADC的模拟量输入可以是任何值, 但数字输出是量化的, 所以实际的模拟输入与数字输出之间存在±1/2LSB的量化误差。
在交流采样应用中, 这种量化误差会产生量化噪声。
图1 理想3位ADC转换特性如果对理想ADC加一恒定直流输入电压, 那么多次采样得到的数字输出值总是相同的, 而且分辨率受量化误差的限制。
如果在这个直流输入信号上叠加一个交流信号, 并用比这交流信号频率高得多的采样频率进行采样, 此时得到的数字输出值将是变化的, 用这些采样结果的平均值表示ADC的转换结果便能得到比用同样ADC高得多的采样分辨率, 这种方法称作过采样(oversampling)。
如果模拟输入电压本身就是交流信号, 则不必另叠加一个交流信号。
采用过采样方法(采样频率远高于输入信号频率)也同样可提高ADC 的分辨率。
由于过采样的采样速率高于输入信号最高频率的许多倍, 这有利于简化抗混叠滤波器的设计, 提高信噪比并改善动态范围。
sigmadeltaadc原理

sigmadeltaadc原理
Σ-Δ模数转换是一种典型的数模转换技术,它利用非线性微分模拟器(Differentiator)把模拟信号转变为进行离散采样的差分脉冲。
Σ-Δ转换技术
有很高的灵敏度,但同时也有一定的复杂性,因为需要大量的计算和设备限制。
Σ-Δ模数转换器中,Σ表示累加器(Accumulator),Δ表示微分器(Differentiator)。
它通常有两个部分,累加(Accumulation)和微分(Differentiation),一般采用了高速積分和微分技术(Sigma-Delta Topology),来完成模拟脉冲的转换。
其中累加(Accumulation)实现的是采样技术,原来的模拟信号在特定的时刻取得一个采样值;累加(Accumulation)把这些采样值累加到心跳的末端;微分(Differentiation)实现的是离散化技术,它使用如
此精密的采样技术,以在心跳的末端释放不同大小的脉冲,从而离散化地表示原始模拟信号。
Σ-Δ模数转换器使得可以使用很少的采样来代表原始模拟信号,但其本质原理却是可以植根于模拟信号的数字信息量的增加,即出现精度的提高。
Σ-Δmodulators的发展为模拟-数字转换技术提供了可靠的仪表精度以及脉冲
转换的灵活性。
英飞凌 dsadc原理

英飞凌 dsadc原理
英飞凌的DSADC(Δ-Σ ADC)模块的工作原理可以概括如下:
首先,差分正弦信号进入DSADC模块后,会经过一个运算放大器,将差分信号做差并放大两倍。
然后,MASH1-1-1调制器将其调制为数字信号,再通过滤波器链进行滤波。
滤波器链中的CIC的降采样率为16,级联阶数为3;两级FIR滤波器的参数固定和降采样率为2。
整流器根据激励信号的相位对返回信号进行翻转,便于信号进行积分;积分后的正/余弦值就是软件算法的输入。
这个值并不在[-1,1]范围内,而是倍乘了一个系数,该系数与激励信号幅值、旋变变比、运放增益、滤波器阶数等都有直接关联。
此外,滤波器链路构建了解调器,该解调器以可配置的输出速率生成结果值。
滤波器链路的元件可以根据应用的要求被激活。
滤波器链路的配置决定了滤波器的衰减和延迟特性,以可配置速率对原始数据样本进行抽取,可以将调制器的输入采样率降低到适合应用的较低结果数据率。
以上内容仅供参考,如需更多信息,建议访问英飞凌官网或咨询相关技术人员。
sigma delta adc原理和及其步进、输入热噪声计算
sigma delta adc原理和及其步进、输入热噪声计算
Sigma Delta ADC(Sigma-Delta Analog-to-Digital Converter)是一种基于高速计数的ADC,其原理是将模拟信号与一个高频时钟进行比较,并将比较结果转换为数字码。
它通过过采样和数据滤波技术,能够在高速采样下实现较高的分辨率和较低的失真。
Sigma Delta ADC的步进过程是通过不断比较模拟输入信号与DAC输出的数字错误值,来调整DAC输出值的大小,使得这个数字错误值的平均值趋近于0。
在一定时间内,ADC通过调整DAC输出的平均值来抵消模拟输入信号的误差,从而实现较高的分辨率。
输入热噪声是指ADC输入端由于温度和杂散电源的影响而产生的噪声。
通常使用热噪声功率谱密度来描述输入热噪声的大小,单位为V/√Hz。
对于Sigma Delta ADC,输入热噪声可以通过计算输入热噪声功率谱密度来获得。
计算输入热噪声功率谱密度的公式如下:
Noise Power = 4 * k * T * R * Δf
其中,k是玻尔兹曼常数 (1.38 * 10^-23 J/K),T是绝对温度(K),R是输入电阻(Ω),Δf是测量带宽 (Hz)。
需要注意的是,Sigma Delta ADC的输入热噪声还受到系统传递函数和滤波器的影响,因此实际的热噪声功率谱密度可能会有所不同。
此外,输入热噪声还与ADC本身的电路设计和增
益等因素有关。
因此,在具体应用中,需要综合考虑以上各个因素来计算和评估Sigma Delta ADC的输入热噪声。
sigma-delta adc的量化过程
sigma-delta adc的量化过程Sigma-Delta ADC(Σ-Δ ADC)是一种常用的模数转换器,它通过采用过采样和噪声整形技术,实现了高精度的模拟信号数字化转换。
本文将介绍Sigma-Delta ADC的量化过程,以及其原理和应用。
让我们了解一下Σ-Δ ADC的基本原理。
Σ-Δ ADC可以看作是一个模拟滤波器和一个数字滤波器的级联,其中模拟滤波器用于滤除高频噪声,数字滤波器用于恢复被过采样信号中的模拟信号。
Σ-Δ ADC的核心思想是在过采样的基础上通过噪声整形技术将噪声推到高频区域,从而提高了系统的动态范围和分辨率。
在Σ-Δ ADC的量化过程中,首先将模拟信号通过一个比特数较高的模数转换器进行采样。
然后,通过一个积分器对模拟信号进行积分,并将积分结果与一个参考电平进行比较。
根据比较结果,Σ-Δ ADC会输出一个1或0的比特,表示模拟信号是否超过了参考电平。
为了更好地理解Σ-Δ ADC的量化过程,可以以一个简单的二进制Σ-Δ ADC为例进行说明。
假设该ADC的比特数为N,那么它将输出一个N位的二进制数。
在量化过程中,如果积分结果大于参考电平,则输出1,否则输出0。
通过这种方式,Σ-Δ ADC可以实现高精度的模拟信号转换。
在实际应用中,Σ-Δ ADC常常用于对低频信号的高精度采样,比如音频和传感器信号采集。
由于Σ-Δ ADC具有较高的动态范围和分辨率,能够抑制高频噪声和共模噪声,因此在音频处理和测量仪器等领域得到了广泛的应用。
除了以上的基本原理和应用外,Σ-Δ ADC还有一些进一步的发展和应用。
例如,Σ-Δ ADC可以通过多级嵌套的方式,实现更高的分辨率和更宽的动态范围。
此外,Σ-Δ ADC还可以结合数字滤波器,实现对不同频率的信号的处理和采样。
总结起来,Σ-Δ ADC是一种基于过采样和噪声整形技术的高精度模数转换器。
它的量化过程通过积分和比较实现,并通过输出二进制数来表示模拟信号的大小。
使用SigmaDeltaADC时容易被忽略的问题
使用SigmaDeltaADC时容易被忽略的问题最近见到不少帖子说,SigmaDelta型ADC不稳定。
其实大多数不是ADC的问题。
而是没有深刻理解SigmaDelta型ADC的原理和内部结构。
∑-△型ADC是一类利用过采样原理来扩展分辨率的模数转换器件,从原理上看,∑-△型ADC利用非常低分辨率的ADC(一般1bit)的ADC通过高速过采样,得到码流后量化得到数字量。
因为1bit ADC 就是一个比较器,1bitDAC也可以用模拟开关来实现;加之滤波和量化工作也是全数字实现的,所以∑-△型ADC更像是数字器件而不是模拟器件。
这最大可能的避免了模拟电路的漂移、批次性问题。
因此∑-△型ADC可以很容易达到高精度和高分辨率。
下面看图4.2:一个带锁存的比较器作为1bitADC,其输出码流分2路,一路给数字滤波和量化用,另一路反馈到减法器。
积分器的作用就是对减法器后的输入信号求平均。
关于∑-△调制和过采样的原理,很多教科书都是搬弄一大堆的公式和定理,证明码流平均值正比输入电压就了事。
没有让读者真正理解,害了不少人。
我觉得,从大家都熟悉的运放负反馈虚短路的知识,很容易理解∑-△调制的原理。
图4.2的整个环路构成典型的负反馈,那么由反馈理论可知,只要比较器(相当于运放)的开环增益足够大,A点会非常接近0V(虚地),即DAC的码流平均值(积分器就是求平均)一定会非常接近输入信号Vin/Vref的值。
数字滤波和量化器功能就是一低通滤波器,就是将码流的平均值(低频量)取出作为ADC转换结果。
上面分析了∑-△型ADC的基本原理。
在实际的∑-△型ADC芯片中,都采用开关电容电路来实现输入、减法器、积分器、基准切换功能。
这样便于纯数字方法实现。
很多∑-△型ADC内置可编程增益放大器(PGA),非常方便与电桥、热电偶等微弱信号传感器连接。
PGA 的实现其实也是靠改变开关电容采样、积分与读出的速度比来实现的,仍然是纯数字电路实现,不存在运算放大器的漂移、失调、上下轨等问题。
(完整版)SigmaDeltaADC原理简单理解
(完整版)SigmaDeltaADC原理简单理解∑?模数转换器概述过采样∑?ADC 的基本结构包括抗混迭滤波器、调制器及降采样低通滤波器,如图3.1所⽰。
抗混迭滤波器将输⼊信号限制在⼀定的带宽之内,对于过采样ADC ,由于输⼊信号带宽0f 远⼩于采样频率sf 的⼀半,抗混迭滤波的通带到阻带之间的过渡带(2s f f -)较宽,缓解了其设计要求,可⽤低阶模拟滤波器实现。
调制器将过采样信号转化为⾼速、低精度的数字信号。
然后降采样滤波器将其转变为Nyquist 频率的⾼精度信号。
调制器可以抑制过采样率ADC 电路引⼊的噪声,⾮线性等误差,这样缓解了它对模拟电路的精度要求。
另外,对于开关电容电路实现的过采样ADC ,⽆需采⽤采样保持电路。
图3.1 ∑?过采样ADC 的结构图本章⾸先介绍了∑?ADC 的⼀些主要性能指标、调制器的⼯作原理、基本结构,然后介绍了调制器的⾮理想因素与误差来源,最后介绍了未深⼊研究的问题与宽带∑?ADC 研究现状。
3.1 ∑?ADC 的⼀些主要性能指标∑?ADC 的主要性能指标为:动态范围(DR)、信噪⽐(SNR)、信噪失真⽐(SNDR)、有效位数(ENOB)以及过载度(OL)。
如图3.2所⽰,图中横轴为输⼊信号的归⼀化值,即/in refV V ,纵轴为SNR 或SNDR ,⼆者均⽤dB 表⽰。
从图3.2中可以看出,当输⼊信号幅度较⼩时,SNR 和SNDR ⼤⼩是相等的;随着输⼊幅度的增加,失真将会降低调制器的性能,因⽽在输⼊幅度较⼤时,SNDR 会⽐SNR ⼩⼀些。
图3.2显⽰了⾮理想调制器的性能⽐理想调制器的性能差⼀些:⼀⽅⾯是由于实际调制器的有限增益引起性能成呈线性下降;另⼀⽅⾯是由于实际调制器过载⽽造成的性能下降。
图3.2 典型的∑?转换器的性能图调制器各相主要性能指标[60]介绍如下:1.信噪⽐(SNR):是指在⼀定的输⼊幅度时,转换器输出信号能量与噪声能量的⽐值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
揭秘Σ-Δ ADC 的工作原理
节选自Maxim 应用笔记AN1870
石忠东 整理
摘要:本文深入介绍了Σ-Δ模拟数字转换器(ADC )的理论背景,特别强调了过采样,噪声整形,滤波和抽取等几个难于理解的有关数字信号的关键概念。
越来越多的应用,诸如过程控制、称重等,都需要高分辨率、高集成度和价格低廉的ADC 。
新型Σ-Δ转换技术恰好可以满足上述需求。
然而,很多设计者并不十分了解这种AD 转换技术,因而更愿意选用传统的逐次比较(SAR )型ADC 。
Σ-Δ转换器的模拟部分非常简单(类似于一个1位ADC ),而数字部分要复杂得多,按照功能可划分为数字滤波和抽取单元。
由于Σ-Δ型ADC 更接近于数字器件,因而其制造成本非常低廉。
Σ-Δ ADC 的工作原理
要理解Σ-Δ型ADC 的工作原理,首先应对以下概念有所了解:过采样、噪声成形、数字滤波和抽取。
1. 过采样
首先,考虑一个传统ADC 的频域传输特性。
输入一个正弦信号,然后以频率S f 采样,按照Nyquist 定理,采样频率至少两倍于输入信号。
从FFT 分析结果可以看到,单音和一系列频率分布于DC 到S 2f 间的随机噪声,如图1所示,这就是所谓的量化噪声,主要是由于有限的ADC 分辨率而造成的。
图1. N 位 ADC 以频率f s 采样单音信号的频谱分析
单音(基频)信号的功率与所有频率的噪声的RMS 功率之和的比值就是信号噪声比(SNR )。
对于一个N 位 ADC ,SNR 可由公式:SNR=6.02N+1.76dB 得到。
为了改善SNR 和更为精确地再现输入信号,对于传统ADC 来讲,必须增加。
如果将采样频率提高一个过采样系数k ,即采样频率为S kf ,再来讨论同样的问题,如图2所示,FFT 分析显示噪声基线降低了,SNR 值虽未改变,但噪声能量却分散到更宽的频率范围。
Σ-Δ
信号幅值
N 位ADC 的信噪比 SNR = 6.02N + 1.76dB
量化噪声
本底噪声平均值(基线)
功率
频域
转换器正是利用了这一原理,具体方法就是在1位 ADC 之后进行数字滤波。
如图3所示,由于大部分噪声位于数字滤波器带宽之外而被滤除,这样,RMS 噪声就降低了,使得Σ-Δ转换器能够从一个低分辨率ADC 获得宽动态范围。
图2. N 位ADC 以频率k f s 采样单音信号的频谱分析
图3. 数字滤波器对噪声频谱的滤除效应
那么,简单的过采样和滤波能否改善SNR 呢?一个1位 ADC 的SNR 为7.78dB (6.02+1.76),每4倍过采样可以使SNR 增加6dB ,SNR 每增加6dB 等效于分辨率增加1-bit 。
这样,采用1位 ADC 进行64倍(即34倍)过采样可以获得4位分辨率,而要获得16位分辨率就必须进行154倍过采样,这是不切实际的。
Σ-Δ转换器采用噪声成形技术消除了这种局限,使得每4倍过采样可增加高于6dB 的SNR 。
2.噪声成形
通过图4所示的一阶Σ-Δ调制器的工作原理,可以理解噪声成形的工作机制。
Σ-Δ调制器包含1个差分放大器、1个积分器、1个比较器以及1个由1位 D/A (1个简单的开关,可以将差分放大器的反相输入接到正或负参考电压)构成的反馈环。
反馈DAC 的作用是使积分器的平均输出电压接近于比较器的参考电平。
功率
K 倍过采样
K 倍过采样
本底噪声平均值
数字滤波器
数字滤波器频响
K 倍过采样
被滤波器滤除的噪声
功率
图4. Σ-Δ调制器框图
调制器输出中“1”的密度正比于输入信号,如果输入电压上升,比较器将产生更多数量的"1",反之亦然。
积分器用来对误差电压求和,对于输入信号表现为低通滤波器,而对于量化噪声则表现为高通滤波。
这样,大部分被推向更高的频段,如图5所示。
与前面的简单过采样相比,总的噪声功率虽未改变,但噪声的分布发生了变化。
图5. Σ-Δ调制器中积分器的作用
如果对噪声整形后的Σ-Δ调制器输出进行数字滤波,将有可能移走比简单过采样中更多的噪声,如图6所示。
这种调制器(一阶)在每两倍的过采样率下可提供9dB 的SNR 改善。
在Σ-Δ调制器中采用更多的积分与求和环节,可以提供更高阶数的量化噪声成形。
例如,如图7中所示,一个二阶Σ-Δ调制器在每两倍的过采样率下可改善SNR 15dB 。
图8显示了Σ-Δ调制器的阶数、过采样率和能够获得的SNR 三者之间的关系。
信号输入
差分 放大器
积分器
1位D/A
比较器 (1位A/D)
去数字 滤波器
功率
信号幅值
积分器对噪声 进行高通滤波 完成噪声成形
噪声成形频谱
图6. 数字滤波器对整形后噪声的滤除效果
图7. 采用多级积分与求和获取更高阶数的量化噪声
图8 信噪比(SNR )与Σ-Δ调制器阶数和过采样率的关系
对整形后的噪声进行滤波
数字 滤波器
信号幅值 数字滤波器 滤除高频噪声
二阶 一阶
二阶环路 15dB 每倍频程 一阶环路 9dB 每倍频程
功率
数字滤波器频响
信噪比(d B )
三阶环路 21dB 每倍频程
过采样率,K
3. 数字滤波和抽取
Σ-Δ调制器以采样速率输出1位数据流,频率可高达MHz 量级。
数字滤波和抽取的目的是从该数据流中提取出有用的信息,并将数据速率降低到可用的水平。
Σ-Δ ADC 中的数字滤波器对1位数据流求平均,滤除目标带宽以外的量化噪声,并改善ADC 的分辨率。
数字滤波器决定了信号带宽、建立时间和阻带抑制。
图9. Σ-Δ ADC 的数字部分框图
Σ-Δ转换器中广泛采用的滤波器拓扑是Sinc 3,一种具有的低通特性的滤波器。
如图10中所示,这种滤波器的一个主要优点是具有陷波特性,可以将陷波点设在和电力线相同的频率,抑制其干扰。
陷波点与输出数据速率(转换时间的倒数)直接相关。
Sinc 3滤波器的建立时间三倍于转换时间。
当陷波点设在60Hz 时(60Hz 数据速率),建立时间为3/60Hz ,即50ms 。
有些应用要求更快的建立时间,而对分辨率的要求较低。
对于这些应用,可以考虑允许用户自行选择Sinc 1或Sinc 3滤波器类型的MAX1400系列Σ-Δ ADC 。
图10. 具有低通特性的Sinc 3
滤波器
Sinc 1滤波器的建立时间只有一个数据周期,对于前面的举例则为1/60Hz ,即16.7ms 。
由于带宽被输出数字滤波器降低,输出数据速率可低于原始采样速率,但仍满足奈奎斯特(Nyquist )定律。
这可以通过在频域保留某些采样而丢弃其余采样来实现,这个过程就是所谓的按M 因子“抽取”。
M 因子为抽取比例,可以是任何整数值。
在选择抽取因子时应该使输出数据速率高于两倍的信号带宽,如图11所示。
这样,如果以频率f s 对输入信号进行采样,滤波后的输出数据速率可降低至f s /M ,而不会丢失任何信息。
1位 数据流
Sinc 3数字低通滤波器
多位 数据
数据 输出
模拟 输入
Σ-Δ 调制器
数字低通 滤波器
抽取 滤波器
衰减比(d B )
频率(Hz )
信号
图11. 抽取不会丢失任何信息
后记:
本文整理节选自Maxim公司的APPLICATION NOTE 1870:Demystifying Sigma-Delta ADCs “/app-notes/index.mvp/id/1870”的前半部分,主要中文文字节选于徐继红编译的《揭开Σ-ΔADC的神秘面纱》的前半部分。
整理此文的初衷是为了便于个人理解Σ-Δ型ADC以及Sinc3数字滤波中抽取比例M因子的取值原则。
附录:
(a) Sinc1(b) Sinc3
附图1. TI公司MSC1210 Σ-ΔADC手册中给出的
Sinc1和Sinc3数字滤波器的频率特性曲线和截止频率
(a) 固定数据输出频率时ENOB与抽取率的关系(b)固定抽取率时ENOB与数据输出频率的关系
附图2. TI公司MSC1210 Σ-ΔADC有效位数(ENOB)与不同的抽取率和数据输出频率之间的关系
(a) Sinc1(b) Sinc3
附图3. CIRRUS LOGIC公司CS553x系列Σ-ΔADC应用文档AN311中给出的
Sinc1和Sinc3数字滤波器的频率特性曲线和倍频程即十倍频程衰减比
附图4. CIRRUS LOGIC公司CS553x系列Σ-ΔADC应用文档AN311中给出的
1~5阶Sinc x数字滤波器的频率特性和倍频程及十倍频程衰减比的对照曲线和数据。
