2011年中考数学创新思维训练(三)
全国各省市2011中考数学真题分类汇编—猜想、规律与探索(附答案)

2011全国各省市中考数学真题分类汇编—猜想、规律与探索(附答案)一、选择题1.(2011赤峰市中考)8.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),……,则第n 个图形的周长是( )(A )2n(B )4n(C )12n + (D )22n +2.(2011山东烟台市中考)8、如图,一串有趣的图案按一定的规律排列,请仔细观察,按此规律第2010个图案是( )3.(2011舟山市中考)9.一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( ▲ ) (A )2010 (B )2011(C )2012(D )20134.(2011湖北武汉市中考) 9.在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x 轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…则边图1图2图3……(第3题)… …红 黄 绿 蓝 紫 红 黄 绿 黄 绿 蓝 紫长为8的正方形内部的整点的个数为( ) A.64. B.49. C.36. D.25.5.(2011潜江市 天门市 仙桃市中考)9.如图,已知直线l :y=33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 4的坐标为( )A .(0,64)B .(0,128)C .(0,256) D .(0,512)6.(2011江苏常州市中考)7.在平面直角坐标系中,正方形ABCD 的顶点分别为A ()1,1、B ()1,1-、C ()1,1--、D ()1,1-,y 轴上有一点P ()2,0。
中考数学创新思维训练题

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载中考数学创新思维训练题地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容2011年中考数学创新思维训练(1)一、细心填一填(本大题共有12小题,15空,每空2分,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)1、-2的倒数是_________, ________.2、9的平方根是__________,-8是_______的立方根.3、用四舍五入所得的数是-2.164,它精确到位.4、计算:cos45= ,tan30= .5、函数y=中,自变量x的取值范围是__________;函数y=中,自变量x的取值范围是_________.6、在实数内分解因式:x4-2x2= .7、一个多边形的每个外角都等于30,这个多边形的内角和为_________度.8、下面一组数据表示初三(1)班23位同学衣服上衣口袋的数目,若任选一位同学,则其上衣口袋的数目为5的概率为 .3,4,2,6,5,5,3,1,4,2,4,2,4,5,10,6,1,5,5,62,10,39、一个矩形的周长为60㎝,其面积为S,则S的取值不超过㎝2.10、⊙O的直径CD与弦AB交于点M,添加条件(写出一个即可)就可得到M是AB的中点.11、如下图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要枚棋子.12、如图所示是由7个完全相同的正方形拼成的图形,请你用一条直线将它分成面积相等的两部分.(在原图上作出).二、精心选一选(本大题共8小题,每题3分,共24分. 在每题所给出的四个选项中,只有一项是符合题意的. 把所选项前的字母代号填在题后的括号内. 相信你一定会选对!)13、已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是()A、0B、1C、2D、-214、下列各式中,与是同类二次根式的是()A、 B、 C、 D、15、如图所示,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再把剩余的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式是()A、B、C、D、16、在直角坐标系中,⊙O的圆心在圆点,半径为3,⊙A的圆心A的坐标为(-,1),半径为1,那么⊙O与⊙A的位置关系为()A、外离B、外切C、内切D、相交17、有十五位同学参加智力竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛()A、平均数B、众数C、最高分数D、中位数18、在“抛一枚均匀硬币”的实验中,如果现在没有硬币,则下面各个试验中哪个不能代替()A、两张扑克,“黑桃” 代替“正面”,“红桃” 代替“反面”B、两个形状大小完全相同,但一红一白的两个乒乓球C、扔一枚图钉D、人数均等的男生、女生,以抽签的方式随机抽取一人19、相信同学们都玩过万花筒,右图是某个万花筒的造型,图中的小三角形均是全等的等边三角形,那么图中的菱形AEFG可以看成是把菱形ABCD以A 为旋转中心()A、顺时针旋转60°得到B、顺时针旋转120°得到C、逆时针旋转60°得到D、逆时针旋转120°得到20、将一张正方形的纸片按下图所示的方式三次折叠,折叠后再按图所示沿MN裁剪,则可得()A、多个等腰直角三角形B、一个等腰直角三角形和一个正方形C、四个相同的正方形D、两个相同的正方形三、认真答一答(本大题共7小题,满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!)21、(本题共有3小题,每小题5分,共15分)(1)计算:(2)已知不等式5(x-2)+8<6(x-1)+7的最小整数解是方程2x-ax=4的解,求a的值.(3)先化简,再求值:,其中x=2.22、(本题满分6分)方格纸中每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.(1)在10×10的方格中(每个小方格的边长为1个单位),画一个面积为1的格点钝角三角形ABC,并标明相应字母.(2)再在方格中画一个格点△DEF,使得△DEF∽△ABC,且相似比为,并加以证明.如图,给出五个条件:①AE平分∠BAD,②BE平分∠ABC,③E是CD的中点,④AE⊥EB,⑤AB=AD+BC(1)请你以其中三个作为命题的条件,写出一个能推出AD∥BC的正确命题,并加以说明;(2)请你以其中三个作为命题的条件,写出一个不一定能推出AD∥BC的正确命题,并举例说明.24、(本题满分6分)夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)2,5,0,5,2,5,6,5,0,5,5,52,5,8,0,5,5,2,5,5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;(2)求出同学的零用钱的平均数、中位数和众数;(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?25、(本题满分8分)某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校. 若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得. 现在学校有30个班级,平均每班50人.(1)作为一名学生,你恰好能得到荣誉的机会有多大?(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?(4)你可以用哪些方法来模拟实验?某市的一家报刊摊点从报社买进一种晚报,其价格为每份0.30元,卖出的价格为0.50元,卖不掉的报纸可以退还给报社,不过每份退还的钱数与退还的报纸的数量关系如下:现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定每天批发给摊点的报纸的数量必须相同.(1)通过在坐标系中(以退还的钱数为纵坐标,退还的报纸数量为横坐标)描出点,分析出退还的钱数y(元)与退还的报纸数量k(份)之间的函数关系式.(2)若该家报刊摊点每天从报社买进的报纸数x份(满足100<x<150),则当买进多少报纸时,毛利润最大?最多可赚多少钱?27、(本题满分8分)在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.小明说:我的设计方案如图(1),其中花园四周小路的宽度相等. 通过解方程,我得到小路的宽为2m或12m.小颖说:我的设计方案如图(2),其中花园中每个角上的扇形相同.(1)你认为小明的结果对吗?请说明理由.(2)请你帮助小颖求出图中的x(精确到0.1m).(3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.四、动脑想一想(本大题共有2小题,共18分. 开动你的脑筋,只要你勇于探索,大胆实践,你一定会获得成功的!)28、(本题满分8分)如图,在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点,(可以与A、B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D.(1)记BP的长为x,△BPM的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;(2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x 的值;若不存在,请说明理由.29、(本题满分10分)如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是ABC的中点,弦DE⊥AB,垂足为F,DE交AC于点G.(1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程)(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由.(3)在满足第(2)问的条件下,已知AF=3,FB=,求AG与GM的比.〖第(1)的结论可直接利用〗1、参考答案一、细心填一填1. ﹣,﹣82. ±3 ,﹣1253. 千分位4. ,5.x≠1 ,x≥3 6 . x(x+)(x-) 7. 1800 8. 9. 225 10. CD⊥AB 11. 179 12. 略二、精心选一选13. C 14. B 15. A 16. C 17. D 18. C 19. D 20. C三、认真答一答21. (1)3;(2)a=4 ;(3) 2x-1 ,3 22. 略23.(1)①②⑤AD∥BC .证明:在AB上取点M,使AM=AD,连结EM,可证△AEM≌△AED,△BEM≌△BCE,∴∠D=∠AME, ∠C=∠BME,故∠D+∠C=∠AME+∠BME=180°∴AD∥BC.(2)①②③ AD∥BC为假命题反例:△ABM中,E是内心,过E作DC⊥EM,显然有,AE平分∠BAM,BE平分∠ABM,ED=EC,但AD不平分于BC.24.(1)0元的频数是5,2元的频数是7,5元的频数是21,6元的频数是5,8元的频数是2.(2)平均数是4.125,中位数是5,众数是5.(3)5元.25.(1);(2),;(3)班级人数、三好生数、模范生数、成绩提高奖人数;(4)用50个小球,其中3个红球、4个白球、5个黑球,其余均位黄球,把它们装进不透明的口袋中搅均,闭着眼从中摸出一个球,则摸到非黄球的机会就是得到荣誉的机会,摸到红球或白球的机会就是当选为三好生和模范生的机会.26.(1)通过作图,知y=mk+n,当0<k<30,且为整数, y=﹣0.1k+0.3;当k≥30 , y=0.02.(2)S=2×0.2x+100×10×0.2-(0.3-y)(x-100)= 4x+200-0.1(x -100)=﹣0.1x+24x-800.当x=﹣=120时,即每天买进120份报纸时,可获最大毛利润为640元.27.(1)设小路的宽为xm,则(16-2x)(12-2x)=×16×12,解得x=2,或x=12(舍去). ∴x=2,故小明的结果不对.(2)四个角上的四个扇形可合并成一个圆,设这个圆的半径为rm,故有r2=×16×12,解得r≈5.5m.(3)依此连结各边的中点得如图的设计方案.28.(1)作PK⊥BC于K,BM=4,AB=10,∵PK∥AC,∴=pk=x,∴y=×4×x=x(0<x<10).(2)①∠PMB=∠B, PM=PB ,MK=KB=2 , =, x=2.5;②∠PMD=∠A, 又∠B =∠B,∴△BPM∽△BAC,∴BP·AB=BM·BC,∴10x=4×8 ,x=3.2,∴存在 x=2.5或3.2.29.(本题仅供学有余力的同学参考)(1)OA=OB,DF=EF,DE=AC,AG=DG,EG=CG.(2)ME=GM. 理由是:连EO并延长交⊙O于点N,连结DN. ∵EM是⊙O的切线,∴∠OEM=90º,∴∠GEM+∠GEN=90º. ∵EN是⊙O的直径,∠N+∠GEN=90º,∴∠N=∠GEM. ∵AB是⊙O的直径,∴∠B+∠BAC=90º,∵∠AGF+∠GAF=90º,∴∠AGF=∠B,∵∠AGF=∠CGE,∴∠CGE=∠B. ∵AC=DE,∴∠N=∠B,∴∠GEM=∠CGE,∴MG=ME.(3)答案:.。
广东省2011年中考数学试卷(含答案)创新1
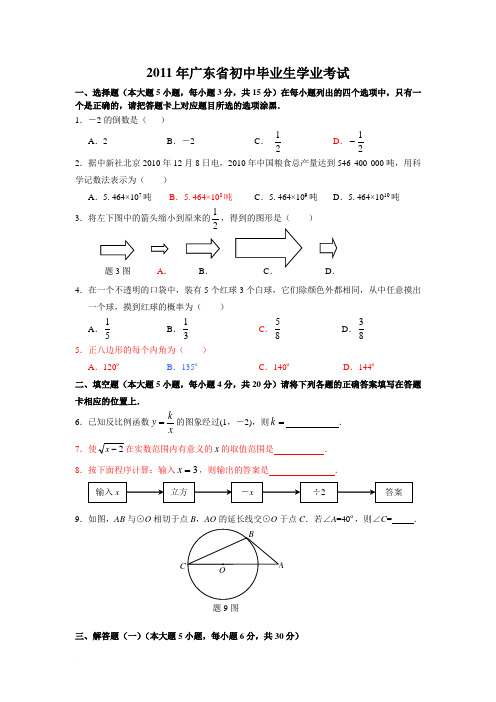
2011年广东省初中毕业生学业考试一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.-2的倒数是( ) A .2 B .-2C .21D .21-2.据中新社北京2010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为( )A .5.464×107吨B .5.464×108吨C .5.464×109吨D .5.464×1010吨3.将左下图中的箭头缩小到原来的21,得到的图形是( )4.在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( ) A .51B .31 C .85 D .835.正八边形的每个内角为( )A .120ºB .135ºC .140ºD .144º二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上. 6.已知反比例函数xky =的图象经过(1,-2),则=k ____________. 7.使2-x 在实数范围内有意义的x 的取值范围是______ _____. 8.按下面程序计算:输入3=x ,则输出的答案是_______________.9.如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C .若∠A =40º,则∠C =_____.三、解答题(一)(本大题5小题,每小题6分,共30分)A .B .D .题3图题9图 B C O A11.计算:(1)20245sin 18)12011(-︒+-. (2)()22()()14a b a b a b +--+-12.解不等式组:⎩⎨⎧-≤-->+128,312x x x ,并把解集在数轴上表示出来.13.已知:如图,E ,F 在AC 上,AD //CB 且AD =CB ,∠D =∠B .求证:AE =CF .15.(本题满分6分)如图所示,A 、B 两城市相距100km .现计划在这两座城市间修筑一条高速公路(即线段AB ),经测量,森林保护中心P 在A 城市的北偏东30°和B 城市的北偏西45°的方向上.已知森林保护区的范围在以P 点为圆心,50km 为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?1.732 1.414)题13图 B D A F EA第15题图BF E P45°30°数学试题 第 3 页 (共 11 页)四、解答题(二)(本大题4小题,每小题7分,共28分)16.肇庆市某施工队负责修建1800米的绿道.为了尽量减少施工对周边环境的影响,实际工作效率比原计划提高了20%,结果提前两天完成.求原计划平均每天修绿道的长度. 19.(本题7分)某校为了了解本校八年级学生课外阅读的喜欢,随机抽取了该校八年级部分学生进行问卷调查(每人只选一种书籍)。
2011中考数学选择题专训(附习题含答案)

2011中考数学选择专训数学选择题的常用解法(方法篇)数学选择专项训练1在中考数学试题中,选择题占相当大的比例,因此,解答选择题对考试成绩影响很大。
解数学选择题,常可以从选择支出发进行思考,充分利用选择支所提供的信息与“只有一个正确答案”的方向,改变解题策略,充分发挥直观的作用,发现其特殊的数量关系和图形位置特征,迅速解题。
下面举例谈谈解数学选择题的五种常用方法,供大家复习时参考。
一. 直接法例1. 若b ab a <0,有意义,则a b a=( )。
A.abB.-abC. -abD. --ab解:根据题设,注意到a <0,直接化简原式,可得-ab 。
选C 。
点拨:直接法就是直接从条件出发,通过合理运算和严密推理,最后推出正确的结果,再对照选择支解答的一种解题思路。
二. 特例法例2. 若a b <-<<010,,则( ) A. ab ab a 2<< B. a ab ab <<2C. ab a ab 2<<D. a ab ab <<2 解:取a b =-=-112,,很容易得到答案为D 。
点拨:特例法就是用符合已知条件的特例或考虑特殊情况、特殊位置,检验选择支或化简已知条件,得出答案。
当已知条件中有范围时可考虑使用特例法。
三. 检验法例3. 方程7312x x -+-=的解是( )A. 3B. 2C. 1D.37解:把四个选择支的数值代入方程7312x x -+-=中,很快就可知道答案为C 。
点拨:检验法就是将选择支分别代入题设中或将题设代入选择支中检验,从而确定答案。
解答本题时若直接解方程,要浪费很多时间和精力。
当结论为具体值时可考虑使用检验法。
四. 排除法例4. 在同一坐标平面内,函数y m x =-()1与y mx x m =++2的图象只可能是( )解:选择支A 中抛物线肯定错误,B 中直线肯定错误(若为抛物线也错误),C 中直线和抛物线不是同时正确的,故选D 。
广东省深圳市中考数学模拟试卷3

深圳市2011年高中阶段学校招生考试数学模拟试卷(三)说明:1.全卷22题,共8页,考试时间90分钟,满分100分.2.答题前,请将考场. 试室号. 座位号. 考生号. 姓名写在试卷密封线内,不得在试卷上作任何标记.3.做选择题时,请将选项的字母代号写在“答题表一”内;做填空题时,请将答案写在"答题表二"内;做解答题时,将解答过程写在指定的位置上.一、选择题(本大题10小题,每题3分,共30分)每小题有4个选项,其中只 有一个正确的,请把正确选项的字母代号填在.............".答题表一....".内.,.否.则.不.给.分. 答 题 表 一 1.9的算术平方根是( ) A .3 B .-3 C .±3 D .81 2.下列各图中,可以是一个正方体的平面展开图的是( )A .B .C .D .3.中国的国土面积为9596960平方千米,把这个数保留三个有效数字,并用科学记数法表示,应为( )A .71059.9⨯B .61060.9⨯C .6106.9⨯D .61059.9⨯4.下列图形中,既是轴对称,又是中心对称图形的是( )5. 已知二次函数y=ax2+bx+c(a≠0)的图象如下图所示,给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a<0;④ abc>0 . 其中所有正确结论的序号是( )A. ③④B. ②③C. ①④D. ①②③6.假设五个相异正整数的平均数是15,中位数是18,则这五个相异正整数中的最大数的最大值为( )A.24 B.32 C.35 D.407.三角形两边长分别是3和6,第三边是方程0862=+-xx的解,则这个三角形的周长是( )A.11 B. 13 C. 11或13 D. 11和138.如右图,滔滔发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30º角,且此时测得1米杆的影长为2米,则电线杆的高度为( )A.9米 B.28米C.()37+米 D.()3214+米9.某商场将一种商品A按标价的9折出售,依然可获利10%,若商品A的标价为33 元,那么该商品的进货价为( )A.31元 B. 30.2元 C. 29.7元 D. 27元10.如下图在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan ∠DBA=51,则AD的长为( )A.2B.2C.1D.22二、填空题(本大题5小题,每小题3分,共15分)请把答案填.....在答题表二内......BDAC答 题 表 二11.在“石头、剪子、布”的游戏中,两人做同样手势的概率是_________12.关于x 的方程233xmx x =+--有增根,则m 的值为_________13.如图13,是按照一定数字规律画出的一行“树型”图.照此规律继续画下去,则图(7)应有的线段条数为_________14.如图1,在矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BC ,垂足为E ,连结DE 交AC 于点P ,过P 作PF ⊥BC ,垂足为F ,则CB CF的值是______________15.如图2,如图,AB 是⊙O 的直径,⊙O 交BC 于D ,DE ⊥AC ,垂足为E ,要使DE 是⊙O 的切线,则图中的线段应满足的条件是___________________________________________或________________________________________三、解答题(本大题共有7小题,共55分)16.(6分)计算:2011(2008)1)tan 45π-︒-+--+-(1) (2) (3) (4) (5) (7)图13图1 D B 图217.(6分)先化简,再求值:)21(42x x x +÷-,其中2008=x .18.(7分)某货船以20海里/时的速度将一批重要物资由A 处运往正西方向的B 处,经16小时的航行到达,到达后必须立即卸货。
2011河北中考数学试题及答案

2011河北中考数学试题及答案2011年河北中考数学试题一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 已知一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 83. 如果一个数的平方等于16,那么这个数是多少?A. ±4B. ±2C. 4D. 24. 一个圆的半径是5,求这个圆的面积。
A. 25πB. 50πC. 75πD. 100π5. 一个数列的前三项是1, 3, 6,求第四项。
A. 10B. 12C. 15D. 206. 一个长方体的长、宽、高分别是2, 3, 4,求其体积。
A. 24B. 26C. 28D. 327. 一个分数的分子是5,分母是8,这个分数化简后是多少?A. 5/8B. 1/2C. 5/4D. 1/18. 一个二次方程x^2 - 5x + 6 = 0的解是什么?A. x = 2, 3B. x = -2, -3C. x = 2, -3D. x = -2, 39. 一个函数f(x) = 2x + 3的反函数是什么?A. f^(-1)(x) = (x-3)/2B. f^(-1)(x) = (x+3)/2C. f^(-1)(x) = (x-2)/3D. f^(-1)(x) = (x+2)/310. 一个正弦函数y = sin(x)的图像,当x增加π时,图像如何变化?A. 向左平移π个单位B. 向右平移π个单位C. 向上平移π个单位D. 向下平移π个单位二、填空题(每题2分,共20分)11. 圆的周长公式是_________。
12. 一个数的绝对值是它到0的距离,例如|-5|=_______。
13. 一个多项式3x^2 - 5x + 2的首项系数是_______。
14. 一个三角形的内角和是_______度。
15. 一个数的对数函数log_a(x),当a=10时,称为_______。
初三数学中考创新思维训练三

一、细心填一填(本大题共有12小题,15空,每空2分,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)1.3的相反数是_________,-2的绝对值是___________. 2.4的算术平方根是__________,-8的立方根是___________.3.据中新社报道:2010年我国粮食产量将达到540 000 000 000千克,这个粮食产量用科学记数法可表示为______________________千克.4.分解因式:x 2-4=_________________. 5.函数y =12x +中,自变量x 的取值范围是___________________; 函数y中,自变量x 的取值范围是___________________.6.如图,已知a ∥b ,∠1=40?,则∠2=_________?.7.一n 边形的内角和等于1080?,那么这个正n 边形的边数n =_________.8.为发展农业经济,致富奔小康,养鸡专业户王大伯2004年养了2000只鸡. 上市前,他随机抽取了10只鸡,称得重量统计如下:根据统计知识,估计王大伯这批鸡的总重量约为_____________千克.9.如图,在⊙O 中,弦AB =1.8cm ,圆周角∠ACB =30?,则⊙O 的直径 为__________cm.10.有一直角梯形零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm , ∠D =120?,则该零件另一腰AB 的长是___________cm.11.两个完全相同的长方体的长、宽、高分别为5cm 、4cm 、3cm , 把它们叠放在一起组成一个新的长方体,在这些长方体中,表 面积最大是__________cm 2.12.一串有黑有白,其排列有一定规律的珠子,被盒子遮住了一部分 (如图),则这串珠子被盒子遮住的部分有_________粒. 二、精心选一选(本大题共8小题,每题3分,共24分. 在每题所给出的四个选项中,只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对!)13.如图,a 、b 、c 在数轴上对应的点分别为A 、B 、C ,则下列结论正确的是 ( )A.ab <0B. a -b >0C. abc <0D. c (a -b )<014)A B C D 15.下列各式中,与分式x y x--的值相等的是( )A .x x y + B .x x y -- C .x x y -+ D .x x y- 16.已知一次函数y =kx +b 的图像如图所示,则当x <0时,y 的取值范围是( )A. y >0B. y <0C. -2<y <0D. y <-2(第6题)ba c21AB C D(第10题)B AC (第13题)(第9题)17.下面的平面图形中,是正方体的平面展开图的是( )1819 )A B .为了了解全国中学生的睡眠状况,采用普查方式 C .为了了解人们保护水资源的意识,采用抽样调查的方式D .对栽人航天器“神州五号”零部件的检查,采用抽样调查的方式20.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏. 游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸就不得奖. 参与这个游戏的观众有三次翻牌的机会(翻过的牌不能再翻). 某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( )A .14 B .15C .16D .320三、认真答一答(本大题共7小题,满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!) 21.(本题共有3小题,每小题5分,共15分)(1)计算:(-2)3+12(2004)0tan60?.(2)解不等式: 12(x -2)<3-x .(3)解方程组:{4,2 5.x y x y -=+=22.(本题满分6分)在如图的12×24的方格形纸中(每个小方格的边长都是1个单位)有一ΔABC . 现先把ΔABC 分别向右、向上平移8个单位和3个单位得到ΔA 1B 1C 1;再以点O 为旋转中心把ΔA 1B 1C 1按顺时针方向旋转90o 得到ΔA 2B 2C 2. 请在所给的方格形纸中作出ΔA 1B 1C 1和 ΔA 2B 2C 2.23.(本题满分8分)如图,给出四个等式:①AE =AD ;②AB =AC 件,另一个作为结论.(1(2)请你至少写出三个这样的正确命题. 24.(本题满分6分)某产品每件成本10间的关系如下表:若日销量y (件)是销售价x (元)的一次函数.(1)求出日销量y (件)与销售价x (元)的函数关系式;(2)要使每日的销售利润最大,每件产品的销售价应定位多少元?此时每日的销售利润是多少? 25.(本题满分6分)如图,有两个可以自由转动的均匀转盘A 、B ,转盘A 被均匀地分成4等分,每份分别标上1,2,3,4四个数字;转盘B 被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字. 有人为甲、乙两人设计了一个游戏,其规则如下:A.B. C. D.(1)同时自由转动转盘A、B;(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字作成积. 如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜(如果转盘A指针指向3,转盘B指针指向5,3×5=15,按规则乙胜).你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.(2)①填写下表:②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数关系式:___________;(3)当水面宽度为36m时,一艘吃水深度(船底部到水面的距离)为1.8m的货船能否在这个河段安全通过?为什么?27.(本题满分9分)某生活小区的居民筹集资金1600元,计划在一块上、下底分别为(如图).(1)他们在ΔAMD和ΔBMC地带上种植太阳花,单价为8元/cm共花了160元,请计算种满ΔBMC地带所需的费用;(2)花木,刚好用完所筹集资金?(3)若梯形ABCD为等腰梯形,面积不变(如图)P,使得ΔAPB≌ΔDPC,且SΔAPD=SΔBPC,,并说出你的理由.四、动脑想一想(本大题共有2小题,共18分.28.(本题满分8分)如图,在平面直角坐标系中,直线l的解析式为y,关于x2x2-2(m+2)x+2m+5=0(m>0)有两个相等的实数根.(1)试求出m的值,并求出经过点A(0,-m)和点D(m,0)的直线解析式;(2)在线段AD上顺次取两B、C,使AB=CD-1,试判断ΔOBC的形状;(3)设直线l与直线AD交于点P,图中是否存在与ΔOAB相似的三角形?如果存在,请直接写出来;如果不存在,请说明理由.29.(本题满分10分)如图,正方形ABCD的边长为12,划分成12×12个小正方形. 将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)图乙×(n -1)的正方形. 如此摆放下去,最后直到纸片盖住 正方形ABCD 的右下角为止. 请你认真观察思考后回答下 列问题:(1)由于正方形纸片边长n 的取值不同,完成摆放时所使用正方形纸 片的张数也不同,请填写下表:(2)设正方形ABCD 被纸片盖住的面积(重合部分只计一次)为S 1,未被盖住的面积为S 2. ①当n =2时,求S 1∶S 2的值;②是否存在使得S 1=S 2的n 值?若存在,请求出这样的n 值;若不存在,请说明理由.参考答案一、细心填一填(本大题共有12小题,15空,每空2分,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)1.-3,2 2. 2,-2 3. 5.4×1011 4. (x +2)(x -2) 5. x ≠-2, x ≥3 6. 140 7. 8 8. 5000 9. 3.6 11. 176 12. 27二、精心选一选(本大题共8小题,每题3分,共24分. 在每题所给出的四个选项中,只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对!) 13. C 14. B 15. D 16. D 17. C 18. A 19. C 20. C三、认真答一答(本大题共7小题,满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!)21. (1)-9;(2)x <83;(3){3,1.x y ==- 22.ΔA 1B 1C 1和ΔA 2B 2C 2如图所示.23.(1)如果AE=AD ,AB=AC ,那么∠B =∠C证明:在ΔABE 和ΔACD 中,∵AE=AD ,∠A =∠A ,AB=AC ,∴ΔABE ≌Δ(2)①如果AE=AD ,AB=AC ,那么OB=OC . ②如果AE=AD ,∠B =∠C ,那么AB=AC . ③如果OB=OC ,∠B =∠C ,那么AE=AD . 24.(1)y =-x +40;(2)当销售价定为25元/件时日销售利润最大,为225元.25.这个游戏不公平.把游戏中由A 、B 两个转盘中所指的两个数字的“积”改成“和”,游戏就公平了. 因为在A 盘和B 盘中指针所指的两个数字作和共有24种情况,而A 盘中每个数字与B 盘中的数字作和得到偶数和奇数的结果都是3,这样这24个和中,偶数和奇数的种数都是12,所以甲和乙获胜的可能性是一样的,这对他们就公平了.26.(1)如图所示; (2)①; ②y =200x 2;(3)当水面宽度为36m ,即x =18m 时,y =1.62m<1.8m , 所以这艘货船不能安全通过该河段.27.(1)∵梯形ABCD 中,AD ∥BC ,∴∠MAD =∠MCB ,∠MDA =∠MBC ,∴ΔMAD ∽ΔMCB ,∴S ΔMAD ∶S ΔMBC =1∶4. ∵种植ΔMAD 地带花费160元,∴S ΔMAD =160÷8=20(m 2),∴S ΔMBC =80(m 2), ∴种植ΔMBC 地带花费640元.(2)设ΔMAD 的高为h 1,ΔMBC 的高为h 2,梯形ABCD 的高为h ,则 S ΔMAD =12×10 h 1=20,∴h 1=4;S ΔMBC =12×10 h 2=80,∴h 2=8,∴h =h 1+h 2=12,∴S 梯形ABCD =12×(AD +BC ) h =180,∴S ΔMAB + S ΔMCD =180-(20+80)=80(m 2).∵160+640+80×12=1760(元),160+640+80×10=1600, ∴应种植茉莉花刚好用完所筹集的资金.(3)点P 在AD 、BC 的中垂线上. 此时,PA=PD ,PB=PC . ∵AB=DC ,∴ΔAPB ≌ΔDPC .设ΔAPD 的高为x ,则ΔBPC 的高为(12-x ), ∴S ΔAPD =12×10 x =5x , S ΔBPC =12×20(12-x )=10(12-x ),由S ΔAPD = S ΔBPC ,即5x =10(12-x ),可得x =8.∴当点P 在AD 、BC 的中垂线上,且与AD 的距离为8cm 时,S ΔAPD = S ΔBPC . 28.(1)由题意得Δ=[-2(m +2)]2-4×2×(2m +5)=0,∴m=∵m >0,∴m.∴点A (0、D0). 设经过A 、D 两点的直线解析式为y =kx +b ,则0,b b ==+⎧⎪⎨⎪⎩解得1,k b ==⎧⎨⎩∴y =x-. (2)作OE ⊥AD 于E ,由(1)得OA=OD,∴AD=∴OE=AE=ED=12AD =∵AB=CD1,∴BE=EC =1,∴OB=OC .在Rt ΔOBE 中,tan ∠OBE=OE BE=ΔOBC 为等边三角形.(3)存在,ΔODC 、ΔOPC 、ΔOPA . 29.(1)依此为11,10,9,8,7(2)S 1=n 2+(12-n )[n 2-(n -1)2]= -n 2+25n -12. ①当n =2时,S 1=34,S 2=110,∴S 1∶S 2=17∶55; ②若S 1=S 2,则有-n 2+25n -12=12×122,即n 2-25n +84=0,解得n 1=4, n 2=21(舍去)。
初中创新思维训练(H30)

第 1 页 共 2 页初中创新思维训练(H30)“《数学周报》杯”2011年全国初中数学竞赛试题(A 卷) 一、选择题(共5小题,每小题7分,满分35分)1、设17-=a ,则代数式12612323--+a a a 的值为( ). (A )24 (B )25 (C )1074+ (D )1274+2、对于任意实数a,b,c,d,定义有序实数对(a ,b )与(c ,d )之间的运算“△”为;(a ,b )△(c ,d )=(a c+bd ,ad +b c )。
如果对于任意实数u ,v ,都有(u ,v )△(x ,y )=(u ,v ),那么(x ,y )为( )。
(A )(0,1) (B )(1,0) (C )(-1,0) (D )(0,-1)3、若0,1>>y x ,且满足y y x yxx xy 3,==,则y x +的值为( )。
(A )1 (B )2 (C )29 (D )211 4、已知点D E ,分别在△ABC 的边AB AC , 上,BE与CD 相交于点F ,设1S S EAD F =四边形,2S S BDF =∆,3S S BCF =∆,4S S CEF =∆,则13S S 与24S S 的大小关系为( ).(A ) 1324S S S S < (B ) 1324S S S S = (C )1324S S S S > (D )不能确定5、设3339912111+++=S ,则4S 的整数部分等于( ). (A )4 (B )5 (C )6 (D )7 二、填空题(共5小题,每小题7分,共35分)6、若关于x 的方程()()0422=+--m x x x 有三个根,且这三个根恰好可以作为一个三角形的三边长,则m 的取值范围是___________.7、一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为5的概率是____________.8、如图,已知点B A ,在直线x y =上,过B A ,分别作y轴的平行线交双曲线xy 1=(x >0)于点D C ,.若AC BD 2=,,则224OD OC -的值为__________.9、若211-+-=x x y 的最大值为a ,最小值为b 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年中考数学创新思维训练(三)
一、填空题(每小题3分,共15分) 1、EFGH 是矩形
ABCD 的内接矩形,且1:3:=FG EF ,1:2:=BC AB ,则=HE AH :
2、某市初三年级举行以班为单位的基层数学团体赛,在各校预赛的基础上,每校选派一个班级中25名同学参加决赛,实验初中三(2)班、三(6)班为该校的候选班级,他们预赛的成绩如下:
得分 50 60 70 80 90 100 人数
三(2) 4 5 10 8 14 9 三(6)
4
4
16
2
12
12
已经算得两个班的平均分都是80分
①利用你学的统计知识,比较 班的实力更均衡些. ②你认为应派 班的25名同学参加决赛. 3、数轴上表示1、
2的对应点分别为A 、B ,点B 关于点A 的对称点C 所示的数是
4、在平面直角坐标系中,直线k x y +-=与双曲线x
y 1=只有一个交点,则k 的值为
5、如图,圆木的横截面圆半径均为r ,则将这七根圆木用绳子扎住,每周所需绳子的长度为 二、(共7分)
如图,AM 是⊙O 的直径,AM BC ⊥,垂足为N ,CD 是弦,交AM 和AB
于点E 、F .
①如果NM EN
=,求证:AB CD ⊥.
②如果弦CD 交AB 于点F ,且AB CD
=,求证:ED EF CE ⋅=2.
三、(共8分)
已知关于x 的方程0127)1(222
=+--+-+b a a x a x
有两个相等的实数根,且满足02=-b a .
①利用根与系数的关系判断这两根的正负情况. ②若将127)1(222+--+-+=b a a x a x y 图象沿对称轴向下移动3个单位,
写出顶点坐标和对称轴方程.
A
B
C
D E F
M
N O
四、(11分) 如图所示,52=AB ,2tan =∠ABC ,5
3
cos =
∠ACB ①求过
A 、
B 、
C 三点的二次函数解析式.
②若D 是AB 的中点,试判断点D 在这条二次函数的图象上吗?并说明理由. ③若y 随x 的增大而减小,求x 的取值范围.
五、(9分)
正方形ABCD 中,有一直径为BC 的半圆,cm BC 2=,现有两点E 、F ,分别从点B 、点A 同时出发,点E 沿线段BA 以s cm /1的速度向点A 运动,点F 沿折线C D A --以s cm /2的速度向点C 运动,设点E 离开B 的
时间为t 秒
①当t 为何值时,线段EF 与BC 平行?
②设21<<t ,当t 为何值时,EF 与半圆相切?
③当21<≤t 时,设EF 与AC 相交于点P ,问点E 、F 运动时,点P 的位置是否发生变化?若变化,请说明理
由;若不发生变化,请给予证明,并求PC AP ⋅的值.
A B
C
D
E
F
P
A B
C
D
E
F
A B
C
D E
F
A
B
C
O
3,参考答案
一、1、1:5;2、①二班②六班;3、22-;4、2±=k ;5、r r π212+
二、证明:①连结BM ,
∵AM 是⊙O 的直径,∴︒=∠90ABM
∵AM BC ⊥,∴CN BN =,BNM ENC ∠=∠ 又NM EN =,∴Rt △CEN ≌Rt △BMN ∴ECB MBC ∠=∠
又∵AM BC ⊥,∴MC BM =,∴MBC A ∠=∠ ∴EBC A ∠=∠ 又AEF NEC ∠=∠ 在△AEF 和△CNE 中 ︒=∠=∠90AFE ENC 即AB CD ⊥
②连结BD 、BE 、AC
∵点E 是BC 垂直平分线AM 上一点,∴EC BE = ∵AB CD =
∴AB CD =,∴BC AD =,∴BDC ACD ∠=∠
又
AE AE AC AB ==,
∴△ABC ≌△ACE
∴BDC ACD ABE ∠=∠=∠
BED ∠是公共角
∴△BED ∽△FEB ,
∴ED EF BE ⋅=2
∴ED EF CE
⋅=2
三、①解:由0)127(4)3(422=+----=∆
b a a a
得03=
-+b a ,又02=-b a 得
2,1==b a
设这个方程的解为1x 、2x 则
04)3(221>=--=+a x x
∴ 1x 、2x 均为正根
② ∵ 2,1==b a
∴ 127)1(222+--+-+=b a a x a x y 可化为:
442+-=x x y ,将此图象向下移动2个单位,得
3)2(2--=x y
顶点)3,2(-,对称轴为2=x
四、解:①
)4,0(A ,)0,2(-B ,)0,3(C ∴
43
2
322++-=x x y
②∵D 是AB
的中点,∴)2,1(-D
∵4)1(3
2
)1(322
2+-⨯+-⨯-≠
∴点D 一在这条二次函数的图象上
③∵
625)21(322+--=x y ,032<-=a 开口向下
∴当2
1
>x 时,y 随x 的增大而减小
五、解:①点E 离开点B t 秒,t BE =,t CF 24-=
要使EF 与BC 平行,则应CF BE =
∴t t 24-=,得3
4
=t
②EF 与半圆相切,作AB FG ⊥于G
在Rt △EFG 中,∵2.22
EF FG EG =+
∴222)24(2)43(t t t
-+=+-
∴2
22+=
t (秒)
③当21<≤t 时,点P 的位置不会发生变化
证明:E 、F 出发t 秒时,t BE = t AE -=2,t CF 24-= ∴
2
1
2442=--=t CF AE 又∵CD AB //,∴△AEP ∽△CFP ∴
2
1
==CF AF PC AP 因此,当21<≤t 时,点P 的位置与t 的取值无关,点P 的位置不会发生变化。
