信号与系统 第三章(第5-7讲)
信号与系统第三章PPT课件

.
它们都是傅里叶级数收敛的充分条件。相当广泛的 信号都能满足Dirichlet条件,因而用傅里叶级数表 示周期信号具有相当的普遍适用性。
几个不满足Dirichlet条件的信号
.
三.Gibbs现象 满足 Dirichlet 条件的信号,其傅里叶级数是如
• “非周期信号都可以用正弦信号的加权积分来 表示”——傅里叶的第二个主要论点
.
傅立叶分析方法的历史
古巴比伦人 “三角函数和” 描述周期性过程、预测天体运
动
1748年 欧拉 振动弦的形状是振荡模的线性组合
1753年 D·伯努利 弦的实际运动可用标准振荡模的线性组合来表示
1759年 拉格朗日 不能用三角级数来表示具有间断点的函数
x[k]h[nk]
x[k]h[n k]
k
.
对时域的任何一个信号 x ( t ) 或者 x ( n ) ,若能将其
表示为下列形式: x(t) a 1 es1 t a 2 es2 t a 3 es3 t
由于 es1t H(s1)es1t
es2t H(s2)es2t
es3t H(s3)es3t
利用齐次性与可加性,有
k
例: y(t)x(t3) ❖ 系统输入为 x(t) ej2t
系统 H(s) ? y(t) ?
H(s) h(t)estdt
❖ 系统输入为 x(t)cos(4t)cos(7t)
系统 y(t) ?
.
*问题:究竟有多大范围的信号可以用复指数信号的 线性组合来表示?
.
3.3 连续时间周期信号的傅里叶级数表示
第k次谐波 e jk 0t 的周期为
信号与系统课后习题与解答第三章
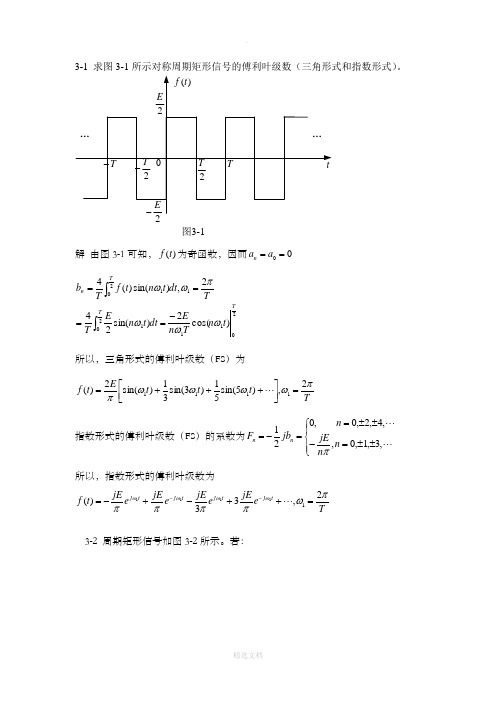
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为Te jE e jE e jEe jEt f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统第三章 连续信号的正交分解

f (t ) Ci gi (t )
i 1
n
第三章连续信号的正交分解
13
理论上讲
f (t ) lim Ci gi (t )
n i 1
n
在使近似式的均方误差最小条件下,可求得
t t1 f (t ) gi (t )dt Ci t 2 gi2 (t )dt t1
均方误差
n t2 2 ( t ) [ f ( t ) crgr ( t )]2 dt t 2 t 1 t 1 r 1
第三章连续信号的正交分解 23
1
若令 n 趋于无限大, 2 (t )的极限等于零 lim 2 (t ) 0
n
则此函数集称为完备正交函数集
第三章连续信号的正交分解
15
定义2:
如果在正交函数集 g1( t ), g 2( t ), gn( t ) 之外, 不存在函数x(t)
t2 2 0 x ( t )dt t1 t2 满足等式 x( t ) gi ( t )dt 0 t1
第三章连续信号的正交分解 8
信号的分量和信号的分解
信号常以时间函数表示,所以信号的分解指的就是 函数的分解。 1、函数的分量 设在区间
t 1 t t 2 内,用函数 f 1(t )
在另一
函数 f 2(t ) 中的分量 C 12 f 2(t ) 来近似的代表 原函数 f 1(t ) 。
f 1(t ) C12 f 2(t )
1 jnt f (t ) An e cn e jnt 2 n n
cn
1 An 称为复傅里叶系数。 2
表明任意周期信号可以表示成 e jn t 的线性组合,加权因 子为 cn 。
《信号与系统》教学大纲

《信号与系统》教学大纲Signals and Systems一、课程教学目标1、任务和地位:《信号与系统》是通信及相关专业的专业基础课,是通信专业的必修课程。
通过本课程的学习,使学生掌握用系统的观点和方法分析求解电子系统的特性,为后续课程(通信理论、网络理论、控制理论、信号处理和信号检测理论等课程)的学习和今后从事专业技术工作打下坚实的基础。
2、知识要求:本课程是信息类各专业本科生继“电路分析基础”课程之后必修的重要主干课程。
该课程主要研究确知信号的特性,线性时不变系统的特性,信号通过线性时不变系统的基本分析方法,以及信号与系统分析方法在某些重要工程领域的应用。
该课程是学习《现代通信原理》、《数字信号处理》等后续课程所必备的基础。
3、能力要求:通过本课程的学习,使学生掌握信号分析与线性系统分析的基本理论及分析方法,能对工程中应用的简单系统建立数学模型,并对数学模型求解。
为适应信息科学与技术的飞速发展,及在相关专业领域的深入学习打下坚实的基础。
同时,通过习题和实验,学生应在分析问题与解决问题的能力及实践技能方面有所提高。
二、教学内容的基本要求和学时分配2、具体要求:第一章信号与系统[目的要求]1.掌握信号、系统的概念,以及它们之间的关系。
2.了解信号的函数表示与图形表示。
3.掌握信号的能量和信号的功率的概念。
4.熟练掌握信号的自变量变换和信号的运算。
5.掌握阶跃信号、冲激信号,及其性质、相互关系。
6.了解系统的性质。
[教学内容]1. 信号、信号的自变量变换。
2. 能量和功率信号的判别方法3. 阶跃信号和冲激信号。
4. 一些典型序列。
5. 连续时间系统和离散时间系统。
6. 系统的性质[重点难点]1. 信号和系统的概念。
2. 能量和功率信号的判别方法3. 信号的自变量变换4. 阶跃信号和冲激信号。
5. 系统的性质。
[教学方法] 课堂讲解[作业] 7道[课时] 6第二章线性时不变系统[目的要求]1. 单位冲激响应的概念。
信号与系统王明泉第三章习题解答

(4)频域分析法分析系统;
(5)系统的无失真传输;
(6)理想低通滤波器;
(7)系统的物理可实现性;
3.3本章的内容摘要
3.3.1信号的正交分解
两个矢量 和 正交的条件是这两个矢量的点乘为零,即:
如果 和 为相互正交的单位矢量,则 和 就构成了一个二维矢量集,而且是二维空间的完备正交矢量集。也就是说,再也找不到另一个矢量 能满足 。在二维矢量空间中的任一矢量 可以精确地用两个正交矢量 和 的线性组合来表示,有
条件1:在一周期内,如果有间断点存在,则间断点的数目应是有限个。
条件2:在一周期内,极大值和极小值的数目应是有限个。
条件3:在一周期内,信号绝对可积,即
(5)周期信号频谱的特点
第一:离散性,此频谱由不连续的谱线组成,每一条谱线代表一个正弦分量,所以此谱称为不连续谱或离散谱。
第二:谐波性,此频谱的每一条谱线只能出现在基波频率 的整数倍频率上。
(a)周期、连续频谱; (b)周期、离散频谱;
(c)连续、非周期频谱; (d)离散、非周期频谱。
答案:(d)
题7、 的傅里叶变换为
答案:
分析:该题为典型信号的调制形式
题8、 的傅里叶变换为
答案:
分析:根据时移和频移性质即可获得
题9、已知信号 如图所示,且其傅里叶变换为
试确定:
(1)
(2)
(3)
解:
(1)将 向左平移一个单位得到
对于奇谐函数,满足 ,当 为偶数时, , ;当 为奇数时, , ,即半波像对称函数的傅里叶级数展开式中只含奇次谐波而不含偶次谐波项。
(4)周期信号傅里叶级数的近似与傅里叶级数的收敛性
一般来说,任意周期函数表示为傅里叶级数时需要无限多项才能完全逼近原函数。但在实际应用中,经常采用有限项级数来代替无限项级数。无穷项与有限项误差平方的平均值定义为均方误差,即 。式中, , 。研究表明, 越大, 越小,当 时, 。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
第3章信号与系统

2011-03
17
• Multirate Filters子模块集
双击图3-4所示的Library:dspfiltering窗口中的Multirate Filters模块 ,将弹出一个新窗口Library:dspmlti4,如图3-7所示。它包含有FIR Decimation模块、FIR Interpolation模块、FIR Rate Conversion模块、CIC Decimation模块和CIC Interpolation模块、Two-Channel Analysis Subband Filter模块、Two-Channel Synthesis Subband Filter模块、Dyadic Analysis Filter Bank模块和Dyadic Synthesis Filter Bank模块等共九个模块。
2011-03
7
3.1.1 信号处理输入模块
Chirp 模块。输出通过“Swept cosine”模式、“Linear”模式、 “Logarithmic”模式和“Quadratic”模式产生的具有指定频率和 时间参数的瞬时频率值的调频信号。 Discrete Impulse 模块。输出一个由“Delay”变量指定延时时间 的离散单位脉冲信号。 N-Sample Enable 模块。输出一个在“N”样本后激活的布尔信号 或者逻辑信号。 Multiphase Clock 模块。输出N相时钟信号。 Identity Matrix模块。输出一个单位矩阵,如果输入的“Matrix size”是个标量,则输出是一个单位方阵,如果输入的“Matrix size”是一个向量,则输出是个不对称的的矩阵,对角线上是1, 其他位置都为零。
图3-5 Filter Designs子模块库
【信号与系统(郑君里)课后答案】第三章习题解答

【信号与系统(郑君⾥)课后答案】第三章习题解答3-1 解题过程:(1)三⾓形式的傅⽴叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅⽴叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn == F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e ? jn ω1t dt T 1 t 0F n =1( a n ? jb n ) F ? n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因⽽a 0 = a n = 0 4 Tb n = T ∫02= 2Eπ n4TE2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 ? cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三⾓形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5Tn = 0, ±2, ±4,F n = ? jb n jE=2 n = 0,± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = ? jE π ej ω1t+ πjE e ? j ω1t ? 3jE π e j 3ω1t + 3jEπ e ? j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅⽴叶变换有如下两种⽅法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章连续信号的正交分解§3-1 引言线性系统分析方法,是将复杂信号分解为简单信号之和(或积分),通过系统对简单信号的响应求解系统对复杂信号的响应。
在上一章所述的时域中,近代时域法将信号分解为冲激信号的积分,根据系统的冲激响应通过卷积计算出系统对信号的响应。
然而,很多信号的特性与频率有着很重要的关系,因此研究信号在频域中的特性可以得到许多极具实用价值的结论,它在工程中也具有很重要的意义。
故此,从本章开始,我们就是研究这方面的问题。
在本章中,我们研究任何将信号分解成与频率有关的函数的叠加。
即在频域中,将信号分解为一系列与频率有关的正弦函数的和(或积分)。
然后,再研究如何通过系统对正弦信号的响应求解系统对原信号的响应。
类似上章所述,通过信号分解的方法求解响应要研究下面几个问题:1)如何将任意信号分解为一系列正弦信号之和(或积分)。
2) 求解系统对各个正弦子信号的响应(这个内容在电路分析课程中已经有详细介绍)。
3) 将各子信号的响应相叠加,从而合成系统对激励信号的响应。
本章将要研究的就是如何对信号进行分解和合成。
§3-2 信号在正交函数集中的分解信号的分解,在某种意义上与矢量的分解有相似之处。
为了形象地说明信号的分解,首先我们讨论矢量的分解。
一、矢量的分解1、矢量的定义:具有大小和方向的量叫做矢量。
2、矢量运算:加,矢量点乘(结果是标量),矢量叉乘。
3、矢量的分解:1) 矢量的单矢量基的分解:A 在1A 上的分量为A 在1A 上的投影:E +=11A A c其中,E 为误差矢量。
而A 在1A 上的垂直投影11c A 的模11A c :11111A A Acos θA Acos θA AA ∙===1c ,从几何或者解析角度,都可以得到使误差E 最小的系数为:1112111A A A AA A A ∙∙=∙=c其中的1c 称为矢量A 和1A 的相似系数。
其它投影情况下误差E 不为最小,见上图。
如果0A 2πA c o s A A 211121=⎪⎭⎫⎝⎛=∙=A A 1c (或01=A A ),则表明A 和1A 相垂直(又称为正交)。
2) 矢量的多矢量基分解:将矢量表示成为一系列标准矢量(基)的线性组合:11∑==+++=ni i i n n c c c c 12211...A A A A A✧ 显然,如果知道了标准矢量i A 和相应的系数i c ,就可以确定任意矢量。
✧ 如何确定最佳的系数i c ?如果矢量i A 两两正交,可以证明:ii i i c A A AA =4、标准矢量基的几个限制条件:1)归一化:标准矢量的模等于1——方便计算; 2)正交化:标准矢量两两正交;3)完备性:可以不失真地组合出任意矢量。
二、信号的分解用与矢量分解相类比的方法,我们也可以推导出信号分解。
1、单个标准信号下的分解:在时间区间),(21t t 内,用)(11t f c 近似任意函数)(t f ,并使误差尽可能小。
1) 如何衡量函数误差的大小?可以采用方均误差:⎰-=21)(1)(2122t t dt t t t t εε2) 最佳系数:⎰⎰=2121)()()()(1111t t t t dtt f t f dt t f t f c (也称为函数)(t f 和)(1t f 的相似系数。
3) 如果01=c (或0)()(211=⎰t t dt t f t f ),则称)(t f 和)(1t f 正交。
4) 如果)(t f 和)(1t f 是复函数,则其方均误差为:⎰⎰⋅-=-=2121)()(1)(1)(*122122t t t t dt t t t t dt t t t t εεεε最佳系数为:⎰⎰=2121)()()()(*11*11t t t t dtt f t f dt t f t f c2、多个标准信号下的分解:将信号表示为多个标准信号的线性组合:∑==+++=ni i i n n t f c t f c t f c t f c t f 12211)()(...)()()(这里的i c 同样难以确定。
但是如果标准函数)(t f i 之间两两正交,则可以证明:⎰⎰=2121)()()()(**t t i i t t i idtt f t f dt t f t f c例:标准信号集:泰勒级数,...,...,,,,132kx x x x , 三角函数:,...sin ,cos ,...,2sin ,2cos ,sin ,cos ,1kt kt t t t t3、对标准信号集的要求: 1)归一化:1)()(21*=⎰t t i i dt t f t f 2)正交化:0)()(21*=⎰t t j i dt t f t f ,j i ≠3)完备性:可以用其线性组合表示任意信号。
完备正交函数集一般都包含无穷多个函数,例如:三角函数集,沃尔什函数集等。
但在实际应用中不可能用无穷多个,只可能用有限个函数,只能近似表示任意函数。
附:矢量与函数的运算与分解比较:§3-3 信号表示为傅里叶级数傅里叶级数是最常用的一种正交函数集。
它在工程中有很广泛的用途。
一、三角函数形式的傅里叶级数这种正交函数集为:{},...sin ,cos ,...,2sin ,2cos ,sin ,cos ,1t k t k t t t t ΩΩΩΩΩΩ其中:T t t ππ2212=-=Ω或将正交函数集表示为:{},...2,1,0)sin(),cos(=ΩΩn t n t n可以证明该函数集满足:1)正交性:函数集中的函数两两相正交。
011=ΩΩ⎰+dt )t m sin()t n cos(Tt tnm dt )t m sin()t n sin(dt )t m cos()t n cos(T t t Tt t ≠⎪⎭⎪⎬⎫=ΩΩ=ΩΩ⎰⎰++0011112)当0≠n 时:2111122Tdt )t n (sin dt )t n (cos Tt tTt t=Ω=Ω⎰⎰++T dt Tt t=⎰+111可以将任意函数f (t)在这个正交函数集中展开(表示成该正交函数集函数的线性组合):()()()()()()()()()∑∞+=Ω+Ω+=+Ω++Ω+Ω+Ω++Ω+Ω+=102121022n n n n n t n sin b t n cos a a ...t n sin b ...t sin b t sin b ...t n cos a ...t cos a t cos a a )t (f其中的系数可以根据§3-2节的结果计算出:⎪⎪⎩⎪⎪⎨⎧=≠Ω=ΩΩ=⎰⎰⎰⎰++++Tt t Tt t T t t T t t n n dt)t (f T n dt )t n cos()t (f T dt )t n (cos dt )t n cos()t (f a 1111111101022⎰⎰⎰+++Ω=ΩΩ=Tt t Tt tTt tn dt )t n sin()t (f T dt)t n (sin dt )t n sin()t (f b 11111122其中n a 的表达不太方便。
为了方便表达,将分解式改写:()()()∑+∞=Ω+Ω+=102n n n t n sin b t n cos a a )t (f则系数为:⎰+Ω=Tt t n dt )t n cos()t (f T a 112⎰+Ω=Tt t n dt )t n sin()t (f T b 112其中,n =0,1,2,……。
所以,信号可以表示成为直流信号和一系列正弦信号之和。
另外一种分解方式:令:22n n n b a A +=,nnn a b arctan -=ϕ,则上面的分解式可以表达成:()∑+∞=ϕ+Ω+=10cos 2)(n n n t n A a t f它可以看成是下列正交信号集:{},...2,1,0)cos(=Ωn t n的平移后的线性组合。
在上面的系数中,n a 和n A 是n 的偶函数;n b 和n ϕ是n 的奇函数;——如果f (t)是实数信号。
上面的分解等式的左右两边的函数是否相等,没有误差?或者,是否随着n 趋向于无穷大,等式右边的函数收敛于左边的函数?Direchlet(狄利克雷)证明,只要满足下面三个条件,等式就收敛:1)f (t)绝对可积,即:∞<⎰+Tt t dt )t (f 112)f (t)在区间内有有限个间断点; 3)f (t)在区间内有有限个极值点。
实际信号大都满足这个条件。
✧ 等式右边是多个周期为T 的函数的和,它仍然是周期为T 的函数。
✧ 这种分解可以用在两个场合:1)研究函数在)T t ,t (+11区间内的分解;2)研究周期为T 的函数在整个时间区间内的分解。
本课程中研究的是2)。
✧ 如果f (t) 周期为T 的函数,为了方便讨论,一般函数的主值区间取⎪⎭⎫ ⎝⎛-2,2T T ✧ 在函数的分解中:20a 称为信号的直流分量;()t cos a Ω1、()t sin b Ω1或)cos(11ϕ+Ωt A 称为信号的基波分量;()t n cos a n Ω、()t n sin a n Ω或)cos(n n t n A ϕ+Ω称为信号的n (n 2≥时)次谐波分量;✧ 实际情况下,n 无法计算到无穷大,只能取有限。
这时,这种正交展开是有误差的。
n 越大,误差越小。
例:方波的傅里叶级数。
(P97)⎪⎩⎪⎨⎧<<-<<=T t T T t t f 21201)( 按照定义公式,可以计算出:()()[]0 2 22020=Ω-Ω=Ω=⎰⎰⎰/T T /T T n dt t n cos dt t n cos Tdt )t n cos()t (f Ta )cos(1)cos(12 )sin()sin(2 )sin()(22/2/02/02/0⎥⎥⎦⎤⎢⎢⎣⎡ΩΩ+ΩΩ-=⎥⎦⎤⎢⎣⎡Ω-Ω=Ω=⎰⎰⎰T T T T T T T n t n n t n n T dt t n dt t n T dt t n t f T b ⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛Ω-ΩΩ+⎪⎭⎫ ⎝⎛-ΩΩ-=偶为数当为奇数当n n n )T n cos()T n cos(n )T n cos(n T 04 211212 π()()()⎥⎦⎤⎢⎣⎡+Ω+Ω+Ω=∴......5sin 513sin 31sin 4)(t t t t fπ对于具有不连续点的函数,即使所取级数的项数无限增大,在不连续处,级数之和仍不收敛于于原函数。
在跃变点附近,出现振荡、超过原函数幅度的过冲。
随着n 趋向于无穷,在函数的间断点附近,其过冲值收敛于函数在这点上的跳变值的8.948987%---Gibbs (吉布斯)现象。
