正三棱锥的内切球与外接球
正三棱锥的内切球与外接球

正三棱锥的内切球与外接球要回答这个问题,先要了解什么是正三棱锥.请看正三棱锥的定义.1.底面是正三角形2.顶点在底面的射影是底面三角形的中心.满足以上两条的三棱锥是正三棱锥.由以上定义可知,正三棱锥底面为正三角形,三个侧面是全等的等腰三角形.要防止和另外一个概念----正四面体混淆.正四面体的要求比正三棱锥更要.每个面都是正三角形的四面体才是正四面体.我们可以说,正四面体是特殊的正三棱锥,正三棱锥具备的性质正四面体都有,而正四面体具备的性质正三棱锥不一定有.下面来说如何寻找正三棱锥的内切球和外接球球心.在棱柱和棱锥的外接球中,谈到了一种方法,就是把符合条件的棱锥和棱柱放入长方体中,从而把问题转化、简化为长方体的外接球的问题.这是处理问题的方法之一.适合这种方法的情况可小结如下:⑴正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥.⑵同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥.⑶若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.⑷若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.今天说说第二种方法,就是利用球的定义确定球心.基本的规律可小结如下:⑴长方体或正方体的外接球的球心是其体对角线的中点.⑵正三棱柱的外接球的球心是上下底面中心连线的中点.⑶直三棱柱的外接球的球心是上下底面三角形外心连线的中点.⑷正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到.我们利用第(4)条结论来研究正三棱锥的外接球球心的位置.举一个具体栗子来说明.外接球球心分析:在正三棱锥的高线上,先假设一个位置,然后构造直角三角形,利用勾股定理求解.从图看出,此正三棱锥的外接球球心在高线PO的延长线上.再来求内切球的球心位置.由正三棱锥的对称性可知,内切球球心也在高线PO上.下面利用等体积法(即算两次体积)求内切球的半径.等体积法已经是第二次提到了,第一次提起是在线面角和点面距中.回到这位朋友的问题上来,外接球球心和内切球球心重合吗显然,多数情况下是不重合的.有童鞋可能会问,有没有重合的时候呢为了回答这个问题,我们作一般化的推导.若底边长刚好等于侧棱长,即正三棱锥变为正四面体时,奇迹发生了.画出图来是这样滴.此时,两心重合于一点,且该点把三棱锥的高分为3:1,长的那段为外接球半径,短的那一段为内切球半径.。
高考数学空间几何体的外接球与内切球常见题型

高考数学空间几何体的外接球与内切球常见题型本文介绍了空间几何体的外接球与内切球的经典类型,其中第一种类型为墙角模型,即三条棱两两垂直,不需要找球心的位置即可求出球半径。
具体方法是找到三条两两垂直的线段,然后使用公式2R=a+b+c或2R=a^2+b^2+c^2来求出R。
例如,在已知各顶点都在同一球面上的正四棱柱的高为4,体积为16的情况下,可以求出该球的表面积为32π。
第二种类型为对棱相等模型,补形为长方体。
在这种情况下,需要找到对棱相等的空间几何体,并补成长方体。
例如,如果三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积为36π。
除此之外,文章还给出了一些具体的例子,如正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积为36π。
同时,文章还提到了一些需要注意的引理,如正三棱锥的对棱互相垂直等。
需要注意的是,文章中存在一些格式错误和明显有问题的段落,需要进行删除或修改。
题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD)首先,我们可以画出一个长方体,标出三组互为异面直线的对棱,如图2-1所示。
设出长方体的长宽高分别为a,b,c,AD=BC=x,AB=CD=y,AC=BD=z,列方程组:a^2+b^2=x^2b+c=yc^2+a^2=z^2根据墙角模型,我们可以得到2R=a+b+c=2(x^2+y^2+z^2)/(x^2+y^2+z^2),化简得到R=sqrt(2)/2*(x^2+y^2+z^2)/(x^2+y^2+z^2),求出R即可。
例2(1)如下图所示三棱锥A-BCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为。
2)在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,则三棱锥A-BCD外接球的表面积为。
3)正四面体的各条棱长都为2,则该正面体外接球的体积为。
专题——几何体的外接球和内切球问题

B.112π
C.1 000π 9
D.5 000 10π 81
※内切球问题 1.正棱锥的内切球.
第一步:先现出内切球的截面图, E, H 分别是两个三角形的外心; 第二步:由 POE 相似于 PDH ,建立等式: OE PO ,解出 r
DH PD
2.任意多面体的内切球:等体积法,
例 3 非直二面角类型
(1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
专题——几何体的外接球和内切球问题
※基础知识:
1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆
长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半;
正三角形的内切圆半径: 3 a 6
外接圆半径: 3 a 3
面体的外接球的球心。 由定义,给出以下简单多面体外接球的球心的结论。
结论 1:正方体或长方体的外接球的球心就是其体对角线的中点,即其外接球的半径 R 满足:
2R2 a2 b2 c2 ,即 R a2 b2 c2
2 结论 2:正棱柱的外接球的球心是上下底面中心的连线的中点,即正棱柱的外接球的半径 R 为: R h 2 r 2 (其中 h 为正棱柱的侧棱长, r 是底面多边形的外接圆的半径)
(1)已知边长为 2 3 的菱形 ABCD 中,BAD 60 ,沿对角线 BD 折成二面角 A BD C 的大
小为120 的四面体,则该四面体的外接球的表面积为
。
第一步:先求出多面体的表面积和体积; 第二步:解出 r 3V S表
例 1、正方体的内切球与其外接球的体积之比为( )
球。
3.球的截面:
用一平面 去截一个球 O ,设 OO 是平面 的垂线段,O 为垂 足,且 OO d ,所得的截面是以球心在截面内的射影为圆心,以
空间几何的体积与表面积 高考数学一轮复习(提升版)(新高考地区专用)
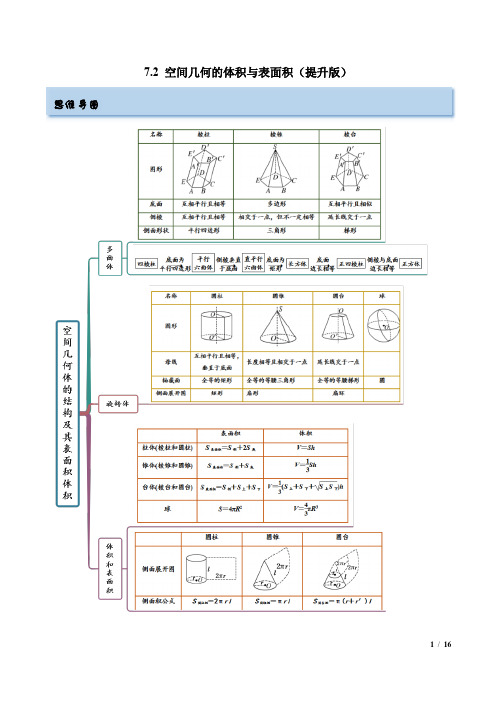
7.2 空间几何的体积与表面积(提升版)思维导图考点一柱锥台表面积【例1-1】(2022·青海)以边长为4的正方形的一边所在直线为旋转轴,将该正方形旋转一周,所得圆柱的侧面积为()A.32πB.16πC.32D.16【答案】A【解析】以边长为4的正方形的一边所在直线为旋转轴,旋转一周得到的旋转体为圆柱,其底面半径4r=,高4h=,故其侧面积224432S r hπππ=⋅=⨯⨯=.故选:A【例1-2】(2022·天津·南开中学模拟预测)已知圆锥PO的母线长与底面直径都等于2,一个圆柱内接于这个圆锥,即圆柱的上底面是圆锥的一个截面,下底面在圆锥的底面内,则圆柱侧面积的最大值为()A.3π2B.3πC.()633π-D.3【答案】A【解析】如图,1AB=,2BE=,3AE=,则30AEB∠=,设DC r=,01r<<,则2EC r=,3DE r=,则33AD AE DE r=-=-,考点呈现例题剖析∴圆柱侧面积为:)()221132π2π3323π23π22S r AD r r r r ⎡⎤⎛⎫=⋅=⋅=-+≤-+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,当12r =时取等号.故选:A . 【一隅三反】1.(2023·全国·高三专题练习)《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥,若某直角圆锥内接于一球(圆锥的顶点和底面上各点均在该球面上),求此圆锥侧面积和球表面积之比( ) A .24B 22C 2D .24π【答案】A【解析】设直角圆锥底面半径为r 2r , ()222rr r -=,所以底面圆的圆心即为外接球的球心,所以外接球半径为r , 所以22224S rl r S r πππ==圆锥侧球故选:A. 2.(2022·福建三明·模拟预测)如图所示的建筑物是号称“神州第一圆楼”的福建土楼——二宜楼,其外形是圆柱形,圆楼直径为73.4m ,忽略二宜楼顶部的屋檐,若二宜楼的外层圆柱墙面的侧面积略小于底面直径为40m ,高为77的圆锥的侧面积的23,则二宜楼外层圆柱墙面的高度可能为( )A .16mB .17mC .18mD .19m【答案】A【解析】底面直径为40m ,高为77m ()2210772090m +=,所以该圆锥的侧面积为220901800cm ππ⋅⋅=,设二宜楼外层圆柱墙面的高度为h ,则由36.72h π⨯1200π=,解得16.3h ≈因为二宜楼的外层圆柱墙面的侧面积略小于底面直径为40m ,高为77的圆锥的侧面积的23, 所以二宜楼外层圆柱墙面的高度可能为16m , 故选:A3.(2022·江苏·阜宁县东沟中学模拟预测)民间娱乐健身工具陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺的立体结构图.已知.底面圆的直径16cm AB =,圆柱体部分的高8cm BC =,圆锥体部分的高6cm CD =,则这个陀螺的表面积是( )A .2192m c πB .2252m c πC .2272m c πD .2336m c π【答案】C【解析】由题意可得圆锥体的母线长为226810l =+=, 所以圆锥体的侧面积为10880ππ⨯=,圆柱体的侧面积为168128ππ⨯=,圆柱的底面面积为2864ππ⨯=, 所以此陀螺的表面积为8012864272ππππ++=(2cm ),故选:C考点二 柱锥台的体积【例2-1】(2022·全国·高三专题练习)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC 是边长为2的正三角形,SC 为球O 的直径,且4SC =,则此棱锥的体积为( )A 42B 43C 82D .42【答案】A【解析】解:因为ABC 是边长为2的正三角形,所以ABC 外接圆的半径12232sin 60r =⋅=︒所以点O 到平面ABC 的距离2226d R r -SC 为球O 的直径,点S 到平面ABC 的距离为462d =此棱锥的体积为2111464222sin 60332ABCV S d =⨯=⨯⨯,故选:A .【例2-2】(2022·天津·高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120︒,腰为3的等腰三角形,则该几何体的体积为( )A .23B .24C .26D .27【答案】D【解析】该几何体由直三棱柱AFD BHC -及直三棱柱DGC AEB -组成,作HM CB ⊥于M ,如图, 因为3,120CH BH CHB ==∠=,所以3332CM BM HM ==, 因为重叠后的底面为正方形,所以33AB BC ==, 在直棱柱AFD BHC -中,AB ⊥平面BHC ,则AB HM ⊥, 由AB BC B ⋂=可得HM ⊥平面ADCB , 设重叠后的EG 与FH 交点为,I则132713813333,=3333=322224I BCDA AFD BHC V V --=⨯=⨯⨯则该几何体的体积为8127222742AFD BHC I BCDA V V V --=-=⨯-=.故选:D. 【例2-3】(2022·湖北·高三阶段练习)已知四面体D ABC -中,1AC BC AD BD ====,则D ABC -体积的最大值为( ) A 42B 32C 23D 3【答案】C【解析】设M 为CD 的中点,连接AM,BM , 设四面体A -BCD 的高为h ,则h AM ≤,由于1AC BC AD BD ====,故ACD BCD ≌ , 则ACD BCD ∠=∠,设π,(0,)2BCD ACD αα∈∠=∠=,则sin sin ,22cos 2cos AM BM BC CD CM BC αααα======, 所以1136D ABC A DBC BCDV V Sh CD BM AM --==⋅≤⋅⋅222222231112cos sin sin cos sin 2cos sin sin ()333232αααααααα++==⋅⋅23, 当且仅当平面ACD 与平面BCD 垂直且sin 2αα=即arctan 2α=时取等号,故选:C 【一隅三反】1.(2022·江苏)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若=2S S 甲乙,则=VV 甲乙( ) A 5B .22C 10D 510【答案】C【解析】设母线长为l ,甲圆锥底面半径为1r ,乙圆锥底面圆半径为2r ,则11222S rl rS r l r ππ===甲乙,所以122r r =,又12222r r l l πππ+=,则121r r l +=,所以1221,33r l r l ==,所以甲圆锥的高221459h l l =-=,乙圆锥的高2221229h l l =-=,所以221122221453931011223r h l V V r h l l ππ==⨯甲乙故选:C. 2.(2022·广西桂林)一个三棱锥S -ABC 的侧棱上各有一个小洞D ,E ,F ,且SD :DA =SE :EB =CF :FS =3:1,则这个容器最多可盛放原来容器的( ) A .89B .49C .5564D .23【答案】C【解析】由题意,这个容器最多可盛放原来容器的比例为DEF ABC S ABC S DEFS ABC S ABC V V V V V ------=,设C 到平面SAB 的距离为h ,则13S ABC C ABS SAB V V Sh --==.又91991646464S DEF F SDE SABSAB C ABS V V S h S h V ---==⨯=⨯=,故915564164DEF ABC S ABC S DEFS ABC S ABCV V V V V -------=== 故选:C3.(2023·全国·高三专题练习)足球起源于中国古代的蹴鞠游戏.“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,如图所示.已知某“鞠”的表面上有四个点,,,P A B C,满足1,PA PA =⊥面ABC ,AC BC ⊥,若23P ABC V -=,则该“鞠”的体积的最小值为( )A .256π B .9πC .92πD .98π【答案】C【解析】取AB 中点为D ,过D 作//OD PA ,且11==22OD PA ,因为PA ⊥平面ABC,所以OD ⊥平面ABC .由于AC BC ⊥,故DA DB DC ==,进而可知OA OB OC OP ===,所以O 是球心,OA 为球的半径.由112==4323P ABC V AC CB PA AC CB -=⨯⋅⋅⇒⋅,又2222=8AB AC BC AC BC =+≥⋅,当且仅当2AC BC ==,等号成立,故此时22AB =所以球半径()2222113+2222R OA OD AB ⎛⎫⎛⎫==+≥ ⎪ ⎪⎝⎭⎝⎭,故min 3=2R ,体积最小值为334439πππ3322R ⎛⎫== ⎪⎝⎭故选:C4.(2023·全国·高三专题练习)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且333l ≤≤ ) A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27]【答案】C【解析】∴ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当326l ≤≤0V '>,当2633l ≤0V '<, 所以当26l =时,正四棱锥的体积V 取最大值,最大值为643, 又3l =时,274V =,33l =814V =,所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.考点三 球的体积与表面积【例3】(2022·甘肃省武威第一中学)如图,半径为4的球O 中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的表面积之差为( )A .64πB .48πC .32πD .16π【答案】D 【解析】如图.设圆柱底面半径为r ,球的半径与圆柱底面夹角为OMN α∠=,则cos 4cos MN r R αα==⋅=,sin 4sin ON R αα=⋅=,∴圆柱的高8sin h α=,∴圆柱的侧面积为232sin2S r h ππα=⋅⋅=⋅,当且仅当4πα=时,sin21α=,圆柱的侧面积最大,为32π, 球的表面积与圆柱的表面积之差为22422(22)64321616R rh πππππππ--⨯=--=.故选:D . 【一隅三反】1.(2022·全国·赣州市第三中学)已知某正三棱锥S ABC -的内切球与外接球的球心恰好重合,如果其内切球的半径为1,其外接球的体积为36π,那么这个三棱锥的表面积为( ) A .24 B .243C .48D .483【答案】B【解析】由题意可知,点S 在底面ABC 内的射影点D 为等边ABC 的中心,取线段BC 的中点E ,连接AE ,则2AD DE =,易知三棱锥S ABC -的外接球球心O 在线段SD 上,设正三棱锥S ABC -的外接球半径为R ,则34363R ππ=,解得3R =,设正三棱锥S ABC -的内切球的半径为r ,则1r =,故314SD R r =+=+=,SD ⊥平面ABC ,AD ⊂平面ABC ,SD AD ∴⊥,易知3OA R ==,则222222AD OA OD R r --=所以,122DE AD ==32AE =26sin 3AEAB π== 由勾股定理可得2226SA SD AD =+=所以,正三棱锥S ABC -是边长为6 因此,正三棱锥S ABC -的表面积为(23426=243故选:B.2.(2022·天津·耀华中学二模)一个圆锥的侧面展开图是一个半圆,则该圆锥的内切球的表面积和圆锥的侧面积的比为( ) A .2:3 B .3:2 C .1:2 D .3:4【答案】A【解析】设圆锥的底面半径为r ,母线长为l ,圆锥的高为h ,内切球的半径为R ,其轴截面如图所示,设O 为内切球球心,因为圆锥的侧面展开图是一个半圆, 所以2l r ππ=,得2l r =,即2PA PB r ==, 所以222243PD PB BD r r r =--, 所以3PO PD OD r R =-=-, 因为POE △∴PBD △,所以PO OEPB BD=, 3r R Rr -=,得3R =, 所以圆锥的内切球的表面积和圆锥的侧面积的比为 22214:4:22:33R rl r r ππππ=⋅=,故选:A3.(2022·山东青岛·二模)《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体,如图,羡除ABCDEF 中,底面ABCD 是正方形,EF ∥平面ABCD ,2EF =,其余棱长都为1,则这个几何体的外接球的体积为( )A 2B .4π3C 82D .4π【答案】B【解析】连接AC ,BD 交于点M ,取EF 的中点O ,则OM ⊥平面ABCD ,,取BC 的中点G ,连接FG ,作GH EF ⊥,垂足为H ,如图所示由题意可知,13,2HF FG ==222HG FG HF =- 所以2OM HG ==2AM =所以221OA OM AM +=,又1OE =, 所以1OA OB OC OD OE OF ======,即这个几何体的外接球的球心为O ,半径为1, 所以这个几何体的外接球的体积为33444ππ1π333V R ==⨯⨯=.故选:B.考点四 空间几何的截面【例4-1】(2022·全国·高三专题练习)已知圆锥的母线长为2,侧面积为23π,则过顶点的截面面积的最大值等于( ) A 3B 2C .3 D .2【答案】D【解析】由圆锥的母线长为2,侧面积为3π,假设底面圆周长为l ,因此12232l π⨯⨯=,故底面圆周长为23π3由于轴截面为腰长为2,底边长为底面圆直径32π3.故当截面为顶角是π2的等腰三角形时面积最大,此时1π22sin 222S =⋅⋅⋅=.故选:D【例4-2】.(2022·湖南·长沙一中模拟预测)(多选)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则( )A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165π C .四面体CDEF 的体积的取值范围为3203⎛⎤⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为22543⎡+⎣,【答案】BCD【解析】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积 为24r π,圆柱的表面积222226r r r r πππ+⋅=, 所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得125225OG ==设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=, 所以平面DEF 截得球的截面面积最小值为165π,故B 正确; 由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈, 又114482DCO S=⨯⨯=,所以123228(0,]33E DCO V d -=⨯∈,故C 正确;由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ',则2222222,2,2,16PP PE P E PF P F P E P F '''''==+++=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,222216PE PF t t +++-所以()222222216241680PE PF t tt t +=++-=+-++()224281442485,48t ⎡⎤=+--++⎣⎦,所以225,43PE PF ⎡+∈+⎣,故D 正确.故选:BCD.【一隅三反】1.(2022·江西鹰潭·二模)《算数术》竹简于上世纪八十年代出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也,叉以高乘之,三十六成一."该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式2136V L h ≈.它实际上是将圆锥体积公式中的圆周率π近似取为3.现有一圆锥底面周长为563,侧面面积为1123,其体积的近似公式为23112V L h ≈,用此π的近似取值(用分数表示)计算过该圆锥顶点的截面面积的最大值为( ) A .15 B .37C .8821D .8【答案】D【解析】若圆锥母线长为l ,底面半径为r ,则156112233l ⨯=,故4l,又5623r π=,故283r π=, 而22133112V r h L h π=≈,则2228356()()31123ππ⨯≈⨯,可得289π=, 所以3r =,若截面顶角θ,当截面为轴截面时2221cos 108r l θ=-=-<,此时2πθπ<<,又截面面积为21sin 8sin 2l θθ=,故当2πθ=时截面面积的最大值为8.故选:D2.(2022·河南·方城第一高级中学)某中学开展劳动实习,学生对圆台体木块进行平面切割,已知圆台的上底面半径为1,下底面半径为2,要求切割面经过圆台的两条母线且使得切割面的面积最大.3则切割面的面积为______3______. 【答案】 2 33【解析】解法一:如图,将圆台1O O 补成圆锥PO ,设圆台1O O 的上、下底面半径分别为r ,R ,高和母线长分别为h ,l ,则()222l h R r =+-.因为等腰梯形ABCD 为过两条母线的截面,设PC x =.APB θ∠=,则r x R x l=+,得rl x R r=-,则()()2221sin sin 22PAB PCD ABCD R r S S S x l x l R r θθ+⎡⎤=-=+-=⎣⎦-△△梯形.∴若33h ,则23l =,0120θ︒<≤︒,当90θ=︒时,切割面的面积最大,最大面积2S =;∴若3h =2l =,060θ︒<︒≤,当60θ=︒时,切割面的面积最大,最大面积33S =解法二:如图,设圆台上底面圆心为1O ,下底面圆心为O ,过两条母线的截面为四边形11ABB A ,可得四边形11ABB A 为等腰梯形.设111AO B AOB θ∠=∠=,圆台的高1O O h =,取11A B ,AB 的中点分别为1C ,D ,连接11O C ,1C D ,OD ,则四边形11O C DO 为直角梯形,过1C 作11C C O O ∥交OD 于点C.因为111O B =,2OB =,所以11cos2O C θ=,111122sin2A B B C θ==,2cos2OD θ=,24sin 2AB BD θ==,所以11cos 2CD OD O C θ=-=,所以221cos 2DC h θ=+则()11221111cos 222ABB A S S AB A B DC h θθ==+⋅=+梯形令sin 2t θ=,因为(]0,θπ∈,所以(]0,1t ∈,则2231S t h =-+(]0,1t ∈.∴当3h 时,2222244333232t t S t t ⎛⎫+- ⎪⎛⎫=-≤= ⎪ ⎪⎝⎭ ⎪⎝⎭,当且仅当2243t t =-,即6t =max 2S =.∴当3h =()22423434S t t t t =--+令2t x =,则(]0,1x ∈,()24224424t t x x x -+=-+=--+,当1x =时,取最大值3.此时max 33S =故答案为:2;333.(2022·青海·海东市第一中学)已知圆锥的底面直径为2323则该圆锥的体积为________. 5π【解析】由题意知:圆锥的底面半径3r =设圆锥的母线长为l ,则2213sin 2323l π⋅==22l =∴圆锥的高22835h l r =--=∴圆锥的体积2153V r h ππ=⋅=.5π.。
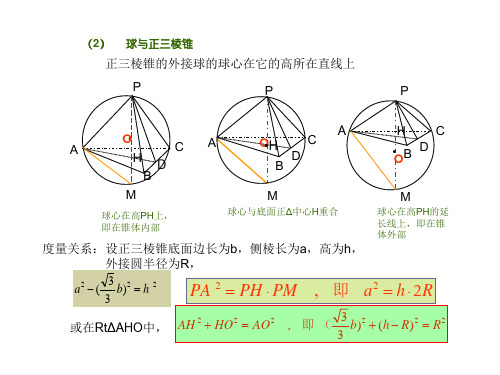
球与正三棱锥和正三棱柱的切接关系讲解
b 2 R 6a 3
P
O
C
D
B
M
由
V锥
1 3
Sh
1 3
3 a2 4
3 a 1 a3 3 12
3
得: a3 12 3
R3 3 a3 3 12 3 4
9
9
如图, 设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且
AB AC 6, AD 2 ,则AD两点间的球面距离
斜高 h 2 a , 高 h a2 ( 3 b)2 a2 6 a2 3 a
2
3
9
3
代入正三棱锥内切球半径公式:
得:
r a 3
3 36
3a
r 3 bh 6h 3 b
OK C HD
B
P
K O
又 正三棱锥外接球半径
R 3a 2
H
D
r 3 3 3 3 3 2 3 1
真题赏析
(2009全国卷Ⅰ理)直三棱柱 ABC A1B1C1 的各顶点都在同一球 面上,若 AB AC AA1 2 , BAC 120 ,则此球的表面积
等于 20。
解:在 ABC 中, AB AC 2 , BAC 120 可得 BC 2 3
由正弦定理,可得 ABC 外接圆半径r=2,设此圆圆心为 O ,
:4
R2
6(2 3)2 3
于A,B,C三点,若球的体积为 4 , 则OP的距离为( B )
3
A. 2 B. 3 C. 1 D. 2
P
2
P
解析:先想象一下图形,画出示意图
因PA与球O相切于点A, ∴OA⊥PA,同理,OB⊥PB,OC⊥PC.
立体几何中的“内切”与“外接”问题的探究(完美版)

立体几何中的“内切”与“外接”问题的探究一、由球心的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球球心。
二、由上述性质可以得出以下多面体外接球的结论:结论1:正方体或长方体的外接球的球心是其体对角线的中点。
结论2:正棱柱的外接球的球心是上下底面中心的连线的中点。
结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
结论4:正棱锥的外接球的球心是在其高上,具体位置可通过计算得到。
结论5:若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
一、定义法例1、 在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解 设矩形对角线的交点为O ,则由矩形对角线互相平分,可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C.二、求正方体、长方体的外接球的有关问题结论1:正方体或长方体的外接球的球心是其体对角线的中点。
①出现“墙角”结构利用构造法(补形法),联系长方体。
【原理】:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=例1、若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ,则有()()()()222223339R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222R a b c =++.②出现正四面体外接球时利用构造法(补形法),联系正方体。
球与正三棱锥和正三棱柱的切接关系

Rt PHD ∽ Rt PKO
PD HD PO KO
6 b h 3 hr r
OK HD 或 sin P OP PD
3 b r 6 hr h
3 bh r 6h 3 b
把有关立体几何的计算转化为平面几何的计算,是最基本的策略。
题目:
正三棱锥P---ABC的侧棱长为1,底面边长为 2 ,它 的四个顶点在同一个球面上,则球的体积为 ( A )
3 3 2R , R 3 2
4 4 3 3 3 V球 R 3 ( ) 3 3 2 2
法二 由AH>PH知:球心O在正三棱锥的高PH的延长线上。在RtΔAHO,有:
( 6 2 3 3 ) (R )2 R 2 , R 3 3 2
题目:
正三棱锥P—ABC的三条侧棱两两互相垂直,则该正三 棱锥的内切球与外接球的半径之比为 ( D )
3
BOC
2
O C B A
②∵OA=OB=OC=1
AOB、AOC都是边长为1的正三角形
而BOC是等腰直角三角形, AB AC 1 , BC 2
ABC是等腰直角三角形, BAC
O A O B A
O C C
2
, ABC的 BC 2 2 2
外接圆圆心是 BC 中点,外接圆半径 r
A. 1: 3 B. 1: (3 3) C. ( 3 1) : 3 D. ( 3 1) : 3
P
解析: 设正三棱锥侧棱长为a ,底面边长为b ,∵三侧棱两 两垂直,∴各侧面都是全等的等腰直角三角形。
b 2 a
斜高 h
A
O
K D
立体几何中的“内切”与“外接”问题的探究(完美版)

立体几何中的“内切”与“外接”问题的探究(完美版)探究立体几何中“内切”与“外接”问题在立体几何中,我们经常遇到“内切”和“外接”的问题。
在研究这些问题之前,我们需要先明确球心的定义。
如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球球心。
根据上述性质,我们可以得出以下多面体外接球的结论:1.正方体或长方体的外接球的球心是其体对角线的中点。
2.正棱柱的外接球的球心是上下底面中心的连线的中点。
3.直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
4.正棱锥的外接球的球心在其高上,具体位置可通过计算得到。
5.若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
接下来我们来探究一下正方体和长方体的外接球的问题。
根据结论1,正方体或长方体的外接球的球心是其体对角线的中点。
我们可以利用构造法(补形法)来解决这类问题。
例如,对于一个长方体,如果从一个顶点出发的三条棱长分别为a、b、c,则体对角线长为√(a^2+b^2+c^2),几何体的外接球直径2R为体对角线长l,因此R=√(a^2+b^2+c^2)/2.举个例子,如果一个三棱锥的三个侧面两两垂直,且侧棱长均为3,则可以将这个三棱锥补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球。
设其外接球的半径为R,则有(2R)^2=3^2+3^2+3^2=27.因此,其外接球的表面积为S=4πR^2=36π。
另外,对于一个矩形ABCD,如果AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为(125π)/(1296)。
最后,如果出现正四面体外接球的问题,我们可以利用构造法(补形法),联系正方体。
一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为多少?解析:由于所有棱长都相等,所以可以构造一个正方体,再寻找棱长相等的四面体。
如图2所示,四面体ABDE满足条件,即AB=AD=AE=BD=DE=BE=2.由此可求得正方体的棱长为1,对角线为$\sqrt{3}$,从而外接球的直径也为$\sqrt{3}$,所以此球的表面积为$4\pi$,故选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正三棱锥的内切球与外接球要回答这个问题,先要了解什么是正三棱锥.
请看正三棱锥的定义.
1.底面是正三角形
2.顶点在底面的射影是底面三角形的中心.满足以上两条的三棱锥是正三棱锥.
由以上定义可知,正三棱锥底面为正三角形,三个侧面是全等的等腰三角形.
要防止和另外一个概念----正四面体混淆.
正四面体的要求比正三棱锥更要.每个面都是正三角形的四面体才是正四面体.我们可以说,正四面体是特殊的正三棱锥,正三棱锥具备的性质正四面体都有,而正四面体具备的性质正三棱锥不一定有.
下面来说如何寻找正三棱锥的内切球和外接球球心.
在棱柱和棱锥的外接球中,谈到了一种方法,就是把符合条件的棱锥和棱柱放入长方体中,从而把问题转化、简化为长方体的外接球的问题.
这是处理问题的方法之一.
适合这种方法的情况可小结如下:
⑴正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥.⑵同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥.
⑶若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.
⑷若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.
今天说说第二种方法,就是利用球的定义确定球心.
基本的规律可小结如下:
⑴长方体或正方体的外接球的球心是其体对角线的中点.
⑵正三棱柱的外接球的球心是上下底面中心连线的中点.
⑶直三棱柱的外接球的球心是上下底面三角形外心连线的中点.
⑷正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到.
我们利用第(4)条结论来研究正三棱锥的外接球球心的位置.
举一个具体栗子来说明.外接球球心分析:在正三棱锥的高线上,先假设一个位置,然后构造直角三角形,利用勾股定理求解.从图看出,此正三棱锥的外接球球心在高线PO的延长线上.
再来求内切球的球心位置.由正三棱锥的对称性可知,内切球球心也在高线PO上.
下面利用等体积法(即算两次体积)求内切球的半径.等体积法已经是第二次提到了,第一次提起是在线面角和点面距中.回到这位朋友的问题上来,外接球球心和内切球球心重合吗
显然,多数情况下是不重合的.
有童鞋可能会问,有没有重合的时候呢
为了回答这个问题,我们作一般化的推导.若底边长刚好等于侧棱长,即正三棱锥变为正四面体时,奇迹发生了.
画出图来是这样滴.
此时,两心重合于一点,且该点把三棱锥的高分为3:1,长的那段为外接球半径,短的那一段为内切球半径.。
