2-电阻电路的化简和等效变换
合集下载
二章电阻电路等效变换
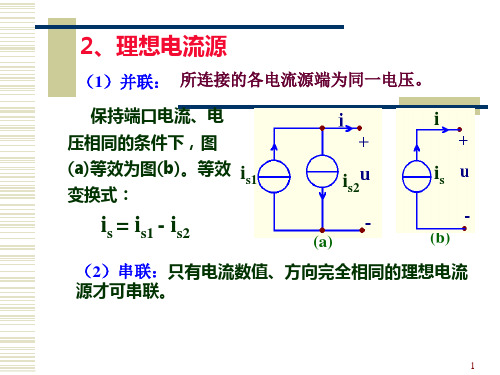
2、理想电流源
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
电工基础实用教程2-1电阻电路的等效简明教程PPT课件

电 工 基 础
例题 1 求图2-1-7 (a)中a、b两端钮间的等效电阻Rab 。(图中电阻的单位为Ω)。
电 工 基 础
解:从图(a)难于看出串、并联关系,为此在 不改变各元件连接关系的前提下,设法改画电路 图。c、d两点等电位,所以c、d两点可重合为一 点,将与e点相连的各元件合并移动得图(b), 可见8Ω与8Ω、2Ω与2Ω都是并联,求它们的等 效电阻得图(c)。化简得图(d),等效化简过 程如图2-1-7所示: 由(d)图可知 R=4+10//10=4+5=9Ω
电 工 基 础
教学重点
1.支路电流法、网孔电流法、节点电压法、叠加定理以及戴维 南定理的应用。 2.电阻电路的化简。 3 .会选择最佳分析方法对电路进行分析与计算。
电 工 基 础
2.1电阻电路的等效
一、电阻的串联及分压 I1 I 2 I 1 串联电路的特点
U U1 U 2 U n
解:分析(a)图可知,图中共有两个星形和三个三角形,如果先 变星形,无论先变哪一个都需变两步才变成简单电路,而且数据 计算不方便;如果变中间的三角形,则需再做一次三角形变换, 且数据计算不便,较烦琐,而变ace和dbf两个三角形时,不仅数 据容易计算,而且两个三角形可以同时进行变换,在一步内变换 成简单电路,因此是最佳方安。 将ace和dbf两个三角形变换成星形,变换过程如下图所示:
R R1 R2 Rn
分压公式
Rn Un U R
电 工 基 础
二、 电阻的并联与分流 1 电阻的并联的特点
U U1 U2 Un
I I1 I 2 I n
1 1 1 1 R R1 R2 Rn
2 分流公式
第二章 电阻电路的等效变换

注意: 注意: 上的电压; (1)变换后 0是两个元件上的电压; )变换后u 两个元件上的电压 控制变量所在支路不能动 (2)受控源的控制变量所在支路不能动。 )受控源的控制变量所在支路不能动。 2. 利用两类约束找关系 利用两类约束 两类约束找关系
1 对回路列KVL: (1 + R 3 + R 4 )i + 2 R 4 u 3 = u S 对回路列 : 2 受控源的控制量: 受控源的控制量: u 3 = R3 i
2、并联等效电阻 、并联等效电阻
(1)等效条件: )等效条件: (2)分流公式: )分流公式:
G
等
=
∑
G
并
Gk ik = G k u = i G等
i1
i2 G2 iS
特殊: 特殊:
G
k
= ∞ ,即 R
k
=
0 ,
i
k
=
i
,
短路处电流 电流源电流 其它电导电流 电流= 电流, 电导电流= ) (短路处电流=电流源电流,其它电导电流=0)
§2-1 引言 -
由时不变线性无源元件、线性受控源和独立电源 时不变线性无源元件 线性受控源和 元件、 组成的电路,称为时不变线性电路,简称线性电 组成的电路,称为时不变线性电路,简称线性电 路。 如果构成电路的无源元件均为线性电阻,则称为 如果构成电路的无源元件均为线性电阻, 构成电路的无源元件均为线性电阻 线性电阻性电路。 线性电阻性电路。电路中电压源的电压或电流源 的电流,可以是直流, 的电流,可以是直流,也可以随时间按某种规律 变化;当电路中的独立电源均为直流电源 直流电源时 变化;当电路中的独立电源均为直流电源时,称 直流电路。 为直流电路。 简单电阻电路的分析与计算 本章为简单电阻电路的分析与计算,着重介绍 本章为简单电阻电路的分析与计算, 等效变换的概念 的概念。 等效变换的概念。
电阻电路的等效变换和化简

(1) 电阻串连时,各电阻消耗的功率与电阻大小成正比 (2) 等效电阻消耗的功率等于各串连电阻消耗功率的总和
返回 上页 下页
2. 电阻并联 (Parallel Connection)
(1) 电路特点
i
+
i1 i2
ik
in
u R1 R2
Rk
Rn
_
(a) 各电阻两端分别接在一起,两端为同一电压 (KVL); (b) 总电流等于流过各并联电阻的电流之和 (KCL)。
3.
b
100 10 60 50
80 R
c
R
2.
5
a 20
15 b
7
6
6
a
b
R
R
d
返回 上页 下页
例 求: Rab
a
b
20
100 10
40
60 50
a
20
120
b
100 60
60
80
a
b
20 100
a
b
100
Rab=70
20 40
100 60
返回 上页 下页
例 求: Rab
20
5a15 b2 Nhomakorabea 缩短无电阻支路
R1
包含
1
a
R3
1d
R12
R31
R1
R2
R3
2
R23
3
2
3
型网络
Y型网络
R2
b
R4
三端 网络
返回 上页 下页
,Y 网络的变形:
型电路 ( 型)
T 型电路 (Y、星 型)
这两个电路当它们的电阻满足一定的关系时,能够相互等效
2-电阻电路的等效变换

§2.3电阻的星形联接与三角形联接 的等效变换 (Y—变换)
一.电阻的 、Y形连接 R1 a R2
R3
b R4
R5 1
R1 R2 2 0 Y形网络 R3 3
包含
1 三端 网络 R31
R12 2 R23 形网络
3
二.电阻的 Υ Δ 变换:
1
R12
R1 R2 R2 R3 R3 R1 R3
选择
练练
对称的电阻星型连接在等效成对称的三角形连接时, 每边的电阻是原来的( )。 A 、2倍; B 、1/2; C、3倍; D、1/3;
应用举例
例: 求图示电路的等效电阻Rab。 2-3 4 4 a a R1 1.5 3 5 2 等效 0.6 Rab 1 Rab R3 R2 1 1 1 1 b b 解: 将电路上面的Δ联接部分等效为Y联接, 3 5 R1 1.5 352 2 1.6 2 5 Rab 4 1.5 6.39 R2 1 2 1.6 352 2 3 R3 0.6 352
30 等 效 c 15
60 d
1 1 1 1 Gcd S 60 30 60 15 1 Rcd 15 Gcd
d
应用举例
例: 求图所示惠斯通电桥的平衡条件。 2-2 解: 电桥平衡时,检流计G的读数为零。 c 因此所谓电桥平衡的条件就是指电 i3 阻R1,R2,R3,R4满足什么关系时, R1 i R3 g 检流计的读数为零。 ig=0时,检流 i1 R5 a d 计所在的支路相当于开路,故有: uac=uab G R2 R4 ucb=0 ug=0 ig=0 i4 i2 ucd=ubd RS b 即: R1i1 R2 i2 , R3 i3 R4 i4 – + uS R1 R2 两式相比有: R3 R4 即电桥平衡的条件是: R1 R4 R2 R3
邱关源《电路》第五版 第二章 电阻电路的等效变换

a
10
10 10 10
b
10
Rab=5
b
10
§2-3 电阻的串联和并联 求解等效电阻时必须注意:
* 首先搞清对何处等效;
* 分清串、并联关系;
* 可改画电路,原则是电阻相互联接关系不能改 变,但电阻位置可变,尽量缩短无阻支路,逐 步等效,逐步化简。 * 等电位点可以短路,电流为零的支路可以开路。 特别注意电路中有无平衡电桥电路。
-
2
§2-5 电压源、电流源的串联和并联 4. 电流源与任意支路串联
iS R i + 1
+
uS
iS + u
1
u
-
2 iS
1
-2
+
u
-
2
§2-5 电压源、电流源的串联和并联 5. 举例
【例1】化简电路。
iS1 =1A
-ห้องสมุดไป่ตู้
+
uS1=2V
1
+
uS2=2V
R1=1
iS2=1A
R2=1
2
§2-6 实际电源的两种模型及其等效变换
2
2
iS
iS iS1 iS2 iSn
iS1 iS 1 iS2 iSn
显然只有电流源 电流相等时,才允 2 许串联。
iS iS1 iS2 iSn
§2-5 电压源、电流源的串联和并联 3. 电压源与任意支路并联
+
uS
i R 1
+
uS
1 iS i
-
2 1
2
+
uS
i
3 R3 i3
i1
第二章:电阻电路的等效变换

Rab RbcRca
b
Rb
c
Ib Ic
b
c
电阻Y形联接 Y
Ra Rb + Rb Rc + Rc Ra Rab = Rc Ra Rb + Rb Rc + Rc Ra Rbc = Ra Ra Rb + Rb Rc + Rc Ra Rca = Rb
(2-7)
Ia
a
Rab RbcRca
Ia
Ra Ib
R1 c R3 R6
a b R5 e (a)
R2 d R4
a
R1 R6 R3 R5 e (b)
R2 c d R4
b
3 电路具有某种对称性时,可在电路中找到一些 等电位点,把等电位点联在一起,不会使电路中各 元件的电位发生变化。
例如: 桥式电路,若 R1 = R3 ,R2 = R4 则电路对称,
b、c 两点等电位;可把b、c联在一起,如图 b) 。
例2-3 :求下列各电路的等效电源 a
2 3 5V
+
+
U
a 2 2V
+
(a)
U
2 5A
3 (b)
+ -
+ 5V (c)
+
U
a
–
–b
–b
a
–b
a
解:
2
+
U
(a)
a 5A 3 (b)
+
U
+
+ –
b 5V (c)
+
U
–
5V
b
b
例2-4 :已知:R1=R2=2 ,R3=R4=1 ;求u0 /uS 。 _ u3 _ u3 + R1 + + + R3 + R4 R3 1 u0 u0 u + + s R4 R2 _ 2u 0.5us 2u _ 3 _ _3 _
b
Rb
c
Ib Ic
b
c
电阻Y形联接 Y
Ra Rb + Rb Rc + Rc Ra Rab = Rc Ra Rb + Rb Rc + Rc Ra Rbc = Ra Ra Rb + Rb Rc + Rc Ra Rca = Rb
(2-7)
Ia
a
Rab RbcRca
Ia
Ra Ib
R1 c R3 R6
a b R5 e (a)
R2 d R4
a
R1 R6 R3 R5 e (b)
R2 c d R4
b
3 电路具有某种对称性时,可在电路中找到一些 等电位点,把等电位点联在一起,不会使电路中各 元件的电位发生变化。
例如: 桥式电路,若 R1 = R3 ,R2 = R4 则电路对称,
b、c 两点等电位;可把b、c联在一起,如图 b) 。
例2-3 :求下列各电路的等效电源 a
2 3 5V
+
+
U
a 2 2V
+
(a)
U
2 5A
3 (b)
+ -
+ 5V (c)
+
U
a
–
–b
–b
a
–b
a
解:
2
+
U
(a)
a 5A 3 (b)
+
U
+
+ –
b 5V (c)
+
U
–
5V
b
b
例2-4 :已知:R1=R2=2 ,R3=R4=1 ;求u0 /uS 。 _ u3 _ u3 + R1 + + + R3 + R4 R3 1 u0 u0 u + + s R4 R2 _ 2u 0.5us 2u _ 3 _ _3 _
第二章 电阻电路等效变换

2、说明下图所示三个电路对端口而言,是否互 为等效电路。
§2-5 实际电源两种模型及其等效变换
一、实际电源的模型 实际电压源
u Us
理想电压源 实际电压源
理想电压源: 0 其特性仅由唯一参数 us来描述,且与外电路无关。
i
实际电压源:其端电压是随着输出电流 的改变而变化的。 原因:实际电压源内部存在电阻,即内 部有损耗。
R31 i3'
i'1 2
R23
i'2 3
2)形等效为Y形,有
R31 R12 R1 R12 R23 R31 R12 R23 R2 R12 R23 R31 R23 R31 R3 R R R 12 23 31
i1'
R12
R31
N1
2、等效电导
a
i i1 G1
+ u b
i2 G2
…
in Gn
a b
i + u Geq N2
N1
i = i1+ i2++ in = G1u+G2u++ Gnu =(G1+ G2+… +Gn)u 令 Geq= G1+ G2+… +Gn=Gk;则有: i = Geq u 可见: Geq= Gk —等效电导 或1 / Req=1/ Rk,Req R k
I
a Is b
I' Rs'
a
b
(3) 理想电压源和理想电流源不能等效互换 a I' a I + Uab' Us Is b b
Us Us IS (不存在) Rs 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ us1 -+ us2 + usn + us -
电压源u 值不相等不能并联! 电压源us值不相等不能并联! a +
Us1
2009.4
Us2 b
目录 上页 下页 返回 退出
郭颖
与理想电压源并联的元件的处理: 与理想电压源并联的元件的处理: a +
E
a Is + b a E b
-
+ E
郭颖
列KVL方程时: KVL方程时 方程时: 与理想电压源并联的 元件可开路去掉来列 方程。 方程。
Rc
C
Rb
相 R∆之 邻 积 RY = 三 R∆之 个 和
目录 上页 下页 返回 退出
Ia a Ra Ib Ic b Rb Rc
C
Y-△变换的公式
Ra Rb +GaGb + Rc Ra Rb Rc Gab = Rab = Ga + Gb + Gc Rc Ra Rb +GbGC + Rc Ra Rb Rc Rbc Gbc = = Ga + Ga + Gc Rb R R + GbGa + Rc Ra R Rc Rca Gca = b = a Rb Ga + Gb + Gc
a I RO
I'
a
Is
b
E
+ -
RO' b
郭颖
2009.4
目录
上页
下页
返回
退出
4、恒压源和恒流源不能等效互换 a I I' a Uab' b
+ E -
b
Is
郭颖
2009.4
目录
上页
下页
返回
退出
例题1 例题1:求I。
R5 R1 E1 + R2 R3 I
+
I=?
R1 U1 = U R1 + R2
R2 U2 = U R1 + R2
应用 降压、限流、调节电压等。 降压、限流、调节电压等。
郭颖 2009.4 目录 上页 下页 返回 退出
二、电阻的并联
特点: 特点: (1)各电阻联接在两个相 (1)各电阻联接在两个 各电阻联接在两个相 同的结点之间; 的结点之间; (2)各电阻两端的电压相 (2)各电阻两端的电压相 同。
E
a Is b a Is Is b
列KCL方程时: KCL方程时 方程时: 与理想电流源串联的元 件可短路去掉列方程。
目录 上页 下页 返回 退出
-
R
b
郭颖 2009.4
二、实际电源的等效变换
I + E – R0 电压源 U = E- IR0 等效变换条件: 等效变换条件: E = ISR0
郭颖 2009.4 目录 上页 下页 返回 退出
郭颖
2009.4
目录
上页
下页
返回
退出
等效电阻等于各电阻之和
R1
R2 R
Rn
R = ∑Ri = R1 + R2 +…+ Rn
i=1
郭颖 2009.4 目录 上页 下页 返回 退出
n
分压公式——以两个电阻串联为例 分压公式——以两个电阻串联为例
I + U – + U1 R1 – + U2 R 2 –
目录 上页 下页 返回 退出
2009.4
RO
b
电流源并联: is=is1+is2+…… 电流源并联:
is1 is2 isn is
电流源i 值不相等不能串联! 电流源is值不相等不能串联!
is1 is2
郭颖
2009.4
目录
上页
下页
返回
退出
与理想电流源串联的元件的处理: 与理想电流源串联的元件的处理: a +
郭颖
2009.4
目录
上页
下页
返回
退出
本章要求
重点 1、理解等效变换的概念; 理解等效变换的概念; 2、掌握实际电源的等效变换; 掌握实际电源的等效变换; 3、掌握输入电阻的概念与计算。 掌握输入电阻的概念与计算。 难点 1、含受控源电阻电路的输入电阻。 含受控源电阻电路的输入电阻。
郭颖
2009.4
I RL IS R0 U + R0 U – RL
+ U –
电流源
U/ R0 = IS– I
U = ISR0 – IR0
等效变换的注意事项
1. 2. 3. 4. 5. “等效”是指对外等效,对内不等效。 等效”是指对外等效,对内不等效。 对外等效 的方向(非关联)。 注意转换前后 E 与 Is 的方向(非关联)。 模型中电压源与电流源的位置不能交换 位置不能交换。 模型中电压源与电流源的位置不能交换。 理想电压源和理想电流源不能等效互换。 理想电流源不能等效互换 理想电压源和理想电流源不能等效互换。 源变换的目的:使尽可能多的E串联、 并联、 源变换的目的:使尽可能多的E串联、IS并联、R 串或并联,以达到减少元件个数的目的, 串或并联,以达到减少元件个数的目的,简化 电路。 电路。 待求支路必须保留。 6. 待求支路必须保留。 含有受控源时,受控源象独立源一样处理, 7. 含有受控源时,受控源象独立源一样处理,但对 控制量应该保留
G5 G12 = G1 + G2 + G5 G1 G25 = G1 + G2 + G5 G2 G35 = G1 + G2 + G5
目录 上页 下页 返回 退出
R4
郭颖
2009.4
2-3 电源的等效变换
一、理想电源串联、并联的化简 理想电源串联、
电压源串联: 电压源串联:us=us1+us2+…… 串联
郭颖 2009.4 目录 上页 下页 返回 退出
1、“等效”是指“对外”等效,“对内”是不 等效”是指“对外”等效, 对内” 等效的
a RO b 例如: RL=∞ 时 例如 RO中不消耗能量 RO'中则消耗能量 中则消耗能量 对内不等效
郭颖 2009.4
I a Is Uab RL RO' Uab' b
I'
+ -E
RL
′ U ab = U ab = E I = I′ = 0
对外等效
目录 上页 下页 返回 退出
2、注意转换前后 E 与 Is 的非关联方向
a I RO I a RO b
E
+ b
Is
RO E
郭颖
I
a Is b
目录
I RO
a
+
2009.4
b
上页 下页 返回 退出
3、模型中电压源与电流源的位置不能交换
目录 上页 下页 返回 退出
电阻对称时
Ra = Rb = Rc = RΥ
Rab = Rbc = Rca = R∆
有: RY=R△/3 或 3RY=R△
郭颖
2009.4
目录
上页
下页
返回
退出
例2-1 求Req。
对R1、R5、R3做△-Y: :
C A
R1 R3 D
R5
R2
B
R4
C A
R31 R53
R15 R2
2Ω Ω + 1Ω U Ω – R"
目录
上页
下页
返回
退出
2. 等位点的应用:可开路,可短路。 等位点的应用:可开路,可短路。 ① 设点法: (适用两结点间有理想导线) 设点法: 适用两结点间有理想导线 理想导线)
R1
a
R2 R7 R5 R4 R3
b
R6
郭颖 2009.4 目录 上页 下页 返回 退出
郭颖 2009.4 目录 上页 下页 返回 退出
Ia
a Rab RbcRca b
△-Y变换的公式
C
Ib Ic
∆ -Y等效变换 等效变换 Ia a Ra Ib Ic b
郭颖 2009.4
RabRca Ra = Rab + Rbc + Rca Rbc Rab Rb = Rab + Rbc + Rca Rca Rbc Rc = Rab + Rbc + Rca
目录
上页
下页
返回
退出
2-1电阻的串联、并联和串并联 电阻的串联、
等效变换的概念
一个电路的某一部分可以用另一个简单电路替 且满足电路变换前后: 代,且满足电路变换前后: 1. 端子上的电流不变; 端子上的电流不变; 2. 端口上的电压不变。 端口上的电压不变。 则我们称这两个电路(对外电路) 等效变换的 则我们称这两个电路(对外电路)是等效变换的。
2
电阻Y 电阻Y形联结
电阻∆ 电阻∆形联结
推导思路:(等效概念)1-2、2-3、3-1间的电压 推导思路: 等效概念) 相等,且流入各个节点(1、2、3)的电流相等, 的电流相等, 相等,且流入各个节点( 分别写出其伏安关系式,各项分别相等从而得 分别写出其伏安关系式, 出Y-∆变换公式。 变换公式。
R6
R2
R4 R6
c d b
a
R1
R3 R5 R7
郭颖
2009.4
目录
上页
下页
返回
退出
② 平衡电桥: 平衡电桥:
C
R1 R3 D
R5
R2
R4
当R1/R3=R2/R4时:C、D两点为等位点。 两点为等位点。 方法一: 方法一:将R5开路 R=(R1+R2)//(R3+R4) ( ( 方法二: 方法二:将R5短路 R=(R1//R3)+(R2 // R4) ( (
电压源u 值不相等不能并联! 电压源us值不相等不能并联! a +
Us1
2009.4
Us2 b
目录 上页 下页 返回 退出
郭颖
与理想电压源并联的元件的处理: 与理想电压源并联的元件的处理: a +
E
a Is + b a E b
-
+ E
郭颖
列KVL方程时: KVL方程时 方程时: 与理想电压源并联的 元件可开路去掉来列 方程。 方程。
Rc
C
Rb
相 R∆之 邻 积 RY = 三 R∆之 个 和
目录 上页 下页 返回 退出
Ia a Ra Ib Ic b Rb Rc
C
Y-△变换的公式
Ra Rb +GaGb + Rc Ra Rb Rc Gab = Rab = Ga + Gb + Gc Rc Ra Rb +GbGC + Rc Ra Rb Rc Rbc Gbc = = Ga + Ga + Gc Rb R R + GbGa + Rc Ra R Rc Rca Gca = b = a Rb Ga + Gb + Gc
a I RO
I'
a
Is
b
E
+ -
RO' b
郭颖
2009.4
目录
上页
下页
返回
退出
4、恒压源和恒流源不能等效互换 a I I' a Uab' b
+ E -
b
Is
郭颖
2009.4
目录
上页
下页
返回
退出
例题1 例题1:求I。
R5 R1 E1 + R2 R3 I
+
I=?
R1 U1 = U R1 + R2
R2 U2 = U R1 + R2
应用 降压、限流、调节电压等。 降压、限流、调节电压等。
郭颖 2009.4 目录 上页 下页 返回 退出
二、电阻的并联
特点: 特点: (1)各电阻联接在两个相 (1)各电阻联接在两个 各电阻联接在两个相 同的结点之间; 的结点之间; (2)各电阻两端的电压相 (2)各电阻两端的电压相 同。
E
a Is b a Is Is b
列KCL方程时: KCL方程时 方程时: 与理想电流源串联的元 件可短路去掉列方程。
目录 上页 下页 返回 退出
-
R
b
郭颖 2009.4
二、实际电源的等效变换
I + E – R0 电压源 U = E- IR0 等效变换条件: 等效变换条件: E = ISR0
郭颖 2009.4 目录 上页 下页 返回 退出
郭颖
2009.4
目录
上页
下页
返回
退出
等效电阻等于各电阻之和
R1
R2 R
Rn
R = ∑Ri = R1 + R2 +…+ Rn
i=1
郭颖 2009.4 目录 上页 下页 返回 退出
n
分压公式——以两个电阻串联为例 分压公式——以两个电阻串联为例
I + U – + U1 R1 – + U2 R 2 –
目录 上页 下页 返回 退出
2009.4
RO
b
电流源并联: is=is1+is2+…… 电流源并联:
is1 is2 isn is
电流源i 值不相等不能串联! 电流源is值不相等不能串联!
is1 is2
郭颖
2009.4
目录
上页
下页
返回
退出
与理想电流源串联的元件的处理: 与理想电流源串联的元件的处理: a +
郭颖
2009.4
目录
上页
下页
返回
退出
本章要求
重点 1、理解等效变换的概念; 理解等效变换的概念; 2、掌握实际电源的等效变换; 掌握实际电源的等效变换; 3、掌握输入电阻的概念与计算。 掌握输入电阻的概念与计算。 难点 1、含受控源电阻电路的输入电阻。 含受控源电阻电路的输入电阻。
郭颖
2009.4
I RL IS R0 U + R0 U – RL
+ U –
电流源
U/ R0 = IS– I
U = ISR0 – IR0
等效变换的注意事项
1. 2. 3. 4. 5. “等效”是指对外等效,对内不等效。 等效”是指对外等效,对内不等效。 对外等效 的方向(非关联)。 注意转换前后 E 与 Is 的方向(非关联)。 模型中电压源与电流源的位置不能交换 位置不能交换。 模型中电压源与电流源的位置不能交换。 理想电压源和理想电流源不能等效互换。 理想电流源不能等效互换 理想电压源和理想电流源不能等效互换。 源变换的目的:使尽可能多的E串联、 并联、 源变换的目的:使尽可能多的E串联、IS并联、R 串或并联,以达到减少元件个数的目的, 串或并联,以达到减少元件个数的目的,简化 电路。 电路。 待求支路必须保留。 6. 待求支路必须保留。 含有受控源时,受控源象独立源一样处理, 7. 含有受控源时,受控源象独立源一样处理,但对 控制量应该保留
G5 G12 = G1 + G2 + G5 G1 G25 = G1 + G2 + G5 G2 G35 = G1 + G2 + G5
目录 上页 下页 返回 退出
R4
郭颖
2009.4
2-3 电源的等效变换
一、理想电源串联、并联的化简 理想电源串联、
电压源串联: 电压源串联:us=us1+us2+…… 串联
郭颖 2009.4 目录 上页 下页 返回 退出
1、“等效”是指“对外”等效,“对内”是不 等效”是指“对外”等效, 对内” 等效的
a RO b 例如: RL=∞ 时 例如 RO中不消耗能量 RO'中则消耗能量 中则消耗能量 对内不等效
郭颖 2009.4
I a Is Uab RL RO' Uab' b
I'
+ -E
RL
′ U ab = U ab = E I = I′ = 0
对外等效
目录 上页 下页 返回 退出
2、注意转换前后 E 与 Is 的非关联方向
a I RO I a RO b
E
+ b
Is
RO E
郭颖
I
a Is b
目录
I RO
a
+
2009.4
b
上页 下页 返回 退出
3、模型中电压源与电流源的位置不能交换
目录 上页 下页 返回 退出
电阻对称时
Ra = Rb = Rc = RΥ
Rab = Rbc = Rca = R∆
有: RY=R△/3 或 3RY=R△
郭颖
2009.4
目录
上页
下页
返回
退出
例2-1 求Req。
对R1、R5、R3做△-Y: :
C A
R1 R3 D
R5
R2
B
R4
C A
R31 R53
R15 R2
2Ω Ω + 1Ω U Ω – R"
目录
上页
下页
返回
退出
2. 等位点的应用:可开路,可短路。 等位点的应用:可开路,可短路。 ① 设点法: (适用两结点间有理想导线) 设点法: 适用两结点间有理想导线 理想导线)
R1
a
R2 R7 R5 R4 R3
b
R6
郭颖 2009.4 目录 上页 下页 返回 退出
郭颖 2009.4 目录 上页 下页 返回 退出
Ia
a Rab RbcRca b
△-Y变换的公式
C
Ib Ic
∆ -Y等效变换 等效变换 Ia a Ra Ib Ic b
郭颖 2009.4
RabRca Ra = Rab + Rbc + Rca Rbc Rab Rb = Rab + Rbc + Rca Rca Rbc Rc = Rab + Rbc + Rca
目录
上页
下页
返回
退出
2-1电阻的串联、并联和串并联 电阻的串联、
等效变换的概念
一个电路的某一部分可以用另一个简单电路替 且满足电路变换前后: 代,且满足电路变换前后: 1. 端子上的电流不变; 端子上的电流不变; 2. 端口上的电压不变。 端口上的电压不变。 则我们称这两个电路(对外电路) 等效变换的 则我们称这两个电路(对外电路)是等效变换的。
2
电阻Y 电阻Y形联结
电阻∆ 电阻∆形联结
推导思路:(等效概念)1-2、2-3、3-1间的电压 推导思路: 等效概念) 相等,且流入各个节点(1、2、3)的电流相等, 的电流相等, 相等,且流入各个节点( 分别写出其伏安关系式,各项分别相等从而得 分别写出其伏安关系式, 出Y-∆变换公式。 变换公式。
R6
R2
R4 R6
c d b
a
R1
R3 R5 R7
郭颖
2009.4
目录
上页
下页
返回
退出
② 平衡电桥: 平衡电桥:
C
R1 R3 D
R5
R2
R4
当R1/R3=R2/R4时:C、D两点为等位点。 两点为等位点。 方法一: 方法一:将R5开路 R=(R1+R2)//(R3+R4) ( ( 方法二: 方法二:将R5短路 R=(R1//R3)+(R2 // R4) ( (
