电路基本分析 电阻电路的等效变换法
电路与电子电路分析：2-1 等效的概念及等效变换分析
电+
压 源
us
-
电压源
i +
uR -
外电路
u us
0
u us iRs
us Rs i
实 际
is
电
流
源
(a) i
u
+ Rs u
is Rs
R
i is u Rs
-
0
is i
电流源
外电路
(a) 对外电路等效：对外VCR曲线完全相同。
u s is Rs
is u s Rs X
7、两种实际电源模型的等效变换
•
a
a
10V
10 1A
10
b
b
例题2 求下图所示电路中的电流i。
解：利用电源的等效变换将图（a）所示电路逐步化
简为图（d）所示电路，变换过程如图（b）、 （c）所示。
2 2
2
6A
6V
2A 2
i 7
3A 2 6A
2A
2
i 7
（a）
（b）
X
解续
2
9A
2A
i
1
7
4V 1
9V
2
i
7
（c）
（d）
由图（d）可求得：i 9 4 0.5A
退出 开始
电阻电路
• 电阻电路，是指电路只由电源和电阻元件组成， 而不包含电容、电感等元件。
• 电流和电压的约束关系都是瞬时的， • 各支路某时刻的电压/电流只取决与该时刻电路
的情况，而与历史时刻无关，因此又称为无记忆 电路。 • 电阻电路各个之路上电流和电压的约束关系即 VCR只是代数方程。
第二章 电阻电路的基本分析方法与定理
电阻的等效变换技巧
电阻的等效变换技巧电阻的等效变换技巧是电路分析中常用的一种方法，通过将电路中的电阻按照等效电路的要求进行变换，可以简化复杂的电路分析问题，提高分析的效率。
下面将介绍电阻的串、并联、三角形转星型等效变换技巧。
1. 串联电阻的等效变换当若干个电阻串联时，可以通过求和的方式得到等效电阻。
假设要将电阻R1、R2、R3串联，则它们的等效电阻为Req = R1 + R2 + R3。
这是因为电流在串联电路中是恒定的，所以电阻的总和就是电流通过的路径上的总阻抗。
2. 并联电阻的等效变换当若干个电阻并联时，可以通过求倒数和再求倒数的方式得到等效电阻。
假设要将电阻R1、R2、R3并联，则它们的等效电阻为Req = (1/R1 + 1/R2 + 1/R3)^-1。
这是因为电压在并联电路中是恒定的，所以电阻的倒数之和的倒数就是电流通过的总阻抗。
3. 三角形转星型等效变换在某些情况下，三角形电阻网络需要转换为星型电阻网络以便于分析。
假设有三个电阻Ra、Rb、Rc构成的三角形网络，可以通过以下公式得到等效电阻值：Rab = (Ra * Rb + Rb * Rc + Rc * Ra) / (Rc)Rac = (Ra * Rb + Rb * Rc + Rc * Ra) / (Rb)Rb= (Ra * Rb + Rb * Rc + Rc * Ra) / (Ra)这是因为在三角形电阻网络中，可以将其中任意两个电阻并联得到一个新的等效电阻，再将得到的等效电阻与剩余的电阻串联，最后得到总的等效电阻。
以上是电阻的等效变换技巧的基本介绍，这些方法可以帮助我们简化复杂的电路分析问题，提高分析的效率。
在实际应用中，可以根据具体情况选择不同的等效变换方法，以便更好地解决问题。
同时，还可以通过使用等效变换技巧，将复杂电路转换为简单的等效电路，以便更好地理解和分析电路的工作原理。
电阻电路的等效变换技术
不能改变电路的结构和参数
电阻电路等效变换不能改变 电路的电压、电流、功率等 参数。
电阻电路等效变换不能改变 电路的元件参数，如电阻、
电容、电感等。
电阻电路等效变换只能改变 电路的连接方式，不能改变 电路的结构和参数。
电阻电路等效变换不能改变 电路的拓扑结构，如串联、
并联、混联等。
07
电阻电路等效变换的发 展趋势
变换过程中，要保证电路的电源和负载不变，如电压、电流、功率等。
变换过程中，要保证电路的稳定性和可靠性，如电路的稳定性、可靠性、 安全性等。
保持元件连接方式不变的原则
电阻电路等效变换时，应保持元件之间的连接方式不变，避免出现错误。 变换过程中，应遵循电路的基本原理，如欧姆定律、基尔霍夫定律等。 变换过程中，应保持电路的拓扑结构不变，避免出现短路或断路。 变换过程中，应保持电路的功率和能量守恒，避免出现能量损失或增加。
复杂电路的等效变换：对于复杂电路，可以采用分压法、分流法等方法进 行等效变换，将复杂电路简化为简单电路，再进行等效变换。
星形电阻网络的等效变换
星形电阻网络的定义：由多个电阻串联或并联组成的网络
等效变换的方法：将星形电阻网络转换为等效的Y形或△形网络
转换步骤：首先确定星形网络的中心点，然后将每个电阻两端的电压和电流分别相加或相减， 得到等效的Y形或△形网络
电阻电路的等效变换 技术
,a click to unlimited possibilities
汇报人：
目录 /目录
01
点击此处添加 目录标题
04
电阻电路等效 变换的应用
02
电阻电路等效 变换的基本概 念
05
电阻电路等效 变换的注意事 项
电路基本分析 第一章 电路分析的基本概念及定律
Chapter 1
Chapter 1
Chapter 1
举例
开关 干电池
电灯
R0 + US （b）
S R1
（a）
（c）
实际电路与电路模型
Chapter 1
四、电路的分类 1.集总参数电路：其电路的几何尺寸l<<电路的工作频率 对应的波长λ。 集总参数电路又分为线性能 定义：一段时间内电路消耗的功率。可表为：
W=P t
若功率随时间变化，则： w
u、i 方向与w的关系：
t
pdt uidt
0
0
i
t
单位：焦耳J
u、i 方向如图示：
w>0，吸收；w<0， 发出。
a
+
u
_
b
Chapter 1
小结： 1.实际电路或实际电路元件可以用理想电路元件或理想 电路元件组合的电路模型进行模拟。
目 录
第一章 电路的基本概念和定律 第二章 电阻电路的等效变换 第三章 电路分析的网络方程法 第四章 正弦交流电路 第五章 谐振与互感电路 第六章三相电路 第七章 非正弦周期电流电路 第八章 动态电路的时域分析
第九章 动态电路的复频域分析
第十章 二端口网络
Chapter 1
第一章
电路分析的基本概念及定律
Chapter 1
教学目的 1.了解实际电路、理想电路元件和电路模型的概念。 2.熟练掌握电流、电压和电功率的概念。 3.理解电位、电动势和能量的概念。
教学内容概述 主要介绍理想电路元件和电路模型的概念以及电路中常 用的物理量：电流、电压和电功率的概念。 教学重点和难点 重点：电流、电压的参考方向及关联参考方向和电功率 的计算。 难点：电功率的计算及对电路发出和吸收功率的判断。
电阻电路的等效变换
2.2 电路的等效变换
1.二端电路（网络）
ik1 Gk1uGk1 Rk2 ik2 Gk2u Gk2 Rk1
例 两电阻的分流：
1 ReqGeq
1 11
R1R2 R1R2
R1 R2
1
i1
G1 Geq
i
R1 11
i R2 i R1 R2
R1 R2
1
i2
G2 i Geq
R2 11
i R1 i R1 R2
R1 R2
i
+
i1
i2
u R1 R2
2
3 2
3
依据：经过等效变换后，与外电路相连的任意两个节点间的电阻阻值相等。
R1
R2
R 12 ( R 23 R 31 ) R 12 R 31 R 23
R2 R3
R 23 ( R 31 R 12 ) R 12 R 31 R 23
R3
R1
R 31 ( R 12 R 23 ) R 12 R 31 R 23
n
等效电阻： R eqR 1R kR n R kR k k 1
串联电路的总电阻等于各分电阻之和，且大于各分电阻。
3）分压公式
uk
RkiRk
u Req
Rk Req
uu
uk1 Rk1i Rk1 uk2 Rk2i Rk2
电压与电阻成正比，因此串联电阻电路可作分压电路。
i
电阻的等效变换
R1 R1 R2
u
u2
R2 R1 R2
u
1.4 电路的分析方法
（2）电阻的并联
i
a + u
b
i1 R1
i2 R2
…
in Rn
N1
i = i1+ i2++ in
= G1u+G2u++ Gnu
=（G1+ G2+… +Gn）u
第一章 电路的基本概念、定律与分析方法
i
a +
u b
Req
N2
i = Gequ
1.4 电路的分析方法
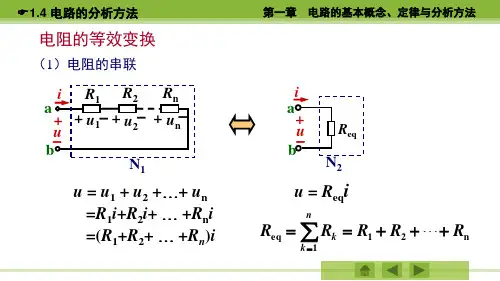
电阻的等效变换
（1）电阻的串联
i R1 R2 Rn
aБайду номын сангаас+
bu
+ u1 + u2 + un
N1
u = u1 + u2 ++ un =R1i+R2i+ +Rni =(R1+R2+ +Rn)i
第一章 电路的基本概念、定律与分析方法
i
a
+
bu
Req
N2
u = Reqi
n
Req Rk R1 R2 Rn k 1
…
in Rn
N1
Req
R1 R2 R1 R2
两个电阻并联时
i1
R2 R1 R2
i
i2
R1 R1 R2
i
1.4 电路的分析方法
第一章 电路的基本概念、定律与分析方法
例1 求解端口ab的等效电阻 。
a
解：1.找到并联电阻进行等效。
电路基础课件-第2章电路的等效变换
THANKS
感谢观看
总结词
降低成本。
详细描述
优化电源配置，提高电源利用率，可以减少对昂贵电源的 需求，从而降低整个电路的成本。
总结词
提升稳定性。
详细描述
合理的电源配置能够提升电路的稳定性，降低因电源问题 导致的故障风险。等效变换在此过程中起到关键作用。
测量仪表的误差分析
总结词
等效变换有助于分析测量仪表的误差来源。
详细描述
05
CATALOGUE
电路的等效变换应用实例
复杂电路的化简
总结词
通过等效变换，将复杂电路简化为简单电路，便于分析 。
详细描述
在复杂电路中，通过使用等效变换的方法，将电路中的 元件进行等效替代或合并，从而简化电路的结构，降低 分析难度。
总结词
提高分析效率。
详细描述
通过等效变换，可以将复杂的电路简化为简单的形式， 从而减少分析时间和计算量，提高分析效率。
电路基础课件-第2 章电路的等效变换
contents
目录
• 等效变换的基本概念 • 电阻电路的等效变换 • 含源一端口网络的等效变换 • 含源二端口网络的等效变换 • 电路的等效变换应用实例
01
CATALOGUE
等效变换的基本概念
等效的定义
等效是指两个电路在某点之前和之后的电流和电压保持不变，即对外电路等效。 等效电路是指一个电路可以代替另一个电路，而不会改变外电路的电流和电压。
04
CATALOGUE
含源二端口网络的等效变换
二端口网络参数方程与等效电路
参数方程
由二端口网络的电压和电流关系，可 以推导出其参数方程，包括Y参数方 程和Z参数方程。
等效电路
电路理论分析-第2章
R1
(R (R
R1) R1)
RA RA
400 0.5 R1 400 0.5
100 0.5 100
电路中的电流为
I U 500 5A 1.8A
R1 100
该电流超过了滑线变阻器的额定电流，在电气工程中是不允许的，
此时的输出电压几乎为零。
10
实例分析1
+ 火线 U_
A
C
零线
B
A点等效电路
R
4 1 1 3
1A
PR I 2 R 3W
U RI 3V
PUS 41 4W
内部
PIS IsU 4 3 12W
PRS I 2Rs 1W
PRS U 2Gs 9W
25
例2 求电压U3
i1 5Ω
2i1
+
6V
3Ω 3Ω
_
解：由于电路中的R3对电流i1无影 响，暂且将其短路；
R1 5 i1
所谓端口上伏安关系相同，即外特性相同，指的是当N1 和N2分别接上同一个外电路时，它们对应端电压相等，对 应端电流相等，相应的外电路的功率也相等，则N1和N2对 外部电路是等效的。
3
§2.1 不含独立源电路的等效变换
一.无源二端网络电阻的串联、并联和混联连接
电阻串联( Series Connection of Resistors )
uS _
º
º
+
+
+
uS1_
uS2_
uS us us1 us2
_
º
20
2. 理想电流源的串联并联
并联
is is1 is2 isn isk
iS1 iS2
电路基本分析第二章电阻电路的等效变换法
Chapter 2
方法二：将Y→△（如下图），自己练习。
1
2Ω
R12
2
1Ω 2Ω
1
2Ω
1Ω
2
1Ω
3
1
1
R12
R13 2 Ω
2
1Ω
2 1Ω
R23
3
1
R12
2
说明:使用△-Y 等效变换公式前，应先标出三个端头标 号，再套用公式计算。
Chapter 2
小结: 1 .一个内部不含独立电源的单口网络对外可以等效为一
电路对外可等效为一个理想电压源us和一个内阻Rs串 联的电压源模型。
Chapter 2
2. n个实际电流源并联：
isn
Gsn
i s2
is1
is3 Gs3
Gs2
i +a Gs1 u
-
b
i＇
a
+
is
Gs
u＇
-
b
由KCL得端口电压电流关系：
i i s 1 i s 2 i s 3 i s n G s 1 G s 2 G s 3 G s n u
解得：
i1
R1R2
R3u12 R2R3
R3R1
R1R2
R2u31 R2R3
R3R1
i2
R1R2
R1u23 R2R3
R3R1
R1R2
R3u12 R2R3
R3R1
i3
R1R2
R2u31 R2R3
R3R1
R1R2
R1u23 R2R3
R3R1
第2章电路分析的基本方法
2Ω
is
2A
2Ω
解： （1） 与电压源并联的R2和与电流源串联的R3不 考虑（等效）
us 2
+ 10V -
- 4V +
4Ω
RL
I 5Ω
+Ω
us 2
- 4V +
4Ω
RL
I
2A
2Ω
us 2
5Ω
+ U -
3A 2Ω
- 4V +
4Ω
RL
I
2Ω
5Ω
+ U -
控制量u1应转换为支路电流表示
u1 = us2+ R2i2 （ 4）
求解得 ：i1=0.43A ，i2=-0.71A，i3=1.14A， u1=0.57V
求解受控源上的电压u2时，不 能延用图（b）所示的电路， 回到原电路即图3-2（a）所 示的电路中进行求解 u2= -R3i3+ us2+R2i2
i1 R i R2 2 1 + il1 + uS1 il2 uS2 – – b
列写的方程
i3
R3
独立回路数为 2 。选 图示的两个独立回路，支 路电流可表示为：
i1 il1 i3 il 2 i2 il 2 il1
网孔电流在网孔中是闭合的，对每个相关结 点均流进一次，流出一次，所以KCL自动满足。 因此网孔电流法是对网孔回路列写KVL方程，方 程数为网孔数。
a
R1
c
b
R2 d
R4 Rab=(R1+R3)//(R2+R4) a b R1 c
R3
R2
d
电桥平衡条件： R1R4=R2R3
电路等效变换
电路等效变换引言电路等效变换是电路分析中的一种重要方法，通过将电路中的一些元件或电路结构进行变换，可以简化复杂的电路，使其更容易分析和计算。
本文将介绍电路等效变换的基本概念和常用方法，以及它在电路分析中的应用。
电路等效变换的基本概念电路等效变换是指在不改变电路的总体功能和性质的前提下，通过对电路进行一系列变换，将原有电路等效为一个简单、方便分析的等效电路。
等效电路与原有电路在某些方面有着相同的性质，可以用来进行电路计算和分析。
常用的电路等效变换方法1. 串、并联电阻的等效变换•串联电阻的等效变换：将串联电阻变换为等效电阻，其阻值等于串联电阻的和。
•并联电阻的等效变换：将并联电阻变换为等效电阻，其阻值等于并联电阻的倒数之和的倒数。
2. 电压源与电流源的等效变换•电压源的等效变换：将电压源变换为等效电流源，其电流等于电压除以等效电阻。
•电流源的等效变换：将电流源变换为等效电压源，其电压等于电流乘以等效电阻。
3. 零电阻与无穷大电阻的等效变换•零电阻的等效变换：将零电阻变换为等效电流源，其电流等于零。
•无穷大电阻的等效变换：将无穷大电阻变换为等效电压源，其电压等于无穷大。
4. 串并联电感和电容的等效变换•串联电感的等效变换：将串联电感变换为等效电感，其电感等于串联电感的和。
•并联电感的等效变换：将并联电感变换为等效电感，其电感等于并联电感的倒数之和的倒数。
•串联电容的等效变换：将串联电容变换为等效电容，其电容等于串联电容的倒数之和的倒数。
•并联电容的等效变换：将并联电容变换为等效电容，其电容等于并联电容的和。
电路等效变换的应用电路等效变换在电路分析和设计中具有广泛的应用。
它可以简化复杂的电路，使电路的分析和计算更加方便。
以下是电路等效变换的一些常见应用：1. 电路简化通过对电路进行等效变换，可以将复杂的电路简化为简单的等效电路，从而减少计算和分析的复杂程度。
2. 电路分析通过对电路中的元件进行等效变换，可以将原始电路转化为等效电路，从而更方便地进行电路分析和计算。
第二章电阻电路的分析
第二章 电阻电路的分析主要内容：定理法：叠加定理、替代定理、戴维南定理（诺顿定理）； 等效变换法：独立电源的等效变换、电阻的Y -Δ转换、移源法； 系统化法：节点电压法、回路电流法。
§2-1 线性电路的性质·叠加定理(superposition theorem)一、 线性电路的概念由线性元件及独立电源组成的电路。
电源的作用是激励，其它元件则是对电源的响应。
二、 线性电路的性质 1、齐次性： 若有图示的线性电路，在单电源激励下，以2R 的电流2i 为输出响应，则容易得到：s u R R R R R R R i 13322132++=由于321,,R R R 为常数，故有：s ku i =2显然，2i 与su 成比例。
在数学中，被称为“齐次性”，而在电路理论中则称为“比例性”。
2、相加性在图示的两激励电路中，若仍以2R 的电流2i 作为输出响应，则有：u+ |2us u+ ||2us s i R R R u R R i 2112121+++=显然，2i 由两项组成，第一项为电压源单独作用时，在电阻上引起的响应，每二项为电流源单独作用时，在电阻上引起的响应，每一项只与某个激励源成比例。
也即，由两个激励所产生的响应，表示为每一个激励单独作用时产生的响应之和。
这在数学中称为“相加性”，在电路理论中则称为“叠加性”。
三、 叠加定理在任何线性电阻电路中，每一元件的电流或电压都是电路中各个独立电源单独作用时在该元件产生的电流或电压的叠加。
叠加性是线性电路的一个根本属性。
注：叠加定理适用于线性电路。
在叠加的各分电路中，不作用的电压源置零（即，电压源用短路代替），不作用的电流源置零（即，电流源用开路代替），电阻不更动，受控源保留在各分电路中。
和分电路中的电压、电流的参考方向可以取为原电路中的相同方向，求和时，应注意各分量前的“+”、“-”号。
原电路的功率不等于按各分电路计算所得的功率叠加，这是因为功率是电压和电流的乘积。
《电工电子技术基础》第2章 电路的基本分析方法
第2章 电路的基本分析方法 ——电源等效变换
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——电源等效变换
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——电源等效变换
如图2.2.11所示，计算电路中流过2 Ω电阻的电流I。
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——叠加定理
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法——戴维宁定理
2.5 戴维宁定理
复杂电路中有时只需要计算其中某一条支路的响应，此时可 以将这条支路划出，而把其余部分看作一个有源二端网络。 有源二端网络 具有两个出线端的内含独立电源的电路 无源二端网络 不含独立电源的二端网络
回路，网孔的数目就等于总的独立回路数。
I1
I3
I2 I II
III
章目录 节首页 上一页 下一页
第2章 电路的基本分析方法 ——支路电流法
4.选取独立结点电流方程和独立回路电压方程组成联列方程组。
I1
I3
I1+I2 － I3=0 R1I1 － R2I2=US1 － US2
I2 I II
R2I2+R3I3=US2
III
5.方程总数等于支路总数，也就是所要求的变量数，方程组
有唯一的解。解方程组，可得到各支路电流I1、I2和I3。
I1
US1(R2 R3 ) R1R2 R2 R3
US2 R3 R3R1
第二章 电路分析的等效变换法
R1R2 R2R3 R3R1 R12 R3 R1R2 R2R3 R3R1 R23 R1 R1R2 R2R3 R3R1 R31 R2
i1 =u12 /R12 – u31 /R31
+
+
5V
_
5V
_
_
2.3.2 电流源的串并联 并联： 可等效成一个理想电流源 i S º iS1 iS2 iSk º 串联: º 2A 2A 2A º º 电流相同的理想电流源 才能串联。但每个电流 iS
º iS= iSk （注意参考方向） º
源的端电压无法确定。 º
2. 3. 3 电压源与电流源的串并联 Is
º
º
º
º
º
º
º
º
º
º
º
º
2.3 电源的等效变换
2.3.1 电压源的串并联 + uS1 _ + uSn _ º
º + uS _
º
串联: uS= uSk ( 注意参考方向。一致， 取+；否则，取 - 。) 并联: 电压相同的电压源才 能并联。但每个电压 源的电流无法确定。 º
º I
º
I
º + 5V º
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 故可以直接用等效电阻计算并联电路“内部”的总功率。 （对照前面：“对外等效”，对内不一定等效。）
2.1.3 电阻的串并联 要求：弄清楚串、并联的概念。 计算举例： 例1.
4 º 2
3 Req = 4∥(2+3∥6) = 2
电路原理教学大纲
教学基本要求一、性质、地位和任务电路原理是电类专业的重要基础课程，其内容包括：电路的基本概念和定律，电阻电路的等效变换法，电路的网络方程分析法，电路基本定理，正弦交流电路，串、并联谐振电路，具有互感的电路，三相交流电路，非正弦周期电流电路，动态电路，二端口网络，磁路等内容。
本课程的主要任务是：使学生掌握电路的基本理论知识、电路基本分析方法，为学习后续课程准备必要的电路理论知识。
二、教学基本要求第一章电路的基本概念和定律1．了解电路和电路模型。
2．熟悉电流、电压、电功率、电能的概念；理解电流、电压的参考方向，及关联参考方向。
3．熟悉电阻元件、电感元件、电容元件及其伏安特性，掌握电阻元件、电感元件、电容元件的功率和能量的计算。
4．熟悉电压源、电流源及其模型。
5．了解电路中的受控源及其四种基本形式。
6．熟练掌握基尔霍夫定律的应用。
第二章电阻电路的等效变换法1．掌握电阻的串并联等效变换。
2．掌握电阻的星形连接与三角形连接的等效变换。
3．掌握电源、受控源的等效变换。
第三章电路的网络方程分析法1．理解电路网络方程分析法的概念。
2．熟练掌握支路电流分析法、网孔电流分析法、节点电位分析法的步骤和规律，并会加以应用。
第四章电路基本定理1．理解叠加定理、替代定理、戴维南定理和诺顿定理。
2．熟练掌握各定理在电路分析中的应用。
第五章正弦交流电路1．了解正弦交流电的基本概念，熟悉正弦交流电的相关参量。
2．掌握正弦量的各种表示方法和它们之间的相互转换。
3．掌握电阻元件、电感元件、电容元件的正弦交流电路的伏安关系，功率消耗及能量转换。
4．理解相量形式的基尔霍夫定律。
5．掌握电阻、电感、电容串联电路和并联电路的电压与电流的关系，及其相量图。
6．掌握正弦交流电路功率的计算方法。
7．了解提高功率因数的原因，理解提高功率因数的方法。
8．熟练掌握相量法在一般正弦交流电路计算中的应用。
第六章串、并联谐振电路1．理解串联谐振的条件及其特点2．理解串联谐振的频率特性及其通用谐振曲线。
电阻串并联等效变换
电阻串并联等效变换电阻串并联等效变换是电路中常用的一种技巧，可以将复杂的电路简化为一个等效电路，方便计算和分析。
本文将介绍电阻串并联等效变换的基本原理、方法和应用。
一、电阻串并联等效变换的基本原理电阻串并联等效变换的基本原理是根据欧姆定律和基尔霍夫定律，将一组电阻串联或并联起来，转化为一个等效电阻。
串联电阻的等效电阻为各电阻之和，即R=R1+R2+R3+...+Rn；并联电阻的等效电阻为各电阻的倒数之和的倒数，即1/R=1/R1+1/R2+1/R3+...+1/Rn。
二、电阻串并联等效变换的方法1. 串联电阻的等效变换方法将一组电阻串联起来，可以将其等效为一个等效电阻。
具体方法如下：（1）将电路中的电阻串联起来，组成一个电阻串。
（2）计算电阻串中各电阻之和，得到等效电阻R。
（3）将等效电阻R代替原电路中的电阻串。
2. 并联电阻的等效变换方法将一组电阻并联起来，可以将其等效为一个等效电阻。
具体方法如下：（1）将电路中的电阻并联起来，组成一个电阻并联。
（2）计算电阻并联中各电阻的倒数之和的倒数，得到等效电阻R。
（3）将等效电阻R代替原电路中的电阻并联。
三、电阻串并联等效变换的应用电阻串并联等效变换在电路分析和设计中具有广泛的应用，可以用于简化电路、计算电路参数和优化电路性能等方面。
1. 电路简化通过电阻串并联等效变换，可以将复杂的电路简化为一个等效电路。
这样可以减少计算量，提高计算精度，方便电路分析和设计。
2. 电路参数计算通过电阻串并联等效变换，可以方便地计算电路中的电阻、电流、电压等参数。
这对于电路分析和设计非常有用。
3. 电路性能优化通过电阻串并联等效变换，可以优化电路的性能，比如降低电路的功耗、提高电路的稳定性、改善电路的响应速度等。
总之，电阻串并联等效变换是电路分析和设计中常用的一种技巧，掌握了这种技巧，可以方便地简化电路、计算电路参数和优化电路性能，提高电路分析和设计的效率和精度。
第2章 电阻电路的等效变换
结论 串联电路的等效电阻等于各分电阻之和。
等效：对外部电路(端钮以外)效果相同。
2.串联电阻上电压的分配
R1
Rk
Rn
i + u1 _ + uk_ + un _
+
u
_
表明
uk
Rk i
Rk
u Req
Rk u Req
u
电压与电阻成正比，因此串联电阻电路可作分压电路。
两个电阻的分压：
i
+ u
u-+__1
等效的目的：化简电路
电阻的串联： Req= Rk
电 阻 电
2.2 电阻的等效变换 ( ，★ )
电阻的并联：Geq= Gk 电阻的Y- 等效变换
uk
ik
Rk GRk eqi
Geq
u
路
电压源串联：uS= uSk
的 等 效
2.3 独立源的等效变换 (，★)
电流源并联: iS= iSk 实际电源两种模型间的等效： uS=iSRS
(3)等效电导等于并联的各电导之和。
Geq=G1+G2+ ... +Gk+ ... +Gn= Gk = 1/Rk
3. 并联电阻的分流： 由 ik u/Rk Gk i u/Req Geq
ik
Gk i Geq
电流分配与
电导成正比
对于两电阻并联，有：
i
+ i1
i2
u_ R1
R2
1 Req
思考与练习
1.等效变换的概 念是什么？“电 路等效就是相等” 这句话对吗？为 什么？
2.电路等效变 换的目的是 什么？
阻容电路 等效变换
阻容电路等效变换1. 引言阻容电路是由电阻（R）和电容（C）组成的电路，是电子工程中常见的一种电路类型。
在分析和设计电路时，经常需要进行等效变换，以简化电路结构、提高计算效率。
本文将介绍阻容电路的等效变换原理、方法和应用。
2. 阻容电路基础2.1 电阻（R）电阻是电路中的基本元件，其特征是阻碍电流通过的能力。
电阻的单位是欧姆（Ω）。
2.2 电容（C）电容是电路中的另一种基本元件，其特征是可以储存电荷。
电容的单位是法拉（F）。
2.3 阻容电路阻容电路是由电阻和电容组成的电路。
在交流电路中，电阻和电容对电流和电压的响应具有不同的特性，因此阻容电路的分析和设计需要考虑这两者的相互影响。
3. 阻容电路等效变换原理3.1 等效电阻（Re）在阻容电路中，电阻和电容可以通过等效电阻进行简化。
等效电阻是指在某些条件下，用一个电阻代替电路中的电阻和电容，使得整体电路的特性保持不变。
3.2 等效电容（Ce）类似地，也可以通过等效电容进行简化，将电路中的电阻和电容替换为一个等效电容，以简化分析和设计过程。
4. 阻容电路等效变换方法4.1 泰勒级数展开法通过泰勒级数展开法，可以将非线性电路近似为线性电路，从而进行等效变换。
这在高频电路中特别有用。
4.2 时域与频域的等效变换在时域和频域之间进行等效变换，常用的方法有拉普拉斯变换和傅里叶变换。
这可以使电路在不同域中的分析更加方便。
5. 阻容电路等效变换应用5.1 信号处理在通信系统和信号处理中，阻容电路的等效变换可以用于滤波器设计和信号传输过程的分析。
5.2 电源管理在电源管理电路中，通过对阻容电路的等效变换，可以更好地优化电源的效率和稳定性。
5.3 放大器设计在放大器设计中，对阻容电路进行等效变换有助于简化电路结构，提高放大器的性能。
6. 结论阻容电路等效变换是电子工程中重要的分析和设计工具之一。
通过等效变换，可以简化复杂的阻容电路，提高计算效率，更好地理解电路的行为。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Req i
+
u
-
1. 特点：并联电阻承受的电压为同一电压。
Chapter 2
2. 等效电阻
R e qu i
u
R u 1 R u 2 R u n
1 R 1 1 R 1 2 R 1 n
即
n
1
Req i1Ri
n
或 Geq Gi
i1
两个电阻并联公式： 1 1 1 Req R1 R2
-
uk
Rk R eq
u
串联电阻具有分压作用，电阻越大，分压越高。
Chapter 2
两个串联电阻的分压公式：
i R1
R2
+
u1 u
u2
-
u1
R1 R1 R2
u
u2
R2 R1 R2
u
条件：u 、u1 、u2 参考方向一致。
Chapter 2
三.并联电阻：
设n个电阻并联 i
i1 i2 R1 R2
in u
2
B
u2 u3
i 3
3
1 i'1
A
u'1
2
i'2
C
u'2 u'3
3 i'3
图中各对应电压、电流相等时，B电路与C电路等效。
即等效条件为： u1 u1 u2 u2 i1 i1 i2 i2
Chapter 2
1.Y 形联接：三个电阻一端连接为一点，另一端分别引出 三个端头。
1
i1
R1
R3
i3
3
R2 i2
即： R 3RY
或：
RY
1 3
R
Chapter 2
例2-2.桥形电路,求等效电阻R12。
1
1
1
1
R1
1
2Ω
2Ω
R2
R3
R12 2
1Ω
3
2
3
R12
2Ω
2
1Ω 2Ω
1Ω 2
1Ω
1Ω 2
解：先标出三个端点,将△ 2、2、1 →Y
22 R1 2120.8
i
R1
R2
+
u
Rn
-
i Req
+
u
-
1.特点：流过串联电阻的电流为同一电流。
Chapter 2
2.等效电阻
R e u i q R 1 i R 2 i R 3 i R n i i R 1 R 2 R n i n 1 R i
3.分压原理： i R1
+
R2 Rk Rn
u+uk -
Chapter 2
第二章 电阻电路的等效变换法
Chapter 2
教学目的 1.深刻理解等效电阻的概念。 2.掌握等效电阻的计算方法。 3.熟练掌握电阻的星形和三角形等效变换。
教学内容概述 本讲主要讲解电阻的串、并联, 星形和三角形等效变换，
即无源二端网络的等效化简。 教学重点和难点
重点:等效电阻的计算。 难点:电阻的星形网络和三角形网络的等效变换。
4A
R1
- ux +
1A R2 ix
ux
-
+
9A R1
R2
ix
6A
③ 求解： ixR 1R 1R 2922 0 10 0 9 6
u x R 2 i x 1 0 6 6 V 0
Chapter 2 2-2.电阻星形联接与三角形联接的等效变换
一.电路等效的一般概念：
1
i1
A
u1
i 2
i1
u12 R12
u31 R31
i2
u23 R23
u12 R12
i3
u31 R31
u23 R23
（2）
Chapter 2
3.利用电路等效概念推出Y-△等效变换公式
由电路等效概念，若Y网络与△网络等效，应满足：
u12 u12 u23u2 3
i1 i1
i2 i2
比较⑴、⑵两式，则有：
u31u3 1
Chapter 2
5.两个电阻的分流公式
i
i1
Req R1
i
R2 R1 R2
i
i1
i2
R1
R2
u
i2
Reqi R2
R1 R1R2
i
使用条件: i1 、i2 及 i 参考方向如上图。
Chapter 2
四.串、并联电路： 等效化简方法：按电阻串联或并联关系进行局部 化简后，重新画出电路，然后再进行简化，进而逐步 化简为一个等效电阻。
R1R2
R3u12 R2R3
R3R1
R1R2
R2u31 R2R3
R3R1
i2
R1R2
R1u23 R2R3
R3R1
R1R2
R3u12 R2R3
R3R1
i3
R1R2
R2u31 R2R3
R3R1
R1R2
R1u23 R2R3
R3R1
（1）
Chapter 2
2.找出△联结端口电压电流关系：
由KCL及Ω定律有:
Chapter 2 2-1 电阻的串、并联等效变换
一.等效电阻的概念：
i
i
u
Req
u
N
任一无源电阻二端网络，在其二端施加独立电源us(或is)， 输入电流为i (或u)，此网络可等效为一电阻，称为等效电阻
Req， 其值为：
RequS i
u Req
iS
Chapter 2
二. 串联电阻：
设n个电阻串联
即
Req
R2R1 R1 R2
Chapter 2
3.n个相等的电阻并联
设R1= R2= = Rn= R 则Geq= nG
其中 G 1 R
∴
R eq
R n
4.分流原理：
i1 i2
i
ik
in
并联电阻具有分流作用，如：R1 R 2
R k Rn
u
ik
uk Rk
Req i Rk
可知电阻 Rk 越大，分流越小，反之Rk 越小，分流越大。
i3 i3
R12R1R2RR2R 33R3R1 R23R1R2RR2R13R3R1 R31R1R2RR2R23R3R1 以上为已知Y求△的等效变换公式。
Chapter 2
将上式联立求解得:
R1
R12
R31R12 R23 R31
R2
R12R23 R12R23R31
R3
R31R23
R12R23R31
以上为已知△求Y的等效变换公式。
Chapter 2
说明： （1）以上两套公式的记忆法：
△→Y：分母为三个电阻的和，分子为三个待求电阻相 邻两电阻之积。
Y→△：分子为电阻两两相乘再相加，分母为待求电阻 对面的电阻。
（2）特例：若R12=R23=R31=R ，则有 R1R2R3RY1 3R 若R1=R2=R3=RY ， 则有 R12=R23=R31=3RY
2
Chapter 2
2.△形联接：三个端钮,每两个端钮之间连接一个电阻。
1
i'1
u'31
R13
u1' 2
R12
R23
3 i3'
i'2
2
u'23
Chapter 2
三.Y-△等效变换
1.找出Y联结端口电压电流关系：
u12R 1i1R 2i2 u23 R 2i2R 3i3
i1i2i30
解得：
i1
Chapter 2
例2-1 在图示电路中应用电阻合并方法求 ux 和 ix 。
4A
解：
14Ω 10Ω
4A R1
ux 15Ω
-
+
1A
20Ω
6Ω
ix
5Ω
6A
- ux +
1A R2 ix
6A
分析: ① R 1 1/0 1 / 1 5 4 2 0 R 2 2/0 5 / 6 1 0
Chapter 2
② 合并电源： 6+4-1=9A