结构动力学问答题答案-武汉理工-研究生
结构动力学习题解答

(4)
将(4)式代入方程(3)可以求得:
A= h
(ω
2
n
−ω
2 2
)
= + 4n ω 2 nω
2 2
6F
;
L 6 K − mω
(
2 2
)
+ 9C ω
2
2
α = arctg
ω n −ω
2
2
= arctg
3Cω 6 K − mω 2
;
(2) 求 f (t ) = δ (t ) 的解; 将 f (t ) = δ (t ) 代入方程(1)得
∑ M ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤: (1)设系统的广义坐标为 θ ,写出系统对于坐标 θ 的动能 T 和势能 U 的 表 达 式 ; 进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
ωn =
=
1 rA
;
1.8 已知图1-37所示振动系统中,匀质杆长为 L,质量为 m,两弹簧刚度皆为 K,阻尼系
̇ = 0时 数为 C,求当初始条件 θ 0 = θ 0
克拉夫《结构动力学》习题答案汇总

第二章 自由振动分析2-1(a ) 由例22T π=22()W K T gπ= 因此 max ()()D t kT νν= 其中 k=0、1、2……T D =0.64sec 如果ξ 很小,T D =T∴ 222200()49.9/0.64sec 386/sec kipsk kips in in π==⇒ 50/k kips in = (b )211lnln n n v v v v δ+≡=δξ=→=1.2ln 0.3330.86δ==0.0529ξ==0.33320.05302δπξξπ=→==⇒ 5.3%ξ= (a ’)D ω=2T πω=T T =249.950/1k kips in ξ==- (c)2c m ξω=W m g=2T πω=4c T gπωξ=T T =241W c Tg πξξ=- 2240.05292000.64sec386/sec 10.0529kipsc in π=-0.539sec/c kips in =⋅ T=T D0.538sec/c kips in =⋅ ⇒0.54sec/c kips in =⋅2-22k mω=→4.47ω== (1/sec ) (0)(0)()sin (0)cos tD D Dv v t et v t ξωξωνωωω-⎡⎤⎛⎫+⎢⎥ ⎪=+⎢⎥ ⎪⎝⎭⎣⎦∴ (0)(0)()sin (0)(0)(0))cos t D D D v v t e t v v v t ξωξωνξωωξωξωωω-⎛⎫⎡⎤+⎧⎫⎡⎤ ⎪⎢⎥=-++-⎨⎬⎢⎥ ⎪⎢⎥⎣⎦⎩⎭⎣⎦⎝⎭()22(0)(0)()(0)cos sin D t D D Dv v t e v t t ξωξωξωωνωωω-⎛⎫⎡⎤++ ⎪⎣⎦=- ⎪ ⎪⎝⎭D ω=→()(0)cos (0)(0)sin t D D D t e v t v v t ξωωνωξωωω-⎛⎫⎡⎤=-+ ⎪⎢⎥⎣⎦⎝⎭()(0)cos tD D t ev t t ξωνωω-⎛⎫⎪= ⎪⎝⎭0.055922(2)(4.47)c cc m ξω=== (a) c=0→0ξ=→D ωω=∴ 5.6(1)sin 4.470.7cos 4.47 1.384.47v t in ==+=- (1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/sec v t in ==-=⇒(1) 1.4v in =-,(1) 1.7/sec v in = (b)c=2.8→0.0559(2.8)0.157ξ==4.41D ω== (1/sec ) (0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e ν-⎡+⎤⎛⎫==+⎪⎢⎥⎝⎭⎣⎦(1)0.764t in ν==-(0.157)(4.41)(1) 5.6cos 4.41 4.41t e ν-⎛⎫== ⎪⎝⎭(1) 1.10/sec t in ν==⇒(1)0.76v in =-,(1) 1.1/sec v in =第三章 谐振荷载反应3-1根据公式有 ()()21sin sin 1R t w t wt ββ⎡⎤=-⎢⎥-⎣⎦0.8wwβ== ()()2.778sin 0.8sin1.25R t wt wt=-将t ω以80°为增量计算)(t R 并绘制曲线如下:80° 160° 240° 320° 400° 480° 560° 640° 720° 800° 00.547 1.71 -0.481 -3.214 0.357 4.33 -0.19 -4.9244.9241.25w w =tω)(t R3-2解:由题意得:22m kips s in =⋅ , 20k kips in = , (0)(0)0v v == ,w w =3.162w rad ===8wt π=(a )0c =()()1sin cos 2R t wt wt wt =-将8wt π=代入上式得:()412.566R t π=-=- (b )0.5c k s =⋅0.50.0395222 3.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得:()7.967R t =- (c ) 2.0c k s =⋅2.00.1582223.162c c c c mw ξ====⨯⨯()()(){}1exp 1cos exp sin 2R t wt wt wt wt ξξξξ=--+-⎡⎤⎡⎤⎣⎦⎣⎦将8wt π=代入上式得:() 3.105R t =-3-3解:(a ):依据共振条件可知:10.983sec w w rad =====由2L T V w π==得:10.9833662.96022wL V ft s ππ⨯===(b ):()()()122max2221212tgo v v ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦1w w β==0.4ξ= 1.2go v in =代入公式可得:max 1.921tv in =(c ):2L T V w π=='45min 66V h ft s ==226611.51336V w rad s ec L ππ⨯'===11.5131.04810.983w w β'===0.4ξ=代入数据得 :()()()122max22212=1.85512tgov v in ξββξβ⎡⎤+⎢⎥=⎢⎥-+⎣⎦3-4解:按照实际情况,当设计一个隔振系统时,将使其在高于临界频率比β=在这种情况下,隔振体系可能有小的阻尼。
结构动力学试题及答案

结构动力学试题及答案(本文按试题和答案格式进行编写)试题一:1. 请问什么是结构动力学?2. 简述结构动力学的研究对象和主要内容。
3. 结构动力学分析常用的方法有哪些?4. 结构动力学分析中常用的数学模型有哪些?5. 结构动力学的应用领域有哪些?答案一:1. 结构动力学是研究结构在外力作用下的动态响应及其稳定性的学科。
2. 结构动力学的研究对象是各种工程结构,主要内容包括结构的振动、冲击响应、瞬态响应和稳态响应等。
3. 结构动力学分析常用的方法有模态分析法、频率响应分析法、时程分析法等。
4. 结构动力学分析中常用的数学模型有单自由度体系、多自由度体系、连续体系等。
5. 结构动力学的应用领域广泛,包括建筑结构工程、桥梁工程、风力发电机组、地震工程等。
试题二:1. 结构动力学分析中,模态分析的基本原理是什么?2. 简述模态分析的步骤和计算方法。
3. 常用的模态分析软件有哪些?4. 请问什么是结构的固有频率和阻尼比?5. 结构的模态振型对结构动力响应有什么影响?答案二:1. 模态分析是基于结构的振动特性,通过求解结构的固有频率、模态振型和阻尼比等参数,来研究结构的动力响应。
2. 模态分析的步骤包括建立结构有限元模型、求解结构的固有频率和模态振型、计算结构的阻尼比等。
常用的计算方法有有限元法、拉普拉斯变换法等。
3. 常用的模态分析软件有ANSYS、ABAQUS、MSC.NASTRAN等。
4. 结构的固有频率是结构在无外力作用下自由振动的频率,阻尼比是结构振动过程中能量耗散的程度。
5. 结构的模态振型对结构动力响应有很大影响,不同的模态振型会导致不同的振动特性和反应。
试题三:1. 结构动力学分析中,频率响应分析的基本原理是什么?2. 简述频率响应分析的步骤和计算方法。
3. 频率响应分析和模态分析有什么区别?4. 结构的频率响应函数和传递函数有什么区别?5. 频率响应分析在结构设计中的应用有哪些?答案三:1. 频率响应分析是研究结构在单频激励下的响应特性,通过求解结构的频率响应函数,来获得结构的响应。
结构动力学习题答案
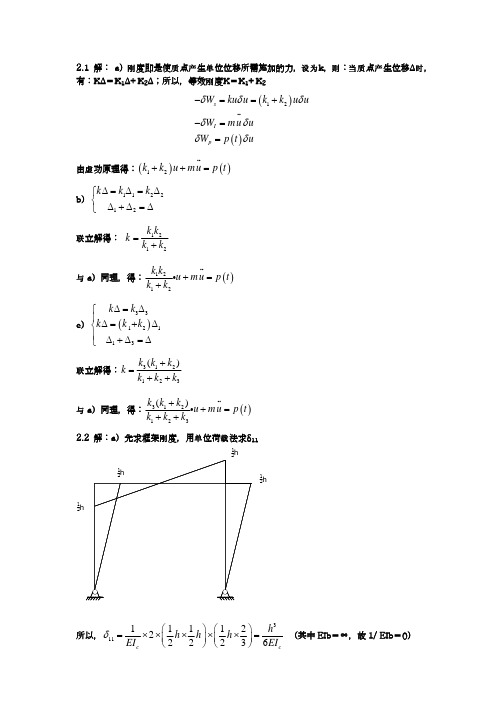
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程: ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时,发生共振有: Rd 1 =
当 w wn = 1 10 时, Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解:
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理: δ Ws
+ δ WI + δ W D +δ W p = 0 得:
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解:
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭
结构动力学问答题答案-武汉理工-研究生

结构动力学问答题答案-武汉理工-研究生《结构动力学》思考题第1章1、对于任一振动系统,可划分为由激励、系统和响应三部分组成。
试结合生活或工程分别举例说明:何为响应求解、环境识别和系统识别?响应求解:结构系统和荷载已知,求响应。
又称响应预估问题,是工程正问题的一种,通常在工程中是指结构系统已知,具体指结构的形状构件及离散元件等,环境识别:主要是荷载的识别,结构和响应已知,求荷载。
属于工程反问题的一种。
在工程中,如已知桥梁的结构和响应,根据这些来反推出桥梁所受到的荷载。
系统识别:荷载和响应已知,求结构的参数或数学模型。
又称为参数识别,是工程反问题的一种,在土木工程领域,房屋、桥梁和大坝等工程结构被视为“系统”,而“识别”意味着由振动实验数据求得结构的动力特性(如频率、阻尼比和振型)。
如模态分析和模态试验技术等基本成型并得到广泛应用。
2、如何从物理意义上理解线性振动系统 解的可叠加性。
求补充!!!!!3、正确理解等效刚度的概念,并求解单自由度系统的固有频率。
复杂系统中存在多个弹性元件时,用等效弹性元件来代替原来所有的弹性元件,等效原则是等效元件刚度等于组合元件刚度,则等效元件的刚度称为等效刚度。
4、正确理解固有频率f 和圆频率ω的物理意义。
固有频率f :物体做自由振动时,振动的频率与初始条件无关,而仅与系统的本身的参数有关(如质量、形状、材质等),它是自由振动周期的倒数,表示单位时间内振动的次数。
圆频率ω: ω=2π/T=2πf 。
即为单位时间内位移矢量在复平面内转动的弧度,又叫做角频率。
它只与系统本身的参数m ,k 有关,而与初始条件无关5、正确理解过阻尼、临界阻尼、欠阻尼的概念。
一个系统受初扰动后不再受外界激励,因为受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。
系统的状态按照阻尼比ζ来划分。
把ζ=0的情况称为无阻尼,即周期运动;把0<ζ<1的情况称为欠阻尼,即系统所受的阻尼力较小,振幅在逐渐减小,最后才达到平衡位置;把ζ>1的情况称为过阻尼,如果阻尼再增大,系统需要较长的时间才能达到平衡;把ζ=1的情况称为临界阻尼,即阻尼的大小刚好使系统作非"周期"运动。
结构力学(专科)——武汉理工大学
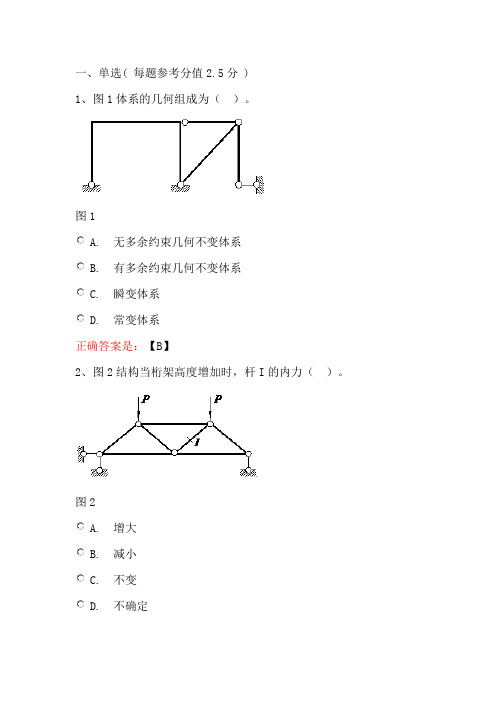
一、单选( 每题参考分值2.5分 )1、图1体系的几何组成为()。
图1A. 无多余约束几何不变体系B. 有多余约束几何不变体系C. 瞬变体系D. 常变体系正确答案是:【B】2、图2结构当桁架高度增加时,杆I的内力()。
图2A. 增大B. 减小C. 不变D. 不确定正确答案是:【C】3、当杆件刚度系数SAB=3i时,杆的B端为()。
A. 自由端B. 固定端C. 铰支承D. 定向支承正确答案是:【C】4、图3结构超静定次数为()。
图3A. 6次B. 7次C. 8次D. 9次正确答案是:【C】5、图1体系的多余约束的个数为()。
图1A. 0个B. 1个C. 2个D. 3个正确答案是:【B】6、拱轴线为合理拱轴线,其横截面上内力为零的是()。
A. 弯矩B. 扭矩C. 轴力D. 支座反力正确答案是:【A】7、图2梁受到三角形荷载作用,A端竖向支座反力的大小为()。
图2A. ql/2B. ql/3C. ql/4D. ql/6正确答案是:【A】8、在力法方程中()。
A.B.C.D. 前三种答案都有可能正确答案是:【D】9、拱的突出持点是竖向荷载下有()。
A. 轴力B. 弯矩C. 竖向力D. 水平推力正确答案是:【D】10、力法典型方程的物理意义是()。
A. 结构的平衡条件B. 结点的平衡条件C. 结构的变形协调条件D. 结构的平衡条件及变形协调条件正确答案是:【C】11、绘制任一量值的影响线时,假定荷载是()。
A. 一个方向不变的单位荷载B. 移动荷载C. 动力荷载D. 可动荷载正确答案是:【A】12、力矩分配法计算得出的结果()。
A. 一定是近似解B. 不是精确解C. 是精确解D. 可能为近似解,也可能是精确解正确答案是:【D】13、图3桁架零杆的个数为()。
图3A. 3个B. 4个C. 5个D. 6个正确答案是:【D】14、图3a结构,EI=常数,取图3b为力法基本体系,则中的和分别等于()。
图3A. Δ,Δ/4B. -Δ,Δ/4C. Δ,-Δ/4D. -Δ,-Δ/4正确答案是:【D】15、叠加原理用于求解静定结构时,需要满足的条件是()。
在线测试题试题库及解答(第十章)结构动力学

在线测试题试题库及解答第十章结构动力学基础一、单项选择题1、结构的主振型与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A2、结构的自振频率与什么有关?A、质量和刚度B、荷载C、初始位移D、初始速度标准答案 A3、单自由度体系在简谐荷载作用下,下列哪种情况内力与位移的动力系数相同?A、均布荷载作用B、荷载作用在质点上与质点运动方向垂直C、荷载不作用在质点上D、惯性力与运动方向共线标准答案 D4、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D5、具有集中质量的体系,其动力计算自由度A、等于其集中质量数B、小于其集中质量数C、大于其集中质量数D、以上都有可能标准答案 D6、当简谐荷载作用于有阻尼的单自由度体系质点上时,若荷载频率远远大于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、重力C、阻尼力D、惯性力标准答案 D7、设ω为结构的自振频率,θ为荷载频率,β为动力系数下列论述正确的是A、ω越大β也越大B、θ/ω越大β也越大C、θ越大β也越大D、θ/ω越接近1,β绝对值越大标准答案 D8、如果体系的阻尼增大,下列论述错误的是A、自由振动的振幅衰减速度加快B、自振周期减小C、动力系数减小D、位移和简谐荷载的相位差变大标准答案 B9、无阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力C、惯性力与弹性力的合力D、没有力标准答案 D10、有阻尼单自由度体系在简谐荷载作用下,共振时与动荷载相平衡的是A、弹性恢复力B、惯性力与弹性力的合力C、惯性力D、阻尼力标准答案 D11、当简谐荷载作用于无阻尼的单自由度体系质点上时,若荷载频率远远小于体系的自振频率时,则此时与动荷载相平衡的主要是A、弹性恢复力B、阻尼力C、惯性力D、重力标准答案 A12、一单自由度振动体系,其阻尼比为ξ,动力系数β,共振时下列结果正确的是A、ξ=0.05,β=10B、ξ=0.1,β=15C、ξ=0.15,β=20D、ξ=0.2,β=25标准答案 A13、一单自由度振动体系,由初始位移0.685cm,初始速度为零产生自由振动,振动一个周期后最大位移为0.50cm,体系的阻尼比为A、ξ=0.05B、ξ=0.10C、ξ=0.15D、ξ=0.20标准答案 A14、在低阻尼体系中不能忽略阻尼对什么的影响?A、频率B、主振型C、周期D、振幅标准答案 D15、单自由度体系受简谐荷载作用,ω为体系自振频率,θ为荷载频率,动位移 y(t)与荷载 P(t) 的关系是A、当θ/ω>1时,y(t)与P(t)同向,当θ/ω<1时,y(t)与P(t)反向。
结构动力学试题及答案

结构动力学试题及答案一、选择题1. 在结构动力学中,下列哪项不是描述结构动力响应的参数?A. 自然频率B. 阻尼比C. 静力平衡D. 模态阻尼2. 以下哪个不是结构动力学分析中的常用方法?A. 模态分析B. 时域分析C. 频域分析D. 静力分析二、简答题1. 简述结构动力学中模态分析的目的和重要性。
2. 描述阻尼对结构动力响应的影响。
三、计算题1. 假设一个单自由度系统,其质量为m,刚度为k,初始位移为x0,初始速度为v0。
若外力为F(t) = F0 * sin(ωt),求该系统在任意时间t的位移响应。
答案一、选择题1. 正确答案:C. 静力平衡解析:静力平衡是静力学的概念,与结构动力学无关。
2. 正确答案:D. 静力分析解析:静力分析是分析结构在静载荷作用下的响应,而结构动力学分析动态载荷下的结构响应。
二、简答题1. 模态分析的目的在于识别结构的自然振动特性,包括自然频率、阻尼比和模态形状。
它的重要性在于:- 预测结构在动态载荷下的响应。
- 为控制结构的振动提供基础数据。
- 优化设计,提高结构的抗震性能。
2. 阻尼对结构动力响应的影响主要表现在:- 减少振动幅度,提高结构的稳定性。
- 改变系统的自然频率和模态形状。
- 影响系统的动态响应时间。
三、计算题1. 单自由度系统的位移响应可以通过以下步骤求解:- 写出系统的动力学方程:m * d²x/dt² + c * dx/dt + k * x = F(t)- 应用初始条件:x(0) = x0, v(0) = v0- 应用外力:F(t) = F0 * sin(ωt)- 通过傅里叶变换或拉普拉斯变换求解方程。
- 应用逆变换得到位移响应的解析解或数值解。
位移响应的一般形式为:x(t) = X * cos(ωt - φ) + Y *sin(ωt - φ),其中X和Y是与系统参数和初始条件有关的常数,φ是相位角。
具体的数值需要根据系统参数和初始条件进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构动力学问答题答案-武汉理工-研究生《结构动力学》思考题第1章1、对于任一振动系统,可划分为由激励、系统和响应三部分组成。
试结合生活或工程分别举例说明:何为响应求解、环境识别和系统识别?响应求解:结构系统和荷载已知,求响应。
又称响应预估问题,是工程正问题的一种,通常在工程中是指结构系统已知,具体指结构的形状构件及离散元件等,环境识别:主要是荷载的识别,结构和响应已知,求荷载。
属于工程反问题的一种。
在工程中,如已知桥梁的结构和响应,根据这些来反推出桥梁所受到的荷载。
系统识别:荷载和响应已知,求结构的参数或数学模型。
又称为参数识别,是工程反问题的一种,在土木工程领域,房屋、桥梁和大坝等工程结构被视为“系统”,而“识别”意味着由振动实验数据求得结构的动力特性(如频率、阻尼比和振型)。
如模态分析和模态试验技术等基本成型并得到广泛应用。
2、如何从物理意义上理解线性振动系统 解的可叠加性。
求补充!!!!!3、正确理解等效刚度的概念,并求解单自由度系统的固有频率。
复杂系统中存在多个弹性元件时,用等效弹性元件来代替原来所有的弹性元件,等效原则是等效元件刚度等于组合元件刚度,则等效元件的刚度称为等效刚度。
4、正确理解固有频率f 和圆频率ω的物理意义。
固有频率f :物体做自由振动时,振动的频率与初始条件无关,而仅与系统的本身的参数有关(如质量、形状、材质等),它是自由振动周期的倒数,表示单位时间内振动的次数。
圆频率ω: ω=2π/T=2πf 。
即为单位时间内位移矢量在复平面内转动的弧度,又叫做角频率。
它只与系统本身的参数m ,k 有关,而与初始条件无关5、正确理解过阻尼、临界阻尼、欠阻尼的概念。
一个系统受初扰动后不再受外界激励,因为受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。
系统的状态按照阻尼比ζ来划分。
把ζ=0的情况称为无阻尼,即周期运动;把0<ζ<1的情况称为欠阻尼,即系统所受的阻尼力较小,振幅在逐渐减小,最后才达到平衡位置;把ζ>1的情况称为过阻尼,如果阻尼再增大,系统需要较长的时间才能达到平衡;把ζ=1的情况称为临界阻尼,即阻尼的大小刚好使系统作非"周期"运动。
1过阻尼:n n ω> (m c n 2/=m k n =ω),特征根为两个负实数,微分方程的解是一条负指数衰减曲线,不会发生往复振动。
2临界阻尼:n n ω=,特征方程的跟为两个相等的实数。
3欠阻尼:n n ω<。
6、正确理解自由振动和强迫振动的概念。
自由振动:没有激振力(动荷载)的作用,振动系统在初始扰动后,仅靠恢复力维持的振动。
强迫振动:振动系统在外界干扰力或干扰位移作用下产生的振动7、)(t f kx x c xm =++一单自由度振动系统的幅-频曲线如图所示,根据频率大致可划分为三个区域,试说明各频段内其物理含义。
(1)当频率比远小于1时,即(ω<<ωn),随着阻尼比的增大,曲线均趋于平缓,放大因子趋近于1,体系振动很慢,惯性力与阻尼力都很小,动荷载主要与弹性力平衡。
(2)当频率比远大于1时,即(ω>>ωn),随着无论阻尼比大小如何,曲线放大因子均趋近于0,体系振动很快,振幅大小主要取决于系统惯性,动荷载主要与惯性力平衡。
(3) 当频率比接近1时,即(ω≈ωn ),振幅迅速增大,即产生共振现象,此时振幅大小与阻尼关系密切,阻尼越大,振幅越大。
1.当1<<β时,放大系数β接近1,基本上与阻尼比无关,表明稳态反应的幅值基本上与静位移相同,由系统刚度控制。
2.当1=β时,稳态反应由阻尼控制,当n ω接近1时,β对阻尼比非常敏感,可为静位移的数倍,说明动力反应的幅值比静位移大很多。
3.当1>>β时,放大系数β随频率比增大而趋于0,基本不受阻尼的影响,稳态反应的幅值由质量控制。
8、一单自由度振动系统,何谓位移共振、速度共振和加速度共振?试说明其物理含义。
位移共振:当β、n ω和f 不变时,改变ω使结构的位移达到极大值的现象称为位移共振速度共振:当β、n ω和f 不变时,改变ω使结构的速度达到极大值的现象称为速度共振加速度共振:当β、n ω和f 不变时,改变ω使结构的加速度达到极大值的现象称为加速度共振9、一单自由度振动系统的位移传递率如图所示,试分析各频率段阻尼比对其响应的影响作用。
(1)n ωω<<1时,位移传递率A/B=1,体系质量的绝对位移与基础的位移相同,两者之间没有相对位移 (2)nωω=2时,位移传递率A/B=1,此时与阻尼无关 (3)nωω≈1时,位移传递率A/B >1,且有峰值,即失振现象 (4)n ωω>2时,位移传递率A/B<1,即质量的振动幅值小于基础运动的幅值,即随着频率比的增大,A/B 减小,此时阻尼比越小越好,但是阻尼比过小会对通过共振区不利。
10、单自由度振动系统旋转矢量法求解的物理含义是什么。
振动系统的弹性力、阻尼力、激振力和惯性力都可以用矢量表示,根据动力平衡,它们的合力为0,这些力应组成一平衡力系,其力多边形应封闭。
11、推导杜哈梅(Duhamel )积分。
略12、 如何理解频率响应函数的物理意义。
频率响应函数表示单位正弦力引起的复反应,频率响应函数是以频率为自变量的函数,它描述了系统输入与输出在不同的频率取值时的对应关系,一般以复数形式表示。
13、阻尼、结构阻尼与等效阻尼的基本概念。
阻尼:泛指振动过程中的能量耗散。
结构阻尼:又叫滞后阻尼,它是来源于结构内部由于振动变形引起能量耗散带来的阻尼等效阻尼:将各种复杂的阻尼折算为等价的粘性阻尼,折算的方法是认为其他阻尼与粘性阻尼在振动一周之内所耗散的能量相等。
14、结合第一章单自由系统的强迫振动,试总结简谐力激励、周期函数力激励、脉冲力激励、阶跃力激励及任意力激励响应的求解方法。
略15、试分析线性振动系统响应谱求解和时间历程响应求解的特点与区别。
响应谱求解:选择一个或多个系统参数使系统满足某些给定条件,使用响应谱来刻划不同结构参数在给定激励下的最大响应。
响应谱求解以任意一个参数为自变量,而时间历程求解以时间为自变量。
第2~3章1、 什么是结构的共振?如何理解其物理意义?当系统的外加激励引起的结构频率与振型与结构自身的固有频率和振型相吻合的时候,产生的结构振幅增大的现象,系统发生共振,共振过程中,外加激励的能量被系统吸收,系统的振幅逐渐增大2、周期信号展开成傅里叶(Fourier )级数∑∞=++=10)sin cos (2)(n n n T t n b t n a a t f ωω如何理解其ω称为基频, ωωn n = 为倍频的含意。
周期信号可以由傅里叶级数分解为一系列的离散谱,其中频率最小的谐波的频率称为基频,基频以外的其他振动频率均为基频的整数倍,称为倍频3、数学上如何理解 ,当 时。
三角函数系中任何两个不同的两个函数的乘积在区间【-π,π】上的积分等于零4、如何准确理解多自由度系统固有频率的内涵。
多自由度系统的特征方程的根称为多自由度系统的固有频率 5、结构的响应是各阶模态共同参与的结果。
试根据模态叠加原理写出其表达式,并扼要地说明各项的物理意义。
{}{}∑==n i i i Y 1)(y η,{}y 为结构在外界激励下的响应;i η为模态参与因子,{})(i Y 为各阶振型6、如何理解结构模态对位移响应的贡献与所对应模态应变能的关系;怎样理解模态截断准则?结构的低阶模态对位移的响应的贡献要大于高阶模态对位移的贡献,但高阶模态对应的模态变形能要远高于低阶模态对应的模态变形能理想的情况下我们希望得到一个结构的完整的模态集,实际应用中这即不可能也不必要。
实际上并非所有的模态对响应的贡献都是相同的。
对低频响应来说,高阶模态的影响较小。
对实际结构而言,我们感兴趣的往往是它的前几阶或十几阶模态,更高的模态常常被舍弃。
这样尽管会造成一点误差,但频响函数的矩阵阶数会大大减小,使工作量大为减小。
这种处理方法称为模态截断。
7、如何理解结构的阻尼和各阶模态的阻尼。
结构的阻尼比是测不出来的,通过共振试验测到的是结构的各阶模态阻尼比8、结构余振波形识别结构第1阶固有频率和阻尼比应注意哪些问题。
求补充!!!!!9、比例阻尼 的物理含义和实质。
假设结构阻尼[C]是质量矩阵[M]和刚度矩阵[K]的线性组合,称为比例阻尼或瑞利阻尼。
10、什么是正则坐标?什么是静力耦合?什么是动力耦合?在正则坐标变换{y}=[Y]{η}中,{η}称为正则坐标,刚度矩阵不为对角矩阵,质量矩阵为对角矩阵,称为静力耦合,质量矩阵不为对角矩阵而刚度矩阵为对角矩阵称为动力耦合。
11、主振型正交的物理内涵是什么?主振型正交的物理意义是各阶模态的能量不能在模态之间相互转化12、对于一线性振动系统,进行模态坐标变换的实质是什么?][][][K M C βα+=0)sin()sin(0=⎰dt t j t i T ωωj i ≠将振动微分方程解耦,使其变成n个独立的线性微分方程组13、动力减振器减振的实质是什么?附加系统产生一个与激振力等大反向的力。
14、试总结多自由度系统运动微分方程建立的常用方法。
达朗贝尔原理,拉格朗日方法,动力平衡法,虚功法,变分法15、试总结多自由度系统求解响应主要分为哪几步进行。
a.建立多自由度系统的振动微分方程b.求出固有频率,主振型,并验证主振型的正交性,得到模态矩阵c.求出正则坐标,利用模态叠加原理求出几何坐标16、列举几个你所知晓的关于向量正交的例子。
多自由体系主振型的正交性,主振型关于质量矩阵,刚度矩阵,阻尼矩阵正交第4章1、在对一振动系统利用里兹法(Ritz)、伽辽金(Galerkin)法或有限元法近似求解时,对其振型函数分别有什么要求?瑞利-里兹法的振型函数满足位移边界条件;伽辽金法满足位移边界条件和应力的边界条件;有限元法需要选定以杆端位移为参数,以单元内任一点的位置坐标为自变量,以杆端位移为参数来表示单元内部任意一点位移。
2、对于一振动系统,可有多种方法近似求出其固有频率,如瑞利法(Rayleigh),里兹法(Ritz)、伽辽金(Galerkin)法或有限元法等。
试问:在众多的近似解与精确值比较时,近似解比精确值是大些、小些、还是不能确定?为什么?近似解比精确解大,由最小势能原理,在所有满足位移边界条件的位移中,真实存在的那一组使总势能取极小值。
3、主振型正交性的物理内涵是什么?见第2,3章4、正确理解结构的振动与波动。
①研究对象不同——振动,是单个质点在平衡位置附近的往复运动;波动,是介质中大量质点依次的集体振动.②力的来源不同——产生振动的回复力,可以由作用在物体上的各种性质的力提供;而引起波动的力,则总是联系介质中各质点的弹力.③运动性质不同——各质点的振动,是变加速运动;而波动是匀速直线运动,传播距离与时间成正比.5、试分析两弹性体碰撞时,与哪些因素有关。
