附表三卡方分布上侧分位数表
三大分布及其分位数

泊松分布的均值和方差相等,且随着均值 的增大,泊松分布逐渐趋近于正态分布。 此外,泊松分布具有可加性,即两个独立 泊松分布的和仍然服从泊松分布。
泊松分布的分位数计算
分位数定义
分位数是指将一个随机变量的概率分 布划分为几个等份的数值点,如中位 数就是50%分位数。
泊松分布分位数计算
泊松分布的分位数可以通过查表或使用 统计软件进行计算。对于给定的泊松分 布参数λ和概率p,可以计算出对应的分分位数的概念
分布
分布是指一组数据在各个取值范围内的频数或频率。在统计 学中,分布通常用概率密度函数或累积分布函数来描述。
分位数
分位数是指将一个随机变量的概率分布范围分为几个等份的 数值点。常用的分位数有四分位数、百分位数等。例如,中 位数就是50%分位数,表示有一半的数据小于或等于该值, 另一半的数据大于该值。
和优化提供理论支持。
生物学和医学
在生物学和医学研究中,泊松分布 可以用来描述放射性物质的衰变次 数、基因突变数等随机事件的发生
次数。
04 指数分布及其分位数
指数分布的定义和性质
定义
01
指数分布是一种连续概率分布,通常用于描述事件之间的时间
间隔。
性质
02
指数分布具有无记忆性,即事件发生的概率与自上次事件发生
排队论
在排队系统中,指数分布可用于描述顾客到达和 服务时间的概率分布,从而分析系统的性能指标 。
金融风险管理
指数分布可用于评估金融风险,如信用风险和市 场风险等,帮助金融机构制定风险管理策略。
05 三大分布的比较与联系
三大分布的特征比较
正态分布
呈钟形曲线,两侧对称,均值、 中位数、众数相等,标准差决定
卡方分布概念及表和查表方法

卡方分布概念及表和查表方法目录1简介2定义3性质4概率表简介分布在数理统计中具有重要意义。
分布是由阿贝(Abbe)于1863年首先提出的,后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K·Pearson)分别于1875年和1900年推导出来,是统计学中的一个非常有用的著名分布。
定义若n个相互独立的随机变量ξ₁、ξ₂、……、ξn,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为分布(chi-square distribution),卡方分布其中参数称为自由度,正如正态分布中均数或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。
记为或者(其中,为限制条件数)。
卡方分布是由正态分布构造而成的一个新的分布,当自由度很大时,分布近似为正态分布。
对于任意正整数x,自由度为的卡方分布是一个随机变量X的机率分布。
性质1) 分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数的增大,分布趋近于正态分布;卡方分布密度曲线下的面积都是1。
2) 分布的均值与方差可以看出,随着自由度的增大,分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
3)不同的自由度决定不同的卡方分布,自由度越小,分布越偏斜。
4) 若互相独立,则:服从分布,自由度为。
5) 分布的均数为自由度,记为E( ) = 。
6) 分布的方差为2倍的自由度( ),记为D( ) = 。
概率表分布不象正态分布那样将所有正态分布的查表都转化为标准正态分布去查,在分布中得对每个分布编制相应的概率值,这通过分布表中列出不同的自由度来表示,卡方分布临界值表在分布表中还需要如标准正态分布表中给出不同P 值一样,列出概率值,只不过这里的概率值是值以上分布曲线以下的概率。
由于分布概率表中要列出很多分布的概率值,所以分布中所给出的P 值就不象标准正态分布中那样给出了400个不同的P 值,而只给出了有代表性的13个值,因此分布概率表的精度就更差,不过给出了常用的几个值,足够在实际中使用了。
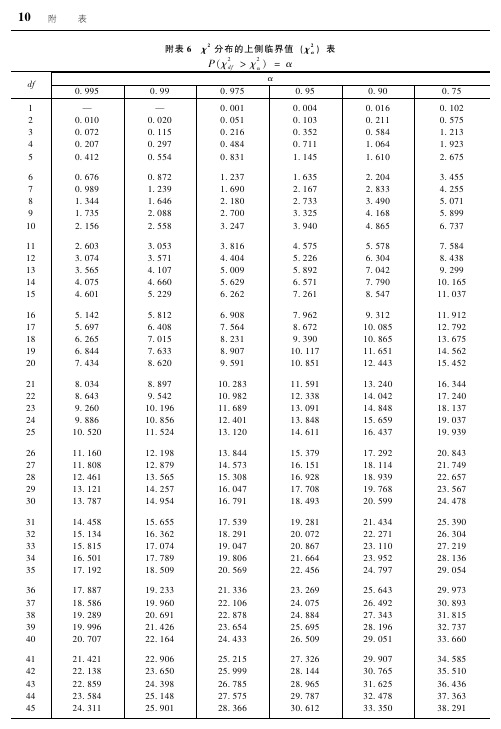
卡方分布的上侧临界值表
!!! !!
*/*"
$/$#& '/)"* ""/#+& "#/)(( "&/*%$
"$/%") "%/+(& )*/*'* )"/$$$ )#/)*'
)+/()& )$/)"( )(/$%% )'/"+" #*/&(%
#)/*** ##/+*' #+/%*& #$/"'" #(/&$$
)#/)$' )+/*(& )+/%%+ )&/$'& )$/&*'
))/'*$ )#/$&* )+/#'% )&/"+% )&/'*"
)&/)"& )&/''' )$/(%& )(/&(& )%/#$$
)(/#)$ )%/"++ )%/'$& )'/(%( #*/$")
*/'*
*/*"$ */)"" */&%+ "/*$+ "/$"*
!+ !!!
卡方分布分位数

卡方分布分位数
卡方分布分位数是统计学中一种重要的分布,可以用来分析和比较不同独立变量之间的相关性。
它是一种对数正态分布,其分布是以同样大小的统计方差来定义的,同时有许多分位数可以用来描述数据的分布。
卡方分位数是通过求解卡方分布函数 f(x) 的积分计算得到的。
卡方分布的分位数表示的是在某一自变量的值固定的情况下,另一自变量的值分布的概率。
卡方分布分位数可以比较两个或多个卡方分布的取值结果,以及比较不同自变量的取值情况。
卡方分位数最常用于卡方检验,用于验证两个或多个变量之间是否存在统计学上的联系性。
此外,卡方分位数也可以用于犯罪学、心理学等多个领域,以分析不同自变量之间的关联性,并进行相关性的衡量。
总的来说,卡方分位数是一种重要的统计工具,也是一种常见的应用于统计分析的技术。
它不仅可以用于评估不同变量之间的相关性,而且可以用于犯罪学、心理学等多个领域,以辅助分析不同环境下的思维行为,提高研究质量。
r语言构造卡方分布的分位数表

r语言构造卡方分布的分位数表卡方分布是统计学中常用的概率分布之一,通常用于统计离散随机变量之间的关系。
卡方分布的密度函数随着自由度的增加而变化,因此在实际应用中需要使用卡方分布的分位数表来进行计算。
卡方分布的分布函数可以用以下公式表示:$F(x)=P(X \lex)=\sum_{i=0}^{\lfloor x \rfloor} \frac{(e^{-\frac{x}{2}})(\frac{x}{2})^i}{i!}$,其中,x是随机变量的取值,自由度为v的卡方分布的期望值为v,方差为2v。
如果要计算x的概率,可以通过查表或使用R语言编程来实现。
在R语言中,可以通过qchisq()函数来计算卡方分布的分位数。
该函数的语法格式为:qchisq(p, df, lower.tail = TRUE, log.p = FALSE),其中p为概率值,df为自由度,lower.tail为计算分位数是采用小于等于还是大于等于概率值,默认为TRUE,表示小于等于概率值的分位数;log.p为概率值是否以对数形式输入,默认为FALSE。
以下是自由度为5的卡方分布的分位数表的部分内容,可以用于计算概率值和分位数:自由度df 0.995 0.990 0.975 0.950 0.9000.100 0.050 0.025 0.010 0.0051 0.000 0.000 0.001 0.004 0.016 2.7063.841 5.024 6.635 7.8792 0.010 0.020 0.051 0.103 0.211 4.6055.991 7.378 9.210 10.5973 0.072 0.115 0.216 0.352 0.584 6.2517.815 9.348 11.345 12.8384 0.207 0.297 0.484 0.711 1.064 7.7799.488 11.143 13.277 14.8605 0.412 0.554 0.831 1.145 1.610 9.23611.070 12.833 15.086 16.7506 0.676 0.872 1.237 1.635 2.20410.645 12.592 14.449 16.812 18.548从表中可以看出,对于自由度为5的卡方分布,当满足95%的置信度时,对应的分位数为11.07。
卡方分布的分位数

卡方分布的分位数
卡方分布的分位数
卡方分位数是用来衡量样本和理论分布之间的偏离程度的度量指标。
它表示理论分布中某个特定分位数点的卡方值,可用来确定样本和理
论分布之间的差异。
在卡方检验中,卡方分位数有两个主要用途:
1)卡方分位数可以用来检验样本的正态性。
如果样本符合正态分布,
那么卡方分位数将与理论值一致。
2)卡方分位数可以用来测量样本和理论分布之间的偏离程度。
如果样
本与理论分布有显著的偏离,那么卡方分位数将显著地不同于理论值。
卡方分位数的计算可以通过统计软件实现。
它的计算公式如下:
卡方分位数=Σ(n-1)/Σ(n-1)*χ2(α,v)
其中n为样本的大小,α为显著性水平,v为自由度,χ2(α,v)
为指定的显著性水平和自由度下的卡方分布的期望值。
总之,卡方分位数是一种有效的度量工具,可以用来测量样本和理论
分布之间的偏离程度,以及检验样本的正态性。
它的计算可以通过统
计软件实现,其计算公式如上所述。
统计学常用分布与其分位数
§1.4 常用的分布及其分位数1. 卡平方分布卡平方分布、t 分布及F 分布都是由正态分布所导出的分布,它们与正态分布一起,是试验统计中常用的分布。
当X 1、X 2、…、Xn 相互独立且都服从N(0,1)时,Z=∑ii X 2 的分布称为自由度等于n 的2χ分布,记作Z ~2χ(n),它的分布密度 p(z )=⎪⎪⎩⎪⎪⎨⎧>⎪⎭⎫ ⎝⎛Γ--,,00,2212122其他z e x n z n n 式中的⎪⎭⎫ ⎝⎛Γ2n =u d e u u n ⎰∞+--012,称为Gamma 函数,且()1Γ=1,⎪⎭⎫ ⎝⎛Γ21=π。
2χ分布是非对称分布,具有可加性,即当Y 与Z 相互独立,且Y ~2χ(n ),Z ~2χ(m ),则Y+Z ~2χ(n+m )。
证明: 先令X 1、X 2、…、X n 、X n+1、X n+2、…、X n+m 相互独立且都服从N(0,1),再根据2χ分布的定义以及上述随机变量的相互独立性,令Y=X 21+X 22+…+X 2n ,Z=X 21+n +X 22+n +…+X 2m n +,Y+Z= X 21+X 22+…+X 2n+ X 21+n +X 22+n +…+X 2m n +, 即可得到Y+Z ~2χ(n +m )。
2. t 分布 若X 与Y 相互独立,且X ~N(0,1),Y ~2χ(n ),则Z =nY X 的分布称为自由度等于n 的t 分布,记作Z ~ t (n ),它的分布密度P(z)=)()(221n nn ΓΓ+2121+-⎪⎪⎭⎫ ⎝⎛+n n z 。
请注意:t 分布的分布密度也是偶函数,且当n>30时,t分布与标准正态分布N(0,1)的密度曲线几乎重叠为一。
这时, t 分布的分布函数值查N(0,1)的分布函数值表便可以得到。
3. F 分布 若X 与Y 相互独立,且X ~2χ(n ),Y ~2χ(m ), 则Z=mY n X的分布称为第一自由度等于n 、第二自由度等于m 的F 分布,记作Z ~F (n , m ),它的分布密度 p(z)=⎪⎪⎪⎩⎪⎪⎪⎨⎧>++-⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛Γ⎪⎭⎫ ⎝⎛+Γ∙。
r语言构造卡方分布的分位数表
r语言构造卡方分布的分位数表一、前言卡方分布是统计学中常用的一种分布,它也是许多统计检验方法中的基础分布。
在进行假设检验时,我们需要利用卡方分布的分位数来判断样本观测值与理论值之间是否存在显著差异。
本文将介绍如何使用R语言构造卡方分布的分位数表。
二、卡方分布卡方分布是指若 $X_1, X_2, \cdots, X_n$ 是 $n$ 个相互独立的标准正态随机变量,那么这 $n$ 个变量的平方和所服从的概率分布就称为自由度为 $n$ 的卡方分布,记作 $\chi^2(n)$。
卡方分布具有以下性质:1. 卡方分布是非负的连续概率分布;2. 卡方分布具有单峰性;3. 卡方分布的期望值为自由度 $n$;4. 卡方分布的形状参数为自由度 $n$。
三、构造卡方分位数表在R语言中,我们可以使用 `qchisq()` 函数来求解卡方分位数。
该函数需要两个参数:第一个参数是要求解的概率值,第二个参数是自由度。
例如,要求解自由度为 $5$,概率为 $0.95$ 的卡方分位数,可以使用如下代码:```rqchisq(0.95, df = 5)```输出结果为:```[1] 11.0705```这表示在自由度为 $5$ 的卡方分布中,概率值为 $0.95$ 对应的分位数为 $11.0705$。
我们可以使用循环语句来构造卡方分位数表。
例如,要构造自由度从$1$ 到 $10$,概率从 $0.05$ 到 $0.95$(步长为 $0.05$)的卡方分位数表,可以使用如下代码:```rdf <- 1:10prob <- seq(0.05, 0.95, by = 0.05)chisq_table <- matrix(nrow = length(df), ncol = length(prob))for (i in 1:length(df)) {for (j in 1:length(prob)) {chisq_table[i, j] <- qchisq(prob[j], df = df[i])}}rownames(chisq_table) <- paste("df =", df)colnames(chisq_table) <- paste("p =", prob)print(chisq_table)```输出结果为:```p = 0.05 p = 0.1 p = 0.15 p = 0.2 p = 0.25 p = 0.3 p = 0.35df = 1 0.00393 0.01579 0.03983 0.07939 0.132830.21072 0.31831df = 2 0.10259 0.21072 0.35241 0.50945 0.693360.90618 1.15035df = 3 0.35185 0.58437 0.83121 1.11514 1.342531.53320 1.81246df = 4 0.71072 1.06362 1.38629 1.64878 1.922562.19839 2.48508df =5 1,14547 1,61031 2,011162,34253 2,73264 3,07694 3,45550 df =6 1,63538 2,20413 2,641653,07057 3,45550 - -df =7 2,16735 2,83311 3,32511 - - - -df =8 - - - - - - -df =9 - - - - - - -df =10 - - - - --p =df =p =p =```四、总结本文介绍了如何使用R语言构造卡方分位数表。
卡方分布分位数
卡方分布分位数
卡方分布分位数是一种常见的统计学应用。
它可以帮助研究者们深入了解一些大量统计数据的特征,以及它们的变化趋势。
它的用途也很广泛,可以用于不同的统计方法、研究领域、学科领域等。
什么是卡方分布分位数?卡方分布分位数是一种统计方法,它利用卡方分布的分布特性来评估不同样本数据的概率密度分布。
假设我们有一组来自不同样本的数据,那么我们用卡方分布分位数来评估这些样本数据之间的关系。
卡方分布分位数可以通过卡方分布的概率密度函数来估计。
概率密度函数是描述随机变量分布的一种函数,它又被称为分布函数。
卡方分布的概率密度函数主要包括两部分,一部分是分布的概率密度函数,另一部分是分位数。
卡方分布的概率密度函数可以表示为:
f(x)=λe^(-λx)*x^(λ-1)
其中λ是常数,它是用来衡量数据的变异性的量。
值越大,说明数据的变异性越大。
它的分位数通过求解以下方程来计算:
P(x)=∫f(t)dt
其中P(x)为该区间的概率值。
卡方分布分位数可用来评估来自不同样本数据的统计关系,因此也可以用来进行回归分析。
卡方分布分位数也可以用于估计分布上的置信区间,并用来测定随机变量的变异性。
卡方分布分位数的实际应
用可以说是非常多的,它可以用于不同的研究领域,如实验设计、统计学、社会科学等等。
总之,卡方分布分位数是一种重要的统计工具,它可以帮助我们更好地了解统计数据,并用于不同研究领域的研究分析。
