单相正弦交流电路
单相正弦交流电路复习资料

单相正弦交流电路复习资料单相正弦交流电路复习资料在我们日常生活中,电力是不可或缺的资源。
而电力的传输和使用离不开电路的支持。
其中,单相正弦交流电路是最常见和基础的一种电路形式。
本文将对单相正弦交流电路进行复习和总结,帮助读者更好地理解和应用这一电路。
一、基本概念1. 交流电和直流电的区别交流电指的是电流方向和大小随时间变化的电流形式。
而直流电则是电流方向和大小保持不变的电流形式。
在单相正弦交流电路中,电流和电压都是交流的。
2. 正弦波的特点正弦波是一种周期性变化的波形,具有以下特点:- 幅值:波峰和波谷的最大偏离值,表示电压或电流的大小。
- 周期:波形重复出现的时间间隔。
- 频率:单位时间内波形重复出现的次数,与周期的倒数成正比。
- 相位:波形相对于某一参考点的位置,用角度表示。
3. 交流电路中的元件单相正弦交流电路由电源、负载和连接二者的导线组成。
其中,电源提供电能,负载是电能的消耗者。
二、基本电路1. 电阻电路电阻电路是最简单的单相正弦交流电路形式。
其中,电流和电压的关系由欧姆定律决定:电压等于电流乘以电阻。
2. 电感电路电感电路中,电感线圈是主要元件。
电感线圈的特点是:当电流变化时,产生感应电动势,抵抗电流的变化。
因此,电感电路中电流和电压之间存在相位差。
3. 电容电路电容电路中,电容器是主要元件。
电容器的特点是:可以存储电荷,当电压变化时,释放或吸收电荷。
因此,电容电路中电流和电压之间存在相位差。
三、复杂电路1. 串联电路串联电路是将多个电阻、电感或电容依次连接起来的电路形式。
在串联电路中,总电压等于各个元件电压之和,总电流相等。
2. 并联电路并联电路是将多个电阻、电感或电容同时连接在一起的电路形式。
在并联电路中,总电流等于各个元件电流之和,总电压相等。
3. RC、RL和RLC电路RC电路由电阻和电容组成,RL电路由电阻和电感组成,RLC电路由电阻、电感和电容组成。
这些电路在实际应用中具有重要作用,可以用于滤波、调节电压和频率等。
单相正弦交流电路

u2 2U2 sin t 2
有效值相量: U1 = U1 ψ1
U2 2 U1
1
U2 = U2 ψ2
设: 幅度: U2 U1
相量图
相位哪一个超前?
相位: 2 1 哪一个滞后?
U2 超前于 U1
例 同频率正弦量相加—— 平行四边形法则
i1 I1m sin(t 1) i2 I2m sin(t 2 )
I解
I2
求:i1+i2=?
I1 = I1 ψ1 I2 = I2 ψ2
2 1
I1
I = I1 + I2
即: i Im sin(t )
问题的提出:但不旋精转确矢。量故可引以入运相用量平的行复四数边运形算法法则。求解,
相量 → 复数表示法 → 复数运算
u
Um
sin(t
)
相量为:
最大值相量:U
m
Um
例 已知 u 220 2 sin(t 235)V , i 10 2 sin(t 45) A
求u和i的初相及两者间的相位关系。
解 u 220 2 sin(t 235)V
220 2 sin(t 125)V
所以,电压u的初相位为-125°, 电流i的初相位为45°。
ui u i 125 45 170 0
直流情 况下容 抗为多 大?
XC与频率成反比;与电容量C成反比
直流下频率f =0,所以XC=∞。C相当于开路。
由于C上u、i 为微分(或积分)的 动态关系,所以C也 是动态元件。
2. 电容元件的功率
(1)瞬时功率 p
p<0
p为正弦波,频率为ui 的2 倍;在一个周期内,L吸 收的电能等于它释放的磁 场能。
单相正弦交流电路
第5章单相正弦交流电路正弦交流电路是电工知识的重要内容,是学习电工与电子技术的理论基础,因此,分析研究正弦交流电路是十分重要的。
本章主要介绍单相正弦交流电的基本概念与表示方法,重点研究单相正弦交流电路的分析与计算,在着重讨论R、L、c单相正弦交流电路的基础上,利用矢量图法分析串、并联电路的电压、电流关系及功率关系。
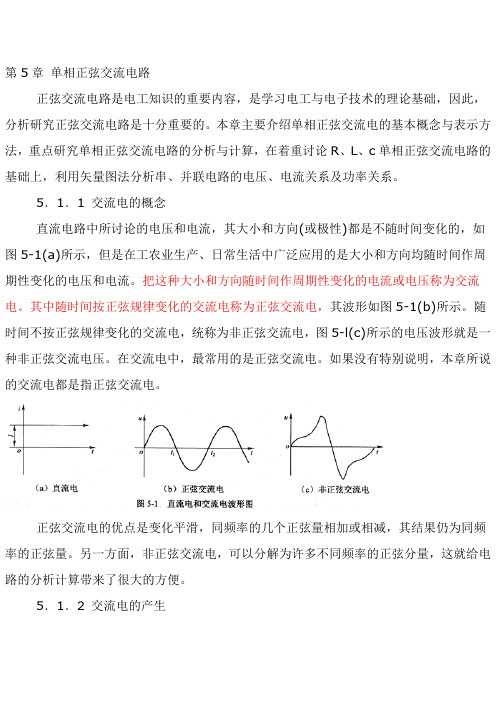
5.1.1 交流电的概念直流电路中所讨论的电压和电流,其大小和方向(或极性)都是不随时间变化的,如图5-1(a)所示,但是在工农业生产、日常生活中广泛应用的是大小和方向均随时间作周期性变化的电压和电流。
把这种大小和方向随时间作周期性变化的电流或电压称为交流电。
其中随时间按正弦规律变化的交流电称为正弦交流电,其波形如图5-1(b)所示。
随时间不按正弦规律变化的交流电,统称为非正弦交流电,图5-l(c)所示的电压波形就是一种非正弦交流电压。
在交流电中,最常用的是正弦交流电。
如果没有特别说明,本章所说的交流电都是指正弦交流电。
正弦交流电的优点是变化平滑,同频率的几个正弦量相加或相减,其结果仍为同频率的正弦量。
另一方面,非正弦交流电,可以分解为许多不同频率的正弦分量,这就给电路的分析计算带来了很大的方便。
5.1.2 交流电的产生正弦交流电是通过单相交流发电机产生的,如图5-2所示。
单相交流发电机由定子和转子组成。
定子中有绕组,且按顺时针方向在磁场中匀速旋转,绕组由于切割磁力线而产生交流电。
在图5—2中1、2、3、4、5、6、7、8的八个小圆圈表示导线截面,由于导线切割磁力线的位置在变化,其电动势e的大小也随之变化。
当导线在位置l时,导线运动方向和磁力线平第97页行,没有切割磁感线,此时电动势e的大小为零。
当导线到位置2时,导线斜方向切割磁力线,导线中产生了电动势。
当导线到位置3时,导线运动方向与磁力线相互垂直,切割磁力线最大。
当导线到位置4时,导线又变为斜方向切割磁感线,导线中产生的电动势又变小。
单相正弦交流电路三要素

正弦交流电的三要素
角频率:
i=Imsin(ωt+ )
0
i
Im
角频率
T
ωt
i
Im
T
表示正弦电流变化的快慢,还有周期T和频率f。
正弦交流电的三要素
初相位:
i=Imsin(ωt+ )
0
i
Im
相位
初相位就是波形起点至坐标原点的角度。 >0,波形“起点”在原点的左边, <0,波形“起点”在原点的右边, 初相位的绝对值不大于π。
φ i
φ u
φ
两个同频率交流电的相位之差。用来φ表示。
φ=φu- φi
相位差等于初相位之差。
u
若φ>0,则电压u先到达正(或负)的最大值,称电压u超前电流i,或称电流i滞后电压u。
02
若φ<0,则电流i先到达正(或负)的最大值,称电流i超前电压u,或称电压u滞后电流i。
03
若φ=0,则电压u与电流i同时到达正(或负)的最大值,称电压u与电流i同相。
正弦电压和电流
实际方向和参考方向一致
实际方向和参考方向相反
+
-
正半周 实际方向和参考方向一致
负半周 实际方向和参考方向相反
正弦交流电的电压和电流是按照正弦规律周期性变化的。
数学表达式:
i=Imsin(ωt+ )
0
i
Im
T
ωt
i
Im
T
在正弦交流电路中各支路的电流、电压都是时间t的正弦函数,分别用英文小写字母“i”和“u”表示。
ωt
i
Im
相位:表示正弦量的变化进程,也称相位角。 初相位:t =0时的相位。
单相交流电路之正弦交流电

单相交流电路之正弦交流电一、正弦交流电的三要素正弦交流电是指其数值大小、方向都按正弦的规律周而复始循环变化的电势电压与电流。
要完全掌握正弦交流电,必须掌握交流电的三要素,数值、频率和角频率,相位关系,正弦交流电的三要素是极大值(或有效值)、频率(或角频率)及相位(或初相位)。
1.正弦交流电的数值1)瞬时值正弦交流电在变化过程中,任意确定时刻t的数值,称为正弦交流电的瞬时值,如图 2 - 15 中的e₁。
瞬时值用小写符号表示,如i、e、u等。
2)最大值正弦交流电的最大值又称极大值,振幅值也可称为极值,是指在变化过程中,正弦交流电出现的最大瞬时值,用符号Eₘ(图 2 - 15)、Iₘ、Uₘ表示。
3)有效值正弦交流电的有效值是衡量它发热做功的一个基本量。
就是说,交流电流和直流电流分别通过同一电阻,如果经过相同时间产生同样热量,则交流电流的有效值等于直流电流的大小。
因此,定义正弦交流电的有效值是从发热做功方面与直流等效的值称为交流电的有效值,从数学角度,它又可以称为方均根值。
有效值用大写符号表示,如E、I、U。
正弦交流电的瞬时值,可以用数学解析式表达,即u=Uₘsin(ωt+φ)正弦交流电的有效值与极大值的关系为或实际上,交流电路的分析与计算过程中,主要用交流电的有效值,例如,电器铭牌上标定的电压、电流,仪表(电流表、电压表)测量的指示值以及计算电路的电压、电流等都是有效值。
2.频率和角频率1)频率和周期(1)频率:是指正弦交流电单位时间(s)内循环变化的次数,用符号f表示,单位为赫兹(Hz).-般50Hz.、60Hz称为工频交流电。
(2)周期:是指正弦交流电每循环一次所经历的时间(s),即正弦交流电从0值到极大值再到0值再变化到负的最大值然后回到0值的过程所经历的时间称,用符号T表示,单位为秒(s)。
频率与周期的关系为f=1/T2) 角频率角频率是指正弦交流电每秒循环变化所经历的弧度(这里指角度),用符号ω表示,单位是弧度/秒(red/s)。
单相交流电路之正弦交流电

变压器:改变电压和电流,实现能量传输和转换
电感:储存磁场能量,阻碍电流变化
导线与开关
导线:连接电源和负载的导线,用于传输电流
开关:控制电路通断的开关,用于保护电路和设备安全
单相交流电路的分析方法
03
阻抗分析法
阻抗分析法的定义:通过分析电路中各元件的阻抗,来求解电路中电流、电压等参数的方法。
添加标题
添加标题
功率分析法
功率的测量方法:使用功率表或电能表进行测量
功率的用途:用于分析电路的能耗和效率
功率的定义:电压与电流的乘积
功率的种类:有功功率、无功功率、视在功率
功率的计算公式:P=UI
相量分析法
相量分析法的基本概念和原理
添加标题
相量分析法在单相交流电路中的应用
添加标题
相量分析法的优点和局限性
并联谐振的条件:当电路中的电感L和电容C的频率相同时,电路中的电流达到最大,这种现象称为并联谐振。
滤波器的工作原理
滤波器是一种能够滤除特定频率信号的电子设备
滤波器的工作原理主要是利用电容、电感等元件的频率特性来实现信号的滤波
滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等类型
滤波器的性能指标主要包括通带增益、阻带衰减、截止频率等
效率:交流电的转换效率,单位为百分比(%)
单相交流电路的组成
02
电源
交流电源:提供交流电能
直流电源:提供直流电能
变压器:将交流电能转换为直流电能
整流器:将交流电能转换为直流电能
滤波器:滤除交流电中的杂波和噪声
稳压器:稳定交流电的电压和频率
负载
电阻:消耗电能,产生热量
电容:储存电场能量,阻碍电压变化
单相正弦交流电路

T 1 1 0.02s ω=2πf =f2×35.104×50=314rad/ s
3.1.3 初相
u=Umsin(ωt+ψ) (ωt+ψ)称为相位。它表示交流电在某一时刻所处的变化状态,决定该时刻瞬时 值的大小、方向和变化趋势。 ψ 称为初相,它表示计时开始时交流电所处的变化状态 幅值、频率和初相分别表示交流电变化的幅度、快慢和起始状态。称为交流电的 三要素。
1.L上电压与电流关系 如 i=Imsinωt 则
电感电路超前 i
XLu=ωLL=d2iπfLL dt
d,9I0Xm0Lds,(tin有Ω)效t称值为的感关L抗I系m,为cfo愈Us=高XtXLLI愈U大m。sin(t
900
)
2. L上功率
p=ui=UmImsin(ωt+900)sinωt =UmImcosωtsinωt=UIsin2ωt 在0-π/2区间p为正值,电感吸收
解:只有同频率的交流电才能进行相量运算 ,所以
=
=ψ1-ψ2=600,如选ψ1=00,则
3.3 单一参数的交流电路
单一参数是指在电路中只有电阻R、电感L或电容C其中的一种 元件。掌握了单一参数在电路中的作用,混合参数电路的分析就很 容易掌握了。
3.3.1电阻电路
1.R上电压与电流关系 如选择 i=Imsinωt
Q
UI
I 2 XC
U2 XC
【例3.在4收】录机的输出电路中,常利用电容来短掉高频干扰信号,
保留音频信号。如高频滤波的电容为0.1μF,干扰信号的频率f1= 1000KHz,音频信号的频率f2=1kHz,求容抗分别为多少?
解:
X C1
1
2f1C
单相正弦交流电路—单一参数元件的电路

幅角:
i 90o
二、 C元件电路的功率
1. 瞬时功率 p
i
u
i
u
C
2 I sin t
2U sin( t 90 )
p i u U I sin 2 t
在关联参考方向下,功率有时大于零,有时小于零,电容元件在电路中的作
用是怎样的呢?
p i u iU I sin2ut
o
U I R
三、 R元件电路的功率
1. 瞬时功率 p:瞬时电压与瞬时电流的乘积
i
u
i I m sin ( t )
u U m sin ( t )
R
U m Im
p u i U m I m sin t
(1 cos 2t )
2
UI (1 cos 2t ) UI UI sin(2t 900 )
U IL
3. 有效值
电压、电流波
形图
u
i
90
定义:
t
X L L 2 fL
则:
U I XL
感抗(Ω)
关于感抗的讨论
感抗( XL ωL 2πfL)是频率的函数,频率越高,感抗越大,频率越低,感抗越
小。电感有通低频,阻高频的特性。
UL I X L
R
+
_
f=0时
e
L
0.45 / 60o ( A)
R
484
i 0.45 2 sin(314t 60o )( A)
P UI 220 0.45 100(W )
在关联参考方向下,功率有时大于零,有时小于零,电感元件在电路中的作
用是怎样的呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与 E 的和为 相量 E 2 1
E E (43.4 j 25 86.6 j50) (129.9 j25)(V) E 1 2
第2章 正弦交流电路 将上式转换成极坐标式为
25 2 2 E E (129 .9) (25) arctan 132 .310.9(V) 129 .9
式中, 小写字母e、u、 i是这些量的瞬时值。
(2-1)
第2章 正弦交流电路 图2.1所示为正弦电动势的波形图。图中横坐标用时间t/s、 弧度ωt/rad或电角度ωt/度(°)表示。
图2.1 正弦电动势波形图
第2章 正弦交流电路
在具有一对磁极的交流发电机中,转子旋转一周,电动势 交变一个周期,所以转子旋转的机械角度等于电动势变化的电 角度。 当发电机具有两对磁极时, 转子旋转一周,电动势交 变两个周期,此时机械角度变化360°,而电动势变化720°机
第2章 正弦交流电路
第2章 正弦交流电路
2.1 正弦交流电的基本概念 2.2 单相正弦交流电路 2.3 三相正弦交流电路 习题
第2章 正弦交流电路
2.1 正弦交流电的基本概念
2.1.1 随时间按正弦函数变化的电动势、 电压和电流总称为正弦 交流电, 它们的表达式为
e Em sin t u U m sin t i I m sin t
2.1.3 正弦交流电的表示法
1. 相量法 用来表示正弦量的复数称为相量。复数是相量法的基础, 所以相量法又称为复数符号法。正弦电动势Em sin(ω t+φ )写成
.
E(cos jsin ) E E
(2-10) .
式中E是表示正弦电动势e的复数,读作相量E。相量E既表达了 电动势e的有效值,又表达了它的初相位。为了区别于只能表示 . 有效值的E,相量E写成E。 式中的j就是虚数
第2章 正弦交流电路
已知 e 50 2 sin(t 30)V, 1 e2 100 2 sin(t 30)V, 求e=e1+e2。 . . 解 设 E2 为参考相量,为使 E2 的初相位等于零,将各相量 . . 的初相位都增加 30°, E1 导前于 E2 的相位差仍为 60°,如图 例2-3
写出i1和i2的正弦函数表达式。
第2章 正弦交流电路
•
2-4 已知u1=70.7 sin(ωt+150°)(V), =50∠30°(V), 角 频率与u1相同。写出 与u2的表达式;计算它们的函数和。
• •
2-5 已知i1=10sin(ωt+30°)(A),i2=10sin(ωt-60°) (A), 用相量法求它们的和及差。
时的相位角。
在图2.2中,e1和e2是两个频率相等的正弦电动势,但是它 们的初相位是不同的。
e1 Em1 sin(t 1 ) e2 Em 2 sin(t 2 )
(2-4)
第2章 正弦交流电路 当 t=0 时, e1=Em1sin(ωt+φ1) , e2=Em2sin(ωt+φ2) ,它们的初
械角度就不等于电角度。 波形图中标出的是电角度或电弧度。
第2章 正弦交流电路
2.1.2
1. 周期、 正弦量交变一次所需的时间称为周期,用字母T表示,单位 为秒(s),如图2.1所示。1s内正弦量的交变次数称为频率, 用 字母f表示,单位为赫兹(Hz ),简称赫。显然,频率与周期互 为倒数,
1 f T
第2章 正弦交流电路
图2.4 复平面的上相量
第2章 正弦交流电路
3. j
j既是一个虚数单位,同时又是一个旋转因子。因为任何
相量与j相乘意味着该相量按逆时针方向旋转了 90°。例如, . 在图2.5中,设相量A的模为1、辐角为30°, 其相量式为
130 cos30 j sin 30 0.866 j0.5 A
φ 为合成相量的辐角,其值为
. . 若欲求E1与E2的差,则
E1 sin arctan E1 cos1 E2
' E E E ( E ) E 1 2 1 2
' 的模和辐角都可以从图2.6所示的相量图上求得。 E
第2章 正弦交流电路
图2.6 相量的加法与减法
2
(2-6)
热效应相等的条件为QAC=QDC, 因此可得交流电的有效值为
1 T 2 I i dt T 0
(2-7)
第2章 正弦交流电路
有效值又称均方根值,用大写字母表示。在正弦交流电中,
代入式(2-7)得其有效值为
1 T 2 1 T 1 cos 2t 2 I I m sin t dt dt T 0 T 0 2 Im 2
式中,电压的有效值为
U=RI
式(2-12)若写成相量式为
(2-13)
U0 RI0 RI U
(2-14)
第2章 正弦交流电路 在任一瞬间,电阻元件中的电流瞬时值与同一瞬间加在电 阻元件两端的电压瞬时值乘积,称为电阻的瞬时功率,用pR来 表示, 即
1 cos 2t pR uR i U m I m sin t U m I m 2 UI (1 cos 2t )
第2章 正弦交流电路 •2-6 在图2.44中,已知I1=10A,I2=20A,U=100 V。(1) 写 出i1、i2、u的正弦函数表达式;(2) 求电流和的有效值; (3) 求电流差的有效值。
图2.44 题2-6的图
第2章 正弦交流电路
第2章 正弦交流电路
2.2 单相正弦交流电路
2.2.1 单一参数的交流电路
相量每乘j一次,意味着逆时针旋转90°。图2.5中画出了相量 . A每次乘j以后的旋转情况。不难证明,相量每乘(-j )一次, 则顺时针旋转90°。
第2章 正弦交流电路
图2.5 相量乘以j
第2章 正弦交流电路 4. 相量的加法和减法 正弦量的加减法可以在相量图上进行。选定一个相量作为参
考相量,假设其初相位为零,画在水平轴上,其他相量就可根
据其与参考相量的相位差而画出。在作相量图时一般不画出坐 标轴。
为参考相量, 导前于 在图2.6中, E E 2 1
要计算
与 E 1
之和,则 E 2
的相位角为φ1。 若 E 2
E E E E 1 2
第2章 正弦交流电路 式中, E为合成相量的模,其值为
E ( E1 cos 1 E2 ) 2 ( E1 sin 1 ) 2
相位角分别为φ1和φ2。因此当φ1≠φ2时, e1和e2的初始值是不相
等的。 两个同频率正弦量的初相位角之差称为相位角差, 简称相 位差,用φ表示。式(2-4)中e1和e2的相位差为
(t 1 ) (t 2 ) 1 2
第2章 正弦交流电路
图2.2 正弦电动势的相位
即
I 0.707I m
I m 2I 1.414I
或
第2章 正弦交流电路 同理得电动势和电压的有效值为
Em Um E ,U 2 2
工程上通常所说的交流电压和交流电流的数值都是指有效 值,如某电器的额定电压为 220 V,某电路的电流为 3 A。交
流电表所测得的数值一般也是有效值。
第2章 正弦交流电路
第2章 正弦交流电路
习 题
2-1 已知Im=10 A,f=50Hz,φ=60°。写出i的正弦函数表达 式;求t=1ms时的i。 2-2 已知u1=141sin(ωt-30°)(V), u2=282sin(ωt+45°(V)。
(1)写出相量式U 1
; U 2
(2)求u1与u2的相位差。
3 j4(A), I 3 j4(A 2-3 已知 I , ) 角频 率都是 ω 0 。 1 2
1 T 0.02(s) 20(ms) 50
所以
ω =2π f=2×50π =100π =314 (rad/s)
在某些设备中需要频率较高的交流电,例如高频电炉所用 的 频 率 可 达 108Hz , 无 线 电 工 程 上 使 用 的 频 率 约 为 105~3×1010Hz。
第2章 正弦交流电路 2. 相位、 初相位和相位差 正弦量在不同的时刻有不同的瞬时值。例如电动势 e=Em sinω t,当t变化时,ω t也变,e的数值随之而变,ω t就称为 正弦量的相位或相位角。 初相位是一个反映正弦量初始值的物理量, 是计时开始
1. 纯R电路 根据图2.8(a)中u和i的参考方向,得电压与电流的一般
关系式为
u Ri
(2-11)
第2章 正弦交流电路
图2.8 (a) 一般表示; (b) 相量表示; (c) 相量图; (d) 波形图
第2章 正弦交流电路 对于正弦电路,设电流为i=Im sinωt, 则电压为
u Ri RIm sin t 2RI sin t 2U sin t
第2章 正弦交流电路
图2.3 同相与反相的正弦量
第2章 正弦交流电路 3. 最大值和有效值 交流电在某一瞬间的数值称为瞬时值,规定用小写字母表
示,例如 e 、 u 、 i ,分别表示正弦电动势、电压、电流的瞬时
值。在一周期内出现的最大瞬时值称为最大值,也称为幅值, 分别用字母Em、Um、Im表示。 最大值只是交流电在变化过程中某一瞬间的数值,不能用 来代表交流电在一段较长的时间内作功的平均效果。交流电的
第2章 正弦交流电路
为参考相位时曾将各相量的初相量增加了 30°, 在设定 E
2
所以在写函数式时,e的初相位要扣除30°,
e e1 e2 132.3 2 sin(t 19.1 30) 132.3 sin(t 10.9)(V)
第2章 正弦交流电路
图2.7 例2-3图
