(完整版)相似三角形中几种常见的辅助线作法(有辅助线)
相似三角形之常用辅助线

相似三角形之常用辅助线在与相似有关得几何证明、计算得过程中,常常需要通过相似三角形,研究两条线段之间得比例关系,或者转移线段或角。
而有些时候,这样得相似三角形在问题中,并不就是十分明显、因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需得结论。
专题一、添加平行线构造“A"“X”型定理:平行于三角形一边得直线与其它两边(或两边延长线)相交,所构成得三角形与原三角形相似。
定理得基本图形:例1、平行四边形ABCD中,E为AB中点,AF:FD=1:2,求AG:GC变式练习:已知在△ABC中,AD就是∠BAC得平分线.求证:、(本题有多种解法,多想想)例2、如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若==2,求BE:EA得比值、变式练习:如图,直线交△ABC得BC,AB两边于D,E,与CA延长线交于F,若错误!= 错误!=2,求BE:E A得比值。
例3、BE=AD,求证:EF·BC=AC·DF变式1、如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE,BC得延长线相交于点F,证明:AB·DF=AC·EF。
例4、已知:如图,在△ABC中,AD为中线,E在AB上,AE=AC,CE交AD于F,EF∶FC=3∶5,EB=8cm,求AB、AC得长、变式:如图,,求。
(试用多种方法解)说明:此题充分展示了添加辅助线,构造相似形得方法与技巧.在解题中方法要灵活,思路要开阔.总结:(1)遇燕尾,作平行,构造字一般行。
(2)引平行线应注意以下几点:1)选点:一般选已知(或求证)中线段得比得前项或后项,在同一直线得线段得端点作为引平行线得EF EF EFEF点。
2)引平行线时尽量使较多已知线段、求证线段成比例。
专题二、作垂线构造相似直角三角形 一、基本图形例1、,,那么吗?试说明AC BD AC BC CA CD ⊥=⋅22理由?(用多种解法)v变式练习:平行四边形ABC D中,CE ⊥A E,CF ⊥AF,求证:A B·AE+AD ·AF=AC 2例2、如图,RtA BC 中,CD 为斜边AB 上得高,E 为CD 得中点,AE 得延长线交B C于F,FG AB 于G,求证:FG =CFBF【练习】1.如图,一直线与△ABC 得边AB,AC 及BC 得延长线分别交于D,E,F 。
相似三角形之常用辅助线

相似三角形之经常运用关心线之马矢奏春创作时间:二O 二一年七月二十九日在与相似有关的几何证实、计算的过程中,经常需要经由过程相似三角形,研究两条线段之间的比例关系,或者转移线段或角.而有些时刻,这样的相似三角形在问题中,其实不是十清晰显.是以,我们需要经由过程添加关心线,机关相似三角形,进而证实所需的结论.专题一、添加平行线机关“A”“X”型定理:平行于三角形一边的直线和其它两边(或两边延长线)订交,所构成的三角形与原三角形相似.定理的底子图形: 例1、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC 变式演习:已知在△ABC 中,AD 是∠BAC 的等分线.求证:. (本题有多种解法,多想想)例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若==2,求BE:EA 的比值.变式演习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC =FEED =2,求BE:EA 的比值.例3、BE =AD,求证:EF·BC=AC·DF变式1、如图,△ABC 中,AB<AC,在AB 、AC 上辨别截取BD=CE,DE,BC 的延长线订交于点F,证实:AB·DF=AC·EF.例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC,CE 交AD 于F,EF∶FC=3∶5,EB=8cm, 求AB 、AC 的长. 变式:如图,,求.(试用多种方法解)说明:此题充分展示了添加关心线,机关相似形的方法和技巧.在解题中方法要灵活,思路要坦荡.总结:(1)遇燕尾,作平行,机关字一般行. (2)引平行线应留心以下几点:1)选点:一般选已知(或求证)中线段的比的前项或后项,在同一贯线的线段的端点作为引平行线的点.2)引平行线时尽量使较多已知线段、求证线段成比例.专题二、作垂线机关相似直角三角形 一、底子图形 例1、情由?(用多种解法)v变式演习:平行四边形ABCD 中,CE⊥AE,CF⊥AF,求证:AB·AE+AD·AF=AC2例2、如图,Rt ABC 中,CD 为斜边AB 上的高,E 为CD 的中点,AE 的延长线交BC 于F,FG AB 于G,求证:FG =CF BFABCDE F ABCDE F A BCDEF ABCDE F ABDEFC【演习】1.如图,一贯线与△ABC 的边AB,AC 及BC 的延长线辨别交于D,E,F.求证:若,则D 是AB 的中点.2.如图,在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延长线上,BD=3CE,DE 交BC 于F,求DF :FE 的值.3.已知:AM :MD=4:1,BD :DC=2:3,求AE :EC. 4、如图,的AB 边和AC 边上各取一点D 和E,且使AD =AE,DE延长线与BC 延长线订交于F,求证:时间:二O 二一年七月二十九日ABC D E FBEA DC F。
相似三角形证明技巧(整理)

相似三角形解题方法、技巧、步骤、辅助线解析一、相似三角形(1)三角形相似的条件: ①;②;③.二、两个三角形相似的六种图形:只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决.三、三角形相似的证题思路:判定两个三角形相似思路:1)先找两对角对应相等(对平行线型找平行线),因为这个条件最简单; 2)再而先找一对角对应相等,且看夹角的两边是否对应成比例; 3)若无对应角相等,则只考虑三组对应边是否成比例;找另一角两角对应相等,两三角形相似找夹边对应成比例两边对应成比例且夹角相等,两三角形相似找夹角相等两边对应成比例且夹角相等,两三角形相似 找第三边也对应成比例三边对应成比例,两三角形相似 找一个直角斜边、直角边对应成比例,两个直角三角形相似找另一角两角对应相等,两三角形相似找两边对应成比例判定定理2 找顶角对应相等判定定理1 找底角对应相等判定定理1 找底和腰对应成比例判定定理3e)相似形的传递性若△1∽△2,△2∽△3,则△1∽△3四、“三点定形法”,即由有关线段的三个不同的端点来确定三角形的方法。
具体做法是:先看比例式前项和后项所代表的两条线段的三个不同的端点能否分别确定一个三角形,若能,则只要证明这两个三角形相似就可以了,这叫做“横定”;若不能,再看每个比的前后两项的两条线段的两条线段的三个不同的端点能否分别确定一个三角形,则只要证明这两个三角形相似就行了,这叫做“竖定”。
有些学生在寻找条件遇到困难时,往往放弃了基本规律而去乱碰乱撞,乱添辅助线,这样反而使问题复杂化,效果并不好,应当运用基本规律去解决问题。
例1、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC. 求证: BAAC AF AE(判断“横定”还是“竖定”? )a)已知一对等b)己知两边对应成比c)己知一个直d)有等腰关例2、如图,CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC、CD于点E、F,AC·AE=AF·AB吗?说明理由。
中考相似三角形之常用辅助线

中考相似三角形之常用辅助线Revised on November 25, 2020相似三角形之常用辅助线在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。
而有些时候,这样的相似三角形在问题中,并不是十分明显。
因此,我们需要通过添加辅助线,构造相似三角形,进而证明所需的结论。
专题一、添加平行线构造“A ”“X ”型定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似.定理的基本图形: 例1、平行四边形ABCD 中,E 为AB 中点,AF :FD =1:2,求AG :GC变式练习:已知在△ABC 中,AD 是∠BAC 的平分线.求证:. (本题有多种解法,多想想)例2、如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若DCBD =FA FC=2,求BE:EA 的比值.变式练习:如图,直线交△ABC 的BC,AB 两边于D,E,与CA 延长线交于F,若BD DC = FEED =2,求BE:EA 的比值.例3、BE =AD ,求证:EF ·BC =AC ·DF变式1、如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB·DF=AC·EF 。
例4、已知:如图,在△ABC 中,AD 为中线,E 在AB 上,AE=AC ,CE 交AD 于F ,EF ∶FC=3∶5,EB=8cm,求AB 、AC 的长.变式:如图,21==DE AE CD BD ,求BFAF。
(试用多种方法解)CDBDAC AB =A B CEF A B C EF A BCEF A BC EF说明:此题充分展示了添加辅助线,构造相似形的方法和技巧.在解题中方法要灵活,思路要开阔. 总结:(1)遇燕尾,作平行,构造 字一般行。
思维特训(十一) 相似三角形中的辅助线作法归类

思维特训(十一) 相似三角形中的辅助线作法归类在添加辅助线时,所添加的辅助线往往能构造出一组或多组相似三角形,或得到成比例的线段,或得出等角、等边,从而为证明三角形相似或进行有关的计算找到等量关系. 作辅助线的方法主要有以下几种:(1)作平行线构造“A ”型或“X ”型相似;(2)作平行线转换线段比;(3)作垂直证明相似.图11-S -1类型一 作平行线构造“A ”型或“X ”型相似1.如图11-S -2,已知平行四边形ABCD 中,对角线AC ,BD 相交于点O ,E 为AB 延长线上一点,OE 交BC 于点F ,若AB =a ,BC =b ,BE =c ,求BF 的长.图11-S -22.如图11-S -3,在△ABC 中,AD 为BC 边上的中线,CF 为任一直线,CF 交AD 于点E ,交AB 于点F .求证:AE DE =2AF BF. 图11-S -33.在一节数学课上,老师出示了这样一个问题让学生探究:如图11-S -4,在△ABC中,D 是BA 延长线上一动点,点F 在BC 上,且CF BF =12,连接DF 交AC 于点E . (1)如图△,当E 恰为DF 的中点时,请求出AD AB的值; (2)如图△,当DE EF =a (a >0)时,请求出AD AB的值(用含a 的代数式表示). 思考片刻后,同学们纷纷表达自己的想法:甲:过点F 作FG △AB 交AC 于点G ,构造相似三角形解决问题;乙:过点F 作FG △AC 交AB 于点G ,构造相似三角形解决问题;丙:过点D 作DG △BC 交CA 的延长线于点G ,构造相似三角形解决问题. 老师说:“这三位同学的想法都可以”.请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问中AD AB的值. 图11-S -4类型二 作平行线转换线段的比4.如图11-S -5,B 为AC 的中点,E 为BD 的中点,求AF AE的值. 图11-S -55.如图11-S -6,已知等边三角形ABC ,D 为AC 边上的一动点,CD =nDA ,连接BD ,M 为线段BD 上一点,∠AMD =60°,连接AM 并延长交BC 于点E .(1)若n =1,则BE CE =______,BM DM=______; (2)若n =2,如图△,求证:BM =6DM ;(3)当n =________时,M 为BD 的中点(直接写出结果,不要求证明).图11-S -66.2019·朝阳 已知:如图11-S -7,在△ABC 中,点D 在AB 上,E 是BC 的延长线上一点,且AD =CE ,连接DE 交AC 于点F .(1)猜想证明:如图△,在△ABC 中,若AB =BC ,学生们发现:DF =EF .下面是两位学生的证明思路:思路1:过点D 作DG △BC ,交AC 于点G ,可通过证△DFG △△EFC 得出结论;思路2:过点E 作EH △AB ,交AC 的延长线于点H ,可通过证△ADF △△HEF 得出结论. 请你参考上面的思路,证明DF =EF (只用一种方法证明即可).(2)类比探究:在(1)的条件下(如图△),过点D 作DM △AC 于点M ,试探究线段AM ,MF ,FC 之间满足的数量关系,并证明你的结论.(3)延伸拓展:如图△,在△ABC 中,若AB =AC ,∠ABC =2△BAC ,AB BC=m ,请你用尺规作图在图△中作出AD 的垂直平分线交AC 于点N (不写作法,只保留作图痕迹),并用含m的代数式直接表示FN AC的值. 图11-S -7类型三 作垂直证相似7.如图11-S -8,在△ABC 中,∠C =90°,D 为边AB 的中点,M ,N 分别为边AC ,CB 上的点,且DM ⊥DN .(1)求证:DM DN =BC AC; (2)若BC =6,AC =8, CM =5,直接写出CN 的长.图11-S -88.如图11-S -9,在△ABC 中,D 是BC 边上的点(不与点B ,C 重合),连接AD . 问题引入:(1)如图△,当D 是BC 边的中点时,S △ABD ∶S △ABC =________;当D 是BC 边上任意一点时,S △ABD ∶S △ABC =________(用图中已有线段表示).探索研究:(2)如图△,在△ABC 中,O 是线段AD 上一点(不与点A ,D 重合),连接BO ,CO ,试猜想S △BOC 与S △ABC 之比应该等于图中哪两条线段之比,并说明理由.拓展应用:(3)如图△,O 是线段AD 上一点(不与点A ,D 重合),连接BO 并延长交AC 于点F ,连接CO 并延长交AB 于点E .试猜想OD AD +OE CE +OF BF的值,并说明理由. 图11-S -99.如图11-S -10,已知一个直角三角形纸片ACB ,其中,∠ACB =90°,AC =4,BC =3,E ,F 分别是AC ,AB 边上的点,连接EF .(1)如图△,若将直角三角形纸片ACB 的一角沿EF 折叠,折叠后点A 落在AB 边上的点D 处,且S 四边形ECBF =3S △EDF ,则AE =________;(2)如图△,若将直角三角形纸片ACB 的一角沿EF 折叠,折叠后点A 落在BC 边上的点M 处,且MF △CA ,求EF 的长;(3)如图△,若FE 的延长线与BC 的延长线相交于点N ,CN =1,CE =47,求AF BF的值. 图11-S -10详解详析1.解:如图,过点O 作OM △BC 交AB 于点M .∵O 是AC 的中点,OM ∥BC ,∴M 是AB 的中点,即MB =12a , ∴OM 是△ABC 的中位线,OM =12BC =12b . ∵OM ∥BC ,∴△BEF ∽△MEO ,∴BF MO =BE ME , 即BF 12b =c a 2+c ,∴BF =bc a +2c . 2.证明:如图,过点D 作DG △CF 交AB 于点G .∵DG ∥CF ,D 为BC 的中点,∴G 为BF 的中点,FG =BG =12BF . ∵EF ∥DG ,∴AE DE =AF GF =AF 12BF =2AF BF . 3.解:(1)甲同学的想法:如图△,过点F 作FG △AB 交AC 于点G ,∴△AED ∽△GEF ,∴AD GF =ED EF. ∵E 为DF 的中点,∴ED =EF ,∴AD =GF .∵FG ∥AB ,∴△CGF ∽△CAB ,∴GF AB =CF CB. ∵CF BF =12,∴CF CB =13,∴AD AB =GF AB =CF CB =13. 乙同学的想法:如图△,过点F 作FG △AC 交AB 于点G ,∴AD AG =ED EF. ∵E 为DF 的中点,∴ED =EF ,∴AD =AG .∵FG ∥AC ,∴AG AB =CF CB. ∵CF BF =12,∴CF CB =13,∴AD AB =AG AB =CF CB =13. 丙同学的想法:如图③,过点D 作DG △BC 交CA 的延长线于点G ,∴∠C =△G ,∠CFE =△GDE ,∴△GDE ∽△CFE ,∴GD CF =ED EF. ∵E 为DF 的中点,∴ED =EF ,∴GD =CF .∵DG ∥BC ,∴∠C =△G ,∠B =△ADG ,∴△ADG ∽△ABC ,∴AD AB =DG BC .∵CF BF =12,∴CF BC =13. ∴AD AB =DG BC =CF BC =13. (2)如图△,过点D 作DG △BC 交CA 的延长线于点G ,∴∠C =△G ,∠CFE =△GDE ,∴△GDE ∽△CFE ,∴GD CF =ED EF. ∵DE EF =a ,∴ED =aEF , ∴DG =aCF .∵DG ∥BC ,∴∠C =△G ,∠B =△ADG ,∴△ADG ∽△ABC ,∴AD AB =DG BC . ∵CF BF =12,∴CF BC =13,即BC =3CF . ∴AD AB =DG BC =aCF 3CF =a 3. 4.解:取CF 的中点G ,连接BG .∵B 为AC 的中点,∴BG AF =12,且BG △AF . 又E 为BD 的中点,∴F 为DG 的中点,△EF BG =12,∴EF AF =14, ∴AF AE =43. 5.解:(1)当n =1时,CD =DA .∵△ABC 是等边三角形,∴BD ⊥AC ,∠BAC =60°,∴∠ADM =90°.又△△AMD =60°,∴∠MAD =30°,∴∠BAE =△BAC -△MAD =30°,即△BAE =△EAD ,∴AE 为△ABC 的中线,∴BE CE=1. 在△AMD 中,DM =12AM (30°角所对的直角边等于斜边的一半). ∵∠BAM =△ABM =30°,∴AM =BM ,∴BM DM=2. (2)证明:△△AMD =△ABD +△BAE =60°,∠CAE +△BAE =60°,∴∠ABD =△CAE .又△BA =AC ,∠BAD =△ACE =60°,∴△BAD △△ACE (ASA),∴AD =CE ,∴CD =BE .如图,过点C 作CF △BD 交AE 的延长线于点F ,∴FC BM =CE BE =AD CD =12①,DM FC =AD AC =13②,由△×△得DM BM =16,∴BM =6DM . (3)△M 为BD 的中点,∴BM =MD .∵△BAD ≌△ACE ,∴AD =CE ,∴CD =BE .∵△AMD ∽△ACE ,△BME ∽△BCD ,△AD AE =MD CE ,BM BC =ME CD, ∴AD =MD ·AE CE ③,CD =BC ·ME BM④, 由△×△得CD =5-12DA ,∴n =5-12. 6.解:(1)思路1:如图△,过点D 作DG △BC ,交AC 于点G .∵AB =BC ,∴∠A =△BCA .∵DG ∥BC ,∴∠DGA =△BCA ,∠DGF =△ECF ,∴∠A =△DGA ,∴DA =DG .∵AD =CE ,∴DG =CE .又△△DFG =△EFC ,∴△DFG ≌△EFC ,∴DF =EF .思路2:如图△,过点E 作EH △AB ,交AC 的延长线于点H .∵AB =BC ,∴∠A =△BCA .∵EH ∥AB ,∴∠A =△H .∵∠ECH =△BCA ,∴∠H =△ECH ,∴CE =EH .∵AD =CE ,∴AD =EH .又△△AFD =△HFE ,∴△DF A ≌△EFH ,∴DF =EF .(2)结论:MF =AM +FC .证明:如图△,由思路1可知:DA =DG ,△DFG ≌△EFC ,∴FG =FC .∵DM ⊥AG ,∴AM =GM .∵MF =FG +GM ,∴MF =AM +FC .(3)AD 的垂直平分线交AC 于点N ,如图△所示.连接DN ,过点D 作DG △CE 交AC 于点G .设DG =a ,BC =b ,则AB =AC =mb ,AD =AG =ma .∵∠ABC =2△BAC ,设△BAC =x ,则△B =△ACB =2x ,∴5x =180°,∴x =36°,∴∠A =36°. ∵NA =ND ,∴∠A =△ADN =36°.∵∠ADG =△B =72°,∴∠NDG =△A =36°.又△△DGN =△AGD ,∴△GDN ∽△GAD ,∴DG 2=GN ·GA .易知DG =DN =AN =a ,∴a 2=(ma -a )·ma ,两边同除以a ,得m 2a -ma -a =0. ∵DG ∥CE ,∴DG ∶CE =FG △FC =DG △DA =1△m .∵CG =mb -ma ,∴FG =1m +1·m (b -a ), ∴FN =GN +FG =ma -a +1m +1m (b -a )=m 2a -a +mb -ma m +1=mb m +1, ∴FN AC =mbm +1mb =1m +1. 7.解:(1)证明:如图,过点D 作DP △BC 于点P ,DQ ⊥AC 于点Q ,∴∠DQM =△DPN =90°.又△△C =90°,∴四边形CPDQ 为矩形,∴∠QDP =90°,即△MDQ +△MDP =90°. ∵DM ⊥DN ,∴∠MDN =90°,即△MDP +△NDP =90°,∴∠MDQ =△NDP ,∴△DMQ ∽△DNP ,∴DM DN =DQ DP. ∵D 为AB 的中点,DQ ∥BC ,DP ∥AC ,∴DQ =12BC ,DP =12AC ,∴DQ DP =BC AC ,∴DM DN=BC AC. (2)由题意得AQ =CQ =4,MQ =CM -CQ =5-4=1,DQ =12BC =3,DP =12AC =4. ∵△DMQ ∽△DNP ,∴MQ NP =DQ DP ,∴NP =43. 又CP =PB =3,∴CN =3-43=53. 8.解:(1)1△2 BD △BC(2)猜想S △BOC 与S △ABC 之比应该等于OD △AD .理由:如图,分别过点O ,A 作BC 的垂线OE ,AF ,垂足分别为E ,F ,∴OE ∥AF ,∴OD ∶AD =OE △AF .∵S △BOC =12BC ·OE ,S △ABC =12BC ·AF , ∴S △BOC ∶S △ABC =⎝⎛⎭⎫12BC ·OE ∶⎝⎛⎭⎫12BC ·AF =OE △AF =OD △AD . (3)猜想OD AD +OE CE +OF BF的值是1.理由如下: 由(2)可知:OD AD +OE CE +OF BF =S △BOC S △ABC +S △BOA S △ABC +S △AOC S △ABC =S △BOC +S △BOA +S △AOC S △ABC =S △ABC S △ABC=1. 9.解:(1)△将△ACB 的一角沿EF 折叠,折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF ,∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF ,∴S △ABC =4S △AEF .在Rt △ABC 中,∵∠ACB =90°,AC =4,BC =3,∴AB =5.∵∠EAF =△BAC ,∴Rt △AEF ∽Rt △ABC ,∴S △AEF S △ABC =(AE AB)2,即(AE 5)2=14,∴AE =2.5. (2)连接AM 交EF 于点O ,如图△,∵将△ACB 的一角沿EF 折叠,折叠后点A 落在BC 边上的点M 处,∴AE =EM ,AF =MF ,∠AFE =∠MFE .∵MF ∥CA ,∴∠AEF =△MFE ,∴∠AEF =△AFE ,∴AE =AF ,∴AE =EM =MF =AF ,∴四边形AEMF 为菱形.设AE =x ,则EM =x ,CE =4-x .∵四边形AEMF 为菱形,∴EM ∥AB ,∴△CME ∽△CBA ,∴CM CB =CE CA =EM AB, 即CM 3=4-x 4=x 5,解得x =209,CM =43. 在Rt △ACM 中,AM =AC 2+CM 2=4103. ∵S 菱形AEMF =12EF ·AM =AE ·CM , ∴EF =2×43×2094103=4109. (3)如图△,过点F 作FH △BC 于点H ,∵EC ∥FH ,∴△NCE ∽△NHF , ∴CN ∶NH =CE △FH ,即1△NH =47∶FH ,∴FH ∶NH =4△7. 设FH =4x ,NH =7x ,则CH =7x -1,BH =3-(7x -1)=4-7x .∵FH ∥AC ,∴△BFH ∽△BAC ,∴BH ∶BC =FH △AC ,即(4-7x )△3=4x △4,解得x =0.4,∴FH =4x =85,BH =4-7x =65.第11页/共11页 在Rt △BFH 中,BF =(65)2+(85)2=2, ∴AF =AB -BF =5-2=3,∴AF BF =32.。
小专题(六) 相似三角形的辅助线添作技巧

小专题(六) 相似三角形的辅助线添作技巧本专题主要通过添加适当的辅助线构造相似三角形,运用相似三角形的知识来解决数学问题.添作辅助线的方法有:添作平行线、添作垂线、连接线段等.类型1 巧添平行线求线段的比1.如图,在△ABC 中,点D ,E 分别在BC ,AC 上,BE 与AD 交于点F ,且BD=DC ,AE ∶AC=1∶3,求AFFD 的值.解:过点A 作AG ∥BC 交BE 的延长线于点G ,那么△AEG ∽△CEB ,△AFG ∽△DFB ,∴AG BC =AE EC =12,又BD=DC , ∴AG=BD ,∴AFFD =AGBD =1.2.如图,在▱ABCD 中,E 是BC 的中点,在AB 上截取BF=12FA ,EF 交BD 于点G ,求BG ∶GD 的值.解:过点E 作EM ∥AB 交BD 于点M ,那么△BFG ∽△MEG ,∴BGGM =BFEM .∵AB ∥CD ,∴EM ∥CD ,∵BE=EC ,∴BM=MD ,∴EM=12CD ,∵BF=12FA ,∴BF=13AB , ∵AB=CD ,∴BFEM =BGGM =23,∵BM=MD ,∴BG ∶GD=2∶8=1∶4.类型2 巧连线段证线段之间的关系3.如图,在正方形ABCD 中,M 为AD 中点,以M 为顶点作∠BMN=∠MBC ,MN 交CD 于点N. 求证:DN=2NC.解:延长MN ,BC 交于点E ,连接MC ,设AB=2a ,那么AM=a ,BM=√5a.由△BAM≌△CDM,那么BM=MC,且∠BCM=∠CBM=∠BMN.∴△BMC∽△BEM.∴BMBE =BCBM,即√5aBE=√5a,∴BE=52a,∴CE=BE-BC=52a-2a=12a.∵四边形ABCD为正方形,∴∠D=∠DCB=90°,即∠D=∠NCE=90°.∵∠DNM=∠CNE,∴△MDN∽△ECN,∴DNNC =MDCE=a12a=2,即DN=2NC.4.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使DG=CF.求证:(1)△ABF∽△FCE;(2)BD⊥GE.解:(1)∵四边形ABCD是矩形,∴∠ABF=∠C=∠ADC=90°,∴∠BAF+∠BFA=90°,由折叠的性质可得∠AFE=∠ADC=90°,∴∠CFE+∠BFA=90°,∴∠BAF=∠CFE,∴△ABF∽△FCE.(2)由(1)知EFAF =FCAB,又EF=ED,AF=AD,FC=GD,∴DEAD=GDAB.又∵∠BAD=∠GDE=90°,∴△BAD∽△GDE,∴∠ADB=∠DEG,又∠ADB+∠BDC=90°,∠DEG+∠BDC=90°,∴BD⊥GE.类型3巧添垂线求线段的长5.如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,点F在边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N,求MN的长.解:过点F作FH⊥AD于点H,交ED于点O,那么FH=AB=2,∵BF=2FC,BC=AD=3,∴BF=AH=2,FC=HD=1,∴AF=√FH 2+AH 2=√22+22=2√2,∵OH ∥AE ,∴HO AE =DH AD =13,∴OH=13AE=13,∴OF=FH-OH=2-13=53,∵AE ∥FO ,∴△AME ∽FMO ,∴AM FM =AE FO ,即AM FM =153=35,∴AM=38AF=3√24,∵AD ∥BF ,∴△AND ∽△FNB ,∴ANFN =AD BF =32,∴AN=35AF=6√25,∴MN=AN-AM=6√25−3√24=9√220. 类型4 巧添垂线求线段的比6.如图,在△ABC 中,AB=AC ,E ,F ,G 分别是BC ,AB ,AC 上一点,∠FEG=2∠B. (1)求证:∠BFE=∠AGE ; (2)假设BECE =12,求EFEG 的值.解:(1)∵2∠B+∠A=180°,∴∠FEG+∠A=180°,∴∠BFE=∠AGE. (2)过点E 作EM ⊥AB 于点M ,作EN ⊥AC 于点N ,∴△EMF ∽△ENG ,∴EFEG =EM EN ,易证△EBM ∽△ECN ,∴EM EN=BECE=12,∴EF EG=12.7.如图,△ABC 中,AB=AC ,∠BAC<60°,D 为BC 延长线上一点,E 为∠ACD 内部一点,且∠ABE=∠ECD=45°,求BE AC的值.解:作AF ⊥BC 于点F ,BG ⊥CE 交EC 的延长线于点G.∵AB=AC ,∴BF=FC=12BC.∵∠ABE=∠ECD=∠BCG=45°,∴∠CBG=45°,BG=√22BC=√2BF.又∵∠ABF=∠EBG ,∴Rt △ABF ∽Rt △EBG ,∴BEAB =BGBF =√2,∴BEAC =√2.8.如图,将一个直角三角板的直角顶点P 放在矩形ABCD 的对角线BD 上滑动,并使其一条直角边始终经过点A ,另一条直角边与BC 相交于点E ,且AD=10,DC=8,求AP ∶PE 的值.解:过点P作PM⊥AB于点M,PN⊥BC于点N,易证△APM∽△EPN,那么AP∶PE=PM∶PN=AD∶DC=10∶8=5∶4.。
模型总结: 相似三角形模型解析及辅助线作法梳理

相似三角形(模型-辅助线)一、本章概述相似作为几何学习的一个重要内容,大量的出现在中考试卷中,它与勾股定理和锐角三角形函数并列为初中几何计算三大工具。
本章重点讲解相似的几个模型,如A字形,8字形,一线三等角等模型。
二、知识回顾1、图形的相似(1)相似图形:形状相同的图形叫做相似图形(2)相似多边形:对应角相等,对应边的比相等。
相似多边形对应边的比为相似比。
2.相似三角形(3)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段的比相等。
(4)相似三角形的判定①预备定理:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等。
②判定定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
③传递性定理:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(5)相似三角形的性质①相似三角形的对应角相等,对应边成比例②相似三角形的周长的比等于相似比;对应线段的比等于相似比;面积比等于相似比的平方。
3.位似(6)多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫做位似图形,这个点叫做位似中心。
(7)在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k。
1.相似基本模型一、本节概述本节重点讲解“A”字形和“8”字形的应用和构造方法,这两个模型是相似三角形中最为基础的两个模型,但应用十分广泛。
1.“A”字形相似2. ”8”字形相似二、典例精析能力目标:1.熟练掌握正A型相似和正8型相似模型:2.借助平行线构造正A型相似和正8型相似模型解决相关问题。
【例1】已知:图下图,AD(1)若E为AD的中点,射线CE交AB于F,则(2)若E为AD上一点,且,射线CE交AB于F,则思维探究:方法一:通过平行线构造相似解析:过A点作A P//BC交CF于点P,“8”字模型A P CD方法二:过A作A H//CF交BC延长线于H,则方法三:作DK//CF交AB于K,则方法四:作DM//AB交CF于M,则AF=DM,( 2 ) 构造平行线,通过线段比解决问题作B P//AD交CF于点P,大家可尝试过其他点作平行线,解答中用了A点和D点,其它的同学们自己尝试。
(完整版)相似三角形中几种常见的辅助线作法(有辅助线)
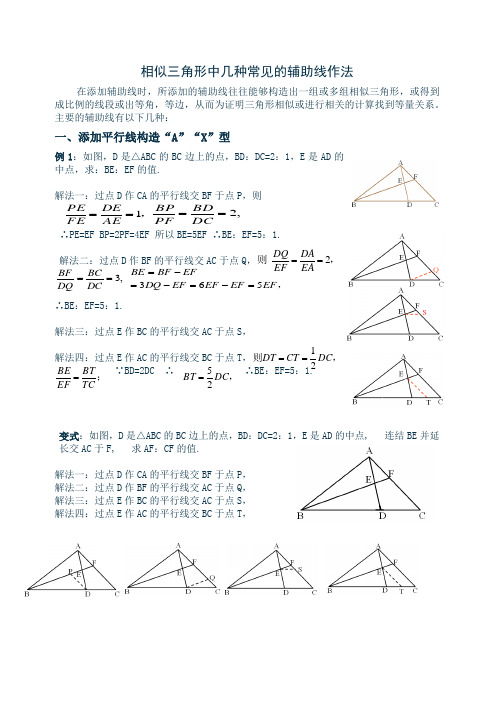
相似三角形中几种常见的辅助线作法在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。
主要的辅助线有以下几种:一、添加平行线构造“A ”“X ”型例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值.解法一:过点D 作CA 的平行线交BF 于点P ,则∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1.解法二:过点D 作BF 的平行线交AC 于点Q ,∴BE :EF=5:1.解法三:过点E 作BC 的平行线交AC 于点S ,解法四:过点E 作AC 的平行线交BC 于点T ,∵BD=2DC ∴ ∴BE :EF=5:1.变式:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,连结BE 并延长交AC 于F,求AF :CF 的值.解法一:过点D 作CA 的平行线交BF 于点P , 解法二:过点D 作BF 的平行线交AC 于点Q , 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T ,,1==AE DE FEPE ,2==DC BD PF BP ,则2==EA DA EF DQ ,3==DCBC DQBF ,EF EF EF EF DQ EF BF BE 563=-=-=-=,则DC CT DT 21==;TC BT EF BE =,DC BT 25=例2:如图,在△ABC 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,DE 延长线与BC 延长线相交于F ,求证:(证明:过点C 作CG//FD 交AB 于G )例3:如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB ·DF=AC ·EF.分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形中几种常见的辅助线作法
在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。
主要的辅助线有以下几种:
一、添加平行线构造“A ”“X ”型
例1:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,求:BE :EF 的值.
解法一:过点D 作CA 的平行线交BF 于点P ,则
∴PE=EF BP=2PF=4EF 所以BE=5EF ∴BE :EF=5:1.
解法二:过点D 作BF 的平行线交AC 于点Q ,
∴BE :EF=5:1.
解法三:过点E 作BC 的平行线交AC 于点S ,
解法四:过点E 作AC 的平行线交BC 于点T ,
∵BD=2DC ∴ ∴BE :EF=5:1.
变式:如图,D 是△ABC 的BC 边上的点,BD :DC=2:1,E 是AD 的中点,
连结BE 并延
长交AC 于F,
求AF :CF 的值.
解法一:过点D 作CA 的平行线交BF 于点P , 解法二:过点D 作BF 的平行线交AC 于点Q , 解法三:过点E 作BC 的平行线交AC 于点S , 解法四:过点E 作AC 的平行线交BC 于点T ,
,
1==AE DE FE
PE ,2==DC BD PF BP ,则2==EA DA EF DQ ,3==DC
BC DQ
BF ,
EF EF EF EF DQ EF BF BE 563=-=-=-=,则DC CT DT 2
1
==;TC BT EF BE =,
DC BT 2
5=
例2:如图,在△ABC 的AB 边和AC 边上各取一点D 和E ,且使AD =AE ,
DE 延长线与BC 延长线相交于F ,求证:
(证明:过点C 作CG//FD 交AB 于G )
例3:如图,△ABC 中,AB<AC ,在AB 、AC 上分别截取BD=CE ,DE ,BC 的延长线相交于点F ,证明:AB ·DF=AC ·EF.
分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。
不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。
. 方法一:过E 作EM//AB ,交BC 于点M ,则△EMC ∽△ABC (两角对应相等,两三角形相似). 方法二:过D 作DN//EC 交BC 于N. 例4:在△ABC 中,D 为AC 上的一点,E 为CB 延长线上的一点,BE=AD ,DE 交AB 于F 。
求证:EF ×BC=AC ×DF
证明:过D 作DG ∥BC 交AB 于G ,则△DFG 和△EFB 相似,
∴
∵BE =AD,∴ 由DG ∥BC 可得△ADG 和△ACB 相似,∴ 即 ∴EF ×BC =AC ×DF.
例5:已知点D 是BC 的中点,过D 点的直线交AC 于E,交BA 的延长线于F,
求证:
CE
BD
CF BF =EC
AE
BF AF =
DG DF BE EF =DG DF AD EF =
DG AD BC AC =DG BC
AD AC
=
分析:利用比例式够造平行线,通过中间比得结论 .
(或利用中点”倍长中线”的思想平移线段EC,使得所得四条线段分
别构成两个三角形.)
例6:已知:在等腰三角形ABC中,AB=AC,BD是高,求证:BC2=2AC·C D
分析:本题的重点在于如何解决“2”倍的问题;让它归属一条线段,
找到这一线段2倍是哪一线段.
例7: 如图,△ABC中,AD是BC边上中线,E是AC上一点,连接ED
且交AB的延长线于F点.求证:AE:EC=AF:BF.
分析:利用前两题的思想方法,借助中点构造中位线,利用平行
与2倍关系的结论,证明所得结论.找到后以比例式所在三角
形与哪个三角形相似.
例8:在∆ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F,求证:BP²=PE·PF
分析:在同一直线上的三条线段成比例,可以通过中间比转化,也可以通过线段相等,把共线的线段转化为两个三角形中的线段,通过相似证明.另外在证明等积式时要先转化为比例式观察相似关系,有利于证明.
二、作垂线构造相似直角三角形
例9:如图从 ABCD 顶点C 向AB 和AD 的延长线引垂线CE 和CF ,垂足分别为E 、F ,
求证:
证明:过B 作BM ⊥AC 于M ,过D 作DN ⊥AC 于N ∴ AM :AE=AB :AC (1)
(1)+(2)得
例10:∆ABC 中,AC=BC ,P 是AB 上一点,Q 是PC 上一点
(不是中点),MN 过Q 且MN ⊥CP ,交AC 、BC 于M 、N ,求证:
证明:过P 作PE ⊥AC 于E ,PF ⊥CB 于F ,则CEPF 为矩形
∴ PF EC ∵ ∠A =∠B=45° ∴Rt ΔAEP=Rt ΔPFB ∴ ∵ EC=PF ∴ (1) 在ΔECP 和ΔCNM 中CP ⊥MN 于Q
∴ ∠QCN+∠QNC=90°又 ∵ ∠QCN+∠QCM=90° ∴∠MCQ=∠CNQ
∴Rt ΔPEC ∽Rt ΔMCN ∴ 即 (2) 由(1)(2)得
三、作延长线构造相似三角形
例11. 如图,在梯形ABCD 中,AD ∥BC ,若∠BCD 的平分线CH ⊥AB 于点H ,BH=3AH ,且四边形AHCD 的面积为21,求△HBC 的面积。
分析:因为问题涉及四边形AHCD ,所以可构造相似三角形。
把问题转化为相似三角形的面积比而加以解决。
解:延长BA 、CD 交于点P ∵CH ⊥AB ,CD 平分∠BCD
∴CB=CP ,且BH=PH ∵BH=3AH ∴PA :AB=1:2 ∴PA :PB=1:3
∵AD ∥BC ∴△PAD ∽△PBC
2AC AF AD AE AB =⋅+⋅CN CM PB PA ::=AM AC AE AB ⋅=⋅)(AN AM AC AN AC AM AC AF AD AE AB +=⋅+⋅=⋅+⋅BCM
ADN ∆≅∆=
//EC
PE PF PE PB PA ==CN EC CM EP =CN CM EC EP =CN
CM PB PA =
91:
:∴△△=PBC PAD S S PBC PCH S S △△∵2
1=72:∴四边形△==AHCD PAD S S 21=AHCD S 四边形∵6=PAD S △∴54=PBC S △27
2
1
==PBC HBC S S △△∴
例12. 如图,RtABC 中,CD 为斜边AB 上的高,E 为CD 的中点,AE 的延长线交BC 于F ,FG 交AB 于G ,求证:FG=CF ·BF
分析:欲证式即 由“三点定形”,ΔBFG 与ΔCFG 会相似吗?显然不可能。
(因为ΔBFG 为Rt Δ),但由E 为CD 的中点,∴可设法构造一个与ΔBFG 相似的三角形来求解。
不妨延长GF 与AC 的延长线交于H ,则 又ED=EC ∴FG=FH 又易证Rt ΔCFH ∽Rt ΔGFB ∴FG ·FH=CF ·BF ∵FG=FH ∴FG2=CF ·BF
四、利用中线的性质构造相似三角形
例13:如图,中,AB ⊥AC ,AE ⊥BC 于E ,D 在AC 边上,若BD=DC=EC=1,求AC.
解:取BC 的中点M ,连AM ∵AB ⊥AC ∴ AM=CM ∴∠1=∠C 又 BD=DC
∴∠DBC=∠DCB ∴∠CAM=∠C=∠DBC ∴ΔMAC ∽ΔDBC ∴ 又 DC=1 MC= BC ∴ (1)
又 Rt ΔAEC ∽Rt ΔBAC 又 ∵ EC=1 ∴ (2)
由(1)(2)得, ∴
小结:利用等腰三角形有公共底角,则这两个三角形相似,取BC 中点M ,构造ΔMAC ∽ΔDBC
是解题关键
FG
CF
BF FG =EC FH ED FG AE AF ==EC
FH ED FG =BF FH FG CF =BC AC DC MC =2122
1BC DC BC MC AC =⋅=BC BC CE AC =⋅=242
1AC AC =32=AC。
