计算题节约里程法

节约里程法训练专题

节约里程法1、已知配送中心P0向5个用户Pj(j=1,2,3,4,5)配送货物，其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示：图中括号内的数字表示客户的需求量（单位：吨），线路的数字表示两结点之间的距离，配送中心有3台2t卡车和2台4t卡车，两者车辆可供用。

需求量P01.5 8 P11.7 8 12 P20.9 6 13 4 P31.4 7 15 9 5 P42.4 10 16 18 16 12 P5（1）试利用节约里程法制定最优的配送方案；（2）设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间。

2、已知配送中心P0向5个用户Pj(j=1,2,3,4,5,)配送货物，其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示：图中括号内的数字表示客户的需求量（单位：吨），线路的数字表示两结点之间的距离，配送中心有（1）试利用节约里程法制定最优的配送方案；（2）设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间。

3、已知配送中心P0向5个用户Pj(j=1,2,3,4,5,)配送货物，其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示：图中括号内的数字表示客户的需求量（单位：吨），线路的数字表示两结点之间的距离，配送中心有（1）试利用节约里程法制定最优的配送方案；（2）设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间。

4、已知配送中心P0向5个用户Pj(j=1,2,3,4,5)配送货物，其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示：图中括号内的数字表示客户的需求量（单位：吨），线路的数字表示两结点之间的距离，配送中心有（1）试利用节约里程法制定最优的配送方案；（2）设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间。

节约里程法练习答案

通过节约里程法，我们可以有效地规划配送路线，减少运输成本和时间成本，提高物流效率。在实际应用中，我们还可以考虑多种车型、装载量等因素对配送方案的影响，以实现更优的配送计划。
优化建议
在实际应用中，可以根据实际情况考虑多种车型、装载量等因素对配送方案的影响，以实现更优的配送计划。例如，如果配送中心有多辆不同装载量的车辆，可以合理分配装载量以提高车辆利用率和减少运输成本。
02
考虑了不同客户之间的距离和需求，能够更好地满足客户需求。
03
考虑了车辆的装载量和行驶时间，能够更好地利用车辆和司机的时间。
反思和讨论
节约里程法在实践中的应用需要考虑更多的实际情况，例如客户的分布、交通状况、路况
等。
节约里程法的计算方法需要进一步优化，以提高计算效率和
准确性。
节约里程法在实践中的应用需要考虑如何更好地与其他运输方式进行协调和配合，以实现
节约里程法练习答案
汇报人：文小库
2023-11-03
CONTENTS
• 练习题目 • 解题思路&问题建模 • 执行计算 • 图表展示 • 结论
01
练习题目
题目描述
• 本练习题目旨在帮助学员掌握节约里程法的计算方法，通过一个具体的实例来演示如何运用该方法进行路线规划。我们将提供两个城市之间的距离和运输成本，并要求计算出一条能够节约成本的运输路线的里程数。
此外，可以考虑使用先进的物流信息系统和技术手段来提高配送效率。例如，利用GIS、GPS等技术手段对配送路线进行优化，以提高运输效率和质量。
04
图表展示
路线图
路线图1
该路线图展示了从起点到终点的实际行驶路线和距离。可以清晰地看出每次行驶的距离和方向，为后续计算节约里程提供基础数据。

节约里程法详解图

例：有一配送（P）具有如图所示的配送网络，其中A-J表示收货站，（）内数字表示发送量（吨），路线上的数字表示道路距离（公里）。

问为使行走距离尽量小，应该如何去求配送线路？假设能够利用的车是2吨车（即最大载重量是2吨）和4吨车两种，并限制车辆一次运行的初步距离是30公里。

解题步骤：1.第一步：作出最短距离矩阵，首先从配送网络图中计算出配送中心与收货点之间以及收货点相互之间的最短距离矩阵，见下表所示：表一：最短距离矩阵（单位：公里）例如：计算A-B的节约里程项目如下：P-A的距离是：a=10P-B的距离是：b=9A-B的距离是：c=4节约里程项目为：a+b-c=10+9-4=15公里3.第三步：节约项目分类，再把节约项目由大到小顺序排列。

（1）.初次解。

线路数：10总行走距离：(10+9+7+8+8+8+3+4+10+7)*2=148公里车辆台数：2吨车10台（2）.二次解。

按节约里程由大到小的顺序，连接A-B，A-J，B-C连接线。

线路数：7总行走距离：148-15-13-11=109公里车辆台数：2吨车6台，4吨车1台（3）.三次解。

其次节约里程最大的是C-D和D-E。

C-D，D-E两者都有可能与二次解的线路A连接，但由于A的车辆载重量与行走距离有限，不能再增加收货点。

为此，略去C-D而连接D-E。

总行走距离：109-10=99公里车辆台数：2吨车5台，4吨车1台（4）.四次解。

接下来节约里程大的是A-I和E-F。

由于A已组合在完成的线路A中，所以略去，不能再增加收货点。

为此，略去A-I 而将E-F连接在线路B上。

线路数：5总行走距离：99-9=90公里车辆台数：2吨车3台，4吨车2台（5）.五次解。

再继续按节约里程由大到小排出I-J，A-C，B-J，B-D，C-E。

由于同一组总有一头或两头包含在已完成的线路A中，不能再作出新的线路。

只考虑把下一组F-G组合在完成的线路B中。

总行走距离：85公里车辆台数：2吨车2台，4吨车2台线路A：4吨车，总行走距离27公里，装载量3.6吨。

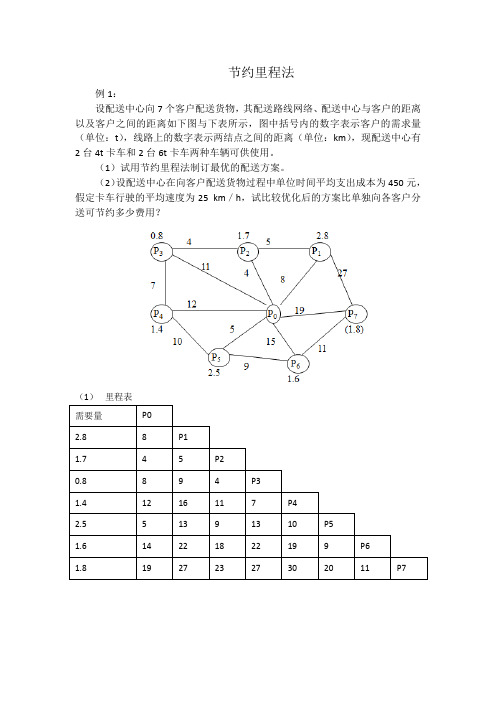
节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7（2）节约里程表需要量P02.8 8 P11.7 4 5（7）P20.8 8 9（7）4（8）P31.4 12 16（4）11（5）7（13）P42.5 5 13（0）9（0）13（0）10（7）P51.6 14 22（0）18（0）22（0）19（7）9（10）P61.8 19 27（0）23（0）27（0）30（1）20（4）11（22）P7（3）节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1（4）配送路线选择节省的配送时间为节省的费用为：例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

计算题节约里程法

节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7（2）节约里程表需要量P02.8 8 P11.7 4 5（7）P20.8 8 9（7）4（8）P31.4 12 16（4）11（5）7（13）P42.5 5 13（0）9（0）13（0）10（7）P51.6 14 22（0）18（0）22（0）19（7）9（10）P61.8 19 27（0）23（0）27（0）30（1）20（4）11（22）P7（3）节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1（4）配送路线选择节省的配送时间为节省的费用为：例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

节约里程法例题

节约里程法例题
问题描述
某公司为了降低员工的交通成本，制定了节约里程法，规定员工在每周的通勤过程中，只能行驶一定的里程数。

具体规定如下：
•每位员工每周最多行驶300公里的里程数；
•员工每行驶一公里，公司会额外支付0.5元。

现在需要使用节约里程法计算员工每周的交通费用。

算法设计
节约里程法的核心思想是根据员工的行驶距离来计算交通费用。

算法的基本步骤如下：
1.设置变量total_mileage为员工总行驶里程数，初始值为0；
2.设置变量total_cost为员工总交通费用，初始值为0；
3.循环执行以下步骤：
–输入本次行驶的里程数mileage；
–如果mileage + total_mileage大于300，则将total_cost 增加300 - total_mileage * 0.5，并将total_mileage更新为300；
–否则，将total_cost增加mileage * 0.5，并将
total_mileage增加mileage；
–如果total_mileage等于300，则退出循环。

4.输出员工总交通费用total_cost。

算法实现
以下是使用Python语言实现节约里程法的代码示例：
```python def calculate_transport_cost(): total_mileage = 0 total_cost = 0
while total_mileage < 300:
mileage = float(input(\。

节约里程法计算公式

节约里程法计算公式
节约里程法的基本思想是在满足所有客户需求的前提下，通过合理规划配送路线，使得配送车辆的行驶总里程最短，从而达到节约运输成本的目的。

其核心计算公式如下：
1. 计算节约里程值（S_ij）
- 设配送中心为P，客户点i和客户点j，d_Pi表示配送中心到客户点i的距离，d_Pj表示配送中心到客户点j的距离，d_ij表示客户点i到客户点j的距离。

- 节约里程值S_ij=d_Pi+d_Pj - d_ij
例如，若配送中心P到客户点A（即i = A）的距离d_PA=10公里，配送中心P到客户点B（即j = B）的距离d_PB=12公里，客户点A到客户点B的距离d_AB=5公里，则节约里程值S_AB=d_PA+d_PB-d_AB=10 + 12-5 = 17公里。

2. 构建配送路线的步骤中的计算（以车辆载重等约束条件为例）
- 计算出所有客户点两两之间的节约里程值S_ij，并按照从大到小的顺序进行排列。

- 然后，从节约里程值最大的组合开始，判断将这两个客户点连接到同一路线是否满足车辆载重、配送时间等约束条件。

- 假设车辆的载重上限为Q，客户点i的货物需求量为q_i，客户点j的货物需求量为q_j。

如果q_i+q_j≤ Q，并且其他约束条件（如配送时间等）也满足，那么就可以将客户点i和客户点j连接到同一路线中。

- 在构建路线的过程中，不断重复这个步骤，直到所有客户点都被分配到合适的配送路线中。

节约里程法在物流配送路线规划等领域有着广泛的应用，通过合理计算节约里程值并考虑各种约束条件，可以有效地优化配送方案，提高物流配送的效率，降低物流成本。

[计算题]节约里程法答案讲解学习

节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）作运输里程表，列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7（2）按节约里程公式求得相应的节约里程数（3）将节约里程按从大到小顺序排列表-4）根据载重量约束与节约里程大小，选择配送路线。

优先择节约里程数最大的连接点：P6-P7、P3-P4最优方案：P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点，所以优先选择P6-P7，又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t（此路线选择一辆6t卡车）因P3-P4为第二大节约里程数连接点，且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t，故选择P0-P4-P3-P2-P0路线3.9t（此路线选择一辆4卡车）最后选P0-P1-P0路线2.8t（此路线选择一辆4卡车）得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=（19+14+5+12+8+4+8）*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

节约里程法

配送案例分析
问题：1.采用节约里程法制定最优的配送方案。
2.设客车行驶的速度平均为40千米/
小时，比较优化后的方案比单独向客户分送
可节约多少时间？
配送案例分析
配送案例分析
第（1）步：作运输里程表，列出配送中心到用户及用户间的最短距离。
配送案例分析
配送案例分析
第（2）步：由运输里程表、按节约里程公式，求得相应的节约里程数，如上表（）内。
8 8
P0 8
3
g
0. 6
配送网络图
1. 5b
9
1 0 7
4
h
0. 8
0. 6j
1 0
0. a7
i
0. 5
• 初始方案运行结果：
• 1、从百家姓配送中心出发，需要设计10条配送线路，分别向10家连锁店配送商品；
• 2、需要10辆2t的配送车辆（每家连锁店的需要量都低于2t），总配送距离为148km。
2)FG的配送货物量1.1T，正好可以与2.9T拼装为一辆4T 货车的载运量，它们相互衔接成为一条配送路线AEGFA。全程为20＋1＋6＋24＝51KM。
3)C,D配送货物量是1.0＋0.7＝1.7T，在货车载重限度内，可以将B点的0.8T货物集中在一起，拼装为一辆2.5T货车的载运量，形成第二条配送路线ABCDA或ADCBA，全程为9＋9＋10＋12＝40KM。
P0
7
辆
J （0.6）
7
（1.5） F
8
3
G 6
4 10
H
（0.6）修正结果：运距——85km，车辆——4t2辆，2t2辆
（0.5） I
修正2套方案：按节约里程大小顺序，组成配送线路。

【管理资料】节约里程法例题计算汇编

顺序排位
1 2 3 4 4 6 6 6 9 9 11 12
连接线
A－ B A－ J B－ C D－ E C－ D A－ I E－ F I－ J A－ C B－ J B－ D C－ E
节约里程
15 13 11 10 10 9 9 9 8 8 7 6
顺序排位
13 13 13 16 16 16 19 19 21 22 22 22
C
D
B
A 0.32
0.24
路线1 2
E
P 路线2 2
J 0.24
F
G
路线3 2
0.16
0.48
H
0.40
图2 配送路线图
I 0.32
从配送路线图可看出，依次确定的三条配送路线均符合配送中心的约束条件，需要2t货车3辆，总走行里程为70km，若简单地每个连锁分店送货，需要2t货车10辆，走行总里程148km。
此课件下载可自行编辑修改，仅供参考！感谢您的支持，我们努力做得更好！谢谢
连接线
F－ G G－ H H－ I B－ I A－ D F－ H B－ E D－ F G－ I C－ J E－ G F－ I
节约里程
5 5 5 4 4 4 3 3 2 1 1 1
第四步：根据节约里程排序表和配送车辆载重及行驶里程等约束条件，渐近绘出如图2所示的配送路线图。
0.32
0.40
0.40
第二步：由最短距离表，利用“节约里程”法计算出各连锁分店之间的节约里程，做出节约里程表（见表3），计算结果有正有负，节约里程为负数时，无实际意义，在表内写0。
表3 节约里程表
A BC DE F GH I J A B C D E F G H I J

节约里程法-应用

节约运输里程法应用
(0.4)
D
(0.8)
C
Байду номын сангаас
5
B (1.5) 4 A
(1.4)
E
8
8
7
线路A：装载量 3.6 运输距离27KM
(0.7)
4
J (0.6)
P
8 3 4 (0.6)
G
3次解：按节约里程的大小，连接C—D 和D—E ，但因为限制，不能连接C—D，所以只能连接D--E 线路数：6条总运输距离：99KM
里程节约法
节约里程的定义
A A a B P c
a
P b （一）
b
（二）
B
运输方式由（一）变成（二），可节省的运输距离为（2a+2b）-（a+b+c）= a+b-c > 0，这一节省的运输距离称为“节约里程”
节约里程法——基本假定
①配送的是同一种货物 ②各客户的坐标及需求量均为已知 ③配送中心有足够的运输能力
I
J (0.6) 10
6 F
G (0.6) H (0.8)
(1.5)
线路数：4条总运输距离：85KM 车辆台数：2吨车2台， 4吨车2台
(0.5)
节约运输里程法应用
(0.4) D 6 (1.4) 8
(0.8) 5
C B (1.5) 4 7 线路A：装载量 3.6 运输距离27KM P 3 7 10 J (0.6) 线路C：装载量 1.3 运输距离 23KM H (0.8) 9 (0.7) A 4
I
F (1.5)
H (0.8)
(0.5)
节约运输里程法应用
(0.4) D 6 7 (0.8) C

[计算题]节约里程法答案

节约里程法例1：设配送中心向7个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。

（1）试用节约里程法制订最优的配送方案。

（2）设配送中心在向客户配送货物过程中单位时间平均支出成本为450元，假定卡车行驶的平均速度为25 km／h，试比较优化后的方案比单独向各客户分送可节约多少费用？（1）作运输里程表，列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7（2）按节约里程公式求得相应的节约里程数（3）将节约里程按从大到小顺序排列表-4）根据载重量约束与节约里程大小，选择配送路线。

优先择节约里程数最大的连接点：P6-P7、P3-P4最优方案：P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点，所以优先选择P6-P7，又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t（此路线选择一辆6t卡车）因P3-P4为第二大节约里程数连接点，且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t，故选择P0-P4-P3-P2-P0路线3.9t（此路线选择一辆4卡车）最后选P0-P1-P0路线2.8t（此路线选择一辆4卡车）得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=（19+14+5+12+8+4+8）*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2：设配送中心向5个客户配送货物，其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示，图中括号内的数字表示客户的需求量（单位：t），线路上的数字表示两结点之间的距离（单位：km），现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

节约里程法练习答案

4. 优化路径
重复合并任务的过程，直到无法再合并或达到满意的路径为止。
5. 评估结果
评估优化后的路径的经济性和效率，选择最佳的送货方案。
Part
05
总结与思考
对节约里程法的理解与思考
节约里程法是一种运筹学中的优化方法，通过合理安排运输路线和车辆调度，实现运输成本的节约和效率的提高。
在节约里程法中，关键在于找出最短路径和最大节约量，这需要运用图论和线性规划等数学工具进行求解。
解答
节约里程法是一种用于解决车辆路径问题的算法，旨在寻找最经济、最有效的车辆行驶路径，以降低运输成本和提高运输效率。
常见问题二解答
问题
节约里程法的基本原理是什么？
VS
解答
节约里程法的基本原理是利用车辆的运输能力来优化行驶路径，通过合并送货路线来减少行驶里程，从而降低运输成本。该方法基于一个简单的原则：如果通过合并两个或多个送货任务，能够减少单次送货的里程数，那么这种合并是有益的。
STEP 02 O-P：8
STEP 03 O-Q：9
P-Q：4
练习题目二及答案
01
02
P-R：3
P-S：5
03
R-S：2
练习题目二及答案
S-E：6
01
E-D：7
02
03
D-C：5
练习题目二及答案
01
C-B：4
02
B-A：2
03
答案：略。
Part
04
常见问题与解答
常见问题一解答
问题
什么是节约里程法？
计算过程与结果
1. 计算任意两个节点（配送中心或客户）之间的距离矩阵。
3. 根据节约里程进行排序，将客户分配给最近的配送中心。

节约里程法

b94b
c795c
d 8 14 10 5 d
e 8 18 14 9 6 e
f 8 18 17 15 13 7 f
g 3 13 12 10 11 10 6 g
h 4 14 13 11 12 12 8 2 h
i 10 11 15 17 18 18 17 11 9 i
ห้องสมุดไป่ตู้
j 7 4 8 13 15 15 15 10 11 8 j
5
5
d
c
b4
6
a
e
4
7 8
7 Q
j
f
3
10
g
h
2
9
i
最佳配送线路
8
配送线路的优化
节约里程法 1、节约里程的基本原理
用一辆车将所有客户的货物装在一起，沿着一条精心选择的最佳路线，将货物送到客户手中。目标：节约车辆、节约费用、缓解交通压力、减少环境污染。
△S = S1 + S2 - S3
1
2、按节约里程法制定配送计划例有一配送中心（Q）要向10个用户配送，配送距离（公里）和需用量（吨）如下图所示。假设：采用最大载重量2吨、4吨、8吨三种汽车，并限定车辆一次运行距离50公里。用节约里程法选择最佳配送路线和车辆的调度。
j 13 8 1 0 0 0 0 0 9
节约里程计算过程
5
第四步：将节约里程按大小顺序排列分类。
节约里程顺序表
分类 Ⅰ
用户连接线
a—b
节约里程
15
分类 Ⅸ
用户连接线
f—g
Ⅱ
a—j
13
Ⅸ
g—h
Ⅲ
b—c
11

节约里程法

=27+34=61(Km) 节约费用:C=(61/25)×45=109.8（元）
7
12 5
P5 （2.5） 9
（1.7） P2
4 8
P1 （2.8）
P0 19
11
（1.6）
P7 （1.8）
配送线路： ①P0→P2→P3→P4→P0（27Km）,派4t车1辆 ②P0→P5→P6→P7→P0(44Km),派6t车1辆 ③P0→P1→P0(16Km),派4t车1辆节约里程数:△S=148－(27+44+16)=61(Km)
设配送中心P0向7个用户Pj配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图1
与下表1所示，图中括号内的数字表示客户的需求量( 单位：t)，线路上的数字表示两结点之间的距离(单位：km)，现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
⑴试用节约里程法制定最优的配送方案。
O 图2
△L=L1－L2=2(a+b)－(a+b+c)=(2a+2b)－a－b－c=a+b－c
2.节约里程法核心思想
节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路，每次使合并后的总运输距离减小的幅度最大，直到达到一辆车的装载限制时，再进行下一辆车的优化。
3.节约里程法的应用
⑵设配送中心在向用户配送货物过程中单位时间平均支出成本为45元，假定卡车行驶的平均速度为25公里/ 小时，试比较优化后的方案比单独向各用户分送可节约多少费用？
（0.8t）
P3
（1.7t） 4
5
P2
7
11
4
（1.4t）P4
12
10

配送管理实务-例6节约里程法解题过程

【例6-3】如图6-8所示为一配送网络。

P为配送中心所在地，A～J为客户所在地，括号内的数字为配送量，单位为吨（t），线路上的数字为道路距离，单位为千米（km）。

图6-8 配送中心的配送网络图为了尽量缩短车辆运行距离，必须求出最佳配送线路。

现有可以利用的车辆是装载量为2吨和4吨的两种厢式货车，并限制车辆一次运行距离在30千米以内。

第一步：首先计算相互之间最短距离，根据图6-8中配送中心至各用户之间、与用户之间的距离，得出最短配送线路距离矩阵，如图6-9所示。

图6-9 最短配送线路距离矩阵第二步：从最短配送线路距离矩阵（图6-9）中计算出各用户之间的配送线路节约行程图（图6-10）。

例如，计算A-B的节约距离。

P-A的距离：a＝10P-B的距离：b＝9A-B的距离：c＝4A＋b－c＝15图6-10 配送线路节约行程图第三步：对节约行程按大小顺序进行排列，配送线路节约行程排序表见表6-13。

表6-13 配送线路节约行程排序表第四步：按照配送线路节约行程排序表(表6-13)，组合成配送路线图。

1）初始解。

如图6-11所示，从配送中心P向各个用户配送。

配送线路10条，总运行距离为148千米。

图6-11 初始解2）二次解。

按照节约行程的大小顺序连接A-B、A—J、B-C。

如图6-12所示，配送线路7条，总运行距离为109千米，需要2吨车6辆，4吨车1辆。

在图中可以看出规划的配送线路工装配量为3．6吨，运行距离为27千米。

图6-12 二次解3）三次解。

按照节约行程大小顺序，应该是C-D和D-E、C-D和D-E都有可能连接到二次解的配送路线工中。

但是由于受车辆装载量和每次运行距离这两个条件的限制，配送线路Ⅰ不能再增加用户，为此不再连接C-D，而连接D-E，组成配送线路Ⅱ，该线路装载量为1．8吨，运行距离22千米。

此时，配送线路共6条，总运行距离99千米，需要2吨汽车5辆，4吨汽车1辆。

4）四次解。

接下来的顺序是A—I、E-F，由于将用户A组合到配送线路Ⅰ中，而且该线路不能扩充用户，所以不再连接A—I。

两个例子节约里程法

30km，4t车一
P0
7
辆
J （0.6）
7
（1.5） F
3
G 6
4 H
线路3：运距23km，
102t车一辆
（0.5）
（0.8）
9
I
（0.6）修正结果：运距——80km，车辆——4t2辆，2t1辆
练习
例：如图所示为配送中心P的配送网络图，某配送中心P向A、B、C、D、E五个客户配送物品。图中边线上的数字表示公路里程（km）。靠近各用户括号里的数字表示对货物的需求量（t）。配送中心备有2t和4t载重量的汽车，汽车一次巡回行驶里程不能超过30km。求解配送路线方案。
j 7 4 8 13 15 15 15 10 11 8 j
最短距离矩阵
准备相关资料：
P
a
b
15 b
第二步：从最短矩阵中，计算用户相互间的节约里程。
c
8
11 c
d
4
7
10 d
e
0
3
6
10 e
f
0
0
0
3
9
f
g
0
0
0
0
1
5
g
h
0
0
0
0
0
4
5
h
i
9
4
0
0
0
1
2
5
i
j
13 8
1
0
0
0
0
0
9
节约里程计算过程
如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时，汽车行驶的总里程L是
L=2（L1+ L2）如果用一辆汽车向A、B两个用户巡回送货，则汽车行驶总里程L′为