管道包扎问题的数学模型论文
管道订购与运输问题-2000年全国数学建模竞赛B题优秀论文
管道订购与运输问题1 问题重述2 基本假设(1)只考虑订购费用和运输费用,不考虑装卸等其它费用. (2)钢管单价与订购量、订购次数、订购日期无关.(3)订购汁划是指对每个厂商的定货数量;运输方案是指具有如下属性的一批记录:管道区间,供应厂商,具体运输路线.(4)将每一单位的管道所在地看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.3 符号说明M :钢厂总数. n :单位管道总数.:i S 第i 个钢厂 :i S 第i 个钢厂的产量上限。
:i p 第i 个钢厂单位钢管的销售价 i A 管道线上第i 个站点。
i d 管道线上第i 个单位管道的位置。
F :总费用。
:ij C 从钢厂(1,2,,)i S i m =到点(1,2,,)j d j n =的最低单位费用。
4 问题的简化求 S AP 矩阵的基本思路是图的最短路算法 . 由于铁路的运输费用与线路的长度不是线性关系 ,必须对铁路网做一些预处理才能套用图的标准最短路算法 . 下面叙述求 S AP 矩阵的过程:1.利用图的标准最短路算法 ,从铁路网络得出图中任两个点之间的最短路径表 T (如果两个点之间不连通 ,认为它们之间的最短路长度为+ ∞ ) .2.利用题中的铁路运价表将 T 中的每个元素 (即最短距离 )转化为运输费用 ,将运输费用表记为 C.3.将公路的长度换算为运输费用 ,由公路路程图 (包括要沿线铺设管道的公路 )得出公路费用图 G,若 i, j 不连通 ,则令 Gij = + ∞ .4.对于任一组 ( i , j)∈ { 1,… n }× { 1,… m } 如果 Cij <+ ∞ ,且小于 Gij ,那么就在公路费用图中加一条边. 即令 Gij = min{Cij , Gij } .5.利用图的标准最短路算法 ,求公路费用图中任一个 S 点到任一个 A 点的最小费用路径 ,得出 S AP 矩阵. 如表 1所示:SAP 矩阵A123 4 5 6 7 8 9 10 11 12 13 14 15 S1 170716031402986 380 205 31 212 642 920 960 1060 1212 1280 14202 215720531902 1716 1110 955 860 712 1142 1420 1460 1560 1712 1780 19203 230722032002 1816 1210 1055 960 862 482 820 860 960 1112 1180 13204 260725032352 2166 1560 1405 1310 1162 842 620 510 610 762 830 9705 255724532252 2066 1460 1305 1210 1112 792 570 330 510 712 730 8706 265725532352 2166 1560 1405 1310 1212 842 620 510 450 262 110 2807 275726532452 2266 1660 1505 1410 1312 992 760 660 560 382 260 205问题分析运输费用等价转换法则:按单位运费相等原则将任意两点间的最短铁路线转换为公路 线.对于铁路线上的任意两点,i j V V ,用F1oyd 算法找出两点间最短铁路路线的长度ij L 查铁路运价表求得ij L ,对应的铁路单位运费ij f ;又设与该段铁路等费用的公路长度为ij l ,则:0.1ij ij f l =⨯由此,我们就在,i j V V 之间用一条等价的公路线来代替,i j V V 间的最短铁路线.如果,i j V V 之间原来就有公路,就选择新旧公路中较短的一条.这样,我们就把铁路运输网络转换成了公路运输网络.销价等价转换法则:按单位费用相等将任意钢厂的单位销价转换为公路单位运价.对于钢厂S i 的销售单价P i ,我们可以虚设一条公路线,连接钢厂S i 及另一虚拟钢厂'i s ,其长度为i l ,并且满足0.1i i l p =⨯;从而将钢厂的销售单价转换成公路运输单价,而新钢厂'i s 的销售价为0.将铁路和销价转换为公路的过程可以由计算机编程实现. 通过上述的分析,我们可以将原问题化为一个相对简单的产量未定的运输问题,利用115A A 到之间的管道距离和钢厂和站点之间的公路距离建立一个产量未定的运输问题的模型.但是由于1215,A A A ,并不能代表所有的实际需求点(实际需求点是n 个单位管道),因此,我们可以用F1oyd 算法进一步算出7个钢厂到所有实际的n 个需求点(对于问题一,n =5171;对于问题三,n =5903)的最短路径,并由此得出一个具有7个供应点、n 个需求点的产址未定的运输模型.6 模型的建立产量未定的运输模型根据假设4,我们可以将每一单位的管道看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.对每个点,我们可以根据该点的位置和最短等价公路距离,求出各钢厂与该点之间最小单位运输费用ij C (销价已经归人运输费用之中了).设总共有m 个供应点(钢厂),n 个需求点,我们就可以得到一个产量未定的运输模型:有m 个供应点、n 个需求点,每个供应点的供应量{0}{500,}i i u s ∈;每个需求点需要1单位,运输单价矩阵为C ,求使得总运输费用最小的运输方案.其数学规划模型: 11minmnij ij i j F C x ===∑∑11{0}{500,}1,2,,..11,2,01nij i j mij i ij x S i ms tx j n x ==⎧∈=⎪⎪⎪==⎨⎪⎪=⎪⎪⎩∑∑或其中: 1112112n m m mn C C C C CC C ⎛⎫⎪=⎪ ⎪⎝⎭为单位费用矩阵 1112112n m m mn x x x X x x x⎛⎫⎪=⎪ ⎪⎝⎭为决策矩阵,也为0-1矩阵 代码如下7 模型的求解对于本题,上述0-1规划规模宏大,现有的一些算法不能胜任,我们必须具体问题具体分析,结合本题实际情况,寻找行之有效的算法.(1)初始方案的改进的最小元素法和改进的伏格尔法 *改进的最小元素法改进的最小元素法又称为贪婪法或瞎子爬山法,它的宗旨是每一步都取当前的最优值算法步骤为,对费用矩阵C 作n 次下列循环:①C 中找一个最小值ij C ; ②令1;ij x =③C 的第j 的所有数据改为+∞;④如果1nij i j x s ==∑,第i 个供应点的供应量已达上限,将C 的第i 行数据全改为+∞。
直通连接水管注射模毕业设计

毕业设计(论文)题目:直通连接水管注射模设计课程:注塑模具设计院(部):专业:机电一体化〔模具方向〕班级:09模具双高(1)姓名:学号:37设计日期:2012-02-12—2012-03-16“塑料成型工艺与模具设计”课程设计任务书目录一、塑件材料工艺分析与设计.................................................. 31.塑料原料材料的分析.................................................... 42.塑料的尺寸精度分析....................................................53.塑件表面质量分析......................................................54.塑件结构分析..........................................................5二、肯定成型设备选择与模塑工艺参数...........................................61.计算塑件的注射量、注射压力、锁模力的计算...............................62.肯定成型工艺参数.......................................................6三、注射模的结构设计.........................................................71.分型面的选择...........................................................72.型腔数量的肯定及型腔的排位.............................................73.标准模架的选用.........................................................84.浇注系统的设计.........................................................81)主流道的设计..........................................................8 2)分流道的设计......................................................... 93)分流道的形状和截面尺寸................................................94)分流道的表面粗糙度....................................................105.型芯型腔的结构设计....................................................106.内模镶件的设计........................................................117.推出机构的设计........................................................118.排气方式的设计........................................................119.冷却系统的设计........................................................12四、注射模成型零件的计算....................................................12五、注射机的有关参数的校核...................................................131.最大注射量的校核.......................................................132.注射压力的校核.........................................................133.锁模力的校核...........................................................134.模具与注射机安装部份相关尺寸校核.......................................13六、装配图..................................................................14七、致谢....................................................................14八、参考文献及资料...........................................................14课题设计名称:直通连接水管的注射模设计塑件图:塑件名称直通连接水管材料UPVC厚度3工件精度MT5设计内容:1、绘制塑件注射模总装图(A0图纸1张)2、编写完善模具设计说明书(按A4打印纸装订)一、塑件材料工艺分析与设计1.塑料原料材料的分析1).硬PVC的特性PVC的特征是:是一种非结晶性材料。
管道包扎

管道包扎一、摘要家庭中的煤气管道或暖气管道以及化工厂中大量的管道在室外的部分经常需要从外部用很长的带子缠绕包扎,从而对管道加以保护。
在包扎过程中总会考虑到材料最省时需要带子的总量,以及在材料稍微多余的情况下如何包扎才能将材料全部用完的问题。
在这里,我们将建立简单的数学模型并借助数学软件MATLAB求解,利用一些参数可以算出所需最短带子的长度为50.400m,这就解决了第一个问题。
在第二个问题中,带子总长M=51.000m,由此我们算出包扎时每次重叠0.004m 就能刚好把带子用完。
二、问题已知直圆管道的长度,用缠绕的方法包扎管道,需用多长的带子?1、设管道长L = 30m , 圆管截面周长C = 50cm, 带子宽W = 30cm,则最少要用多长M的带子才能将管道缠绕包扎上?2、现有带长M=51m,计划将这条带子全部用来缠绕包扎上面的管道。
缠绕时允许带子互相重叠一部分。
应该如何包扎这个管道?(计算结果精确到0.001)三、问题的分析这是一个很实际化、很生活化的问题,但是题目给得很粗糙,在建立数学模型时为了能顺利解决问题,我们需要作出一些假设,如假设管道是直圆管、带子无弹性等。
根据生活经验,我们需要将带子斜着缠绕在管道上,于是为了使带子全部包住管道而且带子间互不重叠就必须得选择一个适当的角度,为此我们将建立一个简单的数学模型来解决这个问题。
但是,实际生活我们又会遇到这样一个问题,买来的带子通常要稍微多于实际所需要的,这时,我们就得另外建立一个模型,来考虑如何将买来的材料用完并且包扎得比较完美的问题。
四、假设1). 管道是直圆管,粗细一致;2). 带子等宽,无弹性,并且带宽要小于圆管截面周长;3). 为保持包扎过程的连续性以减少劳动量,在包扎过程中昼不将带子剪短;4).针对问题1,假设在包扎过程中带子包住管道且带子互不重叠、边缘衔接处没有空隙:5).针对问题2,假设包扎时带子每次重叠的部分相等;6).为表达更加方便,我们假设一些符号表示——W:带宽,C:截面周长, :倾斜角,W*:问题2中模型上的带宽,L:管长,M:带长五、模型的建立及求解1、问题1模型我们设想将带子已经缠绕在管道上使它包住管道且带子互不重叠、边缘衔接处没有空隙,并且从带子一角的A 点沿圆管母线的方向画一条辅助线l ,再在辅助线与带子边缘的交点处画出圆管的横截面的切口线c ,将画有辅助线的带子剪下一段展开。
钢管订购和运输数学建模论文

钢管订购和运输摘要本文建立了一个运输问题的最优化模型。
通过对图(一)的分析,我们首先直观地将路线分成两段,将图分为两个子图建立了模型一, 利用分支定界法求得总费用最优解为1279496万元。
然后对模型一进行优化,得到全线的最优模型二,求得总费用最优解为1278632万元。
通过对最优模型二的分析,我们得出钢厂S1的上限产量和钢厂S6的销价的的变化对运购计划和总费用的影响最大,并给出了数据结果。
我们利用截取和连接的方法将树形图转化成为对线性图进行分析,并给出了一般的解决方法。
对图(二)给出的具体模型,类似与问题一,分别建立了模型三和模型四,求得最优解分别为1408859.4和1403948万元.一、 问题的提出已知有7个钢厂,可生产输送天然气主管道的钢管,用S i 表示(i=1,2,…,7)。
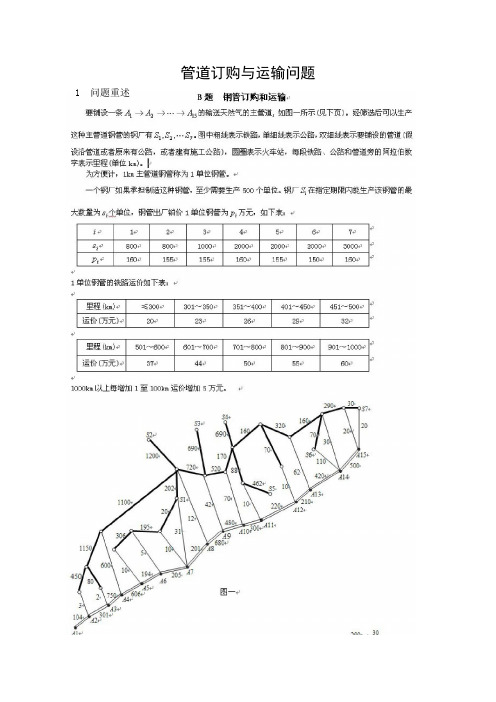
现有15个地点(A 1,A 2,…,A 15),沿着这15个地点铺设一条输送天然气的主管道。
为方便计,1km 主管道称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:i1 2 3 4 5 6 7 i s800 800 1000 2000 2000 2000 3000 i p1601551551601551501601单位钢管的铁路运价如下表:里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600 601~700 701~800 801~900 901~1000运价(万元) 37445055601000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
5.捆扎水管的学问

2014年温州市小学数学小课题评比学校:苍南县钱库小学成员姓名:蔡勤学陈耀坤邓家宝小课题题目:捆扎水管的学问指导教师:林尾维捆扎水管的学问一、问题提出前几天,我们学习了圆的周长,在数学书66页,遇到了一个题目,如图1:图1看见这个问题,我想:这不就是捆扎起来的水管的横截面吗?要计算出它们的周长,到底有没有计算的方法呢?能不能用我们的能力研究出一个简易的方法或者说一个数学公式呢?我们带着这些问题,开始了“捆扎同尺寸的多根圆形管所用绳子长度”的规律的研究。
二、研究过程首先,我们就针对遇到的那个问题进行了解决。
(一)计算2个圆: 4个圆:9个圆:图2 图3 图42×7+7π1 4×7+7π 8×7+7π=2×7+7×3.14 =4×7+7×3.14 =8×7+7×3.14=14+21.98 =28+21.98 =56+21.98=35.98(cm) =49.98(cm) =77.98(cm)这3个计算是我用最简单的方法“数线段”做的——数出线段的数量乘圆的直径加上圆的周长。
但是我们觉得这方法太简单了,所以我们决定找出一个新的计算公式。
1本文π取3.14。
经过计算,我发现图2和图3的线段数都等于它们圆的个数,可是图4的却不等,这是为什么呢? 我们反复观察、比较,终于发现中间那个圆是没有算线段的,那么,算式9-1=8(个),只有其他8个圆有算线段。
不禁,我想出了一个计算公式:绳子的长度=圆的直径×(圆的个数-绳子没有碰到的圆的个数)+圆的周长。
如果出现像图2,图3这样的,绳子没有碰到的圆的个数为0的时候,当然就不算。
这个公式三种情况可以通用。
但,是不是所有的捆扎方式都可以对应这个新的公式呢?(二)提出猜想:我们大胆得提出猜想:无论水管的捆扎方式是怎样的,绳子的长度=圆的直径×(圆的个数-绳子没有碰到的圆的个数)+圆的周长。
全国数模竞赛优秀论文钢管订购与运输的优化模型(浙江师范大学 胡国英 柯 懿 张惠锋) 精品

(1)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二(见附录一)按(1)的要求给出模型和结果。
(二)问题的分析本题要铺设一条A1~A15的天然气管道,使得总费用最小。
可以这样考虑问题:我们可以先把钢厂生产的钢管运到各个站点Ai(i≠1)再往两边运送,再计算出总的费用使之最小。
事实上我们并不知道每个站点上要运去多少货,所以设每个钢厂运往站点的数量为一变量及站点运往两边的钢管量也为变量,再通过图中已知信息相应的列出一些恒等式和约束条件。
为了使问题便于求解,我们把铁路费用及销价相应转换为公路费用(其简化的图示见附录一的图三),又因为铁路运费为一分段函数,故要对一些点之间加线使运费相当。
转换完毕后再利用赋权图的性质求出厂到站点的最短路。
(其具体数据见附录三)(三)模型的假设(1)运钢管过程中若用火车则可直接把钢管运到公路与铁路交接处,即下了火车不上火车。
(2)假设运输单位可提供足够的火车与汽车。
(3)费用计算时按照钢管数量来算,不考虑其他计费方法及因素。
(4)运费中不足整公里部分按整公里计。
(5)假设向每个钢管厂都订购钢管。
(6)设1Km主管道钢管为1单位钢管。
(7)路中铺设的钢管只允许由其相邻站点提供。
(8)不计各个环节中的装卸费用。
(四)符号说明Si: 表示生产钢管的钢厂(i=1,2…7)。
Ai:表示暂存钢管的站点。
(i=1,2…15)X1,+kk 与X1,-kk:分别表示Ak运往A1+k方向的钢管的数量和Ak运往A1-k方向的钢管的数量。
(其中K=2,3…15 X21=104, X16,15=0)Bk :表示存放在Ak处的钢管数量(k=2,3…15).Yij : 表示从Si->Aj所运的钢管数量。
F(Xij ,Yij): 表示总的费用。
(单位:万元)△Pi :表示钢管销价的变化量。
(五)模型的建立与求解题Ⅰ:为了使问题简化,我们可采取如下原则:(1)总费用公路化原则:就是将铁路运费及钢管销价恰当的转换为公路运费。
数学建模论文 打井铺设管道的优化问题
打井铺设管道的优化问题一、提出问题政府打算着手帮助该村解决用水难的问题。
从两方面考虑,一是地质专家经过勘察,在该村附近又找到了8个可供打井的位置,它们的地质构造不同,因而每个位置打井的费用和预计的年产水量也不同,详见表2,而且预计每口水井的年产水量还会以平均每年10%左右的速率减少。
二是从长远考虑,可以通过铺设管道的办法从相隔20公里外的地方把河水引入该村。
铺设管道的费用为P0.51.0(万元),其中Q表示每年的可供水量(万吨/年),L表示管道L66Q长度(公里)。
铺设管道从开工到完成需要三年时间,且每年投资铺设管道的费用为万元的整数倍。
要求完成之后,每年能够通过管道至少提供100万吨水。
政府从2012开始,连续三年,每年最多可提供60万元用于该村打井和铺设管道,为了保证该村从2012至2016这五年间每年分别能至少获得150、160、170、180、190万吨水,请作出一个从2012起三年的打井和铺设管道计划,以使整个计划的总开支尽量节省(不考虑小蓄水池的作用和利息的因素在内)。
表1 现有各水井在近几年的产水量(万吨)二、分析问题题中要求制定一个总费用(决策目标)最小的抗旱(打井,铺设管道)方案,属于优化问题,并且使得该村从2012至2016这五年间每年分别能至少获得150、160、170、180、190万吨水,每年费用不超过60万元。
(此两点为主要约束条件)其他的约束条件有:a.每口井只能在2012开始,连续三年中的其中一年施工b.铺设管道费用为万元整数倍c.由于河位于与该村相隔20公里外的地方,所以管道总长度不小于20公里d.铺设管道需要3年时间,故前3年管道供水量为0,而第4,5年供水量不小于100万吨。
故此模型即为基于以上约束条件的整数规划(最优决策目标)问题。
三、模型假设a.忽略小蓄水池的作用和利息因素b.不考虑意外情况导致所需经费增加c.假设井在年初修建且时间很短,修完之后即可利用,管道铺好后即可用于供水d.假设这五年之内村民需水量基本稳定e.假设井供水量呈稳定规律变化,不考虑其他因素对产水量的影响f.从长远利益考虑,打井和铺设管道两个方案应同时协调进行四、符号说明X ij 0—1变量,表示第i号井在第j年的施工情况,X ij=1第i号井在第j年0表示不施工施工,Xij=Z j 第j年的总费用P j 第j年的铺管道费用L j 第j 年铺管道公里数W j 第j 年的水量Q 管道供水量N j 所有新建的水井在第j年的产水量五、模型建立决策变量为三年间铺设管道和打井的总费用。
布条缠绕圆形管道的问题

布条缠绕圆形管道的问题数学与统计学院2006级5班邓璎函 222006314011216摘要这篇论文通过确定重合点,在已知布条宽度和圆形管道直径的情况下,运用一些简单的几何知识解决了布条与管道轴线的夹角问题。
同时,从管道表面积和布条面积相等的角度,在已知管道长度的情况下,求出了布条的长度。
同时也考虑到了布条两端的影响。
此外,分两种情况考虑了其他形状的管道的布条缠绕问题:布条紧贴于管道缠绕和布条不紧贴贴于管道缠绕。
关键词:重合点表面积紧贴一、问题重述用已知宽度的布条缠绕已知直径的圆形管道,布条应紧密排在一起且不能重叠,求布条与管道轴线的夹角。
此外,在已知管道长度的情况下,还要求出所需布条的长度。
二、模型假设1.布条的厚度可忽略不计,即不会影响结果。
2.布条缠绕在管道上不重叠时可以完全紧密地排在一起。
3.布条是完全没有弹性的。
三、符号说明四、模型建立与求解模型一:夹角α的模型不妨将管道表面展开如图1,黄色部分为缠绕的布条。
由于要求布条完全缠绕于管道上且不重叠,那么A 、B 应该在管道上重合。
则cos d παω=故arccos d ωαπ=模型二:布条长度L 的模型由于布条是完全缠绕于管道上的,且没有重叠,可以从管道表面积和布条面积相等来考虑。
0S dh π=S l ω=且 0S S =,即dh l πω=也即dhl πω=但由于布条两端都成πα-弧度,会有所浪费,因此也考虑两端的影响,即多加上图中AC 段的长度。
sin AC l d πα==故 所需布条长度为AC dhL l l πω=+=+图 1五、模型评价模型在理论上应该是很准确的,但事实上,布条不可能如想象中那样紧密排列,而且布条的厚度也并不是可以忽略不计的。
这些均是影响结果的因素。
六、模型优化优化一:布条厚度的考虑既然布条厚度为一个影响结果的因素,不妨考虑一下布条的厚度。
设布条厚度为k ,圆形管道的横截面如图2。
布条上表面伸展,下表面收缩,中间的长度不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
管道包扎问题的数学模型论文管道包扎问题的数学模型摘要: 本篇论文讨论管道的包扎问题.是一个三维空间的问题我采用剪切的方法把空间问题转化为平面问题建立刚好全部包扎所用带子最短模型和管道包扎出现接缝处重叠模型然后利用数学软件Matlab 求解.在图1 中,求得最短带子包扎的通用表达式并代入题目给出的数据得到第一个问题的最短长度为50.4 米。
在图2 和图3 中,采用近似的处理方法求出管道包扎接缝处重叠带子宽度的表达式代入第二个问题的数据得到带子的重叠宽度为0.004 米.论文的最后对临界角0 和截面是正多边形的管道的情况作进一步的讨论并得到更一般的模型.关键词: 临界角临界点临界长度等量关系1 问题的提出用宽度为0.3m 的带子缠绕包扎圆柱型管道,管道长30m,截面周长为0.5m. 1 如果用带子全部包住管道,最少要用多长的带子,请你给出计算这个最小长度的公式,并且依次计算出所需长度数值. 2 现有一条长度为51m 的带子,想将这条带子全部用于缠绕包扎这个管道,可以使带子的接缝处重叠瘩接.请你给出用这条带子缠绕包扎这个管道的方案.(计算结果精确到0.001m)3 如果管道截面是正三边形正四边形或边数更多的正多边形.2 问题的分析生活的经验告诉我们在包扎圆形管道的过程中如果开始包扎时带子边缘所在的直线与管道母线的夹角过小就可能出现不能把管道全部包扎的现象如果夹角过大就可能出现包扎带子在接缝处重叠的现象. 所以随着夹角的增大总会出现在接缝处恰好接合而没有重叠的情况.这种特殊的情况就是第一问的求解问题称此时包扎带子的长度为临界长度带子边缘所在的直线与管道母线的夹角为临界角管道任一端的带子截口所在边与管道截面的交点称为临界点.如果给定一段带子的长度大于临界长度则总能找到一种包扎方案使得整条带子全都包扎完其中接缝处有重叠. 当管道的截面为正多边形时我们把正多边形的直棱柱管道看作圆形管道的变形来处理即正多边形的直棱柱管道的平面展开图与圆形管道的平面展开图是同样的.3 模型的假设1 管道没有厚度即把管道剪开图看成平面不考虑空间结构2 管道是刚性物体带子也不具备弹性 3 管道截面是圆形或正多边形整条管道粗细均匀 4 包扎过程中带子的宽度不变,带子也不能切断 5 带子没有厚度且两端截口垂直于它的边.即把带子看成一个长方形不考虑空间结构4 符号的约定1)a -----带子的宽度2)b -----管道的长度;3 c -----管道截面的周长4)l ----- 带子的长度5 θ--- 带子截口所在的直线与管道母线的夹角 6 S1 ----- 直角三角形AED 的面积7 S 2 ----- 直角三角形OBF 的面积8 S 3 ---- 四边形COHG 的面积9 x ---- 带子重叠部分的宽度10 y --- 重叠部分的带子长度11 m---- 截面正多边形的边长12 n ---- 截面正多边形的边数.5 模型的建立和求解5.1 刚好全部包扎所用带子最短模型经过临界点沿着管道的母线切开得到矩形ABCD如下图1: 图1 其中矩形ABCD 为管道的侧面展开图三角形AED 为直角三角形四边形OHGC.定理1 直角三角形AED 的面积等于直角三角形OBF 和四边形OHGC 之和. 证明线段BF 和线段CG在空间图形中是重合的故这两线段相等. 把直角三角形OBF 向右移动使BF 与CG 重合则构成直角三角形O HO . 又EDOH OBOCAD 故AED O HO 即定理成立.推论1 沿着管道任一母线剪开得到的平面展开图中管道截面界线的两端分别能组成两个直角三角形且这两个直角三角形的面积相等.由上面的定理 1 和推论可以得出刚好包扎管道所用带子最短的模型: al S1 S 2 S 3 bc 1 S1 a c a 2 2 2 S1 S 2 S 3 求得一般表达式为: bc l c2 a2 a把题目中给出的数据代入一般表达式求得第一问题的临界长度为: 30 0.5 l 0 .5 2 0 .3 2 50.4 米0 .35.2 管道包扎出现接缝处重叠的模型按图1的剪开方法得到管道平面展开图如图2: 图2 其中阴影为带子重叠部分. 命题1 在带子宽度不变的条件下带子相接处重叠的宽度一定相等即图 2 中阴影部分的平行四边形的宽度不改变.5.2.1 求阴影部分的带子的长度. 命题 2 阴影部分的长度比整条包扎带子的长度短线段AE 的长度. 证明由推论 2 阴影部分的宽度相等故可以过图2 的 A 点垂直AE 剪切再把剪切的左边部分图形补到右边如下图3: 图3由图3 可以看出y l AE l c cos5.2.2 利用阴影部分的面积相等得到模型: xy al bc a x c 2 a x 2 y l c cos c 2 a x 2 cos c化简此方程组得: 2 x a c 2 a x 2 xl al bc 0 1利用Matlab 解方程1得到的结果过繁所以为了得到一个比较简单而又接近实际的答案我们作以下处理: 在生活和工作中为了节省材料包扎管道的带子一般不会比临界长度长太多所以可用 c 2 a 2 近似代替c 2 a x 2 求得结果为: a c 2 a 2 bc al x 2 2 c2 a2 l 把第二问题的数据代入方程1得: x 1 0.00357把第二问题的数据代入方程2得: x 2 0.0036由以上计算得到的结果可以看出当带子的长度不太长时用 a c 2 a 2 bc al x 2 c2 a2 l代替这个模型的结果是可以的.且取得第二问题的结果为: x0.004米5.3 截面为正多边形的直棱柱管道模型推理1 对于任何正多边直棱柱的包扎面从临界点沿棱柱的母线剪开得到的剪开平面如图 1 所示包扎方案为临界时如果有带子重合的情形如图 2.类似以上图 1 圆柱管道包扎方案的方法建立模型如下: 5.3.1 包扎正多边直棱柱的临界模型: al S1 S 2 S 3 bmn 1 S1 a mn a 2 2 2 S1 S 2 S 3 解得: mnb l mn 2 a 2 a 5.3.1 包扎正多边直棱柱的有重叠的模型: xy al mnb a x mn 2 a x 2 y l mn cos mn 2 a x 2 cos mn 以mn 2 a 2 代替mn 2 a x 2 解得a mn 2 a 2 mnb al x 2 mn 2 a 2 l6 模型的分析6.1 临界角的讨论 a 临界角0 arcsin 3 c 6.1.1 当0 时带子不能全部包扎整条管道.如果要在角增大即临界角增大的情况下实现全部包扎由3 式可以看出应加大带子的宽度或减小管道截面的周长. 6.1.2 当0 时带子在包扎过程中出现接缝处重叠.如果要在角减小即临界角减小的情况下实现全部包扎由3 式可以看出应减小带子的宽度或增加管道截面的周长.故有以下推理:推理 2 包扎管道的临界角0 随带子宽度的增大而增大管道截面周长的减小而增大随带子宽度的减小而减小管道截面周长的增大而减小.6.2 管道的讨论由推论1、命题1 和推理1可知无论求解模型是圆柱模型或是截面为正多边形的直棱柱其求解过程都是相同的故有以下推理.推理3 管道的包扎方案与管道截面是凸多边形不限边数不限每边的长度或连续的凸封闭曲线无关只与管道截面的周长C、管道长度l 和给定的带子的长度有关.参考文献:1 吕林根. 解析几何〔M〕. 北京:高等教育出版社,2000.2 刘来福. 数学模型与数学建模〔M 北京:北京师范大学出版社20023.姜启源等编.《数学模型》(第三版).北京:高等教育出版社.2003. 》4.姜启源等编.《数学模型(第三版)习题参考解答. 北京:高等教育出版社.2003.5.刘来福,曾文艺.数学模型与数学建模.北京:北京师范大学出版社,19976.杨启帆,边馥萍.数学模型.杭州:浙江大学出版社,19907.叶其孝.中学数学建模M.长沙:湖南出版社.1998.9-108.冯跃峰.对数学教育若干问题的认识J.数学教育学报.1992(1):64-659.卜月华.中学数学建模教与学M.东南大学出版社,2002,310.荆新大.足球中的数学J.数学教学,1993(3)11.廖运章.强调数学理解建模灵活开放.数学通报,2000,12 The study of pipeline bind up’s problem YE Feiwu(Department of mathematics 2000 grade Class Shaoguan College Shaoguan512005Guangdong)Abstract: we will discuss the bind up problems of pipeline in this paper. This problem is athree- figure problem. We can cut the pipeline open and change these plane problems intothree-figure problems. We set up the best of all shot model which use band shot of all and happen tobind up the pipeline entirely and set up the repeated model of which the joint locate appear repeatedthen take the mathematics software to work out the problem. In the fig1 we work out the currencyexpression of best of all bands and make use of the data of subject and gained the answer of thefirst problem is 50.4 meter. In the fig2 and fig3 adopt approximate method to seek out theexpression of the band’s width superposed and make use of the data of subject and gained theanswer of the second problem is 0.004 meter. At the end of the paper we will discuss the critical angle 0 and pipeline of which section ispositive polygon and gained the even more model.Key words: critical angle critical point critical length grade measure relation。
