史上详细的平面曲线的弧长公式计算微积分
弧长的计算公式

弧长的计算公式
弧长的计算公式
弧长计算公式是一个数学公式,为L=n×π×r/180,L=α×r。
其中n是圆心角度数(角度制),r是半径,L是圆心角弧长,α是圆心角度数(弧度制)。
曲线的弧长也称曲线的长度,是曲线的特征之一。
不是所有的曲线都能定义长度,能够定义长度的曲线称为可求长曲线。
扇形面积公式
一条弧和经过这条弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形),它是由圆周的一部分与它所对应的圆心角围成。
S扇=LR/2(L为扇形弧长,R为半径)或π(R^2)*N/360(即扇形的度数)
扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2.
如果其顶角采用弧度单位,则可简化为1/2×弧长×(半径)。
扇形还与三角形有相似之处,上述简化的面积公式亦可看成:1/2×弧长×(半径),与三角形面积:1/2×底×高相似。
史上最详细的平面曲线的弧长公式计算(微积分)

•பைடு நூலகம்
A M0
•Mn1
•
B Mn
MnB,依次用弦将 O
x
相邻两点联结起来, 得到一条内接折线. 记每条弦
的长度为 |M i 1 M i|i , 1 , 2 , ,n ,令 m 1 i n|M ai 1 x M i|.
如果当分点无限增加, 且 0时 ,折线长度的极限
n
lim |
0 i1
Mi1Mi |存在 ,则称此极限为曲线弧
弧长元素为 ds(dx)2(dy)2 r2()r2()d
弧长 s r 2( ) r2( )d .
史上最详细的平面曲线的弧长公式计算(微
9
积分)
7.4 平面曲线的弧长
s r 2( ) r2( )d
例
求极坐标系下曲线
r
asin
3
的长.
3
(a0)(03π)
解
s
r2()r2()d
等于椭圆 y x c1o tas2sitn (0t2π)的周长.
证 设正弦线的弧长等于s1 对称性
π
s120
1y2dx2π 0
1a2co2xsdx
设椭圆的周长为s2
π
s220
(x)2(y)2dt2π 0
(st)i2 n(1a2)(c t)2d o t s
π
2
1a2co2td st
0
π
2
o ax xdxb x
任取小区间 [x,xdx],以对应小切线段的长代替小
弧段的长, 小切线段的长为:
(dx)2 (dy)2 1 y2dx
弧长元素 ds 1 y2dx, 弧长 s b
(弧微分)
a
史上最详细的平面曲线的弧长公式计算(微
高等数学(上)02-62.2 平面曲线的弧长

定义:若在弧痂上任意作内接折线,当折线段的最大 边
长人一0时,折线的长度趋向于一个确定的极限,则称 此极限为曲线弧分的弧长,即
n
"姓財Ml
i=l
并称此曲线弧为可求长的.
/ B=Mn A=Mo
定理:任意光滑曲线孤都是可求长的. (证明略)
若 (p(t), 屮 Q) 连 续
可导,且[。'(。]2+ [“0)]2。0, 则曲线C : {二*)E["]为光滑 曲线; 当/(X)连续可2
因此所求弧长
S=
(6>) + /2(6>) 60
例7.求连续曲线段 "L应如d,的孤长. 解:
•/ cosx> 0, /. s=E
2
<x<^
‘2 dx
二2』2 + (Vcosx)2 dx
例8.计算摆线
x = a(t-smt)(口>0)一 拱(0M〈2m) y = a(l- cos t)
的弧长.
y\
rr2(6>) d<9
= ^a1O2+a1
=oJl + "2 dO :.s = a[2\ll + 02d0 (P349 公式 39)
Jo?Jl + din<9 + Jl + 屮 I2来自22/rI
0
=。兀』1 + 4兀2 + ;m(27T + J]+ 4/ )
(1)曲线弧由直角坐标方程给出:
y = f(x) {a<x<b)
孤长元素(弧微分):
ds = J(dx)2 +(dy)2
y
弧微分的计算

弧微分的计算以弧微分的计算为标题,本文将介绍弧微分的概念、计算方法以及应用。
弧微分是微积分中的重要概念之一,它可以用于描述曲线的性质和计算曲线上的各种量。
通过了解弧微分的概念和计算方法,我们能更好地理解和应用微积分的知识。
让我们来了解一下弧微分的概念。
在平面直角坐标系中,我们可以用方程 y = f(x) 来表示曲线。
曲线上的每一个点都有唯一的坐标 (x, y)。
假设我们从曲线上的一个点 P1(x1, y1) 移动到另一个点 P2(x2, y2),这两个点之间的直线距离称为弧长。
而弧微分就是描述这个弧长的微小变化。
弧微分的计算可以通过微积分中的导数来实现。
我们可以将曲线上的每一个点都看作一个参数 t 的函数,即 x = x(t) 和 y = y(t),其中 t 是参数。
对于曲线上的任意两个点 P1(x1, y1) 和 P2(x2, y2),我们可以将弧长表示为:s = ∫√(dx² + dy²)其中,dx 和 dy 分别表示 x 和 y 的微小变化。
根据导数的定义,我们可以得到:dx = x'(t)dtdy = y'(t)dt将 dx 和 dy 代入弧长的公式中,我们可以得到:s = ∫√(x'(t)²dt² + y'(t)²dt²)化简上式,我们可以得到:s = ∫√(x'(t)² + y'(t)²)dt这个公式描述了弧长和参数t 的关系,可以用来计算曲线上的弧长。
接下来,让我们看一下弧微分的计算方法。
根据弧微分的定义,我们可以得到:ds = √(dx² + dy²)将 dx 和 dy 代入上式中,我们可以得到:ds = √(x'(t)²dt² + y'(t)²dt²)化简上式,我们可以得到:ds = √(x'(t)² + y'(t)²)dt这个公式描述了弧微分和参数 t 的关系,可以用来计算弧微分。
《微积分》第八节 平面曲线的弧长
小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b]上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
作业
P236习题3_8 1(单),2(2),3,4(2), 5,7(1、4),8,10(单)
三、平面曲线的弧长
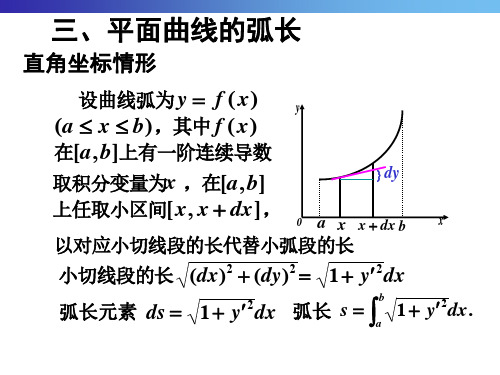
直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a, b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
曲线弧为 ( ) ( )
其中 ( ) 在[ , ]上具有连续导数.
x y
( (
)cos )sin
( )
dx [()cos ()sin]d,
dy [()sin ()cos]d,
ds (dx)2 (dy)2 2( ) 2( )d,
弧长
s
2( ) 2( )d .
例5
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
解
r
3a
sin
3
2
cos
3
1 3
a sin
2
cos
,
3 3
s
r 2( ) r2( )d
3 0
a2
sin
3
牛顿-莱布尼茨公式计算曲线的弧长

牛顿-莱布尼茨公式是微积分中一个非常重要的公式,它可以用来计算曲线的弧长。
在学习微积分的过程中,我们经常会遇到需要计算曲线弧长的情况,而牛顿-莱布尼茨公式提供了一个非常便捷和有效的方法。
让我们来看一下牛顿-莱布尼茨公式的表达式:\[ L = \int_{a}^{b} \sqrt{1 + (f'(x))^2} dx \]这里,\( L \)代表曲线的弧长,\( f(x) \)代表曲线的函数,\( f'(x) \)代表函数的导数。
公式的核心是利用积分来求曲线的弧长,通过对曲线的微小线段进行求和,从而得到整条曲线的长度。
接下来,让我们以一条简单的曲线\( y = x^2 \)为例来演示牛顿-莱布尼茨公式的计算过程。
我们假设要计算曲线在区间[0, 1]上的弧长。
第一步,我们需要求出函数\( y = x^2 \)的导数\( f'(x) \),即\( 2x \)。
我们将\( f'(x) \)带入到公式中,得到:\[ L = \int_{0}^{1} \sqrt{1 + (2x)^2} dx \]接下来,我们可以利用定积分的性质来求解这个积分。
通过简单的换元和分部积分,我们最终可以得到曲线\( y = x^2 \)在区间[0, 1]上的弧长为\( \frac{\sqrt{5} + \ln(2 + \sqrt{5})}{4} \)。
这个结果非常直观地展现了牛顿-莱布尼茨公式的应用。
不仅如此,牛顿-莱布尼茨公式还可以应用于更加复杂的曲线和函数。
无论是求解圆的弧长、椭圆的弧长,还是一些特殊函数的弧长,牛顿-莱布尼茨公式都能够提供一个通用的计算方法。
牛顿-莱布尼茨公式是微积分中非常重要的一个公式,它可以有效地计算曲线的弧长。
通过对曲线的微小线段进行求和,利用积分来得到整条曲线的长度,这个公式为我们提供了一个非常便捷和实用的工具。
在实际应用中,只要我们掌握了牛顿-莱布尼茨公式的计算方法,并灵活运用积分的性质,就可以轻松地解决曲线弧长的计算问题。
弧长 计算公式

弧长计算公式在圆周长上的任意一段弧的长度叫做弧长。
有优弧劣弧之分。
弧长公式:n是圆心角度数,r是半径,a是圆心角弧度。
公式l = n(圆心角)x π(圆周率)x r(半径)/180在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°。
例:半径为1cm,45°的圆心角所对的弧长为l=nπR/180=45×π×1/180=45×3.14×1/180约等于0.785(cm)拓展扇形面积公式:S(扇形面积)=n(圆心角度数)x π(圆周率)x r²【半径的平方(2次方)】/360如果已知他的沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平,就得到圆锥的平面展开图。
它是由一个半径为圆锥体的母线长,弧长等于圆锥体底面圆的周长的扇形和一个圆组成的,这个扇形又叫圆锥的侧面展开图。
补充公式S扇=nπr*2/360=πrnr/360=2πrn/360×1/2r=πrn/180×1/2r所以:S扇=rL/2还可以是S扇=n/360πr²(n为圆心角的度数,L为该扇形对应的弧长。
)圆锥的表面积=圆锥的侧面积+底面圆的面积其中:圆锥体的侧面积=πRL圆锥体的全面积=πRl+πR2π为圆周率≈3.14R为圆锥体底面圆的半径L为圆锥的母线长我们把连接圆锥顶点和底面圆周上任意一点的线段叫作圆锥的母线(注意:不是圆锥的高)是展开扇形的边长n圆锥圆心角=r/l*360 360r/l弧长=圆周长侧面展开图的圆心角求法:n=360r/R=πRr或2πr=nπr/180 n=360r/R 。
如果题目中有切线,经常用的辅助线是链接圆心和切点的半径,得到直角,再用相关知识解题。
扇形的面积扇形是与圆形有关的一种重要图形,其面积与圆心角(顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为n/360*πr^2。
史上最详细的平面曲线的弧长公式计算(微积分)

1 r 3a sin cos a sin cos 3 3 3 3 3
2
10
2
7.4 平面曲线的弧长
例 求阿基米德螺线 r a (a 0)上相应于
从 0到2 π的弧长.
解
o
2π
2πa
x
s
r 2 ( ) r 2 ( )d
a a d a 0
2 2 2
2π
0
2 1d
a [2 π 1 4 π 2 ln( 2 π 1 4 π 2 )]. 2
x x a dx 2
2 2
a x a ln | x x 2 a 2 | C 2
2 2
11
2
7.4 平面曲线的弧长
s
r 2 ( ) r 2 ( )d
3
解 s
r 2 ( ) r 2 ( )d
6 4 2 2
2 a sin a sin cos d 0 3 3 3 2 3π 3 a sin d πa . 0 2 3
s1 2
s2 2
π
π
0
2 2 2 1 a cos xdx 1 y dx 0
2
π
设椭圆的周长为s2
2
0 π
2 2 2 ( x) ( y) dt 20 (sin t ) (1 a )(cos t ) dt
2
2
π
2
0 π
1 a cos tdt
2 2
0
1 a cos xdx s1 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ds (dx)2 (dy)2 2(t) 2(t)dt
弧长 s 2(t) 2(t)dt. 6
7.4 平面曲线的弧长
s 2(t ) 2(t )dt
例 求星形线 x2 3 y2 3 a2 3(a 0)的全长.
x a cos3 t
解
星形线的参数方程为
弧段的长, 小切线段的长为:
(dx)2 (dy)2 1 y2dx
弧长元素 ds 1 y2 dx, 弧长 s b 1 y2 dx.
(弧微分)
a
3
7.4 平面曲线的弧长
(chx) shx
chxdx shx C
s
b a
1 y2 dx
例 悬链线方程 y a (ex a e x a ) ach x
例 计算曲线 y nn 0
sin d 的弧长 (0 x nπ).
解 y n sin x 1 sin x ,
nn
n
s nπ 0
1 sin x dx nx0π n0πt
n dx ndt
π
0
1 sint ndt
π
n 0
sin
t 2
2
cos
t 2
2
2
sin
t 2
cos
t 2
r( r(
) cos ) s in
(
)
为参数的 参数方程
弧长元素为 ds (dx)2 (dy)2 r2( ) r2( )d
弧长 s r 2( ) r2( )d . 9
7.4 平面曲线的弧长
s r 2( ) r2( )d
例
求极坐标系下曲线
r
a sin
3
的长.
3
(a 0) (0 3π)
y
a
sin
3
t
(0 t 2π)
对称性
y
s 4s1 第一象限部分的弧长
π
4 2 ( x)2 ( y)2 dt 0 π
a
aa
O
x
a
4 2 3a sin t cos tdt 0
6a.
7
7.4 平面曲线的弧长
例 证明正弦线 y asin x (0 x 2π) 的弧长
等于椭圆
x y
•
B Mn
Mn B,依次用弦将 O
x
相邻两点联结起来, 得到一条内接折线. 记每条弦
的长度为
|
M i 1 M i
|,
i
1,2,
, n, 令
max |
1in
M i 1 M i
|.
如果当分点无限增加, 且 0时,折线长度的极限
n
lim
0
|
i 1
M i 1 M i
|
存在,
则称此极限为曲线弧
AB的
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
12
7.4 平面曲线的弧长
思考题
闭区间[a, b]上的连续曲线 y = f (x)是否
一定可求长?
解答
不一定. 仅仅有曲线连续还不够, 必须保证曲线光滑才可求长.
13
弧长(长度). 光滑曲线弧是可求长.
2
7.4 平面曲线的弧长
二、直角坐标情形
设曲线弧为y = f (x)
y
y f (x)
(a x b), 其中f (x)在
[a, b]上有一阶连续导数.
现在计算这曲线弧的长度.
取积分变量为x, 在[a, b]上
dy dx
o a x x dx b x
任取小区间 [x, x dx], 以对应小切线段的长代替小
dt
n π sin t cos t dt 4n.
0 2
2
5
7.4 平面曲线的弧长
三、参数方程情形
曲线弧为
x
y
(t), (t)
(
t
)
其中 (t), (t) 在[a, b]上具有连续导数.
现在计算这曲线弧的长度.
取参数t为积分变量, 其变化区间为 [ , ].
对应于 [ , ]上任一小区间 [t,t dt]的小弧段的
2
a
计算介于 x b与x b之间一段弧长度.
解 y ach x , y sh x
y
a
a
a
1 ( y)2
1 sh x 2 a
ch x a
b O
bx
所求弧长为
s
b
ch
x
dx
2
b
ch
xdx
2ash
x
b
2ash
b
.
b a
0a
a0
a
4
7.4 平面曲线的弧长
x
s b 1 y2 dx a
π
2
1 a2 cos2 tdt
0
2 π 1 a2 cos2 xdx s1. 0
8
7.4 平面曲线的弧长
四、极坐标情形
曲线弧为 r r( ) ( )
其中r( )在[ , ]上具有连续导数. 现在计算这曲线弧的长度. 由直角坐标与极坐标的关系:
x
y
r cos r sin
x y
解
s r 2( ) r2( )d
2πa
o
x
2π
2π
a2 2 a2d a
2 1d
0
0
a [2π 1 4π2 ln( 2π 1 4π2 )]. 2
x2 a2dx x x2 a2 a2 ln | x x2 a2 | C
2
2
11
7.4 平面曲线的弧长
四、小结
平面曲线弧长的概念
7.4 平面曲线的弧长
7.4 平面曲线的弧长
弧长的概念 直角坐标情形 参数方程情形 极坐标情形 小结 思考题 作业
7.4 平面曲线的弧长
一、平面曲线弧长的概念
设A、B是曲线 y
Mi
•
弧上的两个端点, 在
M2• M1•
弧上插入分点 A M0 ,
M1, , Mi , , Mn1,
•
A M0
• Mn1
cos t 1 a2 sin t
(0
t
2π) 的周长.
证 设正弦线的弧长等于s1 对称性
π
s1 2 0
1 y2dx 2 π 0
1 a2 cos2 xdx
设椭圆的周长为s2
π
s2 2 0
( x)2 ( y)2dt 2 π 0
(sin t)2 (1 a2 )(cost)2dt
解 s r 2( ) r2( )d
3π 0
a2
sin
3
6
a2sinຫໍສະໝຸດ 34 cos
3
2
d
a 3π sin 2d 3 πa.
0 3
2
r
3a
sin
3
2
cos
3
1 3
a sin
2
3
cos
3
10
7.4 平面曲线的弧长
例 求阿基米德螺线 r a (a 0)上相应于
从0到2π的弧长.
