数学建模-黄灯亮多久
交通灯控制系统中黄灯时间的确定

( 重庆工学院 ,重庆 400050)
Ξ
摘要 : 介绍了电灯的由来 ,探讨了黄灯时间的长短对交通安全正负两方面的影 , 在应用力学和运 动学原理的基础上 ,提出了一种计算黄灯时间的模型 . 分析了模型建立的全部过程 , 最后列出了 黄灯时间的求解公式 . 关 键 词 :黄灯时间 ; 交通控制系统 ; 运动学 中图分类号 :U121 文献标识码 :A 文章编号 :1671 - 0924 (2008) 04 - 0154 - 03
离为 x .
2) 十字路口处同一条路上 2 条停车线之间的
距离为 H.
3) 典型的车辆车身长为 L , 车辆总质量 ( 包括
车身和载重) 为 W .
4) 在刹车时 , 车辆与地面的摩擦系数为 f . 5) 每次黄灯亮的时间为 T. 3. 2 模型假设
通过前面的分析和对问题所涉及的主要量的 确定 , 给出黄灯时间求解模型假设 [ 1 ] :
[3 ] 郑积仕 ,汤志康 . 一种基于模糊神经网络的城市道路
有 代入式 ( 4) , 得 :
t 1 = v0 / ( f g ) v0 x ( t1) = D a = 2f g
交叉口可变相序控制 [J ] . 重庆工学院学报 ,2006 ,20
(5) :143 - 147.
( 9)
将式 ( 2) 和式 ( 9) 代入式 ( 1) , 得黄灯亮的时间
- fW = W d2 x ・ 2 g dt = v0 ( 4)
4 结束语
美国公路安全保险公司的发言人理克德・ 雷 廷表示 ,部分司机在钻黄灯和红灯之间的空子 , 因 此确立黄灯亮的时间实际上是在维护红灯的尊 严 . 同时他又认为 ,增加亮黄灯的时间虽然有一些 好处 ,但他的研究小组发现 , 缩短黄灯时间对习惯 闯红灯的人其实是一个威慑 . 其实 , 保证交通安全 的关键还是所有驾驶员都按正规的操作规范和交 通信号指示来驾驶车辆 [2 - 3 ] .
数学建模-红绿灯问题

红绿灯优化问题摘要红绿灯(交通信号灯)系以规定之时间上交互更迭之光色讯号,设置于交岔路口或其他特殊地点,用以将道路通行权指定给车辆驾驶人与行人,管制其行止及转向之交通管制设施。
为一由电力运转之交通管制设施,以红、黄、绿三色灯号或辅以音响,指示车辆及行人停止、注意与行进,设于交岔路口或其他必地点。
有些红绿灯在设计的时候,由于考虑不周全,环境的发展变化,出现了一系列问题,使得不能真正的方便于人。
为了使红绿灯能真正的方便于人,本文建模过程根据实际情况,考虑诸如道路车辆行驶速度、行人行走速度、车流量、人流量、路段宽度等相关问题,对这些因素进行了数据收集,利用数学方法对其进行了分析,得出了各个影响红绿灯变化的规律及其拟合方程。
一、问题重述灯是用以将道路通行权指定给车辆驾驶人与行人,管制其行止及其转向之交通管制设施,红绿灯灯亮的时间长短问题影响了车辆和行人的通行。
如控制方案不佳,会导致行人和车辆通行的不便,怎样设置才能使红绿灯时间达到最佳。
在日常生活中我们知道红绿灯的表示如下:(一)绿灯亮时,准许车辆通行,但转弯的车辆不得妨碍被放行的直行车辆、行人通行;(二)黄灯亮时,已越过停止线的车辆可以继续通行;(三)红灯亮时,禁止车辆通行。
根据其工作原理我们可以知道,在红绿灯前首先司机会看到黄灯,黄灯亮后变成红灯,红灯亮后,没有通过停止线的车辆则要停止,行人此时过马路。
此后再变绿灯,以此循环。
但由于变化的规律性,地域的差异,红绿灯时间很难达到最佳。
红绿灯时间差的决定因素大体可以归为两个:车流量和人流量。
第一个因素车流量会因为地域经济发展程度而决定。
所谓的地域经济发展程度会影响该地域人们的经济,人们的经济条件则决定车的总量。
第二个因素人流量的主要影响条件也是地域经济发展程度,所以我们把总因素,即红绿灯的时间差因素归纳为地域经济发展因素的影响。
根据路口设置信号灯的交通流量标准表,下表所示:根据路口设置信号灯的交通流量标准表,下表所示:二、模型的建设1、假设公路路面行驶顺畅,所以车辆设为质点,车距相等;2、假设司机的反应时间相同;3、假设车辆离红绿灯较远的速度和离开红绿灯后的速度相等。
十字路口黄灯时间及困境区域的数学模型研究

辆 通行 , 但转 弯 的车 辆 不 得妨 碍被 放 行 的直 行 车 辆 、 人 通行 . 行 黄灯 亮 时 , 已越 过 停 止线 的车辆 可
以继续 通 行 . 灯 亮 时 , 止 车 辆 通 行 . l 近 几 红 禁 ”1
黄 灯 时 间确定 ห้องสมุดไป่ตู้数 学模 型
1 1 保守 黄灯 时间 的数学模 型 阳 .
Vo . 5 No 5 13 .
0C .2 1 t 01
十 字路 口黄 灯 时 间及 困境 区域 的数 学模 型研 究
王 秀 良 乔 木
( 国人 民公 安 大 学 理 科 基 础 部 中 北 京 10 3 ) 0 08
摘 要 : 市 交 通 十 字 路 口是 冲 突 交 通 流 汇 聚 的 节 点 , 全 问题 十分 突 出 , 城 安 黄灯 在 交 通 信 号 系 统 中起
1 =。 、 警
【 ( 一 z ) o o
一 一
对式 ( ) 1 积分 , 初始 条件 ( ) 将 2 代人 , 得
d x
ft- g 4
L/ m
’
—
1 .0
3 .5
—1 1 / S
15 .
4. 0
2. 0
4. 5
2. 5
5. 0
当汽 车在 停 车线前 停 止时 , 由式 ( ) 4 得
0 引
言
该 亮多 长时 间才能 使停 车线 附近 的车辆 安全顺 利 地 通过 路 口呢?本 文建 立 了一个有 效黄 灯时 间 的 数 学模 型 , 在城 市 道 路 十 字路 口黄 灯 时 间确 定 并 为 4S的情况 下 , 析车辆 的安全 停 车距离 . 分
20 0 4年颁 布 的《 中华 人 民共 和 国道 路 交通 安 全 法实施 条 例 》 3 第 8条规 定 , 绿 灯亮 时 , 许 车 “ 准
数学建模-黄灯亮多久
v0
解题过程
第三步 : 下面先计算刹车距离. 设车辆的重量为 W ,车 辆刹车时,水平方向只受到摩擦力fW 作用,其方向 与运动方向相反。设刹车后,汽车走过的位移 x(t ) , 根据牛顿第二定律有如下的微分方程:
W d2 x − fW = g ⋅ dt 2 , dx = v0 , dt t = 0 x(0) = 0.
黄灯亮多久
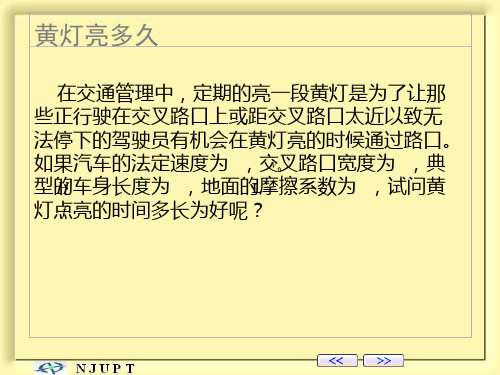
在交通管理中,定期的亮一段黄灯是为了让 那些正行驶在交叉路口上或距交叉路口太近以致 无法停下的驾驶员有机会在黄灯亮的时候通过路 口。如果汽车的法定速度为 v ,交叉路口宽度 为 H ,典型的车身长度为 L ,地面的摩擦系数 为 f ,试问黄灯点亮的时间多长为好呢?
0
应用背景
相关知识点
1.函数最大(小)值的求法 2.高阶可降阶微分方程的解法 3.微分方程的几何应用和简单物理应用
解题过程
第二步 : 因此,如果取
T = t0 + t1 + t2 ,
则选择刹车的驾驶员可以在刹车距离内安全停车; 选择通过路口的驾驶员也有足够时间安全通过路口。 T 所以最佳点亮黄灯时间就归结为求上述 的最小值。 假设汽车以法定速度 通过路口。由于 为常数, t0 v0 而 , L+H
t2 =
所以只有 是需要进一步求得的。
(1)
解题过程
其中 g 为重力加速度,负号是因为速度与摩擦力方 向相反,从而
dv d 2 x = 2 <0 dt dt
.
解题过程
第四步 : 对(1)式积分得 由于车停下后速度为零,所以在(2)式中令 v = 0
v0 得到汽车自刹车至停下所用的时间 t ' = 。 fg
dx v= = − fgt + v0 dt
数学建模简单13个例子讲义.

支 球队中的胜者及轮空者进入下一轮,直至比赛结
束。问共需进行多少场比赛?
一般思维:
36 18 10 4 2 1 18 9 5 2 1 1 36 2 2 2 2 2
逆向思维:
每场比赛淘汰一名失败球队,只有一名冠军,即 就是淘汰了36名球队,因此比赛进行了36场。
4、爬山问题
某人早8时从山下旅店出发沿一条路径上山,下午5 时到达山顶并留宿,次日早8时沿同一路径下山,下午5 时回到旅店,则这人在两天中的同一时刻经过途中的 同—地点,为什么? 解法一: 将两天看作一天,一人两天的运动看作一天两 人同时分别从山下和山顶沿同一路径相反运功,因为 两人同时出发,同时到达目的地,又沿向一路径反向 运动,所以必在中间某一时刻t两人相遇,这说明某人 在两天中的同一时刻经过路途中的同一地点。
1、从包汤圆(饺子)
今天,1公斤面不变,馅比 1公斤多了,问应多包几 个(小一些),还是少包几个(大一些)?
通常,1公斤面, 1公斤馅,包100个汤圆(饺子)
问题
圆面积为S的一个皮,包成体积为V的汤圆。若 分成n个皮,每个圆面积为s,包成体积为v。
S V s v s v
…
s v
( 共 n个 )
定性分析
根据题意,A点的坐标为(-300,0), 单位为km.台风中心的运动轨迹为直 线BC,这里的∠CBA=450,当台风中 心在运动过程中处于以A为圆心、半径 为250 km的圆内(即MN上)时,气象台 A所在地区将遭受台风的影响。 因为圆的方程为: 直线BC的方程为: 当台风中心处于圆内时,有: 解得 其中参数t 为时间(单 位为h)。
马路的宽度D是容易测得的,问题的关键在于L的确定。 为确定L,还应当将L划分为两段:L1和L2。 其中 L1是司机在发现黄灯亮及判断应当刹车的反应 时间内驶过的路程,L2为刹车制动后车辆驶过的路程。 L1较容易计算,交通部门对司机的平均反应时间 t1早有测 算,反应时间过长将考不出驾照),而此街道的行驶速度 v 也是交管部门早已定好的,目的是使交通流量最大,可 另建模型研究,从而L1=v*t1。刹车距离 L2既可用曲线拟 合方法得出,也可利用牛顿第二定律计算出来 黄灯究竟应当亮多久现在已经变得清楚多了。 第一步,先计算出L应多大才能使看见黄灯的司机停 得住车。 第二步,黄灯亮的时间应当让已过线 D 的车顺利穿过马路, L 即T 至少应当达到 (L+D)/v。
交通管理中的黄灯问题数学建模

交通管理中的黄灯问题数学建模
交通管理中的黄灯问题可以通过数学建模来进行研究和分析。
黄灯的作用是提示驾驶员前方即将变为红灯,需要减速慢行。
因此,黄灯时间的设置需要考虑多种因素,如道路交通流量、车辆速度、驾驶员反应时间等。
一种常见的方法是将黄灯问题视为一个动态博弈问题,驾驶员在看到黄灯时需要做出一个决策,即是否继续行驶或者减速停车。
我们可以使用博弈论中的模型来描述驾驶员的行为,例如基本博弈模型或者扩展博弈模型。
另外,我们也可以使用数学模型来研究黄灯时间的设置对道路交通流量的影响。
例如,可以使用交通工程学中的排队论模型来分析黄灯时间对车辆排队等待时间的影响,以及不同黄灯时间设置下的道路交通流量变化情况。
总结起来,交通管理中的黄灯问题可以通过数学建模来进行研究和优化,以提高道路交通的安全性和效率。
数学建模简单13个例子

在这场“价格战”中,我们假设汽油的正常销售价格 保持定常不变,并且假定以上各因素对乙加油站汽油 销售量的影响是线性的.于是乙加油站的汽油销售量 可以由下式给出
返回
13、遗传模型
1.问题分析
所谓常染色体遗传,是指后代从每个亲体的基因 中各继承一个基因从而形成自己的基因型.
如果所考虑的遗传特征是由两个基因A和B控制的, 那么就有三种可能的基因型:AA,AB和BB.
4、爬山问题
某人早8时从山下旅店出发沿一条路径上山,下午5 时到达山顶并留宿,次日早8时沿同一路径下山,下午5 时回到旅店,则这人在两天中的同一时刻经过途中的 同—地点,为什么?
解法一: 将两天看作一天,一人两天的运动看作一天两人 同时分别从山下和山顶沿同一路径相反运功,因为两 人同时出发,同时到达目的地,又沿向一路径反向运 动,所以必在中间某一时刻t两人相遇,这说明某人在 两天中的同一时刻经过路途中的同一地点。
Y
P(x,y)
记v2/ v1=a通常a>1
航母
则 | BP |2 a2 | AP |2 即:
A(0,b)
θ1
x2 (y b) 2 a2 [x2 (y - b)2 ]
O B(0,-b)
θ2 护卫舰
可化为:
X
x2
y
a2 a2
2
11 b
4a 2b2 (a 2 1)2
某人第一天由 A地去B地,第二天由 B地沿原路 返回 A 地。问:在什么条件下,可以保证途中至 少存在一地,此人在两天中的同一时间到达该地。
假如我们换一种想法,把第二天的返回改变成另一 人在同一天由B去A,问题就化为在什么条件下, 两人至少在途中相遇一次,这样结论就很容易得出 了:只要任何一人的到达时间晚于另一人的出发时 间,两人必会在途中相遇。
黄灯时间的确定.

黄灯时间的确定一、问题重述在交通十字路口,都会设置红绿灯。
为了让那些正行驶在交叉路口或离交叉路口太近而无法停下的车辆通过路口,红绿灯转换中间还要亮起一段时间的黄灯。
对于一位驶近交叉路口的驾驶员来说,万万不可处于这样的进退两难的境地:要安全停车则离路口太近;要想在红灯亮之前通过路口又觉太远。
那么,黄灯应亮多长时间才最为合理呢?二、模型假设1.交叉路口处路面为具有一定倾斜角的平面;2.驾驶员在通过交叉路口时,匀速驾驶车辆;3.驾驶员在刹车制动的过程中,将刹车踏板踩到底直到车辆停止;4.车辆未安装防抱死系统(ABS),在刹车制动过程中主动轮抱死;5.仅考虑车辆直行的情况,不考虑转弯和掉头中一些特殊情况的干扰;6.不考虑在人行道中行走的行人对来往车辆通行的影响。
三、变量说明符号符号说明m汽车的质量f路面的滑动摩擦系数g 重力加速度T 黄灯闪烁的时间t0 驾驶员的平均反应时间t1 驾驶员从开始刹车到停车所用的时间t2 驾驶员匀速通过交叉路口所用的时间l 汽车的长度L 交叉路口的宽度a 交叉路口处路面的倾斜角v0 驶近交叉路口的汽车的速度X1 刹车制动过程中位移随时间的变化函数X2 匀速通过路口走过的位移量四、模型的分析驾驶员在遇到绿灯变黄灯的情况下,在经过短暂的思考过后,会有两种动作:其一是判断不能安全通过路口,这时候我们假设驾驶员全力刹车以保证可以安全停止车辆,即停在停车线以内;其二是判断可以安全通过路口,这时候我们假设驾驶员以不变的速度匀速安全通过路口。
通过建立数学模型我们可以求得在第一种情况下驾驶员的刹车距离和刹车时间,刹车距离的意义就是在距离停车线的距离为大于或等于刹车距离的那些正在行驶的车辆可以安全停止,然而对于那些距离小于刹车距离的车辆,它们不能安全通过,于是考虑让他们可以安全通过,根据第二种情况匀速通过,可以求得距离停车线最远的那辆车所能安全通过的最大时间,将这两个时间取最大值然后加上驾驶员的反应时间得到的就是我们所要求得黄灯闪烁时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在 x(0) 0的条件下,对(2)式再积分得到
x(t)12fg2tv0t
(3)
从而刹车距离
x(t ') D v02 .
(4)
2 fg
解题过程
第五步 : 由(4)式得
所以
t1
D v0
v0 2 fg
,
T2vf0gLv0Ht0 .
对 T关于 v 0 求导数,令 T 0 0 得到驻 点 v0 2fg(LH) ,所以当 v0 2fg(LH)时, T有 极小值
顺便地,我们还可以求得使 T取最小值时的法 定速度v0 7.67(m/s)=27.6(km/h),此时T *= 4.91s。
进一步的问题
即使给了充分的停车时间,仍有许多驾驶员企 图加速想抢在红灯亮之前冲过交叉路口。但驾驶员 们并不知道什么时候红绿灯转为红灯。有一种“倒 数”型的红绿灯可以部分地解决这个问题,在黄灯 亮的最后几秒钟内,黄灯上显示出一窜倒着数的数 字,它们准确地警告驾驶员红绿灯何时将变为红色。 这种系统在我国的部分城市正使用着,它成功地降 低了事故发生率。
fW
W g
d d
2x t2
,
dx dt
t 0
v0,
x(0) 0.
(1)
解题过程
其中 g为重力加速度,负号是因为速度与摩擦力方
向相反,从而
dv d2x dt dt2 0
.
解题过程
第四步 : 对(1)式积分得
由于车停下后速v度为ddxt零,f所gt以v0在(2)式中(令2)v 0 得到汽车自刹车至停下所用的时间 t ' v 0 。
设驾驶员作出决定的反应时间为 t 0 ,通过刹车 距离的时间为 t1 ,通过路口和一个车身距离的时间 为 t 2 ,黄灯点亮的时间为 T 。
解题过程
第二步 :
因此,如果取
Tt0 t1t2,
则选择刹车的驾驶员可以在刹车距离内安全停车;
选择通过路口的驾驶员也有足够时间安全通过路口。
所以最佳点亮黄灯时间就归结为求上述 的最T 小值。
4.92
经验法(s) 2
45
5.39
3
60
6.16
4
75
7.03
5
数学实验
表中的“经验法”是按如下“经验”得到:对法 定的迫近速度的每个15 km/h亮黄灯1秒。我们注意 到,经验法的结果一律比我们预测的黄灯状态短些。 这使人想起,许多交叉路口的设计很可能使车辆在 绿灯转为红灯时正处在交叉路口上。
T*miTn
2(LH) fg
t0
数学实验
借助于Mathematica可以描绘出 T关于 v 0 的图 像。假设t0 1 s ,L5m ,H10m 。另外,我们 将接受公路工程师提出的具有代表性的数据 f 0.2.
在Mathematica软件中输入如下程序:
Plot[v/(2*0.2*9.8)+(5+10)/v+1, {v, 0, 30}]
假设汽车以法定速度 通过路口。由于 为常数,
而
v0
t0
所以只有 是需要进t一2 步L求v0H得的。,
t1
解题过程
第三步 : 下面先计算刹车距离. 设车辆的重量为 W ,车
辆刹车时,水平方向只受到摩擦力 f W作用,其方向 与运动方向相反。设刹车后,汽车走过的位移 x (t ), 根据牛顿第二定律有如下的微分方程:
运行后得到如下 T关于
m/s。
40 T(s)
v 0的图像,其中
的v 0 单位为:
30
20
10
v (0 m/s)
5
10
15
20
25
30
数学实验
当 v0 30、45、60、75(km/h ),也即约8.3, 12.5, 16.7,20.8(m/ )时, 的值T如下表所 示:
v0 (km/h)
30
T (s)
黄灯亮多久
在交通管理中,定期的亮一段黄灯是为了让 那些正行驶在交叉路口上或距交叉路口太近以致 无法停下的驾驶员有机会在黄灯亮的时候通过路 口。如果汽车的法定速度为 v 0 ,交叉路口宽度 为 H,典型的车身长度为 L ,地面的摩擦系数 为 f ,试问黄灯点亮的时间多长为好呢?
应用背景
相关知识点
1.函数最大(小)值的求法 2.高阶可降阶微分方程的解法 3.微分方程的几何应用和简单物理应用
解题方法
通过建立汽车刹车的微分方程,求出汽车通 过刹车距离、路口宽度和一个车身的行驶时间, 再求黄灯亮时的最小值,解决黄灯亮时问题。
解题过程
第一步 :
驶近交叉路口的驾驶员看到黄灯信号时首先要 作出决定:是停车还是通过路口。如果选择停车, 他必须有足够的停车距离;如果选择通过路口,他 必须有足够的时间安全通过路口。
