数学与应用数学专业课程设置一览表
数学与应用数学大一课表

数学与应用数学大一课表
数学与应用数学专业大一的课程通常包括以下内容:
1. 数学分析:这是数学与应用数学专业最重要的基础课程之一,主要学习函数的极限、连续、可微、可积等性质,以及实数和复数的性质和运算。
2. 高等代数:该课程主要学习线性方程组、矩阵、行列式、向量空间、线性变换等知识,掌握基本的代数知识。
3. 概率论与数理统计:该课程主要学习概率论和数理统计的基本概念、随机变量、随机过程、参数估计、假设检验等知识,掌握概率论与数理统计的基本方法和应用。
4. 微分方程:该课程主要学习常微分方程和偏微分方程的基本理论和方法,掌握求解微分方程的基本技巧。
5. 实变函数与泛函分析:该课程主要学习实变函数和泛函分析的基本概念和方法,包括集合论、测度论、积分论、函数空间等。
6. 数值分析:该课程主要学习数值计算的基本原理和方法,包括线性代数方程组的数值解法、插值与拟合、数值积分与微分等。
7. 离散数学:该课程主要学习离散数学的基本概念和方法,包括图论、组合数学、离散概率论等。
8. 计算机基础:该课程主要学习计算机的基本原理和编程语言,包括计算机组成原理、数据结构与算法、C++或Python编程等。
以上是一般情况下数学与应用数学专业大一的课程表,具体课程设置可能因学校而异。
数学与应用数学专业课程设置及简介

数学与应用数学专业课程设置及简介来源:理学院时间:2005年8月2日14:27 点击:5603数学系数学与应用数学专业(S)四年制教学中共开设相关专业课程26门,其中专业基础课3门,包括:数学分析、高等代数、解析几何;专业课12门,包括:常微分方程、中学数学解题研究、中学数学教材分析、数学教育概论、计算方法、初等数论、离散数学、近世代数、实变函数论、复变函数论、概率论、数理统计;专业选修课11门,包括:专业英语、泛函分析、点集拓扑、数学实验、数学模型、数学分析选讲、高等代数选讲、线性规划、数学史、数学竞赛教程。
各门课程简介如下:一、数学分析内容简介:数学分析是数学专业的一门重要的专业基础课程,是高等数学理论的基础,也是所有本科专业学生的必修课程,这门课程的学好与否,直接影响到后续课程如复变函数、实变函数以及拓扑学等课程的学习。
该课程首先详细介绍了极限理论,用极限理论作为工具,讨论了函数,特别是连续函数的导数与徽分;不定积分与定积分;级数理论;多元函数微分学以及多元函数积分学等理论。
通过这门课的学习,应该使学生掌握函数的微积分理论的基本理论和基本方法,能应用这些理论和方法解决分析中提出的理论和实际问题,为后续课程的学习打下良好的基础。
该课程重点是极限理论和微积分理论,难点是实数连续性定理及级数理论。
先修课要求:中学数学教材及参考书:《数学分析讲义》刘玉琏傅沛仁编高等教育出版社二、高等代数内容简介:高等代数是数学教育专业的一门重要基础课。
高等代数是高等师范院校数学专业一门重要基础课,是中学代数的继续和提高,通过这一课程的教学,可以使学生初步掌握基本的系统的代数知识和抽象的严格的代数方法,以加深对中学数学的理解,并为进一步学习打下基础.本课程的主要内容是多项式理论,线性代数理论两部分。
多项式理论主要讨论一元多项式和因式分解理论。
线性代数部分包括矩阵、线性空间、线性变换、欧氏空间和二次型等内容。
先修课要求:中学数学教材及参考书:《高等代数》北大数学系代数几何教研室王萼芳编高等教育出版社三、解析几何内容简介:解析几何是师范本科院校数学教育专业的一门重要基础课,其特点是用代数观点来研究几何问题,即:设法把空间的几何结构有系统的代数化、数量化。
数学与应用数学专业(金融数学)本科学分制培养方案

数学与应用数学专业(金融数学)本科学分制培养方案专业名称:数学与应用数学(金融数学)专业代码: 070101一、培养目标本专业培养德、智、体、美全面发展,掌握数学科学的基本理论与基本方法,具备运用数学知识、使用计算机解决实际问题的能力,能在金融证券、投资、保险等经济部门、科研部门和政府部门从事经济分析、金融产品设计的涉外复合型应用人才。
二、培养规格本专业学生主要学习数学和应用数学的基本理论、基本方法,受到数学建模、计算机和数学软件方面的基本训练,在数学理论和它的应用两方面都受到良好的教育,具有较高的科学素养和较强的创新意识,具备科学研究、教学、解决实际问题及软件开发等方面的基本能力和较强的更新知识的能力。
毕业生应达到以下要求:(一)知识要求具有比较扎实的数学基础,受到严格的科学思维训练,初步掌握数学科学的思想方法;具有应用数学知识建立数学模型以解决实际问题的初步能力和进行数学教学的能力;了解数学科学发展的历史概况以及当代数学的某些新发展和应用前景;了解金融数学学科的若干最新进展及相近学科的一般原理与知识;能熟练使用计算机(包括常用语言、工具及数学软件),具有编写简单程序的能力;有较强的语言表达能力,掌握资料查询、文献检索以及运用现代信息技术获取相关信息的基本方法,具有一定的科学研究能力;掌握金融数学、经济学和金融学的基本理论和方法,具备运用所学的数学与金融分析方法进行经济、金融信息分析与数学处理的能力;熟练掌握一门外语,具有较强的听、说、读、写、译能力。
(二)素质要求本专业毕业的学生应具有良好的思想道德品质、较强的法制观念和诚信意识;较高的人文、科学和艺术修养;较强的现代意识和人际交往意识;科学的思维方法、求实创新精神、专业分析的素养;健康的体魄和健全的心里素质。
(三)能力要求具有宽广的国际视野,较强跨文化沟通能力;较强的自主学习能力;利用计算机网络获取、利用、管理信息的能力;了解金融数学学科的若干最新进展及相近学科的一般原理与知识,能够运用相关软件进行金融数值计算,具有金融风险管理及证券投资的模拟试验能力。
数学与应用数学师范 本科课程

数学与应用数学师范本科课程
数学与应用数学师范本科课程通常包括以下内容:
1. 高等数学:包括微积分、线性代数、常微分方程等内容,是数学学科的基础课程。
2. 概率论与数理统计:是数学学科中的一个重要分支,包括概率分布、随机变量、样本调查等内容。
3. 数学分析:是对数学的进一步深入研究,包括实分析、复分析、泛函分析等内容。
4. 抽象代数:是对数学中基本概念抽象化的研究,包括群论、环论、域论等内容。
5. 数值计算:是将数学与计算机科学相结合的分支,包括数值分析、计算方法等。
6. 拓扑学:是数学中一个重要分支,研究集合、空间之间的结构和连续性,包括初等拓扑学和代数拓扑学。
7. 数学建模:是将数学方法应用于现实问题的分支,其中包括数学模型的建立和解决方法的研究。
8. 数学教育:是培养数学教师的必修课程,包括数学教法、课程设计等内容。
以上课程是数学与应用数学师范专业本科课程的主要内容,涵盖了数学学科的主要分支及其应用。
应用数学专业课程

应用数学专业课程
【原创实用版】
目录
1.应用数学专业简介
2.应用数学专业课程设置
3.应用数学专业的就业方向
4.应用数学专业的发展前景
正文
一、应用数学专业简介
应用数学专业是一门以数学为基础,以应用为目的的学科,旨在培养掌握数学基本理论和方法,能在工程、物理、经济、金融等领域从事科学研究、技术开发和应用的高级专门人才。
应用数学专业的学生需要具备良好的数学素养、较强的逻辑思维能力和扎实的计算机基础。
二、应用数学专业课程设置
应用数学专业的课程设置主要包括基础课程和专业课程两个方面。
基础课程主要包括:高等数学、线性代数、概率论与数理统计、微分方程、数学建模等。
专业课程主要包括:运筹学、控制论、信息论、密码学、生物数学、经济数学、金融数学等。
三、应用数学专业的就业方向
应用数学专业的毕业生在就业市场上有着广泛的选择,可以在工程、物理、经济、金融等领域从事科学研究、技术开发和应用工作。
具体的就业方向有:教育科研、软件开发、金融投资、企业管理等。
四、应用数学专业的发展前景
随着我国经济的快速发展,应用数学专业的发展前景十分广阔。
数学与应用数学专业培养计划
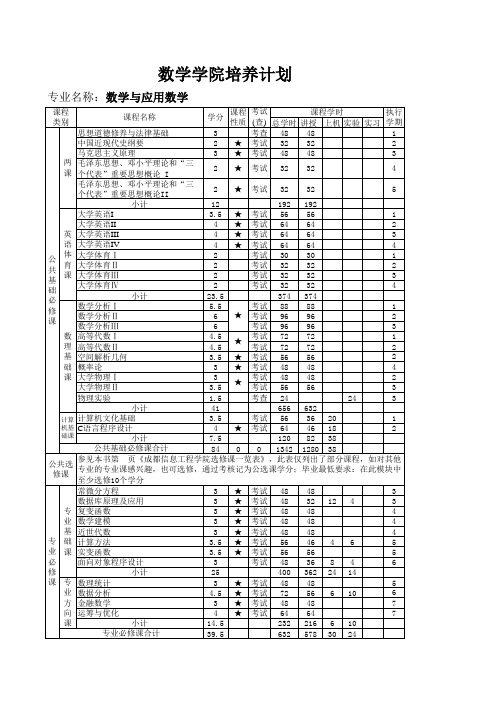
★ ★
考查 72 考试 48 考试 16 考试 16 考试 16 考查 4周 考查 12周 96
1.5 2 1.5 3 3 3 2 3 3 2 3 3 3.5 2.5 2 3 2 2 2 2 3 3.5 2 3 2.5 3 66 1 1 1 1 3 1 1 1 4 11 25 180
考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查 考查
数学学院培养计划
专业名称:数学与应用数学 数学与应用数学
课程 类别 课程名称 学分 思想道德修养与法律基础 3 2 中国近现代史纲要 马克思主义原理 3 毛泽东思想、邓小平理论和“三 2 ★ 考试 32 32 4 个代表”重要思想概论 I 毛泽东思想、邓小平理论和“三 2 ★ 考试 32 32 5 个代表”重要思想概论II 12 192 192 小计 3.5 ★ 考试 56 56 1 大学英语I 4 ★ 考试 64 64 2 大学英语II 4 ★ 考试 64 64 3 大学英语III 4 ★ 考试 64 64 4 大学英语IV 大学体育Ⅰ 2 考试 30 30 1 大学体育Ⅱ 2 考试 32 32 2 大学体育Ⅲ 2 考试 32 32 3 大学体育Ⅳ 2 考试 32 32 4 23.5 374 374 小计 数学分析Ⅰ 5.5 考试 88 88 1 ★ 考试 96 数学分析Ⅱ 6 96 2 数学分析Ⅲ 6 考试 96 96 3 高等代数Ⅰ 4.5 考试 72 72 1 ★ 高等代数Ⅱ 4.5 考试 72 72 2 2 空间解析几何 3.5 ★ 考试 56 56 概率论 3 ★ 考试 48 48 4 大学物理Ⅰ 3 考试 48 48 2 ★ 大学物理Ⅱ 3.5 考试 56 56 3 物理实验 1.5 考查 24 24 3 41 656 632 小计 计算机文化基础 3.5 考试 56 36 20 1 4 ★ 考试 64 46 18 2 C语言程序设计 7.5 120 82 38 小计 84 0 0 1342 1280 38 公共基础必修课合计 参见本书第 页《成都信息工程学院选修课一览表》,此表仅列出了部分课程,如对其 他专业的专业课感兴趣,也可选修,通过考核记为公选课学分;毕业最低要求:在此模 块中至少选修10个学分 常微分方程 3 ★ 考试 48 48 3 数据库原理及应用 3 ★ 考试 48 32 12 4 3 复变函数 3 ★ 考试 48 48 4 数学建模 3 ★ 考试 48 48 4 3 ★ 考试 48 48 4 近世代数 计算方法 3.5 ★ 考试 56 46 4 6 5 实变函数 3.5 ★ 考试 56 56 5 面向对象程序设计 3 考试 48 36 8 4 6 25 400 362 24 14 小计 3 ★ 考试 48 48 5 数理统计 6 ★ 考试 72 56 6 10 数据分析 4.5 7 3 ★ 考试 48 48 金融数学 7 4 ★ 考试 64 64 运筹与优化 6 14.5 232 216 10 小计 39.5 632 578 30 24 专业必修课合计 课程学时 课程 考试 执行 性质 (查) 总学时 讲授 上机 实验 实习 学期 考查 48 48 1 ★ 考试 32 32 2 ★ 考试 48 48 3
数学与应用数学专业课程设置及简介[1]
![数学与应用数学专业课程设置及简介[1]](https://img.taocdn.com/s3/m/0119739d9fc3d5bbfd0a79563c1ec5da50e2d629.png)
数学与应用数学专业课程设置与简介来源: 理学院时间: 2005年8月2日14:27 点击: 5603数学系数学与应用数学专业(S)四年制教学中共开设相关专业课程26门, 其中专业基础课3门, 包括: 数学分析、高等代数、解析几何;专业课12门, 包括: 常微分方程、中学数学解题研究、中学数学教材分析、数学教育概论、计算方法、初等数论、离散数学、近世代数、实变函数论、复变函数论、概率论、数理统计;专业选修课11门, 包括: 专业英语、泛函分析、点集拓扑、数学实验、数学模型、数学分析选讲、高等代数选讲、线性规划、数学史、数学竞赛教程。
各门课程简介如下:一、数学分析内容简介: 数学分析是数学专业的一门重要的专业基础课程, 是高等数学理论的基础, 也是所有本科专业学生的必修课程, 这门课程的学好与否, 直接影响到后续课程如复变函数、实变函数以与拓扑学等课程的学习。
该课程首先详细介绍了极限理论, 用极限理论作为工具, 讨论了函数, 特别是连续函数的导数与徽分;不定积分与定积分;级数理论;多元函数微分学以与多元函数积分学等理论。
通过这门课的学习, 应该使学生掌握函数的微积分理论的基本理论和基本方法, 能应用这些理论和方法解决分析中提出的理论和实际问题, 为后续课程的学习打下良好的基础。
该课程重点是极限理论和微积分理论, 难点是实数连续性定理与级数理论。
先修课要求:中学数学教材与参考书: 《数学分析讲义》刘玉琏傅沛仁编高等教育出版社二、高等代数内容简介: 高等代数是数学教育专业的一门重要基础课。
高等代数是高等师范院校数学专业一门重要基础课,是中学代数的继续和提高,通过这一课程的教学,可以使学生初步掌握基本的系统的代数知识和抽象的严格的代数方法,以加深对中学数学的理解,并为进一步学习打下基础.本课程的主要内容是多项式理论, 线性代数理论两部分。
多项式理论主要讨论一元多项式和因式分解理论。
线性代数部分包括矩阵、线性空间、线性变换、欧氏空间和二次型等内容。
2019河南师范大学课程计划总表和分学年课程设置一览表-数学与应用数学

备注
上课时间为4-12周 军训2周
上课时间为1-9周 上课时间为10-18周
必修课
第二 学年
大学英语Ⅳ
3
4
大学体育Ⅳ
1
2
教育学
2
3
必修课
现代教育技术
2
2
中华优秀传统文化概论
1
2
第四学期 (春)
抽象代数
3
3
复变函数
3
3
微分几何
3
3
合计
21
2
26
中学生品德发展与道德教育
1
2
特殊教育概论
0.5
2
选修课
3
3
图论
3
3
组合数学
3
3
金融数学
2
3
合计
32
1
39
1-6学期
必修课
第七学期 (秋)
第四 学年
选修课
必修课
第八学期 (春) 选修课
教育实践
合计 现代数学与中学数学
Python数据分析 合计
毕业论文或毕业设计 第二课堂 合计
合计
6
0
6
1121源自3262
0
8
含见习3周(第2~5学 期);校内实习2周 (第7学期),校外实 习8周(第7学期), 校内研习5周(含观摩 教学比赛准备1周,第 7学期)
大学生心理健康教育 教师口语
数学分析(一) 解析几何 合计
中国近现代史纲要 大学英语Ⅱ 大学体育II 音乐鉴赏 美术鉴赏
大学语文或应用写作 大学生职业规划 教师职业道德 数学分析(二) 高等代数(一) 大学物理I 大学物理实验I 合计 C程序设计 中学生心理辅导
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
MA330 偏微分方程续论(A) 2.0 34 34
8
MA333
代数拓扑
3.0 51 51
8
能力贡献
素质贡献
数学与应用数学专业课程设置一览表
课程 代码
课程名称
学时分配
排
推
总总
课理
荐
学学
分 时 学 论实实其 学
时 教验习他 期
学
知识贡献
MA414
组合数学
3.0 51 51
8
MA418 李群与李代数
拓扑学基础
4.0 68 68
6
MA308
泛函分析
4.0 68 68
6
总 12.0 204
非基地班学生须修满此模块全部学分。基地班学生选此模块课程可充抵专业方向选修课基本学分。
MA335
随机过程
4.0 68 68
5
MA309 偏微分方程数值解 4.0 68 68
6
MA336
图与网络
4.0 68 68
6
专业教育课程
须修满全部
MA122 数学分析(1) 5.0 119 119
1
MA134 高等代数与解析几 5.0 119 119
1
何(A类)(1)
CS048 C++程序设计(A类) 3.0 48 48
2
MA123 数学分析(A类)(2) 5.0 119 119
2
MA135 高等代数与解析几 5.0 119 119
2.0 34 34
7
EM405 流体力学简介
2.0 32 32 32
8
MA424
最优控制
3.0 51 51
8
总 30.0 503
专业实践类课程
实验课程
必修课
须修满全部
PH028 大学物理实验(1) 1.0 26 26
2
PH029 大学物理实验(2) 1.0 26 26
3
军事技能训练
总 2.0 52
必修课
总 12.0 204
所有学生全部修业期间须修满20学分。其中基地班学生在专业方向选修A组中须至少选修12学分作为基本学分。
MA218 现代数学选讲
1.0 17 17
4
MA313
动力系统
3.0 51 51
6
MA323 群与代数表示论 3.0 51 51
6
MA327 复变函数续论(A) 2.0 34 34
3.0 51 51
8
MA440 微分几何续论
3.0 48 48
8
MA441 非线性泛函分析基础 3.0 48 48
8
总 44.0 739
所有学生全部修业期间须修满20学分。其中基地班学生在专业方向选修A组中须至少选修12学分作为基本学分。
CS430
数据结构B
2.0 32 32 32
3
MA322
数学规划
个性化教育课程
个性化教育课程
选修课
全部修业期间须修满10学分。 除本专业培养方案中通识教育课程、专业教育课程、实践教育课程三个模块要求学分之外的所有学分均可计入。
2
何(A类)(2)
PH001 大学物理(A类)(1) 4.0 68 68
2
MA220 数学分析(A类)(3) 4.0 85 85
3
PH002 大学物理(A类)(2) 4.0 68 68
3
专业类
总 35.0 745
必修课
须修满全部
MA103
初等数论
2.0 34 34
1
MA202
常微分方程
4.0 68 68
体育(2)
1.0 34 34
2
PE003
体育(3)
1.0 34 34
3
PE004
体育(4)
1.0 34 34
4
TH004
军事理论
1.0 17 17
2
通识核心类
总 25.0 513
最低要求为12学分。须在人文学科、社会科学、工程科学与技术3个模块课程中各至少选修1门课程或2学分.其余学 分可在4个模块课程中任意选修。
各类别学分要求如下
工程科学与技术 2.0
人文学科
2.0
社会科学
2.0
通识教育实践
总 6.0
必修课
须修满全部
XP000 通识教育实践活动 2.0 34 34
2
数学与应用数学专业课程设置一览表
课程 代码
课程名称
学时分配
排
推
总总
课理
荐
学学
分 时 学 论实实其 学
时 教验习他 期
学
知识贡献
基础类 必修课
总 2.0 34
1
TH007 马克思主义基本原理 3.0 48 48 32
16 3
TH012 毛泽东思想和中国特色社 6.0 96
会主义理论体系概论
EN025 大学基础英语(1) 3.0 68
96 48 68
48 4 1
EN026 大学基础英语(2) 3.0 68 68
2
PE001
体育(1)
1.0 34 34
1
PE002
7
MA348 科学计算(2) 3.0 48 48
7
MA400
代数几何
2.0 34 34
7
MA401
微分流形
3.0 51 51
7
MA417
代数数论
2.0 34 34
7
MA421
广义函数
2.0 34 34
7
MA428 非线性数学物理方法 2.0 34 34
7
MA429
编码与密码
2.0 34 34
7
MA329 常微分方程续论(A) 2.0 34 34
能力贡献
素质贡献
数学与应用数学专业课程设置一览表
课程 代码
课程名称
学时分配
排
推
总总
课理
荐
学学
分 时 学 论实实其 学
时 教验习他 期
学
须修满全部
TH010
军训
3.0 51 51
2
专业综合训练
总 3.0 51
必修课
知识贡献
须修满全部
BS420 毕业设计(数学) 12.0 204 204
8
总 12.0 204
3
MA226 科学计算(1) 4.0 68 68
3
MA204
抽象代数
4.0 68 68
4
MA205
复变函数
4.0 68 68
4
MA206
概率论
4.0 68 68
4
MA301
实变函数
4.0 68 68
5
MA302
偏微分方程
4.0 68 68
5
MA306
数理统计
4.0 68 68
5
MA321
数学建模
3.0 51 51
3.0 51 51
5
MA310 运筹学(B类) 3.0 51 51
6
MA324
数量经济学
3.0 51 51
6
MA363 科学与工程问题的并行计 3.0 48 48源自6算MA403
数理金融
3.0 51 51
7
MA406
多元统计
3.0 51 51
7
MA411 时间序列分析
3.0 51 51
7
MA430 科学计算选讲
6
能力贡献
素质贡献
数学与应用数学专业课程设置一览表
课程 代码
课程名称
学时分配
排
推
总总
课理
荐
学学
分 时 学 论实实其 学
时 教验习他 期
学
知识贡献
选修课
总 37.0 629
基地班学生须修满此模块全部学分。非基地班学生选此模块课程可充抵专业方向选修课学分。
MA303
微分几何
4.0 68 68
5
MA307
数学与应用数学专业课程设置一览表
课程 代码
课程名称
学时分配
排
推
总总
课理
荐
学学
分 时 学 论实实其 学
时 教验习他 期
学
知识贡献
能力贡献
素质贡献
公共课程类 必修课
通识教育课程
须修满全部
TH000 思想道德修养与法律基础 3.0 48 48 32
16 2
TH021 中国近现代史纲要 2.0 32 32 32
