组合弹簧的设计与计算
弹簧设计计算

弹簧设计计算弹簧在材料选定后,设计时需要计算出弹簧刚度F、中径D、钢丝直径d、有效圈数n、变形量f。
以下面弹簧设计为例;1.计算弹簧受力:假设弹簧端克服1个标准大气压,即推动钢球,则弹簧受力为:F=PA=1×105N/mm2×πd12 /4其中d1——钢球通道直径弹簧还须克服钢球下降重力:G=mρV=m×4ρπR3/3其中R——钢球半径弹簧受合力:F合=F+G考虑制造加工因素,增加1.2倍系数F′=1.2F合2.选材料:(一般选用碳素弹簧钢丝65Mn或琴钢丝)以65Mn为例,钢丝直径d=1.4mm3.查表计算许用应力:查弹簧手册8-10表中Ⅰ类载荷的弹簧考虑(根据阀弹簧受力情况而言) 材料的抗拉强度σb与钢丝直径d有关查表2-30(选用D组): σb=2150~2450Mpa安全系数K=1.1~1.3, 可取K=1.2, 则σb=1791.7~2041.7 Mpa因此σb=1791.7Mpa(下限值)查表2-103,取切变模量G=78.8×103Mpa查表8-10,取许用切应力τs==0.5σb=0.3×1791.7=537.51Mpa 4.选择弹簧旋绕比C:根据表8-4初步选取C=105.计算钢丝直径:d≥1.6√KFC/[τ]其中K——曲度系数,取K=1.1~1.3F——弹簧受力6.计算弹簧中径:D=C d7.计算弹簧有效圈数:n=Gd4f/8FD3则总圈数n总=n+n1(查表8-6)8.计算试验载荷:Fs=πd3τs/8D9.自由高度:H0=nt+1.5d其中:t——初步估计节距t=d+f/n+δ1(δ1=0.1d)查表8-7系列值H0取整数10.节距计算:t=(H0-1.5d)/n11.弹簧螺旋角:(此值一般符合=5°~9°)α=arctan(t/πD)12.弹簧的稳定性验算:(b<5.3,即可满足稳定性要求=b=H0/D13.展开长度:L=πDn1/cosα14.弹簧刚度:F′=Gd4/8D3n14.弹簧载荷:F= F′×f15.弹簧试验变形:fs= Fs/ F其中在绘制弹簧图纸时,压紧弹簧时的长度L1(即受装配积压时的长度) 下弹簧对应受力F1,在阀开启时弹簧压缩的长度L2=L1+f,对应弹簧受力F2 例如:ZYB-1416N15-306H0=68.5 mm,装配时弹簧被压缩至37mm,阀开启时再次压缩8mm则L1=37,L2=37+8=45F1=37×F′F2=45 F′验算比较L2与Fs/ F的大小:若L2>Fs/ F′重新设计刚度;反之设计合理。
弹簧设计的计算公式

弹簧设计的计算公式
常见的弹簧设计绝大部分是压缩螺旋弹簧或拉伸螺旋弹簧。
这两种弹簧设计,涉及下面的项目。
在这里将关于a),b),c)进行解说。
a)在使用范围内,弹簧负载和形变量:弹簧常数
b)安装弹簧的空间:长度x外形
c)弹簧的固定方法:弹簧的两端形状和固定方法
d)其他:弹簧刚度(永久变形),疲劳度
(1)弹簧常数和弹簧形状尺寸的关系式
弹簧的形变量和负载(力)的关系。
P =k x δ
P:弹簧负载
k:弹簧常数
δ:弹簧挠度(形变量)
(k:弹簧常数)用弹簧材料特性和弹簧形状可以用下述公式表达。
这个公式压缩螺旋弹簧和拉伸螺旋弹簧都适用。
k =P/δ=G x d4/8 x n x D3 ・・・(A)
G:横向弹性系数(杨氏模量)
d:线径
n:有效匝数
D:平均线圈直径
通过使公式(A)变形,暂时设定D(平均线圈直径),d(线径),
k(弹簧常数)来计算有效匝数:n,或者根据已知的P,D,d,n ,来计算形变量:δ。
(2)弹簧的长度、外形的设计
弹簧长度是根据(允许形变量)与弹簧载荷之间的关系来选择和设计的。
(允许形变量)是会使弹簧变形或损坏的最大变形量(参考图1)。
弹簧设计计算

D(mm)
K1
Fc(N)
100
0.686
62724.63
100
0.686
15846.15
100
0.686
9093.29
分别为959219N和15846N)均大于工作载荷F(13186.81N),所 。
F/Fc 0.210 0.832 荷F下的变形量)
4*E 824000
1-μ² 0.91
碟簧片数 5
0.384
.2-2查得)
Fσ(许用载荷)/N 48000 13100 8610
f=0.75·h0 f(变形量)/mm
1.65 2.1 2.63
σⅡ或σⅢ/Mpa
1420 1050 1240
t代替
5/32
0.15625
H0/t 1.366666667
H0/t-1 0.366666667
C2验算
(H0/t-1)²
h0(碟簧压平时
H0
变形量)/mm (自由高度)/mm
A100
100
51
6
2.2
8.2
B100
100
51
3.5
2.8
6.3
C100
100
51
2.7
3.5
6.2
由C=D/d=100/51=1.96 从表7.2-5查得系数 K1=0.686
D(外径)/mm d(内径)/mm
C
100
51
1.96
⑴ 采用A系列外径D=100mm 碟形复合组合弹簧(A100-1GB/T1972-1992)
Fc(N)
h0/t
A100
2.2
6
13186.81
机械设计——弹簧机构设计

“弹簧”被组入到各种机构中,发挥出弹簧各自的作用。
但相对于显著的要素部件来说,它担当的是辅助的角色。
但是,它与可靠性、高速运动性能、小型轻量化和操作性等之间有很深的关系。
即使在今后的技术进步中,弹簧也是一种重要的LCA部件。
弹簧的种类和特点「弹簧」按照形状分类如下。
【表1】按照形状分类的弹簧种类施加在弹簧上的负载:P和挠度(形变量):δ成比例(线性)关系,根据「胡克定律」。
比例常数k称为「弹簧常数」。
【图1】显示了负载和形变之间的关系。
在这个图中,斜度表示弹簧常数:k。
利用这一特性,我们设计和制造了测量物体重量的“弹簧秤”、需要一定力量动作的安全阀用弹簧等。
(2)具有不同负载特性的弹簧弹簧的负载-形变关系除了上述(1)所述的线性特性以外,还有非线性的弹簧。
以压缩螺旋弹簧为例,其中负载和形变为非线性特性的有以下3种。
非线性压缩螺旋弹簧中[1]螺旋直径,[2]间距和[3]线径中的至少一个以上的设计参数,通过变换螺旋弹簧的位置,负载的增加,来实现线条或线条与座位表面相互接触。
・在拉伸弹簧中,即使在无负载的状态下,弹簧圈之间相互作用的力:可以形成初张力。
・这种初张力在由密着状态形成时,通过弹簧线在螺旋方向紧密缠绕扭转而获得的。
・在通过冷成型紧密卷绕加工形成弹簧的情况下,尽管在一定程度上产生了初张力,但是主动形成初始张力的弹簧被称为有初始张力的弹簧。
・没有初张力的弹簧和有初张力的弹簧的负载-形变量特性如下所示。
(【图1】)・【图1】的拉伸弹簧负载-形变量关系式用【公式A】来表示。
有初张力的弹簧拉伸弹簧的负载-形变量关系式用【公式B】来表示。
【公式A】负载P(N)=弹簧常量k(N/mm)x形变量δ(mm)【公式B】荷重P(N)=初张力Pi(N)由下述公式算出。
+弹簧常量k(N/mm)x形变量δ(mm)・初张力Pi(3)拉伸弹簧的各种形状拉伸螺旋弹簧的形状在弹簧特性面上有时不具有非线性,大致有圆筒形和双重拉伸两种。
弹簧参数尺寸及计算公式

弹簧参数尺寸及计算公式弹簧是一种用来储存和释放机械能的装置,应用广泛于机械、汽车、电器等领域。
弹簧的参数、尺寸以及计算公式对于设计和选择弹簧十分重要。
1.弹簧的参数:- 预压力(Preload):弹簧在未加载之前的初始压力。
- 弹性系数(Spring Constant):弹簧在单位变形下的恢复力。
- 卸载长度(Unloaded Length):未加载时的弹簧长度。
- 动载荷(Dynamic Load):弹簧所承受的变动力。
- 疲劳寿命(Fatigue Life):弹簧能够承受的循环加载次数。
2.弹簧的尺寸:- 线径(Wire Diameter):弹簧材料的直径,决定着弹簧的承载能力。
- 外径(Outer Diameter):弹簧的最大直径。
- 内径(Inner Diameter):弹簧的最小直径。
- 组件高度(Solid Height):弹簧在最大压缩状态下的高度。
- 活动齿数(Active Coils):弹簧上具有弹性的齿数。
- 紧齿数(Total Coils):弹簧上总共的齿数。
3.弹簧的计算公式:-弹性系数(K)的计算公式:K=Gd^4/(8Na^3)其中,G为剪切模量,d为线径,N为齿数,a为活动齿数。
-预压力(P)的计算公式:P=K*δ其中,δ为弹簧的压缩/拉伸变形量。
-力(F)的计算公式:F=K*δ弹簧所受的力正比于弹性系数与变形量之积。
-弹簧的伸长(δ)计算公式:δ=(F*L)/(K*Gd^4)其中,L为弹簧的长度。
-弹簧的疲劳寿命(Nf)计算公式:Nf=(C*S^b)/(F^b)其中,C为常数,S为应力幅值(一般为弹簧的最大变形量)。
以上公式仅为常见的弹簧计算公式,实际应用中可能还需要考虑更多的因素,如安全系数、材料的疲劳强度等。
总结起来,弹簧的参数、尺寸和计算公式对于弹簧的设计和选择至关重要。
具体的参数和尺寸根据实际应用需求和弹簧类型来确定,而计算公式则是根据力学原理和材料特性推导得出的。
弹簧的k值计算公式(二)

弹簧的k值计算公式(二)弹簧的k值计算公式弹簧的k值(弹性系数)是衡量弹簧强度和刚度的重要参数。
在弹簧的设计和应用过程中,计算k值是必不可少的步骤。
本文将列举几种常见的弹簧k值计算公式,并用例子进行说明。
1. 无扭转弹簧的k值计算公式线圈弹簧(拉伸弹簧)的k值计算公式:k = (G * d⁴) / (8 * D³ * n)其中:k:弹簧的k值(N/m)G:弹簧材料的剪切模量(N/m²)d:弹簧线径(m)D:弹簧直径(m)n:弹簧总匝数(个)例如,假设有一个线径为(5mm)、直径为(40mm)的线圈弹簧,弹簧材料的剪切模量为80 × 10^9 N/m²,总匝数为10个。
那么可以通过上述公式计算出该弹簧的k值:k = (80 × 10^9 * ()^4) / (8 * ()^3 * 10)≈ 15784 N/m因此,该线圈弹簧的k值约为15784 N/m。
扭转弹簧(扭簧)的k值计算公式:k = (G * d⁴) / (32 * D³ * n)其中的符号意义与线圈弹簧的公式相同。
2. 有扭转弹簧的k值计算公式杆弹簧(压簧)的k值计算公式:k = (E * d⁴) / (8 * D³ * n)其中:k:弹簧的k值(N/m)E:弹簧材料的弹性模量(N/m²)d:弹簧线径(m)D:弹簧直径(m)n:弹簧总匝数(个)例如,假设有一个线径为(5mm)、直径为(40mm)的杆弹簧,弹簧材料的弹性模量为200 × 10^9 N/m²,总匝数为20个。
那么可以通过上述公式计算出该弹簧的k值:k = (200 × 10^9 * ()^4) / (8 * ()^3 * 20)≈ 312500 N/m因此,该杆弹簧的k值约为312500 N/m。
总结弹簧的k值计算公式是根据弹簧的材料、几何尺寸和总匝数等参数进行推导的。
最好的弹簧计算公式
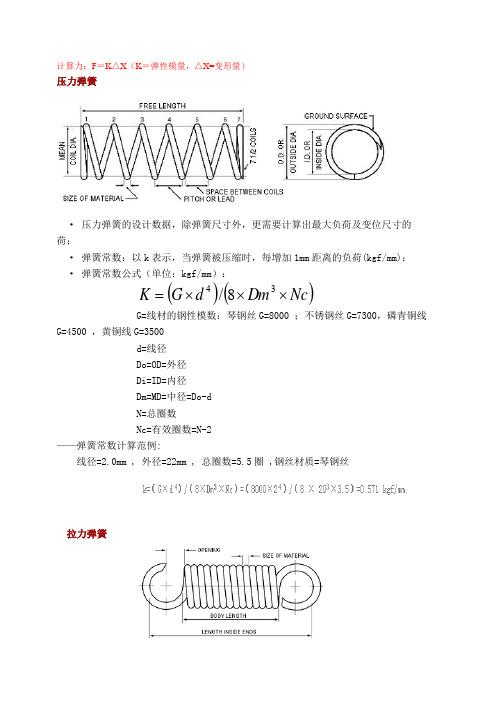
计算力:F =K △X (K =弹性模量,△X=变形量)压力弹簧· 压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的荷;· 弹簧常数:以k 表示,当弹簧被压缩时,每增加1mm 距离的负荷(kgf/mm); · 弹簧常数公式(单位:kgf/mm ):()()Nc Dm d G K ⨯⨯⨯=348/G=线材的钢性模数:琴钢丝G=8000 ;不锈钢丝G=7300,磷青铜线G=4500 ,黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2——弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。
拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不平均的现象。
所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。
· 初张力=P-(k×F1)=最大负荷-(弹簧常数×拉伸长度)扭力弹簧· 弹簧常数:以 k 表示,当弹簧被扭转时,每增加1°扭转角的负荷 (kgf/mm).· 弹簧常数公式(单位:kgf/mm):()()R4⨯⨯/=1167⨯K⨯pN⨯DmdEE=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。
弹簧设计计算过程

弹簧设计计算已知条件:最小工作压力:F1=15N最大工作压力:F2=210N工作行程:h=15.5mm弹簧外径:D=17mm弹簧直径:d=3mm计算步骤:1),弹簧中径: D2=D-d=17-3=14mm2),弹簧指数C : 214 4.73D C d === 3),弹簧工作圈数n :21321()7700015.5322.1(22)8()8(21015)G d n F F C λλ-⨯⨯===-⨯-取 (查表得 剪切弹性模数G=77000)4),修正变形量λ1和λ2(1)最小工作载荷F1 :2112315.5770003F =F 21014.1822 4.7N λλ-⨯⨯-=-=⨯⨯⨯⨯3()Gd 8n c (2)弹簧刚度j : 212101512.58/15.5F F j N mm h --=== (3)变形量λ1和λ21114.1 1.1212.58F mm j λ=== 2221016.6912.58F mm j λ=== 5),弹簧圈间隙δ:216.690.10.13 1.0622d mm n λδ=+=+⨯=(取1mm ) 6)弹簧节距P :P=δ+d=1+3=4mm 7)弹簧自由高度H 0:01(0.5)221(240.5)392.5H n n d mm δ=+-=⨯+-⨯= (总圈数 n 1=n+2=24)8)实际极限载荷F lim :lim 12.58221276.76F jn N δ==⨯⨯=弹簧的最大压缩量也就是最大工作负荷下的变形量F:F=Pn/P' 式中:Pn--最大工作负荷,N. Pn=πd^3/(3KD) [ τ ]式中:d--弹簧钢丝直径,mm. D--弹簧中径,mm. K--曲度系数,K=(4c-1)/(4c-4)+ 0.615/c c=D/d[ τ ]--弹簧的许用应力,MPa.P'--弹簧刚度,N/mm. P'=(Pn-P1)/h. 式中:P1--最小工作负荷,N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合弹簧的设计与计算
组合弹簧是一种由多个弹簧组成的复合弹簧,具有结构简单、能量密度高、工作稳定可靠等特点。
组合弹簧的设计与计算是一项重要的工作,需要考虑弹簧的材料、尺寸、弹性系数、刚度、阻尼等因素,以保证其满足要求的工作条件。
设计组合弹簧时,首先需要确定所需的弹簧力和工作环境,然后根据弹簧的工作原理和参数,选择合适的材料和尺寸进行设计。
在设计中,需要考虑各个弹簧之间的相互影响和协调,以保证组合弹簧的整体性能。
计算组合弹簧的弹性系数、刚度和阻尼等参数,可以采用经验公式、数值模拟和试验等方法。
其中,经验公式主要适用于设计简单的组合弹簧,数值模拟可以较准确地模拟组合弹簧的工作性能,试验则可以验证模拟结果和设计方案的可行性。
总之,组合弹簧的设计与计算是一项复杂而重要的工作,需要综合考虑多个因素,以保证组合弹簧能够满足工程要求。
- 1 -。
