BBS挑战100浙教版数学九上二次函数及图像练习及答案
浙教版九年级上册数学第1章 二次函数含答案

浙教版九年级上册数学第1章二次函数含答案一、单选题(共15题,共计45分)1、已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过()A.一、二、三象限B.一、二、四象限C.一、三、四象限D.一、二、三、四象限.2、抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论是()A.③④B.②④C.②③D.①④3、二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的图象,则关于x的方程ax2+bx+c=m有实数根的条件是()A.m≥﹣2B.m≥5C.m≥0D.m>44、已知二次函数y=ax²-8ax(a为常数)的图象不经过第二象限,在自变量x 的值满足2≤x≤3时,其对应的函数值y的最大值为3,则a的值为()A. B. C. D.5、若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为()A.0 5B.0 1C.﹣4 5D.﹣4 16、把函数的图像向下平移2个单位长度,所得到的新函数的解析式是()A. B. C. D.7、已知一次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是()A.1B.2C.3D.48、函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为A.1B.2C.3D.49、二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是()A.①④B.②④C.①②③D.①②③④10、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是A.a>0B.3是方程ax 2+bx+c=0的一个根C.a+b+c=0D.当x <1时,y随x的增大而减小11、已知二次函数y=1﹣3x+5x2,则其二次项系数a,一次项系数b,常数项c分别是()A.a=1,b=﹣3,c=5B.a=1,b=3,c=5C.a=5,b=3,c=1 D.a=5,b=﹣3,c=112、关于二次函数的下列结论,不正确的是()A.图象的开口向上B.当时,y随x的增大而减小C.图象经过点D.图象的对称轴是直线13、下列结论中,不正确的有()①反比例函数y=的函数值y随x的增大而减小;②任意三点确定一个圆;③圆既是轴对称图形又是中心对称图形;④二次函数y=x2-2x-3(x≥1)的函数值y随x的增大而减小;⑤平分弦的直径垂直于弦;⑥相等的圆周角所对的弧相等.A.2个B.3个C.4个D.5个14、如图,在同一平面直角坐标系中,函数与的图象可能是().A. B. C. D.15、当a-1≤x≤a时,函数y=x2-2x+1的最小值为1,则a的值为( )A.1B.2C.1或2D.0或3二、填空题(共10题,共计30分)16、若抛物线y=x2﹣6x+m与x轴没有交点,则m的取值范围是________.17、函数y=2x2﹣3x+4经过第________象限.18、将y=2x2﹣12x﹣12变为y=a(x﹣m)2+n的形式,则m•n=________.19、形状与抛物线y=2x2﹣3x+1的图象形状相同,但开口方向不同,顶点坐标是(0,﹣5)的抛物线的关系式为________.20、已知二次函数的顶点坐标为(1,4),且其图象经过点(-2,-5),求此二次函数的解析式________.21、函数y=x2+2x-8与y轴的交点坐标是________.22、二次函数的图象如图所示,则y<0时自变量x的取值范围是________ .23、已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:x …﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …y … 3 ﹣2 ﹣5 ﹣6 ﹣5 …则关于x的一元二次方程ax2+bx+c=﹣2的根是________.24、若是二次函数,则m=________.25、二次函数y=ax2+bx+c (a≠0)(a≠0,a,b,C为常数)的图象,若关于x的一元二次方程ax2+bx+c=m有实数根,则m的取值范围是________.三、解答题(共5题,共计25分)26、如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.(1)求点D的坐标;(2)求经过O、D、B三点的抛物线的函数关系式.27、国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A,B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同,销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系式yA =﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系式yB=﹣x+14.(1)求A、B两种型号的汽车的进货单价;(2)已知A型汽车的售价比B型汽车的售价高2万元/台,设B型汽车售价为t万元/台.每周销售这两种车的总利润为W万元,求W与t的函数关系式,A、B两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?28、如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B 两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P 是直线BC下方的抛物线上一动点。
浙教版九年级上册数学第1章 二次函数 含答案

浙教版九年级上册数学第1章二次函数含答案一、单选题(共15题,共计45分)1、已知抛物线y=ax2+2ax+4(0<a<3),A(x1, y1)B(x2,y2)是抛物线上两点,若x1>x2,且x1+x2=1-a, 则()A.y1< y2B.y1= y2C.y1> y2D.y1与y2的大小不能确定2、已知二次函数的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是()A.abc<0B.b=2aC.a+b+c=0D.2a+b3、已知二次函数的图象如图所示,下列结论中正确的个数是()①;②;③;④;⑤(为实数,且)A.2个B.3个C.4个D.5个4、二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①ab<0;②b2>4ac;③a+b+c<0;④3a+c<0.其中正确的是()A.①④B.②④C.①②③D.①②③④5、如图,抛物线与轴相交于、两点,与轴相交于点,点在抛物线上,且. 与轴相交于点,过点的直线平行于轴,与抛物线交于,两点,则线段的长为()A. B.3 C. D.6、已知二次函数y=x2+2x+2,图象的顶点为A,图象与y轴交于点B,O为坐标原点,则AB的长等于()A.1B.C.D.7、如图,抛物线y=ax2+bx+c经过(﹣1,0)和(0,﹣1)两点,则抛物线y=cx2+bx+a的图象大致为()A. B. C.D.8、抛物线的顶点坐标是()A. B. C. D.9、将抛物线y=x2+1 绕原点O旋转180°,则旋转后的抛物线的解析式为()A.y=-x 2B.y=-x 2+1C.y=-x 2-1D.y=x-110、已知二次函数y=﹣(x﹣a)2﹣b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是()A. B. C. D.11、下列函数中是二次函数的有()①y=x+;②y=3(x-1)2+2;③y=(x+3)2-2x2;④.A.1个B.2个C.3个D.4个12、已知二次函数y=ax2+bx+c,其中a<0,若函数图象与x轴的两个交点均在负半轴,则下列判断错误的是()A.abc<0B.b>0C.c<0D.b+c<013、已知抛物线y=-x2+(6-2m)x-m2+3的对称轴在y轴的右侧,当x>2时,y的值随着x值的增大而减小,点P是抛物线上的点,设P的纵坐标为t,若t≤3,则m的取值范围是()A.m≥B. ≤m<3C.m<3D.1≤m<314、如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是图中的()A. B. C.D.15、将抛物线y=3x2向右平移两个单位,再向下平移4个单位,所得抛物线是()A. B. C. D.二、填空题(共10题,共计30分)16、对某条线段的长度进行了3次测量,得到3个结果(单位:mm)9.9,10.1,10.0,若用a作为这条线段长度的近似值,当10.0mm时,最小.对另一条线段的长度进行了n次测量,得到n个结果(单位:mm)x1, x2,…x n ,若用x作为这条线段长度的近似值,当x=________mm时,(x﹣x1)2+(x﹣x2)2+…+(x﹣xn)2最小.17、根据下列表格的对应值:请你写出方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个近似解________(精确到0.1).x 2 3 2.5 2.7 2.6 2.65ax2+bx+c ﹣1 1 ﹣0.25 0.19 ﹣0.04 0.072518、抛物线图象如图,下列结论中正确的是________(填序号即可)①;②不等式的解为;③;④.19、已知抛物线y=x2+bx+c经过点A(0,5)、B(4,5),那么此抛物线的对称轴是________.20、二次函数的顶点坐标是________.21、当x=________时,二次函数y=x2﹣2x+6有最小值________.22、如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围________.23、如图,二次函数的图象经过点,对称轴为直线下列个结论:;;;;.其中正确的结论为________. (注:只填写正确结论的序号)24、已知二次函数y=x2﹣bx(b为常数),当2≤x≤5时,函数y有最小值﹣1,则b的值为________.25、已知二次函数y=ax2+bx+c中,自变量x与函数y的部分对应值如下表:x …-2 0 2 3 …y …8 0 0 3 …当x=-1时,y=________.三、解答题(共5题,共计25分)26、我们知道任何实数的平方一定是一个非负数,即:(a+b)2≥0,且﹣(a+b)2≤0.据此,我们可以得到下面的推理:∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,而(x+1)2≥0∴(x+1)2+2≥2,故x2+2x+3的最小值是2.试根据以上方法判断代数式3y2﹣6y+11是否存在最大值或最小值?若有,请求出它的最大值或最小值.27、四边形ABCD是平行四边形,AB=3,AD=,高DE=2.建立如图所示的平面直角坐标系,其中点A与坐标原点O重合.(1)求BC边所在直线的解析式;(2)设点F为直线BC与y轴的交点,求经过点B,D,F的抛物线解析式;(3)判断▱ABCD的对角线的交点G是否在(2)中的抛物线上,并说明理由.28、某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.每台机器产生的次品数p(千件)与每台机器的日产量x(千件)(生产条件要求4≤x≤12)之间变化关系如表:日产量x(千件/台)… 5 6 7 8 9 …次品数p(千件/台)…0.7 0.6 0.7 1 1.5 …已知每生产1千件合格的元件可以盈利1.6千元,但没生产1千件次品将亏损0.4千元.(利润=盈利﹣亏损)(1)观察并分析表中p与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识求出p(千件)与x(千件)的函数解析式;(2)设该工厂每天生产这种元件所获得的利润为y(千元),试将y表示x的函数;并求当每台机器的日产量x(千件)为多少时所获得的利润最大,最大利润为多少?29、某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.30、如图,已知抛物线y=-+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程;(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN 的最大值;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.参考答案一、单选题(共15题,共计45分)1、A2、D3、A4、C5、C6、B7、B8、A9、C10、B11、B12、B13、B14、C15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
浙教版数学 九年级上册第1章 1.2.1 二次函数的图象 同步练习(含答案)

浙教版九年级上册第一章二次函数1.2.1二次函数的图象同步练习一、选择题(共10*3=30分)1. 抛物线y =x 2-mx -m 2+1的图象过原点,则m 的值为( )A .0B .1C .-1D .±12. 如图,在平面直角坐标系中的函数图象的表达式应是( )A .y =x 2B .y =x 2 3223C .y =x 2D .y =x 234433. 如图,在Rt △AOB 中,AB ⊥OB ,且AB =OB =3,设直线x =t 截此三角形所得阴影部分的面积为S ,则S 与t 之间的函数关系的图象为下列选项中的( )4 已知a≠0,在同一平面直角坐标系中,函数y =ax 与y =ax 2的图象有可能是( )5. 抛物线y =x 2-6x +5的顶点坐标为( )A .(3,-4)B .(3,4)C .(-3,-4)D .(-3,4)6. 某烟花厂为北京APEC 会议举行焰火表演特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h =-t 2+20t +1.若这种礼炮在点火升空到最高点52时引爆,则从点火到引爆需要的时间为( )A .3 sB .4 sC .5 sD .6 s7. 在同一平面直角坐标系中,将抛物线y =2x 2+4x -3先向右平移2个单位,再向下平移1个单位后得到的函数图象的顶点坐标是( )A .(-3,-6)B .(1,-4)C .(1,-6)D .(-3,-4)8. 将抛物线y =x2+bx +c 先向右平移2个单位,再向下平移3个单位,所得图象的函数表达式为y =(x -1)2-4,则b ,c 的值为( )A .b =2,c =-6B .b =2,c =0C .b =-6,c =8D .b =-6,c =29. 向空中发射一枚炮弹,设第x s 时上升的高度为y m ,且时间与上升高度的关系式为y =ax 2+bx +c(a≠0).若此炮弹在第7 s 与第14 s 时上升的高度相等,则在下列时间中炮弹所在位置高度最高的是( )A .第8 sB .第10 sC .第12 sD .第15 s 10. 二次函数y =ax 2+bx +c(a≠0)的图象如图所示,对称轴是直线x =1,下列结论:①ab <0;②a +b +2c <0;③3a +c <0.其中正确的是( )A .①③B .②③C .①②D .①②③二、填空题(共8*3=24分)11.函数y =-x 2的对称轴是______,顶点坐标是_______,开口____,顶点是抛物线的23____.12. 已知抛物线y =ax 2(a≠0)与双曲线y = 的交点的横坐标大于零,则a____0(填“>”或2x “<”).13. 若y =(2-m)x m2-3是二次函数,且它的图象的开口向上,则m =____;此时当x =____时,y 有最____值.14. )已知下列函数:①y =x 2;②y =-x 2;③y =(x -1)2+2.其中,图象通过平移可以得到函数y =x 2+2x -3的图象的有_______.(填序号)15. )若二次函数y =2x 2-bx +3的对称轴是直线x =1,则b 的值为____.16. 抛物线y =x2-6x +5的顶点坐标为__________.17. 已知抛物线y =(1-m)x2除顶点外,其余各点均在x 轴的下方,则m 的取值范围为________.18. 如图所示,从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)的函数关系式是h =9.8t -4.9t 2,那么小球运动中的最大高度h 最大=_______.三、解答题(共66分)19. (6分)在如图所示的直角坐标系中,画出下列函数的图象:①y =x 2;②y =2x 2;③y =-x 2;④y =-2x 2.对比图象,说出表达式中二次项系数a 对抛物线的形状有什么影响?20. (6分)已知二次函数y=ax2(a≠0)的图象经过点(-2,4).(1)求a的值,并写出这个二次函数的表达式;(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图象的位置.21. (6分)已知直线y=kx+b经过点A(2,0),且与抛物线y=ax2(a≠0)相交于B,C(-2,4)两点.(1)求直线和抛物线的表达式;(2)在同一平面直角坐标系中画出它们的图象;(3)求△AOC的面积.22. (6分)一个涵洞的截面成如图所示的抛物线,现测得,当水面宽AB =1.6 m 时,涵洞顶点O 到水面的距离为2.4 m ,ED 离水面1.5 m ,则涵洞宽ED 是多少?是否会超过1 m ?[提示:设该涵洞截面所成抛物线的表达式为y =ax 2(a <0)]23. (6分)如图,已知抛物线①y =x2,②y =-x2,在x 轴上有一动点P 从原点出发,以每12秒2 cm 的速度沿x 轴正方向运动,出发t s 后,过点P 作与y 轴平行的直线交抛物线①于点A ,交抛物线②于点B ,过A ,B 分别作x 轴的平行线交抛物线①于点D ,交抛物线②于点C.(1)求点B ,点D 的坐标(用含t 的式子表示);(2)当点P 运动多少秒时,四边形ABCD 为正方形?24. (8分)如图,已知直线l过A(4,0)和B(0,4)两点,且它与二次函数y=ax2的图象在第一象限内交于点P.若△AOP的面积为,求二次函数y=ax2的表达式.25. (8分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的表达式;(2)若点M是抛物线对称轴上一动点,求AM+OM的最小值.26.(10分)(邵阳中考)如图所示,已知二次函数y=-2x2-4x的图象E,将其向右平移2个单位后得到图象F.(1)求图象F的函数表达式;(2)设抛物线F与x轴相交于点O,B(点B位于点O的右侧),顶点为C,点A位于y轴的负半轴上,且到x轴的距离等于点C到x轴的距离的2倍,求直线AB的函数表达式.27.(10分)如果二次函数的二次项系数为1,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;(2)探究下列问题:①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数;②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?参考答案1-5 DDDCA6-10 BCBBB11. y轴向下最高点12. >13. 1,0,小14. ①③15. 5 216. (3,-4)17. m>118. 419. 解:列表如下:x-2-1012y=x241014y=2x282028y=-x2-4-10-1-4y=-2x2-8-20-2-8描点:以所列表中的数据作为点的坐标在平面直角坐标系中描点;连线:用平滑的线连结,如图所示:由图象可知:a的绝对值相同,两条抛物线的形状就相同;|a|越大,开口越小.20. 解:(1)把(-2,4)代入y=ax2,得a=1,∴y=x2.(2)顶点为(0,0),对称轴为y 轴,开口向上,图象(除顶点外)在x 轴上方.21. 解:(1)y=-x+2,y=x 2.(2)如图所示.(3)过点C 作CD ⊥x 轴于点D ,则C0=4,.S △AOC =0A·CD=×2×4=4.121222. 解:设该涵洞截面所成抛物线的表达式为y=ax 2(a<0),由题意可得点B(0.8,-2.4),∵点B 在抛物线上,∴2.4=0.64a,∴a=-,154∴y=-x 2154即y=-x 2=-(2.4-1.5)时,154解得x=±,65∴ED=m,265∵<1265∴涵洞宽ED 是,不会超过1m.26523. 解:(1)B(2t ,一2t 2),D (一2t,4t 2).(2)要使四边形ABCD 为正方形,则有AD=AB ,即4t=6t 2,.t=或0(舍去),即点P 运23动s 时,四边形ABCD 为正方形.2324. 解:设直线的表达式为y=kx+b,将点A,B 的坐标代入y=kx+b,得,解得k=-1,b=4.{4k +b =0,b =4,)∴y=-x+4.设点P 的坐标为(x,y)且x>0,y>0.∵S △AOP =,∴×4y=921292解得y=.94当y=-x+4=时,解得x=,∴P(,).94747494将点P 的坐标代入y=ax 2,得=a×,944916解得a=,3649∴二次函数y=ax 2的表达式为y=x 2364925. 解:(1)把A (一2,一4),0(0,0),B (2,0)三点代入y=ax 2+bx +c,得解得。
二次函数的图象 浙教版九年级数学上册同步练习(含答案)
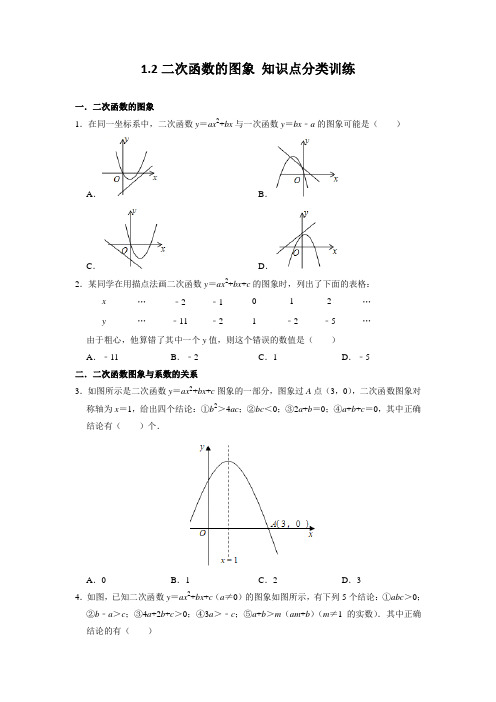
1.2二次函数的图象知识点分类训练一.二次函数的图象1.在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx﹣a的图象可能是()A.B.C.D.2.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:x…﹣2﹣1012…y…﹣11﹣21﹣2﹣5…由于粗心,他算错了其中一个y值,则这个错误的数值是()A.﹣11B.﹣2C.1D.﹣5二.二次函数图象与系数的关系3.如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论有()个.A.0B.1C.2D.34.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>﹣c;⑤a+b>m(am+b)(m≠1的实数).其中正确结论的有()A.①②③B.②③⑤C.②③④D.③④⑤5.如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是()A.﹣3<P<﹣1B.﹣6<P<0C.﹣3<P<0D.﹣6<P<﹣3 6.如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,则以下四个结论中:①abc>0,②2a+b=0,③4a+b2<4ac,④3a+c<0.正确的个数是()A.1B.2C.3D.47.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为()A.B.C.D.8.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣,y2)在该图象上,则y1>y2.其中正确的结论是(填入正确结论的序号).9.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,对称轴是直线x=﹣1,点B的坐标为(1,0).下面的四个结论:①AB=4;②b2﹣4ac>0;③ab<0;④a﹣b+c<0,其中正确的结论是(填写序号).三.二次函数图象上点的坐标特征10.若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3﹣m,n)、D(,y2)、E(2,y3),则y1、y2、y3的大小关系是()A.y1<y2<y3B.y1<y3<y2C.y3<y2<y1D.y2<y3<y1 11.已知(﹣3,y1),(﹣2,y2),(1,y3)是抛物线y=﹣3x2﹣12x+m上的点,则()A.y3<y2<y1B.y3<y1<y2C.y2<y3<y1D.y1<y3<y2 12.已知二次函数y=ax2﹣2ax+1(a<0)图象上三点A(﹣1,y1),B(2,y2)C(4,y3),则y1、y2、y3的大小关系为()A.y1<y2<y3B.y2<y1<y3C.y1<y3<y2D.y3<y1<y2 13.已知点A(x1,y1),B(x2,y2)均在抛物线y=ax2+2ax+4(0<a<3)上,若x1<x2,x1+x2=1﹣a,则()A.y1>y2B.y1<y2C.y1=y2D.y1与y2大小不能确定14.已知函数y=x2﹣2mx+2021(m为常数)的图象上有三点:A(x1,y1),B(x2,y2),C (x3,y3),其中x1=﹣+m,x2=+m,x3=m﹣1,则y1、y2、y3的大小关系是()A.y1<y3<y2B.y3<y1<y2C.y1<y2<y3D.y2<y3<y1 15.已知A(x1,2022),B(x2,2022)是二次函数y=ax2+bx+5(a≠0)的图象上两点,则当x=x1+x2时,二次函数的值是()A.B.C.2022D.516.若直线y=x+m与抛物线y=x2+3x有交点,则m的取值范围是()A.m≥﹣1B.m≤﹣1C.m>1D.m<117.已知函数y=﹣(x﹣1)2图象上两点A(2,y1),B(a,y2),其中a>2,则y1与y2的大小关系是y1y2(填“<”、“>”或“=”)18.当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为.19.已知点(﹣1,m)、(2,n)在二次函数y=ax2﹣2ax﹣1的图象上,如果m>n,那么a0(用“>”或“<”连接).20.如果点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,那么m的值为.21.已知二次函数y=ax2﹣2ax+c(a<0)图象上的两点(x1,y1)和(3,y2),若y1>y2,则x1的取值范围是.22.已知二次函数y=ax2+bx+c中,自变量x与函数y的部分对应值如下表:x…﹣2023…y…8003…当x=﹣1时,y=.23.二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:x…﹣2﹣1012…y…﹣7﹣1355…则的值为.24.已知点A(a,m)、B(b,m)、P(a+b,n)为抛物线y=x2﹣2x﹣2上的点,则n=.25.已知二次函数y=a(x﹣1)2﹣4的图象经过点(3,0).(1)求a的值;(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y2时,求m、n之间的数量关系.四.二次函数图象与几何变换26.抛物线y=x2+4x+5是由抛物线y=x2+1经过某种平移得到,则这个平移可以表述为()A.向左平移1个单位B.向左平移2个单位C.向右平移1个单位D.向右平移2个单位27.二次函数y=x2的图象平移后经过点(2,0),则下列平移方法正确的是()A.向左平移2个单位,向下平移2个单位B.向左平移1个单位,向上平移2个单位C.向右平移1个单位,向下平移1个单位D.向右平移2个单位,向上平移1个单位28.二次函数y=﹣2x2+4x+1的图象如何移动就得到y=﹣2x2的图象()A.向左移动1个单位,向上移动3个单位B.向右移动1个单位,向上移动3个单位C.向左移动1个单位,向下移动3个单位D.向右移动1个单位,向下移动3个单位29.将抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位,那么得到的抛物线的表达式为.30.将抛物线y=ax2+bx﹣1向上平移3个单位长度后,经过点(﹣2,5),则8a﹣4b﹣11的值是.31.把抛物线y=2x2﹣4x+3向左平移1个单位长度,得到的抛物线的解析式为.32.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移5个单位,得到抛物线y=x2+4x ﹣1,则a+b+c=.33.已知二次函数y1=x2+2x﹣3的图象如图所示.将此函数图象向右平移2个单位得抛物线y2的图象,则阴影部分的面积为.34.如图,将函数y=(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是.35.如图,抛物线y1=﹣x2+2向右平移1个单位得到抛物线y2,回答下列问题:(1)抛物线y2的顶点坐标;(2)阴影部分的面积S=;(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,求抛物线y3的解析式.36.把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q.(1)求顶点P的坐标;(2)写出平移过程;(3)求图中阴影部分的面积.参考答案一.二次函数的图象1.解:由方程组得ax2=﹣a,∵a≠0∴x2=﹣1,该方程无实数根,故二次函数与一次函数图象无交点,排除B.A:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;但是一次函数b为一次项系数,图象显示从左向右上升,b>0,两者矛盾,故A错;C:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;b为一次函数的一次项系数,图象显示从左向右下降,b<0,两者相符,故C正确;D:二次函数的图象应过原点,此选项不符,故D错.故选:C.2.解:由函数图象关于对称轴对称,得(﹣1,﹣2),(0,1),(1,﹣2)在函数图象上,把(﹣1,﹣2),(0,1),(1,﹣2)代入函数解析式,得,解得,函数解析式为y=﹣3x2+1当x=2时,y=﹣11,故选:D.二.二次函数图象与系数的关系3.解:由图象知和x轴有两个交点,∴Δ=b2﹣4ac>0,∴b2>4ac,故①正确;由图象知,图象与y轴交点在x轴的上方,且二次函数图象对称轴为x=1,∴c>0,∵﹣=1,a<0,∴b>0,即bc>0,2a+b=0,∴②不正确,③正确;由图象知,当x=1时y=ax2+bx+c=a×12+b×1+c=a+b+c>0,∴④不正确,综合上述:正确的个数是2,故选:C.4.解:①∵对称轴在y轴的右侧,∴ab<0,由图象可知:c>0,∴abc<0,故①不正确;②当x=﹣1时,y=a﹣b+c<0,∴b﹣a>c,故②正确;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c>0,故③正确;④∵x=﹣=1,∴b=﹣2a,∵a﹣b+c<0,∴a+2a+c<0,3a<﹣c,故④不正确;⑤当x=1时,y的值最大.此时,y=a+b+c,而当x=m时,y=am2+bm+c,所以a+b+c>am2+bm+c(m≠1),故a+b>am2+bm,即a+b>m(am+b),故⑤正确.故②③⑤正确.故选:B.5.解:∵抛物线y=ax2+bx+c(c≠0)过点(﹣1,0)和点(0,﹣3),∴0=a﹣b+c,﹣3=c,∴b=a﹣3,∵当x=1时,y=ax2+bx+c=a+b+c,∴P=a+b+c=a+a﹣3﹣3=2a﹣6,∵顶点在第四象限,a>0,∴b=a﹣3<0,∴a<3,∴0<a<3,∴﹣6<2a﹣6<0,即﹣6<P<0.故选:B.6.解:①根据抛物线开口向下可知:a<0,因为对称轴在y轴右侧,所以b>0,因为抛物线与y轴正半轴相交,所以c>0,所以abc<0,所以①错误;②因为抛物线对称轴是直线x=1,即﹣=1,所以b=﹣2a,所以b+2a=0,所以②正确;③∵b=﹣2a,∴b2=4a2,如果4a+b2<4ac,那么4a+4a2<4ac,∵a<0,∴c<1+a,而根据抛物线与y轴的交点,可知c>1,∴结论③错误;④当x=﹣1时,y<0,即a﹣b+c<0,因为b=﹣2a,所以3a+c<0,所以④正确.所以正确的是②④,共2个.故选:B.7.解:∵a<0,∴抛物线的开口方向向下,故第三个选项错误;∵c<0,∴抛物线与y轴的交点为在y轴的负半轴上,故第一个选项错误;∵a<0、b>0,对称轴为x=>0,∴对称轴在y轴右侧,故第四个选项错误.故选:B.8.解:∵二次函数开口向下,且与y轴的交点在x轴上方,∴a<0,c>0,∵对称轴为x=1,∴﹣=1,∴b=﹣2a>0,∴abc<0,故①、③都不正确;∵当x=﹣1时,y<0,∴a﹣b+c<0,故②正确;由抛物线的对称性可知抛物线与x轴的另一交点在2和3之间,∴当x=2时,y>0,∴4a+2b+c>0,故④正确;∵抛物线开口向下,对称轴为x=1,∴当x<1时,y随x的增大而增大,∵﹣2<﹣,∴y1<y2,故⑤不正确;综上可知正确的为②④,故答案为:②④.9.解:∵抛物线对称轴是直线x=﹣1,点B的坐标为(1,0),∴A(﹣3,0),∴AB=4,故选项①正确;∵抛物线与x轴有两个交点,∴b2﹣4ac>0,故选项②正确;∵抛物线开口向上,∴a>0,∵抛物线对称轴在y轴左侧,∴a,b同号,∴ab>0,故选项③错误;当x=﹣1时,y=a﹣b+c此时最小,为负数,故选项④正确;故答案为:①②④.三.二次函数图象上点的坐标特征10.解:∵经过A(m,n)、C(3﹣m,n),∴二次函数的对称轴x=,∵B(0,y1)、D(,y2)、E(2,y3)与对称轴的距离B最远,D最近,∵|a|>0,∴y1>y3>y2;故选:D.11.解:抛物线的对称轴为直线x=﹣=﹣2,∵a=﹣3<0,∴x=﹣2时,函数值最大,又∵﹣3到﹣2的距离比1到﹣2的距离小,∴y3<y1<y2.故选:B.12.解:y=ax2﹣2ax+1(a<0),对称轴是直线x=﹣=1,即二次函数的开口向下,对称轴是直线x=1,即在对称轴的右侧y随x的增大而减小,A点关于直线x=1的对称点是D(3,y1),∵2<3<4,∴y2>y1>y3,故选:D.13.解:将点A(x1,y1),B(x2,y2)分别代入y=ax2+2ax+4(0<a<3)中,得:y1=ax12+2ax1+4﹣﹣﹣﹣①,y2=ax22+2ax2+4﹣﹣﹣﹣②,②﹣①得:y2﹣y1=(x2﹣x1)[a(3﹣a)],因为x1<x2,3﹣a>0,则y2﹣y1>0,即y1<y2.故选:B.14.解:y=x2﹣2mx+2021=(x﹣m)2﹣m2+2021,∴抛物线开口向上,对称轴为:直线x=m,当x>m时,y随x的增大而增大,由对称性得:x1=﹣+m与x=m+的y值相等,x3=m﹣1与x=m+1的y值相等,且,∴+m<m+1<m+,∴y2<y3<y1;故选:D.15.解:∵A(x1,2022),B(x2,2022)是二次函数y=ax2+bx+5(a≠0)的图象上两点,又∵点A、B的纵坐标相同,∴A、B关于对称轴x=﹣对称,∴x=x1+x2=﹣,∴a+b(﹣)+5=5;故选:D.16.解:令x+m=x2+3x,则x2+2x﹣m=0,令△=22﹣4×1×(﹣m)≥0,解得,m≥﹣1,故选:A.17.解:∵函数y=﹣(x﹣1)2,∴函数的对称轴是直线x=1,开口向下,∵函数图象上两点A(2,y1),B(a,y2),a>2,∴y1>y2,故答案为:>.18.解:∵当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3=(x﹣1)2+2的函数值相等,∴以m、n为横坐标的点关于直线x=1对称,则=1,∴m+n=2,∵x=m+n,∴x=2,函数y=4﹣4+3=3.故答案为3.19.解:∵二次函数的解析式为y=ax2﹣2ax﹣1,∴该抛物线对称轴为x=1,∵|﹣1﹣1|>|2﹣1|,且m>n,∴a>0.故答案为:>.20.解:由点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,得(﹣1,4)与(m,4)关于对称轴x=1对称,m﹣1=1﹣(﹣1),解得m=3,故答案为:3.21.解:∵y1>y2,∴a﹣2ax1+c>9a﹣6a+c,∴a﹣2ax1﹣3a>0,∵a<0,∴函数y=a﹣2ax1﹣3a开口向下,令a﹣2ax1﹣3a=0,解得x1=﹣1或3,画出函数图象示意图:由图象可得,当﹣1<x<3时,a﹣2ax1﹣3a>0,∴x1的取值范围是﹣1<x1<3,故答案为:﹣1<x1<3.22.解:依据表格可知抛物线的对称轴为x=1,∴当x=﹣1时与x=3时函数值相同,∴当x=﹣1时,y=3.故答案为:3.23.解:∵x=1、x=2时的函数值都是﹣1相等,∴此函数图象的对称轴为直线x=﹣==,即=﹣.故答案为:﹣.24.解:∵抛物线解析式为y=x2﹣2x﹣2=(x﹣1)2﹣3,∴该抛物线的对称轴是直线x=1,又∵点A(a,m)和B(b,m)关于直线x=1对称,∴=1,∴a+b=2,把(2,n)代入抛物线的解析式得,n=22﹣2×2﹣2=﹣2.故答案是:﹣2.25.解:(1)将(3,0)代入y=a(x﹣1)2﹣4,得0=4a﹣4,解得a=1;(2)方法一:根据题意,得y1=(m﹣1)2﹣4,y2=(m+n﹣1)2﹣4,∵y1=y2,∴(m﹣1)2﹣4=(m+n﹣1)2﹣4,即(m﹣1)2=(m+n﹣1)2,∵n>0,∴m﹣1=﹣(m+n﹣1),化简,得2m+n=2;方法二:∵函数y=(x﹣1)2﹣4的图象的对称轴是经过点(1,﹣4),且平行于y轴的直线,∴m+n﹣1=1﹣m,化简,得2m+n=2.四.二次函数图象与几何变换26.解:原抛物线的顶点为(0,1),新抛物线的顶点为(﹣2,1),∴是抛物线y=x2+1向左平移2个单位得到,故选:B.27.解:A、平移后的解析式为y=(x+2)2﹣2,当x=2时,y=14,本选项不符合题意.B、平移后的解析式为y=(x+1)2+2,当x=2时,y=11,本选项不符合题意.C、平移后的解析式为y=(x﹣1)2﹣1,当x=2时,y=0,函数图象经过(2,0),本选项符合题意.D、平移后的解析式为y=(x﹣2)2+1,当x=2时,y=1,本选项不符合题意.故选:C.28.解:二次函数y=﹣2x2+4x+1的顶点坐标为(1,3),y=﹣2x2的顶点坐标为(0,0),∴向左移动1个单位,向下移动3个单位.故选:C.29.解:抛物线y=2(x﹣1)2+2向左平移3个单位,再向下平移4个单位得到y=2(x﹣1+3)2+2﹣4=2(x+2)2﹣2.故得到抛物线的解析式为y=2(x+2)2﹣2.故答案为:y=2(x+2)2﹣2.30.解:将抛物线y=ax2+bx﹣1向上平移3个单位长度后,表达式为:y=ax2+bx+2,∵经过点(﹣2,5),代入得:4a﹣2b=3,则8a﹣4b﹣11=2(4a﹣2b)﹣11=2×3﹣11=﹣5,故答案为:﹣5.31.解:∵y=2x2﹣4x+3=2(x﹣1)2+1,∴向左平移1个单位长度得到的抛物线的解析式为y=2(x+1﹣1)2+1=2x2+1,故答案为:y=2x2+1.32.解:平移后的抛物线y=x2+4x﹣1=(x+2)2﹣5,顶点为(﹣2,﹣5),根据平移规律,得原抛物线顶点坐标为(0,0),又平移不改变二次项系数,∴原抛物线解析式为y=x2,∴a=1,b=c=0,∴a+b+c=1,故答案为1.33.解:由题意知,y1=x2+2x﹣3=(x+1)2﹣4,则顶点坐标是(﹣1,﹣4).所以,阴影部分的面积为:2×4=8.故答案是:8.34.解:∵函数y=(x﹣2)2+1的图象过点A(1,m),B(4,n),∴m=(1﹣2)2+1=,n=(4﹣2)2+1=3,∴A(1,),B(4,3),过A作AC∥x轴,交B′B的延长线于点C,则C(4,),∴AC=4﹣1=3,∵曲线段AB扫过的面积为9(图中的阴影部分),∴AC•AA′=3AA′=9,∴AA′=3,即将函数y=(x﹣2)2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象,∴新图象的函数表达式是y=(x﹣2)2 +4.故答案是:y=(x﹣2)2 +4.35.解:(1)读图找到最高点的坐标即可.故抛物线y2的顶点坐标为(1,2);(2)把阴影部分进行平移,可得到阴影部分的面积即为图中两个方格的面积=1×2=2;(3)由题意可得:抛物线y3的顶点与抛物线y2的顶点关于原O成中心对称.所以抛物线y3的顶点坐标为(﹣1,﹣2),于是可设抛物线y3的解析式为:y=a(x+1)2﹣2.由对称性得a=1,所以y3=(x+1)2﹣2.36.解:(1)平移的抛物线解析式为y=(x+6)x=x2+3x=(x+3)2﹣,所以顶点P的坐标为(﹣3,﹣);(2)把抛物线y=x2先向左平移3个单位,再向下平移个单位即可得到抛物线y=(x+3)2﹣;(3)图中阴影部分的面积=S△OPQ=×3×9=.。
浙教版九年级上册数学第1章 二次函数含答案(精练)

浙教版九年级上册数学第1章二次函数含答案一、单选题(共15题,共计45分)1、将抛物线y=x2向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为()A.y=(x﹣2)2+3B.y=(x+2)2+2C.y=(x﹣3)2+2D.y=(x+3)2+22、关于二次函数y=-2(x-3) +5的最大值,下列说法正确的是( )A.最大值是3B.最大值是-3C.最大值是5D.最大值是-53、抛物线y=x2﹣bx+8的顶点在x轴上,则b的值一定为()A.4B.﹣4C.2或﹣2D.4 或﹣44、抛物线y=x2-2x-1上有点P(-1,y1)和Q (m,y2),若y1>y2,则m的取值范围为( )A.m>-1B.m<-1C.-1<m<3D.-1≤m<35、二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.当x=﹣1或x=2时,y=0D.当x>0时,y随x的增大而增大6、抛物线y=-2x2+1的对称轴是()A.直线x=B.直线x=-C.直线x=2D.直线x=07、如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.其中正确的个数是()A.1B.2C.3D.48、已知二次函数y=x2+bx-2的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是().A.(1,0)B.(2,0)C.(-2,0)D.(-1,0)9、抛物线的顶点坐标是()A. B. C. D.10、抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3,则b、c的值为()A.b=2,c=2B.b=2,c=0C.b=﹣2,c=﹣1D.b=﹣3,c=211、抛物线向左平移8个单位,再向下平移9个单位后,所得抛物线关系式是()A. (x+8)2-9B. (x-8) 2+9C. (x-8) 2-9D.(x+8) 2+912、已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是()A.abc>0B.a+b+c>0C.c<0D.b<013、对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是()A.开口向下B.对称轴是x=﹣1C.顶点坐标是(1,2)D.与x 轴有两个交点14、小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为()A.4.4B.3.4C.2.4D.1.415、将函数y=x2+x的图象向右平移a(a>0)个单位,得到函数y=x2﹣3x+2的图象,则a的值为()A.1B.2C.3D.4二、填空题(共10题,共计30分)16、若抛物线y=ax2经过点A ( ,-9),则其解析式为________。
浙教版九年级上册数学第1章 二次函数含答案

浙教版九年级上册数学第1章二次函数含答案一、单选题(共15题,共计45分)1、在平面直角坐标系中,二次函数 y1=﹣x2+4x 和一次函数 y2=2x 的图象如图所示,那么不等式﹣x2+4x>2x 的解集是()A.x<0B.0<x<4C.0<x<2D.2<x<42、已知抛物线,与轴的一个交点为,则代数式的值为()A. B. C. D.3、已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0;④的最小值为3.其中,正确结论的个数为()A.1个B.2个C.3个D.4个4、在直角坐标系中,把抛物线y=x2+4向上平移2个单位长度,再向右平移3个单位长度,可得到抛物线的解析式为()A.y=(x﹣3)2+2B.y=(x﹣3)2+6C.y=(x+3)2+2 D.y=(x+3)2+65、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个结论①a、b同号②当x=1和x=3时函数值相等③4a+b=0④当y=-2时x的值只能取0其中正确的个数A.1个B.2个C.3个D.4个6、抛物线的顶点在()A.x轴正半轴上B.x轴负半轴上C.y轴正半轴上D.y轴负半轴上7、一条开口向上的抛物线的顶点坐标是(﹣1,2),则它有()A.最大值1B.最大值﹣1C.最小值2D.最小值﹣28、已知二次函数y=ax2+bx+c(a≠0,a,b,c为常数)的y与x的部分对应值如下表:x 3.23 3.24 3.25 3.26y ﹣0.06 ﹣0.08 ﹣0.03 0.09判断方程ax2+bx+c=0的一个解x的取值范围是()A.3<x<3.23B.3.23<x<3.24C.3.24<x<3.25D.3.25<x <3.269、已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如下面右图所示,则函数y=ax+b的图象可能正确的是()A. B. C. D.10、二次函数与的图象与x轴有交点,则k的取值范围是A. B. 且 C. D. 且11、如图,点A,B的坐标分别为(1,4)和(4,4),抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )A.-3B.1C.5D.812、如图,已知抛物线的对称轴为直线,与x轴的两个交点是A,B,其中点A的坐标为,则下列结论:①;②;③点B的坐标是;④点、是抛物线上的两点,若,则,其中正确结论的个数是()A.1个B.2个C.3个D.4个13、已知抛物线y=ax2+b x+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )A.a>0B.b<0C.c<0D.a+b+c>014、下列函数中,属于二次函数的是 ( )A. B. C. D.15、下列关于函数的图象说法:①图象是一条抛物线;②开口向下;③对称轴是y轴;④顶点(0,0),其中正确的有()A.1个B.2个C.3个D.4个二、填空题(共10题,共计30分)16、将抛物线向上平移个单位,再向左平移个单位后,得到的抛物线的顶点坐标是________.17、对称轴为的抛物线如图所示,与x 轴分别交于点,,,有下列五个结论:①;②;③(t为实数);④当时,y随x增大而增大;⑤若方程的两个实数根分别为,,且,则,.其中结论错误的是________.18、已知函数,当时,此函数的最大值是________,最小值是________.19、已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(﹣2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是________20、抛物线y=x2+mx+4与x轴仅有一个交点,则该交点的坐标是________.21、对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是________.22、已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x的方程ax2+bx+c的两个根分别是x1=1.3和x2=________。
浙教版九年级数学上1.2二次函数的图像(2)同步练习含答案

1.2二次函数的图像(二)一、选择题1.抛物线y=-3x 2一点到x 轴的距离是3,则该点的横坐标是( )A .-27 B.1 C.-1 D.1或-12.将二次函数y=x 2的图象向右平移一个单位长度,再向上平移3个单位长度所得的图象解析式为( )A. y=(x ﹣1)2+3B. y=(x+1)2+3C.y=(x ﹣1)2﹣3D. y=(x+1)2﹣3 3.图象的顶点为(-2,-2),且经过原点的二次函数的关系式是( )A .y=(x+2)2-2B .y=(x-2)2-2C .y=2(x+2)2-2D .y=2(x-2)2-24.已知抛物线的顶点坐标是,则和的值分别是( ) A.2,4 B. C.2, D.,0 ★5.已知抛物线c bx ax y ++=2与x 轴的一个交点(1,0)对称轴为直线x =-1,则该抛物线与轴另一个交点坐标为( )A.(-3,0)B.(-2,0)C.(2,0)D.无法确二、填空题6.将二次函数22(1)4y x =--+的图象向左平移2个单位长度,再向下平移3个单位长度,得到函数解析式为: . 7.已知m ,n 是方程2230x x +-=的两个实数根,则m 2﹣mn +3m +n =8.对于二次函数, 已知当由1增加到2时,函数值减少3,则常数的值是9.如果二次函数16的图象顶点的横坐标为1,则的值为 . ★10.设抛物线y=ax 2+bx+c (a ≠0)过A (0,2),B (4,3),C 三点,其中点C 在直线x=2上,且点C 到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 ___________ .三、解答题11.已知抛物线y=-x2+bx+c 经过点A(3,0),B(-1,0) 求抛物线的解析式,求抛物线顶点坐标12.已知二次函数y=x2-2x-1.(1)求此二次函数的图象与x轴的交点坐标;(2)二次函数y=x2的图象如图所示,将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2-2x-1的图象13.已知二次函数y=(x+1)2 -4,指出函数图象的开口方向、对称轴和顶点坐标。
浙教版九年级上册数学第1章 二次函数含答案

浙教版九年级上册数学第1章二次函数含答案一、单选题(共15题,共计45分)1、二次函数的大致图象如图所示,关于该二次函数,下列说法错误的是()A.函数有最小值B.对称轴是直线x=C.当x< ,y随x的增大而减小D.当 -1 < x < 2时,y>02、如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac<b2,④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是()A.①②③B.①②④C.②③④D.③④⑤3、如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于C点,图中虚线为抛物线的对称轴,则下列正确的是( )A.a<0B.b<0C.c>0D.b 2-4ac<04、抛物线y=x2, y=-3x2, y=x2的图象开口最大的是()A.y= x 2B.y=-3x 2C.y=x 2D.无法确定5、已知抛物线与x轴没有交点,过、、、四点,则的大小关系是( )A. B. C. D.6、已知二次函数y=﹣x2+2x﹣3,用配方法化为y=a(x﹣h)2+k的形式,结果是()A.y=﹣(x﹣1)2﹣2B.y=﹣(x﹣1)2+2C.y=﹣(x﹣1)2+4 D.y=﹣(x+1)2﹣47、关于x的二次函数y=a(x+1)(x﹣m),其图象的对称轴在y轴的右侧,则实数a、m应满足()A.a>0,m<﹣1B.a>0,m>1C.a≠0,0<m<1D.a≠0,m >18、抛物线y= x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为()A.y = x 2+ 2x + 1B.y = x 2 + 2x - 2C.y = x 2 - 2x -1 D.y = x2 - 2x + 19、如图,抛物线与x轴交于点A和B,线段AB的长为2,则k的值是()A.3B.−3C.−4D.−510、如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为()A.6B.12C.18D.2411、若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x2﹣16),则符合条件的点P()A.有且只有1个B.有且只有2个C.有且只有3个D.有无穷多个12、已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )A.有最大值2,有最小值-2.5B.有最大值2,有最小值1.5C.有最大值1.5,有最小值-2.5D.有最大值2,无最小值13、若抛物线y=x2-2x+m的最低点的纵坐标为n,则m-n的值是()A.-1B.C.1D.214、如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y 轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①a﹣b+c<0;②2a+b+c>0;③x(αx+b)≤a+b;④a>﹣1.其中正确的有()A. 4个B.3个C.2个D.1个15、抛物线y=(x-2)2+1是由抛物线影响y=x2平移得到的,下列对于抛物线y=x2的平移过程叙述正确的是()A.先向右平移2个单位,再向上平移1个单位B.先向右平移2个单位,再向下平移1个单位C.先向左平移2个单位,再向上平移1个单位 D.先向左平移2个单位,再向下平移1个单位二、填空题(共10题,共计30分)16、如图,抛物线的对称轴为直线,与轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①;②方程的两个根是;③;④当时,的取值范围是;⑤当时,随增大而增大;其中结论正确有________.17、函数与的图象及交点如图所示,则不等式x2<x+2的解集是________.18、已知二次函数()图象的顶点在第二象限,且过点(1,0),则________0(用“<、>、、、=”填写).19、若二次函数(、为常数)的图象如图,则的值为________20、抛物线经过点A(0,3),B(2,3),抛物线的对称轴为________.21、若二次函数y=2x2经过平移后顶点的坐标为(﹣2,3),则平移后的解析式为________.22、把函数y=x2+3的图象向下平移1个单位长度得到的图象对应的函数关系式为________.23、已知二次函数y=m (x﹣1)( x﹣4)的图象与x轴交于A,B两点(点A 在点B的左边),顶点为C,将该二次函数的图象关于x轴翻折,所得图象的顶点为D.若四边形ACBD为正方形,则m的值为________.24、将抛物线y=-x2-4x(-4≤x≤0)沿y轴折叠后得另一条抛物线,若直线y=x+b与这两条抛物线共有3个公共点,则b的取值范围为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数及图像练习
一、选择题:
1、[2014·兰州]抛物线3)1(2--=x y 的对称轴是( )
A 、y 轴
B 直线1-=x
C 、直线1=x
D 、直线3-=x
2、已知x 是实数,且满足01)2)(2(=---x x x ,则相应的二次函数12++=x x y 的值为( )
A 、13或3
B 、7或3
C 、3
D 、13或7或3
3、抛物线432+--=x x y 与坐标轴的交点个数是( )
A 、3
B 、2
C 、1
D 、0
4、将抛物线342+-=x x y 平移,使它平移后的顶点为(﹣2,4),则需将该抛物线( )
A 、先向右平移4个单位,再向上平移5个单位
B 、先向右平移4个单位,再向下平移5个单位
C 、先向左平移4个单位,再向上平移5个单位
D 、先向左平移4个单位,再向下平移5个单位
5、抛物线32-+=bx ax y 经过点(2,4),则代数式8a +4b +1的值为( )
A 、3
B 、9
C 、15
D 、—15
6、[2014·遵义]已知抛物线bx ax y +=2和直线b ax y +=在同一坐标系内的图象如图,
其中正确的是( ) A B C D 7、如图,平面直角坐标系内二次函数12+=x y 的图象通过A ,B 两点,且坐标分别为
(a ,
429),(b ,4
29),则AB 的长度为( ) A 、5 B 、425 C 、2
29 D 、229 8、某市举办了苏迪曼杯羽毛球混合团体锦标赛,在比赛中,某次羽毛球的运动线路可以看做是抛物线c bx x y ++-=24
1的一部分(如图),其中出球点B 离地面O 点的距离是1m ,球落地点A 到O 点的距离是4m ,那么这条抛物线的表达式是( )
A 、14
3412++-
=x x y B 、14
3412-+-=x x y C 、14
3412+--=x x y
D 、143412---=x x y 9、如图,平面直角坐标系中,两条抛物线有相同的对称轴,
则下列关系正确的是( )
A 、h k n m >=,
B 、h k n m <=,
C 、h k n m =>,
D 、h k n m =<,
10、坐标平面上,若移动二次函数6)176)(175(2+--=x x y 的图象,使其与x 轴交于两点,且此两点的距离为1单位,则移动方式可为下列哪一种( )
A 、向上移动3单位
B 、向下移动3单位
C 、向上移动6单位
D 、向下移动6单位
二、填空题
11、若函数3)2()4(22+++-=x k x k y 是二次函数,则k
12、[2014·天津]抛物线322+-=x x y 的顶点坐标是
13、若函数122++=x mx y 的图象与x 轴只有一个公共点,则常数m 的值是 14、抛物线c bx x y ++=2的图象如图所示,则它关于y 轴对称的抛物线表达式是
(第14题图) (第15题图) (第16题图)
15、已知二次函数c bx ax y ++=2的图象如图所示,有下列5个结论:①abc <0;②b <a +c ;③4a +2b +c >0;④2c <3b ;⑤a +b <m (am +b )(m ≠1的实数),其中正确结论的序号有
16、如图,抛物线的顶点为P (—2,2),与y 轴交于点A (0,3),若平移该抛物线使其顶
点P 沿直线移动到‘P (2,—2),点A 的对应点为’A ,则抛物线上PA 段扫过的区域(阴
影部分)的面积为
三、解答题
17、已知二次函数c x ax y +-=32,当2-=x 时,函数值是1-;当1=x 时,函数值是4-.求这个二次函数的表达式。
18、如图,抛物线4)1(2+-=x a y 与x 轴交于点A ,B ,与y 轴交于点C ,过点C 作CD ∥x 轴交抛物线的对称轴于点D ,连结BD ,已知点A 的坐标为(1-,0).
(1)求该抛物线的表达式;
(2)求梯形COBD 的面积.
19、已知某二次函数图象的顶点是)21
(,-,且过点)2
30(, (1)求此抛物线的表达式;
(2)求证:对任意实数m ,点(m ,2m -)都不在这个二次函数的图象上.
20、现将抛物线c bx ax y ++=2先向左平移3个单位,再向下平移2个单位,的到抛物线
122
12++-=x x y .求原抛物线的表达式.
21、如图,二次函数c bx x y ++=2的图象经过点M (1,2-),N (1-,6). (1)求二次函数c bx x y ++=2的表达式;
(2)把Rt △ABC 放在坐标系内,其中∠CAB=90°,点A ,B 的坐标分别为点(1,0), (4,0),BC=5.将△ABC 沿x 轴向右平移,当点C 落在抛物线上时,求△ABC 平移的距离.
22、如图,抛物线221+-=x y 向右平移1个单位得到抛物线2y ,回答下列问题:
(1)抛物线2y 的顶点坐标为 ;
(2)阴影部分的面积S= ;
(3)若再将抛物线2y 绕原点O 旋转180°得到抛
物线3y ,求抛物线3y 的表达式.
23、对于二次函数)0(2≠++=a c bx ax y ,如果当x 取任意整数时,函数值y 都是整数,那么我们把该函数的图象叫做整点抛物线,例如:222++=x x y .
(1)请你写出一个二次项系数的绝对值小于1的整点抛物线的表达式 (不必证明);
(2)请探索:是否存在二次项系数的绝对值小于
21的整点抛物线?若存在,请写出其中一条抛物线的表达式;若不存在,请说明理由.
24、已知抛物线)0(322≠++=a x ax y 有如下两个特点:①无论实数a 怎么变化其顶点都在某一条直线l 上;②若把顶点的横坐标减少
a 1,纵坐标增加a 1分别作为点A 的横、纵坐标,把顶点的横坐标增加
a 1,纵坐标增加a 1分别作为点B 的横、纵坐标,则A ,B 两点也在抛物线)0(322≠++=a x ax y 上.
(1)求出当实数a 变化时,抛物线)0(322
≠++=a x ax y 的顶点所在直线l 的表达式;
(2)请找出在直线l 上但不是该抛物线顶点的所有点,并说明理由;
(3)你能根据特点②的启示,对一般二次函数)0(2≠++=a c bx ax y 提出一个猜想吗?请用数字语言把你的猜想表达出来,并给予证明.
23、
24、。
