贵州师范大学硕士研究生入学考试大纲(复试)
贵州师范大学《教育技术学基础(含研究方法)》2020年考研专业课复试大纲

贵州师范大学硕士研究生入学考试大纲(复试)(科目:教育技术学基础)本科目复试内容包括“教育技术学导论”和“教育技术学研究方法”两部分。
一、考查目标(一)教育技术学导论1.考生对教育技术学的基础知识、基本概念和基本理论的掌握情况;2.考生对信息技术支持的教与学相关基础知识、基本理论的掌握情况;3.考生对国家关于教育信息化方面有关方针、近期政策及其影响的熟悉程度;4.考生对教育信息技术新领域、新发展、新动态的熟悉情况。
(二)教育技术学研究方法1.考生对教育技术学研究的基本理论、基本概念及常用研究方法的熟悉程度;2.考生开展科学研究和实际工作的能力,从实践问题中选择有价值的、新颖的、可行的研究方法,运用教育技术学的基本理论与常用方法分析、解决教育技术学领域的理论与实践问题;3.考生对教育技术学研究设计、数据分析与处理过程、途径与常用工具软件的掌握情况。
二、考查范围(一)教育技术学导论1.教育技术概述教育技术的本质、教育技术定义与内涵;教育技术的产生、形成与发展过程;教育技术学的学科性质及研究范畴;教育技术的理论基础(学习理论、教学理论、传播与媒体理论、系统科学理论、信息科学理论等)。
2.信息技术支持的教与学信息化教学设计理论、实践与应用;学习资源的开发与应用;信息化环境下的教学模式;信息化教学策略与教学方法;信息化教学评价方法与过程。
3.教育信息化建设教育信息化的概念、特征及其对教育改革的影响;教育信息化领域最新政策文件。
4.教育信息技术新领域、新发展、新动态网络与在线教育、创客与STEAN教育、人工智能与教育大数据、云技术等前沿发展与动态;教育信息技术前沿发展对教育的作用与影响。
(二)教育技术学研究方法1.教育技术学研究概述教育研究的概念与内涵;。
贵州师范大学计算数学《数值分析》考研复试大纲

贵州师范大学硕士研究生入学考试大纲(复试)(科目名称:数值分析)一、考查目标本《考试大纲适用于贵州师范大学数学科学学院数学专业硕士研究生入学考试复试。
数值分析是高等院校数学与应用数学、信息与计算科学等理工科专业的一门专业核心必修课程。
它是一门内容丰富,研究方法深刻,有自身理论体系的课程。
其研究对象是解决各种数学问题的数值计算程序、方法与相关理论。
1、考试目的测试考生对数值计算方法的基本原理和基本方法的掌握,以及对数值分析的理解及基本应用能力。
考生应该掌握拉格朗日插值方法、数值积分、数值微分、方程求根、线性代数方程组的数值解法,并有应用这些方法解决和分析数值计算中常见问题的基本能力。
《数值分析》是我校数学科学学院招收全日制硕士研究生而设置的具有选拔性质的复试科目,其目的是考察学生是否具备本学科计算数学专业硕士研究生学习所要求的水平,为我校数学科学学院择优选拔硕士研究生提供依据。
2、考试的基本要求要求学生了解和掌握这门课程所涉及的各种常用的数值计算公式、数值方法的构造原理及适用范围,为今后用计算机去有效地解决实际问题打下基础。
(1)掌握算法的基本原理和思想,包括算法的构造、算法处理的技巧、误差分析、收敛性和稳定性等基本理论。
(2)掌握误差与有效数字定义、函数插值与逼近的方法、积分与微分的数值计算方法、线性方程组的数值解法、非线性方程根的求解方法。
(3)掌握各种算法的理论分析;了解主要算法的设计思路。
二、考试形式与试卷结构(一)试卷成绩及考试时间本试卷满分为100分。
考试时间为180分钟。
(二)答题方式闭卷,笔试;所有题目全部为必答题。
(三)试卷内容数值计算中的误差、拉格朗日插值方法、数值积分、数值微分、方程求根、线性代数方程组的数值解法(四)试卷题型结构计算题、证明题。
三、考查范围1、数值计算中的误差了解误差的四种来源,特别是截断误差和舍入误差。
理解误差,误差限,有效数字的概念以及它们之间的相互关系。
贵州师范大学《地理信息系统》2020年考研专业课复试大纲

贵州师范大学硕士研究生入学考试大纲(复试)
(科目:地理信息系统)
一、考查目标
全日制攻读硕士学位入学考试《地理信息系统》考试,要求学生系统掌握地理信息系统的基础理论,了解地理信息系统的产生背景、功能、应用领域及发展方向;掌握GIS的基本概念、GIS的数据结构、GIS数据输入存储编辑方法、GIS空间分析方法、GIS产品等知识点;懂得如何利用GIS去解决实际问题的
思路。
二、考试形式与试卷结构
(一)试卷成绩:
本试卷满分为100分。
(二)答题方式:口试。
注:复试时不能带资料进场。
(三)试卷内容结构
1、GIS功能、应用领域及发展方向
2、GIS的基本概念
3、GIS的数据结构
4、GIS数据处理与数据库
5、GIS空间分析方法
(四)试卷题型结构
1、名词解释:2小题,每小题15分,共30分
2、问答题:2小题,每小题35分,共70分
三、考查范围
系统掌握地理信息系统的基础理论,了解地理信息系统的产生背景、功能、应用领域及发展方向;掌握GIS的基本概念、GIS的数据结构、GIS数据输入
存储编辑方法、GIS空间分析方法、GIS产品等知识点;懂得如何利用GIS去
1。
贵州师范大学《复变函数》2020年考研专业课复试大纲

贵州师范大学2020年硕士研究生招生复试大纲(科目:复变函数)一、考查目标本考试大纲适用于贵州师范大学数学科学学院数学专业硕士研究生入学考试复试。
复变函数论是数学与应用数学本科专业开设的一门专业核心必修课,也是数学分析课程的深入与延续;随着科学技术的不断发展,复变函数在越来越多的领域得到应用,如计算机科学、天文学、物理学、生物学、工程技术学等等。
因此,复变函数是基础数学专业和应用数学专业的一门非常重要的、不可缺少的课程。
(一)考试目的测试考生掌握该课程的基本概念及其性质,掌握复变函数中解析函数、柯西积分定理、柯西积分公式、解析函数的泰勒展开与罗朗展开等方面的基础知识和基本方法,要求能用这些理论和方法解决有关问题的能力。
《复变函数》是我校数学科学学院招收全日制硕士研究生而设置的具有选拔性质的复试科目,其目的是考察学生是否具备本学科基础数学专业硕士研究生学习所要求的水平,为我校数学科学学院择优选拔硕士研究生提供依据。
(二)考试的基本要求要求学生了解和掌握复变函数论的基本理论和方法,获得独立地分析和解决某些相关理论和实际问题的能力。
为以后硕士阶段进一步学习其他课程,以及将来从事教学,科研及其他实际工作打好基础。
(1)了解复变函数与实二元函数的关系、解析函数与调和函数的关系、解析函数零点的孤立性与解析函数的唯一性定理、最大模原理、双边幂级数的敛散性及其和函数的解析性等基本理论。
(2)掌握复数概念及各种表示、复变函数的极限与连续性、解析函数的定义及其简单性质,熟练掌握解析函数的等价刻划定理特别是柯西-黎曼条件、复变函数的积分的定义、复积分的计算方法、柯西积分定理、柯西积分公式与高阶导数公式、柯西不等式、刘维尔定理、摩勒拉定理、复数项级数敛散性的定义及其收敛性的两个刻划定理、幂级数收敛半径的求法、一些初等函数的泰勒展开式、洛朗定理、孤立奇点的三种类型及其判别法。
二、考试形式与试卷结构(一)试卷成绩及考试时间本试卷满分为100分。
贵州师范大学《音乐学院》2020年考研专业课复试大纲
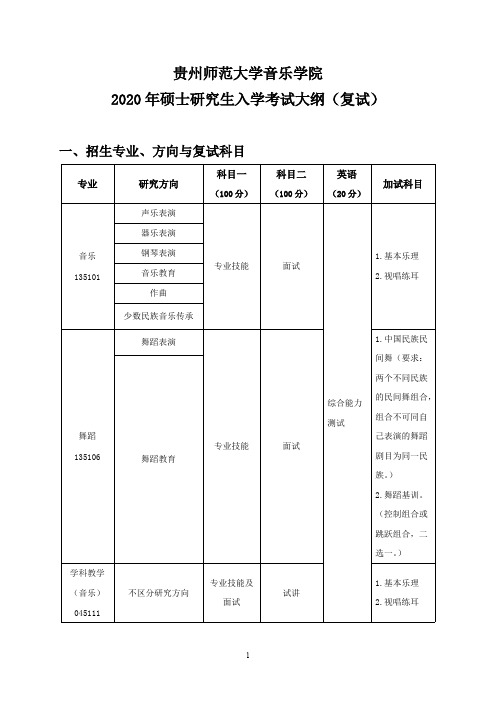
舞蹈教育
专业技能
学科教学 (音乐) 045111
不区分研究方向
专业技能及 面试
面试 试讲
1.中国民族民
间舞(要求:
两个不同民族
综合能力 测试
的民间舞组合, 组合不可同自 己表演的舞蹈
剧目为同一民
族。)
2.舞蹈基训。
(控制组合或
跳跃组合,二
选一。)
1.基本乐理 2.视唱练耳
1
二、复试内容与要求
音乐
专业
研究 方向
科目一(专业技能)100 分
科目二 英语 (面试) 20
100 分 分
声乐表演
美声唱法演唱中外歌曲六首,要求涵盖歌剧咏叹调两 首(中外作品均可)、两首艺术歌曲(一首中国作品, 一首外国作品)、两首近现代创作歌曲,要求用两种 不同国家的原文演唱外国作品不低于两首。
民族唱法演唱歌曲六首,要求涵盖中国民族歌剧选段、 戏曲选段、中国民歌、创作民歌。
器乐表演
背谱演奏作品四首,下列内容选考其一: 1. 管弦乐器。要求练习曲一首、大、中型乐曲二首和 奏鸣曲或协奏曲的一个乐章。 2. 中国乐器。要求大、中型以上含不同时期的作品四 首。
现场抽签 回答问题
口试
钢琴表演
背谱演奏中外作品四首。涵盖练习曲、复调、奏鸣曲、 中外乐曲。练习曲要求演奏肖邦(作品 10 之 3、6, 作品 25 之 2、7、9 除外)、李斯特或其它相应水平以 上的练习曲,奏鸣曲要求至少一个快板乐章。
试讲:时 长 15 分 钟,试讲 口试 内容自选。
3
作曲
1.提交原创作品三首。 2、演奏钢琴曲 1 首,车尔尼 849 程度以上(含)作品。
少数民族 音乐传承
音乐教育
贵州师范大学《分析化学》2020年考研专业课复试大纲

贵州师范大学2020年硕士研究生入学考试大纲(复试)(科目:材料化学专业代码:070302 专业名称:分析化学)一、考查目标全日制攻读分析化学专业硕士学位入学考试(复试)材料化学科目的考试内容包括无机化学、有机化学和材料科学基础三部分。
要求考生系统掌握材料化学的基本概念、基本知识、基础理论和基本方法,并能运用相关理论和方法分析解决有关材料化学的实际问题,尤其是关于无机合成、有机合成与材料的组织、结构、性能之间的关系及其变化规律相关内容。
二、考查范围分为以下三个部分,各知识点如下。
第一部分无机化学部分1、波函数、电子层的概念,描述电子运动状态的四个量子数的物理意义、取值规律和合理组合。
2、掌握价键理论及杂化轨道理论,理解杂化对分子性质的影响,能用杂化轨道理论解释一般分子和离子的空间构型。
3、了解晶体学基本概念,掌握晶体的特征,了解晶胞参数的定义以及体心、面心和底心晶胞的概念。
掌握原子晶体和分子晶体基本特征及性质。
4、掌握理想气体状态方程及混合气体分压定律,化学热力学四个最重要的状态函数—热力学能、焓、吉布斯自由能和熵及它们的变化的初步概念;理解化学反应等温式的含义并会用其求算∆r G和K平衡;根据吉布斯一亥姆霍兹公式理解∆G与∆H及∆S的关系,会讨论温度对化学反应自发性的影响。
5、理解化学平衡常数意义,Gibbs自由能与平衡常数之间关系,掌握浓度、压力、温度对化学平衡的影响,掌握平衡移动原理(吕·查德里原理)。
6、掌握浓度、温度及催化剂对反应速率的影响;理解碰撞理论和过渡态理论,理解有效碰撞、活化分子、活化能的概念。
7、理解溶解度、溶液浓度的表示方法,掌握稀溶液的依数性;了解强电解质溶液的相关概念。
1。
贵州师范大学《遗传学大纲》2020年考研专业课复试大纲

贵州师范大学硕士研究生入学考试大纲
(复试)
(科目:遗传学)
一、考查目标:
本《遗传学》考试大纲适用于2020年贵州师范大学生命科学相关专业的硕士研究生入学复试考试。
遗传学的主要内容包括经典遗传学、细胞遗传学、分子遗传学和发育遗传学等。
要求考生掌握基本概念、原理,从个体、细胞、和分子水平对遗传学有较完整和系统的认识,掌握遗传学的基本规律和应用,熟悉遗传学的基本概念及规律,并能综合、灵活运用所学知识分析问题和解决问题。
二、考核形式与结构
(一)考试成绩:本部分考核满分为100分。
(二)答题方式:口述回答问题
(三)试题类型:综合性问答题
三、考试范围与要求:
(一)孟德尔遗传
通过本章教学,使学生了解孟德尔如何通过植物杂交实验得出遗传分离规律和自由组合规律的。
掌握孟德尔遗传规律的内容及其所需的必要条件。
理解如何进行遗传分析,以及如何判断实际遗传分离比例是否符合孟德尔遗传规律的理论遗传模式。
(二)遗传的染色体学说
了解染色体结构,模式动植物的染色体数目。
理解染色体在细胞分裂过程中的动态变化,在生命周期中的数目变化。
掌握染色体行为与遗传因子的平行关系。
(三)基因互作及其与环境的关系
通过本章教学,使学生了解基因型与表现型的关系,理解性状的多基因决定和基因的多效性。
掌握基因间相互作用。
理解环境对基因表型的影响效应。
(四)基因的连锁与交换
了解连锁与交换的基本证据。
掌握连锁与交换定律的内容,以及基因连锁与否的判断方法。
理解连锁与交换的生物学意义。
(五)性别决定与伴性基因的遗传
1。
贵州师范大学硕士硕士研究生入学考试大纲

贵州师范大学硕士硕士研究生入学考试大纲(复试)(科目名称:通信工程基础)一、考查目标要求考生系统深入地掌握《通信原理》的基本知识、基本理论,并且能灵活运用,对信号进行分析。
重点考察了解和掌握现代通信系统的基本原理和分析方法,掌握模拟和数字通信系统的组成、调制和解调原理及性能,掌握数字信号基带传输和载波传输的基本技术、模拟信号数字传输系统的基本原理、同步原理和纠错编码的基本概念。
二、考试形式与试卷结构(一)试卷成绩本试卷满分为100分,考试时间为120分钟。
(二)答题方式复试分笔试与面试两部分,以面试为主,根据需要适当必试。
其中,笔试为闭卷考试。
(三)试卷内容结构各部分内容所占分值为:通信系统的模型、数字通信的特点、平均信息量的计算、信息速率、频带利用率定义约占15分;随机过程的概念、高斯白噪声及带限噪声的定义、噪声的功率谱密度与相关函数的关系约占15分;恒参、随参信道的定义及特点、频率选择性衰落的原因约占15分;各种调制方式的原理、抗噪声性能、数字基带信号传输与码间串扰约占30分; 数字带通传输系统、模拟信号的数字传输和差错控制编码约占25分。
三、考查范围(一)考试内容一、通信系统组成1. 通信的基本概念2. 通信系统的组成3. 通信系统分类与通信方式4. 信息及其度量5. 通信系统主要性能指标二、信号1. 确知信号的频域性质2. 确知信号的时域性质三、平稳随机过程1. 平稳随机过程2. 平稳随机过程通过线性系统四、信道与编码1. 信道的数学模型2. 信道容量3. 纠错编码的基本原理4. 线性分组码五、模拟调制1. 幅度调制的原理2. 线性调制系统的抗噪声性能六、数字基带传输系统1. 数字基带信号传输与码间串扰2. 无码间串扰的基带传输特性七、数字带通传输系统1. 二进制数字调制原理八、模拟信号的数字传输1. 模拟信号的抽样2. 模拟脉冲调制3. 抽样信号的量化4. 脉冲编码调制5. 增量调制四、参考书目樊昌信、曹丽娜编著《通信原理》(第6版)(国防工业出版社,2006年,9月)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贵州师范大学硕士研究生入学考试大纲(复试)
(科目代码:科目名称:运筹学)
一、考查目标
本考试大纲适用于贵州师范大学数学科学学院数学专业学术型硕士研究生入学考试复试。
运筹学是大学数学系本科学生的一门重要课程。
要求考生了解运筹学的形成和发展,认识运筹学的性质和特点,掌握运筹学的工作步骤和模型,熟练地掌握运筹学的基本思想、基本理论、基本方法,通过相关实际问题的解决来进一步掌握运筹学的建模方法、算法设计、程序编写,并在此基础上,能独立解决生产实践中相关的简单优化问题。
1考试目的
《运筹学》是我校数学科学学院为招收全日制硕士研究生而设置的具有选拔性质的复试科目,其目的是考察学生是否具备本学科各专业硕士研究生学习所要求的水平,为我校数学科学学院择优选拔硕士研究生提供依据。
2考试的基本要求
要求考生比较系统地掌握运筹学的基本思想、基本理论和基本方法,并在此基础上,能独立解决生产实践中相关的简单优化问题。
二、考试形式与试卷结构
(一)试卷成绩及考试时间
本试卷满分为100分。
考试时间为120分钟。
(二)答题方式
闭卷,笔试;所有题目全部为必答题。
(三)试卷内容结构
线性规划与目标规划约占45%,整数规划约占15%,网络计划约占15%,存储轮约占10%,对策论约占:15%。
(四)试卷题型结构
单项选择题、填空题、判断题、简答题、解答题。
三、考查范围
线性规划与单纯形法
(一)学习目的与要求
通过本章的学习,应掌握线性规划的数学模型,相关基本概念,图解法,单
纯形法及运用线性规划求解相关实际问题。
(二)考核知识点与考核要求
(1)凸集、凸组合:识记
(2)线性规划的数学模型及标准型:识记、理解
(3)线性规划的几何意义:识记、理解
(4)图解法:简单应用
(5)单纯形法、人工变量法:简单应用
(6)运用线性规划求解相关实际问题:综合应用
对偶理论与灵敏度分析
(一)学习目的与要求
通过本章的学习,应掌握原问题和对偶问题之间的关系,对偶单纯形法,灵敏度分析及运用对偶理论和灵敏度分析求解相关实际问题。
(二)考核知识点与考核要求
(1)原问题与对偶问题之间的关系:识记、理解
(2)对偶单纯形法:简单应用
(3)灵敏度分析:简单应用
(4)运用对偶理论和灵敏度分析求解相关实际问题:综合应用
运输问题
(一)学习目的与要求
通过本章的学习,应掌握运输问题的数学模型和特点,表上作业法及运用表上作业法求解相关运输问题。
(二)考核知识点与考核要求
(1)运输问题的数学模型及特点:识记、理解
(2)产销平衡问题和产销不平衡问题:理解
(3)产销不平衡问题转换为产销平衡问题:简单应用
(4)表上作业法:简单应用
(5)运用表上作业法求解相关运输问题:综合应用
线性目标规划
(一)学习目的与要求
通过本章的学习,应掌握线性目标规划的数学模型和特点,解线性目标规划的图解法和单纯形法及运用目标规划求解相关实际问题。
(二)考核知识点与考核要求
(1)线性目标规划的数学模型和特点:识记、理解
(2)解线性目标规划的图解法:理解、简单应用
(3)解线性目标规划的单纯形法:理解、简单应用
(4)运用目标规划求解相关实际问题:综合应用
整数线性规划
(一)学习目的与要求
通过本章的学习,应掌握整数线性规划的数学模型和特点,分支定界法,割平面法,0-1整数线性规划的数学模型和特点,指派问题的数学模型和特点及运用整数线性规划求解相关实际问题。
(二)考核知识点与考核要求
(1)整数线性规划的数学模型和特点:识记、理解
(2)0-1整数线性规划的数学模型和特点:识记、理解
(3)指派问题的数学模型和特点:识记、理解
(4)分支定界法、割平面法:简单应用
(5)隐枚举法:简单应用
(6)匈牙利法:简单应用
(7)运用整数线性规划求解相关实际问题:综合应用
网络计划
(一)学习目的与要求
通过本章的学习,应掌握网络计划的相关概念,绘制网络计划图,网络计划图的时间参数计算,网络计划的优化及运用网络计划求解相关实际问题。
(二)考核知识点与考核要求
(1)网络计划的相关概念:识记
(2)绘制网络计划图:理解、简单应用
(3)网络计划图的时间参数计算:理解、简单应用
(4)网络计划的优化:简单应用
(5)运用网络计划求解相关实际问题:综合应用
存储论
(一)学习目的与要求
通过本章的学习,应掌握存储论的基本概念,四种确定性存储问题的数学模型及特点及运用存储论求解简单的确定性存储问题。
(二)考核知识点与考核要求
(1)存储论的基本概念:识记、理解
(2)四种确定性存储问题的数学模型及特点:识记、理解
(3)运用存储论求解简单的确定性存储问题:综合应用
对策论基础
(一)学习目的与要求
通过本章的学习,应掌握对策行为的三个基本要素,对策的分类,矩阵对策的数学模型和特点,矩阵对策的混合策略,矩阵对策的公式法、图解法和方程组法及运用矩阵对策求解相关实际问题。
(二)考核知识点与考核要求
(1)对策行为的三个基本要素:识记
(2)对策的分类:识记
(3)矩阵对策的数学模型和特点:识记、理解
(4)矩阵对策的混合策略:理解
(5)矩阵对策的公式法、图解法和方程组法:简单应用
(6)运用矩阵对策求解相关实际问题:综合应用
四、样题
一、单项选择题(每小题3分,共15分)
1、下列描述正确的是()。
A、线性规划的可行域是凸集
B、线性规划的可行域不是凸集
C、线性规划的可行域可能是凸集,也可能不是凸集
D、以上选项都不对
二、填空题(每小题3分,共15分)
1、线性规划数学模型的标准形式是__ __。
三、判断题(每小题3分,共15分)
1、如果线性规划问题存在最优解,那么最优解一定可以在其可行域的某个顶点处达到。
( )
四、简答题(每小题3分,共12分)
1、简述求解线性规划的单纯形算法的基本思想。
五、解答题(共43分)
1、(12分)已知线性规划:
12
121212
max z x x 2x 5x 166x 5x 30x ,x 0=++≤⎧⎪+≤⎨⎪≥⎩ (1) 用图解法求解该线性规划问题(4分);
(2) 用单纯形算法求解该线性规划问题(5分);
(3) 写出该线性规划的对偶问题(3分)。
