人教版九年级数学下册27.2.2相似三角形的性质同步练习-精编版
人教版九年级数学下第二十七章 27.2.2第9课时相似三角形的性质练习及答案

第9课时相似三角形的性质1.若△ABC ~△A ′B 'C ′,相似比为1∶2,则△ABC 与△A 'B ′C '的周长的比为( )A .2∶1B .1∶2C .4∶1D .1∶42.已知△ABC ∽△DEF ,若面积比为4∶9,则它们对应高的比是( )A .4∶9B .16∶81C .3∶5D .2∶33.△ABC 与△DEF 是相似三角形,且△ABC 与△DEF 的相似比是1∶2,已知△ABC 的面积是3,则△DEF 的面积是( )A .3B .6C .9D .124.已知△ABC ∽△DEF ,且它们的周长之比为1∶3,则它们的相似比为 .5.如果把一个多边形改成和它相似的多边形,面积缩小为原来的41,那么边长缩小为原来的_________.6.如图,已知△ADE ∽△ABC ,且AD =6,AE =4,AB =12,求CD 的长.7.如图,△ADE ∽△ABC , = ,△ABC 的面积为18,求△ADE 的面积.8.已知△ABC ∽△A ′B ′C ′,AB A ′B ′=12,AB 边上的中线CD =4 cm ,△ABC 的周长为20 cm ,△A ′B ′C ′的面积是64 cm 2.(1)求A ′B ′边上的中线C ′D ′的长;(2)求△A ′B ′C ′的周长.1.B2.D3.D4.1∶35.126.解∶∵△ADE ∽△ABC , ∴ = ,∵AD=6,AE=4,AB=12,∴=,∴AC=8,∴CD=AC-AD=8-6=2.7.解∶∵=,∴=,∵△ADE∽△ABC,=,∴△ADE与△ABC的面积比为,又△ABC的面积为18,∴△ADE的面积为2,8.解:(1)∵△ABC∽△A′B′C′,ABA′B′=12,AB边上的中线CD=4 cm,∴CDC′D′=ABA′B′=12,∴C′D′=4×2=8(cm).(2)∵△ABC∽△A′B′C′,ABA′B′=12,△ABC的周长为20 cm,∴△ABC的周长△A′B′C′的周长=ABA′B′=12,∴△A′B′C′的周长=20×2=40(cm).。
九年级数学下册 第二十七章 相似 27.2 相似三角形 27.2.2 相似三角形的性质同步练习 (新版)新人教版

课时作业(十一)[27.2.2 相似三角形的性质]一、选择题1.2017·重庆若△ABC ∽△DEF ,且相似比为3∶2,则△ABC 与△DEF 的对应高的比为( ) A .3∶2 B .3∶5 C .9∶4 D .4∶92.若两个相似三角形的对应中线的比为3∶4,则它们对应角平分线的比为( ) A .1∶16 B .16∶9 C .4∶3 D .3∶43.已知△ABC ∽△DEF ,且它们的周长之比为1∶9,则△ABC 与△DEF 对应高的比为( ) A .1∶3 B .1∶9 C .1∶18 D .1∶814.2017·连云港如图K -11-1,已知△ABC ∽△DEF ,AB ∶DE =1∶2,则下列等式中一定成立的是( )图K -11-1A.BC DF =12B.∠A 的度数∠D 的度数=12C.△ABC 的面积△DEF 的面积=12D.△ABC 的周长△DEF 的周长=125.2017·永州如图K -11-2,在△ABC 中,D 是AB 边上的一点,若∠ACD =∠B ,AD =1,AC =2,△ADC 的面积为1,则△BCD 的面积为( )图K -11-2A .1B .2C .3D .4 6.如图K -11-3,在Rt △ABC 中,AD 为斜边BC 上的高,若S △CAD =3S △ABD ,则AB ∶AC 等于( ) 链接听课例3归纳总结图K -11-3A .1∶3B .1∶4C .1∶ 3D .1∶27.如图K -11-4,D ,E 分别是△ABC 的边AB ,BC 上的点,DE ∥AC .若S △BDE ∶S △CDE =1∶3,则S △DOE ∶S △AOC 的值为( )图K -11-4A.13B.14C.19D.1168.如图K -11-5,四边形ABCD 和四边形CEFG 都是正方形,点G 在线段CD 上,连接BG ,DE ,DE 和FG 相交于点O .设AB =a ,CG =b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③DG GC =GO CE;④(a -b )2·S △EFO =b 2·S △DGO .其中正确的有( )图K -11-5A .4个B .3个C .2个D .1个 二、填空题9.2018·连云港如图K -11-6,△ABC 中,点D ,E 分别在AB ,AC 上,DE ∥BC ,AD ∶DB =1∶2,则△ADE 与△ABC 的面积的比为________.图K -11-610.若△ABC ∽△A ′B ′C ′,BC =18 cm ,CA =15 cm ,AB =21 cm ,△A ′B ′C ′的最短边长为5 cm ,则△A ′B ′C ′的周长为________.11.如图K -11-7,在▱ABCD 中,E 是边AD 的中点,EC 交对角线BD 于点F ,若S △DEC =3,则S △BCF =________.图K -11-712.如图K -11-8,Rt △AOB 的一条直角边OB 在x 轴上,双曲线y =k x(x >0)经过斜边OA 的中点C ,与另一条直角边交于点D .若S △OCD =9,则S △OBD 的值为________.图K -11-8三、解答题13.如图K -11-9,在△ABC 中,DE ∥BC ,EF ∥AB ,已知△ADE 和△EFC 的面积分别为4 cm 2和9 cm 2,求△ABC 的面积.图K -11-914.如图K -11-10,在△ABC 中,D ,E 分别是AB ,AC 上的点,△ADE ∽△ACB ,相似比为AD ∶AC =2∶3,△ABC 的角平分线AF 交DE 于点G ,交BC 于点F .求AG 与GF 的比.图K -11-1015.如图K -11-11所示,在▱ABCD 中,E 是CD 延长线上的一点,BE 与AD 交于点F ,DE =12CD .(1)求证:△ABF ∽△CEB ;(2)若△DEF 的面积为2,求▱ABCD 的面积. 链接听课例3归纳总结图K -11-11数形结合如图K -11-12,有一块三角形余料ABC ,它的边BC =120 mm ,高AD =80 mm.要把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB ,AC 上.问加工成的正方形零件的边长为多少毫米?小颖解得此题的答案为48 mm.小颖善于反思,她又提出了如下的问题:(1)如果原题中所要加工的零件是一个矩形,且此矩形由两个并排放置的正方形组成,如图K -11-13,此时,这个矩形零件的相邻两边长又分别是多少毫米?请你计算.(2)如果原题中所要加工的零件只是一个矩形,如图K-11-14,这样,此矩形零件的相邻两边长就不能确定,但这个矩形的面积有最大值,求矩形面积达到这个最大值时矩形零件的相邻两边长.图K-11-12图K-11-13图K-11-14详解详析[课堂达标] 1.A 2.D3.[解析] B ∵△ABC 与△DEF 的周长之比为1∶9,∴△ABC 与△DEF 的相似比为1∶9, ∴△ABC 与△DEF 对应高的比为1∶9.4.[解析] D 已知△ABC ∽△DEF ,且相似比为1∶2,A 选项中BC 与DF 不是对应边;B 选项中的∠A 和∠D 是一对对应角,根据“相似三角形的对应角相等”可得∠A =∠D ;根据“相似三角形的面积比等于相似比的平方”可得△ABC 与△DEF 的面积比是1∶4;根据“相似三角形的周长比等于相似比”可得△ABC 与△DEF 的周长比是1∶2.因此A ,B ,C 选项错误,D 选项正确.5.[解析] C ∵∠ACD =∠B ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AB =AD AC ,∴2AB =12,∴AB =4,∴S △ACD S △ABC =(AC AB )2,∴1S △ABC =(24)2,∴S △ABC =4,∴S △BCD =S △ABC -S △ACD =4-1=3.6.[解析] C 由题意可得△CAD ∽△ABD ,∴S △ABD S △CAD =⎝ ⎛⎭⎪⎫AB AC 2=13,∴AB AC =13. 7.[解析] D ∵S △BDE ∶S △CDE =1∶3,∴BE ∶EC =1∶3,∴BE ∶BC =1∶4.∵DE ∥AC ,∴DE AC =BE BC =14,△DOE ∽△COA ,∴S △DOE ∶S △AOC =(DE AC )2=116.8.[解析] B ①由BC =DC ,∠BCG =∠DCE ,CG =CE ,可证△BCG ≌△DCE(SAS),故①正确. ②延长BG 交DE 于点H ,由①可得∠CDE =∠CBG.∵∠DGH =∠BGC(对顶角相等), ∴∠DHG =∠BCG =90°,即BG ⊥DE ,故②正确.③由△DGO ∽△DCE 可得DG DC =GOCE,故③不正确.④易知△EFO ∽△DGO ,S △EFO S △DGO 等于相似比的平方,即S △EFO S △DGO =⎝ ⎛⎭⎪⎫EF DG 2=b2(a -b )2,∴(a -b)2·S △EFO =b 2·S △DGO ,故④正确. 9.[答案] 1∶9[解析] ∵DE ∥BC ,AD ∶DB =1∶2,∴AD AB =13,△ADE ∽△ABC ,∴S △ADE S △ABC =19.故答案为1∶9.10.[答案] 18 cm 11.[答案] 4[解析] ∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC , ∴△DEF ∽△BCF , ∴EF CF =DE BC ,S △DEF S △BCF =(DE BC )2. ∵E 是边AD 的中点,∴DE =12AD =12BC ,∴EF CF =DE BC =12,∴EF EC =13, ∴S △DEF =13S △DEC =1,S △DEF S △BCF =14,∴S △BCF =4. 12.[答案] 6[解析] 如图,过点C 作CE ⊥x∵在Rt △OAB 中,∠OBA =90°, ∴CE ∥AB.∵C 为Rt △AOB 的斜边OA 的中点,∴CE 为Rt △AOB 的中位线,且S △OCD =S △ACD ,∴△OEC ∽△OBA ,且OC OA =12.∵双曲线所对应的函数解析式是y =kx,∴S △OBD =S △COE =12k ,∴S △AOB =4S △COE =2k.由S △AOB -S △OBD =S △OAD =2S △OCD =18,得2k -12k =18,解得k =12,∴S △OBD =12k =6.故答案为6.13.解:∵DE ∥BC ,EF ∥AB , ∴△ADE ∽△ABC ∽△EFC , ∴⎝ ⎛⎭⎪⎫AE EC 2=S △ADE S △EFC =49, ∴AE EC =23,则AE AC =25, 故S △ADE S △ABC =⎝ ⎛⎭⎪⎫AE AC 2=425. ∵S △ADE =4 cm 2,∴S △ABC =25 cm 2.14.解:∵△ADE ∽△ACB , ∴∠ADG =∠C.∵AF 是△ABC 的角平分线, ∴∠DAG =∠FAC , ∴△ADG ∽△ACF , ∴AD AC =AG AF . ∵AD AC =23,∴AG AF =23, ∴AG ∶GF =2∶1. 15.[解析] (1)由平行四边形的对角相等,对边平行,证得△ABF ∽△CEB ;(2)由△DEF ∽△CEB ,△DEF ∽△ABF ,根据相似三角形的面积比等于相似比的平方可以求出△ABF 和△BCE 的面积,从而▱ABCD 的面积可求.解:(1)证明:∵四边形ABCD 是平行四边形, ∴∠A =∠C ,AB ∥CD , ∴∠ABF =∠CEB , ∴△ABF ∽△CEB.(2)∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB 綊CD ,∴△DEF ∽△CEB ,△DEF ∽△ABF.∵DE =12CD ,∴EC =3DE ,∴S △DEF S △CEB =(DE EC )2=19,S △DEF S △ABF =(DE AB )2=14. ∵S △DEF =2,∴S △CEB =18,S △ABF =8,∴S 四边形BCDF =S △CEB -S △DEF =16,∴S ▱ABCD =S 四边形BCDF +S △ABF =16+8=24. [素养提升]解:(1)∵四边形PNMQ 是矩形, ∴PN ∥QM ,∴△APN ∽△ABC , ∴PN BC =AE AD. 设PQ =ED =x mm ,则PN =2x mm ,AE =(80-x)mm , ∴2x 120=80-x 80, 解得x =2407,则2x =4807.这个矩形零件的相邻两边长分别是2407 mm 和4807mm.(2)∵四边形PNMQ 是矩形, ∴PN ∥QM ,∴△APN ∽△ABC , ∴PN BC =AE AD. 设PQ =ED =x mm ,则AE =(80-x)mm , ∴PN 120=80-x 80, 即PN =80-x 80·120=3(80-x )2,∴S 矩形PNMQ =PN·PQ=3(80-x )2·x=-32x 2+120x =-32(x -40)2+2400,∴当x =40时,S 矩形PNMQ 有最大值2400,此时PN =3×(80-40)2=60(mm).∴矩形面积达到最大值时矩形零件的相邻两边长分别为40 mm ,60 mm.。
人教版九年级下册数学 27.2相似三角形 同步练习(含解析)

27.2相似三角形同步练习一.选择题1.如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是()A.150°B.147°C.135°D.120°2.两个相似三角形对应角平分线的比为4:3,那么这两个三角形的面积的比是()A.2:3B.4:9C.16:36D.16:93.下列条件中,不能判断△ABC与△DEF相似的是()A.∠A=∠D,∠B=∠F B.且∠B=∠DC.D.且∠A=∠D4.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中能判断△ABC∽△AED 的是()①∠AED=∠B;②∠ADE=∠C;③=;④=.A.①②B.①②③C.①②④D.①②③④5.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为()A.5:7B.10:4C.25:4D.25:496.已知点E、F分别在△ABC的AB、AC边上,则下列判断正确的是()A.若△AEF与△ABC相似,则EF∥BCB.若AE×BE=AF×FC,则△AEF与△ABC相似C.若,则△AEF与△ABC相似D.若AF•BE=AE•FC,则△AEF与△ABC相似7.如图,在△ABC,D是BC上一点,BD:CD=1:2,E是AD上一点,DE:AE=1:2,连接CE,CE的延长线交AB于F,则AF:AB为()A.1:2B.2:3C.4:3D.4:78.如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则△DEF与四边形EFCO的面积比为()A.1:4B.1:5C.1:6D.1:79.如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△P AD 与△PBC相似,则这样的点P有()A.1 个B.2 个C.3 个D.4 个10.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于F,连接DF,若BF=,BC =3,则DF=()A.4B.3C.2D.二.填空题11.已知△ABC∽△A′B′C′,且AB=3cm,A′B′=5cm,则相似比为.12.如图,△ABC中,CA=CB,点E在BC边上,点D在AC边上,连接AE、DE,若AB =AE,2∠AEB+∠ADE=180°,BE=8,CD=,则CE=.13.如图,在△ABC中,若DE∥BC,EF∥CD,AE=2EC,则AF:FD:DB=.14.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则的值是.15.如图,在矩形ABCD中,AD=2,AB=4,E、F分别是AB、CD边上的动点,EF⊥AC,则AF+CE的最小值为.三.解答题16.如图,点P是菱形ABCD的对角线AC上一点,连接DP并延长,交AB于点F,交CB 的延长线于点E.求证:(1)△APB≌△APD;(2)PD2=PE•PF.17.如图,在△ABC中,点D、E分别在AB、AC上,DE、BC的延长线相交于点F,且EF•DF=CF•BF.求证:△CAB∽△DAE.18.如图,AF,AG分别是△ABC和△ADE的高,∠BAF=∠DAG.(1)求证:△ABC∽△ADE;(2)若DE=3,,求BC的长.参考答案一.选择题1.解:∵△ABC∽△DCA,∴∠BAC=∠D=117°,∠DAC=∠B=33°,∴∠BAD=∠BAC+∠DAC=150°,故选:A.2.解:∵两个相似三角形对应角平分线的比为4:3,∴它们的相似比为4:3,∴它们的面积比为16:9.故选:D.3.解:A、∠A=∠D,∠B=∠F,可以得出△ABC∽△DFE,故此选项不合题意;B、=且∠B=∠D,不是两边成比例且夹角相等,故此选项符合题意;C、==,可以得出△ABC∽△DEF,故此选项不合题意;D、=且∠A=∠D,可以得出△ABC∽△DEF,故此选项不合题意;故选:B.4.解:∵∠A=∠A,∴∠AED=∠B或∠ADE=∠C时,△ABC∽△AED.∵=,∴=∵∠A=∠A,∴△ABC∽△AED,故①②③可以判断三角形相似,故选:B.5.解:设DE=5k,EC=2k,则CD=7k,∵四边形ABCD是平行四边形,∴AB=CD=7k,DE∥AB,∴△DEF∽△BAF,∴===,故选:D.6.解:选项A错误,∵△AEF与△ABC相似,可能是∠AEF=∠C,推不出EF∥BC.选项B错误,由AE×BE=AF×FC,推不出△AEF与△ABC相似.选项C错误,由,推不出△AEF与△ABC相似.选项D正确.理由:∵AF•BE=AE•FC,∴=,∴EF∥BC,∴△AEF∽△ABC.故选:D.7.解:过D作DH∥AB交CF于H,如图,∵DH∥BF,∴=,∵BD:CD=1:2,∴CD:BC=2:3,∴BF=DH,∵DH∥AF,∴==2,∴AF=2DH,∴AF:BF=2DH:DH=4:3,∴AF:AB=4:7.故选:D.8.解:∵四边形ABCD是平行四边形,∴BO=DO,AB∥CD,∵E为OD的中点,∴DE=EO=DO,∴BO=2EO,BE=3DE,∵DF∥AB,∴△DFE∽△BAE,∴=()2=,设S△DEF=x,则S△BEA=9x,∵BO=2OE,∴S△AOB=6x=S△DOC,∴四边形EFCO的面积=5x,∴△DEF与四边形EFCO的面积比=1:5,故选:B.9.解:∵AB⊥BC,∴∠B=90°.∵AD∥BC∴∠A=180°﹣∠B=90°,∴∠P AD=∠PBC=90°.设DP的长为x,则CP长为6﹣x.若AB边上存在P点,使△P AD与△PBC相似,那么分两种情况:①若△APD∽△BPC,则DP:CP=AD:BC,即x:(6﹣x)=3:4,解得:x=②若△APD∽△BPC,则DP:PC=AD:BC,即x:4=3:(6﹣x),整理得:x2﹣6x+12=0,∵△<0,这种情形不存在,∴满足条件的点P的个数是1个,故选:A.10.解:如图,连接BD,∵∠AEF=∠BEA,∠AFE=∠BAE=90°,∴△AEF∽△BEA,∴=,∵AE=ED,∴=,又∵∠FED=∠DEB,∴△FED∽△DEB,∴∠EFD=∠EDB,∵∠EFD+∠DFC=90°,∠EDB+∠ODC=90°,∴∠DFC=∠ODC,∵在矩形ABCD中,OC=AC,OD=BD,AC=BD,∴OD=OC,∴∠OCD=∠ODC,∴∠DFC=∠OCD,∴DF=DC,在Rt△BCF中,FC===2,∵AD∥BC,∴△AEF∽△CBF,∴==,∴AF=FC=,∴AB===3,∴DF=3,故选:B.二.填空题11.解:由题意得,=,∵△ABC∽△A′B′C′,∴△ABC与△A′B′C′的相似比为=,故答案为:.12.解:如图,过点A作AM⊥BE于E,过点D作DN⊥EC于N,∵CA=CB,AB=AE,∴∠B=∠CAB,∠B=∠AEB,∴∠B=∠CAB=∠AEB,∵∠B+∠BAC+∠C=180°,∠B+∠AEB+∠BAE=180°,∴∠C=∠BAE,∴2∠AEB+∠C=180°,又∵2∠AEB+∠ADE=180°,∴∠C=∠ADE,又∵∠ADE=∠C+∠DEC,∴∠C=∠DEC,∴DE=DC=,∵AB=AE,AM⊥BE,DE=CC,DN⊥EC,∴BM=ME=BE=4,EN=NC=EC,AM∥DN,∴△CDN∽△CAM,∴,∴,∴EC=12,EC=﹣5(不合题意舍去),故答案为:12.13.解:∵EF∥CD,AE=2EC,∴==2,∵DE∥BC,∴==2,设DF=m,则AF=2m,AD=3m,DB=m,∴AF:DF:DB=2m:m:m=4:2:3.故答案为:4:2:3.14.解:∵DE∥AC,∴△DOE∽△COA,∴=()2=,∴=,∵DE∥AC,∴△BDE∽△BAC,∴=,∴=,故答案为:.15.解:如图所示:设DF=x,则FC=4﹣x;过点C作CG∥EF,且CG=EF,连接FG,当点A、F、G三点共线时,AF+FG的最值小;∵CG∥EF,且CG=EF,∴四边形CEFG是平行四边形;∴EC∥FG,EC=FG,又∵点A、F、G三点共线,∴AF∥EC,又∵四边形ABCD是矩形,∴AE∥DC,∠D=90°,∴四边形AECF是平行四边形,∴OA=OC,OE=OF,又∵EF⊥AC,AF=CF=4﹣x,在Rt△ADF中,由勾股定理得:AD2+DF2=AF2,又∵AD=2,DF=x,则FC=4﹣x,∴22+x2=(4﹣x)2,解得:x=,∴AF=,在Rt△ADC中,由勾股定理得:AD2+DC2=AC2,∴AC=,∴AO=,又∵OF∥CG,∴△AOF∽△ACG,∴=,∴AG=5,又∵AG=AF+FG,FG=EC,∴AF+EC=5,故答案为5.三.解答题16.证明:(1)∵四边形ABCD是菱形,∴AB=AD,∠BAC=∠DAC,在△ABP和△ADP中,,∴△ABP≌△ADP(SAS);(2)∵△ABP≌△ADP,∴PB=PD,∠ADP=∠ABP,∵AD∥BC,∴∠ADP=∠E,∴∠E=∠ABP,又∵∠FPB=∠EPB,∴△EPB∽△BPF,∴,∴PB2=PE•PF,∴PD2=PE•PF.17.证明:∵EF•DF=CF•BF.∴,∵∠EFC=∠BFD,∴△EFC∽△BFD,∴∠CEF=∠B,∴∠B=∠AED,∵∠CAB=∠DAE,∴△CAB∽△DAE.18.(1)证明:∵AF,AG分别是△ABC和△ADE的高,∴AF⊥BC,AG⊥DE,∴∠AFB=90°,∠AGD=90°,∴∠BAF+∠B=90°,∠DAG+∠ADG=90°,∵∠BAF=∠DAG,∴∠B=∠ADG,又∵∠EAD=∠BAC,∴△ABC∽△ADE;(2)解:∵△ADE∽△ABC,∴,∵,BC=3,∴,∴BC=.。
【九年级】九年级数学下27.2相似三角形(一)同步练习(人教版有答案和解释)

【九年级】九年级数学下27.2相似三角形(一)同步练习(人教版有答案和解释)27.2相似三角形同步练习(一)一、单选题(本大题共15个子题,每个子题得3分,共计45分)1、如图,在中,已知于点,则图中相似三角形共有().a、对b.对c、对d.对2.如图所示,如果直线已知,且直线和,,分别与点,,,,,,,,,相交,则的值为()3、如图,已知,,则().4.同时,身高1.6米的小华在阳光下的影子长度为0.8米。
如果一棵树的阴影长度是4.8米,那么树的高度是()a.米b、仪表c.米d、仪表5、下列四组线段中,不成构成比例线段的是().A.b.Cd.6.如果是这样,可以得到比例公式()a.Bc.D7、在运动会上,裁判员测得小明与小华跳远成绩分别是米,厘米,则线段与的比值是().A.b.Cd.8.如果三个顶点的纵坐标保持不变,横坐标分别乘以,新点依次连接,则得到的三角形与原始三角形之间的位置关系为()a.原三角形向轴的负方向平移一个单位即为所得三角形b、关于原点对称c.关于轴对称d、关于轴对称9、如图,在中,,若,则()A.b.Cd.10.如果一个直角三角形的两边分别是和,而另一个类似的直角三角形的边分别是和,那么()a.有无数个b、超过,但有限c.可以有个d、只有一个11、与是位似图形,且与的位似比是,已知的面积是,则的面积是()A.d.12.如图所示,为了测量学校旗杆的高度,晓东使用长度为的竹竿作为测量工具移动竹竿,使竹竿顶部和旗杆顶部的阴影落在地面上的同一点上。
此时,竹竿距离此点较远,旗杆高度为()下在墙上形成的影子如图所示.若,则这个三角尺的周长与它在墙上形成的影子的周长的比是()14.如果和的值为()a.D15、如图,已知,那么添加下列一个条件后,仍无法判定的是()D二、填空题(本大题共有5小题,每小题5分,共25分)16.假设两个相似多边形的相似比为,它们对应边的比率等于____________________;,面积比等于__17、测量旗杆高度的方法都是依据___________的原理而设计的.引理:平行于三角形一边并与另两边相交的直线。
人教版数学九年级下册 第27章 相似 27.2 相似三角形 27.2.2相似三角形的判定 同步训
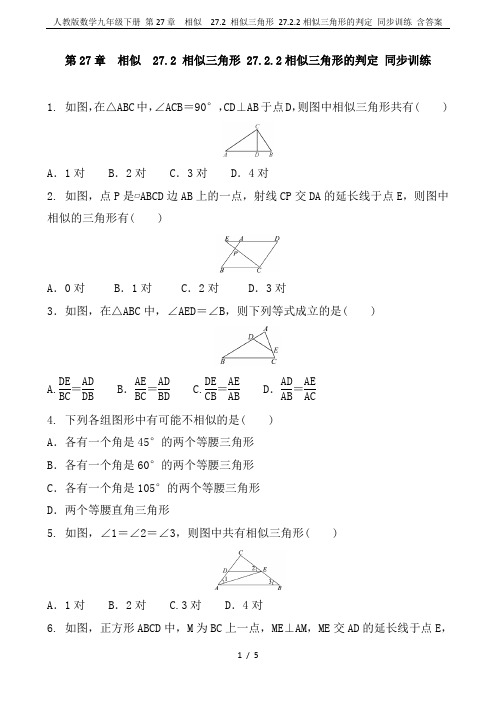
第27章 相似 27.2 相似三角形 27.2.2相似三角形的判定 同步训练1. 如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,则图中相似三角形共有( )A .1对B .2对C .3对D .4对2. 如图,点P 是▱ABCD 边AB 上的一点,射线CP 交DA 的延长线于点E ,则图中相似的三角形有( )A .0对B .1对C .2对D .3对3.如图,在△ABC 中,∠AED =∠B ,则下列等式成立的是( )A.DE BC =AD DB B .AE BC =AD BD C.DE CB =AE AB D .AD AB =AE AC 4. 下列各组图形中有可能不相似的是( ) A .各有一个角是45°的两个等腰三角形 B .各有一个角是60°的两个等腰三角形 C .各有一个角是105°的两个等腰三角形 D .两个等腰直角三角形5. 如图,∠1=∠2=∠3,则图中共有相似三角形( )A .1对B .2对 C.3对 D .4对6. 如图,正方形ABCD 中,M 为BC 上一点,ME ⊥AM ,ME 交AD 的延长线于点E ,若AB =12,BM =5,则DE 的长为( )A .18B .1095 C.965 D .2537. 如图,有三个三角形,其中相似的是 .8. 如图,∠1=∠2,∠B =∠E ,△ABC 与△AED 相似吗?为什么?9. 如图,正方形ABCD 中,点E 、F 、G 分别在AB 、BC 、CD 上,且∠EFG =90°.求证:△EFB ∽△FCG.10. 如图已知,在△ABC 中,CD ⊥AB ,BE ⊥AC ,BE 交CD 于点O.求证:△ABE ∽△OCE.11.如图,在▱ABCD 中,AD =10cm ,CD =5cm ,E 为AD 上一点,且BE =BC ,CE =CD ,则DE = cm.12.如图,正方形ABCD 中,BC =2,点M 是边AB 的中点,连接DM ,DM 与AC 交于点P ,点E 在DC 上,点F 在DP 上,且∠DFE =45°,若PF =56,则CE = . 13. 如图,D 是△ABC 的边BC 上一点,E 为边AD 上一点.若∠1=∠B ,CD =CE ,试说明△ACE ∽△BAD.14. 如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE∶CP=2∶3,求AE的长.参考答案: 1---6 CDCAD B 7. ①与②8. 解:△ABC ∽△AED ,∵∠1=∠2,∴∠1+∠DAC =∠2+∠DAC ,∴∠BAC =∠EAD ,在△ABC 和△AED 中,∵∠B =∠E ,∠BAC =∠EAD ,∴△ABC ∽△AED. 9. 证明:∵四边形ABCD 是正方形,∴∠B =∠C =90°,∴BEF +∠BFE =90°,∵∠EFG =90°,∴∠BFE =∠CFG ,∴△EFB ∽△FCG.10. 证明:因为CD ⊥AB ,BE ⊥AC ,所以∠AEB =∠ADC =90°.又∠A =∠A ,所以∠ABE =∠OCE.又因为∠AEB =∠OEC ,所以△ABE ∽△OCE. 11. 2.5 12. 7613. 证明:∵CD =CE ,∴∠CED =∠CDE ,即∠B +∠3=∠1+∠2,又∠1=∠B ,∴∠2=∠3,∴△ACE ∽△BAD.14. (1)证明:∵AB =AD ,AC 平分∠BAD ,∴AC ⊥BD ,∴∠ACD +∠BDC =90°,∵AC =AD ,∴∠ACD =∠ADC ,∴∠ADC +∠BDC =90°,∵PD ⊥AD ,∴∠ADC +∠PDC =90°,∴∠BDC =∠PDC ;(2)解:过点C 作CM ⊥PD 于点M ,∵∠BDC =∠PDC ,∴CE =CM ,∵∠CMP =∠ADP =90°,∠P =∠P ,∴△CPM ∽△APD ,∴ CM AD =PCPA ,设CM =CE =x ,∵CE ∶CP =2∶3,∴PC =32x ,∵AB =AD =AC =1,∴x 1=32x 32x +1,解得:x =13,故AE =1-13=23.。
人教版数学九年级下册数学:27.2.2 相似三角形的性质 同步练习(附答案)

27.2.2 相似三角形的性质1.已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为34,则△ABC 与△DEF 对应中线的比为( )A.34B.43C.916D.1692.若△ABC ∽△A ′B ′C ′,AB =16 cm ,A ′B ′=4 cm ,AD 平分∠BAC ,A ′D ′平分∠B ′A ′C ′,A ′D ′=3 cm ,则AD = cm.3.已知:△ABC ∽△A ′B ′C ′,AB =4 cm ,A ′B ′=10 cm ,AE 是△ABC 的一条高,AE =4.8 cm.求△A ′B ′C ′中对应高线A ′E ′的长.4.若△ABC ∽△A ′B ′C ′,相似比为1∶3,则△ABC 与△A ′B ′C ′周长的比为( )A .1∶3B .3∶1C .1∶9D .9∶15.如图,在△ABC 中,D ,E 分别是AB ,AC 上的点,DE ∥BC ,且AD =13AB ,则△ADE 的周长与△ABC 的周长的比为 .6.两三角形的相似比是2∶3,则其面积之比是( )A.2∶ 3 B .2∶3 C .4∶9 D .8:27 7.若两个相似三角形的周长比为2∶3,则它们的面积比是 . 8.如图,D ,E 分别是△ABC 的边AB ,AC 上的中点,则S △ADE ∶S △ABC = .9.如图,平行于BC 的直线DE 把△ABC 分成的两部分面积相等,则ADAB= .10.某小区广场有两块相似三角形的草坪,相似比为2∶3,面积差是30 m 2,则小区广场两块相似三角形的草坪面积分别是 .11.如图,在▱ABCD 中,E 是AD 边上的中点,连接BE ,并延长BE 交CD 延长线于点F ,则△EDF 与△BCF 的周长之比是( )A .1∶2B .1∶3C .1∶4D .1∶512.如图,在△ABC 中,点D 在AB 上,BD =2AD ,DE ∥BC 交AC 于点E ,则下列结论不正确的是( )A .BC =3DE B.BD BA =CE CA C .△ADE ∽△ABC D .S △ADE =13S △ABC13.如图,在▱ABCD 中,E 是AB 的中点,EC 交BD 于点F ,则△BEF 与△DCB 的面积比为( )A.13B.14 C.15 D.1614.已知△ABC 与△A ′B ′C ′中,∠C =∠C ′=90°,∠A =∠A ′,BC =6,AC =8,A ′B ′=20,则△A ′B ′C ′的斜边上的高为 .15.在△ABC 中,AB =9,AC =12,BC =18,D 为AC 上一点,AD =4,在AB 上取一点E ,得到△ADE ,若这两个三角形相似,则它们的周长之比是 .16.如图,在△ABC 中,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC ,CF ,EG 分别是△ABC 与△ADE 的中线,已知AD ∶DB =4∶3,AB =18 cm ,EG =4 cm ,求CF 的长.17.如图,▱ABCD中,AE∶EB=2∶3,DE交AC于点F.(1)求证:△AEF∽△CDF;(2)求△AEF与△CDF的周长之比;(3)如果△CDF的面积为20 cm2,求△AEF的面积.18.如图,P为▱ABCD边AD上一点,E,F分别是PB,PC(靠近点P)的三等分点,△PEF,△PDC,△PAB的面积分别为S1,S2,S3,若AD=2,AB=23,∠A=60°,则S1+S2+S3的值为.参考答案: 1.A 2. 12 .3.解:∵△ABC ∽△A ′B ′C ′, ∴AE A ′E ′=AB A ′B ′.∴ 4.8A ′E ′=410. ∴A ′E ′=12 cm. 4.A 5.1∶3. 6.C 7. 4∶9. 8. 1∶4.9210.24__m 2、54__m 2. 11.A 12.D 13.D 14.485.15.4∶9或1∶3. 16.解:∵AD ∶DB =4∶3, ∴AD ∶AB =4∶7. ∵DE ∥BC , ∴△ABC ∽△ADE.∵CF ,EG 分别是△ABC 与△ADE 的中线, ∴AD AB =EG CF .∴47=4CF . ∴CF =7 cm.17.解:(1)证明:∵四边形ABCD 是平行四边形, ∴DC ∥AB. ∴△AEF ∽△CDF.(2)∵四边形ABCD 是平行四边形, ∴DC =AB.∵AE ∶EB =2∶3,设AE =2k ,则BE =3k ,DC =5k.又∵△AEF ∽△CDF , ∴C △AEF C △CDF =AE DC =25. ∴△AEF 与△CDF 的周长之比为2∶5. (3)∵△AEF ∽△CDF , ∴S △AEF S △CDF =(AE DC)2. ∵AE DC =25,△CDF 的面积为20 cm 2, ∴△AEF 的面积为165 cm 2.18.103.。
人教版九年级数学下册 27.2.2相似三角形的性质 同步导练 含答案

人教版九年级数学下册 27.2.2相似三角形的性质 同步导练一、选择题1.如图,已知直线a∥b∥c,直线m 分别交直线a ,b ,c 于点A ,B ,C ,直线n 分别交直线a ,b ,c 于点D ,E ,F ,若21=BC AB ,则EFDE 等于( )A.31 B.21 C.32 D.12.已知△ABC∽△A′B′C′且21''=B A AB ,则S △ABC :S△A′B′C′为( ) A.1:2B.2:1C.1:4D.4:13.在△ABC 和△A′B′C′中,∠A=∠A′=90°,添加下列条件不能判定两个三角形相似的是( )A.∠B=∠B′B.''''C A AC B A AB = C.''''C B BC B A AB = D.''''C A AC C B AB =4.下列能判定△ABC∽△A′B′C′的条件是( ). A.''''C A AC B A AB = B.''''C A AC B A AB =,且∠A=∠A′ C.''''C A B A BC AB =,且∠B=∠C′ D ''C A AC BC AB =,且∠B=∠B′ 5.如图,已知AB∥CD∥EF,AF 交BE 于点H ,下列结论中错误的是( ) A.HC BH =HDAH B.CE BC =DF AD C.DFHD =HE HC D.CE BE =DF AF6.在Rt△ABC 和Rt△DEF 中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )A .∠A=55°,∠D=35°B .AC=9,BC=12,DF=6,EF=8C .AC=3,BC=4,DF=6,DE=8D .AB=10,AC=8,DE=15,EF=97.若△ABC 与△DEF 满足下列条件,其中使△ABC 与△DEF 相似的是( )A.AB=3,BC=6,AC=9;DE=2,EF=4,DF=6B.AB=4,BC=6,AC=8;DE=20,EF=10,DF=15C.AB=1,BC=2,AC=2;DE=6,EF=3,DF=5D.AB=1,BC=5,AC=3;DE=15,EF=25,DF=68.已知△ABC∽△A′B′C′,AD和A′D′分别是△ABC,△A′B′C′的对角平分线,且AD:A′D′=5:4,下列结论:①AC:A′C′=5:4;②△ABC与△A′B′C′的对应中线之比为5:4;③△ABC的周长:△A′B′C′的周长=5:4;④△AB C的面积:△A′B′C′的面积=5:4.其中正确的结论有()A.1个B.2个C.3个D.4个9.如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上,若△ADG,△BED,△CFG的面积分别是1,3,1,则正方形的边长为()A.2B.3C.2D.2210.如图,在□ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是()A.5B.8.2C.6.4D.1.8二、填空题11.底角相等的两个等腰三角形相似.(填“一定”或“不一定”)12.如图,∠C=∠E=90°,AC=3,BC=5,AE=2,则DE= .13.一个直角三角形的两边长分别为3和6,另一个直角三角形的这两边长分别为2和4,那么这两个直角三角形相似.(填“一定”、“不一定”或“一定不”)14.△ABC和△A′B′C′相似,记作,相似三角形的比叫,当相似比为1时,两个三角形 .15.若两个三角形相似,相似比为8:9,则它们对应角平分线之比是,若其中较小三角形的一条角平分线的长为6cm,则另一个三角形对应角平分线的长为.16.如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为 .17.如果两个三角形的三组对应边,那么这两个三角形相似.18.如图所示,它们是两个相似的平行四边形,根据条件可知,∠α=,m= .三、解答题19.如图,小明想测量电线杆AB 的高度,结果发现电线杆AB 的影子正好落在坡面CD 和地面BC 上,已知CD 与地面成30°角,CD=4m ,BC=10m ,且此时测得1m 高的标杆在地面上的影长为2m ,根据以上数据求电线杆AB 的高度.(结果保留根号)20.如图,在平面直角坐标系xOy 中,直线y=-x+3与x 轴交于点C ,与直线AD 交于点A (34,35),点D 的坐标为(0,1).(1)求直线AD 的解析式;(2)直线AD 与x 轴交于点B ,若点E 是直线AD 上一动点(不与点B 重合),当△BOD 与△BCE 相似时,求点E 的坐标.21.如图,在△ABC 中,已知AB=AC=5,BC=6,且△ABC≌△DEF.将△DEF 与△ABC 重合在一起,△ABC 不动,△DEF 运动,并满足:点E 在边BC 上沿点B 到点C 的方向运动,且DE 始终经过点A ,EF 与AC 交于点M.(1)求证:△ABE∽△ECM;(2)探究:在△DEF 运动的过程中,重叠部分能否构成等腰三角形,若能,求出BE 的长;若不能,请说明理由;(3)求当线段AM 最短时的长度.22.如图所示,在平面直角坐标系中,点A 的坐标为(8,0),点B 的坐标为(0,6),C 是线段AB 的中点.请问在y 轴上是否存在一点P ,使得以P 、B 、C 为顶点的三角形与△AOB 相似?若存在,求出点P 的坐标;若不存在,请说明理由.23.已知:如图,在□ABCD 中,E 是BC 边上一点,且BE=21EC ,BD ,AE 相交于F 点.(1)求△BEF 的周长与△AFD 的周长之比;(2)若△BEF 的面积为6cm 2,求△AFD 的面积.24.如图,在△ABC 中,DE∥BC,S △ADE :S 四边形DBCE =9:16,求AD:DB 的值.解:∵DE∥BC,∴△ADE∽△ABC,∴S△ADE:S四边形DBCE= (AD:DB)2.又∵S△ADE:S四边形DBCE=9:16,∴(AD:DB)2=9:16,∴AD:DB=3:4.以上解答是否正确?若不正确,请给予改正.答案1-10.BCDBC,CACCD11.一定 12.3813.不一定14.△ABC∽△A′B′C′,对应边,相似比,全等 15.8:9,427cm. 16.817.的比相等18.125°,12.19.20.21.(1)证明:∵AB=AC,∴∠B=∠C.∵△ABC≌△DEF,∴∠AEF=∠B,又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,∴∠CEM=∠BAE,∴△ABE∽△ECM;(2)能.解:∵∠AEF=∠B=∠C,且∠AME>∠C,∴∠AME>∠AEF,∴AE≠AM;当AE=EM时,则△ABE≌△ECM,∴CE=AB=5,∴BE=BC-EC=6-5=1,当AM=EM时,则∠MAE=∠MEA,∴∠MAE+∠BAE=∠MEA+∠CEM,即∠CAB=∠CEA.又∵∠C=∠C,22.解:存在这样的P点.理由如下:∵∠AOB=90°,OA=8,OB=6,∴AB=10.∵C是线段AB的中点,∴BC=5.∵∠ABO是公共角,23.解:(1)∵四边形ABCD 是平行四边形, ∴AD∥BC,AD=BC ,∴△BEF∽△DAF. ∵BE=21EC , ∴BE:AD=BE:BC=1:3,∴△BEF 与△AFD 的周长之比为1:3.(2)由(1)可知△BEF∽△DAF,且相似比为1:3, ∴S△BEF:S△AFD=1:9.又∵S△BEF=6cm2,∴S△AFD=54cm2.24.解:不正确,改正如下:∵S△ADE :S四边形DBCE=9:16,∴S△ADE:S△ABC=9:25,∵DE∥BC,∴△ADE∽△ABC.∴S△ADE :S△ABC=(AD:AB)2,∴(AD:AB)2=9:25 ∴AD:AB=3:5,∴AD:DB=3:2.。
人教版九年级数学下册 27.2.2 相似三角形的性质同步测试及答案【新】

相似三角形的性质1. 已知△ABC ∽△DEF ,若△ABC 与△DEF 的相似比为3∶4,则△ABC 与△DEF 的面积之比为( D )A .4∶3B .3∶4C .16∶9D .9∶162. 如图27-2-41,AB ∥CD ,AO OD =23,则△AOB 的周长与△DOC 的周长比是 ( D )图27-2-41A.25B.32C.49D.233.两个相似多边形的面积比是9∶16,其中较小多边形的周长为36 cm ,则较大多边形的周长为( A )A .48 cmB .54 cmC .56 cmD .64 cm4.如图27-2-42,在△ABC 中,点D ,E 分别是AB ,AC 的中点,则下列结论不正确的是( D )A .BC =2DEB .△ADE ∽△ABCC.AD AE =AB AC D .S △ABC =3S △ADE【解析】 ∵在△ABC 中,点D ,E 分别是边AB ,AC 的中点,∴DE ∥BC ,DE =12BC ,∴BC =2DE ,故A 正确;∵DE ∥BC ,∴△ADE ∽△ABC ,故B 正确;∴AD AE =AB AC,故C 正确;∵DE 是△ABC 的中位线,∴S △ABC =4S △ADE ,故D 错误.5.如图27-2-43,边长为4的等边△ABC 中,DE 为中位线,则四边形BCED 的面积为( B )A .2 3B .3 3C .4 3D .6 3【解析】 作DF ⊥BC 于F ,∵边长为4的等边△ABC 中,DE 为中位线,∴DE =2,BD =2,∠B =60°,∴BF =1,DF =BD 2-BF 2=22-12=3,∴四边形BCED 的面积为12DF ·(DE +BC )=12×3×(2+4)=3 3.故选B. 6.在△ABC 和△DEF 中,AB =2DE ,AC =2DF ,∠A =∠D ,如果△ABC 的周长是16,面积是12,那么△DEF 的周长、面积依次为( A )A .8,3B .8,6C .4,3D .4,6【解析】 ∵AB =2DE ,AC =2DF ,∴AB DE =AC DF=2,又∠A =∠D ,∴△ABC ∽△DEF ,且相似比为2,∴△ABC 与△DEF 的周长比为2,面积比为4,又∵△ABC 的周长为16,面积为12,∴△DEF 的周长为16×12=8,△DEF 的面积为12×14=3. 7. 如图27-2-44,在△ABC 中,点D ,E 分别在边AB ,AC 上,且AE AB =AD AC =12,则S △ADE ∶S 四边形BCED 的值为( C )图27-2-44A .1∶ 3 B. 1∶2C. 1∶3D. 1∶48.已知△ABC ∽△A ′B ′C ′,相似比为3∶4,若△ABC 的周长为6,则△A ′B ′C ′的周长为__8__.【解析】 ∵△ABC ∽△A ′B ′C ′,∴△ABC 的周长∶△A ′B ′C ′的周长=3∶4,∵△ABC 的周长为6,∴△A ′B ′C ′的周长=6×43=8. 9.已知△ABC ∽△DEF ,△ABC 的周长为3,△DEF 的周长为1,则△ABC 与△DEF 的面积之比为__9∶1__.【解析】 ∵△ABC ∽△DEF ,△ABC 的周长为3,△DEF 的周长为1,∴△ABC 与△DEF 的相似比是3∶1,的面积之比为9∶1.10.如图27-2-45,在△ABC 中,DE ∥BC ,DE 分别交边AB ,AC 于D ,E 两点,若AD ∶AB =1∶3,则△ADE 与△ABC 的面积比为__1∶9__.11.一天,某校数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度,来评估这些深坑对河道的影响,如图27-2-46是同学们选择(确保测量过程中无安全隐患)的测量对象,测量方案如下:①先测量出沙坑坑沿圆周的周长约为34.54米;②甲同学直立于沙坑坑沿圆周所在平面上,经过适当调整自己所处的位置,当他位于点B 时,恰好他的视线经过沙坑坑沿圆周上的一点A 看到坑底S (甲同学的视线起点C 与点A 、点S 三点共线).经测量:AB =1.2米,BC =1.6米. (圆锥的高).(π取3.14,结果精确到0.1米)解:如图,取圆锥底面圆圆心O ,连接OS ,OA , 则∠O =∠ABC =90°,OS ∥BC ,∴∠ACB =∠ASO ,∴△SOA ∽△CBA ,∴OS BC =OA AB ,即OS =OA ·BC AB. ∵OA =34.542π≈5.5,BC =1.6,AB =1.2, ∴OS ≈5.5×1.61.2≈7.3, ∴“圆锥形坑”的深度约为7.3米.12. 已知△ABC ∽△DEF ,DE AB =23,△ABC 的周长是12 cm ,面积是30 cm 2. (1)求△DEF 的周长;(2)求△DEF 的面积.解:(1)∵DE AB =23, ∴△DEF 的周长=12×23=8(cm); (2)∵DE AB =23, ∴△DEF 的面积=30×(23)2=1313(cm 2).13.如图27-2-47,四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于O ,AD =1,BC =4,则△AOD 与△BOC 的面积比等于( D )图27-2-47A.12B.14C.18D.11614.如图27-2-48,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD 于点F ,点E 是AB 的中点,连接EF .(1)求证:EF ∥BC ;(2)若△ABD 的面积是6,求四边形BDFE 的面积.【解析】 (1)证明EF 为△ABD 的中位线;(2)利用相似三角形的面积比等于相似比的平方求解. 解:(1)证明:∵DC =AC ,∴△ACD 为等腰三角形.∵CF 平分∠ACD ,∴F 为AD 的中点.∵E 为AB 的中点,∴EF 为△ABD 的中位线,∴EF ∥BC .(2)由(1)得EF ∥BC ,∴△AEF ∽△ABD . ∵EF BD =12,∴S △AEF ∶S △ABD =1∶4, ∴S 四边形BDFE ∶S △ABD = 3∶4.∵S △ABD =6,∴S 四边形BDFE =92. 15.[2013·泰安]如图27-2-49,四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点.图27-2-49(1)求证:AC 2=AB ·AD ;(2)求证:CE ∥AD ; (3)若AD =4,AB =6,求ACAF的值.解:(1)证明:∵AC 平分∠DAB ,∴∠DAC =∠CAB .又∵∠ADC =∠ACB =90°,∴△ADC ∽△ACB .∴AD AC =AC AB. ∴AC 2=AB ·AD .(2)证明:∵E 为AB 的中点, ∴CE =12AB =AE , ∠EAC =∠ECA .∵AC 平分∠DAB ,∴∠CAD =∠CAB .∴∠DAC =∠ECA .∴CE ∥AD .(3)∵CE ∥AD ,∴∠DAF =∠ECF ,∠ADF =∠CEF ,∴△AFD ∽△CFE ,∴AD CE =AF CF.∵CE =12AB , ∴CE =12×6=3. 又∵AD =4,由AD CE =AF CF 得43=AF CF, ∴AF AC =47. ∴AC AF =74.16. 已知:如图27-2-50,△ABC 中,AB =AC ,AD 是中线,P 是AD 上一点,过C 作CF ∥AB ,延长BP 交AC 于E ,交CF 于F .求证:BP 2=PE ·PF .图27-2-50证明: 连接PC ,∵AB =AC ,AD 是中线,∴AD 是△ABC 的对称轴.∴PC =PB ,∠PCE =∠ABP .∵CF ∥AB ,∴∠PFC =∠ABP (两直线平行,内错角相等),∴∠PCE =∠PFC .又∵∠CPE =∠EPC ,∴△EPC ∽△CPF . ∴PC PE =PF PC(相似三角形的对应边成比例).∴PC 2=PE ·PF .∵PC =BP ,∴BP 2=PE ·PF .17. 我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如有关线段比、面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题:(1)若O 是△ABC 的重心(如图1),连结AO 并延长交BC 于D ,证明:AO AD =23; (2)若AD 是△ABC 的一条中线(如图2),O 是AD 上一点,且满足AO AD =23,试判断O 是△ABC 的重心吗?如果是,请证明;如果不是,请说明理由;(3)若O 是△ABC 的重心,过O 的一条直线分别与AB ,AC 相交于G ,H (均不与△ABC 的顶点重合)(如图3),S 四边形BCHG .S △AGH 分别表示四边形BCHG 和△AGH 的面积,试探究S 四边形BCHG S △AGH的最大值.图27-2-51解:(1)证明:连接BO 并延长交AC 于点E ,连接DE ,则DE 为△ABC 的中位线,∴DE ∥AB ,∴△EDO ≌△BAO ,∴DO AO =DE AB =12,∴AO AD =23.(2)是,证明:连接BO 并延长交AC 于点E ,过点D 作DF ∥BE 交AC 于点F ,则△AOE ∽△ADF , ∴AE AF =AO AD =23,∴AE =2EF ,又∵△CDF ∽△CBE ,∴CF CE =CD CB =12, ∴EF =FC ,∴AE =CE ,即点E 为AC 中点,∴点O 为△ABC 的重心.(3)54.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形的性质及应用练习卷
一、填空题
1、已知两个相似三角形的相似比为 3,则它们的周长比为
;
2、若△ABC ∽△A ′B′C′,且
AB 3 A B 4
,△ABC 的周长为 12cm , △
则A ′B′C′的周长为
;
3、如图 1,在△ABC 中,中线 BE 、CD 相交于点 G ,则
DE
BC
S
=
;
△GED
:
△S GBC
= ;
4、如图 2,在△ABC 中, ∠B=∠AED,AB=5,AD=3,CE=6,则 AE=
;
5、如图 3,△ABC 中,M 是 AB 的中点,N 在 BC 上,BC=2AB ,∠BMN=∠C , △则
∽△ ,
相似比为
,
BN NC
= ;
,
6、如图 4,在梯形 ABCD 中,AD∥BC
=4:9,则 :S =
△S ADE
△:S BCE △S ABD
△ABC
;
7、如图 5,在△ABC 中,BC=12cm ,点 D 、F 是 AB 的三等分点,点 E 、G 是 AC 的三等分点,则
DE+FG+BC= ;
D
A
E
D
A
E
M A
A
E
D
F
D
A
E G
B
C
C B
C B
C
B
8、两个相似三角形的周长分别为 5cm 和 16cm ,则它们的对应角的平分线的比为 ; 9、
两个三角形的面积之比为 2:3 ,则它们对应角平分线的比为 ,对应边的高的比
为
;对应边的中线的比
周长的比
图 5
C
10、已知有两个三角形相似,一个边长分别为 2、3、4,另一个三角形最长边长为 12,则 x 、y 的 值为 ;
二、选择题
11、下列多边形一定相似的为( )
A 、两个矩形
B 、两个菱形
C 、两个正方形
D 、两个平行四边形
12、在△ABC 中,BC=15cm ,CA=45cm ,AB=63cm ,另一个和它相似的三角形的最短边是 5cm ,则最长 边是( )
A 、18cm
B 、21cm
C 、24cm
D 、19.5cm
13、如图,在△ABC 中,高 BD 、CE 交于点 O ,下列结论错误的是( )
A
A 、CO·CE=CD·CA
B 、OE·OC=OD·OB E
D
C 、AD·AC=AE·AB
D 、CO·DO=BO·EO
O
B
C
B G 图 4
N
图 2
图 1
图 3
14、已知,在△ABC中,∠ACB=900,CD⊥AB于D,若BC=5,CD=3,则AD的长为()A、
2.25B、2.5C、2.75D、3
15、如图,正方形ABCD的边BC在等腰直角三角形PQR的底边QR上,
Q 其余两个顶点A、D在PQ、PR上,则PA:PQ等于()B
A、1:3
B、1:2
C、1:3
D、2:3A
C
16、如图,D、E分别是△ABC的边AB、AC上的点,BD AE
==3,
AD CE
P
A
D R
且∠AED=∠B,则△AED与△ABC的面积比是()D
A、1:2
B、1:3
C、1:4
D、4:9
三、解答题B
E
C
17、如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD·BE。
C
A D E B
18、已知,如图,在△ABC中,DE∥BC,AD=5,BD=3,求S的值。
△
:S ADE △BCed A
D
B
19、已知正方形ABCD,过C的直线分别交AD、AB的延长线于点E、F,且AE=15,AF=10,求正方
形ABCD的边长。
E C
20、已知,如图,在等边△CDE中,A、B分别是ED、DE的延长线上的点,且D E
的度数。
2=AD·EB,求∠ACB
C
A D E B
21、已知,如图,在△ABC中,∠C=600,AD⊥BC于D,BE⊥AC于E,试说△明CDE∽△。
CBA
A
E
22、已知,如图,F为ABCD边DC延长线上一点,连结AF,交BC于G,交BD于E,试说明AE2=EG·EF
B
D C
D C
F
E G
A B
24.△ABC中,∠C=900,D,E分别是AB,AC上的点,AD·AB=AE·AC,求证ED⊥AB
26、已知等腰三角形ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F,
求证:BF2=EF·EG
27、已知:在△ABC中,∠BAC=900 AD⊥BC于D,P为AD中点,BP延长线交AC于E,EF⊥BC于F
求证:EF2=AE·AC
28、
如图,平行四边形ABCD中,
BE3
E是B C上的一点,,AE交B D于点F,
EC4A
D
BF 6cm,求BE
DA
及DF的值。
F
B
E C
相似三角形及其判定练习
一、选择题:
1.下列判断正确的是()
A.两个直角三角形相似
B.两个相似三角形一定全等
C.
凡等边三角形都相似 D.所有等腰三角形都相似
2.下列各对三角形中一定不相似的是()
A.
△ABC中,∠A=54°,∠B=78°△A′B′C′中,∠C′=48°,∠B′=78°
△B.ABC中,∠C=90°,AC=4cm,BC=3cm
△A′B′C′中,∠C′=90°,A′C′=12cm,B′C′=15cm
C.△ABC中,∠B=90°,AB=5,AC=13
△A′B′C′中,∠B′=90°,A′B′=2.5a,B′C′=6a
△D.ABC中,∠C=90°,∠A=45°,AB=5
△A′B′C′中,∠A′=45°,A′B′=5
3.如图,AB∥CD,AC、BD交于O,BO=7,DO=3,AC=25,
则Ao长为()
4如图,已知△ABC中D为AC中点,AB=5,AC=7,∠AED=∠C,则ED=。
5在梯形ABCD中,AB∥CD,AC平分∠DAB,DC:AB=1:1.5,则AD:BC=。
6如图18在△R t A B C中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=,BD=。
3
45
6
7.已知:AC⊥BD,DE⊥AB,AC、ED交于F,BC=3,FC=1,BD=5,则AC=。
8.已知□:AB C D中E为AD的中点,AF:AB=1:6,EF与AC交于M。
求:AM:AC。
