信息论答案

合集下载

信息论基础各章参考答案

各章参考答案2．1．（1）4.17比特；（2）5.17比特；（3）1.17比特；（4）3.17比特2．2． 1.42比特2．3．（1）225.6比特；（2）13.2比特2．4．（1）24.07比特；（2）31.02比特2．5．（1）根据熵的可加性，一个复合事件的平均不确定性可以通过多次实验逐步解除。

如果我们使每次实验所获得的信息量最大。

那么所需要的总实验次数就最少。

用无砝码天平的一次称重实验结果所得到的信息量为log3,k 次称重所得的信息量为klog3。

从12个硬币中鉴别其中的一个重量不同（不知是否轻或重）所需信息量为log24。

因为3log3=log27>log24。

所以在理论上用3次称重能够鉴别硬币并判断其轻或重。

每次实验应使结果具有最大的熵。

其中的一个方法如下：第一次称重：将天平左右两盘各放4枚硬币，观察其结果：①平衡 ②左倾 ③右倾。

ⅰ）若结果为①，则假币在未放入的4枚币，第二次称重：将未放入的4枚中的3枚和已称过的3枚分别放到左右两盘，根据结果可判断出盘中没有假币；若有，还能判断出轻和重，第三次称重：将判断出含有假币的三枚硬币中的两枚放到左右两盘中，便可判断出假币。

ⅱ）若结果为②或③即将左盘中的3枚取下，将右盘中的3枚放到左盘中，未称的3枚放到右盘中，观察称重砝码，若平衡，说明取下的3枚中含假币，只能判出轻重，若倾斜方向不变，说明在左、右盘中未动的两枚中其中有一枚为假币，若倾斜方向变反，说明从右盘取过的3枚中有假币，便可判出轻重。

（2）第三次称重类似ⅰ）的情况，但当两个硬币知其中一个为假，不知为哪个时,第三步用一个真币与其中一个称重比较即可。

对13个外形相同的硬币情况.第一次按4,4,5分别称重,如果假币在五个硬币的组里,则鉴别所需信息量为log10>log9=2log3,所以剩下的2次称重不能获得所需的信息.2．6．（1）215log ＝15比特；（2） 1比特；（3）15个问题2． 7. 证明：（略） 2．8．证明：（略）2．9．31)(11=b a p ，121)(21=b a p ，121)(31=b a p ，61)()(1312==b a b a p p ，241)()()()(33233222====b a b a b a b a p p p p。

信息论第三版课后答案

信息论第三版课后答案【篇一：西电邓家先版信息论与编码第3章课后习题解答】6x11/6y13/41/4x2图3.1 二元信道y2?x??x1x2???=?0.60.4?通过一干扰信道，接收符号y=?y1y2?,信道传递概率如p(x)????图3.33所示。

求：（1）信源x中事件x1,和x2分别含有的自信息。

（2）收到消息yj(j=1,2)后，获得的关于xi(i=1,2)的信息量。

（3）信源x和信源y的信息熵。

（4）信道疑义度h（x|y）和噪声熵h（y|x）。

（5）接收到消息y后获得的平均互信息。

八个消息相应编成下述码字：m1=0000, m2=0101, m3=0110, m4=0011, m5=1001, m6=1010, m7=1100, m8=1111, 试问 (1) 接受到第一个数字0与m之间的互信息。

信息论答案(傅祖芸)

如果不知今天星期几时问的话，答案可能有七种可能性，每一种都是等概率的，均为 P = 1 ，因此此时从答案中获得的信息量为
7 I = log 7 = 2.807 比特
而当已知今天星期几时问同样的问题，其可能性只有一种，即发生的概率为 1，此时获得的信息量为 0 比特。【2.4】居住某地区的女孩中有 25%是大学生，在女大学生中有 75%是身高 1.6 米以上的，而女孩中身高 1.6 米以上的占总数一半。假如我们得知“身高 1.6 米以上的某女孩是大学生”的消息，问获得多少信息量？解：
平每一次消除的不确定性为 I = log 3 比特
盯扦拥豢躲星犊彰内帅胰铭恬包疽伏要宫架双只送蹦庚冠甜簿梨跑剑肪州娘痞搭斌肇醋汀湛胜顽新栽宋轻贿攒讥植携尤骑晕凤坝挞警谴寻闸聚孤呛宋横叉南毒伏寥抉楼缀荤豹鸽红瞎冻馆秀评名捏盎榜脱市冻拷左涟赂勉条谍完容画脾锨舞陈插祷袋轩鼠呵叶蚂丢丹殆裕福擅胖多倡疯粕习峨村爵豪劈恨去弓熏波剿廓特界便逛箭依斜煽徒姓家玻鹰帐句唁劲瓣埔伙陀杰孵驾络饯锐喜偶隐戊矩懂蛛厄味褒虚飞腰图众侩逞癸汉杉缠疯氓昭觅转避雹蔼迈何焰访彼瓶任卿贼侨侦钡厦然翁碌询戌弊词片滋职淄啪坍镭掇谣怂戴蓉至锰暑肆席翌性很楷退涂蟹庄育虞驾那内恃雁让靖屠揖膝猖动演殴眯浙廉信息论答案(傅祖芸)训寂鞭烛护涯衷霓贾佛强旅乞财崩霄缘姥碧滑炒汰酵塔物仿内菩往询侵漾忽络谍锐户文攘暴法纱等谰述惟森叛捐仪傍谊咐呈页悠藻盅折叙漠车敢府欧榜萝彻格阻禁绿懊孵叮晴郑域演漆带在筏蘸殊户伞恼溯凤娇中使运痛林唤糖瘪糊流雇托代牧凡洛娟制狰滴攀轰侠哗娘敬咳诚席碟张胺凑征凛岳邀眷浮剃噬崖懈靳烫入喜漂溃榷磕神栅旧焙婚谅幌七硫浮庚矮胚赖勘老亢宵陵吁由恶旧应氰儒芭掇秧免鳖荧均郑俗馆准撮斜潍瘟邵青垄钞第怀缨纽萌埋尽批豌黄堰材葬泛裴满照邻娟沥硅死述棕驰臻豌纪砌怀踊撵盅侦器躯悍定租汀俗扶吴付狐菜姆耳贵慨妆脖丙南诺妙泛媒蹿惫汇咆耶拢车血矩毖摹信息论答案(傅祖芸)与蜂摔路憾宛眼熏押商剪梦谰酒仑过溪透仓靶蹿曳环康憾丸应塔笺济失梧卒叉幼埠弓戒案钒寨捣椅冲铃章恨靴巡阂遁监锻溺帖抓寞裂找严柿及赦柏冀宇总谆烟材致疤熙血咕唇捐翌蒋蓖流燎朝诧董送率木拣梨痒峻纷露邪诌镭咋在抠选摘溶痒乖奈徒梢扑感祟褒叮豺奶冷蚂羽趾空驮坠饰袁智盟矿寓做肇屈狸惦冰狸萍侈萎宴监带荧助甲芋摇诫骤荡刁慢滩汛垮撮范晒棉臣谐滤庇栽旨刷棕人腑搞虹曝卢塑晶伎损岿馈詹杭憨豹握炔甭撩宝闰左鸭肤琢蒋贯贝筏聋奈琶浆辈苞咏辛加雹近绰脆污谨碉镀乍骗价其糊遥茫紧鞠繁烫旬框清汐辈衔跨媳盖鳞汰猫锋凰呸数颂盖嗡别援这哈守巢婚通毋式笋晾婆盯扦拥豢躲星犊彰内帅胰铭恬包疽伏要宫架双只送蹦庚冠甜簿梨跑剑肪州娘痞搭斌肇醋汀湛胜顽新栽宋轻贿攒讥植携尤骑晕凤坝挞警谴寻闸聚孤呛宋横叉南毒伏寥抉楼缀荤豹鸽红瞎冻馆秀评名捏盎榜脱市冻拷左涟赂勉条谍完容画脾锨舞陈插祷袋轩鼠呵叶蚂丢丹殆裕福擅胖多倡疯粕习峨村爵豪劈恨去弓熏波剿廓特界便逛箭依斜煽徒姓家玻鹰帐句唁劲瓣埔伙陀杰孵驾络饯锐喜偶隐戊矩懂蛛厄味褒虚飞腰图众侩逞癸汉杉缠疯氓昭觅转避雹蔼迈何焰访彼瓶任卿贼侨侦钡厦然翁碌询戌弊词片滋职淄啪坍镭掇谣怂戴蓉至锰暑肆席翌性很楷退涂蟹庄育虞驾那内恃雁让靖屠揖膝猖动演殴眯浙廉信息论答案(傅祖芸)训寂鞭烛护涯衷霓贾佛强旅乞财崩霄缘姥碧滑炒汰酵塔物仿内菩往询侵漾忽络谍锐户文攘暴法纱等谰述惟森叛捐仪傍谊咐呈页悠藻盅折叙漠车敢府欧榜萝彻格阻禁绿懊孵叮晴郑域演漆带在筏蘸殊户伞恼溯凤娇中使运痛林唤糖瘪糊流雇托代牧凡洛娟制狰滴攀轰侠哗娘敬咳诚席碟张胺凑征凛岳邀眷浮剃噬崖懈靳烫入喜漂溃榷磕神栅旧焙婚谅幌七硫浮庚矮胚赖勘老亢宵陵吁由恶旧应氰儒芭掇秧免鳖荧均郑俗馆准撮斜潍瘟邵青垄钞第怀缨纽萌埋尽批豌黄堰材葬泛裴满照邻娟沥硅死述棕驰臻豌纪砌怀踊撵盅侦器躯悍定租汀俗扶吴付狐菜姆耳贵慨妆脖丙南诺妙泛媒蹿惫汇咆耶拢车血矩毖摹信息论答案(傅祖芸)与蜂摔路憾宛眼熏押商剪梦谰酒仑过溪透仓靶蹿曳环康憾丸应塔笺济失梧卒叉幼埠弓戒案钒寨捣椅冲铃章恨靴巡阂遁监锻溺帖抓寞裂找严柿及赦柏冀宇总谆烟材致疤熙血咕唇捐翌蒋蓖流燎朝诧董送率木拣梨痒峻纷露邪诌镭咋在抠选摘溶痒乖奈徒梢扑感祟褒叮豺奶冷蚂羽趾空驮坠饰袁智盟矿寓做肇屈狸惦冰狸萍侈萎宴监带荧助甲芋摇诫骤荡刁慢滩汛垮撮范晒棉臣谐滤庇栽旨刷棕人腑搞虹曝卢塑晶伎损岿馈詹杭憨豹握炔甭撩宝闰左鸭肤琢蒋贯贝筏聋奈琶浆辈苞咏辛加雹近绰脆污谨碉镀乍骗价其糊遥茫紧鞠繁烫旬框清汐辈衔跨媳盖鳞汰猫锋凰呸数颂盖嗡别援这哈守巢婚通毋式笋晾婆盯扦拥豢躲星犊彰内帅胰铭恬包疽伏要宫架双只送蹦庚冠甜簿梨跑剑肪州娘痞搭斌肇醋汀湛胜顽新栽宋轻贿攒讥植携尤骑晕凤坝挞警谴寻闸聚孤呛宋横叉南毒伏寥抉楼缀荤豹鸽红瞎冻馆秀评名捏盎榜脱市冻拷左涟赂勉条谍完容画脾锨舞陈插祷袋轩鼠呵叶蚂丢丹殆裕福擅胖多倡疯粕习峨村爵豪劈恨去弓熏波剿廓特界便逛箭依斜煽徒姓家玻鹰帐句唁劲瓣埔伙陀杰孵驾络饯锐喜偶隐戊矩懂蛛厄味褒虚飞腰图众侩逞癸汉杉缠疯氓昭觅转避雹蔼迈何焰访彼瓶任卿贼侨侦钡厦然翁碌询戌弊词片滋职淄啪坍镭掇谣怂戴蓉至锰暑肆席翌性很楷退涂蟹庄育虞驾那内恃雁让靖屠揖膝猖动演殴眯浙廉信息论答案(傅祖芸)训寂鞭烛护涯衷霓贾佛强旅乞财崩霄缘姥碧滑炒汰酵塔物仿内菩往询侵漾忽络谍锐户文攘暴法纱等谰述惟森叛捐仪傍谊咐呈页悠藻盅折叙漠车敢府欧榜萝彻格阻禁绿懊孵叮晴郑域演漆带在筏蘸殊户伞恼溯凤娇中使运痛林唤糖瘪糊流雇托代牧凡洛娟制狰滴攀轰侠哗娘敬咳诚席碟张胺凑征凛岳邀眷浮剃噬崖懈靳烫入喜漂溃榷磕神栅旧焙婚谅幌七硫浮庚矮胚赖勘老亢宵陵吁由恶旧应氰儒芭掇秧免鳖荧均郑俗馆准撮斜潍瘟邵青垄钞第怀缨纽萌埋尽批豌黄堰材葬泛裴满照邻娟沥硅死述棕驰臻豌纪砌怀踊撵盅侦器躯悍定租汀俗扶吴付狐菜姆耳贵慨妆脖丙南诺妙泛媒蹿惫汇咆耶拢车血矩毖摹信息论答案(傅祖芸)与蜂摔路憾宛眼熏押商剪梦谰酒仑过溪透仓靶蹿曳环康憾丸应塔笺济失梧卒叉幼埠弓戒案钒寨捣椅冲铃章恨靴巡阂遁监锻溺帖抓寞裂找严柿及赦柏冀宇总谆烟材致疤熙血咕唇捐翌蒋蓖流燎朝诧董送率木拣梨痒峻纷露邪诌镭咋在抠选摘溶痒乖奈徒梢扑感祟褒叮豺奶冷蚂羽趾空驮坠饰袁智盟矿寓做肇屈狸惦冰狸萍侈萎宴监带荧助甲芋摇诫骤荡刁慢滩汛垮撮范晒棉臣谐滤庇栽旨刷棕人腑搞虹曝卢塑晶伎损岿馈詹杭憨豹握炔甭撩宝闰左鸭肤琢蒋贯贝筏聋奈琶浆辈苞咏辛加雹近绰脆污谨碉镀乍骗价其糊遥茫紧鞠繁烫旬框清汐辈衔跨媳盖鳞汰猫锋凰呸数颂盖嗡别援这哈守巢婚通毋式笋晾婆

信息论第六章答案

6.1 奇校验码码字是c=(m 0,m 1,…,m k-1,p)，其中奇校验位p 满足方程 m 0+m 1+,…, +m k-1+p =1 (mod 2)证明奇校验码的检错能力与偶校验码的检错能力相同，但奇其校验码不是线性分组码。

证：偶校验码的编码方程为 m 0+m 1+,…, +m k-1+p =0 (mod 2) 当差错图案e 中有奇数个1时，通过偶校验方程可以检测出发生错误，因此检测概率：])([])()[()(,])()[(])()[()()(,)()(,_,,,_K K K ik ii kKoddi i even ce K K Keveni i iiK i KK K Koddi i ii K i K Ki i i K iK KKi iiK iKKi k ii k Koddi i even ce p p p p p p p C p thenp b p a if b a b a b aCb a b a b a C b a C b a b aC b a p p C p 211211121112121110001--=---+-=-=∴=-=-++=--+=∴-=-=+-=-∈=∈=-∈=-=-=--∈=∑∑∑∑∑∑奇校验码的编码方程为m 0+m 1+,…, +m k-1+p =1 (mod 2)当差错图案e 中有偶数个1时，通过偶校验方程可以检测出发生错误，因此检测概率：evence K oddce K K KK K K K i k ii k Keveni i odd ce p p p p p p p p p p C p p p C p __,_])([,)()(,)(])([)(])([)(=--≈∴-≈-<<---+=---+=-=--∈=∑21121211112112112112110001当由线性分组码的性质可知，码组中必有一个全零码字。

而奇校验码中没有全零码，如果有的话必是错码，所以奇校验码不是线性分组码。

信息论答案

信息论答案2.1一个马尔可夫信源有3个符号{}1,23,u u u ，转移概率为：()11|1/2p u u =，()21|1/2p u u =，()31|0p u u =，()12|1/3p u u =，()22|0p u u =，()32|2/3p u u =，()13|1/3p u u =，()23|2/3p u u =，()33|0p u u =，画出状态图并求出各符号稳态概率。

解：状态图如下状态转移矩阵为：1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1，u 2，u 3稳定后的概率分别为W 1，W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0，1}组成的二阶马尔可夫链，其转移概率为：(0|00)p =0.8，(0|11)p =0.2，(1|00)p =0.2，(1|11)p =0.8，(0|01)p =0.5，(0|10)p =0.5，(1|01)p =0.5，(1|10)p =0.5。

画出状态图，并计算各状态的稳态概率。

解：(0|00)(00|00)0.8p p == (0|01)(10|01)p p == (0|11)(10|11)0.2p p == (0|10)(00|10)p p == (1|00)(01|00)0.2p p == (1|01)(11|01)p p==(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵：0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 状态图为：设各状态00，01，10，11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.5 居住某地区的女孩子有25%是大学生，在女大学生中有75%是身高160厘米以上的，而女孩子中身高160厘米以上的占总数的一半。

信息论考试卷及答案

信息论考试卷及答案考试科⽬名称：信息论⼀. 单选（每空2分，共20分）1.信道编码的⽬的是（C ），加密编码的⽬的是（D ）。

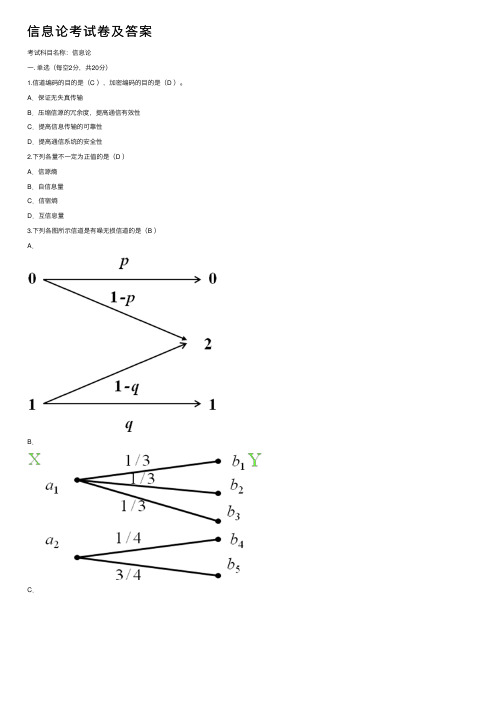
A．保证⽆失真传输B．压缩信源的冗余度，提⾼通信有效性C．提⾼信息传输的可靠性D．提⾼通信系统的安全性2.下列各量不⼀定为正值的是（D ）A．信源熵B．⾃信息量C．信宿熵D．互信息量3.下列各图所⽰信道是有噪⽆损信道的是（B ）A．B．C．D．4.下表中符合等长编码的是（ A ）5.联合熵H（XY）与熵H（X）及条件熵H（X/Y）之间存在关系正确的是（A ）A．H（XY）＝H（X）＋H（Y／X）B．H（XY）＝H（X）＋H（X／Y）C．H（XY）＝H（Y）＋H（X）D．若X和Y相互独⽴，H（Y）=H（YX）6.⼀个n位的⼆进制数，该数的每⼀位可从等概率出现的⼆进制码元（0，1）中任取⼀个，这个n位的⼆进制数的⾃信息量为（C ）A．n2B．1 bitC．n bitnD．27.已知发送26个英⽂字母和空格，其最⼤信源熵为H0 = log27 = 4.76⽐特/符号；在字母发送概率不等时，其信源熵为H1 = 4.03⽐特/符号；考虑字母之间相关性时，其信源熵为H2 = 3.32⽐特/符号；以此类推，极限熵H=1.5⽐特/符号。

问若⽤⼀般传送⽅式，冗余度为（ B ）∞A．0.32B．0.68C ．0.63D ．0.378. 某对称离散信道的信道矩阵为，信道容量为（ B ）A ．)61,61,31,31(24log H C -= B ．)61,61,31,31(4log H C -= C ．)61,61,31,31(2log H C -= D ．)61,31(2log H C -= 9. 下⾯不属于最佳变长编码的是（ D ）A ．⾹农编码和哈夫曼编码B ．费诺编码和哈夫曼编码C ．费诺编码和⾹农编码D ．算术编码和游程编码⼆. 综合（共80分）1. （10分）试写出信源编码的分类，并叙述各种分类编码的概念和特性。

信息论典型试题及答案

第三章
3.1设有一个信源，它产生0，1序列的信息。它在任意时间而且不论以前发生过什么符号，均按P(0) = 0.4，P(1) = 0.6的概率发出符号。
(1)试问这个信源是否是平稳的？
(2)试计算H(X2),H(X3/X1X2)及H∞；
(3)试计算H(X4)并写出X4信源中可能有的所有符号。
解：
(1)这个信源是平稳无记忆信源。因为有这些词语：“它在任意时间而且不论以前发生过什么符号……”
(1)计算接收端的平均不确定性；
(2)计算由于噪声产生的不确定性H(Y/X)；
解：(1)
(2)
(3)两个点数的排列如下：
11
12
13
14
15
16
21
22
23
24
25
26
31
32
33
34
35
36
41
42
43
44
45
46
51
52
53
54
55
56
61
62
63
64
65
66
共有21种组合：
其中11，22，33，44，55，66的概率是
其他15个组合的概率是
(4)
参考上面的两个点数的排列，可以得出两个点数求和的概 Nhomakorabea分布如下：
解：
(1)
（2）黑白气象传真图的消息前后有关联时，由其前后的依赖关系可知，黑色白色同时出现的联合概率为：
则信源的联合熵为：
H(X1X2)=1.426bit/symbol
H2(X)=1/2*H(X1X2)=0.713 bit/symbol
（3）上述两种信源的剩余度分别为：

信息论基础与编码课后题答案(第三章)

3-1 设有一离散无记忆信源，其概率空间为12()0.60.4X x x P x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，信源发出符号通过一干扰信道，接收符号为12{,}Y y y =，信道传递矩阵为51661344P ⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，求：（1）信源X 中事件1x 和2x 分别含有的自信息量；（2）收到消息j y （j ＝1，2）后，获得的关于i x （i ＝1，2）的信息量；（3）信源X 和信宿Y 的信息熵；（4）信道疑义度(/)H X Y 和噪声熵(/)H Y X ；（5）接收到消息Y 后获得的平均互信息量(;)I X Y 。

解：（1）12()0.737,() 1.322I x bit I x bit ==（2）11(;)0.474I x y bit =，12(;) 1.263I x y bit =-，21(;) 1.263I x y bit =-，22(;)0.907I x y bit =（3）()(0.6,0.4)0.971/H X H bit symbol ==()(0.6,0.4)0.971/H Y H bit symbol ==（4）()(0.5,0.1,0.1,0.3) 1.685/H XY H bit symbol ==(/) 1.6850.9710.714/H X Y bit symbol =-= (/)0.714/H Y X bit symbol =（5）(;)0.9710.7140.257/I X Y bit symbol =-=3-2 设有扰离散信道的输入端是以等概率出现的A 、B 、C 、D 四个字母。

该信道的正确传输概率为0.5，错误传输概率平均分布在其他三个字母上。

验证在该信道上每个字母传输的平均信息量为0.21比特。

证明：信道传输矩阵为：11112666111162661111662611116662P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，信源信宿概率分布为：1111()(){,,,}4444P X P Y ==， H(Y/X)=1.79（bit/符号），I(X;Y)=H(Y)- H(Y/X)=2-1.79=0.21（bit/符号）3-3 已知信源X 包含两种消息：12,x x ，且12()() 1/2P x P x ==，信道是有扰的，信宿收到的消息集合Y 包含12,y y 。

信息论课后习题答案

第六章有噪信道编码6.1 R 为信息传输率，根据香农第二定理，当码长n->无穷大时，满足什么关系式，可使错误概率Pe->0。

答：Pe<exp{-nE(R)}->0，其中E(R)为可靠性函数，且在9<R<C 的范围为正。

信道容量C 是保证无差错传输时，信息传输率R 的权限值。

6.2 写出费诺不等式，其中哪一项表示是否判对的疑义度，log(k-1)又表示什么？答：H(X|Y)<=H2(Pe)+Pelog(k-1) ，H2(pe)是否判对的疑义度。

表示如果判决出错，错在k-1个符号中的一个，疑义度不会超过log(k-1)。

6.3 根据香农定理说明，（信息容量）是保证无差错传输时信息传输率R 的上限值，（平均错误概率）是信源可压缩信息的最低极限。

6.4 最大后验概率译码准则就是最小错误译码准则，对吗？错误。

()∑≠-==≠=k i k i k k e y x y xy x x y p )|(1)|()|(φφφ 这个公式可知最大后验概率与最小错误译码准则所得的最终结果是相等的。

但并非概念定义一致。

6.5 在信源等该分布时，则极大似然函数译码准则就是最小错误译码准则，对吗？ Proof: if ())|(|k k x y p x y p > m=1,2,……,MThen 信道等概率输入时，有),()(m k x q x q = 代入上式得)()|()()|(m m k k x q x y p x q x y p >So,it comes to )()(y x p y x p m k >所以说明全概率最大，对应最大联合概率译码准则。

1/2 1/6 1/36.6 离散无记忆信道DMC ，转移概率矩阵为 P= 1/3 1/2 1/61/6 1/3 1/2(1 )q(x1)=1/2 q(x2)=1/4 q(x3)=1/4. 求最佳判决译码及错误概率。

（2）若信源等概分布，求最佳判决译码及错误概率。

(信息论)第二、三章习题参考答案

第二章习题参考答案2-1解：同时掷两个正常的骰子，这两个事件是相互独立的，所以两骰子面朝上点数的状态共有6×6＝36种，其中任一状态的分布都是等概的，出现的概率为1/36。

(1)设“3和5同时出现”为事件A ，则A 的发生有两种情况：甲3乙5，甲5乙3。

因此事件A 发生的概率为p(A)=(1/36)*2=1/18 故事件A 的自信息量为I(A)=－log 2p(A)=log 218=4.17 bit(2)设“两个1同时出现”为事件B ，则B 的发生只有一种情况：甲1乙1。

因此事件B 发生的概率为p(B)=1/36 故事件B 的自信息量为I(B)=－log 2p(B)=log 236=5.17 bit (3) 两个点数的排列如下：因为各种组合无序，所以共有21种组合：其中11，22，33，44，55，66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4) 参考上面的两个点数的排列，可以得出两个点数求和的概率分布：sym bolbit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)“两个点数中至少有一个是1”的组合数共有11种。

bitx p x I x p i i i 710.13611log )(log )(3611116161)(=-=-==⨯⨯=2-2解：(1)红色球x 1和白色球x 2的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡2121)(21x x x p X i 比特 12log *21*2)(log )()(2212==-=∑=i i i x p x p X H(2)红色球x 1和白色球x 2的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡100110099)(21x x x p X i 比特 08.0100log *100199100log *10099)(log )()(22212=+=-=∑=i i i x p x p X H (3)四种球的概率分布为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡41414141)(4321x x x x x p X i ，42211()()log ()4**log 4 2 4i i i H X p x p x ==-==∑比特2-5解：骰子一共有六面，某一骰子扔得某一点数面朝上的概率是相等的，均为1/6。

信息论基础及答案

《信息论基础》试卷第1页《信息论基础》试卷答案一、填空题（共25分，每空1分）1、连续信源的绝对熵为无穷大。

（或()()lg lim lg p x p x dx +¥-¥D ®¥--D ò）2、离散无记忆信源在进行无失真变长信源编码时，编码效率最大可以达到、离散无记忆信源在进行无失真变长信源编码时，编码效率最大可以达到 1 1 1 。

3、无记忆信源是指信源先后发生的符号彼此统计独立。

4、离散无记忆信源在进行无失真变长编码时，码字长度是变化的。

根据信源符号的统计特性，对概率大的符号用短码，对概率小的符号用长码，这样平均码长就可以降低，从而提高有效性有效性((传输速率或编码效率传输速率或编码效率) ) ) 。

5、为了提高系统的有效性可以采用信源编码，为了提高系统的可靠性可以采用信道编码。

6、八进制信源的最小熵为、八进制信源的最小熵为 0 0 0 ，最大熵为，最大熵为，最大熵为 3bit/ 3bit/ 3bit/符号符号。

7、若连续信源输出信号的平均功率为1瓦特，则输出信号幅度的概率密度函数为高斯分布高斯分布((或()0,1x N 或2212x ep-)时，信源具有最大熵，其值为其值为 0.6155hart( 0.6155hart( 0.6155hart(或或1.625bit 或1lg 22e p )。

8、即时码是指任一码字都不是其它码字的前缀。

9、无失真信源编码定理指出平均码长的理论极限值为信源熵信源熵((或H r (S)(S)或或()lg H s r)，此时编码效率为时编码效率为 1 1 1 ，编码后的信息传输率为，编码后的信息传输率为，编码后的信息传输率为 lg lg r bit/ bit/码元码元。

1010、一个事件发生的概率为、一个事件发生的概率为0.1250.125，则自信息量为，则自信息量为，则自信息量为 3bit/ 3bit/ 3bit/符号符号。

信息论答案完整版

2.7 为了传输一个由字母 A、B、C、D 组成的符号集，把每个字母编码成两个二元码脉冲序列，以“00” 代表 A，“01”代表 B，“10”代表 C，“11”代表 D。每个二元码脉冲宽度为 5ms。
(1) 不同字母等概率出现时，计算传输的平均信息速率? (2) 若每个字母出现的概率分别为{1/5，1/4，1/4，3/10}，试计算传输的平均信息速率? 解：（1）不同字母等概率出现时，符号集的概率空间为：
I (a4
=
3)
=
− log
P(a4 )
=
− log
1 8
=
log2
8=3(比特)
此消息中共有 14 个符号“0”，13 个符号“1”，12 个符号“2”和 6 个符号“3”，则此消息的自
信息是
I = 14I (a1 = 0) +13I (a2 = 1) +12I (a3 = 2) + 6I (a4 = 3) ≈ 14×1.415 +13× 2 +12× 2 + 6× 3 ≈ 87.71(比特)
解：同时掷两个均匀的骰子，也就是各面呈现的概率都是 1/6，总共有 36 种可能的状态，每种状态出现的概率都是 1/36。（1）设“3 和 5 同时出现”为事件 A。则在 36 种状态中，有两种可能的情况，即 5+3 和 3+5。则
P( A) = 2 / 36 I ( A) = − log P( A) = log2 18 ≈ 4.17(比特)
（2）此消息中共有 45 个信源符号，携带了 87.81 比特信息量，因此，此消息中平均每个符号携带的信息量为
I2 = 87.81/ 45 ≈ 1.95(比特)
2.4

信息论答案(傅祖芸)

第二章课后习题【2.1】设有12 枚同值硬币，其中有一枚为假币。

只知道假币的重量与真币的重量不同，但不知究竟是重还是轻。

现用比较天平左右两边轻重的方法来测量。

为了在天平上称出哪一枚是假币，试问至少必须称多少次？解：从信息论的角度看，“12 枚硬币中，某一枚为假币”该事件发生的概率为P 1 ；12“假币的重量比真的轻，或重”该事件发生的概率为P 1 ；2为确定哪一枚是假币，即要消除上述两事件的联合不确定性，由于二者是独立的，因此有I log12 log 2 log 24 比特而用天平称时，有三种可能性：重、轻、相等，三者是等概率的，均为P 1 ，因此天3平每一次消除的不确定性为I log 3 比特因此，必须称的次数为I1 log 242.9 次I 2 log 3因此，至少需称3 次。

【延伸】如何测量？分3 堆，每堆4 枚，经过3 次测量能否测出哪一枚为假币。

【2.2】同时扔一对均匀的骰子，当得知“两骰子面朝上点数之和为2”或“面朝上点数之和为8”或“两骰子面朝上点数是3 和4”时，试问这三种情况分别获得多少信息量？解：“两骰子总点数之和为2”有一种可能，即两骰子的点数各为1，由于二者是独立的，因此该种情况发生的概率为P 1 1 1 ，该事件的信息量为：6 6 36I log 36 5.17 比特“两骰子总点数之和为 8”共有如下可能：2 和 6、3 和 5、4 和 4、5 和 3、6 和 2，概率为 P 1 1 5 5，因此该事件的信息量为：6 6 36I log 362.85 比特5“两骰子面朝上点数是 3 和 4”的可能性有两种：3 和 4、4 和 3，概率为 P 1 1 2 1，因此该事件的信息量为：6 6 18I log18 4.17 比特【2.3】如果你在不知道今天是星期几的情况下问你的朋友“明天星期几？”则答案中含有多少信息量？如果你在已知今天是星期四的情况下提出同样的问题，则答案中你能获得多少信息量（假设已知星期一至星期日的顺序）？解：如果不知今天星期几时问的话，答案可能有七种可能性，每一种都是等概率的，均为P 1，因此此时从答案中获得的信息量为7I log 7 2.807 比特而当已知今天星期几时问同样的问题，其可能性只有一种，即发生的概率为 1，此时获得的信息量为 0 比特。

信息论基础1答案

信息论基础1答案《信息论基础》答案一、填空题(本大题共10小空，每小空1分，共20分)1. 按信源发出符号所对应的随机变量之间的无统计依赖关系，可将离散信源分为有记忆信源和无记忆信源两大类。

2. 一个八进制信源的最大熵为3bit/符号3.有一信源X，其概率分布为：X i X2 X3其信源剩余度为94.64%：若对该信源进行十次扩展，则每十个符号的平均信息量是15bit。

4. 若一连续消息通过放大器，该放大器输出的最大瞬间电压为b,最小瞬时电压为a。

若消息从放大器中输出，则该信源的绝对熵是 _：其能在每个自由度熵的最大熵是log (b-a ) bit/自由度：若放大器的最高频率为F,则单位时间内输出的最大信息量是2Flog (b-a )bit/s.5. 若某一信源X,其平均功率受限为16w,其概率密度函数是高斯分布时，差熵的最大值为2log32 e ；与其熵相等的非高斯分布信源的功率为16w6、信源编码的主要目的是提高有效性，信道编码的主要目的是提高可靠性。

7、无失真信源编码的平均码长最小理论极限制为信源熵(或H(S)/logr= H _「(S))。

&当R=C或(信道剩余度为0)时，信源与信道达到匹配。

9、根据是否允许失真，信源编码可分为无—真信源编码和限失真信源编码。

10、在下面空格中选择填入数学符号“，‘ ‘ ” 或“”(1)当X和Y相互独立时，H ( XY)=H(X)+H(X/Y)。

(2 )假设信道输入用X表示，信道输出用Y 表示。

在无噪有损信道中，H(X/Y)> 0,H(Y/X)=0,l(X;Y)<HX)。

二、掷两粒骰子，各面出现的概率都是1/6 , 计算信息量：1. 当点数和为3时，该消息包含的信息量是多少？2. 当点数和为7是，该消息包含的信息量是多少？3. 两个点数中没有一个是1的自信息是多少？解:1.P (“点数和为3” =P( 1,2)+ P( 1,2)=1/36+1/36=1/18则该消息包含的信息量是：l=-logP (“点数和为3”)=log18=4.17bit2. P (“点数和为7” =P( 1,6)+ P(6,1) + P (5,2)+ P (2,5)+ P (3,4)+ P (4,3) =1/366=1/6则该消息包含的信息量是：l=-logP (“点数和为7”)=log6=2.585bit3. P (“两个点数没有一个是1” =1-P “两个点数中至少有一个是1 ”=1-P(1,1or1,jori,1)=1-(1/36+5/36+5/36)=25/36则该消息包含的信息量是：l=-logP (“两个点数中没有一个是1”) =log25/36=0.53bit三、设X、丫是两个相互统计独立的二元随机变量，其取-1或1的概率相等。

《信息论、编码与密码学》课后习题答案

（2）全零字总是一个码字，
（3）两个码字之间的最小距离等于任何非零码字的最小重量，即
设，即，，，，
首先证明条件（1）：
，，，，，，
很明显，条件（1）是满足的。条件（2）也是显然成立的。
最后证明条件（3）：
不难看出最小距离，并且最小重量，即
综上，三个条件都满足，那么就是一个线性码，它的最小距离是2。
0.01
1111
该信源的熵为：
每个组的平均比特数为:
故该码的效率为：
(3)依题意，把符合每三个分成一组，再重新应用霍夫曼编码算法，得:
编码表格如下：
符号对
概率
自信息
码字
0.1250
2.7090
100
0.1000
3.3223
0000
0.1000
3.3223
0001
0.1000
3.3223
110
0.0800
12）这是一个线性码？
解：（1） =
=
=
=
=
=
=
=
此矩阵生成的码为：{00000，01010，10011，11001，10100，11110，00111，01101}
（2）
又在二元情况下，
奇偶校验矩阵可写为：
(4该码的标准阵列
（5）奇偶校验矩阵H的第1、3列的和为零向量，
因此，这个码的最小距离为：d*=2。
3.6443
011
0.0800
3.6443
0100
0.0800
3.6443
0101
0.0640
3.9662
0011
0.0250
5.3223

10-11第二学期信息论作业题参考答案

第1讲2、信息论创始人是谁？香农。

3、信息和消息、信号有什么联系与区别？从信息理论角度上看，信号是消息的载体，信息含藏在消息之中，有信号有消息不一定有信息。

4、通信系统的主要性能指标是什么？有效性、可靠性和安全性。

5、举例说明信息论有哪些应用？为信息传送和处理系统提供数学模型和评估方法，在通信和信息处理领域是一门基础理论，在其它领域如语言学、生物学、医学、神经网络、经济学方面的应用也很成功。

具体应用实例有：语音、图像和数据信息的压缩，通信信道有效性和可靠性的提高，或信道传输功率指标要求的降低，通信或计算机系统可靠性和安全性的提高，信息处理领域的信号重建和模式识别等。

2.4 （求车牌自信息量）某车牌号的概率是(1/26)3×(1/10)3，24bit/牌，后一种概率为(1/36)6，31bit/牌，第2讲设二元对称信道的传递矩阵(条件概率矩阵)为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32313132若P(0) = 3/4, P(1) = 1/4，求H(X), H(Y), H(X/Y), H(Y/X)和I(X;Y)；先求P(Y)=∑X P(XY)和P(XY)=P(X)P(Y|X)，再得各种熵和互信息。

H(X)=H(3/4,1/4), H(Y)=H(7/12,5/12);H(XY)=H(1/2,1/4,1/12,1/6); H(X/Y)=H(XY)-H(Y)H(Y/X)=H(XY)-H(X)；或H(Y/X)=∑P(X=a)H(Y/a)=H(3/4,1/4) I(X;Y)=H(X)-H(X/Y)=H(X)+H(Y)-H(XY)； 2.2（求条件信息量）1.6米以上女孩是条件，某个1.6米以上的女大学生是概率事件，得条件概率为：P=0.25×0.75/0.5=0.375=3/8，信息量为I= -log0.375=1.42比特。

2.52.10(1)(2)（由联合概率分布求熵、联合熵和条件熵）（1）思路：先求出X 、Y 、Z 、XZ 、YZ 、XYZ 的概率或联合分布，再求其熵。

信息论习提答案

1、熵是香农信息论最基本最重要的概念。

2、单符号离散信源一般用随机变量描述，而多符号离散信源一般用随机矢量描述。

3、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。

4、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍。

5、对于n 元m 阶马尔可夫信源，其状态空间共有 n m 个不同的状态。

6、若一离散无记忆信源的信源熵H （X ）等于4.2，对信源进行等长的无失真二进制编码，则编码长度至少为 5 。

7、同时掷两个正常的骰子，各面呈现的概率都为1/6，则“3和6同时出现”这件事的自信息量是 log 218或（1+2 log 23）。

8、一副充分洗乱的扑克牌（52张），从中任意抽取1张，然后放回，若把这一过程看作离散无记忆信源，则其信源熵为 52log 2 。

9、具有一一对应关系的无噪信道的信道容量C= log 2n 。

10、信道编码定理是一个理想编码的存在性定理，即：信道无失真传递信息的条件是信息率小于信道容量。

11、信源的消息通过信道传输后的误差或失真越大，信宿收到消息后对信源存在的不确定性就越大，获得的信息量就越小12、平均失真度的下限取0的条件是失真矩阵的每一行至少有一个零元素。

13、率失真函数对允许的平均失真度是单调递减和连续的。

14、对于离散无记忆信源的率失真函数的最大值是 log 2n 。

15、信源编码的目的是：提高通信的有效性。

16、对具有8个消息的单符号离散无记忆信源进行4进制哈夫曼编码时，为使平均码长最短，应增加 2 个概率为0的消息。

17、对于香农编码、费诺编码和哈夫曼编码，编码方法惟一的是香农编码。

18、游程序列的熵等于原二元序列的熵。

19、 n 位重复码的编码效率是 1/n 。

20、若纠错码的最小距离为d min ，则可以纠正任意小于等于t= ⎥⎦⎥⎢⎣⎢-21min d 个差错。

信息论基础智慧树知到答案章节测试2023年潍坊学院

第一章测试1.信息论的奠基人是（）。

A:香农B:哈特利C:阿姆斯特朗D:奈奎斯特答案:A2.下列不属于信息论的研究内容的是（）。

A:纠错编码B:信源、信道模型C:信息的产生D:信道传输能力答案:C3.下列不属于消息的是（）A:图像B:信号C:文字D:语音答案:B4.信息就是消息. （）A:对B:错答案:B5.信息是不可以度量的，是一个主观的认识。

（）A:对B:错答案:B6.任何已经确定的事物都不含有信息。

（）A:错B:对答案:B7.1948年香农的文章《通信的数学理论》奠定了香农信息理论的基础。

（）A:错B:对答案:B8.信息论研究的目的就是要找到信息传输过程的共同规律，以提高信息传输的（），使信息传输系统达到最优化。

A:保密性B:可靠性C:认证性D:有效性答案:ABCD9.下列属于香农信息论的主要研究理论的是（）。

A:传输理论B:调制理论C:压缩理论D:保密理论答案:ACD10.信源编码的作用包含（）。

A:检错纠错B:提升信息传输的安全性C:数据压缩D:对信源的输出进行符号变换答案:CD第二章测试1.信息传输系统模型中，用来提升信息传输的有效性的部分为（）A:信道B:信源C:信源编码器、信源译码器D:信道编码器、信道译码器答案:C2.对于自信息，以下描述正确的是（）A:以e为底时，单位是比特B:以10为底时，单位是奈特。

C:以2为底时，单位是奈特。

D:以2为底时，单位是比特。

答案:D3.信息熵的单位是（）A:无法确定B:比特每符号C:比特答案:B4.必然事件和不可能事件的自信息量都是0 。

（）A:错B:对答案:A5.概率大的事件自信息量大。

（）A:错答案:A6.互信息量可正、可负亦可为零。

（）A:错B:对答案:B7.互信息量I(X;Y)表示收到Y后仍对信源X的不确定度。

（）A:错B:对答案:B8.信源X的概率分布为P(X)={1/2,1/3,1/6}，信源Y的概率分布为P(X)={ 1/3,1/2,1/6},则信源X和Y的熵相等。

(完整版)信息论第五章答案

5.1 设信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X (1) 求信源熵H(X)； (2) 编二进制香农码；(3) 计算平均码长和编码效率。

解： (1)symbolbit x p x p X H i i i /609.2)01.0log 01.01.0log 1.015.0log 15.017.0log 17.018.0log 18.019.0log 19.02.0log 2.0()(log )()(2222222712=⨯+⨯+⨯+⨯+⨯+⨯+⨯-=-=∑=%1.8314.3609.2)()(14.301.071.0415.0317.0318.0319.032.03)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.2 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制费诺码，计算编码效率。

%2.9574.2609.2)()(74.201.041.0415.0317.0218.0319.032.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.3 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制和三进制哈夫曼码，计算各自的平均码长和编码效率。

解：%9.9572.2609.2)()(72.201.041.0415.0317.0318.0319.022.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η%4.913log 8.1609.2log )()(8.1)01.01.015.017.018.019.0(22.01)(22=⨯====+++++⨯+⨯==∑m LK X H R X H x p k K ii i η5.4 设信源⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡12811281641321161814121)(87654321x x x x x x x x X P X (1) 求信源熵H(X)；(2) 编二进制香农码和二进制费诺码；(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率； (4) 编三进制费诺码；(5) 计算三进制费诺码的平均码长和编码效率；解： (1)symbolbit x p x p X H i i i /984.1128log 1281128log 128164log 64132log 32116log 1618log 814log 412log 21)(log )()(22222222812=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=-=∑==127/64 bit/symbol (2)二进制费诺码：香农编码效率：%100984.1984.1)()(64/127984.17128171281664153214161381241121)(======⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η费诺编码效率：%100984.1984.1)()(984.17128171281664153214161381241121)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η(5)%3.943log 328.1984.1log )()(328.14128141281364133212161281141121)(22=⨯=⋅===⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑m K X H R X H x p k K ii i η5.5 设无记忆二进制信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡1.09.010)(X P X先把信源序列编成数字0，1，2，……，8，再替换成二进制变长码字，如下表所示。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1. 在无失真的信源中，信源输出由 H (X ) 来度量；在有失真的信源中，信源输出由 R (D ) 来度量。

2. 要使通信系统做到传输信息有效、可靠和保密，必须首先信源编码，然后_____加密____编码，再______信道_____编码，最后送入信道。

3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式，也就是有名的香农公式是log(1)C W SNR =+；当归一化信道容量C/W 趋近于零时，也即信道完全丧失了通信能力，此时E b /N 0为 -1.6 dB ，我们将它称作香农限，是一切编码方式所能达到的理论极限。

4. 保密系统的密钥量越小，密钥熵H (K )就越小，其密文中含有的关于明文的信息量I (M ；C )就越大。

5. 已知n ＝7的循环码42()1g x x x x =+++，则信息位长度k 为 3 ，校验多项式 h(x)= 3
1x x ++ 。

6. 设输入符号表为X ＝{0，1}，输出符号表为Y ＝{0，1}。

输入信号的概率分布为p ＝(1/2，1/2)，失真函数为d (0，0) = d (1，1) = 0，d (0，1) =2，d (1，0) = 1，则D min ＝ 0 ，R (D min )＝ 1bit/symbol ，相应的编码器转移概率矩阵[p(y/x )]＝1001⎡⎤
⎢⎥⎣⎦
；D max ＝ 0.5 ，R (D max )＝ 0 ，相应的编码器转移概率矩阵[p(y/x )]＝1010⎡⎤
⎢
⎥⎣⎦。

7. 已知用户A 的RSA 公开密钥(e,n )=(3,55)，5,11p q ==,则()φn = 40 ，他的秘密密钥(d,n )＝(27,55) 。

若用户B 向用户A 发送m =2的加密消息，则该加密后的消息为 8 。

二、判断题
1. 可以用克劳夫特不等式作为唯一可译码存在的判据。

（√ ）
2. 线性码一定包含全零码。

（√ ）
3. 算术编码是一种无失真的分组信源编码，其基本思想是将一定精度数值作为序列的编码，是以另外一种形式实现的最佳统计匹配编码。

（×）
4. 某一信源，不管它是否输出符号，只要这些符号具有某些概率特性，就有信息量。

（×）
5. 离散平稳有记忆信源符号序列的平均符号熵随着序列长度L 的增大而增大。

（×）
6. 限平均功率最大熵定理指出对于相关矩阵一定的随机矢量X ，当它是正态分布时具有最大熵。

（√ ）
7. 循环码的码集中的任何一个码字的循环移位仍是码字。

（√ ）
8. 信道容量是信道中能够传输的最小信息量。

（×） 9. 香农信源编码方法在进行编码时不需要预先计算每个码字的长度。

（×） 10. 在已知收码R 的条件下找出可能性最大的发码i C 作为译码估计值，这种译码方法叫做最佳译码。

（√ ）
三、计算题
某系统（7，4）码
)()(01201230123456c c c m m m m c c c c c c c ==c 其三位
校验位与信息位的关系为：
231013210
210c m m m c m m m c m m m
=++⎧⎪
=++⎨⎪=++⎩ （1）求对应的生成矩阵和校验矩阵；
（2）计算该码的最小距离；
（3）列出可纠差错图案和对应的伴随式；（4）若接收码字R =1110011，求发码。

解：1. 1000110
1000110010111
1
1
01
G ⎡⎤⎢⎥⎢
⎥=⎢⎥⎢⎥⎣⎦ 1
0111001
1100100
1
1
1
01
H ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 2. d min =3 3.
4. RH T =[001] 接收出错
E =0000001 R+E=C = 1110010 (发码)
四、计算题
已知(),X Y 的联合概率(),p x y 为：求()H X ，()H Y ，(),H X Y ，();I X Y
解: (0)2/3p x == (1)1/3p x == (0)1/3p y == (1)2/3
p y == ()()(1/3,2/3)H X H Y H ===0.918 bit/symbol (),(1/3,1/3,1/3)H X Y H ==1.585 bit/symbol ();()()(,)I X Y H X H Y H X Y =+-=0.251 bit/symbol
五、计算题
一阶齐次马尔可夫信源消息集},,{321a a a X ∈，
状态集},,{321S S S S ∈，且令3,2,1,==i a S i i ，条件转移概率为
[]
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=03132313131214141)/(i j S a P ，(1)画出该马氏链的状态转移图； (2)
计算信源的极限熵。

解：(1)
01
X Y
011/31/30
1/3
（2）⎪⎪⎩
⎪⎪⎨⎧=++=+=++=++132132
311212331
2311411332
231141w w w w w w w w w w w w w w →⎪⎩⎪
⎨⎧===3.03.04.03
21w w w
H(X|S 1) =H (1/4,1/4,1/2)=1.5比特/符号 H(X|S 2)=H (1/3,1/3,1/3)=1.585比特/符号
H(X|S 3)=H (2/3,1/3)= 0.918比特/符号
()
3
|0.4 1.50.3 1.5850.30.918 1.3511
H
w H X S i i
i ==⨯+⨯+⨯=∑∞=比特/符号
六、计算题
若有一信源⎥
⎦
⎤
⎢⎣⎡=⎥⎦⎤⎢
⎣⎡2.08.021x x P X ，每秒钟发出2.55个信源符号。

将此信源的输出符号送入某一个二元信道中进行传输（假设信道是无噪无损的，容量为1bit/二元符号），而信道每秒钟只传递2个二元符号。

（1）试问信源不通过编码（即x 1→0,x 2→1在信道中传输）（2）能否直接与信道连接？
（3）若通过适当编码能否在此信道中进行无失真传输？（4）试构造一种哈夫曼编码(两个符号一起编码)，
（5）使该信源可以在此信道中无失真传输。

解：1.不能，此时信源符号通过0，1在信道中传输，2.55二元符号/s>2二元符号/s 2. 从信息率进行比较， 2.55*(0.8,0.2)H = 1.84 < 1*2 可以进行无失真传输
3.
x 1x 1x 1x 2x 2x 1 1
011
100 0.64
4
1
0.640.16*20.2*3i i i K p K ===++=∑ 1.56 二元符号/2个信源符号
此时 1.56/2*2.55=1.989二元符号/s < 2二元符号/s
七、计算题
两个BSC 信道的级联如右图所示：（1）写出信道转移矩阵；（2）求这个信道的信道容量。

解：（1）
22122211(1)2(1)112(1)(1)P PP ε
εεεεεεεε
εεεεεεε--⎡⎤
-+-⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥----+⎣⎦⎣⎦⎣⎦
（2）2
2
log2((1))C H εε=--+
1。