实验六傅里叶变换及其反变换
傅里叶变换及反变换
1 2{F [j(0) ]F [j(0) ] }
F ( j )
1
m 0 m
P( j)
( )
( )
0
0
0
R( j)
1 2
0
0
0
F ( j )
1
m 0 m
f (t)
r(t)
y1(t)
低通
滤波
y(t)
cos(0t) cos(0t)
R( j)
1 2
0 ( )
0
P( j)
0 ( )
§4.5 连续时间傅里叶变换的性质
复习
F(j)= f(t)ejtdt
f(t)21 F(j)ejtd
1 唯一性: 2 线性特性: 3 奇偶特性: 4 共轭特性: 5 对称特性: 6 时域展缩特性: 7 时移特性:
9 时域微分特性: 10 频域微分特性: 11 时域卷积定理: 12 频域卷积定理:
偶信号的频谱是偶函数,奇信 号的频谱是奇函数。
F(j) f(t)ejtdt令t
f()ejd f()关e于jtd F(j)
f(t) F (j) , 则 f* (t) F * ( j)
证F (: j)= f (t)ejtd可 t F 得 *(j)= f*(t)ejtdt
F *(j)= f *(t)ejtdt
0
1 4
20
0
0
Y1( j)
1
1
2
4
0
20
Y ( j) 1
2
0
4.7 傅里叶反 变换
要解决的问题:由F( jw)求 f(t)
f(t)21 F (j)ejtd
利用傅里叶变换的互易对称性 部分分式展开
傅里叶变换原理

傅里叶变换原理
傅里叶变换是一种数学工具,用于将一个函数(通常是时域上的函数)转换为另一个函数(通常是频域上的函数)。
傅里叶变换的原理包括两个核心思想:信号可以表示为不同频率的正弦波的叠加,以及通过计算信号与不同频率正弦波之间的相关性来获得频谱信息。
一维连续时域信号在傅立叶域的变换公式可以表示为:
F(w) = ∫[从-∞到+∞] f(t) * e^(-j*w*t) dt
其中,F(w)表示频域信号,f(t)表示时域信号,e^(-j*w*t)表示
复指数函数,w表示角频率。
傅里叶变换的逆变换公式可以表示为:
f(t) = 1/2π ∫[从-∞到+∞] F(w) * e^(j*w*t) dw
其中,f(t)表示时域信号,F(w)表示频域信号,e^(j*w*t)表示
复指数函数,w表示角频率。
傅里叶变换在信号处理、图像处理、通信系统等领域广泛应用。
通过将信号从时域转换到频域,可以分析信号的频率成分、滤波、降噪等。
同时,傅里叶变换也可以通过逆变换将频域信号转换回时域,实现信号的还原和复原。
除了一维傅里叶变换,还存在二维和多维傅里叶变换,用于处理二维图像和多维信号。
二维傅里叶变换可以将二维图像转换到频域进行图像增强、滤波等处理,多维傅里叶变换可以对多
维信号进行频域分析。
总之,傅里叶变换是一种重要的数学工具,能够将时域信号转换到频域,通过分析频域信号可以获得信号的频率成分和特征,广泛应用于信号处理和图像处理领域。
图像的傅里叶变换、反变换地实现

课程大作业实验报告图像傅里叶变幻、反变换的实现课程名称:数字图像处理组长:王文雄学号:200730590323 年级专业班级:07通信3班成员一:庞柱坚学号:200730590318 年级专业班级:07通信3班成员二:王弥光学号:200730590322年级专业班级:07通信3班成员三:学号:年级专业班级:07通信3班指导教师邓继忠报告提交日期2010年6月1日项目答辩日期2010年6月1日目录1. 项目要求 (4)2. 项目开发环境 (4)3. 系统分析 (4)3.1. 系统的主要功能分析 (4)3.2. 系统的关键问题及解决方法(或思路) (7)4. 系统设计 (11)4.1. 程序流程图及说明 (11)4.2. 程序主要模块(或功能)介绍 (12)4.2.1. 一维FFT 和IFFT (12)4.2.2. 二维图像FFT 和IFFT: (14)5. 实验结果与分析 (15)5.1. 实验结果 (15)5.2. 项目的创新之处 (16)5.3. 存在问题及改进设想 (17)6. 心得体会 (17)6.1. 系统开发的体会 (17)6.2. 对本门课程的改进意见或建议 (18)7. 附件一 (19)1.项目要求1.基本要求:自修教材相关内容(P52-74)或其它参考资料,在CVI下编程对尺寸为2N(N 为正整数)的图像进行FFT(快速傅里叶变换)和(快速傅里叶反变换)。
(不能利用CVI下的函数)2.题目拓展:编程实现任意大小图像的二维傅立叶的变换与反变换。
2.项目开发环境项目开发环境主要分为软件环境和硬件环境软件:Lab Windows/CVI和IMAQ_Vision for LabWindows/CVI。
Lab Windows/CVI 是美国National Instrument(简称NI)公司开发的基于C语言的虚拟仪器开发平台,适用于自动测试、自动控制、测试仪器通信、测试硬件控制、信号分析及图像处理等软件的开发。
函数的傅里叶变换和反变换的性质

函数的傅里叶变换和反变换的性质傅里叶变换和反变换是函数分析中非常重要的概念,它们在信号处理和通信领域等多个应用中都有广泛的应用。
在本文中,我们将讨论傅里叶变换和反变换的性质,以期对函数分析、信号处理以及数学等领域更深入的了解。
一、傅里叶变换的性质傅里叶变换的定义是:任何函数可以表示成以时间为自变量的正弦和余弦函数的无穷级数的形式。
也就是说,将任何函数分解成一系列的正弦和余弦函数后,我们就可以用傅里叶变换来进行函数的处理和操作。
傅里叶变换可以分为离散和连续两种形式,而它们都具有一些很重要的性质。
下面将分别介绍这些性质:1. 线性性傅里叶变换具有线性性,也就是说如果对于两个函数 f(t) 和g(t),它们的傅里叶变换分别是F(ω) 和G(ω),那么对于函数 a ×f(t) + b × g(t)(其中 a 和 b 是任意实数),它的傅里叶变换就是 a × F(ω) + b × G(ω)。
2. 卷积定理卷积定理说明了傅里叶变换中频域的卷积运算可以通过时域中的乘积运算来实现。
如果函数 f(t) 和 g(t) 的傅里叶变换分别是F(ω) 和G(ω),那么它们在时域的卷积 f(t) * g(t) 的傅里叶变换就是F(ω) × G(ω)。
3. 改变函数的时间和频率如果函数 f(t) 的傅里叶变换是F(ω),而f(t − τ) 表示 f(t) 向右平移τ 个单位,那么f(t − τ) 的傅里叶变换就是F(ω) × e^{- iωτ}。
同样的道理,如果 f(t) 的傅里叶变换是F(ω),而 f(at) 表示将 f(t) 的时间宽度缩小到原来的 a 倍,那么 f(at) 的傅里叶变换就是 (1/a) ×F(ω/a)。
二、傅里叶反变换的性质与傅里叶变换相对应的是傅里叶反变换,它可以将函数由频域转换到时域。
傅里叶反变换的定义是:如果一个函数的傅里叶变换为F(ω),那么它的傅里叶反变换就是:f(t) = (1/2π) × ∫_{-∞}^{∞} F(ω) e^{iωt} dω同样的,傅里叶反变换也有一些很重要的性质:1. 线性性傅里叶反变换与傅里叶变换一样具有线性性,也就是说,如果一个函数的傅里叶变换为F(ω),而另一个函数的傅里叶变换为G(ω),那么对于函数a × F(ω) +b × G(ω),它的傅里叶反变换就是a × f(t) + b × g(t)。
如何进行傅里叶逆变换

如何进行傅里叶逆变换傅里叶逆变换是信号处理中常用的一种数学工具,用于将频域信号转换为时域信号。
在本文中,我们将介绍如何进行傅里叶逆变换,并探讨其在实际应用中的重要性。
一、傅里叶逆变换的定义和基本原理傅里叶逆变换是傅里叶变换的逆运算,用于将频域信号转换为时域信号。
在数学上,傅里叶逆变换可以通过以下公式表示:f(t) = ∫F(ω)e^(jωt)dω其中,f(t)表示时域信号,F(ω)表示频域信号,e^(jωt)是欧拉公式中的复指数函数。
二、傅里叶逆变换的步骤进行傅里叶逆变换的步骤如下:1. 将频域信号F(ω)表示为复指数形式,即F(ω) = |F(ω)|e^(jφ),其中|F(ω)|表示幅度,φ表示相位。
2. 将复指数形式的频域信号F(ω)代入傅里叶逆变换公式中,得到时域信号f(t)。
3. 对时域信号f(t)进行必要的处理,如幅度调整、相位校正等。
三、傅里叶逆变换的应用傅里叶逆变换在信号处理领域有着广泛的应用,以下是其中几个重要的应用领域:1. 通信系统:在数字通信系统中,傅里叶逆变换用于将频域信号转换为时域信号,以实现信号的解调和恢复。
2. 图像处理:在图像处理中,傅里叶逆变换用于将图像的频域表示转换为时域表示,以实现图像的恢复和增强。
3. 音频处理:在音频处理中,傅里叶逆变换用于将音频信号的频域表示转换为时域表示,以实现音频的解码和还原。
4. 控制系统:在控制系统中,傅里叶逆变换用于将频域信号转换为时域信号,以实现系统的状态估计和控制。
四、傅里叶逆变换的数值计算方法傅里叶逆变换的数值计算方法有多种,其中最常用的方法是快速傅里叶逆变换(IFFT)。
快速傅里叶逆变换是一种高效的算法,能够在计算复杂度较低的情况下实现傅里叶逆变换。
五、总结傅里叶逆变换是信号处理中重要的数学工具,用于将频域信号转换为时域信号。
通过傅里叶逆变换,我们可以实现信号的解调、图像的恢复、音频的解码等应用。
在实际应用中,我们可以利用快速傅里叶逆变换等数值计算方法来高效地进行傅里叶逆变换操作。
傅里叶变换及反变换课件

• 傅里叶变换概述 • 傅里叶正变换 • 傅里叶反变换 • 傅里叶变换的应用 • 傅里叶变换的实践操作
目录
01
傅里叶变换概述
傅里叶变换的定义
傅里叶变换是一种数学工具,用于将一个时间域的信号转换为其频域表示。在数 学上,它被定义为函数f(t)与其复指数函数e^(iωt)之间的积分变换。
定义函数
定义需要变换的函数 ,例如正弦函数、余 弦函数等。
进行傅里叶变换
使用fft库中的fft函 数进行傅里叶变换。
绘图
使用matplotlib库将 变换后的结果绘制成 图形。
感谢观看
THANKS
通过傅里叶正变换,可以将一个复杂的信号分解成多个简 单的正弦波分量,每个分量都有自己的频率、幅度和相位 。这种分解方式有助于更好地理解信号的组成和特性,在 信号处理、通信、图像处理等领域有广泛应用。
03
傅里叶反变换
傅里叶反变换的定义
傅里叶反变换是数学和工程领域中常用的工具,用于将频域函数转换回时域函数。 它与傅里叶变换是逆操作,通过傅里叶反变换可以将频域信息还原为时域信息。
积分运算的取值范围是整个实数 轴,代表着所有可能的频率成分
。
傅里叶反变换的物理意义
傅里叶反变换的物理意义在于将频域 信息还原为时域信息,从而可以分析 信号的时域特性。
例如,在音频处理中,傅里叶反变换 可以将音频信号从频域转换回时域, 以便更好地感知声音的细节和变化。
通过傅里叶反变换,可以了解信号在 不同时间点的强度和相位变化,这对 于信号处理和通信系统等领域非常重 要。
数值计算和绘图。
定义函数
定义需要变换的函数,例如正 弦函数、余弦函数等。
进行傅里叶变换
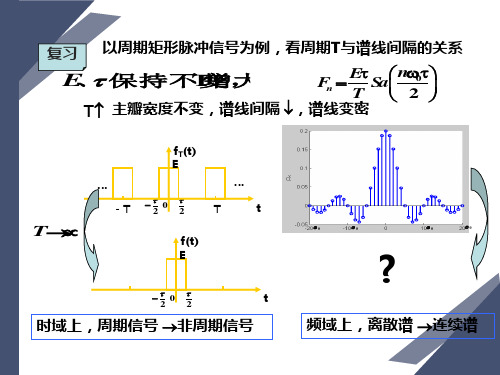
实验六 调制定理

0 2 4 6 8 10 t 1/2/ abs((w-2 ) heaviside(w-2 )+(w+2 ) heaviside(w+2 )-2 w heaviside(w)) 1.5
-8
-6
sin( t)/( t) 1.5 1 0.5 0 -0.5 -10
-8
-6
0 2 4 t abs(-heaviside(w+ )+heaviside(w-))
-4
-2
6
8
10
1.5
1
0.5
0
-80
-60
-40
-20
0 w
20
40
60
80
图 6.1.1 调制信号时域和频域图
sin( t)/( t) cos(10 t) 1 0.5 0 -0.5 -1 -10
-4
-2
1
0.5
0
-80
-60
-40
-20
0 w
20
40
60
80
图 6.2.1 调制信号时域和频域图
sin( t)/( t) sin( t)/( t) cos(20 t) 1 0.5 0 -0.5 -1 -10
0 2 4 6 8 10 t e(w+20 )+(w+22 ) heaviside(w+22 )+(40 -2 w) heaviside(w-20 )+w heaviside(w-18 )+18 heav 1
-8
-6
-4
-2
傅里叶变换及反变换

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X ( j) x(t)e jt dt
6.1
x(t)
1 2
X(
j)e jt d
6.2
连续时间傅里叶变换主要用来描述连续时间非周期信号的频谱。按照教材中的说法,任
意非周期信号,如果满足狄里克利条件,那么,它可以被看作是由无穷多个不同频率(这些 频率都是非常的接近)的周期复指数信号 ejt 的线性组合构成的,每个频率所对应的周期复 指数信号 ejt 称为频率分量(frequency component),其相对幅度为对应频率的|X(j)|之值, 其相位为对应频率的 X(j)的相位。 X(j)通常为关于的复函数,可以按照复数的极坐标表示方法表示为: X(j)=| X(j)|ej X(j) 其中,| X(j)|称为 x(t)的幅度谱,而X(j)则称为 x(t)的相位谱。
%绘制幅度谱
im = imag(Fw);
%计算 F(w)的虚部
re = real(Fw);
%计算 F(w)的实部
phase = atan(im/re);
%计算相位谱
subplot(313);
ezplot(phase);
%绘制相位谱
请输入 a=6
>> syms t v w x phase im re;
的傅里叶反变换
f(t)。
>> syms t v w x phase im re;
%定义符号变量
Fw =1/(1+w^2);
f=fourier(Fw,t)
subplot(311);
ezplot(f);
%绘制 f(t)的时域波形
axis([-1 2.5 0 1.1]);
subplot(312); ezplot(abs(Fw)); im = imag(Fw); re = real(Fw); phase = atan(im/re); subplot(313); ezplot(phase);
实验六 傅里叶变换及其反变换
6.1 实验目的 1.学会运用 MATLAB 求连续时间信号的傅里叶变换; 2.学会运用 MATLAB 求连续时间信号的傅里叶反变换; 3.学会运用 MATLAB 求连续时间信号的频谱图。
6.2实验原理及实例分析 1.连续时间信号傅里叶变换----CTFT
傅里叶变换在信号分析中具有非常重要的意义,它主要是用来进行信号的频谱分析的。 傅里叶变换和其逆变换定义如下:
1. 设双边指数信号 f(t) = e-a|t| (a>0),用 MATLAB 编程求其傅里叶变换,绘出频谱图。要求
由键盘交互式地设置 a 的值,观察当 a 逐渐趋于 0 时,其频谱函数的变化趋势。
>> syms t v w x phase im re;
%定义符号变量
a=input('请输入 a=');
ezplot(abs(Fw));
%绘制幅度谱
im = imag(Fw);
%计算 F(w)的虚部
re = real(Fw);
%计算 F(w)的实部
phase = atan(im/re);
%计算相位谱
subplot(313);
ezplot(phase);
%绘制相位谱
请输入 a=2
2.求
F ()
1 12
%绘制幅度谱 %计算 F(w)的虚部
%计算 F(w)的实部 %计算相位谱
%绘制相位谱
f=
(pi*heaviside(t))/exp(t) + pi*heaviside(-t)*exp(t)
X ( j) x(t)e jt dt lim x(kT )e jkT T
T 0 k
若信号为时限信号,当时间间隔 T 取得足够小时,上式可演变为:
N
X ( j) T x(kT )e jkT k N
[x(t1 ), x(t2 ),, x(t2N 1 )] [e jt1 , e jt2 ,, e jt2N 1 ]T
f = exp(-a*abs(t)) ;
%f(t)= exp(-a*abs(t))
Fw = fourier(f);
%求傅里叶变换
subplot(311);
ezplot(f);
%绘制 f(t)的时域波形
axis([-1 2.5 0 1.1]);
subplot(312);
ezplot(abs(Fw));
谱图。
syms t v w x phase im re;
%定义符号变量
f = exp(-2*t)*sym('Heaviside(t)');
%f(t)=exp(-2*t)*u(t)
Fw = fourier(f);
%求傅里叶变换
subplot(311);
ezplot(f);
%绘制f(t)的时域波形
axis([-1 2.5 0 1.1]);
subplot(312);
ezplot(abs(Fw));
%绘制幅度谱
im = imag(Fw);
%计算F(w)的虚部
re = real(Fw); phase = atan(im/re); subplot(313); ezplot(phase); %End
%计算F(w)的实部 %计算相位谱
%绘制相位谱
给定一个连续时间非周期信号 x(t),它的频谱也是连续且非周期的。对于连续时间周期
信号,也可以用傅里变换来表示其频谱,其特点是,连续时间周期信号的傅里叶变换时有冲
激序列构成的,是离散的——这是连续时间周期信号的傅里叶变换的基本特征。
2.用 MATLAB 实现 CTFT 的计算
MATLAB 进行傅里叶变换有两种方法,一种利用符号运算的方法计算,另一种是数值计算。
2) MATLAB 数值计算求解法 符号运算求解法的局限性在于,如果返回函数中有诸如δ(t)等项,则用 ezplot( )函数无法 作图。对某些信号求变换时,其返回函数可能包含一些不能直接用符号表达的式子,因而也 不返回函数作图。故有必要给出连续信号傅里叶变换的数值计算法。
采用数值计算算法的理论依据是:
%定义符号变量
a=input('请输入 a=');
f = exp(-a*abs(t)) ;
%f(t)= exp(-a*abs(t))
Fw = fourier(f);
%求傅里叶变换
subplot(311);
ezplot(f);
%绘制 f(t)的时域波形
axis([-1 2.5 0 1.1]);
subplot(312);
上式用 MATLAB 表示为: X=x*exp(-j*t’*w)*T
其中 X 为信号 x(t)的傅里叶变换,w 为频率Ω,T 为时间步长。 相应的 MATLAB 程序:
T = 0.01; dw = 0.1;
%时间和频率变化的步长
t = -10:T:10;
w = -4*pi:dw:4*pi;
%X(j)可以按照下面的矩阵运算来进行:
1) MATLAB 符号运算求解法
MATLAB 符 号 数 学 工 具 箱 提 供 了 直 接 求 解 傅 里 叶 变 换 与 傅 里 叶 反 变 换 的 函 数
fourier( )及 ifourier( )。常用的是:F=fourier(f) 默认返回值是关于ω的函数。
f=fourier(F,t) 返回值是关于 t 的函数 例:利用 MATLAB 求单边指数信号 f(t) = e-2tu(t)的傅里叶变换,画出 f(t)及其幅度谱和相位
X=x *exp(-j*t'*)*T %傅里叶变换
X1=abs(X);
%计算幅度谱
phai=angle(X);
%计算相位谱
为了使计算结果能够直观地表现出来,还需要用绘图函数将时间信号 x(t),信号的幅度谱 |X(j)|和相位谱 X(j)分别以图形的方式表现出来,并对图形加以适当的标注。
6.3 编程练习
