MAtlab 傅里叶变换 实验报告
MATLAB实验二傅里叶分析与应用

实验二傅里叶分析及应用一、实验目的(一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义2、学会使用Matlab分析周期信号的频谱特性(二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质1、学会运用Matlab求连续时间信号的傅里叶变换2、学会运用Matlab求连续时间信号的频谱图3、学会运用Matlab分析连续时间信号的傅里叶变换的性质(三)掌握使用Matlab完成信号抽样并验证抽样定理1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化3、学会运用MATLAB对抽样后的信号进行重建二、实验条件Win7系统,MATLAB R2015a三、实验内容1、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
符号运算法数值运算法012345t(20 π ex p(-3 t) heaviside(t) - 8 π ex p(-5 t) heaviside(t))/(2 π)2、试用Matlab 命令求的傅里叶反变换,并绘出其时域信号图。
两个单边指数脉冲的叠加3、已知门函数自身卷积为三角波信号,试用Matlab 命令验证FT 的时域卷积定理。
Code :syms t ; fw =sym('10/(3+i*w)-4/(5+i*w)');ft = ifourier(fw, t); ezplot(ft), grid on ;Code :f = sym('heaviside(t+1) - heaviside(t-1)'); fw = simplify(fourier(f)); F = fw.*fw; subplot(211);ezplot(abs(F), [-9, 9]), grid on title('FW^2') tri =sym('(t+2)*heaviside(t+2)-2*t*heaviside(t)+(t-2)*heaviside(t-2)'); Ftri = fourier(tri); F = simplify(Ftri); subplot(212);ezplot(abs(F), [-9, 9]), grid on ; title('tri FT')4、设有两个不同频率的余弦信号,频率分别为,;现在使用抽样频率对这三个信号进行抽样,使用MATLAB 命令画出各抽样信号的波形和频谱,并分析其频率混叠现象> > > > > > > > > >Code :f1 = 100; % f1 = 100 hz ts = 1/4000;% sample = 4000hz dt = 0.0001;t1 = -0.007:dt:0.007; ft = cos(2*f1*pi*t1);subplot(221); plot(t1, ft), grid on ;axis([-0.006 0.006 -1.5 1.5]) xlabel('Time/s'),ylabel('f(t)') title('Cosine curve');N = 5000; k = -N:N; w = 2*pi*k/((2*N+1)*dt); fw = ft*dt*exp(-1i*t1'*w); subplot(222);plot(w, abs(fw)); grid on ; axis([-20000 20000 0 0.005]); t2 = -0.007:ts:0.007;fst = cos(2*f1*pi*t2);subplot(223);plot(t1, ft, ':'),hold onstem(t2, fst), grid on ;axis([-0.006 0.006 -1.5 1.5])xlabel('Time/s'),ylabel('fs(t)')title('Sample signal'); hold offfsw=ts*fst*exp(-1i*t2'*w);subplot(224); plot(w, abs(fsw)),grid onaxis([-20000 20000 0 0.006])xlabel('\omega'),ylabel('fsw')title(' Sample freq spectrum');-505x 10-3-11Time/s f (t )Cosine curve-2-1012x 104012345-3ωf (w )Cos freq spectrum-505x 10-3-11Time/sf s (t )Sample signal-2-1012x 1040246-3ωf s wSample freq spectrumx 10-3-101Time/s f (t )Cosine curvex 104012345-3ωf (w )Cos freq spectrum-505x 10-3-11Time/sf s (t )Sample signal-2-1012x 1040246-3ωf s wSample freq spectrumf1 = 100Hz将代码中f1设为3800即可↓f2 = 3800Hz-0.500.51Sa(t)0.511.5Sa(t) freq spectrum-0.500.51Sampling signal0.511.5spectrum of Sampling signal5、结合抽样定理,利用MATLAB 编程实现信号经过冲激脉冲抽样后得到的抽样信号及其频谱[建议:冲激脉冲的周期分别取4*pi/3 s 、pi s 、2*pi/3 s 三种情况对比],并利用构建信号。
MAtlab-傅里叶变换-实验报告(同名21543)

陕西科技大学实验报告班级信工142 学号22 姓名何岩实验组别实验日期___________ 室温_______________ 报告日期__________________ 成绩报告内容:(目的和要求,原理,步骤,数据,计算,小结等)1.求信号的离散时间傅立叶变换并分析其周期性和对称性;给定正弦信号x(t)=2*cos(2*pi*10*t),fs=100HZ, 求其DTFT (a)代码:f=10;T=1/f;w=-10:0.2:10;t1=0:0.0001:1;t2=0:0.01:1;n1=-2; n2=8; n0=0; n=n 1:0.01: n2;x5=[ n>=0.01];x1=2*cos(2*f*pi*t1);x2=2*cos(2*f*pi*t2);x3=(exp(-j)4(t2'*w));x4=x2*x3;subplot(2,2,1);plot(t1,x1);axis([0 1 1.1*mi n(x2) 1.1*max(x2)]);xlabel('x( n)');ylabel('x( n)');title('原信号x1');xlabel('t');ylabel('x1');subplot(2,2,3);stem(t2,x2);axis([0 1 1.1*mi n(x2) 1.1*max(x2)]);title(' 原信号采样结果x2');xlabel('t');ylabel('x2');subplot(2,2,2);stem( n, x5);axis([0 1 1.1*mi n(x5) 1.1*max(x5)]);xlabel(' n');ylabel('x2');title(' 采样函数x2');subplot(2,2,4);stem(t2,x4);axis([0 1 -0.2+1.1*mi n(x4) 1.1*max(x4)]);xlabel('t');ylabel('x4');title('DTFT 结果x4');(b)结果:2.用以下两个有限长序列来验证DTFT勺线性、卷积和共轭特性; x1( n)=[1 2 3 4 5 6 7 8 9 10 11 12];x2( n)=R 10( n)⑴线性:(a)代码:w=li nspace(-8,8,10000);nx仁[0:11]; nx2=[0:9];x1=[1 2 3 4 5 6 7 8 9 10 11 12];x2=[1 1 1 1 1 1 1 1 1 1];x3=[x2,zeros(1,(le ngth(x1)-le ngth(x2)))];x4=2*x1+3*x3;X1=x1*exp(-j* nx1'*w);% 频率特性X3=x3*exp(-j* nx1'*w);% 频率特性X4=x4*exp(-j* nx1'*w);% 频率特性subplot(5,3,1),stem( nx1,x1),axis([-1,13,0,15]);title('x1').n DTFT结果川原信号0 05 1眉信寻采率结臭心ylabel('x (n)');subplot(5,3,2),stem( nx2,x2),axis([-1,13,0,5]);title('x2');subplot(5,3,3),stem( nx1,x4),axis([-1,13,0,26]);title('x4=2*x1+3*x 3');subplot(5,3,4),plot(w,abs(X1)); ylabel(' 幅度') subplot(5,3,7),plot(w,a ngle(X1));ylabel(' 相位') subplot(5,3,10),plot(w,real(X1));ylabel(' 实部') subplot(5,3,13),plot(w,imag(X1)); ylabel(' 虚部') subplot(5,3,5),plot(w,abs(X3)); subplot(5,3,8),plot(w,a ngle(X3)); subplot(5,3,11),plot(w,real(X3)); subplot(5,3,14),plot(w,imag(X3)); subplot(5,3,6),plot(w,abs(X4)); subplot(5,3,9),plot(w,a ngle(X4)); subplot(5,3,12),plot(w,real(X4));subplot(5,3,15),plot(w,imag(X4));(b)结果:⑵卷积:(a )代码:nx1= 0:11; nx2=0:9; nx3=0:20;w=li nspace(-8,8,40); %w=[-8,8]分 10000 份x1=[1 2 3 4 5 6 7 8 9 10 11 12]; x2=[1 1 1 1 1 1 1 1 1 1]; x3=conv(x1,x2);% x1 卷积 x2x4=x1*exp(-j*nx1'*w);% x1 频率特性 x5=x2*exp(-j* nx2'*w);% x2 频率特性 x6=x3*exp(-j*nx3'*w);% x1x7=x4.*x5;卷积x2频率特性subplot(2,2,1),stem( nx1,x1),axis([-1,15,0,15]),title('x1'); subplot(2,2,2),stem( nx2,x2),axis([-1,15,0,5]),title('x2'); subplot(2,1,2),stem(nx3,x3),axis([-1,25,0,80]);title('x1卷积 x2 结xl0 5 10 15l DC 0一叫0 101DCi ----- * ------ n■1Q 0 10^JUQ-"w50 10E■-10 Tin □1U0 ©zZ1010 10果x3');figure,subplot(2,2,1),stem(x4,'filled'),title('x1 的DTFT吉果x4');subplot(2,2,2),stem(x5,'filled'),title('x2 的DTFT吉果x5');subplot(2,2,3),stem(x6,'filled'),title('x3 的DTFT吉果x6');subplot(2,2,4),stem(x7,'filled'),title('x4 的DTFT吉果x7'); figure,subplot(3,2,1),stem(w,abs(x6)). ylabel(' 幅度'),title('x1积x2 的DTFT');subplot(4,2,3),stem(w,a ngle(x6)),ylabel(' 相位')subplot(4,2,5),stem(w,real(x6)),ylabel(' 实部')subplot(4,2,7),stem(w,imag(x6)),ylabel(' 虚部')subplot(4,2,2),stem(w,abs(x7)), title('x1 与x2 的DTFT的乘积');subplot(4,2,4),stem(w,a ngle(x7));subplot(4,2,6),stem(w,real(x7));subplot(4,2,8),stem(w,imag(x7));(b)结果:*1巷视说箔畢內10J5330-100泊的(JTFT结畀汕□10 2 口3Q 4Q⑶共轭:(a )代码:xln=[1 2 3 4 5 6 7 8 9 10 11 12]; w=-10:10;N1= le ngth(x1 n); n1=0:N1-1; x1=real(x1 n); x2=imag(x1 n); x2n=x1-j*x2;X 仁 x2 n*(exp(-j)4( n1'*w)); X2=x1 n*(exp(j)4( n1'*w)); x3=real(X2); x4=imag(X2); X2=x3-j*x4;figure,subplot(211);stem(w,X1,'.');title('x1 n 共轭的 DTFT');subplot(212);stem(w,X2,'.');title('x1 n的 DTFT 取共轭且反折');的「JFTH1三汀的「TFT 笊乘祀(b)结果:-10 -B -S3.求LTI系统的频率响应给定系统H( Z) =B (Z) /A (Z), A=[0.98777 -0.31183 0.0256] B=[0.98997 0.989 0.98997],求系统的幅频响应和相频响应。
傅里叶变换及带通滤波器仿真Matlab试验报告
傅里叶变换及带通滤波器仿真Matlab试验报告一.实验目的1.学习软件matlab的编辑语言、绘图、函数等功能的运用2.了解傅里叶级数的复数形式表示方波,并运用matlab绘出。
3.熟悉带通滤波器的工作原理,并用matlab仿真带通滤波器,绘出相应的图形,最后用pspice验证。
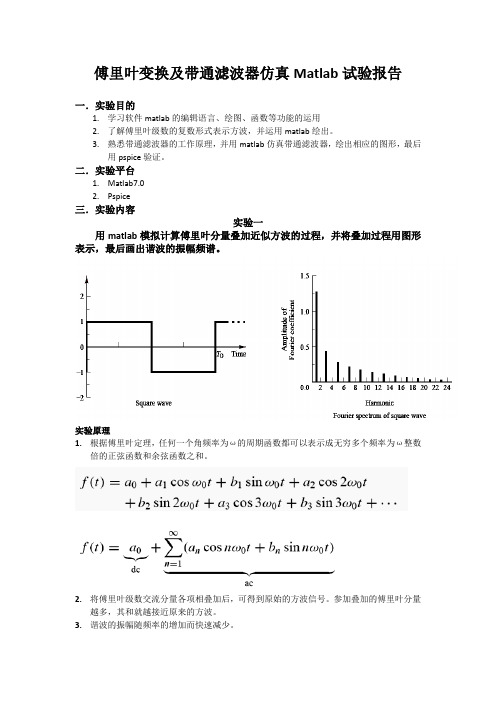
二.实验平台1. Matlab7.02. Pspice三.实验内容实验一用matlab模拟计算傅里叶分量叠加近似方波的过程,并将叠加过程用图形表示,最后画出谐波的振幅频谱。
实验原理1.根据傅里叶定理,任何一个角频率为ω的周期函数都可以表示成无穷多个频率为ω整数倍的正弦函数和余弦函数之和。
2.将傅里叶级数交流分量各项相叠加后,可得到原始的方波信号。
参加叠加的傅里叶分量越多,其和就越接近原来的方波。
3.谐波的振幅随频率的增加而快速减少。
实验步骤1.设计叠加傅里叶交流分量的算法。
2.打开Matlab,编辑程序实现算法。
3.运用Matlab的绘图函数将叠加过程用图形表示。
4.用Matlab绘出振幅频谱图。
实验程序代码%时间t从0到2,每隔0.001秒取一点t=0:0.001:pi;y=0;%通过循环绘出a小于等于5和a=16时的图像for a=1:6n=2*a-1y=y+4./(n*pi)*sin(n*pi*t);figure(1)subplot(2,3,a);plot(t,y,'-g')xlabel('Time');ylabel('F');ends=0;for b=1:16s=s+4./((b*2-1)*pi)*sin((b*2-1)*pi*t);endplot(t,s,'-g')%绘出振幅频谱图像figure(2)k=1:2:12;A=4./(k*pi);bar(k,A,0.1);实验结果傅里叶波形图振幅频谱图实验结果分析与结论1.根据傅里叶波形图可以看出,通过逐项叠加傅里叶级数交流分量可以形成原始方波。
matlab fft谱分析实验报告

matlab fft谱分析实验报告Matlab FFT谱分析实验报告引言谱分析是一种常用的信号处理技术,用于研究信号的频率成分和能量分布。
傅里叶变换是一种常见的谱分析方法,而Matlab中的FFT函数则是实现傅里叶变换的强大工具。
本实验旨在通过使用Matlab中的FFT函数对不同类型的信号进行谱分析,探索其在实际应用中的作用和价值。
实验方法1. 生成信号首先,我们使用Matlab中的函数生成几种不同类型的信号,包括正弦信号、方波信号和噪声信号。
通过调整信号的频率、幅度和噪声水平,我们可以模拟不同的实际场景。
2. 调用FFT函数接下来,我们使用Matlab中的FFT函数对生成的信号进行频谱分析。
FFT函数将信号从时域转换到频域,提供了信号在不同频率上的能量分布情况。
3. 绘制频谱图通过调用Matlab中的绘图函数,我们可以将FFT函数输出的频谱数据可视化为频谱图。
频谱图通常以频率为横轴,能量或幅度为纵轴,展示了信号在不同频率上的能量分布情况。
实验结果1. 正弦信号的频谱分析我们首先对一个频率为50Hz、幅度为1的正弦信号进行频谱分析。
结果显示,该信号在50Hz附近有一个明显的峰值,表示信号主要由50Hz频率成分组成。
2. 方波信号的频谱分析接下来,我们对一个频率为10Hz、幅度为1的方波信号进行频谱分析。
由于方波信号包含丰富的谐波成分,频谱图中出现了多个峰值,每个峰值对应一个谐波成分。
3. 噪声信号的频谱分析最后,我们对一个包含高斯噪声的信号进行频谱分析。
噪声信号的频谱图呈现出平坦的能量分布,没有明显的峰值。
这说明噪声信号在各个频率上都有一定的能量分布,没有明显的频率成分。
讨论与分析通过对不同类型信号的频谱分析,我们可以得出以下结论:1. 正弦信号的频谱图呈现出一个明显的峰值,表示信号主要由该频率成分组成。
这对于识别和分析周期性信号非常有用。
2. 方波信号的频谱图呈现出多个峰值,每个峰值对应一个谐波成分。
傅里叶变换matlab实验总结

傅里叶变换matlab实验总结(完整)快速傅里叶变换fft的Matlab实现实验报告尊敬的读者朋友们:一、实验目的1在理论学习的基础上,通过本实验加深对快速傅立叶变换的理解;2熟悉并掌握按时间抽取FFT算法的程序;3了解应用FFT进行信号频谱分析过程中可能出现的问题,例如混淆、泄漏、栅栏效应等,以便在实际中正确应用FFT。
二、实验内容1仔细分析教材第六章‘时间抽取法FFT'的算法结构,编制出相应的用FFT进行信号分析的C语言(或MATLAB语言)程序;用MATLAB语言编写的FFT源程序如下:%%输入数据f、N、T及是否补零clc;clear;f=input('输入信号频率f:');N=input('输入采样点数N:');T=input(’输入采样间隔T:');C=input('信号是否补零(补零输入1,不补零输入0):’); %补零则输入1,不补则输入0if(C==0)t=0:T:(N—1)*T;=in(2*pift);b=0;eleb=input(’输入补零的个数:');while(log2(N+b),=fi(log2(N+b)))b=input(’输入错误,请重新输入补零的个数:’);endt=0:T:(N+b—1)*T;=in(2*pi*f*t)。
(t<=(N—1)*T);end%%fft算法的实现A=bitrevorder();% 将序列按二进制倒序N=N+b;M=log2(N);% M为蝶形算法的层数W=ep(—j2pi、N);for L=1:1:M% 第L层蝶形算法B=2^L、2;%B为每层蝶形算法进行加减运算的两个数的间隔K=N、(2^L);%K为每层蝶形算法中独立模块的个数for k=0:1:K-1for J=0:1:B-1p=J2^(M—L);%p是W的指数q=A(k2^L+J+1);%用q来代替运算前面那个数A(k2^L+J+1)=q+W^p*A(k2^L+J+B+1);A(k*2^L+J+B+1)=q—W^p*A(k*2^L+J+B+1);endendend%%画模特性的频谱图z=ab(A);% 取模z=z。
数字信号matlab实验快速傅里叶变换及其应用技术

实验三 快速傅里叶变换及其应用上机实验内容一、观察高斯序列的时域和幅频特性,固定信号xa(n)中参数p=8,改变q 的值,分别等于2,4,8,观察他们的时域和幅频特性,了解党q 取不同的值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8,13,14,观察参数p 变化对信号序列的时域及幅频特性的影响,注意p 等于多少时,会发生明显的泄露现象,混叠是否也随之出现? (1)P=8,q=2,4,8时, 程序如下:n=0:15;N=16;p=8;q1=2;q2=4;q3=8; figure(1)x1n=exp(-((n-p1).^2/q)); subplot(3,2,1),stem(n,x1n,'.') x2n=exp(-((n-p2).^2/q)); subplot(3,2,3),stem(n,x2n,'.') x3n=exp(-((n-p3).^2/q)); subplot(3,2,5),stem(n,x3n,'.') x1k=fft(x1n,N);subplot(3,2,2),stem(n,x1k,'.') x2k=fft(x2n,N);subplot(3,2,4),stem(n,x2k,'.') x3k=fft(x3n,N);subplot(3,2,6),stem(n,x3k,'.') 波形如下:0510150510155101505101505101551015p固定时,当p从2变化到8时,时域波形变化缓慢,低频分量增加,频谱泄露和混叠减小。
(2)q=8,p=8,13,14时,程序类同上波形如下:051015051015固定q=8时,当p从8变化到14,窗口位置偏移,受窗口宽度的影响,波形在高处截断产生严重的频谱泄露。
二、观察衰减正弦序列xb(n)的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现位置是否正确,注意频谱的形状,会出幅频特性曲线,改变f,使f分别等于0.4375,0.5625,观察着两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄露现象,说明产生的原因。
信号与系统matlab实验傅里叶分析及应用报告答案

实验二傅里叶分析及应用姓名学号班级一、实验目的(一)掌握使用Matlab进行周期信号傅里叶级数展开和频谱分析1、学会使用Matlab分析傅里叶级数展开,深入理解傅里叶级数的物理含义2、学会使用Matlab分析周期信号的频谱特性(二)掌握使用Matlab求解信号的傅里叶变换并分析傅里叶变换的性质1、学会运用Matlab求连续时间信号的傅里叶变换2、学会运用Matlab求连续时间信号的频谱图3、学会运用Matlab分析连续时间信号的傅里叶变换的性质(三)掌握使用Matlab完成信号抽样并验证抽样定理1、学会运用MATLAB完成信号抽样以及对抽样信号的频谱进行分析2、学会运用MATLAB改变抽样时间间隔,观察抽样后信号的频谱变化3、学会运用MATLAB对抽样后的信号进行重建二、实验条件需要一台PC机和一定的matlab编程能力三、实验内容2、分别利用Matlab符号运算求解法和数值计算法求下图所示信号的FT,并画出其频谱图(包括幅度谱和相位谱)[注:图中时间单位为:毫秒(ms)]。
符号运算法: Ft=sym('t*(Heaviside(t+2)-Heaviside(t+1))+Heaviside(t+1)-Heaviside(t-1)+(-t)*(Heavi side(t-1)-Heaviside(t-2))'); Fw = fourier(Ft); ezplot(abs(Fw)),grid on; phase = atan(imag(Fw)/real(Fw)); ezplot(phase);grid on; title('|F|'); title('phase');3、试用Matlab 命令求ωωωj 54-j 310)F(j ++=的傅里叶反变换,并绘出其时域信号图。
[注意:(1)写代码时j i]syms tFw = sym('10/(3+iw)-4/(5+iw)');ft = ifourier(Fw,t);F = abs(ft);ezplot(F,[-3,3]),grid on;4、已知门函数自身卷积为三角波信号,试用Matlab命令验证FT的时域卷积定理。
[经验]matlab完成傅里叶变换
![[经验]matlab完成傅里叶变换](https://img.taocdn.com/s3/m/4ed7ec0ac381e53a580216fc700abb68a982adcf.png)
一、傅立叶变化的原理;(1)原理正交级数的展开是其理论基础!将一个在时域收敛的函数展开成一系列不同频率谐波的叠加,从而达到解决周期函数问题的目的。
在此基础上进行推广,从而可以对一个非周期函数进行时频变换。
从分析的角度看,他是用简单的函数去逼近(或代替)复杂函数,从几何的角度看,它是以一族正交函数为基向量,将函数空间进行正交分解,相应的系数即为坐标。
从变幻的角度的看,他建立了周期函数与序列之间的对应关系;而从物理意义上看,他将信号分解为一些列的简谐波的复合,从而建立了频谱理论。
当然Fourier积分建立在傅氏积分基础上,一个函数除了要满足狄氏条件外,一般来说还要在积分域上绝对可积,才有古典意义下的傅氏变换。
引入衰减因子e^(-st),从而有了Laplace变换。
(好像走远了)。
(2)计算方法连续傅里叶变换将平方可积的函数f(t)表示成复指数函数的积分或级数形式。
这是将频率域的函数F(ω)表示为时间域的函数f(t)的积分形式。
连续傅里叶变换的逆变换 (inverse Fourier transform)为即将时间域的函数f(t)表示为频率域的函数F(ω)的积分。
一般可称函数f(t)为原函数,而称函数F(ω)为傅里叶变换的像函数,原函数和像函数构成一个傅里叶变换对(transform pair)。
二、傅立叶变换的应用;DFT 在诸多多领域中有着重要应用,下面仅是颉取的几个例子。
需要指出的是,所有DFT 的实际应用都依赖于计算离散傅里叶变换及其逆变换的快速算法,即快速傅里叶变换(快速傅里叶变换(即FFT )是计算离散傅里叶变换及其逆变换的快速算法。
)。
(1)、频谱分析DFT 是连续傅里叶变换的近似。
因此可以对连续信号x(t)均匀采样并截断以得到有限长的离散序列,对这一序列作离散傅里叶变换,可以分析连续信号x(t)频谱的性质。
前面还提到DFT 应用于频谱分析需要注意的两个问题:即采样可能导致信号混叠和截断信号引起的频谱泄漏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
班级信工142 学号 22 姓名何岩实验组别实验日期室温报告日期成绩报告内容:(目的和要求,原理,步骤,数据,计算,小结等)1.求信号的离散时间傅立叶变换并分析其周期性和对称性;给定正弦信号x(t)=2*cos(2*pi*10*t),fs=100HZ,求其DTFT。
(a)代码:f=10;T=1/f;w=-10:0.2:10;t1=0:0.0001:1;t2=0:0.01:1;n1=-2;n2=8;n0=0;n=n1:0.01:n2;x5=[n>=0.01];x1=2*cos(2*f*pi*t1);x2=2*cos(2*f*pi*t2);x3=(exp(-j).^(t2'*w));x4=x2*x3;subplot(2,2,1);plot(t1,x1);axis([0 1 1.1*min(x2) 1.1*max(x2)]);xlabel('x(n)');ylabel('x(n)');title('原信号x1');xlabel('t');ylabel('x1');subplot(2,2,3);stem(t2,x2);axis([0 1 1.1*min(x2) 1.1*max(x2)]);title('原信号采样结果x2');xlabel('t');ylabel('x2');subplot(2,2,2);stem(n,x5);axis([0 1 1.1*min(x5) 1.1*max(x5)]);xlabel('n');ylabel('x2');title('采样函数x2');subplot(2,2,4);stem(t2,x4);axis([0 1 -0.2+1.1*min(x4) 1.1*max(x4)]);xlabel('t');ylabel('x4');title('DTFT结果x4');(b)结果:2.用以下两个有限长序列来验证DTFT的线性、卷积和共轭特性;(n)x1(n)=[1 2 3 4 5 6 7 8 9 10 11 12];x2(n)=R10(1)线性:(a)代码:w=linspace(-8,8,10000);nx1=[0:11]; nx2=[0:9];x1=[1 2 3 4 5 6 7 8 9 10 11 12];x2=[1 1 1 1 1 1 1 1 1 1];x3=[x2,zeros(1,(length(x1)-length(x2)))];x4=2*x1+3*x3;X1=x1*exp(-j*nx1'*w);%频率特性X3=x3*exp(-j*nx1'*w);%频率特性X4=x4*exp(-j*nx1'*w);%频率特性subplot(5,3,1),stem(nx1,x1),axis([-1,13,0,15]);title('x1'), ylabel('x(n)'); subplot(5,3,2),stem(nx2,x2),axis([-1,13,0,5]);title('x2');subplot(5,3,3),stem(nx1,x4),axis([-1,13,0,26]);title('x4=2*x1+3*x3'); subplot(5,3,4),plot(w,abs(X1)); ylabel('幅度')subplot(5,3,7),plot(w,angle(X1));ylabel('相位')subplot(5,3,10),plot(w,real(X1));ylabel('实部')subplot(5,3,13),plot(w,imag(X1)); ylabel('虚部')subplot(5,3,5),plot(w,abs(X3));subplot(5,3,8),plot(w,angle(X3));subplot(5,3,11),plot(w,real(X3));subplot(5,3,14),plot(w,imag(X3));subplot(5,3,6),plot(w,abs(X4));subplot(5,3,9),plot(w,angle(X4));subplot(5,3,12),plot(w,real(X4));subplot(5,3,15),plot(w,imag(X4));(b)结果:(2)卷积:(a)代码:nx1=0:11; nx2=0:9; nx3=0:20;w=linspace(-8,8,40); %w=[-8,8]分10000份x1=[1 2 3 4 5 6 7 8 9 10 11 12];x2=[1 1 1 1 1 1 1 1 1 1];x3=conv(x1,x2);% x1卷积x2x4=x1*exp(-j*nx1'*w);% x1频率特性x5=x2*exp(-j*nx2'*w);% x2频率特性x6=x3*exp(-j*nx3'*w);% x1卷积x2频率特性x7=x4.*x5;subplot(2,2,1),stem(nx1,x1),axis([-1,15,0,15]),title('x1');subplot(2,2,2),stem(nx2,x2),axis([-1,15,0,5]),title('x2');subplot(2,1,2),stem(nx3,x3),axis([-1,25,0,80]);title('x1卷积x2结果x3'); figure,subplot(2,2,1),stem(x4,'filled'),title('x1的DTFT结果x4');subplot(2,2,2),stem(x5,'filled'),title('x2的DTFT结果x5');subplot(2,2,3),stem(x6,'filled'),title('x3的DTFT结果x6');subplot(2,2,4),stem(x7,'filled'),title('x4的DTFT结果x7'); figure,subplot(3,2,1),stem(w,abs(x6)), ylabel('幅度'),title('x1卷积x2的DTFT');subplot(4,2,3),stem(w,angle(x6)),ylabel('相位')subplot(4,2,5),stem(w,real(x6)),ylabel('实部')subplot(4,2,7),stem(w,imag(x6)),ylabel('虚部')subplot(4,2,2),stem(w,abs(x7)), title('x1与x2的DTFT的乘积');subplot(4,2,4),stem(w,angle(x7));subplot(4,2,6),stem(w,real(x7));subplot(4,2,8),stem(w,imag(x7));(b)结果:(3)共轭:(a)代码:x1n=[1 2 3 4 5 6 7 8 9 10 11 12];w=-10:10;N1=length(x1n);n1=0:N1-1;x1=real(x1n);x2=imag(x1n);x2n=x1-j*x2;X1=x2n*(exp(-j).^(n1'*w));X2=x1n*(exp(j).^(n1'*w));x3=real(X2);x4=imag(X2);X2=x3-j*x4;figure,subplot(211);stem(w,X1,'.');title('x1n共轭的DTFT');subplot(212);stem(w,X2,'.');title('x1n的DTFT取共轭且反折');(b)结果:3. 求LTI系统的频率响应给定系统H(Z)=B(Z)/A(Z),A=[0.98777 -0.31183 0.0256]B=[0.98997 0.989 0.98997],求系统的幅频响应和相频响应。
(要求使用filter(B,A,δ(n))求解。
(a)结果:A=[0.98777 -0.31183 0.0256];B=[0.98997 0.989 0.98997];C=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]y=filter(B,A,C);subplot(2,2,1);stem(y,'.');title('原始序列');mag=abs(y);ph=angle(y);ph=ph*180/pi;subplot(2,2,2);stem(mag,'.');title('幅频特性');xlabel('时间信号n');ylabel('信号幅度');subplot(2,2,3);stem(ph,'.');title('相频特性');xlabel('时间信号n');ylabel('信号相位');(b)结果:4. 采样和频谱混叠给定信号x(t)=100*exp(-100*t)*cos(2*pi*500*t),求该信号的频谱;当采样频率分别为fs1=2000HZ,fs2=1000HZ;fs3=500HZ;fs4=200HZ,时输出序列的DTFT。
(a)代码:x=100*exp(-100*t).*cos(2*pi*500*t);t=-2:0.1:2;w=-10:0.1:10;y=x*(exp(-j).^(t'*w));subplot(2,1,1),plot(t,x);subplot(2,1,2),plot(w,y);title('原始信号的频谱');figure,fs1=2000;Ts1=1/fs1;n1=-2:Ts1:2;fs2=1000;Ts2=1/fs2;n2=-2:Ts2:2;fs3=500;Ts3=1/fs3;n3=-2:Ts3:2;fs4=200;Ts4=1/fs4;n4=-2:Ts4:2;x1=100.*exp(-100*n1).*cos(2*pi*500*n1);y1=x1*(exp(-j).^(n1'*w));subplot(221);plot(w,y1);title('经2000Hz采样后信号的DTFT');x2=100.*exp(-100*n2).*cos(2*pi*500*n2);y2=x2*(exp(-j).^(n2'*w));subplot(222);plot(w,y2);title('经1000Hz采样后信号的DTFT');x3=100.*exp(-100*n3).*cos(2*pi*500*n3); y3=x3*(exp(-j).^(n3'*w));subplot(223);plot(w,y3);title('经500Hz采样后信号的DTFT');x4=100.*exp(-100*n4).*cos(2*pi*500*n4);y4=x4*(exp(-j).^(n4'*w));subplot(224);plot(w,y4);title('经200Hz采样后信号的DTFT');(b)结果:收获及感想:DFT针对的是有限长数字信号的傅立叶变换或傅立叶时频分析问题。
