【高中数学课件】必修4任意角ppt课件
合集下载
人教版必修四年级数学《任意角》PPT教学课件

S={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°, k∈Z} = {β|β = 90°+ 2k·180°, k∈Z}∪{β|β = 90°+ (2k + 1)·180°,k∈Z}={β|β=90°+n·180°,n∈Z}.
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
知识迁移 1:
终边在射线上的角如何表示?
S | k 360 , k Z
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
解 S={α|α=k·360°,k∈Z}∪{α|α=k·360°+180°,k∈Z} ={α |α =2k ·180°,k ∈Z}∪{α |α =(2k +1)·180°,k ∈Z} ={α |α =n ·180°,n ∈Z}.
《任意角》
·人教版必修四数学PPT课件·
优品老师
目 录
一 学习目标 二 新课导入 三 新课讲授
四 课堂检测 五 课堂总结
一 学习目标
·学习目标·
(1)推广角的概念、引入大于角和负角; (2)理解并掌握正角、负角、零角的定义; (3)理解任意角以及象限角的概念; (4)掌握所有与角终边相同的角(包括角)的表示方法; (5)树立运动变化观点,深刻理解推广后的角的概念;
一般地,所有与角α 终边相同的角,连同角α 在内,可构成一个集合S={β|β=α +k·360°, k∈Z},即任一与角α 终边相同的角,都可以表示成角α 与整数个周角的和.
注意: (1)α 为任意角. (2)k·360°与α 之间是“+”号,k·360°-α 可理解为k·360°+(-α ). (3)相等的角终边一定相同;终边相同的角不一定相等,终边相同的角有无数多个,它们相差360°的整数倍. (4)k∈Z这一条件不能少.
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
知识迁移 1:
终边在射线上的角如何表示?
S | k 360 , k Z
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
解 S={α|α=k·360°,k∈Z}∪{α|α=k·360°+180°,k∈Z} ={α |α =2k ·180°,k ∈Z}∪{α |α =(2k +1)·180°,k ∈Z} ={α |α =n ·180°,n ∈Z}.
《任意角》
·人教版必修四数学PPT课件·
优品老师
目 录
一 学习目标 二 新课导入 三 新课讲授
四 课堂检测 五 课堂总结
一 学习目标
·学习目标·
(1)推广角的概念、引入大于角和负角; (2)理解并掌握正角、负角、零角的定义; (3)理解任意角以及象限角的概念; (4)掌握所有与角终边相同的角(包括角)的表示方法; (5)树立运动变化观点,深刻理解推广后的角的概念;
一般地,所有与角α 终边相同的角,连同角α 在内,可构成一个集合S={β|β=α +k·360°, k∈Z},即任一与角α 终边相同的角,都可以表示成角α 与整数个周角的和.
注意: (1)α 为任意角. (2)k·360°与α 之间是“+”号,k·360°-α 可理解为k·360°+(-α ). (3)相等的角终边一定相同;终边相同的角不一定相等,终边相同的角有无数多个,它们相差360°的整数倍. (4)k∈Z这一条件不能少.
人教A版高中数学必修四第一章 1.1.1任意角公开课教学课件 (共21张PPT)

列各角终边相同的角,并判定它们是第 几象限角.
(1) 120 ;(2) 6600 ;
(1) 120 ; (2)6600 ;
解:∵ 120 240 (1) 360
∴与 120 角终边相同的角是 240 角,
它是第三象限的角;
(2)ቤተ መጻሕፍቲ ባይዱ 660 300 1 360
∴与660 角终边相同的角是300角,
3、下列说法中,正确的是( )
A.第一象限的角是锐角
B.锐角是第一象限的角
C.小于90°的角是锐角
D.终边相同的角一定相
等
4、把-1485°转化为α+k·360°(0°≤α<360°, k∈Z)
的形式是( )
A.45°-4×360°
B.-45°-4×360°
C.-45°-5×360° D.315°-5×360°
的元素是
363 14 2 360 356 46,
363 14 1 360 3 14,
363 14 0 360 363 14.
变式训练:
写出下列各角终边相同的角的集合, 并把集合中适合不等式 - 720 0 360 0 的元素 写出来: (1)1303018′(2)- 2250
小结:
四、终边相同的角及其表示方法
注:所有与角 终边相同的角,连同角
在内,可以构成一个集合
{ | k 360 0, k Z}
即任一与角 终边相同的角,都可以表示
成角 与整数个周角的和。
说明:终边相同 的角不一定相 等,相等的角终
边一定相同
五、例题分析:
【例1】在 0 ~ 360 间,找出与下
y -3300
3900
300
x
o
300 =300+0x3600
(1) 120 ;(2) 6600 ;
(1) 120 ; (2)6600 ;
解:∵ 120 240 (1) 360
∴与 120 角终边相同的角是 240 角,
它是第三象限的角;
(2)ቤተ መጻሕፍቲ ባይዱ 660 300 1 360
∴与660 角终边相同的角是300角,
3、下列说法中,正确的是( )
A.第一象限的角是锐角
B.锐角是第一象限的角
C.小于90°的角是锐角
D.终边相同的角一定相
等
4、把-1485°转化为α+k·360°(0°≤α<360°, k∈Z)
的形式是( )
A.45°-4×360°
B.-45°-4×360°
C.-45°-5×360° D.315°-5×360°
的元素是
363 14 2 360 356 46,
363 14 1 360 3 14,
363 14 0 360 363 14.
变式训练:
写出下列各角终边相同的角的集合, 并把集合中适合不等式 - 720 0 360 0 的元素 写出来: (1)1303018′(2)- 2250
小结:
四、终边相同的角及其表示方法
注:所有与角 终边相同的角,连同角
在内,可以构成一个集合
{ | k 360 0, k Z}
即任一与角 终边相同的角,都可以表示
成角 与整数个周角的和。
说明:终边相同 的角不一定相 等,相等的角终
边一定相同
五、例题分析:
【例1】在 0 ~ 360 间,找出与下
y -3300
3900
300
x
o
300 =300+0x3600
必修4任意角课件

四、与 终边相同的角的集合为
S { | k 360 , k Z}
o
注:(1) K ∈ Z
(3)K· 360°与 之间是“+”号, (4)终边相同的角不一定相等,但相等的 角终边一定相同,终边相同的角有无数多个, 它们相差360°的整数倍。
(2) 是任意角
• 写出终边在X轴上的角的集合 • 写出终边在坐标轴上的角的集合
o o o o
例3、写出终边在下列阴影部分内的角的集合
问题2、你的手表慢了10分钟,你应该怎样将它校准? 如果你的手表快了10分钟你应该怎么做?如果你的 手表快了1.5个小时,你又如何将它校准?
二、角的分类 逆时针旋转得到的角叫 正角 顺时针旋转得到的角叫 负角
不发生旋转得到的角叫 零角
三、在坐标系中讨论角—象限角
如果角的终边落在了坐标轴上, 就认为这个角不属于任何象限。
必修4
1.1.1 任意角
一、 “角”的定 B 义:
顶 点
终边 B
α
o
A
始边
O
A
(1)由一个顶点发出的两条射线所组成的图形(静态定义)
(2)一条射线绕着端点从一个位置旋转到另一个位置 所组成的图形. (动态定义)
记法:角α或 ∠A0B,也可简记为α
问题1、初中学过的角,范围是什么?(00,3600]
(1)锐角一定是第一象限角; (2)第一象限角一定是锐角; (3)第一象限角一定小于第二象限角; (4)小于90°的角都是锐角。
思考:将角放在坐标系中,给定一个角,就 有唯一的一条终边与之对应。反之,对于坐 标系中的任意一条射线,以它为终边的角是 否唯一?如果不唯一,那么终边相同的角有 什么关系?
高中数学必修四:1.1.1《任意角》 PPT课件 图文
精讲领学
例题1 写出与下列各角终边相同的角的集合S,并把S中在 360~720范围的角写出来.
( 1 ) 6 0 ;( 2 ) 2 1 ;( 3 ) 3 6 3 1 4
解: ( 1 ) S {| k 3 6 0 6 0 , k Z }300,60,420
( 2 ) S {| k 3 6 0 2 1 , k Z }21,339,699
2、下列角中终边与330°相同的角是( ) A.30° B.-30° C.630° D.-630°
3、把-1485°转化为α+k·360° (0°≤α<360°, k∈Z)的形式是( ) A.45°-4×360° B.-45°-4×360° C.-45°-5×360° D.315°-5×360°
反馈固学
1.1.1 任意角
第一课时
(1)推广角的概念;理解并掌握正角、负角、零角的定义; (2)理解任意角以及象限角的概念; (3)掌握所有与角终边相同的角(包括角)的表示方法; (4)树立运动变化观点,深刻理解推广后的角的概念;
思考:那么工人在拧紧或拧松螺丝时,转动的角度 如何表示才比较合适?
逆时 针
4、下列结论中正确的是( ) A.小于90°的角是锐角 B.第二象限的角是钝角 C.相等的角终边一定相同 D.终边相同的角一定相等
5:任意两个角的数量大小可以相加、相减.
例如50°+80°=130°, 50°-80°=-30°, 你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角. -30°是以50°角的终边为始边,顺时针旋转80°所成的角.
注3:(1) 为任意角 (2) k Z这一条件必不可少;
(3) 终边相同的角不一定相等, 终边相等的角有无数多个,它们相差3600的整数倍.
高中数学必修四《任意角》PPT

为了研究方便,我们常在平面直角坐标系中来
讨论角.角的顶点与坐标原点重合,角的始边与x轴 的非负半轴重合.
(1)角的终边在第几象限,就说这个角是第几
象限角;
(2)角的终边在坐标轴上,则此角不属于任何
一个象限.
y
y
o
x
o
x
概念剖析
给出下列四个命题,其中 正确的有__①__②__③__④___
① -75°是第四象限角; ② 215°是第三象限角; ③ 475°是第二象限角; ④ -315°是第一象限角.
1.1.1 任意角
春
夏
秋
冬
月相
潮汐
摩天轮
三角函数 月相
潮汐
摩天轮
知识回顾:
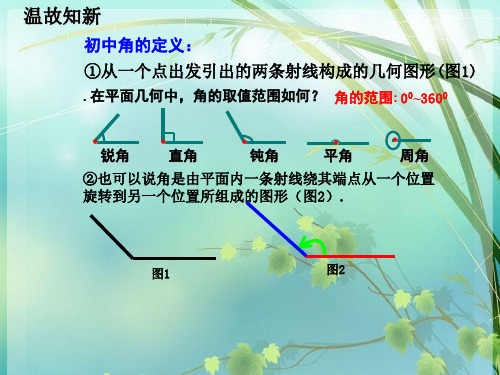
初中教材中是如何定义角的?
一点出发的两条
B
射线所围成的图形.
α
0 α 360 O
A
跳水
既要考虑旋转量,又要考虑旋转方向
任意角的概念
角可以看成是平面内一条射线绕着端点从一 个位置旋转到另一个位置所成的图形.
思考:
1.锐角是第几象限角?第一象 限角一定是锐角吗?
2.第二象限角一定比第一象限 角大吗?
请同学们在平面直角坐标系内分别 作出下列各角:
① -225°;② 135°; ③ 495°.
y
o
225
y
135
x
o
x
?
一般地 ,所有与角α终边相同的角, 连同角α在内,可构成一个集合
y
α | α 90 180 2k 180 ,k Z o
x
α | α 90 2k 180 ,k Z
α | α 90 (2k 1) 180 ,k Z
高中数学必修4《第一章三角函数》精品课件:1.1.1任意角

S={α|α=45°+k·180°,k∈Z}.
S={ -315°,-135°,45°,225°, 405°,585°}
课堂小结
Office组件之word2007
1.角的概念推广 正角、负角、零角、象限角
2.终边相同的角
3.终边在x轴、y轴上的角的表示
4.终边在各个象限上的角的表示
Office组件之word2007
思考2:终边在x轴上的角的集合表示
终边在x轴上:S={α|α=k·180°,k∈Z};
新课教学
Office组件之word2007
思考3:终边在y轴非正半轴、非负半轴
上的角分别如何表示?
y轴非负半轴:α= 90°+k·360°,k∈Z ; y轴非正半轴:α= 270°+k·360°,k∈Z .
思考4:终边在y轴上的角的集合表示
y
x o
知识探究(三):终边相同的角 Office组件之word2007
思考1:-32°,328°,-392°是第几 象限的角?这些角有什么内在联系?
y
328° o
-392° x
-32°
新课教学
Office组件之word2007
思考2:与-32°角终边相同的角有多 少个?这些角与-32°角在数量上相 差多少?
Office组件之word2007
1.1.1 任意角
知识探究(一):角的概念的推广
Office组件之word2007
复习:角的定义 角是由平面内一条射线绕其端点从
一个位置旋转到另一个位置所组成的 图形(如图).
B
始边
终边
A O
顶点
新课教学
Office组件之word2007
思考1:你认为将一条射线绕其端点按逆时针方向旋
高中数学人教版A版必修4《任意角的三角函数》优质PPT课件

第一章 三角函数
§1.2 任意角的三函数
明目标、知重点
内容 索引
01 明目标
知重点
填要点 记疑缺
04
明目标、知重点
明目标、知重点 1.通过借助单位圆理解并掌握任意角的三角函数定义, 了解三角函数是以实数为自变量的函数. 2.借助任意角的三角函数的定义理解并掌握正弦、余弦、 正切函数在各象限内的符号. 3.通过对任意角的三角函数定义的理解,掌握终边相同 角的同一三角函数值相等.
明目标、知重点
(2)sin(-1 320°)cos 1 110°+cos(-1 020°)sin 750°+tan 495°. 解 原式=sin(-4×360°+120°)cos(3×360°+30°)+ cos (-3×360°+60°)sin(2×360°+30°)+tan(360°+135°) =sin 120°cos 30°+cos 60°sin 30°+tan 135°
明目标、知重点
(2)cos α=xr(r>0),因此cos α的符号与x的符号相同,当α的终边 在第一、四象限时,cos α>0;当α的终边在第二、三象限时, cos α<0. (3)tan α=yx,因此tan α的符号由x、y确定,当α终边在第一、三 象限时,xy>0,tan α>0;当α终边在第二、四象限时,xy<0, tan α<0.
明目标、知重点
当堂测·查疑缺
1234
1.已知角α的终边经过点(-4,3),则cos α等于( D )
4
3
A.5
B.5
C.-35
D.-45
解析 因为角 α 的终边经过点(-4,3),所以 x=-4,y=3,r=5,
所以 cos α=xr=-45.
§1.2 任意角的三函数
明目标、知重点
内容 索引
01 明目标
知重点
填要点 记疑缺
04
明目标、知重点
明目标、知重点 1.通过借助单位圆理解并掌握任意角的三角函数定义, 了解三角函数是以实数为自变量的函数. 2.借助任意角的三角函数的定义理解并掌握正弦、余弦、 正切函数在各象限内的符号. 3.通过对任意角的三角函数定义的理解,掌握终边相同 角的同一三角函数值相等.
明目标、知重点
(2)sin(-1 320°)cos 1 110°+cos(-1 020°)sin 750°+tan 495°. 解 原式=sin(-4×360°+120°)cos(3×360°+30°)+ cos (-3×360°+60°)sin(2×360°+30°)+tan(360°+135°) =sin 120°cos 30°+cos 60°sin 30°+tan 135°
明目标、知重点
(2)cos α=xr(r>0),因此cos α的符号与x的符号相同,当α的终边 在第一、四象限时,cos α>0;当α的终边在第二、三象限时, cos α<0. (3)tan α=yx,因此tan α的符号由x、y确定,当α终边在第一、三 象限时,xy>0,tan α>0;当α终边在第二、四象限时,xy<0, tan α<0.
明目标、知重点
当堂测·查疑缺
1234
1.已知角α的终边经过点(-4,3),则cos α等于( D )
4
3
A.5
B.5
C.-35
D.-45
解析 因为角 α 的终边经过点(-4,3),所以 x=-4,y=3,r=5,
所以 cos α=xr=-45.
人教A版高中数学必修四任意角的三角函数教学PPT精品课件

概念拓展
课堂小结
类比
当r=1
情景《引三入角函数概》整念体复设习计 概念探究
【概念再探】
概念形成
概念应用
概念拓展
课堂小结
y
单位圆:
r=1
直角坐标系中,以原点为圆
O
x
心,以单位长为半径的圆。
情景《引三入角函数概》整念体复设习计 概念探究
【概念形成】
概念形成
概念应用
概念拓展
课堂小结
y
O
x
情景《引三入角函数概》整念体复设习计 概念探究
【概念复习】
概念形成
概念应用
概念拓展
课堂小结
直角三角形中 线段比
情景《引三入角函数概》整念体复设习计 概念探究
【概念初探】
概念形成
概念应用
概念拓展
课堂小结
y
y
O
x
线段比--坐标比
情景《引三入角函数概》整念体复设习计 概念探究
【探究发现】
概念形成
概念应用
概念拓展
课堂小结
类比
?
演示,观察 相应的坐标比值。
人教A版必修四第一章
《任意角的三角函数》
情景《引三入角函数概》整念体复设习计 概念探究 概念形成 概念应用 概念拓展 课堂小结
情景《引三入角函数概》整念体复设习计 概念探究 概念形成 概念应用 概念拓展 课堂小结 y
O r=1 P
x
〰〰〰 〰〰〰 〰〰〰 〰〰〰 〰〰〰 〰〰 〰〰 〰〰〰
情景《引三入角函数概》整念体复设习计 概念探究 概念形成 概念应用 概念拓展 课堂小结 y
情景《引三入角函数概》整念体复设习计 概念探究
【探究发现】
