重复测量、协方差、多变量描述
心理学统计第五部分重复测量方差分析

心理学统计第五部分重复测量方差分析在心理学研究中,有时候研究者需要评估一个或多个因素对参与者的多个测量结果的影响。
这种情况下,重复测量方差分析(Repeated Measures Analysis of Variance,简称为RM ANOVA)是一种常用的统计方法。
重复测量方差分析是一种比较多个组内变量平均数差异的方法,它比较了每个组内变量的差异以及每个组间变量的差异。
与传统的方差分析不同,重复测量方差分析考虑了相同参与者在不同条件下的多次测量结果,因此能够更准确地评估因素对测量结果的影响。
首先,我们需要明确的是,在重复测量方差分析中,我们的因变量是一个连续的测量结果,而自变量是一个或多个处理条件。
例如,我们可能想要评估一个新药物是否对人们的注意力产生影响,我们可以将注意力测量结果作为因变量,而药物与安慰剂作为自变量。
重复测量方差分析有三个基本的假设。
首先,我们假设不同处理条件下的测量结果的总平均数相等,即每组的平均值相等。
其次,我们假设各个处理条件下的测量结果有一定的方差。
最后,我们假设不同处理条件下的测量结果相互独立。
重复测量方差分析有一些优点和注意事项。
首先,这种方法可以减少误差变异,因为我们可以通过比较同一参与者在不同条件下的测量结果来消除参与者间的差异。
其次,重复测量方差分析可以提高统计功效,以便检测到小的差异。
然而,我们需要注意确保多次测量结果之间的独立性,以及在数据分析中正确处理可能的违反方差齐性和正态分布的情况。
总结起来,重复测量方差分析是一种常用的心理学统计方法,用于评估一个或多个因素对参与者的多个测量结果的影响。
它是一种有效的方法,可以提供关于不同处理条件之间差异的信息。
在分析数据时,我们需要检查数据的正态性和方差齐性,并使用适当的修正方法来应对违反这些假设的情况。
重复测量方差分析为心理学研究提供了一个强有力的统计工具,使得研究者能够更好地理解和解释影响行为和心理过程的因素。
重复测量设计资料的方差分析SPSS操作

重复测量设计资料的方差分析SPSS操作重复测量方差分析的基本概述:被试对象在接受不同处理后,对同一因变量(测试指标)在不同时点上进行多次测量所得的资料,称为重复测量资料。
这里的重复并不是单一的反复,而是在多个时点上的测量。
这种资料的特点是其定量观测指标的数值会随着时间的变化而发生动态变化,并且各时点上的数值是不满足相互独立的假设的。
因此不能用方差分析的方法直接进行处理。
如果在期初、期中、期末分别测量学生的电脑能力,则这是单变量重复测量问题。
如果分别在三个时期测量学生的电脑和数学成绩,则是多变量重复测量的问题。
重复测量资料的方差分析需满足的前提条件:1、一般方差分析的正态性和方差齐性检验。
2、协方差矩阵的球形对称性或者复合对称性;需要进行球形检验,检验对称性。
原假设:协方差满足球形对称。
当拒绝球形假设时,结果中还有其他表可以检验,见例题中的分析。
被试对象处理测量时间1 2 3 4…………m1 1 ………………………………………….2 1 ………………………………………….. ………………………………………………………………………………………………………….N1 1 …………………………………………..N1+1 2 …………………………………………. …………………………………………………………………………………………………………N2 2 …………………………………………………….例:为研究新减肥药和现有减肥药的效果是否不同,以及肥胖者在服药后不同时间体重的变化情况,将40名体重指标BMIF27的肥胖者随机分为两组,一组用新药,另一组用现有减肥药;坚持服药6个月,期间禁止使用任何影响体重的药物,而且被试对象行为、饮食、运动与服药前平衡期保持一致;分别测得0周、8周、16周、24周的体重资料;试对其进行方差分析。
Spss数据格式片段如下:1、正态性和方差齐性检验对4个不同时点上的体重变量进行检验使用科莫格洛夫—斯米诺夫检验只要16周第二种处理不显著,其他都显著不为0.可认为正态性假设基本成立。
重复测量数据的统计方法

重复测量数据的统计方法重复测量数据的统计方法是指对同一变量进行多次测量所得到的数据进行分析和统计的方法。
在科学研究、生产实践和社会调查中,常常需要对同一指标进行多次观测,例如实验重复测量、调查问卷中多次回答同一个问题等。
重复测量数据的统计方法可以帮助研究者更准确地估计数据的平均值、方差和其他统计指标,从而提高数据分析的可靠性和科学性。
在进行重复测量数据的统计分析时,常用的方法包括重复测量方差分析、重复测量t检验、可重复性分析和相关性分析等。
下面将分别对这些方法进行详细介绍。
首先,重复测量方差分析(Repeated measures analysis of variance,简称RM-ANOVA)是一种常用的分析重复测量数据的方法。
它通过对多个测量间的变异进行分析,判断测量效应是否显著。
RM-ANOVA 通常分为单因素重复测量方差分析和多因素重复测量方差分析两种。
在进行RM-ANOVA分析时,需要对数据的正态性进行检验,并对数据进行变换或采用非参数方法进行分析。
此外,RM-ANOVA还可用于分析数据的交互作用,即测量效应是否受到其他因素的影响。
其次,重复测量t检验(Repeated measures t-test)是一种用于比较两个或多个相关样本均值是否存在显著差异的统计方法。
它适用于重复测量数据且样本数较小的情况。
重复测量t检验的原理是对多次测量的差值进行统计分析,并与一个已知平均差异的理论值进行比较。
通过比较差异的大小和统计显著性水平,来判断差异是否真实存在。
第三,可重复性分析(Intraclass correlation coefficient,简称ICC)是一种用来评估重复测量数据可靠性和一致性的方法。
ICC通常通过计算同一个变量在不同测量间的相关性来评估数据的可重复性。
ICC的值介于0和1之间,数值越接近1说明数据的可靠性越高。
可重复性分析可用于评估测量工具的稳定性、不同测量者之间的一致性以及相同测量者在不同时间点的一致性等。
重复测量方差分析

重复测量方差分析1.理论重复测量:指对同一批研究对象先后施加不同的实验(或在不同的场合)进行测量。
重复测量方差分析:研究在不同的实验或(不同场合)之间是否有差异,或条件和处理间交互项是否有差异。
变量应满足:因变量为连续型随机变量,因素为分类变量。
正态性:不同条件下的个体取自相互独立的随机样本,其总体需满足近似正态分布。
方差齐性:不同条件下的总体方差相等。
满足球形假设:因变量的方差-协方差矩阵满足球形交互项项两两比较结果需要借助语法。
图1交互项两两比较语法2.重复测量方差分析操作步骤操作步骤第一步:首先将数据导入spss中并进行赋值,后点击分析、一般线性模型、重复测量。
图2重复测量方差分析操作步骤第一步操作步骤第二步:进入图中对话框后首先定义主体因子名及实验次数点击添加,后添加测量名称(先在测量名称框中输入名称、后点击添加)点击定义。
图3定义因子操作步骤第三步:定义完成后进入图中对话框后、先将对应的变量放入对应的变量框中,点击事后比较将因子框内的因子放入事后比较框中,勾选假定等方差(LSD)、不假定等方差(塔姆黑尼),点击继续。
图4事后比较勾选操作步骤第四步:点击选项将因子框中的因子放入平均值框中,勾选描述统计、齐性检验,点击继续、确定。
图5选项勾选然后重复测量方差分析的主体间因子、描述统计、等同性检验、主体内效应检验、主体因子事后比较结果就出来了。
图6描述统计结果图7主体内效应操作步骤第一步:点击分析、一般线性模型、重复测量。
图8操作步骤第一步第二步:点击定义。
图9点击定义第三步:进入图中对话框后,点击粘贴。
图10点击粘贴第四步:进入语法编辑窗:在红色框内放入对应的语法(可参考图中语法进行编辑),后选中语法点击红色框内的绿色箭头。
图11语法编写5.交互项结果然后重复测量方差分析的主体因子和因子交互项的主体内因子、主体间因子、描述统计、博克斯等同性酱油结果就出来了。
图12描述统计主体内效应检验、主体内对比检验、误差方差的莱文等同性检验。
SPSS多因素方差分析(一般线性模型):重复测量

SPSS多因素⽅差分析(⼀般线性模型):重复测量⼀、GLM重复测量(分析-⼀般线性模型-重复度量)1、概念:“GLM 重复测量”过程在对每个主体或个案多次执⾏相同的测量时提供⽅差分析。
如果指定了主体间因⼦,这些因⼦会将总体划分成组。
通过使⽤此⼀般线性模型过程您可以检验关于主体间因⼦和主体内因⼦的效应的原假设。
可以调查因⼦之间的交互以及单个因⼦的效应。
另外,还可以包含常数协变量的效应以及协变量与主体间因⼦的交互。
在双重多变量重复测量设计中,因变量表⽰主体内因⼦不同⽔平的多个变量的测量。
例如,您可能在三个不同的时间对每个主体同时测量了脉搏和呼吸。
“GLM 重复测量”过程提供了对重复测量数据的单变量和多变量分析。
平衡与⾮平衡模型均可进⾏检验。
如果模型中的每个单元包含相同的个案数,则设计是平衡的。
在多变量模型中,模型中的效应引起的平⽅和以及误差平⽅和以矩阵形式表⽰,⽽不是以单变量分析中的标量形式表⽰。
这些矩阵称为SSCP(平⽅和与叉积)矩阵。
除了检验假设,“GLM 重复测量”过程还⽣成参数估计。
常⽤的先验对⽐可⽤于对主体间因⼦执⾏假设检验。
另外,在整体的F 检验已显⽰显著性之后,可以使⽤两两⽐较检验评估指定均值之间的差值。
估计边际均值为模型中的单元提供了预测均值估计值,且这些均值的轮廓图(交互图)允许您轻松对其中⼀些关系进⾏可视化。
残差、预测值、Cook 距离以及杠杆值可以另存为数据⽂件中检查假设的新变量。
另外还提供残差SSCP 矩阵(残差的平⽅和与叉积的⽅形矩阵)、残差协⽅差矩阵(残差SSCP 矩阵除以残差的⾃由度)和残差相关矩阵(残差协⽅差矩阵的标准化形式)。
WLS 权重允许您指定⼀个变量,⽤来针对加权最⼩平⽅(WLS) 分析为观察值赋予不同权重,这样也许可以补偿测量的不同精确度。
2、⽰例。
根据学⽣的焦虑程度检验的得分将⼗⼆个学⽣分配到⾼或低焦虑程度组。
焦虑等级被认为是主体间因⼦,因为它会将主体划分成组。
第三讲重复测量资料的方差分析
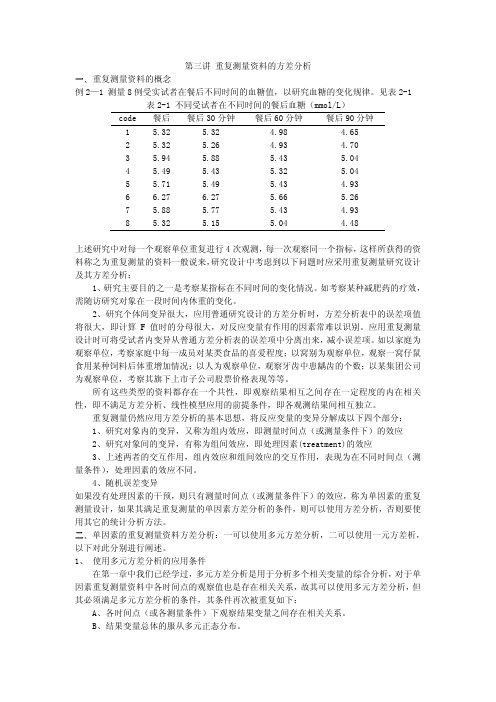
第三讲 重复测量资料的方差分析一、重复测量资料的概念例2—1 测量8例受实试者在餐后不同时间的血糖值,以研究血糖的变化规律。
见表2-1 表2-1 不同受试者在不同时间的餐后血糖(mmol/L)code 餐后 餐后30分钟 餐后60分钟 餐后90分钟1 5.32 5.32 4.98 4.652 5.32 5.26 4.93 4.703 5.94 5.88 5.43 5.044 5.49 5.43 5.32 5.045 5.71 5.49 5.43 4.936 6.27 6.27 5.66 5.267 5.88 5.77 5.43 4.938 5.32 5.15 5.04 4.48上述研究中对每一个观察单位重复进行4次观测,每一次观察同一个指标,这样所获得的资料称之为重复测量的资料一般说来,研究设计中考虑到以下问题时应采用重复测量研究设计及其方差分析:1、研究主要目的之一是考察某指标在不同时间的变化情况。
如考察某种减肥药的疗效,需随访研究对象在一段时间内休重的变化。
2、研究个体间变异很大,应用普通研究设计的方差分析时,方差分析表中的误差项值将很大,即计算F值时的分母很大,对反应变量有作用的因素常难以识别。
应用重复测量设计时可将受试者内变异从普通方差分析表的误差项中分离出来,减小误差项。
如以家庭为观察单位,考察家庭中每一成员对某类食品的喜爱程度;以窝别为观察单位,观察一窝仔鼠食用某种饲料后体重增加情况;以人为观察单位,观察牙齿中患龋齿的个数;以某集团公司为观察单位,考察其旗下上市子公司股票价格表现等等。
所有这些类型的资料都存在一个共性,即观察结果相互之间存在一定程度的内在相关性,即不满足方差分析、线性模型应用的前提条件,即各观测结果间相互独立。
重复测量仍然应用方差分析的基本思想,将反应变量的变异分解成以下四个部分:1、研究对象内的变异,又称为组内效应,即测量时间点(或测量条件下)的效应2、研究对象间的变异,有称为组间效应,即处理因素(treatment)的效应3、上述两者的交互作用,组内效应和组间效应的交互作用,表现为在不同时间点(测量条件),处理因素的效应不同。
多元方差分析与重复测量方差分析

多元方差分析与重复测量方差分析多元方差分析(MANOVA)是一种多变量分析方法,它将多个因变量同时考虑在内,通过比较组别之间的多个平均值来进行分析。
多元方差分析的核心思想是基于协方差矩阵的比较,通过检验各个组别的协方差矩阵是否相等来判断组别之间的差异是否显著。
多元方差分析可以同时比较多个因变量之间的差异,从而避免了多次进行单变量方差分析可能带来的问题。
重复测量方差分析(Repeated Measures ANOVA)也是一种常用的分析方法,主要用于分析同一组个体在不同时间点或不同实验条件下的多次测量结果之间的差异。
重复测量方差分析通常包括对同一组个体在不同时间点或实验条件下的多次测量结果进行统计分析,以比较各个时间点或实验条件之间的平均差异是否显著。
它通过考虑同一组个体之间的相关性,来提高统计分析的效果。
与多元方差分析不同,重复测量方差分析主要关注不同时间点或不同实验条件下的变化趋势和差异,而不是直接比较组别之间的差异。
重复测量方差分析可以用于研究个体在一段时间内的发展趋势,或在不同实验条件下的变化情况,从而揭示出时间和实验因素对变量的影响。
数据结构方面,多元方差分析通常要求每个组别有多个观测值,每个观测值都对应于多个因变量的取值。
而重复测量方差分析要求在相同的个体或实验单位上进行多次测量,并将多次测量结果作为相同个体或实验单位的多个观测值。
分析方法方面,多元方差分析主要依赖协方差矩阵的比较来进行统计推断。
而重复测量方差分析通常使用协方差矩阵的分解来提取主要成分,并通过分析主要成分之间的差异来进行统计推断。
综上所述,多元方差分析和重复测量方差分析是两种常用的统计分析方法,它们在数据结构和分析方法上存在一些差异。
多元方差分析主要用于比较不同组别之间的平均差异,而重复测量方差分析主要用于分析同一组个体在不同时间点或实验条件下的多次测量结果之间的差异。
选择合适的方法需要根据具体问题和数据特点来决定。
以上就是对多元方差分析与重复测量方差分析的详细介绍。
关于重复测量方差分析的理论介绍

关于重复测量方差分析的理论介绍发表时间:2018-02-07T10:33:40.283Z 来源:《心理医生》2017年36期作者:魏雨晨[导读] 重复测量方差分析是方差分析的一种,因此,我将先介绍方差分析。
(闽南师范大学教育科学学院福建漳州 363000)【摘要】重复测量方差分析是方差分析的一种。
本文将先介绍方差分析的基本概念、结构、适用范围、事后比较的方法。
然后引入重复测量方差分析的概念,介绍它的主要优点,需要满足的假设条件,以及它的缺点和改进方法。
【关键词】重复测量方差分析;球形假设;事后比较【中图分类号】R181.3 【文献标识码】A 【文章编号】1007-8231(2017)36-0294-031.概述重复测量方差分析是方差分析的一种,因此,我将先介绍方差分析。
方差分析所研究的是自变量与因变量之间的关系,它和回归分析类似。
两者的因变量常取为属量变量。
而回归分析与方差分析的主要不同在,前者的自变量常取为属量变量,而且需要实现假设自变量与因变量的关系为直线或曲线等函数。
方差分析则无上二项条件。
因此,相对而言,方差分析的应用范围更广更大,而成为资料分析时不可或缺的工具。
我们知道方差分析是t检验的扩展。
t检验用于两个样本或两种条件实验的情况。
而方差分析适用于两个及以上样本或条件的情况。
当样本或条件为两个时,方差分析和t检验的结果相同。
但是当多于两个时,方差分析优于t检验。
其中涉及到I型错误。
当α设定在0.05水平时,实际上是说,拒绝虚无假设意味要冒5%的错误风险。
在仅有两组的实验中,只需计算一次t值。
换句话说,就是我们随机从t分布中抽取一个t值,它大于或等于临界值的概率为0.05。
当实验涉及多次t比较时,那就不是从t分布中取一个t值,而是20个。
这样得到大于或等于临界值的t值的概率就会增加。
犯I型错误的概率会因为多次比较而增加。
方差分析是一种分析多组实验的统计方法。
运用F检验可进行整体的比较,它可辨别各组平均数是否有显著差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
值进行校正。
注意事项
各组例数相等;
“球对称”检验:如果不满足“球对称”假
设,需用“球对称”悉数对自由度进行校正;
无平行对照的单组重复测量数据分析:如果
满足“球对称”假设,重复测量数据的方差
分析和随机区组方差分析等价。
重复测量数据统计分析常见的误用情况
重复进行各时间点的t检验,必然增加假阳性
重复测量设计和随机区组设计的区别:
1、重复测量设计各时间点是固定的,不能随机分 配,而随机区组设计各组接受的处理可随机分配;
2、重复测量设计各时间点的观察结果有相关关系, 分析各时间点的差异需满足“球对称”,而随机区 组设计各处理组间的观察结果彼此独立,各处理间 比较无需满足“球对称”。
表12-3 不同放置时间后受试者血糖浓度(mmol/L) 受试者 编号
第十二章 重复测量设计的方差分析
第一节 重复测量资料的数据特征 (repeated measurement data)
表12-1 高血压患者治疗前后的舒张压(mmHg) 编号
1 2
治疗前
130 124
治疗后
114 110
差值
16 14
……
9
……
126
……
108
……
18
10
124
106
18
前后测量设计和配对设计
F
总
处理 区组
误差 处理+误差 修正均数
表13-7 随机区组设计资料的协方差分析计算表模式 (右半部分)
变异来源 处理+误差 修正均数 误差
估计误差
自由度 残差平方和 23 2 21 2225.36 463.95 2689.31 231.98 105.97 MS
F
P
2.19 >0.05
结论:在扣除进食量因素的影响后,三组大
A饲料 X1 15 13 …… 14 17 Y1 85 83 …… 84 90 X2 17 16 …… 19 18 B饲料 Y2 97 90 …… 99 94 C饲料 X3 22 24 …… 30 32 Y3 89 91 …… 105 110
协方差分析的基本思想
将线性回归分析与方差分析结合起来的一种
表12-9 不考虑组别的SS分解
变异来源 总 自由度 4n-1 离均差平方和(SS)
SS总 = X C
2
组间(观察对象)
组内(重复测量)
2n-1
2n
1 M2 j C 2 1 SS组内 X 2 M 2 j 2 SS组间
表中n为每个处理组中观察对象的例数,X为 每个观察结果,M为每个观察对象前后两次 观察的合计,C为校正系数。
N-G-1
SSa=SST-SSE
SS E
2 ˆ (Y j Y j )
MSa
MSE
MSa/MSE
表13-5 完全随机设计资料的协方差分析计算表模式 (右半部分)
变异来源 总 修正均数 组内(误差)
估计误差
自由度 残差平方和 22 2 20 934.84 707.20 227.64 MS
配对设计可随机分配同一对子的试验单位,
前后测量设计不能同期观察试验结果;
配对设计比较两种处理的差别,前后测量设
计比较某种处理前后的差别;
前后测量设计假定测量时间对观察结果没有
影响。
前后测量设计和配对设计
配对设计要求每组观察结果和差值相互独立,
且服从正态分布,前后测量设计差值通常与
前一次观察存在相关关系;
白鼠的总体增重均数差异无统计学意义。
第十四章
多变量数据的
统计描述和统计推断
表14-1 15名正常成年男子的血脂含量
序号
1 2 ……
甘油三酯
1.06 0.98 ……
总胆固醇
2.56 2.42 ……
高密度脂蛋白
1.93 1.80 ……
15 均数
标准差
1.03 1.020
0.0058
3.25 2.729
多组比较
重复测量资料的多变量分析 轮廓分析
各组协变量与观察指标存在线性回归关系;
各组回归方程的斜率相同(回归线平行);
协变量的要求
连续性变量;
不能影响处理因素;
协变量的取值应在施加处理因素前已获得;
如果协变量的取值是在施加处理因素后,应
不受处理因素的影响。
修正均数
实际上修正均数是协变量取值固定在其总均
数时观察指标的均数;
… S1m … S2 m 1 S jk l jk … … n 1 … S mm
相关矩阵
由多个任意两个变量的相关系数构成的矩阵。
r11 r R 21 … rm1
r1m r22 … r2 m r jk … … … rm 2 … rmm r12 …
表12-8 考虑干预和时间因素的SS分解
变异来源 处理组间 干预(A) 时间(B)
AB交互作用
自由度 离均差平方和(SS) 3 1 1
1
SS处理 1 2 (T1 T22 T32 T42 )-C n
SS A
SS B
1 2 2 (A1 A2 )-C 2n
1 2 2 (B1 B2 )-C 2n
统计方法;
将未加或难以控制的因素(混杂因素)对观
察指标的影响看作是协变量;
建立协变量与应变量之间的线性回归关系;
将协变量的值化为相等;
对观察指标的修正均数进行比较。
协方差分析的应用条件
各组观察指标服从正态分布;
各组观察指标彼此独立;
各组观察指标的总体方差相同(方差齐性);
SS AB SS处理 SS A SSB
表中n为各组的例数,I为A因素的水平数,J为B因素的水平数, A为A因素不同水平的合计数,B为B因素不同水平的合计数, C为校正悉数。
表12-10 重复测量设计两因素两水平的方差分析表
变异来源
组间(对象)
自由度
2n-1
SS
SS组间
MS
F
干预(A)
组间误差 组内(重复) 时间(B) AB交互作用 组内误差
结论
经对修正均数的多重比较的结果显示,服用
A饲料后猪增重的修正均数(94.95)与服用B饲
料后的修正均数(99.50)的差别无统计学意义,
但都高于服用C饲料的修正均数(82.18)。
第三节 随机区组设计资料的 协方差分析
表13-6 三组大白鼠的进食量与增重
区组 1 2 A组 X1 256.9 271.6 Y1 27.0 41.7 X2 260.3 271.1 B组 Y2 32.0 47.1 X3 544.7 481.2 C组 Y3 160.3 96.1
<0.01 <0.01
结论
不同处理对高血压患者的舒张压没有影响;
测量前后舒张压有改变;
测量前后与处理组间有交互作用,说明处理
组和对照组治疗前后的舒张压变化不同。两
组治疗后的差别大于治疗前的差别,说明治
疗有效。
重复测量数据的两因素多水平分析
方差分析的方法与两因素两水平的相似;
如果拒绝“球对称”,需对FB和FAB检验界
修正均数只是用来比较时用的,其本身没有
实际意义;
协变量均数间的差别应进行假设检验; 协方差分析对协变量均数差别不大的资料检
验效果较好。
第二节
完全随机设计资料的 协方差分析
表13-2 完全随机设计资料的协方差分析计算表模式
离均差平方和及积和 自由度 lXX lXY lYY 自由度 残差平方和 MS 估计误差 F
变异 来源
总
组间
组内
修正 均数
表13-3 完全随机设计资料的协方差分析计算表模式 (左半部分)
离均差平方和及积和
变异 来源
自由 度
lXX
∑X2-CX
∑((∑Xj)2/nj)-CX ∑X2- ∑(∑Xj)2/nj
lXY
∑Y2-CY
Σ((∑Yj)2/nj)-CY ∑Y2- ∑(∑Yj)2/nj
lYY
∑XY-CXY
∑((∑Xj)(∑Yj)/nj)-CXY ∑XY-∑((∑Xj)(∑Yj)/nj)
总
组间 组内
N-1
G-1 N -G
表13-3 完全随机设计资料的协方差分析计算表模式 (右半部分)
估计误差
变异来源
自由度 总 N-2 残差平方和
2 ˆ SST = (Y Y )
MS
F
修正均数
组内(误差)
G-3
F
P
353.60 31.07 <0.01 11.38
结论:在扣除初始体重因素的影响后,三组
猪的总体增重均数差异有统计学意义。
修正均数的计算
Y Yj bc ( X j X )
* j
组内l XY bc 组内l XX
修正均数的多重比较:q检验
q | YA* YB* | SY X 组间l XX [1 ] n0 (a 1)组间l XX
l12 … l1m n l22 … l2 m l jk ( X ij X j )( X ik X k ) … … … i 1 lm 2 … lmm
协方差矩阵
由多个任意两个变量的协方差构成的矩阵。
S11 S 21 S … S m1
S12 S 22 … Sm 2
1 2 …… 7 8 放置时间(分) 0 5.32 5.32 …… 5.88 5.32 45 5.32 5.26 …… 5.77 5.15 90 4.98 4.93 …… 5.43 5.04 135 4.65 4.70 …… 4.93 4.48
