重庆市永川中学高中数学第18周练习一(立体几何1)
重庆市永川中学校2023-2024学年高一下学期6月月考数学试题

重庆市永川中学校2023-2024学年高一下学期6月月考数学试题一、单选题1.复数()i 3i z =+在复平面内对应的点所在的象限为( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知向量()1,1a =-r ,()2,1b =r ,()2,c λ=r .若()2c a b +∥r r r ,则λ=( ) A .12- B .0 C .12 D .83.设a 、b 是不同的两条直线,α、β是不同的两个平面,下列说法正确的有( ) A .a α⊥,b β⊂,,⊥a b 则αβ⊥B .α//β,a α⊥,b //β,则a b ⊥r rC .,,a b αβ⊂⊂且//,//,a b βα则//αβD .//,//,a b a β则b β//4.直三棱柱111ABC A B C -中,若90BAC ∠=︒,1AB AC AA ==,则异面直线1BA 与1AC 所成的角等于A .30°B .45°C .60°D .90°5.已知四边形ABCD 是矩形,||4AB =u u u r ,||3BC =u u u r ,则CA DB ⋅=u u u r u u u r ( )A .25B .-7C .7D .-25 6.某居民小区户主人数和户主对住房户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用比例分配的分层随机抽样方法抽取25%的户主作为样本进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )A .400,32B .400,36C .480,32D .480,367.已知圆台上、下底面半径分别为1,2,侧面积为6π,则这个圆台的体积为( )A B . C D 8.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c .已知3B π=,8a =,cos cos 6b A a B +=,点O 是ABC V 的外心,若BO xBA yBC =+u u u r u u u r u u u r ,则x y +=( )A .712B .2336C .2536D .2936二、多选题9.已知平面向量()0,1a =r ,()b =r ,则下列说法正确的有( ) A .7a b +=r rB .()()30a b a b +⋅-=-r r r rC .向量a b +r r 在a r 上的投影向量为D .向量a b +r r 与a r 的夹角为3π10.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知2b =,ABC S =V cos cos 2cos 0c B b C a A +-=,则有( )A .a =B .2C π= C .3A π= D .2c =11.如图,直四棱柱1111ABCD A B C D -的底面是梯形,AB CD ∥,AD DC ⊥,4BC CD ==,12DD AB ==,P 是棱1CC 的中点.Q 是棱11C D 上一动点(不包含端点),则( )A . AC 与平面BPQ 有可能平行B .11B D 与平面BPQ 有可能平行C .三角形BPQD .三棱锥A BPQ -的体积为定值三、填空题12.一组数据按从小到大的顺序排列为1,2,2,x ,5,10,其中5x ≠,已知该组数据的中位数是众数的32倍,则该组数据的标准差为. 13.已知ABC V 的内角,,A B C 所对的边分别,,a b c ,角π=3A .若AM 是CAB ∠的平分线,交BC 于M ,且3AM =,则+2AB AC 的最小值为. 14.在三棱锥S ABC -中,底面ABC 为边长为3的正三角形,侧棱SA ⊥底面ABC ,若三棱锥的外接球的体积为36π,则该三棱锥的体积为.四、解答题15.在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c .已知222sin sin sin sin sin A C A C B +=+.(1)求角B 的大小;(2)若b =ABC V ABC V 的周长. 16.2022年4月16日,神舟13号载人飞船返回舱在东风着陆场成功着陆,这趟神奇之旅意义非凡,尤其是“天宫课堂”在广大学生心中引起强烈反响,激起了他们对太空知识的浓厚兴趣.某中学在进行太空知识讲座后,从全校学生中随机抽取了200名学生进行笔试(试卷满分100分),并记录下他们的成绩,将数据分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],并整理得到如下频率分布直方图.(1)求这部分学生成绩的中位数、平均数(同组数据用该组区间的中点值作代表);(2)为了更好的了解学生对太空知识的掌握情况,学校决定在成绩高的第4、5组中用分层抽样的方法抽取6名学生,进行第二轮面试,最终从这6名学生中随机抽取2人参加市太空知识竞赛,求90分(包括90分)以上的同学恰有1人被抽到的概率.17.已知四棱锥P ABCD -满足:四边形ABCD 为正方形,△P AD 为等边三角形,且平面P AD ⊥平面ABCD ,2AD =,E 为P A 的中点.(1)证明:PC ∥平面BDE ;(2)求直线PC 和平面ABCD 所成角的正切值.18.如图,在四棱锥-P ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为菱形,60ADC ∠=︒,4PA AD ==,E 为AD 的中点.(1)求证:平面PCE ⊥平面PAD ;(2)求二面角A PD C --的平面角的正弦值.19.由于某地连晴高温,森林防灭火形势严峻,某部门安排了甲、乙两名森林防火护林员对该区域开展巡查.现甲、乙两名森林防火护林员同时从A 地出发,乙沿着正西方向巡视走了3km 后到达D 点,甲向正南方向巡视若干公里后到达B 点,又沿着南偏西60°的方向巡视走到了C 点,经过测量发现60ACD ∠=︒.设ACB θ∠=,如图所示.(1)设甲护林员巡视走过的路程为S AB BC=+,请用θ表示S,并求S的最大值;△区域范围内储备应急物资,求(2)为了强化应急应战准备工作,有关部门决定在BCD△区域面积的最大值.BCD。
重庆一中高2018级高一(下)第一次周考数学试卷(精品)

高2018级高一(下)第一次周考数学试卷班级: 姓名: 2016.2.28一、选择题:(本大题12个小题,每小题5分,共60分)在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合{}{}224,log 0x A x B x x =≤=>,则A B ⋂=( )A 、[]1,2B 、(]1,2C 、()0,1D 、(]0,1 2、已知扇形的中心角为3π,半径为2,则其面积为( ) A .6π B .34π C .3π D .32π 3、 585sin 的值为( )A .22-B .22C .23-D .234、下列说法正确的是( )A.若向量a b 与同向,且a b > ,则a b >B.若,//,a b b c //则a c //C.单位向量都是共线向量D.单位向量的模都相等5、三个数2)3.0(=a ,3.0log 2=b ,3.02=c 之间的大小关系是( )A .b c a <<B .c b a <<C .c a b <<D .a c b <<6、已知函数()1254x f x x =+-,则()f x 的零点所在的区间为( ) A 、()0,1 B 、()1,2C 、()2,3D 、()3,4 7、要得到函数x y cos =的图象,只需要将函数)32sin(π+=x y 图像上的所有点( ) A.先向左平移6π个单位长度,再把横坐标伸长到原来的2倍(纵坐标不变), B.先向左平移12π个单位长度,再把横坐标缩短到原来的21(纵坐标不变), C.横坐标伸长到原来的2倍(纵坐标不变),再向左平移6π个单位长度D.横坐标伸长到原来的2倍(纵坐标不变),再向左平移3π个单位长度 8、已知函数)sin(2ϕω+=x y (2,0πϕω<>)的部分图象如图所示,则此函数的解析式为( )A.)62sin(2π-x B .)44sin(2π+x C .)62sin(2π+x D .)64sin(2π+x9、已知定义在R 上的奇函数()f x 满足()()4f x f x +=恒成立,且()11f =,()()()201620172018f f f ++的值为( )A 、0B 、1C 、2D 、310、)120tan 3(10cos 70tan - 等于( )A .1B .2C .﹣1D .﹣2 11、已知关于x 的方程01242=-+⋅+m m x x 有实根,则实数m 的取值范围是( )A .⎥⎦⎤⎢⎣⎡-332,332 B.⎪⎪⎭⎫⎢⎣⎡-1,332 C .⎥⎦⎤⎢⎣⎡-1,332 D .⎥⎦⎤⎢⎣⎡332,1 12、已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的解1x 、2x 、3x 、4x ,且1234x x x x <<<,则()3122341x x x x x ++的取值范围为( ) A 、()1,-+∞ B 、(]1,1- C 、(),1-∞ D 、[)1,1-二、填空题:(本大题4个小题,每小题5分,共20分)13、函数3)4lg(--=x x y 的定义域是 14、化简:=++++AF BC FD CA DB15、当[)π2,0∈t 时,函数)cos 1)(sin 1()(t t t f ++=的最大值为16、已知函数)(x f y =对任意的R x ∈,都有0)1()5(=-++x f x f ,若方程0)(=x f 有且仅有7个不同的实数解,则这7个实数解之和为三、解答题:(本大题6个小题,共70分)(必须写出必要的文字说明、演算步骤或推理过程).17、(1)求值:06.0lg 61lg )01.0()412(25325.02120++-⋅+⎪⎭⎫ ⎝⎛-- (2)已知⎪⎭⎫ ⎝⎛∈⎪⎭⎫ ⎝⎛∈=+=ππβπαβαα,2,2,0,31)sin(,322cos ,求βcos 的值.18、设集合{}{}222|40,|2(1)10A x x x B x x a x a =+==+++-=.(1)求集合A ;(2)若= A B A ,求a 的取值范围。
重庆市第一中学新高中数学立体几何多选题专题复习含解析
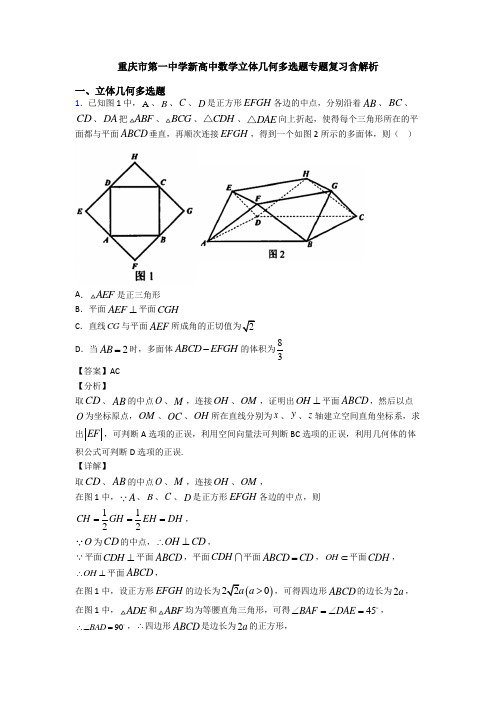
重庆市第一中学新高中数学立体几何多选题专题复习含解析一、立体几何多选题1.已知图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起,使得每个三角形所在的平面都与平面ABCD 垂直,再顺次连接EFGH ,得到一个如图2所示的多面体,则( )A .AEF 是正三角形B .平面AEF ⊥平面CGHC .直线CG 与平面AEF 2D .当2AB =时,多面体ABCD EFGH -的体积为83 【答案】AC【分析】取CD 、AB 的中点O 、M ,连接OH 、OM ,证明出OH ⊥平面ABCD ,然后以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,求出EF ,可判断A 选项的正误,利用空间向量法可判断BC 选项的正误,利用几何体的体积公式可判断D 选项的正误.【详解】取CD 、AB 的中点O 、M ,连接OH 、OM ,在图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,则1122CH GH EH DH ===, O 为CD 的中点,OH CD ∴⊥,平面CDH ⊥平面ABCD ,平面CDH平面ABCD CD =,OH ⊂平面CDH ,OH ∴⊥平面ABCD , 在图1中,设正方形EFGH 的边长为()220a a >,可得四边形ABCD 的边长为2a , 在图1中,ADE 和ABF 均为等腰直角三角形,可得45BAF DAE ∠=∠=, 90BAD ∴∠=,∴四边形ABCD 是边长为2a 的正方形,O 、M 分别为CD 、AB 的中点,则//OC BM 且OC BM =,且90OCB ∠=, 所以,四边形OCBM 为矩形,所以,OM CD ⊥,以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项,由空间中两点间的距离公式可得2AE AF EF a ===, 所以,AEF 是正三角形,A 选项正确;对于B 选项,设平面AEF 的法向量为()111,,m x y z =,(),0,AE a a =-,()0,,AF a a =,由111100m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩,取11z =,则11x =,11y =-,则()1,1,1m =-, 设平面CGH 的法向量为()222,,n x y z =,(),0,CG a a =,()0,,CH a a =-, 由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩,取21z =-,可得21x =,21y =-,则()1,1,1n =--, ()22111110m n ⋅=+--⨯=≠,所以,平面AEF 与平面CGH 不垂直,B 选项错误;对于C 选项,6cos ,23CG mCG m a CG m ⋅<>===⨯⋅, 设直线CG 与平面AEF 所成角为θ,则sin 6θ=,23cos 1sin θθ=-=, 所以,sin tan 2cos θθθ==,C 选项正确; 对于D 选项,以ABCD 为底面,以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -,则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点,因为2AB =,即1a =,则1OH =,长方体1111ABCD A B C D -的体积为2214V =⨯=,11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△, 因此,多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=, D 选项错误.故选:AC.【点睛】方法点睛:计算线面角,一般有如下几种方法:(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin h lθ=(l 为斜线段长),进而可求得线面角; (3)建立空间直角坐标系,利用向量法求解,设a 为直线l 的方向向量,n 为平面的法向量,则线面角θ的正弦值为sin cos ,a n θ=<>.2.如图所示,正三角形ABC 中,D ,E 分别为边AB ,AC 的中点,其中AB =8,把△ADE 沿着DE 翻折至A 'DE 位置,使得二面角A '-DE -B 为60°,则下列选项中正确的是( )A .点A '到平面BCED 的距离为3B .直线A 'D 与直线CE 所成的角的余弦值为58 C .A 'D ⊥BDD .四棱锥A '-BCED 237【答案】ABD【分析】作AM ⊥DE ,交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .利用线面垂直的判定定理判定CD ⊥平面A'MN ,利用面面垂直的判定定理与性质定理得到'A 到平面面BCED 的高A'H ,并根据二面角的平面角,在直角三角形中计算求得A'H 的值,从而判定A;根据异面直线所成角的定义找到∠A'DN 就是直线A'D 与CE 所成的角,利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N ,在利用外接球的球心的性质进行得到四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,经过计算求解可得半径从而判定D.【详解】如图所示,作AM ⊥DE ,交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .则A'M ⊥DE ,MN ⊥DE , ,∵'A M ∩MN =M ,∴CD ⊥平面A'MN ,又∵CD ⊂平面ABDC ,∴平面A'MN ⊥平面ABDC ,在平面A'MN 中作A'H ⊥MN ,则A'H ⊥平面BCED ,∵二面角A'-DE -B 为60°,∴∠A'EF =60°,∵正三角形ABC 中,AB =8,∴AN =∴A'M ,∴A'H =A'M sin60°=3,故A 正确; 连接DN ,易得DN ‖EC ,DN =EC =4,∠A'DN 就是直线A'D 与CE 所成的角,DN =DA'=4,A'N =A'M ,cos ∠A'DN =22441252448+-=⨯⨯,故B 正确;A'D =DB =4,==,∴222A D DB A B '≠'+,∴A'D 与BD 不垂直,故C 错误’易得NB =NC =ND =NG =4,∴N 为底面梯形BCED 的外接圆的圆心,设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,若O 在平面BCED 上方,入图①所示:设ON =x ,外接球的半径为R ,过O 作A'H 的垂线,垂足为P ,则HP =x ,易得()2222243x x R +=-+=,解得23x =-,舍去; 故O 在平面BCED 下方,如图②所示: 设ON =x ,外接球的半径为R ,过O 作A'H 的垂线,垂足为P ,则HP =x ,易得()2222243x x R +=++=, 解得23x =,∴244371699R ⨯=+=,R ∴=故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题,涉及二面角问题,异面直线所成的角,用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算,余弦定理等,属综合性较强的题目,关键是利用线面垂直,面面垂直的判定和性质进行空间关系和结构的判定,注意球心在四棱锥的底面上方和下方的讨论与验证.3.在长方体1111ABCD A B C D -中,4AB BC ==,18AA =,点P 在线段11A C 上,M 为AB 的中点,则( )A .BD ⊥平面PACB .当P 为11AC 的中点时,四棱锥P ABCD -外接球半径为72C .三棱锥A PCD -体积为定值D .过点M 作长方体1111ABCD A B C D -的外接球截面,所得截面圆的面积的最小值为4π【答案】ACD【分析】利用线面垂直的判定定理可判断A 选项的正误;判断出四棱锥P ABCD -为正四棱锥,求出该四棱锥的外接球半径,可判断B 选项的正误;利用等体积法可判断C 选项的正误;计算出截面圆半径的最小值,求出截面圆面积的最小值,可判断D 选项的正误.【详解】对于A 选项,因为AB BC =,所以,矩形ABCD 为正方形,所以,BD AC ⊥, 在长方体1111ABCD A B C D -中,1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1BD AA ∴⊥, 1AC AA A ⋂=,AC 、1AA ⊂平面PAC ,所以,BD ⊥平面PAC ,A 选项正确;对于B 选项,当点P 为11A C 的中点时,PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形,所以,四棱锥P ABCD -为正四棱锥, 取AC 的中点N ,则PN平面ABCD ,且四棱锥P ABCD -的外接球球心在直线PN 上,设该四棱锥的外接球半径为R ,由几何关系可得222PN R AN R -+=,即2288R R -+=,解得92R =,B 选项错误; 对于C 选项,2114822ACD S AD CD =⋅=⨯=, 三棱锥P ACD -的高为18AA =,因此,116433A PCD P ACD ACD V V S AA --==⋅=△,C 选项正确; 对于D 选项,设长方体1111ABCD A B C D -的外接球球心为E ,则E 为1BD 的中点, 连接EN 、MN ,则1142EN DD ==,122MN AD ==, E 、N 分别为1BD 、BD 的中点,则1//EN DD ,1DD ⊥平面ABCD ,EN ∴⊥平面ABCD ,MN ⊂平面ABCD ,EN MN ∴⊥,EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α,点E 到平面α的距离为d ,直线EM 与平面α所成的角为θ,则sin d EM θθ==≤当且仅当2πθ=时,等号成立,长方体1111ABCD A B C D -的外接球半径为R '==,所以,截面圆的半径()()222226252r R d '=-≥-=,因此,截面圆面积的最小值为4π,D 选项正确.故选:ACD.【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;②利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径; ③定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.4.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点M 10D .过B ,E ,M 的平面截正方体所得截面面积的最小值为10【答案】BCD【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM 平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI 10,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AG D E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时221335322D N ⎛⎫=+= ⎪⎝⎭,223110EF =+=1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM 平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NF D F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,其长度为10,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=,故D 选项正确;故选:BCD【点睛】 本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD 选项,通过//BM 平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.5.在直角梯形ABCD 中,2ABC BCD π∠=∠=,1AB BC ==,2DC =,E 为DC 中点,现将ADE 沿AE 折起,得到一个四棱锥D ABCE -,则下列命题正确的有( ) A .在ADE 沿AE 折起的过程中,四棱锥D ABCE -体积的最大值为13 B .在ADE 沿AE 折起的过程中,异面直线AD 与BC 所成的角恒为4π C .在ADE 沿AE 折起的过程中,二面角A EC D --的大小为45︒D .在四棱锥D ABCE -中,当D 在EC 上的射影恰好为EC 的中点F 时,DB 与平面ABCE所成的角的正切为155 【答案】ABD 【分析】 对于A ,四棱锥D ABCE -的底面面积是固定值,要使得体积最大,需要平面DAE ⊥平面ABCE ,此时DE CE ⊥,可求得1133D ABCE ABCE V S DE -=⋅=可判断A ;对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,由翻折前可知4DAE π∠=可判断B ;对于C ,利用线面垂直的判定定理,结合翻折前可知AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的在大小为2π判断C ;对于D ,利用线面垂直的判定定理可知DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,15tan DF DBF BF ∠==,可判断D 正确;【详解】对于A ,ADE 沿AE 折起得到四棱锥D ABCE -,由四棱锥底面面积是固定值,要使得体积最大,需要四棱锥的高最大,即平面DAE ⊥平面ABCE ,此时DE CE ⊥,由已知得1DE =,则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=,故A 正确; 对于B ,在ADE 沿AE 折起的过程中,//AE BC ,所以异面直线AD 与AE 所成的角即为AD 与BC 所成角,又1AB BC ==,2DC =,E 为DC 中点,可知4DAE π∠=,即异面直线AD 与BC 所成的角恒为4π,故B 正确; 对于C ,由翻折前知,,AE EC AE ED ⊥⊥,且EC ED E =,则AE ⊥平面DEC ,又AE ⊂平面ABCE ,所以平面DEC ⊥平面ABCE ,即二面角A EC D --的大小为2π,故C 错误; 对于D ,如图连接,DF BF ,由C 选项知,AE ⊥平面DEC ,又DF ⊂平面DEC ,则AE DF ⊥,又由已知得EC DF ⊥,且EC AE E ⋂=,则DF ⊥平面ABCE ,所以DBF ∠为直线DB 与平面ABCE 所成的角,在直角DFB △中,222222113122152tan 5511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭,所以DB 与平面ABCE 所成的角的正切为155,故D 正确; 故选:ABD 【点睛】关键点睛:本题考查立体几何综合问题,求体积,求线线角,线面角,面面角,解题的关键要熟悉几种角的定义,通过平移法找到线线角,通过证垂直找到线面角和面面角,再结合三角形求出角,考查了学生的逻辑推理能力,转化能力与运算求解能力,属于难题.6.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan 5θ=,故D 正确,得到答案. 【详解】当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确; 若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==,设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.7.如图,点O 是正四面体P ABC -底面ABC 的中心,过点O 的直线交AC ,BC 于点M ,N ,S 是棱PC 上的点,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,则( )A .若//MN 平面PAB ,则//AB RQ B .存在点S 与直线MN ,使PC ⊥平面SRQC .存在点S 与直线MN ,使()0PS PQ PR ⋅+= D .111PQPRPS++是常数【答案】ABD 【分析】对于选项A ,根据线面平行的性质定理,进行推理判断即可;对于选项B ,当直线MN 平行于直线AB , 13SC PC =时,通过线面垂直的判定定理,证明此时PC ⊥平面SRQ ,即可证明,存在点S 与直线MN ,使PC ⊥平面SRQ ;对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=,利用线面垂直的判定定理可证得PC ⊥平面PAB ,此时通过反证法说明矛盾性,即可判断; 对于选项D ,利用S PQR O PSR O PSQ O PQR V V V V ----=++,即可求得111PQPRPS++是常数.【详解】 对于选项A , 若//MN 平面PAB ,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,∴平面SMN 平面PAB =RQ ,又MN ⊂平面SMN ,//MN 平面PAB ,∴//MN RQ ,点O 在面ABC 上,过点O 的直线交AC ,BC 于点M ,N ,∴MN ⊂平面ABC ,又//MN 平面PAB ,平面ABC平面PAB AB =,∴//MN AB , ∴//AB RQ ,故A 正确; 对于选项B ,当直线MN 平行于直线AB ,S 为线段PC 上靠近C 的三等分点,即13SC PC =,此时PC ⊥平面SRQ ,以下给出证明: 在正四面体P ABC -中,设各棱长为a ,∴ABC ,PBC ,PAC △,PAB △均为正三角形,点O 为ABC 的中心,//MN AB ,∴由正三角形中的性质,易得23CN CM a ==, 在CNS 中,23CN a =,13SC a =,3SCN π∠=,∴由余弦定理得,3SN a ==, ∴222249SC SN a CN +==,则SN PC ⊥, 同理,SM PC ⊥,又SM SN S =,SM ⊂平面SRQ ,SN ⊂平面SRQ ,∴PC ⊥平面SRQ ,∴存在点S 与直线MN ,使PC ⊥平面SRQ ,故B 正确; 对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=, 设QR 中点为K ,则2PQ PR PK +=,∴PS PK ⊥,即PC PK ⊥,()cos cos 0PC AB PC PB PA PC PB CPB PC PA CPA ⋅=⋅-=⋅∠-⋅∠=,∴PC AB ⊥,又易知AB 与PK 为相交直线,AB 与PK 均在平面PQR 上,∴PC ⊥平面PQR ,即PC ⊥平面PAB ,与正四面体P ABC -相矛盾,所以假设不成立, 故C 错误; 对于选项D ,易知点O 到面PBC ,面PAC ,面PAB 的距离相等,记为d , 记PC 与平面PAB 所处角的平面角为α,α为常数,则sin α也为常数, 则点S 到PQR 的距离为sin PS α, 又13sin 234PQRSPQ PR PQ PR π=⋅=⋅ ∴()()1133sin sin sin 33412S PQR PQRV PS S PS PQ PR PQ PR PS ααα-=⋅=⋅⋅=⋅⋅, 又13sin 234PSRSPS PR PS PR π=⋅=⋅, 13sin 234PSQS PS PQ PS PQ π=⋅=⋅, 13sin 234PQRSPQ PR PQ PR π=⋅=⋅, ()3S PQR O PSR O PSQ O PQR V V V V d PS PR PS PQ PQ PR ----=++=⋅+⋅+⋅, ∴()33sin 1212PQ PR PS d PS PR PS PQ PQ PR α⋅⋅=⋅+⋅+⋅, ∴111sin d PQPRPSα++=为常数,故D 正确. 故选:ABD. 【点睛】本题考查了线面平行的性质定理、线面垂直的判定定理,考查了三棱锥体积的计算,考查了向量的运算,考查了转化能力与探究能力,属于较难题.8.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.9.如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则()A.直线BD1⊥平面A1C1DB.三棱锥P﹣A1C1D的体积为定值C.异面直线AP与A1D所成角的取值范用是[45°,90°]D.直线C1P与平面A1C1D6【答案】ABD【分析】在A中,推导出A1C1⊥BD1,DC1⊥BD1,从而直线BD1⊥平面A1C1D;在B中,由B1C∥平面A1C1D,得到P到平面A1C1D的距离为定值,再由△A1C1D的面积是定值,从而三棱锥P ﹣A1C1D的体积为定值;在C中,异面直线AP与A1D所成角的取值范用是[60°,90°];在D 中,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线C1P与平面A1C1D 6.【详解】解:在A中,∵A1C1⊥B1D1,A1C1⊥BB1,B1D1∩BB1=B1,∴A1C1⊥平面BB1D1,∴A1C1⊥BD1,同理,DC1⊥BD1,∵A1C1∩DC1=C1,∴直线BD1⊥平面A1C1D,故A正确;在B中,∵A1D∥B1C,A1D⊂平面A1C1D,B1C⊄平面A1C1D,∴B1C∥平面A1C1D,∵点P 在线段B 1C 上运动,∴P 到平面A 1C 1D 的距离为定值,又△A 1C 1D 的面积是定值,∴三棱锥P ﹣A 1C 1D 的体积为定值,故B 正确; 在C 中,异面直线AP 与A 1D 所成角的取值范用是[60°,90°],故C 错误;在D 中,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系, 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1,P (a ,1,a ),则D (0,0,0),A 1(1,0,1),C 1(0,1,1),1DA =(1,0,1),1DC =(0,1,1),1C P =(a ,0,a ﹣1), 设平面A 1C 1D 的法向量(),,n x y z =,则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x =1,得1,1,1n,∴直线C 1P 与平面A 1C 1D 所成角的正弦值为:11||||||C P n C P n ⋅⋅=22(1)3a a +-⋅=21132()22a ⋅-+,∴当a =12时,直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为6,故D 正确. 故选:ABD .【点睛】求直线与平面所成的角的一般步骤:(1)、①找直线与平面所成的角,即通过找直线在平面上的射影来完成;②计算,要把直线与平面所成的角转化到一个三角形中求解; (2)、用空间向量坐标公式求解.10.如图所示,在棱长为1的正方体1111ABCD A B C D -中,过对角线1BD 的一个平面交棱1AA 于点E ,交棱1CC 于点F ,得四边形1BFD E ,在以下结论中,正确的是( )A .四边形1BFD E 有可能是梯形B .四边形1BFD E 在底面ABCD 内的投影一定是正方形C .四边形1BFDE 有可能垂直于平面11BB D D D .四边形1BFD E 面积的最小值为62【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形;1BFD E 在底面ABCD 内的投影是四边形ABCD ;当与两条棱上的交点是中点时,四边形1BFD E 垂直于面11BB D D ;当E ,F 分别是两条棱的中点时,四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E , 如图所示,因为平面11//ABB A 平面11DCC D ,且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =,因此,同理1//D E BF ,故四边形1BFD E 为平行四边形,因此A 错误;对于选项B ,四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ,因此B 正确; 对于选项C ,当点E F 、分别为11,AA CC 的中点时,EF ⊥平面11BB D D ,又EF ⊂平面1BFD E ,则平面1BFD E ⊥平面11BB D D ,因此C 正确;对于选项D ,当F 点到线段1BD 的距离最小时,此时平行四边形1BFD E 的面积最小,此时点E F 、分别为11,AA CC 的中点,此时最小值为162322=,因此D 正确. 故选:BCD【点睛】关键点睛:解题的关键是理解想象出要画的平面是怎么样的平面,有哪些特殊的性质,考虑全面即可正确解题.。
2023-2024学年重庆市十八中高一数学上学期第一次月考卷附答案解析

2023-2024学年重庆市十八中高一数学上学期第一次月考卷全卷满分150分,考试时间120分钟.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}N 13A x x =∈-<<,{}22B x x =-≤<,则A B = ()A .{}12x x -<<B .{}0,1C .{}1,2D .{}0,1,22.命题“20000,560x x x ∃>-+>”的否定是()A .20,560x x x ∀≤-+≤B .20,560x x x ∀>-+≤C .2000R,560x x x ∃≤-+≤D .20000,560x x x ∃>-+≤3.一个等腰三角形的底边长是6,腰长是一元二次方程27120x x -+=的一根,则此三角形的周长是()A .12B .13C .14D .12或144.二次函数2y ax bx c =++(a ,b ,c 为常数且0a ≠)的图象如图所示,则一次函数y ax b =+与反比例函数cy x =的图象可能是()A.B .C .D.5.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m ,再由乙猜这个小球上的数字,记为n.如果m ,n 满足1m n -≤,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是()A .14B .38C .12D .586.若{|1,Z}6k A x x k ==+∈,1{|,Z}32k B x x k ==+∈,21{|,Z}32k C x x k ==+∈,则这三个集合间的关系是()A .ABC ⊆⊆B .A C B ⊆⊆C .C B A ⊆⊆D .C A B⊆⊆7.如图,在Rt ABC △中,90ACB ∠=︒,将ABC 绕顶点C 逆时针旋转得到A B C ''' ,M 是BC 的中点,P 是A B ''的中点,连接PM .若2BC =,30BAC ∠=︒,则线段PM 的最大值是()A .4B .3C .2D .18.记{}max ,a b 为a ,b 两数的最大值,当正数x ,()y x y >变化时,24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭的最小值为()A .4B .5C .6D .7二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.9.如图中阴影部分所表示的集合是()A .()U N M ⋂ðB .()U M N ⋂ðC .()()UM N N⋃⋂ðD .()()UM N N⋂⋂ð10.如图,在直角坐标系中,直线122y x =-.与坐标轴交于A 、B 两点,与双曲线2(0)ky x x =>交于点C ,过点C 作CD x ⊥轴,垂足为D ,且OA AD =,则以下结论中正确结论的有()A .ADB ADCS S =△△B .当03x <<时,12y y <C .如图,当3x =时,83EF =D .当0x >时,1y 随x 的增大而增大,2y 随x 的增大而减小11.已知正实数x ,y 满足1x y +=,则()A .40x y xy +-≥B .221x y +≥C .111112x y ⎛⎫⎛⎫++≥ ⎪ ⎪⎝⎭⎝⎭D .14912x y +≥+12.对于集合{}22,,M a a x y x y ==-∈∈Z Z.给出如下结论,其中正确的结论是()A .如果1a M ∈,2a M ∈,那么12a a M ∈B .如果1a M ∈,2a M∈,那么12a a M+∈C .如果{}21,B b b n n ==+∈N .那么B M⊆D .若{}2,C c c n n ==∈N .对于c C ∀∈,则有c M∈三、填空题:本题共4小题,每小题5分,共20分.13.设a ,b ∈R ,若集合{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则2a b -=.14.如图,直径8AB =的半圆,绕B 点顺时针旋转30︒,此时点A 到了点A ',则图中阴影部分的面积是.15.已知两个命题p :0xy ≥,q :x y x y+=+,则p 是q 的条件(充分不必要,必要不充分,充要,既不充分又不必要).16.对于一个各数位数字均不为零的四位自然数m ,若千位与百位数字之和等于十位与个位数字之和,则称m 为“一致数”.设一个“一致数”m abcd =满足8a ≤且1d =.将m 的千位与十位数字对调,百位与个位数字对调得到新数m '.并记()101m m F m '+=;一个两位数102N a b =+,将N 的各个数位数字之和记为()G N ;当()()243F mG N a k --=+(k 为整数)时,则所有满足条件的“一致数”m 中,满足()G N 为偶数时,k 的值为,m 的值为.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知集合{}123,0A x a x a a =-<+,{}24B x x =-<<.(1)当2a =时,求A B ⋃;(2)若A B ⋂=∅,求实数a 的取值范围.18.2023年以来,某区把垃圾分类纳入积分,建立文明账户,市民以行动换积分,以积分转习惯.区政府为了了解4月份甲、乙两个社区居民垃圾换积分的情况,分别从甲、乙两个社区各抽取10人,记录下他们的积分(单位:分),并进行整理和分析(积分用x 表示,共分为4组::70A x <;:7080B x ≤<,:8090C x ≤<,:90100D x ≤≤),下面给出了部分信息:甲社区10人的积分:47,56,68,71,83,83,85,90,91,94;乙社区10人的积分在C 组中的积分分数为:81,83,84,84;两组数据的平均数,中位数,众数如下表所示:社区平均数中位数众数甲76.883b 乙76.8a84乙社区积分等级扇形图根据以上信息,解答下列问题:(1)填空:=a ______,b =______,m =______;(2)根据以上数据,你认为哪个社区在此次垃圾分类换积分活动中表现更好,请说明理由(一条即可);(3)若4月份甲社区有700人参与活动,乙社区有800人参与活动,请估计4月份甲、乙两个社区积分在80分以上(包括80分)的一共有多少人?19.已知集合{}22A x x =-≤≤,集合50x B x x -⎧⎫=≤⎨⎬⎩⎭.(1)设a 为实数,若集合{}321C x a x a =≤≤+,且()C A B ⊆ ,求a 的取值范围;(2)设m 为实数,集合12D x m x m ⎧⎫=≤≤+⎨⎬⎩⎭,若“()x A B ∈U ”是“x D ∈”的必要不充分条件,判断满足条件的m 是否存在,若存在,求m的取值范围;若不存在,请说明理由.20.如图,一沙尘暴中心在A 地南偏西60︒的方向的B 处,正迅速向正东方向移动,经过一段时间,沙尘暴中心位于A 地西南方向的C 处,且120BC =千米.(1)求A ,C 之间的距离(保留准确值);(2)距沙尘暴中心200千米的范围为受沙尘暴影响的区域,沙尘暴中心由点C 处开始将沿南偏东75︒的CP方向移动,请说明A 地是否会受到这次沙尘暴的影响? 1.41≈ 1.73≈ 2.45≈).21.(1)已知11a b -≤+≤,11a b -≤-≤,求23a b +的取值范围;(2)若实数a ,b ,c 满足2226a b c ++=.试判断221112a b +++与21123c -+的大小并说明理由.22.如图,在平面直角坐标系中,抛物线()250y ax bx a =++≠与x 轴交于点()1,0A -,()5,0B ,与y轴交于点C.点D 是抛物线对称轴上的一点,纵坐标为-5,P 是线段BC 上方抛物线上的一个动点,连接BP ,DP .(1)求抛物线的解析式;(2)当BDP △的面积取最大值时,求点P 的坐标和BDP △的面积的最大值;(3)将抛物线()250y ax bx a =++≠沿着射线BD 平移,使得新抛物线经过点D.新抛物线与x 轴交于E ,F 两点(点E 在点F 左侧),与y 轴交于点G ,点M 是新抛物线上的一动点,点N 是坐标平面上一点,当以点E ,G ,M ,N 为顶点的四边形是矩形时,写出所有符合条件的点M 的坐标,并写出求解点M 的坐标的其中一种情况的过程.1.B【分析】先求集合A ,再根据交集运算求解.【详解】由题意可得:{}0,1,2A =,所以{}0,1A B = .故选:B.2.B【分析】特称命题的否定:存在改任意并否定原结论,即可写出原命题的否定.【详解】由特称命题的否定为全称命题,则原命题的否定为20,560x x x ∀>-+≤.故选:B 3.C【分析】解方程并结合三角形的性质可得腰长为4,进而可得结果.【详解】因为27120x x -+=,解得3x =或4x =,且336+=,不合题意;4486+=>,符合题意,可知:腰长为4,所以此三角形的周长是44614++=.故选:C.4.A【分析】根据二次函数的开口方向、对称轴的位置、在纵轴的交点坐标的正负判断,,a b c 的正负性,再结合反比例函数、一次函数的图象特征逐一判断即可.【详解】由二次函数的图象可知:开口向上,因此0a >;对称轴为002bx b a =->⇒<,当0x =时,0y c =<;因为0c <,所以反比例函数cy x =的图象在二、四象限,排除BC ;因为0a >,0b <,所以一次函数y ax b =+的图象经过第一、三、四象限,故排除D ,故选:A 5.D【分析】根据古典概型的计算公式,结合绝对值不等式进行求解即可.【详解】根据题意,m ,n 的情况如下:()()()()()()()()6,6,6,7,6,8,6,9,7,6,7,7,7,8,7,9,()()()()()()()()8,6,8,7,8,8,8,9,9,6,9,7,9,8,9,9,共16种情况,其中m ,n 满足1m n -≤的情况如下:()()()()()()()()()()6,6,6,7,7,6,7,7,7,8,8,7,8,8,8,9,9,8,9,9,共10种情况,所以两人“心领神会”的概率是105168=,故选:D 6.C【分析】分析给定的三个集合的约束条件,探讨它们的关系即可判断作答.【详解】依题意,6(3)3{|,Z}{|,Z}66k k A x x k x x k +++==∈==∈,23{|,Z}6k B x x k +==∈,43223{|,Z}{|,Z}66k k C x x k x x k +⨯+==∈==∈,而{|3,Z}Z x x k k =+∈=,{偶数}{|2,Z}x x k k ==∈,因此集合C 中的任意元素都是集合B 中的元素,即有C B ⊆,集合B 中的每一个元素都是集合A 中的元素,即B A ⊆,所以C B A ⊆⊆.故选:C 7.B【分析】根据旋转变换的性质,结合三角形三边关系进行求解即可.【详解】在Rt ABC △中,90ACB ∠=︒,2BC =,30BAC ∠=︒,所以4AB =,因为M 是BC 的中点,所以112CM BC ==,因为ABC 绕顶点C 逆时针旋转得到A B C ''' ,所以4A B ''=,90A CB ''∠=︒,因为P 是A B ''的中点,所以122PC A B ''==,由三角形三边关系,得CP CM PM +>,当旋转到,,P C M 在一条直线上,且C 位于,P M 之间时,PM 有最大值,最大值为213+=,故选:B8.A【分析】根据题中定义,结合基本不等式进行求解即可.【详解】由24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭可得:2t x ≥,4()t y x y ≥-,所以有242()t x y x y ≥+-,因为x ,y 是正数,且x y >,所以224416()2y x y x y x y ≥=-+-⎛⎫ ⎪⎝⎭,当且仅当y x y =-时取等号,即当2x y =时取等号,于是有222416284()t x x t y x y x ≥+≥+≥=⇒≥-,当且仅当2216x x =时取等号,即当2,1x y ==时取等号,所以t 的最小值为4,故选:A【点睛】关键点睛:本题的关键是理解{}max ,a b 的含义,由24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭得到2t x ≥,4()t y x y ≥-.9.AD【分析】根据Venn 图,结合集合运算的概念即可得出答案.【详解】A 选项:U M =+①②ð,则U N M = ②ð,故A 正确;B 选项:U N =+④①ð,则U M N = ④ð,故B 错误;C 选项:()①= U M N ð,则()()UM N N ⋃⋂=∅ð,故C 错误;D 选项:()②+④①=+ U M N ð,()UM N N ⎡⎤⋂⋂=⎣⎦②ð,故D 正确.故选:AD.10.AC【分析】A 项,通过证明OBA CDA ≅ 即可得出结论;B 项,利用函数图象的交点即可得出结论;C 项,计算出3x =时12,y y的值,即可求出EF 的长;D 项,根据函数图象即可得出两函数增减性.【详解】由题意,A 选项,对于直线122y x =-,令0x =,得到2y =;令0y =,得到1x =,∴(1,0),(0,2)A B -,即1,2OA OB ==,在OBA △和CDA 中,90,,AOB ADC OAB DAC OA AD︒∠=∠=∠=∠=∴()OBA CDA AAS ≅ ∴()2,1,2,2CD OB OA AD C ====,∴ADB ADCS S =△△(同底等高三角形面积相等),A 正确;B 项,把点C 坐标代入反比例解析式得:4k =,即24y x =,由函数图象得:当02x <<时,12y y <,B 错误;C 项,当3x =时,1244,3y y ==,∴43348EF ==-,C 正确;D 项,当0x >时,1y随x 的增大而增大,2y 随x 的增大,D 错误;故选:AC.11.AD2x y +≤,即14≤xy ,所以选项A 正确;而222()122x y x y ++≥=可判断B 错误;将1111x y ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭展开并结合14≤xy 可知C 错误;观察D 项分母可知12x y ++=,利用基本不等式“1”的妙用求最值,即可知D 正确.【详解】对于A2x y+≤,即14≤xy ,所以41xy x y ≤=+,即40x y xy +-≥;当且仅当12x y ==时,等号成立,故A 正确;对于B ,根据不等式222()122x y x y ++≥=,当且仅当12x y ==时,等号成立;所以B 错误;对于C ,1111112111119x y x y x y xy xy xy xy ⎛⎫+⎛⎫++=+++=++=+≥ ⎪ ⎪⎝⎭⎝⎭,当且仅当12x y ==时,等号成立;故C 错误;对于D ,根据1x y +=,观察分母可知12x y ++=为定值,则1411411419(1)145121212y x x y x y x y x y ⎛⎫⎛⎫⎛⎫++=+++=+++≥+= ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭,当且仅当21,33x y ==时,等号成立;故D 正确.故选:AD.12.AC【分析】对于A :设2222111222,a x y a x y =-=-,则()()221212121221x x y y x y x a a y =+-+,进而分析判断;对于B :先说明2M ∉,再取特值121a a ==,分析判断;对于C :令1x n =+,,y n n =∈Z ,可知对任意b B ∈,均有b M ∈,所以B M ⊆,故C 正确;对于D :取特值121a a ==,分析判断.【详解】对于选项A :因为1a M ∈,2a M∈,设22221112221212,,,,,a x y a x y x x y y =-=-∈Z ,则()()()()()()222222221222222112212121221121212221x y x y x x y y x y x y x x y x y y a y x a =--=+-+=+-+,因为1212,,,x x y y ∈Z ,则12121221,x x y y x y x y +∈+∈Z Z,所以12a a M ∈,故A 正确;对于选项B :因为2222a x y x y=-=-,不妨设,,x y x y ≥∈Z,若x y=,则22a x y =-=;若1x y =+,则()2222121a x y y y y =-=+-=+为奇数;若2x y ≥+,则()()22222414a x y y y y =-≥+-=+≥;综上可知:2M ∉.显然22101M -=∈,令121a a ==,则122a a M +=∉,故B 错误;对于选项C :令1x n =+,,y n n =∈Z ,则()2222121b x y n n n M =-=+-=+∈,即对任意b B ∈,均有b M ∈,所以B M ⊆,故C 正确;对于选项D :由选项B 可知:2,2C M ∈∉,故D 错误.故选:AC.13.0【分析】利用集合相等以及0a ≠,可得0a b +=,即1ba =-,代入原式可得,ab 的值,进而求出答案.【详解】由题意可知:0a ≠,因为{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则0a b +=,可得1b a =-,则{}{1,0,}0,1,a b =-,可得11a b =-⎧⎨=⎩,且满足0a b +=,所以()22110a b -=--=.故答案为:0.14.16π3【分析】由题意可知:阴影部分为以B 点为圆心,AB 为半径的扇形和以A B '为直径的半圆,减去以AB 为直径的半圆,进而结合扇形面积公式运算求解.【详解】由题意可知:阴影部分为以B 点为圆心,AB 为半径的扇形和以A B '为直径的半圆,减去以AB 为直径的半圆,且AB A B '=,即两个半圆的面积相等,则阴影部分的面积即为以B 点为圆心,AB 为半径的扇形得面积,为23016ππ83603︒⨯⨯=︒.故答案为:16π3.15.充要【分析】根据充分条件和必要条件的定义分析判断即可【详解】当0xy ≥时,若,x y 中至少有一个为零,则x y x y+=+成立,若0,0x y >>,则x y x y x y +=+=+,若0,0x y <<,则x y x y x y +=--=+,综上,当0xy ≥时,x y x y+=+成立,故充分性成立;当x y x y+=+时,()()22x y x y +=+,即222222x xy y x xy y ++=++,整理得xy xy=,所以0xy ≥成立,故必要性成立;所以p 是q 的充要条件.故答案为:充要16.6±2231【分析】设一个“一致数”m abcd =满足8a ≤且1d =,得出()()243F m G N a k --=+,然后分类讨论即可求解.【详解】解:设一个“一致数”m abcd =满足18a ≤≤且1,110d a b c a b =+=+⇒+≤,则1000100101m a b c =+++,100010010m c a b '=+++,所以10101011010101()10101101101m m a b c F m a b c '++++===+++,一个两位数102N a b =+,将N 的各个数位数字之和记为()G N ,则()()42529b G N a b b G N a b ≤=+≥=+-时,,时,,因为()()243F mG N a k --=+,即2210101224431591b a b c a b a k k a b +++---=≤=++-,时,,22101012+94315935a b c a b a k k a b b +++---=+=+-≥时,,,因为满足()G N 为偶数时,则5b ≥时a 奇为数,4b ≤时a 为偶数,逐项代入检验可得:当2,2a b ==时,则2366,3k k c ==±=,,当8,4;5,8a b a b ====时,则214410k a b =+>,,故舍去;所以2231m =.故答案为:6±;2231.【点睛】关键点睛:本题的关键是将m 表示成1000100101a b c +++,然后再分类讨论.17.(1){}27x x -<<(2)[5,)+∞【分析】(1)根据集合并集的定义进行求解即可;(2)根据集合交集运算的性质进行求解即可.【详解】(1)因为2a =,所以{}17A x x =<<,而{}24B x x =-<<,所以{}27A B x x ⋃=-<<;(2)因为A B ⋂=∅,所以14a -≥,或232a +≤-,由145a a -≥⇒≥,显然满足0a >;由52322a a +≤-⇒≤-,而0a >,所以不存在这种情况,综上所述:实数a 的取值范围[5,)+∞18.(1)83.5,83,30a b m ===(2)乙社区在此次垃圾分类换积分活动中表现更好,理由见解析(3)980【分析】(1)找出甲社区中出现次数最多的数据,即可求得b 的值,根据乙社区的扇形统计图,计算出,A B 两组的人数,再结合C 组的人数可求出a 的值,利用D 组的数除以10可求出m 的值,(2)从中位数和众数的解度进行分析即可,(3)分别利用总数乘以甲乙两个社区积分在80分以上所占的百分比,将积相加即可.【详解】(1)因为甲社区中出现次数最多的数据为83,所以83b =,由乙社区的扇形统计图可得乙社区A 组人数为1010%1⨯=,B 组人数为1020%2⨯=人,因为乙社区10人的积分在C 组中的积分分数为:81,83,84,84,所以乙社区的积分从小到大排列,第5个和第6个数据分别为83,84,所以1(8384)83.52a =⨯+=,因为乙社区D 组人数为101243---=人,所以D 组人数所占的百分比为3100%30%10⨯=,所以30m =,(2)乙社区在此次垃圾分类换积分活动中表现更好,理由如下:因为甲乙两个社区积分的平均数相同,但是乙社区的中位数和众数均比甲社区高,所以乙社区在此次垃圾分类换积分活动中表现更好,(3)因为甲社区积分在80分以上(包括80分)的人数所占的比例为60.610=,乙社区积分在80分以上(包括80分)的人数所占的比例为70.710=,所以4月份甲、乙两个社区积分在80分以上(包括80分)的一共有0.67000.7800980⨯+⨯=人.19.(1)10,(1,)2⎛⎤⋃+∞ ⎥⎝⎦(2)92,2⎡⎤-⎢⎥⎣⎦【分析】(1)化简集合,通过()C A B ⊆ 即可分类讨论求出a 的取值范围;(2)求出A B ⋃,利用“()x A B ∈U ”是“x D ∈”的必要不充分条件即可求出m 的取值范围.【详解】(1)由题意,化简集合,{}22A x x =-≤≤,{}05B x x =<≤,∴(0,2]A B ⋂=,在{}321C x a x a =≤≤+中,()C A B ⊆ ,当C =∅时,2131a a a +<⇒>,满足题意;当C ≠∅时,1a ≤,此时21210302a a a +≤⎧⇒<≤⎨>⎩综上,a 的取值范围为10,(1,)2⎛⎤⋃+∞ ⎥⎝⎦.(2)由题意及(1)得,{}22A x x =-≤≤,{}05B x x =<≤,∴[2,5]A B =-U ,在12D x m x m ⎧⎫=≤≤+⎨⎬⎩⎭中,“()x A B ∈U ”是“x D ∈”的必要不充分条件,∴2152m m ≥-⎧⎪⎨+≤⎪⎩(等号不同时成立)922m ⇒-≤≤∴满足条件的m 存在,取值范围是92,2⎡⎤-⎢⎥⎣⎦.20.(1)A ,C之间的距离60千米(2)A 地不会受到这次沙尘暴的影响【分析】(1)过A 作AD BD ⊥,垂足为D ,设AC m =千米,可得CD千米,BD 千米,再结合题意列式求解即可;(2)过A 作AE CP ⊥,垂足为E ,可得200.4AE ≈千米,对比分析即可.【详解】(1)过A 作AD BD ⊥,垂足为D ,设AC m =千米,在Rt ACD △中,可知:45CAD ∠=︒,可得2sin 2CD AD AC CAD m==∠=千米,在Rt △ABD 中,可知:60BAD ∠=︒,可得tan BD AD BAD =∠=千米,由题意可得:BD CD BC -=,即6212022m m -=,解得60m =,所以A ,C之间的距离60千米.(2)过A 作AE CP ⊥,垂足为E ,在Rt ACE 中,可知:60ACE ∠=︒,可得(sin 60303200.4AE AC ACE =∠=⨯≈千米,因为200.4200>,所以A 地不会受到这次沙尘暴的影响.21.(1)[]3,3-;(2)22211111223a b c +>-+++,理由见详解【分析】(1)根据题意可得()()512322a b a b a b +=+--,结合不等式性质运算求解;(2)令2221,2,3m a n b t c =+=+=+,可得112m n t++=,根据“1”的应用结合基本不等式运分析判断.【详解】(1)设()()()()23a b x a b y a b a x y b x y +=++-=++-,其中,x y ∈R ,则23x y x y +=⎧⎨-=⎩,解得5212x y ⎧=⎪⎪⎨⎪=-⎪⎩,即()()512322a b a b a b ⎛⎫+=++-- ⎪⎝⎭,因为11a b -≤+≤,11a b -≤-≤,则()555222a b -≤+≤,()111222a b -≤--≤,可得3233a b -≤+≤,所以23a b +的取值范围为[]3,3-;(2)令2221,2,3m a n b t c =+=+=+,则2221,2,3m a n b t c -=-=-=,可得()()()22212366a b c m n t m n t ++=-+-+-=++-=,即112m n t++=,则111111131212m n t n m t m n t m n t m n t m n m t t n ⎡⎤++⎛⎫⎛⎫⎛⎫⎛⎫++=++=++++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦133124⎛⎫≥+++= ⎪ ⎪⎝⎭,当且仅当n mm n t m m t t n n t ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩,即2224,3,2,1m n t a b c ======时,等号成立,可得2221111113112342m n t a b c ++=++≥>+++,即22211111223a b c +>-+++.22.(1)245y x x =-++(2)7299,636P ⎛⎫ ⎪⎝⎭,52924(3)()1,4-,()2,5-,⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】(1)将()1,0A -,()5,0B 代入抛物线即可得出解析式;(2)过点P 作//PQ BD ,得出PQ ,PB 的解析式,即可求出点P 的坐标和BDP △的面积的最大值;(3)求出平移二次函数的解析式,设出点M 坐标,构造矩形,即可求出点M 的坐标.【详解】(1)由题意,在()250y ax bx a =++≠中,()1,0A -,()5,0B 501,,255504a b a a b b ⎧-+==-⎧⎨⎨++==⎩⎩∴抛物线的函数表达式是:245y x x =-++.(2)由题意及(1)得,如下图1,抛物线的对称轴是直线1522x -+==,(2,5)D ∴-,(5,0)B ,∴直线BD 的解析式是:52533y x =-,过点P 作//PQ BD ,∴可设PQ 的解析式是:53y x b=+,由25453x x x b -++=+得27(5)03x x b -+-=,BPD 面积最大,∴方程由两个相等实数根,2706x ⎛⎫∴-= ⎪⎝⎭,7,6x ∴=当76x =时,277299456636y ⎛⎫=-+⨯+= ⎪⎝⎭,7299,636P ⎛⎫∴ ⎪⎝⎭,如图2,(5,0), B ∴直线PB 的解析式是:136566y x =-+,∴当2x =时,132y =,1323(5)22DE ∴=--=,1237529522624BDP S ⎛⎫∴=⨯⨯-=⎪⎝⎭ ,即BDP △的最大面积是52924.(3)由题意,(1)及(2)得,在245y x x =-++中,(5,0),(2,5)B D -平移后的关系式是2(1)4y x =-++,2(1)40,x ∴-++=解得:1x =或3-,∴(3,0),(0,3)E G -,如图3,当点M 落在抛物线2(1)4y x =-++的顶点(1,4)-时,90EGM ︒∠=,∵//,MN EG MN EG =,∴1(1,4)M -,NE ∴的解析式是3y x =--,∴2(1)43x x -++=--,解得:3x =-(舍)或2∴2(2,5)(5,2)M N '--,,当EG 是对角线时,设点()21,23M m m m --+,由22211M E M G EG +=得()()22222222(3)23233x x x x x x++--+++--=+,∴1234113,0,,22x x x x -+--=-===,∴点M 坐标为()1,4-,()2,5-,⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭.。
(完整)高一立体几何经典例题

立体几何周练命题人---王利军一、选择题(每小题5分,共60分)1、线段AB 在平面α内,则直线AB 与平面α的位置关系是A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A B C D -中,下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1B C 成60角5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行; (3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有A 、1B 、2C 、3D 、47、在空间四边形ABCD 各边AB BC CD DA 、、、上分别取E F G H 、、、四点,如果与EF GH 、能相交于点P ,那么 A 、点必P 在直线AC 上 B 、点P 必在直线BD 上C 、点P 必在平面ABC 内D 、点P 必在平面ABC 外 8、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有A 、0个B 、1个C 、2个D 、3个 9、一个棱柱是正四棱柱的条件是A 、底面是正方形,有两个侧面是矩形B 、底面是正方形,有两个侧面垂直于底面C 、底面是菱形,且有一个顶点处的三条棱两两垂直D 、每个侧面都是全等矩形的四棱柱10、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个B 1C 1A 1D 1BACD三棱锥后,剩下的凸多面体的体积是 A 、23 B 、76 C 、45 D 、5611、已知二面角AB αβ--的平面角是锐角θ,α内一点C 到β的距离为3,点C 到棱AB的距离为4,那么tan θ的值等于A 、34B 、35C D12、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为A 、2VB 、3VC 、4VD 、5V13.设α、β、r 是互不重合的平面,m ,n 是互不重合的直线,给出四个命题: ①若m ⊥α,m ⊥β,则α∥β ②若α⊥r ,β⊥r ,则α∥β ③若m ⊥α,m ∥β,则α⊥β ④若m ∥α,n ⊥α,则m ⊥n 其中正确命题的个数是( )A .1B .2C .3D .414.△ABC 是边长为1的正三角形,那么△ABC 的斜二测平面直观图C B A '''∆的面积为( )A .43 B .83 C .86 D .166 15.设正方体的表面积为242cm ,一个球内切于该正方体,那么这个球的体积是 ( ) A .π343cm B .π63cm C .π383cm D .π3323cm16.四面体S ABC -中,各个侧面都是边长为a 的正三角形,,E F 分别是SC 和AB 的中点,则异面直线EF 与SA 所成的角等于( ) A .090 B .060 C .045 D .030 17.三个平面把空间分成7部分时,它们的交线有( )A.1条 B.2条 C.3条 D.1条或2条18.在长方体1111ABCD A B C D -,底面是边长为2的正方形,高为4,QPC'B'A'C BA则点1A 到截面11AB D 的距离为( )A .83 B . 38 C .43 D . 3419.直三棱柱111ABC A B C -中,各侧棱和底面的边长均为a ,点D 是1CC 上任意一点,连接11,,,A B BD A D AD ,则三棱锥1A A BD -的体积为( )A .361a B .3123a C .363a D .3121a 20.下列说法不正确的....是( ) A .空间中,一组对边平行且相等的四边形是一定是平行四边形;B .同一平面的两条垂线一定共面;C .过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;D .过一条直线有且只有一个平面与已知平面垂直. 二.解答题1.(本题满分12分) 在三棱锥V —ABC 中,VA=VB=AC=BC=2,AB=32,VC=1,求二面角V —AB —C 的大小.3主视图左视图俯视图ACDQ DBPCANM2.已知某几何体的三视图如下图所示,其中俯视图为正三角形,设D为AA1的中点。
重庆市永川中学校2018学年高一下学期期末考试数学试题

高一年下学期期末考数学科试卷(2018.18)考试时间:120分钟 试卷总分:150分 本试卷分第I 卷和第II 卷两部分 第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.某校高一共有10个班,编号1至10,某项调查要从中抽取三个班作为样本,现用抽签法抽取样本,每次抽取一个号码,共抽3次,设五班第一次被抽到的可能性为a ,第二次被抽到的可能性为b ,则( ) A.103=a ,92=b B. 101=a ,91=b C. 103=a ,103=b D. 101=a ,101=b 2.下列事件为随机事件的是( )A.平时的百分制考试中,小强的考试成绩为118分B.边长为a ,b 的长方形面积为abC.100个零件中2个次品,98个正品,从中取出2个,2个都是次品D.抛一个硬币,落地后正面朝上或反面朝上3.某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )A.抽样方法是一种分层抽样B.该班级男生成绩的平均数必小于该班级女生成绩的平均数C.抽样方法是一种系统抽样D.这五名女生成绩的标准差必小于这五名男生成绩的标准差 4.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米5319石,验得米内夹谷,抽样取米一把,数得252粒内夹谷28粒,则这批米内夹谷约为 ( ) A.490石B. 540石C.590石D. 640石5.如图,设A ,B 两点在河的两岸,一测量者在A 所在的同侧河岸边选定一点C ,测出AC 的距离为50 m ,∠ACB =45°,∠CAB =118°后,就可以计算出A ,B 两点的距离为( ). A. 50 3 mB. 50 2 mC. 25 2 mD. 2522m6.在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其它7个小长方形的面积和的41,且样本容量为200,则第8组的频数为( ) A. 40B. 50C. 0.2D. 0.257.对某同学的6次数学测试成绩(满分100分)进行统计,作出如图所示茎叶图,给出关于该同学数学成绩的以下说法:①极差是12;②众数是85;③中位数是84;④平均数是85, 正确的是( ) A. ③④B.②④C.①③D. ①②8.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为 0.8155y x =-,后因某未知原因第5组数据的y 值模糊不清,此位置数据记为m (如下表所示),则利用回归方程可求得实数m 的值为( )A 、8B 、8.1C 、8.2D 、8.39.在Excel 中产生区间上均匀随机数的函数为“rand( )”,在用计算机模拟估计函数x y cos =的图象和x 轴在区间[]ππ,-上部分围成的图形面积时,随机点),(11b a 与该区域内的点),(b a 的坐标变换公式为( ) A.112),1(b b a a =-=πB. )1(2),1(211-=-=b b a a πC. 12,211+=-=b b a a ππD. 12,211-=+-=b b a a ππ10.阅读如图所示的语句:当输入的m=168,n=72时,输出的结果用5进制表示是( ) A.)5(143 B.)5(44 C.)5(22D.)5(6第10题11.在以原点O 为圆心,1为半径的单位圆上有两点B A 、,︒=∠120AOB ,点C 是劣弧 AB(较短的弧)上一点,射线OC 与线段AB 交于点M ,则OM B ∆为钝角三角形的概率( )A.21B.32 C.43 D.65 12.设函数()f x 的定义域为R , ()()()(),2f x f x f x f x -==-, 当[]0,1x ∈时,()3f x x =, 则函数()()()cos g x x f x π=-在区间(]1,3-上的所有零点的和为( ).A . 11B .12C . 7D .8第II 卷(非选择题,共90分)二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。
重庆市永川中学高中数学第18周练习一(立体几何1).

立体几何(1)1.设m,n 是不同的直线,,αβ是不同的平面,下列命题中正确的是(B )A .若m//,,,n m n αβαβ⊥⊥⊥则B .若m//,,//,n m n αβαβ⊥⊥则C .若m//,,,//n m n αβαβ⊥⊥则D .若m//,,//,//n m n αβαβ⊥则2.直三棱柱111ABC A B C -中,090=∠BCA ,M N 、分别是1111A B A C 、的中点,1BC CA CC ==,则BM 与AN 所成的角的余弦值为(D )A .110B .25C D 3.在三棱锥ABC S -中,底面是边长为1的等边三角形,侧棱长均为2,⊥SO 底面ABC ,O 为垂足,则侧棱SA 与底面ABC 所成角的余弦值为(D )A .23B .21C .33D .634.如图,正方体1111ABCD A B C D -的棱长为1,点M 是面对角线1A B 上的动点,则1AM MD + 5.在正四面体A -BCD 中,棱长为4,M 是BC 的中点,点P 在线段AM 上运动(P 不与A ,M 重合),过点P 作直线l ⊥平面ABC ,l 与平面BCD 交于点Q ,给出下列命题:①BC ⊥平面AMD ; ②Q 点一定在直线DM 上; ③V C -AMD =4 2.其中正确的是_①② ______6.如图是一个空间几何体的三视图,则该几何体的外接球的表面积为__.8π __7,已知两异面直线a ,b 所成的角为π3,直线l 分别与a ,b 所成的角都是θ,则θ的取值范围是________.[答案] [π6,π2]1. 若正四面体S —ABC 的面ABC 内有一动点P 分别到平面SAB 、平面SBC 、平面SAC 的距离成等差数列,则点P 的轨迹是(A )A .一条线段B .一个点C .一段圆弧D .抛物线的一段8,如图,在平行四边形ABCD 中,CD =1,∠BCD =60°,且BD⊥CD,正方形ADEF 和平面ABCD 成直二面角,G ,H 分别是DF ,BE 的中点.(1)求证:BD⊥平面CDE ;(2)求证:GH∥平面CDE ; (3)求三棱锥D -CEF 的体积.答案:(1)证明:平面ADEF⊥平面ABCD ,交线为AD , ∵ED ⊥AD ,∴ED ⊥平面ABCD.∴ED⊥BD. 又∵BD⊥CD,CD ∩ED =D ,∴BD ⊥平面CDE. (2)证明:连接EA ,则G 是AE 的中点, 在△EAB 中,GH ∥AB ,又∵AB∥CD,∴GH ∥CD.又∵GH 平面CDE ,∴GH ∥平面CDE. (3)解析:设Rt △BCD 中BC 边上的高为h ,依题意:12×2×h =12×1×3,∴h =32,即点C 到平面DEF 的距离为32. ∴V D -CEF =V C -DEF =13×12×2×2×32=33.9,已知正三棱柱ABC -A 1B 1C 1的各棱长都是4,E 是BC 的中点,动点F 在侧棱CC 1上,且不与点C 重合.(1)当CF =1时,求证:EF ⊥A 1C ;(2)设二面角C -AF -E 的大小为θ,求tan θ的最小值.9,解法1:(1)建立如图3所示的空间直角坐标系,则由已知可得A (0,0,0),B (23,2,0),C (0,4,0),A 1(0,0,4),E (3,3,0),F (0,4,1),于是CA 1→=(0,-4,4),EF →=(-3,1,1),则CA 1→·EF →=(0,-4,4)·(-3,1,1)=0-4+4=0,故EF ⊥A 1C .(2)设CF =λ,(0<λ≤4),平面AEF 的一个法向量为m =(x ,y ,z ),则由(1)得F (0,4,λ),AE →=(3,3,0),AF →=(0,4,λ),于是由m ⊥AE →,m ⊥AF →可得⎩⎪⎨⎪⎧m ·AE →=0,m ·AF →=0,即⎩⎨⎧3x +3y =0,4y +λz =0.取m =(3λ,-λ,4).又由直三棱柱的性质可取侧面AC 1的一个法向量为n =(1,0,0), 于是由θ为锐角可得cos θ=|m ·n ||m |·|n |=3λ2λ2+4,sin θ=λ2+162λ2+4, 所以tan θ=λ2+163λ=13+163λ2. 由0<λ≤4,得1λ≥14,即tan θ≥13+13=63, 故当λ=4,即点F 与点C 1重合时,tan θ取得最小值63. 10,如图,在ABC ∆中,090C ∠=,AC BC a ==,点P 在边AB 上,设(0)AP PB λλ=>,过点P 作//PE BC 交AC 于E ,作//PF AC 交BC 于F 。
重庆市第十八中学2023-2024学年高一下学期期中考试数学试题(含答案)

重庆市第十八中学2023-2024学年高一下学期期中考试数学试题考试说明:1.考试时间120分钟 2.试题总分150分 3.试卷页数2页一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 的三个内角所对边的长分别为,若,,,则( )A. B.C. 4D.2. 复数的共轭复数等于( )A. B. C. D. 3. 若,是空间两条不同的直线,,是空间两个不同的平面,那么下列命题成立的是( )A 若,,则 B. 若,,则C. 若,,则 D. 若,,则4. 如图所示是水平放置的的直观图,其中,则原是一个( )A. 等边三角形B. 直角三角形C. 等腰三角形D. 等腰直角三角形5. 已知分别是三内角的对边,且满足,则的形状是( )A. 等腰三角形B. 直角三角形C. 等腰或直角三角形D. 等腰直角三角形6. 在边长为2的正方形中,是的中点,点在线段上运动,则的取值范围是( )A. B. C. D.7. 已知是平面内的一点,若,,且向量在向量上的投影向量.ABC V ,,A B C ,,a b c 3cos 5B =5c =3a =b =()32z i i =-z 23i--23i-+23i-23i+m n αβ//m α//n α//m n//αβm α⊂//m β//m α//αβ//m β//m αn ⊂α//m nABC V 1A O B O C O ''''''===ABC V ,,a b c ABC V ,,A B C sin cos a C a C b c +=+ABC V ABCD M BC E AB EM EC ⋅[]2,6[]28,[]0,2[]0,4M ABC AB AC ⊥ 2AM AB AC =+ BA BC为,则( )A. B. C. D. 8. 在中,的角平分线交于点,若,,则的面积的最小值为( )A.B. C.D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 已知平面向量,,且,则( )A. B. C. D. 10. 如图所示,在正方体中,,分别为棱,的中点,则下列四个结论正确的是( )A. 直线与是相交直线B. 直线与是平行直线C. 直线与是异面直线D. 直线与是异面直线11. 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上:以小斜幂乘大斜幂,减上,余四约之,为实:一为从隅,开平方得积可用公式(其中为三角形的三边和面积)表示.在中,分别为角所对的边,若,则下列命题正确的是()A B. C. 面积的最大值是 D..34BC u uu r MAC ∠=15306075ABC V ABC ∠BD AC D 2BD =π3ABC ∠=ABC V ()2,a m = ()1,1b =-22a b a b +=- 2m =π,3a b =a b⊥ a =1111ABCD A B C D -M N 11C D 1C C AM 1CC AM BN BN 1MB AM 1DD S =a b c S 、、、ABC V a b c 、、、、A B C 2a =()1tan A A C ==c a =ABC V ABC V三、填空题:本题共3小题,每小题5分,共15分.12. 已知复数,(为虚数单位)在复平面上对应的点分别为,则的面积为______.13. 已知在中,内角所对边分别为,点是的重心,且,则角的大小为______.14. 已知圆锥底面圆的直径为12,高为8,若球在圆锥内,则球的表面积的最大值为______,若在圆锥内放置一个棱长为的正四面体,且正四面体能任意转动,则的最大值为______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知,,向量与的夹角.(1)若,求值;(2)求.16. 已知在中,内角所对的边分别为,分别以为直角边的等腰直角三角形的面积依次是,且(1)求;(2)若,求面积.17. 如图,是圆柱的底面直径,是圆柱的母线且,点是圆柱底面圆周上的点.(1)求圆柱的侧面积和体积;(2)若,是的中点,点在线段上,求的最小值.18. 如图,直四棱柱的底面为菱形,,,,分别为上一点且,.的的的12i z =+212i z =-+i 12,Z Z 12V OZ Z ABC V ,,A B C ,,a b c G ABC V 0357a b c GA GB GC ++=C SO 1O SO 1O SO a a 2= a 3b = a b 2π3θ=()a kb a +⊥k 32a b +ABC V ,,A B C ,,a b c ,,a b c 123,,S S S 123S S S +=C 3cos ,25A a ==ABC V AB AP 4AB AP ==C 2AC =D PB E AP CE DE +1111ABCD A B C D -120ADC ∠=︒16BB =3AB =,M N 1,BC AA 4AN =2BM =(1)证明:平面;(2)平面将该直四棱柱分成两部分,记这两部分中较大的体积为;较小的体积为,求的值.19. 如图1所示,在中,点在线段上,满足,是线段上的点,且满足,线段与线段交于点.(1)若,求实数的值;(2)若,求实数的值;(3)如图2,过点的直线与边分别交于点,设,;(ⅰ)求的最大值;(ⅱ)设的面积为,四边形的面积为,求的取值范围.//BN 1AMD 1AMD 1V 2V 12V V ABC V D BC 2CD DB =G AB 32AG GB =CG AD O AD xAB y AC =+,x y AO t AD =t O ,AB AC ,E F EB AE λ= ()0,0FC AF μλμ=>>λμAEF △1S BEFC 2S 21S S重庆市第十八中学2023-2024学年高一下学期期中考试数学试题简要答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.【1题答案】【答案】C【2题答案】【答案】C【3题答案】【答案】B【4题答案】【答案】C【5题答案】【答案】B【6题答案】【答案】A【7题答案】【答案】C【8题答案】【答案】D二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.【9题答案】【答案】ACD【10题答案】【答案】CD【11题答案】【答案】AD三、填空题:本题共3小题,每小题5分,共15分.【12题答案】【答案】##【13题答案】【答案】【14题答案】【答案】①.②. 四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.【15题答案】【答案】(1) (2)【16题答案】【答案】(1); (2).【17题答案】【答案】(1),; (2)【18题答案】【答案】(1)证明略 (2)【19题答案】【答案】(1), (2)(3)(ⅰ);(ⅱ)52 2.52π336π436π3C =ABC S =V 16π16π411313x =23y =2393223,4934⎛⎤ ⎥⎝⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何(1)
1.设m,n 是不同的直线,,αβ是不同的平面,下列命题中正确的是(B )
A .若m//,,,n m n αβαβ⊥⊥⊥则
B .若m//,,//,n m n αβαβ⊥⊥则
C .若m//,,,//n m n αβαβ⊥⊥则
D .若m//,,//,//n m n αβαβ⊥则
2.直三棱柱111ABC A B C -中,0
90=∠BCA ,M N 、分别是1111A B A C 、的中点,
1BC CA CC ==,则BM 与AN 所成的角的余弦值为(D )
A .110
B .25
C D 3.在三棱锥ABC S -中,底面是边长为1的等边三角形,侧棱长均为2,⊥SO 底面ABC ,O 为垂足,则侧棱SA 与底面ABC 所成角的余弦值为(D )
A .23
B .2
1 C .33 D .
63 4.如图,正方体1111ABCD A B C D -的棱长为1,点M 是面对角线1A B 上的动点,则
1AM MD + 5.在正四面体A -BCD 中,棱长为4,M 是BC 的中点,点P 在线
段AM 上运动(P 不与A ,M 重合),过点P 作直线l ⊥平面ABC ,l 与平面BCD 交于点Q ,给出下列命题:
①BC ⊥平面AMD ; ②Q 点一定在直线DM 上; ③V C -AMD =4 2.
其中正确的是_①② ______
6.如图是一个空间几何体的三视图,则该几何体的外接球的表面积为__.8π __
7,已知两异面直线a ,b 所成的角为π
3,直线l 分别与a ,b 所成的角都是θ,则θ的取
值范围是________.
[答案] [π6,π
2
]
1. 若正四面体S —ABC 的面ABC 内有一动点P 分别到平面SAB 、平面SBC 、平面SAC 的距
离成等差数列,则点P 的轨迹是(A )
A .一条线段
B .一个点
C .一段圆弧
D .抛物线的一段
8,如图,在平行四边形ABCD 中,CD =1,∠BCD =60°,且BD⊥CD,正方形ADEF 和平面ABCD 成直二面角,G ,H 分别是DF ,BE 的中点.
(1)求证:BD⊥平面CDE ;
(2)求证:GH∥平面CDE ; (3)求三棱锥D -CEF 的体积.
答案:(1)证明:平面ADEF⊥平面ABCD ,交线为AD , ∵ED ⊥AD ,∴ED ⊥平面ABCD.∴ED⊥BD. 又∵BD⊥CD,CD ∩ED =D ,∴BD ⊥平面CDE. (2)证明:连接EA ,则G 是AE 的中点, 在△EAB 中,GH ∥AB ,
又∵AB∥CD,∴GH ∥CD.又∵GH 平面CDE ,∴GH ∥平面CDE. (3)解析:设Rt △BCD 中BC 边上的高为h ,
依题意:12×2×h =1
2×1×3,
∴h =
32,即点C 到平面DEF 的距离为32
. ∴V D -CEF =V C -DEF =13×12×2×2×32=33
.
9,已知正三棱柱ABC -A 1B 1C 1的各棱长都是4,E 是BC 的中点,动点F 在侧棱CC 1上,且不与点C 重合.
(1)当CF =1时,求证:EF ⊥A 1C ;
(2)设二面角C -AF -E 的大小为θ,求tan θ的最小值.
9,解法1:(1)建立如图3所示的空间直角坐标系,则由已知可得
A (0,0,0),
B (23,2,0),
C (0,4,0),A 1(0,0,4),E (3,3,0),F (0,4,1),
于是CA 1→=(0,-4,4),EF →
=(-3,1,1),
则CA 1→·EF →
=(0,-4,4)·(-3,1,1)=0-4+4=0,故EF ⊥A 1C .
(2)设CF =λ,(0<λ≤4),平面AEF 的一个法向量为m =(x ,y ,z ),则由(1)得
F (0,4,λ),
AE →
=(3,3,0),AF →=(0,4,λ),于是由m ⊥AE →,m ⊥AF →
可得
⎩⎪⎨
⎪⎧
m ·AE →=0,m ·AF →=0,
即⎩⎨
⎧
3x +3y =0,
4y +λz =0.
取m =(3λ,-λ,4).
又由直三棱柱的性质可取侧面AC 1的一个法向量为n =(1,0,0), 于是由θ为锐角可得cos θ=|m ·n ||m |·|n |=3λ2λ2+4,sin θ=λ2
+16
2λ2
+4, 所以tan θ=
λ2
+163λ
=
13+163λ
2. 由0<λ≤4,得1λ≥1
4
,即tan θ≥
13+13=63
, 故当λ=4,即点F 与点C 1重合时,tan θ取得最小值
63
. 10,如图,在ABC ∆中,0
90C ∠=,AC BC a ==,点P 在边AB 上,
设(0)AP PB λλ=>,过点P 作//PE BC 交AC 于E ,作//PF AC 交BC 于F 。
沿PE 将APE ∆翻折成,A PE '∆使平面A PE '⊥平面ABC ;沿PF 将BPF ∆翻折成,B PF '∆使平面B PF '⊥平面ABC 。
(1)求证://B C '平面A PE ';
(2)是否存在正实数λ,使得二面角C A B P ''--的大小为0
90?若存在,求出λ的值;若不存在,请说明理由。
10解析:(1)以G 点为原点,GP GC GB 、、为x 轴、y 轴、
z 轴建立空间直角坐标系,则B (2,0,0),C (0,2,0),
P (0,0,4),故E (1,1,0),GE =(1,1,0), PC =(0,2,4)。
1010
20
22cos =⋅>=
<PC GE ,, ∴GE 与PC 所成的余弦值为
10
10
. (2)平面PBG 的单位法向量n =(0,±1,0) ∵)02
323(4343,,-===
BC AD GD , ∴点D 到平面PBG 的距离为⋅GD |n |=
2
3
. (3)设F (0,y ,z ),则)2
3
23()02323()0(z y z y ,,,,,,-=--=。
∵GC DF ⊥,∴0=⋅GC DF , 即032)020()2
323
(=-=⋅-
y z y ,,,,, ∴23=
y , 又PC PF λ=,即(0,2
3
,z -4)=λ(0,2,-4), ∴z =1, 故F (0,23,1) ,)1210()3230(-=-=,,,,,FC PF ,∴
FC
PF 3PF
PC =。
