初一奥数 第5讲 平行线的判定与性质(2)定稿
平行线的性质ppt课件

等的线段,得到关键点的对应点;
(4) 连: 按原图顺次连结对应点 .
知4-讲
特别警示
确定一个图形平行移动后的位置需要三个条件:
(1)图形原来的位置;
(2)平行移动的方向;
(3)平行移动的距离.
这三个条件缺一不可.
知4-练
例4 如图 4.2-33,现要把方格纸(每个小正方形的边长均为
知1-讲
特别警示
1. 两条直线平行是前提,只有在这个前提下才
有同位角相等.
2. 按格式进行书写时,顺序不能颠倒,与判定
不能混淆.
知1-讲
3. 平行线的性质与平行线的判定的区别
(1) 平行线的判定是根据两角的数量关系得到两条直线的位
置关系,而平行线的性质是根据两条直线的位置关系得
到两角的数量关系;
又∵ EG 平分∠ BEF,∴∠ BEG=
∠
BEF=70° .
∵ AB ∥ CD, ∴∠ 2= ∠ BEG=70° .
答案:A
知2-练
2-1. [中 考·烟 台]一杆 古 秤 在 称 物 时 的状 态 如 图
所 示,已 知∠ 1=102°,则 ∠ 2 的度数为
78°
______.
感悟新知
知识点 3 平行线的性质3
若是,可直接求出;若不是,还需要
通过中间角进行转化 .
知1-练
1-1. [中考·台州]用一张等宽的纸条折成如图所示的图
140° .
案,若∠ 1=20 ° ,则 ∠ 2的度数为_______
感悟新知
知识点 2 平行线的性质2
知2-讲
1. 性质 2 两条平行直线被第三条直线所截,内错角相等 .
七年级数学上册第5章相交线与平行线5.2平行线3平行线的性质说课稿新版华东师大版

平行线的性质一、教材分析1、教材的地位与作用《行线的性质》是华东师大版七年级数学上册的内容,本节课是在学生已经学习了并了解了平行线的概念,经历了两条直线被第三条直线所截同位角相等、内错角相等、同旁内角互补可以判定两条直线平行的判定及性质的基础上进行教学的。
这节课是空间与图形领域的基础知识,在以后的学习中经常要用到。
它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础,学好这部分内容至关重要。
2、教学重点、难点教学重点:平行的三个性质特征。
教学难点:怎样区分性质和判定。
3、学生情况分析七年级的学生刚正式接触几何知识,对平行线的性质和判定定理仅仅记住、理解而已,中等生对该部分的综合应用很不熟练,整个推理过程很难独自完成,很难做到有理有据的推理,这一方面与学生的接受能力有关,对新知识接受快的同学能够模仿书写推理过程;另一方面与学生的思维阶段有关,七年级学生的抽象的逻辑推理能力发展刚刚起步,所以对平行线的推理过程很难规范。
二、教学目标分析根据数学课程标准的要求和教学内容的特点,以及学生的实际情况制定如下目标:知识与技能:探索平行线的性质和判定定理,会用平行线的性质和判定定理进行简单的计算、证明了解平行线的性质和判定的区别。
过程与方法:通过学生观察,培养他们主动探索与合作能力,使学生领会数形结合、转化的数学思想和方法,从而提高学生分析问题和解决问题的能力。
情感、态度与价值观:情境的创设,使学生认识到数学来源于生活又为生活服务,从而认识到数学的重要性。
通过对平行线的性质的推导过程,培养学生严密的思维能力。
三、说教法、学法新课程的理念要求培养学生自主学习,学生是主体,教师起的是主导作用。
为了让学生真正成为课堂的主人,这节课我选用下面教学方法:小组合作法和自主探究法,作为复习课,平行线的性质及判定定理学生已经记住了,但是不能综合应用,所以在本节课上多强调小组合作和自主探究,希望学生能在合作好探究中有所收获,掌握平行线的判断和平行线性质的综合运用来解决几何问题的推理过程。
(新人教版)数学七年级下册:5.3.1《平行线的性质(第2课时)》教学设计(两套)

5.3.2平行线的性质(第2课时)平行线的性质(二)教学目标1.经历观察、操作、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力.2.理解两条平行线的距离的含义,了解命题的含义,会区分命题的题设和结论.3.能够综合运用平行线性质和判定解题. 重点、难点重点:平行线性质和判定综合应用,两条平行的距离,命题等概念. 难点:平行线性质和判定灵活运用. 教学过程 一、复习引入1.平行线的判定方法有哪些?(注意:平行线的判定方法三种,另外还有平行公理的推论)2.平行线的性质有哪些.3.完成下面填空.已知:如图,BE 是AB 的延长线,AD ∥BC,AB ∥CD,若∠D=100°,则∠C=_____, ∠A=______,∠CBE=________.4.a ⊥b,c ⊥b,那么a 与c 的位置关系如何?为什么?cb二、进行新课1.例1 已知:如上图,a ∥c,a ⊥b,直线b 与c 垂直吗?为什么?学生容易判断出直线b 与c 垂直.鉴于这一点,教师应引导学生思考:(1)要说明b ⊥c,根据两条直线互相垂直的意义, 需要从它们所成的角中说明某个角是90°,是哪一个角?通过什么途径得来?(2)已知a ⊥b,这个“形”通过哪个“数”来说理,即哪个角是90°.(3)上述两角应该有某种直接关系,如同位角关系、内错角关系、同旁内角关系,你能确定它们吗?让学生写出说理过程,师生共同评价三种不同的说理. 2.实践与探究(1)下列各图中,已知AB ∥EF,点C 任意选取(在AB 、EF 之间,又在BF 的左侧).请测量各图中∠B 、∠C 、∠F通过上述实践,试猜想∠B 、∠F 、∠C 之间的关系,写出这种关系,试加以说明.E D C B AFECBAFECBA(1) (2) 教师投影题目:学生依据题意,画出类似图(1)、图(2)的图形,测量并填表,并猜想:∠B+∠F=∠C.在进行说理前,教师让学生思考:平行线的性质对解题有什么帮助? 教师视学生情况进一步引导:①虽然AB ∥EF,但是∠B 与∠F 不是同位角,也不是内错角或同旁内角. 不能确定它们之间关系.②∠B 与∠C 是直线AB 、CF 被直线BC 所截而成的内错角,但是AB 与CF 不平行.能不能创造条件,应用平行线性质,学生自然想到过点C 作CD ∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.③如果要说明∠F=∠FCD,只要说明CD 与EF 平行,你能做到这一点吗?以上分析后,学生先推理说明, 师生交流,教师给出说理过程.FEDCB A作CD ∥AB,因为AB ∥EF,CD ∥AB,所以CD ∥EF(两条直线都与第三条直线平行, 这两条直线也互相平行).所以∠F=∠FCD(两直线平行,内错角相等).因为CD ∥AB.所以∠B=∠BCD(两直线平行,内错角相等).所以∠B+∠F=∠BCF. (2)教师投影课本P23探究的图(图5.3-4)及文字.①学生读题思考:线段B 1C 1,B 2C 2……B 5C 5都与两条平行线的横线A 1B 5和A 2C 5垂直吗?它们的长度相等吗?②学生实践操作,得出结论:线段B 1C 1,B 2C 2……,B 5C 5同时垂直于两条平行直线A1B5和A 2C 5,并且它们的长度相等.③师生给两条平行线的距离下定义.学生分清线段B 1C 1的特征:第一点线段B 1C 1两端点分别在两条平行线上,即它是夹在这两条平行线间的线段,第二点线段B 1C 1同时垂直这两条平行线. 教师板书定义:(像线段B 1C 1)同时垂直于两条平行线, 并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.④利用点到直线的距离来定义两条平行线的距离.F EDCBA教师画AB ∥CD,在CD 上任取一点E,作EF ⊥AB,垂足为F.学生思考:EF 是否垂直直线CD?垂线段EF 的长度d 是平行线AB 、CD 的距离吗? 这两个问题学生不难回答,教师归纳:两条平行线间的距离可以理解为:两条平行线中,一条直线上任意一点到另一条直线的距离.教师强调:两条平行线的距离处处相等,而不随垂线段的位置改变而改变. 3.了解命题和它的构成.(1)教师给出下列语句,学生分析语句的特点.①如果两条直线都与第三条直线平行,那么这条直线也互相平行; ②等式两边都加同一个数,结果仍是等式; ③对顶角相等;④如果两条直线不平行,那么同位角不相等.这些语句都是对某一件事情作出“是”或“不是”的判断. (2)给出命题的定义.判断一件事情的语句,叫做命题.教师指出上述四个语句都是命题,而语句“画AB ∥CD”没有判断成分,不是命题.教师让学生举例说明是命题和不是命题的语句. (3)命题的组成.①命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项. ②命题的形成.命题通常写成“如果……,那么……”的形式,“如果”后接的部分是题设,“那么”后接的部分是结论.有的命题没有写成“如果……,那么……”的形式,题设与结论不明显,这时要分清命题判断了什么事情,有什么已知事项,再改写成“如果……,那么……”形式. 师生共同分析上述四个命题的题设和结论,重点分析第②、③语句. 第②命题中,“存在一个等式”而且“这等式两边加同一个数”是题设, “结果仍是等式”是结论。
初中数学华师大版七上5.平行线的判定课件

文字叙述 同位角 相等 两直线平行
_内___错__角__相等 两直线平行
___同__旁__内__角互补 两直线平行
符号语言 ∵ ∠1=∠2 (已知) ∴a∥b
∵ ∠3=∠2 (已知) ∴a∥b
图形 c
1a 34
2
∵ ∠2+∠4=180° (已知)
b
∴a∥b
方法归纳
方法一:平行线的定义:在同一平面内,不相交的两 条直线就是平行线. 方法二:如果两条直线都和第三条直线平行,那么这 两条直线也互相平行. 方法三:同位角相等,两直线平行. 方法四:内错角相等,两直线平行. 方法五:同旁内角互补,两直线平行. 方法六:在同一平面内,垂直于同一条直线的两条直 线平行.
求证:AB∥CE.请完成下列推理过程:证明:∵CD平分∠ECF,
∴∠ECD=
(
).∵∠ACB=∠FCD (
),∴∠ECD=∠ACB (
)∵∠B=∠ACB,∴∠B=∠
(
∠D)CF.∴A角B∥平C分E线(定义
).
对顶角相等
等量代换
ECD 等量代换 同位角相等,两直线平行
课堂总结
两条直线平行的判定定理:
故选:B.
2.如图,现有如下条件:①∠1=∠4;②∠2=∠3;③∠B=∠D;④∠B
=∠DCE;⑤∠D+∠DCB=180°.其中能判断AB∥DC的有( B ) A.①②③ B.②④ C.①③⑤ D.①②④
解:①当∠1=∠4时,由“内错角相等,两直线平行”可以判定AD∥BC, 不能判定AB∥DC,不符合题意;②当∠2=∠3时,由“内错角相等,两直 线平行”可以判定AB∥DC,符合题意;③由∠B=∠D不能判定AB∥DC, 不符合题意;④当∠B=∠DCE时,由“同位角相等,两直线平行”可以判 定AB∥DC,符合题意;⑤当∠D+∠DCB=180°时,由“同旁内角互补,两 直线平行”可以判定AD∥BC,不能判定AB∥DC,不符合题意.
七年级数学平行线的性质5(PPT)5-2

两条平行线被第三条直线所截,内错角相等. 简单地说:两直线平内角互补. 简单地说:两直线平行,同旁内角互补.
别人结婚。 【逼近】ī动靠近;接近:小艇~了岸边|天色已经~黄昏|脚步声从远处渐渐~。 【逼良为娼】ī逼迫良家妇女当娼妓,也比喻迫使正直安分的 人去做坏事。 【逼命】ī动①指用暴力威胁人。②比喻催促得十分紧急,使人感到紧张,难以应付:真~!这么重的任务,三天内怎能完成! 【逼平】ī动体 育比赛中,处于劣势的一方经过努力,迫使; 少儿英语教育加盟 少儿英语教育加盟 ;对手接受平局。 【逼迫】ī动紧紧地催促; 用压力促使:在环境的~下,他开始变得勤奋了。 【逼抢】ī动紧逼着争抢(多用于足球、篮球等球类比赛):~凶狠。 【逼上梁山】ī《水浒传》中有林冲 等人为官府所迫,上梁山造反的情节。后用来比喻被迫进行反抗或不得不做某种事。 【逼视】ī动向前靠近目标,紧紧盯着:光彩夺目,不可~|在众人的~ 下,他显得局促不安了。 【逼问】ī动强迫被问者回答:无论怎么~,他就是不说。 【逼肖】ī〈书〉动很相似:虽是绢花,却与真花~。 【逼仄】ī〈书〉形 (地方)狭窄:~小径|居室~。 【逼债】ī∥动逼迫人还债。 【逼真】ī形①极像真的:情节~|这个老虎画得十分~。②真切:看得~|听得~。 【??】 (鎞)ī〈书〉①钗。②篦子。 【鲾】(鰏)ī名鱼,身体小而侧扁,略呈卵圆形,青褐色,口小,鳞细。生活在近海。种类很多,有牙鲾、鹿斑鲾等。 【荸】 [荸荠](?)名①多年生草本植物,通常栽培在水田里,地下茎扁圆形,皮红褐色或黑褐色,肉白色,可以吃,也可制淀粉。②这种植物的地下茎。‖有的 地区叫地栗或马蹄。 【鼻】①名鼻子:~梁|~音。②〈书〉开创:~祖。 【鼻翅儿】名鼻翼的通称。 【鼻窦】名鼻旁窦的通称。 【鼻化元音】ī见页〖元 音〗。 【鼻尖】(~儿)名鼻子末端最突出的部分。也叫鼻子尖儿。 【鼻疽】名马、驴、骡的一种传染病,由鼻疽杆菌引起,在内脏、鼻腔黏膜和皮下形成
平行线的性质定理和判定定理课件

简单说成:同旁内角互补,两直线平行. ∵ ∠1+ ∠2=180°, ∴ a∥b.
证明一个命题的一般步骤: (1)弄清题设和结论;
a1 b2
c
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
【议一议】 据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为 什么? 通过这个操作活动,得 到了什么结论?
每一个命题都有逆命题,只要将原命题的条件改成 结论,并将结论改成条件,便可得到原命题的逆命题.
但是原命题正确,它的逆命题未必正确.例如真命 题“对顶角相等”的逆命题为“相等的角是对顶角”, 此命题就是假命题.
【跟踪训练】
1.举例说明下列命题的逆命题是假命题. (1)如果一个整数的个位数字是5 ,那么这个整数能被 5整除. 逆命题:如果一个整数能被5整除,那么这个整数的个位 数字是5. 例如,10能被5整除,但它的个位数字是0. (2)如果两个角都是直角,那么这两个角相等. 逆命题:如果两个角相等,那么这两个角是直角. 例如,60°= 60°,但这两个角不是直角.
4.到一个角的两边距离相等的点,在这个角的平分线上.
条件:到一个角的两边距离相等的点. 结论:它在这个角的平分线上. 逆命题:角平分线上的点到角两边的距离相等. 5.线段的垂直平分线上的点到这条线段的两个端点的距离相等. 条件:线段垂直平分线上的点. 结论:它到这条线段的两个端点的距离相等. 逆命题:到一条线段的两个端点的距离相等的点在这条线段 的垂直平分线上.
a
∵∠1+∠2=180°, ∴ a∥b.
b
c
1
2
c
初一年级奥数定理大全:平行线的判定

【导语】平⾏线是指在同⼀平⾯内永不相交的两条直线,判定平⾏线的⽅法包括1.同位⾓相等,两直线平⾏2.内错⾓相等,两直线平⾏3.同旁内⾓互补,两直线平⾏。
下⾯是为⼤家带来的初⼀年级奥数定理⼤全:平⾏线的判定,欢迎⼤家阅读。
1、平⾏线的概念
在同⼀个平⾯内,不相交的两条直线叫做平⾏线。
平⾏⽤符号“‖”表⽰,如“AB‖CD”,读作“AB平⾏于CD”。
同⼀平⾯内,两条直线的位置关系只有两种:相交或平⾏。
注意:
(1)平⾏线是⽆限延伸的,⽆论怎样延伸也不相交。
(2)当遇到线段、射线平⾏时,指的是线段、射线所在的直线平⾏。
2、平⾏线公理及其推论
平⾏公理:经过直线外⼀点,有且只有⼀条直线与这条直线平⾏。
推论:如果两条直线都和第三条直线平⾏,那么这两条直线也互相平⾏。
3、平⾏线的判定
平⾏线的判定公理:两条直线被第三条直线所截,如果同位⾓相等,那么两直线平⾏。
简称:同位⾓相等,两直线平⾏。
平⾏线的两条判定定理:
(1)两条直线被第三条直线所截,如果内错⾓相等,那么两直线平⾏。
简称:内错⾓相等,两直线平⾏。
(2)两条直线被第三条直线所截,如果同旁内⾓互补,那么两直线平⾏。
简称:同旁内⾓互补,两直线平⾏。
补充平⾏线的判定⽅法:
(1)平⾏于同⼀条直线的两直线平⾏。
(2)垂直于同⼀条直线的两直线平⾏。
(3)平⾏线的定义。
4、平⾏线的性质
(1)两直线平⾏,同位⾓相等。
(2)两直线平⾏,内错⾓相等。
(3)两直线平⾏,同旁内⾓互补。
七年级数学5.2.2平行线的判定PPT课件
如图:B= D=45°, C=135°,
问图中有哪些直线平行?
A
D
答:AB//CD,AD//BC B
C
∵ B=45°(已知)
C=135°(已知) B+ C=180° AB//CD(同旁内角互补,两直线平行) 同理:AD//BC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
纸条,
(点阵中相邻的四个点构成正方形).
E
G
A
B
C
D
F
H
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
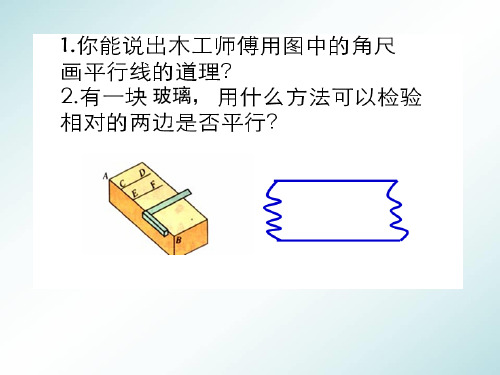
画平行线的事 实
同位角相等, 两直线平行。
同旁内角互补, 两直线平行。
内错角相等, 两直线平行。
判定方法3 两条直线被第三条直线所截,如果 同旁内角互补,那么这两条直线平行
简单说成:同旁内角互补,两直线平行
1a
几何语言: ∵∠1+∠4=1800(已知)
3
4
2b
∴a∥b(同旁内角互补,两直线平行)
想一想 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
简记为“垂直于同一直线的两直线平行”。
∵ a⊥b,a⊥c(已知) ∴ b//c(垂直于同一直线的两条直线平行)
a
1
c
2
b
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五讲 平行线的判定与性质(2)
例1:能否在平面上画出7条直线(任意3条都不共点)使得它们中的每条直线都恰与另3条直线相交?如果能,请画出一例,如果不能,请简述理由。
例2:如图:已知直线a ∥b ,直线AB 交a 与b 于A 、B ,AC 平分∠1,CB 平分∠2.求证∠C=0
90.
练习:如图所示,已知AE ∥BD ,∠1=3∠2,∠2=0
25,求∠C.
例3:如图所示,直线l 的同侧有三点A 、B 、C ,且AB ∥l ,BC ∥l ,求证A 、B 、C 三点在同一条直线上。
练习:如图所示,1AA ∥2BA ,求∠1A -∠1B +∠2A 的值。
例4:有7条直线两两相交,试证明在所有的交角中至少有一个角小于0
27。
2
1b
a C
B
A
F
2
1
E
D
C B
B 1
A 1
A 2B
A
例5:如图AB ∥CD ,∠D =2∠B ,,,AD a CD b AB ==则等于( )
A .1
22a b + .B a b +
.C 2a b -
.D 1
42
b a -
例6:如图‚△AFG 的面积为55‚△A C G 面积为44‚△BFG 面积为77‚则△
AEG 的面积等于( ) A .27 B .28
C .29
D .30
例7:如图‚已知:AB ∥CD ‚∠B =∠C ‚求证:CE ∥BF .
练习:如图‚.已知:AB ∥CD ‚∠1=∠2 ‚求证:∠E =∠F .
例8:如图‚.已知∠B =0
25‚锐角∠0
45BCD =‚∠0
30CDE =‚∠0
10E =‚ 求证:AB ∥∥EF .
练习:如图‚.已知AB ∥CD ‚BE 平分∠ABC ‚DE 平分∠∠ADC . 求证:∠1
2
E =(∠A +∠C ).
G F
E C
B
A
D
C
B
A
G F E D
C B A 21
G F
E
D
C B A F E
D
C
B
A E D
C
B
A
竞赛训练: 一、填空题
1.直线上分布着99个点,我们来标出以这些点为端点的一切可能的线段的中点,那么互不重合的中点至少有___________个。
2.平面上有10 个点,其4个点在一条直线上,其余再无三点共线,则连接这些点的直线共有__________条。
3.如图,两组平行线相交得4个角a 、b 、d 、g 的度数均为质数(a>0
90>b ),则这4 个角的度数有__________组解。
4. 3条直线两两相交,且不过同一个点,那么到3条直线等距离的点有______________个。
5.如图,已知AB ∥CD ,∠1=∠2,则∠E 与∠F 的大小关系是___________.
6.如图,AK ∥OL ,OM ∥BN ,0100KAB ∠=,0
110ABN ∠=,则x ∠=_________.
7.如图,若AB ∥CD ,EF 与AB 、CD 分别相交于F 、E ,∠1=0
40,FC 平分
∠EFA ,则∠EFC =_________________.
8.如图,已知BD ∥EF ,可得出相等的角有____________对。
9.如图,直线AB CD 、相交于点O ,PE ⊥AB 于点F ,如果∠0
50AOC =,那么∠
EPF =________________
二.解答下列各题
1.如图,AB ∥CD ,EF ∥CD ,∠0
50ABC =,∠0
150CEF =,求∠x .
d
g b a 21F E
D C B A X °110°
100°N M L K 1F E D C
B A F E D C
B A O F E
D
C B
A X °
150°
50
°
F E
D
C
B
A
2.如图,已知AB ∥CD 。
求证:∠B +∠F +∠D =∠E +∠G .
3.如图,已知AC ∥DE ,DC ∥FE ,且CD 平分∠BCA ,求证:EF 平分∠BED 。
4.已知:如图,AB ∥CD ,分别探讨下列四个图形中∠APC 与∠PAB 、∠PCD 的关系,并请你加以证明。
5.在直线MN 的同侧有A ,B 两点,请在MN 上找一点P ,使PA PB 最大。
(A ,B 到MN 的距离不等)。
6.如图,在一条河的两岸有A ,B 两个村庄,现要在河上建一座小桥,桥的方向与河流垂直。
设河的宽度不变,试问:桥建在何处,才能使从A 到B 的距离最短?
7.如图,是一台球桌示意图,把球从M 点击出使求与AB 边碰撞后返回,再与CD 边碰撞,最后进入BC 边上的中袋,请设计一条球的最短路线。
G
F
E
D C
B
A
F
E
D
C B
A P
D C B A P
D C B A P
C B A P
D
C B A B
A。
