用MATLAB实现基于混沌的图像置乱加密算法
基于混沌图像加密算法的研究【matlab源码】

毕业论文(设计)题目学院学院专业学生姓名学号年级级指导教师教务处制表基于混沌图像加密算法的研究一、程序说明本团队长期从事matlab编程与仿真工作,擅长各类毕业设计、数据处理、图表绘制、理论分析等,程序代做、数据分析具体信息联系二、写作思路与程序示例随着互联网技术的快速发展,多媒体应用越来越广泛。
数字图像在多媒体信息领域扮演着重要角色,数字图像能够传递表达直观丰富的信息。
互联网是个开放的平台,在网络上传输数字图像很容易遭到篡改和窃取等安全问题。
在互联网安全隐患问题越来越突出的情况下,为了能够保障数字图像在网络传输中的安全,最直接有效的方法就是对数字图像进行加密。
本文主要分为三个部分:第一部分主要研究相关理论,包括混沌理论、密码学理论、图像加密置乱算法和扩散算法、评价混沌图像加密安全性的标准、常见基于混沌的图像加密算法。
重点研究了基于变换域的图像加密算法、相邻像素间异或图像加密算法、基于DNA编码的混沌图像加密算法以及基于分数阶傅里叶变换的混沌图像加密算法等,并给出部分算法的matlab仿真实验。
第二部分提出基于小波变换和中国剩余定理(CRT)的混沌加密图像分存算法。
在现有混沌图像加密算法和图像分存技术的基础上,提出基于小波变换和CRT的混沌加密图像分存算法。
该算法通过对原始图像进行Logistic混沌扩散加密,二级小波分解,低频系数进行Chebyshev混沌系统置乱,低频系数和高频系数进行小波重构,得到重构后的加密图像,最后采用基于CRT的分存技术对小波重构后加密图像进行分存,得到最终加密子图像。
小波变换、混沌扩散加密、混沌置乱加密和分存技术这种组合算法,能够提高加密图像的安全。
对提出的算法进行matlab实验仿真,并对实验结果进行相邻像素相关性分析等,结果表明本算法的密钥敏感性强,相邻像素相关性小,安全性比较高。
第三部分提出基于Contourlet(CT)变换的混沌图像加密算法。
CT变换是在Curvelet变换基础上提出的,CT变换在处理图像细节特征(纹理和轮廓)上,要比小波变换更具有优势。
数字图像加密算法的研究与实现

数字图像加密算法的研究与实现摘要数字图像加密是进行数字图像信息保密的一种手段。
随着信息技术的飞速发展,数字图像在各个领域中有着极为广泛的运用,那么数字图像中所包含的信息安全性应受到重视。
数字图像本身具有数据量较大的特点,用传统的的加密方法往往无法达到加密的要求,许多学者对数字图像的信息安全性进行了多次研究并提出了许多强而有效的算法。
本文研究并实现了一种基于混沌序列置乱的数字图像加密算法,通过密钥产生混沌序列,将该混沌序列进行逻辑排序,并以此排列方法对数字图像进行加密。
该算法隐私性较强,在数字图像的加密和解密过程中均需要密钥的参与,因此不知道密钥的用户无法恢复数字图像,具有良好的保密性。
关键词:数字图像混沌加密数据隐藏AbstractDigital image encryption algorithm is a method about keeping the information of digital image secret.With the quick development of informational technology,the digital image has been utilized in many areas,so the security of message that digital images carry should be paid attention.Particularly ,digital images have the characteristic of a large amount of data,it can not meet demands about encryption that encrypting data in traditional way,which leads to a lot of scholars have spent much time and energy on researching the security about digital image information and illustrated many effective algorithm.This article discuss and illustrate a kind of digital image encryption algorithm based on chaotic array disruption,producing chaotic array according to the key,then logically arranging existed chaotic array,finally encrypt digital image with same logic.It shows better privacy.This process requires keys participating in both encryption and deciphering,so anyone does not know the key who can not rebuild the original image.Key words:digital image chaotic encryption hiding data目录摘要 (I)Abstract (II)绪论 (1)1数字图像加密的基础理论 (4)1.1密码学的介绍 (4)1.2 图像加密技术 (4)1.3数字图像的置乱 (5)1.4混沌加密简介 (5)1.5混沌加密安全性分析 (6)2开发工具简介 (8)3基于混沌的数字图像加密算法 (11)3.1数字图像混沌加密算法总体设计 (11)3.2 数字图像混沌加密算法 (11)3.3数字图像混沌解密算法 (13)4实验仿真与结果 (14)4.1编程实现相关函数及其方法 (14)4.2仿真结果 (14)4.2.1非彩色图像实验仿真 (14)4.2.2彩色图像实验仿真 (16)结论 (18)附录1混沌加密与混沌解密算法代码 (19)绪论计算机和网络的飞速发展为多媒体数字产品的使用、传播提供了极其便利的途径,然而由于数字产品具有极易被复制和修改的特性,使得数字作品的信息安全问题和版权保护成为迫切需要解决的难题。
基于三维混沌映射的彩色图像置乱加密

3 图像 加密与解密 算法
( 3 . 3 ) 当计算机的精度为 1 O 一 1 5 时, 若只考虑 , x 1 时, 密钥空间为 2 1 0 3 0 。 y l ( i ) = m o d ( q I + 姆 / J i / 2 5 5 ) , 1 ) ( 3 . 4 ) 若再考虑其他的密钥 , 则密钥 空间几乎达 到无穷 大 , 足够抵抗穷举 z l ( i ) = o r o d ( ( 1 l + t b / 4 . / 2 5 5 ) , 1 ) ( 3 . 5 ) 攻击 。 4 . 2 统计 分 析 由此产生 的 1 , y 1 , z l 序列用于 图像 分块 置乱和RG B 分量置乱 。 3 . 2 加 密 与解 密步 骤 统计分析 的性能是用来表征采用加密算法 中混迭和扩散性能 本论文采用 分块置乱 的方 法 , 但单独使用分块 处理会 引起块 的强度是否可 以抵抗统计攻击。 我们可以从加密 图像的直方 图和相
一 岍
d z
一
( 2 . 2 )
其 中a = 3 5 , b = 3 , c =2 8 , 此系统处于混沌状态 。
为2 5 6 × 2 5 6 序列进行处理 , 按 式把其转化成 1 3 的实数序列 , 如式3 . 6 。 利用 烈 序列对每一 列进行上下 翻转。 当 丽 =1 时, 则上移一位 , 溉 =2时则上移2 位, 麒 =3 时相 当于保 持不变。 经过此操作 , 彩 色 图像的各个分量之 间对应位置 的像素值进行相应的置乱 , 以此破坏
案 l f 掣
安 全 技 术
2 . 2 Ch e n 映射 的元素为 { 1 , 3 , 9 , 1 l } . . _ …, 其他分 块按 同样 的方式进行置乱 。 C h e n 映射是一种普通 的三维混沌映射 。 混沌系统表述如式2 . 2 ( 2 ) R G B 分量置乱 。 按上述步骤对整个彩色图像进行分块置乱 , 所示 : 整个 图像 的像 素值 位置 发生 变化 , 但是像素值 并没有 发生变化 且 d x , 、 R G B 三个分量之 间的相关性没有破坏 , 容 易遭 受明文攻 击。 把位置 【 一 ) 置乱后 的R G B图像转换成3 * 6 5 5 3 6 的矩 阵。 利用L o g i s t i c  ̄生 的长度
图像加密中测试混沌系统性能的0-1测试0-1Test方法与MATLAB实现代码
图像加密中测试混沌系统性能的0-1测试0-1Test⽅法与MATLAB
实现代码
因为博主学习与实验的原因,需要对混沌系统的性能进⾏测试,⽆奈代码有问题,于是上⽹后找到了0-1测试的代码,经过调试成功运⾏。
⽤到的⽅法与0-1测试的原理在⽂献:The 0-1 Test for Chaos: A Review中写了,感兴趣可以⾃⾏了解。
z1test⽤法
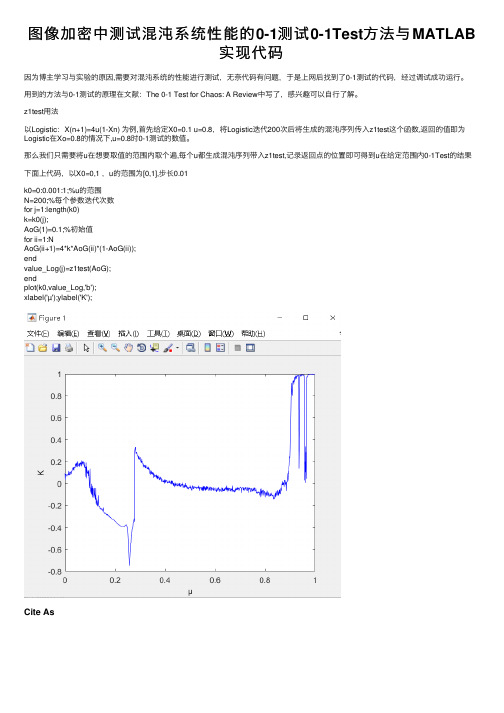
以Logistic:X(n+1)=4u(1-Xn) 为例,⾸先给定X0=0.1 u=0.8,将Logistic迭代200次后将⽣成的混沌序列传⼊z1test这个函数,返回的值即为Logistic在Xo=0.8的情况下,u=0.8时0-1测试的数值。
那么我们只需要将u在想要取值的范围内取个遍,每个u都⽣成混沌序列带⼊z1test,记录返回点的位置即可得到u在给定范围内0-1Test的结果下⾯上代码,以X0=0,1 ,u的范围为[0,1],步长0.01
k0=0:0.001:1;%u的范围
N=200;%每个参数迭代次数
for j=1:length(k0)
k=k0(j);
AoG(1)=0.1;%初始值
for ii=1:N
AoG(ii+1)=4*k*AoG(ii)*(1-AoG(ii));
end
value_Log(j)=z1test(AoG);
end
plot(k0,value_Log,'b');
xlabel('µ');ylabel('K');
Cite As。
基于混沌序列的通用数字图像加密算法

基于混沌序列的通用数字图像加密算法沌序列,然后根据子密钥及图像类型将其转换为无符号整数序列,最后再依次与对应的像素值进行异或运算以实现置换加用评价指标对加密效果与安全性进行分析。
理论分析与实验结果表明,该算法密钥空间大,具有良好的加密效果、安全统计特性,且抗干忧能力较强。
键词 :数字图像加密 ;像素置换 ;混沌序列 ;Logistic 映射Universal Digital Image Encryption Algorithm Base on Chaotic SequenceLU Shou-dong(School of Information and Statisticsof, FiGuangxinanceandUniversity Economics ,Nanning,Guangxi 530003,China ) stract: In order to protect digital aimage's universal digitalinformation, image encryption algorithm based on is chaoticpropo sequencetly, according tokey the and the size of image, a chaoticis generated. sequence Then, according to the sub-key and the type of im chaotic sequenceis converted to an unsigned integer sequence. Lastly, pixelwill permutation be realizedby usencryptioning theXOR opera ween the unsigned integer sequence and each turn.corresponding The effect piofxel encryption value inis and al s osecurity analyzed by u evaluation index. Theoretical analysis and experimental results show that the algorithm has aeff large space of key, a good encryptionrity and statistical characteristics,a strong anti -anoisebility.words: digital image encryption; pixel permutation; sequenc; Logistice chaoticmapping引言可改变图像的直方图,因此安全性更好。
基于混沌理论的图像加密算法设计与实现

基于混沌理论的图像加密算法设计与实现基于混沌理论的图像加密算法设计与实现摘要:随着信息技术的发展和普及,图像在各个领域扮演着越来越重要的角色。
为了保护图像数据的安全性和机密性,图像加密技术成为研究的热点之一。
混沌理论以其高度的不可预测性和不确定性,成为图像加密领域的重要工具之一。
本文基于混沌理论,设计了一种新的图像加密算法,并对其进行了实现。
结果表明,该算法在加密图像的同时,能够保护图像中的信息不被恶意攻击者获取。
关键词:混沌理论;图像加密;信息安全1. 引言图像加密技术是信息安全领域的重要研究内容,它在保护图像数据的安全性和机密性方面发挥着重要作用。
随着计算机技术的不断发展,传统的加密算法逐渐暴露出一些不足之处,例如加密速度慢、加密强度不高等。
混沌理论以其高度的不可预测性和不确定性,成为图像加密领域的重要工具之一。
本文基于混沌理论,设计了一种新的图像加密算法,并对其进行了实现。
2. 混沌理论的基本原理混沌理论是一种描述非线性动力学系统行为的数学理论。
混沌过程具有高度不可预测性和不确定性,其输出表现出一种看似随机而实际上具有确定性的行为。
混沌理论广泛应用于密码学领域,可以产生高度随机的密钥序列。
3. 图像加密算法的设计本文设计的图像加密算法主要包括三个步骤:密钥生成、混沌映射和像素置换。
其中,密钥生成通过混沌映射生成高度随机的密钥序列。
混沌映射是基于混沌系统的一种映射算法,可以产生类似随机数的序列。
像素置换是通过对图像像素的位置进行重新排列来实现加密过程。
具体算法的设计步骤如下:步骤1:密钥生成选择合适的混沌系统,并设置初始值。
通过迭代计算,得到一系列具有高度随机性的密钥序列。
步骤2:混沌映射将生成的密钥序列应用于需要加密的图像。
通过对每个像素值进行异或操作,实现加密过程。
步骤3:像素置换对加密后的图像进行像素位置的重新排列。
可以采用一定的规则,如置换矩阵或者混沌映射算法进行像素位置的调整。
4. 图像加密算法的实现本文采用MATLAB编程语言实现了基于混沌理论的图像加密算法。
在Matlab中使用图像加密和解密技术

在Matlab中使用图像加密和解密技术图像加密和解密技术是保护图像信息安全的重要手段之一。
在信息时代,随着图像的广泛应用,图像加密和解密技术的需求也日益增加。
Matlab作为一种常用的科学计算软件,提供了丰富的工具和函数,使得图像加密和解密变得更加便捷和高效。
一、图像加密技术的基本原理图像加密技术通过对图像进行转换和混淆操作,使得原始图像的信息变得不可读取,达到保护图像信息安全的目的。
常见的图像加密技术包括置乱、替换、混淆等方法。
1.置乱方法:通过对图像的像素点进行置换操作,改变像素点的位置,使得原始图像的信息难以被还原。
常见的置乱方法有置乱矩阵法、置乱像素法等。
2.替换方法:通过对图像的像素点进行替换操作,改变像素点的值,使得原始图像的信息无法被识别。
常见的替换方法有置乱像素法、置乱位值法等。
3.混淆方法:通过对图像的像素点进行逻辑运算、异或运算等操作,改变像素点的值,使得原始图像的信息无法被解读。
常见的混淆方法有异或混淆法、逻辑运算混淆法等。
二、图像加密的Matlab实现在Matlab中,图像加密和解密的实现通常可以借助于图像处理工具箱和编程语言的支持。
下面以置乱方法为例,介绍如何在Matlab中实现图像加密。
1.图像置乱:首先,需要读取待加密的图像文件,并将其转换为Matlab支持的矩阵格式。
可以使用imread函数读取图像文件,得到灰度图像矩阵。
然后,使用randperm函数生成一个随机的置乱矩阵,该矩阵用于置乱图像的像素点位置。
可以使用reshape函数将矩阵转换为一维数组,再将图像矩阵按照置乱矩阵进行置乱操作。
最后,使用imwrite函数将置乱后的图像矩阵写入新的图像文件中,完成图像置乱操作。
2.图像解密:与图像加密相反,图像解密需要使用与加密相对应的逆操作。
在这里,我们需要使用与置乱相反的矩阵,将置乱后的图像还原为原始图像。
首先,读取已经加密的图像文件,并将其转换为Matlab支持的矩阵格式。
基于MATLAB的图像加密与解密技术研究

基于MATLAB的图像加密与解密技术研究图像加密与解密技术是信息安全领域中的重要研究内容,随着计算机和通信技术的不断发展,保护图像信息的安全性变得尤为重要。
本文将探讨基于MATLAB的图像加密与解密技术研究,包括加密算法、解密算法以及实验结果分析等内容。
一、图像加密技术概述图像加密技术是通过某种算法将原始图像转换为看似随机的形式,以保护图像内容不被未经授权的用户访问。
常见的图像加密算法包括DES、AES等对称加密算法以及RSA、ECC等非对称加密算法。
在MATLAB环境下,可以利用这些算法对图像进行加密处理。
二、基于MATLAB的图像加密算法实现在MATLAB中,可以使用各种加密算法对图像进行加密处理。
其中,DES算法是一种较为经典的对称加密算法,通过设置密钥对图像进行加密。
AES算法则是一种更为高级的对称加密算法,具有更高的安全性。
此外,还可以利用MATLAB实现非对称加密算法RSA对图像进行加密。
三、图像解密技术概述图像解密技术是将经过加密处理的图像恢复为原始图像的过程。
在解密过程中,需要使用相同的密钥或者解密算法来还原原始图像。
解密过程需要确保安全性和正确性,以保证解密后的图像与原始图像一致。
四、基于MATLAB的图像解密算法实现在MATLAB环境下,可以编写相应的解密算法来对经过加密处理的图像进行解密操作。
根据所采用的加密算法不同,解密过程也会有所差异。
通过编写相应的MATLAB代码,可以实现对DES、AES等对称加密算法以及RSA等非对称加密算法进行解密操作。
五、实验结果分析与讨论通过实验验证基于MATLAB的图像加密与解密技术,在不同场景下对不同类型的图像进行了加密和解密处理。
实验结果表明,在合适选择加密算法和参数设置的情况下,可以有效保护图像信息的安全性,并且能够高效地还原原始图像。
结语综上所述,基于MATLAB的图像加密与解密技术研究具有重要意义,可以有效保护图像信息的安全性,防止未经授权访问和篡改。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用MATLAB实现基于混沌的图像置乱加密算法
由于图像文件的加密有其自身的要求,传统的文字加密方法不适合图像文件加密。
为此,我们在混沌映射加密算法的基础上,提出了一种利用Logistic混沌序列对图像像素点置乱实现加密的算法,那么,我们今天借助MATLAB软件平台,看看基于混沌的图像置乱加密算法如何实现。
一、基于混沌的图像置乱加密算法
本文提出的基于混沌的图像置乱加密算法示意图如图1所示。
加密算法如下:首先,数字图像B大小为M×N(M是图像B的行像素数,N是图像B的列像素数),将A的第j行连接到j-1行后面(j=2,3,A,M),形成长度为M×N的序列C。
其次,用Logistic混沌映射产生一个长度为的混沌序列{k1,k2,A,kM×N},并构造等差序列D:{1,2,3,A,M×N-1,M×N}。
再次,将所产生的混沌序列{k1,k2,A,kM×N}的M×N个值由小到大排序,形成有序序列{k1′,k2′,A’,kM×N’},确定序列{k1,k2,A,kM×N}中的每个ki在有序序列{k1′,k2′,A’,kM×N’}中的编号,形成置换地址集合{t1,t2,A,tM×N},其中ti为集合{1,2,A,M×N}中的一个;按置换地址集合{t1,t2,A,tM×N}对序列C进行置换,将其第i个像素置换至第ti列,i=1,2,A,M×N,得到C’。
将等差序列D做相同置换,得到D’。
最后,B’是一个M×N的矩阵,B’(i ,j)=C’((i-1)×M+j),其中i=1,2,A,M;j=i=1,2,A,N,则B’就是加密后的图像文件。
解密算法与加密算法相似,不同之处在于第3步中,以序列C’代替随机序列{k1,k2,A,kM×N},即可实现图像的解密。
二、用MATLAB的实现基于混沌的图像置乱加密算法
本文借助MATLAB软件平台,使用MATLAB提供的文本编辑器进行编程实现加密功能。
根据前面加密的思路,把加密算法的编程分为三个主要模块:首先,构造一个与原图a等高等宽的矩阵b加在图像矩阵a后面形成复合矩阵c:
b=zeros(m1,n1);
ifm1>=n1
ifm1>n1
fore=1:n1
b=(e,e);
end
……
else
fore=1:n1
end
fore=1:(n1-m1)
b((m1+e-1),e)=m1+e-1
end
end
c=zeros(m1*2,n1);
c=zeros(m1*2,1);
c=[b,a];
然后,用Logitic映射产生混沌序列:
……
forn=1:n1+100x(n+1)=q*x(n)*(1-x(n));
endn=101:1:n1+100;
y(n-100)=x(n);
……
最后,采用冒泡法将产生的混沌序列值由小到大进行排序,并利用同样的换序条理依次对复合矩阵的列和行进行打乱排序:
forf=1:n1-1forh=f:n1ify(f)>y(h)k=y(f); y(f)=y(h);
y(h)=k;
c1=c(:,f);
c(:,f)=c(:,h);
c(:,h)=c1;
end
……
forh=g:m1
if y(f>y<h)
k=y(f)
y(f)=y(h)
y(h)=k;
d1=d(:,f);
d(:,f)=d(:,h);
d(:h)=d;
end
……
解密的程序与加密的相反。
三、基于混沌的图像置乱加密算法效果分析
利用Logistic混沌序列对图像像素点置乱对图像文件加密,其效果要比用Logistic混沌序列直接对图像文件加密好,令x0=0.3001,图2(b)为用Logistic混沌序列直接对图像文件爱你进行加密的图像,图2(c)为用Logistic混沌序列对图像像素点置乱对图像文件进行加密的图像,图2(d)为其的解密图像文件。
由图2(b)和(c)图可见,原图像的人物和轮廓已经全部覆盖,无法分辨出原图像的细节信息。
但从效果上来看,采用图像置乱与混沌映射结合的加密方法所得到的加密效果要优于直接用混沌进行加密的方法。
下面,针对日常生活中遇到的图像破损问题,对本文算法的抗破损能力进行研究。
当受损区域大小为图像面积7.76%时,恢复的图像仍然比较清晰(如图3(a)、
(d));受损区域大小为图像面积18.63%时,恢复的图像效果开始变差,出现零星的黑点(如图3(b)、(e));受损区域大小为图像面积25.36%时,恢复的图像效果不理想,布满黑点(如图3(b)、(e))。
原图任意区域的像素在置乱图中是均匀分布的,置乱图受损区域的形状及所处的位置不同对恢复图像所造成的影响有限。
图4中(a)、(b)、(c)是三幅遭到损坏的密图,受损区域(黑色)形状不同,位置不同,只有大小是相同的,均为2500个像素点(为图像面积12.94%)。
(a)、(b)、(c)的恢复图像分别为(d)、(e)、(f),三幅恢复图像的效果没有明显差别。
因此,可以认为恢复图像的效果取决于受损区域的面积大小,而受损区域的形状、位置产生的影响很小,只要其面积不大于原图面的20%,就能够恢复出比较理想的图像。
