413-夫琅禾费单缝衍射
夫朗禾费单缝衍射
夫朗禾费单缝衍射
朗禾费单缝衍射是一项经过精心改良的传统服装设计技法。
它通常用
于创造褶皱结构。
传统朗禾费单缝衍射是由单线运用双重夹子实现，而现
代朗禾费单缝衍射也有很多因素影响着它实际的形状，并增强了它的美感
细节和质感。
从结构上来说，朗禾费单缝衍射的基本技巧是在一件衣服的前后及侧
面都进行缝衍射的工作，使衣服的缝衍射柔软灵活，同时也给衣物带来复
杂而丰富的褶皱结构，增加了它们的光泽和柔韧性。
而此外，朗禾费单缝
衍射也可以给予准确的体积解决方案，营造出有度比例的曲线线条，同时，将对任何时候的空间穿衣流行进行完美的行驶。
朗禾费单缝衍射在设计方面可以实现很多不同的风格，从高级礼服到
复杂裙装，从紧凑的衣服到宽松的衣服，它都是一个有效的解决方案，展
现出创意的设计，推动时尚发展。
此外，朗禾费单缝衍射在服装结构上提
供了灵活性。
它可以帮助衣服更好地贴合身体，使衣服形状更加完美，而
不会影响舒适度和自由度。
朗禾费单缝衍射在服装设计中越来越受到重视，不仅被广大服装设计
师用于礼服、裙装、夹克等，用以提升整体气质，而且也可以把它应用于
床上用品、decora缝制以及座椅等非服装行业的设计领域中。
朗禾费单缝
衍射有利于提高服装的穿着性能，对改善夹克衫和礼服的体量，以及增加从微观到宏观的大小曲线，总得而言提高了服装的外观和质感。
夫琅禾费单缝衍射光强分布的研究
姓名：程佳丽 学号：200807034129 专业：物理学（师范）——夫琅禾费单缝衍射光强分布的研究夫琅禾费单缝衍射光强分布的研究（Research Of Fraunhofer Single Slot Diffraction Of LightIntensity Distribution）姓名：程佳丽专业：物理学（师范）班级：08级物教班摘要：我们在光学中学习了有关夫琅禾费单缝衍射和圆孔衍射的内容，本文主要是对夫琅禾费单缝衍射光强的计算公式进行数学推导以及拓展，并且根据推导的数学公式对夫琅禾费单缝衍射光强分布情况进行讨论，对夫琅禾费单缝衍射的特点进行分析介绍。
关键词：夫琅禾费单缝衍射（Fraunhofer single slot diffraction）、光强（Light intensity）、光强分布（Light intensity distribution）、最大值（Maximum）引言：光的衍射是光的波动性的重要现象之一。
衍射现象即波在传播过程中不沿直线传播，而是向各方向绕射的现象。
而光绕过障碍物偏离直线传播而进入几何阴影，并在屏幕上出现光强分布不均匀的现象，称为光的衍射。
在衍射现象中，把平行光束的衍射现象，称为夫琅禾费衍射。
夫琅禾费衍射在光学研究中有着重要意义，它主要包括单缝衍射、圆孔衍射。
这里我重点介绍夫琅禾费单缝衍射的光强分布特点。
一、夫琅禾费单缝衍射实验装置与衍射图样的特点。
所谓夫琅禾费衍射是指光源、衍射屏和观察屏三者之间都是相距无限远的衍射情况。
即相当于入射光和衍射光都是平行的情况。
在这种情况下计算衍射花样中光强的分布时，数学运算就比较简单。
所谓光源在无限远，实际上就是把光源置于第一个透镜的焦平面上，使之成为平行光束；所谓观察角在无限远，实际上是在第二个透镜的焦平面上观察衍射花样。
由于透镜的会聚，衍射花样的光强将比菲涅耳衍射花样的光强大大增加。
夫琅禾费单缝衍射包含着衍射现象的许多主要特征。
夫琅和费单缝衍射实验报告
夫琅和费单缝衍射实验报告夫琅和费单缝衍射实验报告夫琅和费单缝衍射实验是光学领域中的一项重要实验，它揭示了光的波动性质。
本文将介绍夫琅和费单缝衍射实验的原理、实验装置和实验结果，并探讨其对光学理论的贡献。
一、实验原理夫琅和费单缝衍射实验是基于光的波动性质而进行的。
当光通过一个狭缝时，光波会发生衍射现象，即光波会弯曲并扩散到周围空间。
夫琅和费单缝衍射实验利用单缝的特性来观察光的衍射现象，从而揭示光的波动性。
二、实验装置夫琅和费单缝衍射实验的装置相对简单，主要包括光源、单缝、屏幕和测量仪器。
光源可以使用激光器或者单色光源，确保光的单色性。
单缝通常是一个细长的狭缝，可以是金属制成。
屏幕用于接收光的衍射图样，可以是白色的墙壁或者特制的屏幕。
测量仪器可以是尺子或者显微镜，用于测量衍射图样的尺寸。
三、实验过程实验开始时，将光源对准单缝，并调整光源的位置和角度，使得光线垂直射向单缝。
然后，在屏幕上观察到的光的衍射图样。
根据实验需要，可以调整单缝的宽度和光源的强度，观察不同条件下的衍射现象。
四、实验结果夫琅和费单缝衍射实验的结果是一系列明暗相间的条纹，称为衍射图样。
衍射图样的中央区域亮度最高，称为中央极大。
中央极大两侧是一系列暗条纹，称为暗纹。
暗纹两侧又是一系列亮条纹，称为亮纹。
亮纹和暗纹的宽度和间距与单缝的宽度和入射光的波长有关。
五、实验分析夫琅和费单缝衍射实验的结果可以用光的波动理论解释。
当光通过单缝时，光波会向前传播，并在缝后形成球面波。
这些球面波相互干涉，形成衍射图样。
中央极大对应光波的相干增强，而亮纹和暗纹对应光波的相干减弱。
夫琅和费单缝衍射实验的结果还验证了赫兹斯普龙光波理论。
根据赫兹斯普龙光波理论，光波可以看作是一系列波长和振幅不同的波组成的。
夫琅和费单缝衍射实验的结果与赫兹斯普龙光波理论预测的衍射图样相吻合，进一步证明了光的波动性。
六、实验应用夫琅和费单缝衍射实验的结果在实际应用中有着广泛的应用。
夫琅禾费单缝衍射
当 = 2 时，可将缝分成四个“半波带”，
它们发的光在 P 处两两相消，又形成暗纹……
菲涅耳半波带的数目决定于 bsin
P•
•
•
2
f
对应沿方向衍射
的平行光狭缝，波 阵面可分半波带数
k
b sin
2
1、k 由 b、、 确定。
2、k 不一定是整数。
三、单缝衍射明暗条纹条件
由半波带法可得明暗纹条件为：
a sin1
0 21
1 sin1
中央明纹
1
a
k 1
k2
0
2
a
上式为中央明纹角宽度
中央明纹线宽度
x
x0
2 x1
2
ftg 0
2
f 0
2 f
a
xk
k2
x0
2 f
a
(a, )
其他明纹宽度
0 2 1
f
k 1 O中明央纹
a sin k k
tg k
xk f
tg k sin k
xk
k
f
a
f xk a
0.017 0.047
0.047 0.017
-2( /a) -( /a) 0 /a 2( /a) sin
中央极大值对应的明条纹称 中央明纹。 中央极大值两侧的其他明条纹称 次极大。
明纹暗纹的图示
sin Δ x / f
中央亮纹的半角宽
1
x
f
（1）明纹宽度
中央明纹：两个一级暗纹间的距离，
为1
1
级暗纹对应的衍射角
xkk
条纹散开了 b
光通量减少，
清晰度变差。
分析与讨论：
夫琅禾费单缝衍射
(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m
[B]
矩形孔的夫琅禾费衍射
两个正交迭置的狭缝（设宽度分别为a、b） 衍射光在x, y方向的衍射角分别为
x, y
衍射光场：两个按正交方向展开的单缝衍射场的乘积
I(P)
I
0
s i n
2
s i n
2
远去的汽车头灯
最小分辨角：
S1
D
*
1
1.22
D
* S2
0 I
表达式中的波长 是指衍射光场在像方空间所处介质
中的波长
眼睛（正常人眼） a=D/2=1mm，n=1，n'=1.336，
0=550nm，f '=2.2cm
角分辨极限： m=0.610/n'a ≈2.511×10-4 rad
线分辨极限：
0m=0.610/na ≈3.355×10-4 rad
分辨本领:
1 R
min
光学系统对被观察对象微小细节的分辨能力
These photographs of an automobile’s headlights were taken at the greater and greater distances from the camera.
远去的汽车头灯
两个按正交方向展开的单缝衍射场的乘积衍射光在xy方向的衍射角分别为其中矩形远场衍射振幅三维图矩形孔的夫琅禾费衍射图样矩形远场衍射强度三维图24设圆孔的直径为d与p点对应的衍射角为衍射屏观察屏中央亮斑爱里斑变小第一暗圈所包围的中央亮斑叫做爱里斑airydisk线半径
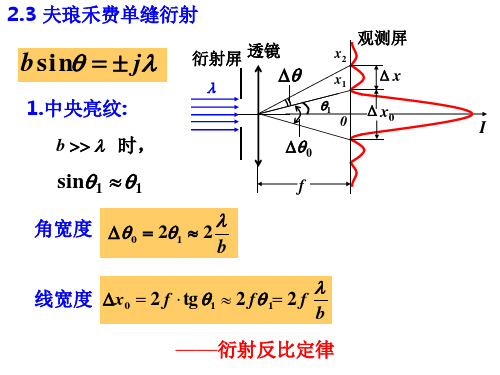
2.3 夫琅禾费单缝衍射
bsin j
实验一夫琅和费单缝衍射实验
实验一夫琅和费单缝衍射实验
一夫琅和费单缝衍射实验是物理学上一项经典的实验，用以验证光是电磁波的结论。
它始于1837年由丹麦物理学家一夫琅和及其同事费单缝提出，采用的装置简单，结论明显，可以准确地验证光是电磁波的性质。
实验可以利用喷洒装置，简单构成，喷出一束射线穿过一个扩孔，然后遇到一片玻璃板，在另一侧可以看到屏幕上出现一组条纹，条纹的间距从远到近逐渐减少，毛细血管末端状则从宽变窄。
实验装置一夫琅费单缝实验使用的主要装置有：一个灯，一个孔成像板，一片玻璃板，一个屏幕，和一个调节螺杆。
其中灯可以利用日光进行，也可以须熄的灯进行，孔成像板由两个平行板和几段螺纹连接构成，玻璃板要以一定角度，屏幕黑白反差强烈，利于观察，调节螺杆可以调节玻璃板和孔成像板之间的距离，来调节条纹之间的间距。
实验原理一夫琅费单缝实验的原理是：灯束穿过孔成像板扩散之后，碰到玻璃板被反射，形成一个新的束线，经过玻璃板到达屏幕，这条新的束线发出的射线一进一出，但是由于它经过玻璃板的一侧与另一侧的距离不同，会发生波前锋现象，导致射线在屏幕上呈现出两种交叠的状态，形成条纹状。
实验结论从实验结果可见，当调节螺杆调节玻璃板与孔成像板之间的距离时，条纹的数量和间距会发生明显变化，这实验表明：光确实是电磁波，光分解为螺旋状电磁波，具有波长，波场的特性，具有反射，折射，吸收，衍射等这实验也被广泛应用于声学，它也证实了谱的物理意义。
总结一夫琅和费单缝实验是用来验证光是电磁波的经典实验，它表明射线经过扩孔可以分散，经过反射或折射的时候，会发生波前锋现象，从而可以在屏幕上看到交叠的条纹。
它不仅证明了光是电磁波，还是一种证实了谱物理意义的经典实验，被广泛用于声学实验。
《夫琅禾费单缝衍射》课件
。
引入新技术与新方法
随着科技的发展，可以引入新的技术 和方法来研究衍射现象，例如计算机
模拟和人工智能等。
THANKS 感谢观看
05 结论与展望
本课程的主要结论
衍射现象的描述
详细解释了夫琅禾费单缝衍射的物理现象，包括 衍射波的分布、衍射角与波长的关系等。
数学模型的建立
介绍了如何通过波动光学理论建立夫琅禾费单缝 衍射的数学模型，并进行了数值模拟。
实验验证
通过实验手段验证了数学模型的准确性，并分析 了实验误差。
对未来研究的建议
分析了缝宽变化对衍射图样和光强分布的影响，得出了缝宽 增大时，衍射现象越明显的结论。
理论预测与实验结果的比较
将实验结果与理论预测进行了比较，验证了理论模型的正确 性。
结果与理论的比较
理论模型介绍
介绍了衍射的理论模型，包括波动理论和光的衍射公式等。
实验结果与理论预测的符合程度
详细分析了实验结果与理论预测的符合程度，证明了实验结果的可靠性和准确性 。
深入研究多缝衍射
可以进一步研究多缝衍射的现象，探索其与单缝衍射的异同点。
引入非线性效应
考虑在衍射过程中引入非线性效应，研究其对衍射结果的影响。
提高实验精度
通过改进实验设备和方法，提高衍射实验的精度和可靠性。
课程展望
拓展应用领域
探讨夫琅禾费单缝衍射在光学、信息 处理和其他相关领域的应用前景。
加强理论与实践结合
根据实验数据，分析夫琅禾费单 缝衍射的规律和特点，并与理论 值进行比较。
04 结果与讨论
实验结果展示
实验数据记录
详细记录了实验过程中测量的数据，包括不同缝宽下的衍射图样和对应的测量 结果。
单缝夫琅禾费衍射原理
单缝夫琅禾费衍射原理嘿，朋友们！今天咱们来唠唠单缝夫琅禾费衍射这个超级有趣的物理现象，就像走进了一个微观世界里的魔法光影剧场。
想象一下，单缝就像一个超级挑剔的门卫，光线呢，就像是一群想要闯进派对的小光子精灵。
这个单缝的宽度啊，窄得就像一根头发丝儿那么精细，对光线来说简直就是一道难以逾越的窄门。
当光线这个调皮的家伙冲向单缝时，就好像一群蚂蚁冲向一个小得可怜的洞口，它们可不会规规矩矩地排成一队走过去。
光子精灵们开始各自施展魔法，它们的路径变得歪歪扭扭，就像喝醉了酒的小虫子。
然后呢，在单缝后面的屏幕上，就出现了神奇的光影画面。
中间最亮的部分，那简直就是光子精灵们开大会的地方，明亮得像太阳落在了屏幕上，这个叫做中央亮纹。
它就像是光的国王，端坐在中间，周围的光线都像是它的臣民，众星捧月般围绕着。
而两边那些逐渐暗下去的条纹啊，就像是国王的卫队，离国王越远，卫队的士兵就越少，光也就越暗。
这些条纹就像是用光绘制出来的神秘花纹，有的宽，有的窄，就像斑马的条纹一样不规则又很有规律。
如果把这个过程比作一场音乐会，单缝就是那个独特的乐器，光线就是乐手，屏幕就是舞台。
不同的光线弹奏出不同的旋律，最后在舞台上呈现出这奇妙的光影音乐秀。
这个单缝夫琅禾费衍射的原理啊，就像是一个神秘的魔法咒语。
光线按照这个咒语，在微观世界里表演着一场盛大的光影舞蹈。
每一个光子都像是一个训练有素的舞者，它们知道自己该怎么扭动，怎么排列，才能在屏幕上画出那一幅幅美丽的光影画卷。
有时候我就在想，这微观世界里的光线就像是一群有自己想法的小捣蛋鬼。
单缝就像是一个给它们设置好的游戏关卡，它们要想尽办法突破这个关卡，然后在屏幕上留下自己独特的痕迹。
这就像我们小时候玩游戏，在一个小小的空间里创造出大大的乐趣。
在这个微观的光影世界里，单缝夫琅禾费衍射就像是一个永远也挖掘不完的宝藏。
每一次研究它，就像是探险家发现了新的宝藏岛屿，总会有新的惊喜和奇妙之处等待着我们去发现。
浙江省大学物理试题库413-夫琅禾费单缝衍射
浙江工商大学 学校 413 条目的4类题型式样及交稿式样1. 选择题题号：41311001 分值：3分难度系数等级：1在单缝夫琅禾费衍射实验中，波长为的单色光垂直入射在宽度为a ＝4的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为 (A) 2 个。
(B) 4 个。
(C) 6 个。
(D) 8 个。
[ ]答案：（B ）题号：41311002 分值：3分难度系数等级：1一束波长为的平行单色光垂直入射到一单缝AB 上，装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为 (A)．(B) ．(C) 3/ 2 ． (D) 2 ．[ ]答案：（B ）题号：41312003 分值：3分难度系数等级：2在如图所示的单缝夫琅禾费衍射实验中，若将单缝沿透镜光轴方向向透镜平移，则屏幕上的衍射条纹(A) 间距变大。
(B) 间距变小。
(C) 不发生变化。
(D) 间距不变，但明暗条纹的位置交替变化。
［ ］答案：（C ）题号：41312004 分值：3分CfD LABλ屏幕fL单缝λ难度系数等级：2在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小。
(B) 对应的衍射角变大。
(C) 对应的衍射角也不变。
(D) 光强也不变。
［］答案：（B）题号：41314005分值：3分难度系数等级：4一单色平行光束垂直照射在宽度为1.0 mm的单缝上，在缝后放一焦距为2.0 m的会聚透镜．已知位于透镜焦平面处的屏幕上的中央明条纹宽度为 2.0 mm，则入射光波长约为(1nm=10−9m)(A) 100 nm (B) 400 nm(C) 500 nm (D) 600 nm［］答案：（C）题号：41312006分值：3分难度系数等级：2在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹(A) 宽度变小。
浙江省大学物理试题库413-夫琅禾费单缝衍射教学文案
浙江省大学物理试题库413-夫琅禾费单缝衍射浙江工商大学 学校 413 条目的4类题型式样及交稿式样1. 选择题 题号：41311001 分值：3分 难度系数等级：1在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a ＝4 λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为 (A) 2 个。
(B) 4 个。
(C) 6 个。
(D) 8 个。
[ ]答案：（B ）题号：41311002 分值：3分 难度系数等级：1一束波长为λ的平行单色光垂直入射到一单缝AB 上，装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为(A) λ / 2．(B) λ．(C) 3λ / 2 ． (D) 2λ ．[ ]答案：（B ）题号：41312003 分值：3分屏难度系数等级：2在如图所示的单缝夫琅禾费衍射实验中，若将单缝沿透镜光轴方向向透镜平移，则屏幕上的衍射条纹(A) 间距变大。
(B) 间距变小。
(C) 不发生变化。
(D) 间距不变，但明暗条纹的位置交替变化。
［ ］答案：（C ）题号：41312004 分值：3分 难度系数等级：2在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹(A) 对应的衍射角变小。
(B) 对应的衍射角变大。
(C) 对应的衍射角也不变。
(D) 光强也不变。
［ ］ 答案：（B ）题号：41314005 分值：3分 难度系数等级：4屏幕一单色平行光束垂直照射在宽度为1.0 mm的单缝上，在缝后放一焦距为2.0 m的会聚透镜．已知位于透镜焦平面处的屏幕上的中央明条纹宽度为2.0 mm，则入射光波长约为 (1nm=10−9m)(A) 100 nm (B) 400 nm(C) 500 nm (D) 600 nm［］答案：（C）题号：41312006分值：3分难度系数等级：2在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹(A) 宽度变小。
夫琅禾费单缝衍射公式
夫琅禾费单缝衍射公式1. 什么是夫琅禾费单缝衍射？好家伙，今天咱们聊聊一个神奇的现象——单缝衍射。
别看名字听起来复杂，实际上这就是光的一种神奇行为。
想象一下，你在阳光下打着一个小小的洞，光透过这个缝隙后，就像水流过一个狭窄的地方一样，开始波动。
这种波动就叫“衍射”，而夫琅禾费则是这项技术的老前辈之一，给它起了个名字，听起来特别牛逼！在科学的世界里，夫琅禾费就是个大佬，他发现了光在通过狭缝的时候，会像一个大明星一样，开始发散、变形，最后形成一些特别有趣的图案。
简单点说，就是光并不总是直线走，它也喜欢在缝隙中“逛逛”，变得有些“顽皮”。
这可不是光的任性，而是它的本性。
2. 单缝衍射的公式好吧，话不多说，进入正题。
单缝衍射的公式其实也不难理解。
公式的样子是这样的：a sin theta = n lambda 。
这里的“a” 是缝的宽度，“θ” 是衍射角，“n” 是一个整数，代表衍射的级数，“λ” 则是光的波长。
听起来有点复杂，但别担心，咱们慢慢来，像吃麻辣火锅一样，细嚼慢咽！首先，缝的宽度“a”就像是一个小小的门，越窄，光透过后就越疯狂。
如果你把门打开得大一点，光就乖乖的直走，没什么好玩的。
如果门太小，光一进去就开始“逛”，形成了一个个花花绿绿的光斑，像是在开派对，特别热闹！然后是“θ”，就是光散开的方向。
光是个调皮捣蛋的家伙，喜欢向不同的方向乱跑，而“θ”就是记录这些方向的好帮手。
每当你看到那些漂亮的条纹图案，实际上就是光在争先恐后想要找到出口的结果。
3. 衍射现象的应用说到这里，很多朋友可能会问：“这个衍射有什么用啊？”嘿嘿，别着急，应用可多了去了！首先，单缝衍射在科学实验中可是个老帮手，尤其是在光学仪器中。
比如，显微镜和望远镜就常常用到这招，帮我们看清那些微小的细节。
再者，衍射现象也应用在音乐里。
听过古典音乐的朋友可能会发现，音色的变化和光的衍射有异曲同工之妙。
音乐的和声就像光的干涉，让不同的音波交织在一起，产生出美妙的旋律。
夫琅禾费衍射求单缝宽度的不确定度
夫琅禾费衍射求单缝宽度的不确定度夫琅禾费衍射是一种重要的物理现象，它可以通过衍射花样来确定物体的尺寸，比如单缝宽度。
单缝宽度的不确定度是指在测量过程中可能存在的误差范围。
这篇文章将从夫琅禾费衍射的原理入手，详细介绍如何求出单缝宽度的不确定度。
夫琅禾费衍射原理夫琅禾费衍射是指，当光通过一个孔或一个缝时，在远离该孔或该缝处出现一系列交替明暗的亮纹和暗纹。
这一现象可以通过夫琅禾费衍射公式进行计算。
当光线通过单缝时，光线将被弯曲，并在缝后的屏幕上形成一系列明暗条纹。
这些条纹的宽度可以用夫琅禾费公式来计算，即：d sinθ = mλ其中d是缝的宽度，θ是光线和屏幕的垂直角度，m是亮条纹的次数（从中央开始），λ是光的波长。
为了测量单缝的宽度，我们将需要测量夫琅禾费衍射实验中的一些参数，包括衍射角度和亮纹的数量。
这些参数将被用于计算单缝的宽度。
测量单缝宽度的不确定度在夫琅禾费衍射实验中，我们需要测量的主要参数是亮条纹的次数和衍射角度。
对于亮条纹的次数，我们需要测量从中央开始的亮条纹数量。
对于衍射角度，我们需要测量屏幕和缝之间的角度，这个角度可以通过三角函数计算，公式如下：sinθ = (mλ)/d为了求出单缝宽度的不确定度，我们需要考虑两个方面：实验误差和计算误差。
实验误差主要来自于实验仪器和人为因素，比如光源的不稳定性、仪器的读数误差、仪器制造方面的误差以及人为误差等。
对于光源的不稳定性，我们可以采用一些措施来减小误差范围。
比如可以使用相对稳定的LED光源，或是在测量过程中保持光源的稳定状态。
对于仪器读数误差，我们可以在测量过程中进行多次测量，并取其平均值。
此外，我们也可以使用数字仪器，来避免读数误差。
对于仪器制造方面的误差，我们可以使用高精度的仪器，来减小其误差。
同时，在对仪器进行校准时也可以进一步减小误差，保证其精度和准确度。
对于人为误差，我们可以通过培训实验人员和严格控制实验条件等措施来减小误差。
计算误差主要来自于数据的不确定度，其中包括亮条纹数量和衍射角度的不确定度。
《夫琅禾费单缝衍射》课件
阐述夫琅禾费单缝衍射的实验装置和操作步骤
介绍夫琅禾费单缝衍射的基本概念和原理
物理学专业学生
物理教师
科研人员
对光学和衍射感兴趣的公众
PART THREE
夫琅禾费单缝衍射是衍射的一种形式
衍射现象：光通过单缝后，在屏幕上形成明暗相间的条纹
衍射条纹：随着缝宽的增加，明暗相间的条纹逐渐变得模糊不清
定义：在远场条件下，将点光源发出的光通过单缝，经过远处的屏幕进行衍射
在光学信号处理和图像处理中的应用
在光学通信和光电子技术中的应用
在光学测量和检测技术中的应用
光学干涉测量
光学信息处理
光学精密测量
光学通信
光学仪器设计：夫琅禾费单缝衍射用于设计各种光学仪器，如望远镜、显微镜等，提高仪器的分辨率和成像质量。
激光技术：在激光技术中，夫琅禾费单缝衍射可用于控制激光束的形状和大小，提高激光加工的精度和效率。
PART FOUR
夫琅禾费单缝衍射装置
实验操作步骤：包括光路调整、测量数据和结果分析等
单缝衍射装置：包括单缝、屏幕和测量尺
光源：激光或单色光源
记录数据：在不同缝宽下，记录衍射条纹的位置和宽度
分析数据：根据记录的数据，分析缝宽与衍射条纹之间的关系
得出结论：总结实验结果，得出夫琅禾费单缝衍射的规律
光学通信：在光纤通信中，夫琅禾费单缝衍射可用于调制光信号，提高通信系统的传输速率和稳定性。
生物医学：在生物医学领域，夫琅禾费单缝衍射可用于研究生物分子结构和功能，为疾病诊断和治疗提供有力支持。
PART SIX
在未来，夫琅禾费单缝衍射的研究前景将更加广阔
夫琅禾费单缝衍射在光学领域的应用越来越广泛
汇报人：
,
夫琅禾费单缝衍射光强分析与探讨 修改
夫琅禾费单缝衍射光强分析与探讨摘要：在夫琅禾费单缝衍射实验中,如果在透镜的物方焦面内沿着某一圆周改变光源S的位置,让透镜出射的单色平面光波都以相同的入射角H0入射到单缝衍射屏上,则单缝衍射光强分布均会发生改变,说明衍射图样的光强分布不仅和入射角H0以及衍射角H有关,而且和光源S的位置有关;考虑单缝衍射屏上光波相位的分布和平面光波的入射方位(即光源S的位置)的关系,采用矢量图解法对单缝衍射因子进行分析及计算,得到了全面的夫琅禾费单缝衍射光强公式。
关键词：单缝衍射;光强;光程差;斜入射目录1 夫琅禾费单缝衍射（一） (1)的物方焦点时的装置及现象 (1)1.1 单色点光源S位于透镜L11.2 用积分法来求夫琅禾费单缝衍射的光强………………………………（）1.3 衍射光强的极值分布条件及特点………………………………………（）2 夫琅禾费单缝衍射（二）……………………………………………………（）2.1 单色点光源S位于透镜L的物方焦面上时的装置……………………（）12.2 单缝衍射因子分析及计算………………………………………………（）3 总结…………………………………………………………………………（）1 夫琅禾费单缝衍射（一）1.1 单色点光源S位于透镜L的物方焦点时的装置及现象1如图1所示,单色点光源S置于凸透镜L1的物方焦平面上,从点光源发出的光经过透镜以后变成平行光,垂直射到宽度约为十分之几毫米的狭缝上。
缝后置一凸透镜L2,在L2象方焦平面上放置接收屏,则屏上显现出由一系列不连续的明亮短线组成的衍射图样,如图1[1]所示。
改变缝的宽度,衍射图样也发生变化,缝越宽,衍射图样越收缩,当缝宽足够大时(远大于波长),则衍射图样缩成一点,这就是点光源S在透镜中所成的象。
狭缝对光波在方向上的限制,使光在x方向上产生衍射,生成一系列沿x方向排列的明亮的短线,这些短线好像是点光源的一个扩展开的象。
如果用氮生在光器作为光源,则可以把透镜L1去掉,使激光直接照射在单缝上,并且去掉L2,在缝后足够远处(几米)屏上可观察到夫琅禾费衍射图样。
413-夫琅禾费单缝衍射
413夫琅禾费单缝衍射1. 选择题1～5 BBCBA 6～8 BDD2. 判断题1～4 错对对错3. 填空题1，答案：7.6×10-2 mm ； 2，答案：6； 3，答案：4； 4，答案：3.0 mm ； 5，答案：λ / sin θ； 6，答案：1×10-6m ； 7，答案：2； 8，答案：30°。
4. 计算题1，解答及评分标准：(1) 由单缝衍射暗纹公式得111sin λθ=a 222sin λθ=a （2分） 由题意可知 21θθ= , 21sin sin θθ=代入上式可得 212λλ= （3分）(2) 211112sin λλθk k a == (k 1 = 1, 2, ……) a k /2sin 211λθ=222sin λθk a = (k 2 = 1, 2, ……) （2分） a k /sin 222λθ= 若k 2 = 2k 1，则θ1 = θ2，即λ1的任一k 1级极小都有λ2的2k 1级极小与之重合． （3分）2，解答及评分标准：(1) 对于第一级暗纹，有a sin ϕ 1≈λ因ϕ 1很小，故tg ϕ 1≈sin ϕ 1 = λ / a （2分）故中央明纹宽度∆x 0 = 2f tg ϕ 1=2f λ / a = 1.2 cm （3分） (2) 对于第二级暗纹，有 a sin ϕ 2≈2λ （2分）x 2 = f tg ϕ 2≈f sin ϕ 2 =2f λ / a = 1.2 cm （3分）3，解答及评分标准：设第三级暗纹在ϕ3方向上，则有a sin ϕ3 = 3λ此暗纹到中心的距离为 x 3 = f tg ϕ3 （4分） 因为ϕ3很小，可认为tg ϕ3≈sin ϕ3，所以x 3≈3f λ / a ．两侧第三级暗纹的距离是 2 x 3 = 6f λ / a = 8.0mm∴λ = (2x 3) a / 6f （4分）= 500 nm （2分）4，解答及评分标准：单缝衍射第1个暗纹条件和位置坐标x 1为： a sin θ1 = λa f f f x /sin tg 111λθθ≈≈= (∵θ1很小) （3分）单缝衍射第2个暗纹条件和位置坐标x 2为： a sin θ2 = 2λa f f f x /2sin tg 222λθθ≈≈= (∵θ2很小) （3分）单缝衍射中央亮纹旁第一个亮纹的宽度 ()a a f x x x //2121λλ-≈-=∆= f λ / a =1.00×5.00×10-7 / (1.00×10-4) m （4分）=5.00 mmL θ2 θ1 Cx 2 x 1 ∆x f。
夫琅禾费单缝衍射实验报告
夫琅禾费单缝衍射实验报告夫琅禾费单缝衍射实验报告夫琅禾费单缝衍射实验是一项经典的物理实验，它揭示了光的波动性质以及光的传播中的干涉现象。
在这个实验中，我们使用一束单色光通过一个细缝，观察光的衍射现象，并记录下实验结果。
实验装置主要包括一束单色光源、一个细缝和一个屏幕。
在实验开始前，我们首先要保证实验环境的稳定性，排除干扰因素。
然后，我们调整光源的位置，使其与细缝保持适当的距离。
接下来，我们将光源打开，并将屏幕放置在光源的后方，以观察光的衍射现象。
当光通过细缝时，光的波动性质会导致光的传播方向发生改变，从而形成衍射现象。
在屏幕上，我们可以观察到一系列明暗相间的条纹，这些条纹被称为衍射条纹。
通过观察这些衍射条纹，我们可以得出一些有关光的性质的重要结论。
首先，我们可以观察到衍射条纹的中央区域最亮，这是因为在中央区域，光的传播方向发生的改变最小，光的干涉最强。
而在离中央区域越远的地方，光的干涉逐渐减弱，导致条纹变暗。
这一现象表明，光的波动性质使得光在传播过程中发生了干涉。
其次，我们还可以观察到衍射条纹的间距随着细缝的宽度减小而增大。
这是因为细缝的宽度决定了光的传播方向发生改变的程度。
当细缝宽度较大时，光的传播方向改变较小，导致衍射条纹的间距较小；而当细缝宽度较小时，光的传播方向改变较大，导致衍射条纹的间距较大。
通过这一现象，我们可以推断出光的波长与细缝宽度之间存在着一定的关系。
在实验过程中，我们还可以进一步探究夫琅禾费单缝衍射实验的一些特殊现象。
例如，当细缝的宽度非常小，接近光的波长时，我们可以观察到衍射条纹的中央区域出现明亮的中央峰。
这是因为在这种情况下，光的传播方向几乎没有发生改变，导致中央峰的亮度最大。
这一现象被称为夫琅禾费衍射。
除了夫琅禾费衍射外，我们还可以观察到衍射条纹的形状随着光源的波长变化而变化。
当光源的波长增大时，衍射条纹的间距也随之增大；而当光源的波长减小时，衍射条纹的间距也随之减小。
夫琅禾费单缝衍射解释依据
夫琅禾费单缝衍射解释依据夫琅禾费单缝衍射是指在光学镜片或其他光学元件中的缝隙处，光线在进入或离开这些元件时发生的衍射现象。
这种现象常见于光学镜片、光纤、晶体、半导体器件等光学元件中，并在日常生活中也有许多应用。
夫琅禾费单缝衍射解释依据主要源于波动电磁学理论，即光是一种电磁波，具有波长和频率的特性。
在光学镜片或其他光学元件中的缝隙处，光线会受到环境中物体的干扰，使其在空间中传播的路径发生变化，产生衍射现象。
夫琅禾费单缝衍射可以通过几何光学理论来解释。
根据几何光学的原理，光线在进入或离开光学元件时，其方向会受到物体的干扰而发生改变。
这种改变的程度取决于光线与物体的入射角度以及物体的形状和尺寸。
当光线与物体的入射角度较小时，其方向改变较小，衍射现象较弱；当光线与物体的入射角度较大时，其方向改变较大，衍射现象较强。
因此，夫琅禾费单缝衍射的强度与光线与物体的入射角度有关。
此外，夫琅禾费单缝衍射还可以通过电磁学理论来解释。
电磁学理论认为，光是一种电磁波，具有波长和频率的特性。
当光线在进入或离开光学元件时，其会受到物体的电磁场干扰，使其方向发生改变。
由于光线的波长不同，其在物体电磁场中的反应也不同，因此夫琅禾费单缝衍射的强度也与光线的波长有关。
当光线的波长较短时，其受到物体电磁场的干扰较强，衍射现象较强；当光线的波长较长时，其受到物体电磁场的干扰较弱，衍射现象较弱。
夫琅禾费单缝衍射在日常生活中有着广泛的应用，例如在光学镜片、光纤、晶体、半导体器件等光学元件中都有着重要的应用。
此外，夫琅禾费单缝衍射还可以用于光学测量、光学通信、光学显示器件等领域。
总的来说，夫琅禾费单缝衍射是指在光学镜片或其他光学元件中的缝隙处，光线在进入或离开这些元件时发生的衍射现象。
夫琅禾费单缝衍射的解释依据主要源于波动电磁学理论和几何光学理论，并在日常生活中有着广泛的应用。
夫琅禾费单缝衍射实验报告
夫琅禾费单缝衍射实验报告1.引言1.1 概述概述部分的内容可以描述夫琅禾费单缝衍射实验的背景和意义。
请参考下面的范例："夫琅禾费单缝衍射实验是一种经典的光学实验，用于研究光的衍射现象。
衍射是光线通过一个缝隙或物体边缘时发生的现象，它使光线朝不同的方向传播，产生特定的干涉图样。
夫琅禾费单缝衍射实验通过将单缝放置在光源和屏幕之间，研究光线经过缝隙后在屏幕上形成的衍射图案。
夫琅禾费单缝衍射实验具有重要的理论和实际意义。
在理论方面，通过观察和解释夫琅禾费单缝衍射实验的结果，我们能够深入了解光的波动性和光的干涉衍射现象。
实验结果与理论模型的对应关系，可以验证光的波动理论的准确性，并对光学现象的性质进行定量描述。
在实际应用中，夫琅禾费单缝衍射实验被广泛应用于光学仪器的设计和光学材料的研究。
通过精确控制和调节单缝的尺寸和光源的参数，可以实现对光的干涉衍射特性的精确测量和调控，为光学器件和光学系统的优化提供理论和实验基础。
本文将详细介绍夫琅禾费单缝衍射实验的原理和过程，并通过实验结果的分析与讨论，总结实验的关键点和注意事项。
通过本文的阐述，读者将能够了解夫琅禾费单缝衍射实验的原理和应用，以及在实验中应该注意的问题，为进一步深入研究和应用光学学科打下坚实的基础。
"1.2 文章结构本文主要介绍了夫琅禾费单缝衍射实验的原理和过程以及实验结果的分析和总结。
文章内容按照以下结构进行组织：第一部分为引言，包括概述、文章结构和目的。
在概述中，简要介绍了夫琅禾费单缝衍射实验的背景和重要性。
文章结构部分（本部分）详细说明了本文的组织结构，使读者可以清晰地了解整个文档的内容安排。
目的部分明确了本次实验的目的是什么，通过实验我们可以得到哪些信息和结论。
第二部分是正文，主要分为两个小节。
第一小节介绍了夫琅禾费单缝衍射实验的原理，详细解释了光在通过单缝时的衍射现象以及衍射图样的特点。
第二小节描述了夫琅禾费单缝衍射实验的具体过程，包括实验器材的准备、实验步骤的具体操作以及数据的记录方式。
C03P041夫朗禾费单缝衍射
sin sin a E ( ) Ca sin a
光强
sin I I0
2
sin 其中 a
I 0 Ca
2
各级亮条纹光强不相等，中央最大值的光强最大， 次极大值都远小于中央最大值
平面波：E(z, t ) Aexpkz t 复振幅：E(z) Aexpikz
平行光垂直入射，波面与衍射平面平行， 波面上的复振幅为常数，设为1
1 E x1 t ( x1 ) 0 x1 a / 2 x1 a / 2
P点的复振幅分布为
a/2
2).波长越长，衍射现象也越明显；用白光为光源，中央亮纹为白色，其他 各级条纹呈现彩色。
3) 当
a
0 ，衍射现象不明显，
a
波动光学过渡到几 所以衍射条纹形状和位置均不变。
5）若光源偏离光轴，这时为平行光非垂直入射。在缝前造成的最
大光程差为 a sin i ，结果使得衍射条纹偏离光轴。
C
exp ikz1 ik e xp x 2 y 2 ikz1 2 z1
对于单缝,不需要考虑y1
E x C E x1 exp(i 2 ux1 )dx1
E(x1):衍射屏上的复振幅分布
单缝衍射屏的振幅透过率函数为
1 t ( x1 ) 0 x1 a / 2 x1 a / 2
小结
暗纹位置
a sin n
a
0.4
0.2
-1.43 -2.45
-10
1.43 2.45
0
浙江省大学物理试题库413 夫琅禾费单缝衍射
在单缝的夫琅禾费衍射实验中，屏上第三级暗纹对应于单缝处波面可划分为 __________ 个半波带。 答案：6
题号：41331003 分值：2 分 难度系数等级：1
波长为的单色光垂直入射在缝宽 a=4的单缝上．对应于衍射角=30°，单缝处的波 面可划分为______________个半波带。 答案：4
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
413夫琅禾费单缝衍射
1. 选择题
1，在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度为a ＝4 λ的单缝上，
对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为
(A) 2 个。
(B) 4 个。
(C) 6 个。
(D) 8 个。
[ ]
2，一束波长为λ的平行单色光垂直入射到一单缝AB 上，
装置如图．在屏幕D 上形成衍射图样，如果P 是中央亮纹一侧第一个暗纹所在的位置，则BC 的长度为
(A) λ / 2． (B) λ． (C) 3λ / 2 ． (D) 2λ ．
[ ]
3，在如图所示的单缝夫琅禾费衍射实验中，若将
单缝沿透镜光轴方向向透镜平移，则屏幕上的衍射条
纹 (A) 间距变大。
(B) 间距变小。
(C) 不发生变化。
(D) 间距不变，但明暗条纹的位置交替变化。
［ ］
4，在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮
纹的中心位置不变外，各级衍射条纹
(A) 对应的衍射角变小。
(B) 对应的衍射角变大。
(C) 对应的衍射角也不变。
(D) 光强也不变。
［ ］
5，在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹 (A) 宽度变小。
(B) 宽度变大。
(C) 宽度不变，且中心强度也不变。
(D) 宽度不变，但中心强度增大。
［ ］
6，在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹 (A) 宽度变小；
屏幕
(B) 宽度变大；
(C) 宽度不变，且中心强度也不变；
(D) 宽度不变，但中心强度变小。
［］7，在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成3个半波带，则缝宽度a等于
(A) λ．(B) 1.5 λ．
(C) 2 λ．(D) 3 λ．
［］8，在白光垂直照射单缝而产生的衍射图样中，波长为λ1的光的第3级明纹与波长为λ2-的光的第4级明纹相重合，则这两种光的波长之比λ1 /λ2为
(A) 3/4 (B) 4/3
(C) 7/9 (D) 9/7
［］2. 判断题
1，对应衍射角不为零的衍射屏上某处，如果能将做夫琅和费单缝衍射的波面分割成偶数个半波带，则在屏幕上该处将呈现明条纹。
2，对应衍射角不为零的衍射屏上某处，如果能将做夫琅和费单缝衍射的波面分割成奇数个半波带，在屏幕上该处将呈现明条纹。
3，在用半波带法求解单缝夫琅和费衍射时，当衍射角不为零时，任何两个相邻的、完整的波带所发出的子波在屏幕上同一点引起的光振动将完全相互抵消。
4，用半波带法讨论单缝衍射暗条纹中心的条件时，与中央明条纹旁第二个暗条纹中心相对应的半波带的数目是2。
3. 填空题
1，He－Ne激光器发出λ=632.8 nm (1nm=10-9 m)的平行光束，垂直照射到一单缝上，在距单缝3 m远的屏上观察夫琅禾费衍射图样，测得两个第二级暗纹间的距离是10 cm，则单缝的宽度a=________．
2，在单缝的夫琅禾费衍射实验中，屏上第三级暗纹对应于单缝处波面可划分为__________ 个半波带。
3，波长为λ的单色光垂直入射在缝宽a=4λ的单缝上．对应于衍射角ϕ=30°，单缝处的波面可划分为______________个半波带。
4，在单缝夫琅禾费衍射实验中，设第一级暗纹的衍射角很小，若钠黄光(λ1≈589 nm) 中央明纹宽度为 4.0 mm，则λ2=442 nm (1 nm = 10-9m)的蓝紫色光的中央明纹宽度为
____________________
5，将波长为λ的平行单色光垂直投射于一狭缝上，若对应于衍射图样的第一级暗纹位置的衍射角的绝对值为θ，则缝的宽度等于________________。
6，如果单缝夫琅禾费衍射的第一级暗纹发生在衍射角为30°的方位上，所用单色光波长λ=500 nm (1 nm = 10-9 m)，则单缝宽度为_____________________m．
7，在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射在宽度为a=2λ的单缝上，对应于衍射角为30︒方向，单缝处的波面可分成的半波带数目为________个。
8，在单缝夫琅禾费衍射实验中，波长为λ的单色光垂直入射在宽度a=5λ的单缝上．对应于衍射角ϕ的方向上若单缝处波面恰好可分成5个半波带，则衍射角ϕ=_______________．
4. 计算题
1，在某个单缝衍射实验中，光源发出的光含有两种波长λ1和λ2，垂直入射于单缝上．假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合，试问
(1) 这两种波长之间有何关系？
(2) 在这两种波长的光所形成的衍射图样中，是否还有其他极小相重合？
2，波长为600 nm (1 nm=10-9 m)的单色光垂直入射到宽度为a=0.10 mm的单缝上，观察夫琅禾费衍射图样，透镜焦距f=1.0 m，屏在透镜的焦平面处．求：
(1) 中央衍射明条纹的宽度∆x0；
(2) 第二级暗纹离透镜焦点的距离x2．
3，某种单色平行光垂直入射在单缝上，单缝宽a = 0.15 mm．缝后放一个焦距f = 400 mm 的凸透镜，在透镜的焦平面上，测得中央明条纹两侧的两个第三级暗条纹之间的距离为8.0 mm，求入射光的波长。
4，在单缝的夫琅禾费衍射中，缝宽a=0.100 mm，平行光垂直入射在单缝上，波长λ=500 nm，会聚透镜的焦距f =1.00 m．求中央亮纹旁的第一个亮纹的宽度∆x．(1 nm =10–9 m)。