matlab基础与指导应用部分习题问题详解
MATLAB语言基础与应用(第二版)第5章 习题答案
第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答：>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答：>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布，用二次曲线拟合。
MATLAB习题与答案详解
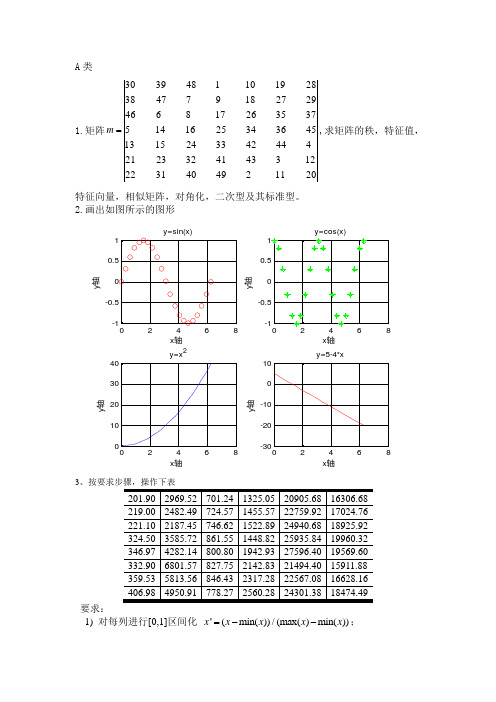
A 类1.矩阵20112494031221234341322321444423324151345363425161453735261786462927189747382819101483930=m ,求矩阵的秩，特征值，特征向量，相似矩阵，对角化，二次型及其标准型。
2.画出如图所示的图形y=sin(x)x 轴y 轴y=cos(x)x 轴y轴2468010203040y=x 2x 轴y 轴2468-30-20-10010y=5-4*xx 轴y轴3要求：1) 对每列进行[0,1]区间化 '(min())/(max()min())x x x x x =--；2) 把区间化后的表的右边3列，连接在左边3列下边，构成16行3列的表；3) 把16行3列进行转置，得到3行16列的表。
然后对列进行操作，把3行16列的表变成一列，后转置成一行，得到最终的结果。
4、下表为81)2) 把任意两点距离的表中，自己到自己的距离，转变成无穷大5.附件1给出了100个学生的学号和五门课程成绩。
1)求五门课总分最高分和最低分及相应学生的学号。
2)设计一个成绩查询系统，要求输入某学生的学号能够返回该学生各科成绩，总分以及在100个人中的名次。
B类（三选二）6.假设排列着100个乒乓球，由两个人轮流拿球装入口袋，能拿到第100个乒乓球的人为胜利者。
条件是：每次拿球者至少要拿1个，但最多不能超过5个，问：如果你是最先拿球的人，你该拿几个？以后怎么拿就能保证你能得到第100个乒乓球？7、模拟猫跑一条轨迹，轨迹为倒“8”字，轨迹如下：（条件自行拟定）8.当一个球从h米自由下落后,被地面弹起h1,再一次下落,直至平衡,如图所示,请模拟这个过程。
1 2 3 4 5 6 7 8x 4.22 7.92 6.56 8.49 6.79 7.43 6.55 7.06y 9.16 9.59 0.36 9.34 7.58 3.92 1.71 0.32。
MATLAB基础及其应用教程周开利邓春晖课后答案
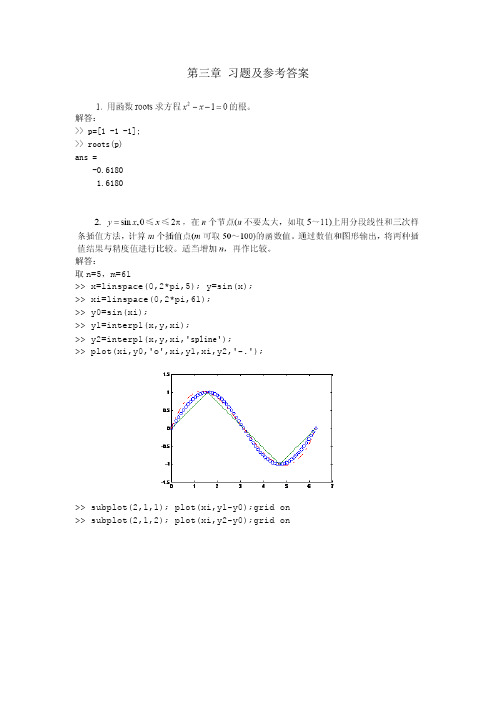
第三章习题及参考答案解答：>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答：取n=5，m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on >> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11，m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答：>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.'); >> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较，都合理，误差也相近。
MATLAB实验及答案详解
>> C3
C3 =
9 22 2
8 19 -6
36 88 3
>> D1
D1 =
2 -2 3
655
16 -10 3
>> D2
D2 =
0.5000 -2.0000 0.3333
0.6667 5.0000 0.2000
1.0000 -10.0000 3.0000
>> D3
D3 =
141
4 25 1
16 100 9
5.0000 - 5.0000i 6.0000 - 6.0000i
②求矩阵的逆矩阵
>> B=[1 2;3 4];
>> B1=inv(B) 运行后显示：
B1 = -2.0000 1.0000 1.5000 -0.5000
>> B2=B^(-1) 运行后显示： B2 =
-2.0000 1.0000 1.5000 -0.5000 ③关于矩阵求幂 >>A=[1 2;3 4]; B=[ 2 1;3 2]; >>A.^B 运行后显示： ans =
>>A=[1,2,3;4,5,6] 运行后显示： A= 123 456
在命令窗口输入：
>>b=A(1,2)
运行后显示：b =2
在命令窗口输入：
>>A(2,3)=-3
运行后显示：A =
123
4 5 -3
矩阵的操作
>>A=[1,2,3;4,5,6;7,8,9]
>>B=diag(A) %X 为矩阵时，V=diag(X,k)得到列向量 V，它取自 X 的第 K 个对角
MATLAB及其应用课后习题解答
5
“MATLAB 及其应用”课程作业
图 4- 2 画出函数图像
第5章
1． 已知椭圆的长、短轴 a 4, b 2 ，用“小红点线”画如下图所示的椭圆
x a cos t 。 y b sin t
（提示：参量 t ；点的大小；axis equal） 答 ： 运 行 :clf; a=4;b=2;t=0:pi/80:2*pi;x=a*cos(t);y=b*sin(t);plot(x,y,’r’,’markersize’,15);axis equal;xlabel(‘x’);ylabel(‘y’);shg;结果如图 5-1 所示：
1
“MATLAB 及其应用”课程作业
a5=sin(sym(pi/4)+exp(sym(0.7+pi/3))); a6=sin(sym(pi/4)+sym(exp(0.7+pi/3))); a7=sin(sym(pi/4+exp(0.7+pi/3))); a8=sym(sin(pi/4+exp(0.7+pi/3))); da2 = vpa(a1-a2,30) da3 = vpa(a1-a3,30) da4 = vpa(a1-a4,30) da5 = vpa(a1-a5,30) da6 = vpa(a1-a6,30) da7 = vpa(a1-a7,30) da8 = vpa(a1-a8,30) 结果如图 2-2 所示： 只有 a2 是精准的，观察可知，这是由 于 sym('Num')和 sym(Num)的区别带来 图 2- 2 vpa 观察误差 的前者以字符串的形式传给符号运算内 核，可以保留完整的精度；而后者经过浮点数运算之后再转换为符号类型，存在精度损 失。 3．在不加专门指定的情况下，以下符号表达式中的哪一个变量被认为是独立自由变量。 sym('sin(w*t)') , sym('a*exp(-X)' ) , sym('z*exp(j*th)') 答：分别为 w,a,z，具体图 2-3 所示。
matlab基础与应用部分习题答案
作业一4、写出完成下列操作的命令。
(1)将矩阵 A 第2~5 行中第1,3,5 列元素赋给矩阵B。
>> M=[0:1:48];>> A=reshape(M,7,7)0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 476 13 20 27 34 41 48 >> B=A(2:5,1:2:5)B =1 15 292 16 303 17 314 18 32( 2)删除矩阵 A 的第七行元素。
>> A(7,:)=[]A =0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 47 (3) 将矩阵A 的每个元素值加30。
>> A=A+30A =30 37 44 51 58 65 7231 38 45 52 59 66 7332 39 46 53 60 67 7433 40 47 54 61 68 7534 41 48 55 62 69 7635 42 49 56 63 70 77(4 求矩阵A 的大小和维素。
sizeA = size(A)dA = ndims(A) sizeA = dA =2(5)将向量t的0元素用机器零来代替。
>> t=[1 2 3 4 0 5];t =1 2 3 4 0 5>> find(t==0)ans =5>> t(5)=epst =1.00002.00003.00004.0000 0.00005.0000(6)将含有12个元素的向量x 转换成3*4 矩阵。
>> x=[0:11]x =0 1 2 3 4 5 6 7 8 9 10 >>11 y=reshape(x,3,4)y =0 3 6 91 4 7 102 5 8 117)求一个字符串的ASCII。
matlab习题与解答
matlab习题与解答MATLAB 习题与解答习题1：利用if 语句根据不同的输入a 值，获取响应的计算因子，()()()[]()0.01,560.03,80.05,0,40.00,a or a a Lfactor a else==??>?=?∈ MatLab 代码：a=input('请输入a ：');if a==5||a==6Lfactor=0.01elseif a>8Lfactor=0.03elseif a>=0&&a<=4Lfactor=0.05elseLfactor=0end运行结果：习题2：了解max 函数，执行v=[12 3.4 32 12 43]; [a n]=max(v)，其中a 返回v 的最大值，n 返回v 中最大值a 的位置。
独立编制一段程序，实现matlab 内部函数max 的功能。
MatLab 代码：v=[12 3.4 32 12 43]; [a n]=max(v)a=v(1);n=1;for i=2:length(v)if a<v(i)< bdsfid="88" p=""></v(i)<>a=v(i);n=i;endend[a n]输出结果：习题3：执行vpa(pi,20), 解释vpa函数的功能MatLab 代码：vpa(pi,20)运行结果：vpa函数功能：matlab控制运算精度用的是digits和vpa这两个函数，digits用于规定运算精度，凡是用需要控制精度的，我们都对运算表达式使用vpa函数。
习题4：求解如下方程组：4x+2y-z=23x-y+2z=1012x+3y=8MatLab 代码：A=[4 2 -1;3 -1 2;12 3 0];b=[2;10;8];A\b运行结果：习题5：创建矩阵[-1 6 15 –7 -2 -4 -6]并选出其中非正元素组成一个新的向量s1，并对s1进行升序排列行程矩阵s2 。
Matlab基础与应用教程答案
第1章一、思考题4.( 1) B=A(2:5,1:2:5)(2)A(7)=[](3)A=A+30(4)size(A)( 5) t(find(t==0))=eps(6)t=reshape(x,3,4)(7)abs('matlab')(8)char(93)5.A=[97,67,34,10;-78,75,65,5;32,5,-23,-59;0,-12,54,7] (1)B=A(1:3,:)C=A(:,1:2)D=A(2:4,3:4)E=B*C(2)A(find(A>=50 & A<=100)) 二、实验题=-74/180*pi;y=-27/180*pi;sin(x*x+y*y)/sqrt(tan(abs(x+y)))+pi一・・,exp*a).*sin(a+=[2,4;,5];log(x+sqrt(1+x.*x))/24.A=[3,54,2;34,-45,7;87,90,15];B=[1,-2,67;2,8,74;9,3,0];(1)A*Bans =129 432 41977 -407 - 1052402 591 12489A.*Bans =3 -108 13468 -360 518783 270 0(2) A A3ans =-28917 240246 -4368137883 -259101 27669171333 252504 38673A.A3ans =27 157464 839304 -91125 343658503 729000 3375( 3) A/Bans =B/A ans =（4）[A,B]ans =3 54 2 1 -2 6734 -45 7 2 8 7487 90 15 9 3 0[&[1,3],:)砂2]ans =3 54 287 90 15600 183 -81684 282 72615 6 825=1+2i;b=3+4i; c=exp(pi*i/6) c =+ c+a*b/(a+b) ans =+ 第2章一、思考题=0; for n=0:63s=s+2A n;end disp(s)n=0:63;s=sum(2.An)二、实验题1.x=input( ' 输入一个四位整数：' );y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,1 0)] z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)2. gh=input( ' 输入工号' ); h=input( ' 输入工时' );dj=84;if h>120gz=dj*120+*dj*(h-120);elseif h<60gz=dj*h-700;else gz=dj*h;end format bank; display([gh,gz])3. 循环结构n=input( 'input n:' );s=0;for k=1:n s=s+1/k A2;end display(sqrt(s*6)) 向量运算n=input( 'input n:' ); k=1:n;display(sqrt(sum(1./k.A2)*6))4.y=0;k=0;while y<3k=k+1; y=y+1/(2*k-1);end display([k-1,y-1/(2*k-1)])5.x0=0;x=1;k=0;a=input( 'a=' ); b=input( 'b=' );while abs(x-x0)>=1e-5 && k<500 x0=x;x=a/(b+x0);k=k+1;end display([k,x]); display([(-b+sqrt(bA2+4*a))/2,(-b-sqrt(bA2+4*a))/2]);6.y=fun(40)/(fun(30)+fun(20))(1)函数文件function f=fun(n) f=n+log(nA2+5);(2)函数文件function f=fun(n) a=1:n;f=sum(a.*(a+1));第3章一、思考题4.t=0::;y=sqrt(3)/2*exp(-4*t).*sin(4*sqrt(3)*t+pi/3);5.x=-10::10; y=linspace(-6,6,size(x,2))z=x.A3+3*x.*y.A2;plot3(x,y,z)6.x=100:100:400;y=100:100:400;z=[636,697,624,478;698,712,630,478;680,674,598,412;662,626,552,334]; [X,Y]=meshgrid(x,y);mesh(X,Y,z)二、实验题1.( 1 ) x=-10::10;plot(x,x-x.A3/3/2)( 2) plot(x,exp(-x.*x/2)/2/pi)(3)x=-8::8;plot(x,sqrt((64-x.*x)/2))( 4) t=0:pi/100:6*pi;plot(t.*sin(t),t.*cos(t))2.( 1) x1=linspace(0,1,100);y1=2*;t=linspace(0,pi,100);x=sin(3*t).*cos(t);y=sin(3*t).*sin(t);plot(x1,y1,'r-',x,y,'b:');text,1,'y='); text,,'x=sin(3t)cos(t)');text,,'y=sin(3t)sin(t)');(2)subplot(1,2,1);scatter(x1,y1,10)title('y=');subplot(1,2,2);scatter(x,y,10)3.subplot(1,2,1);x=1:1:100; y=sin(1./x);plot(x,y) subplot(1,2,2);fplot('sin(1/x)',[1,100])4.subplot(2,2,1);bar(t,y);subplot(2,2,2);stairs(t,y);subplot(2,2,3);stem(t,y) subplot(2,2,4); semilogy(t,y);3.theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); fi=linspace(0,2*pi,100);a=1 r=a.*(1+cos(fi));polar(fi,r);4.plot3(x,y,z);t=0::1;x=t;y=t.A2;z=t.A3;plot3(x,y,z);7.x=-30::0;y=0::30; [x,y]=meshgrid(x,y);z=10.*sin(sqrt(x.A2+y.A2))./sqrt(1+x.A2+y.A2); meshc(x,y,z);8. x=linspace(-3,3,100);y=linspace(-3,3,100);[x y]=meshgrid(x,y);fxy=-5./(1+x.A2+y.A2);i=find(abs(x)<= & abs(y)<=; fxy(i)=NaN;surf(x,y,fxy)9.u=linspace(1,10,100);v=linspace(-pi,pi,100); [u,v]=meshgrid(u,v);x=3.*u.*sin(v);y=2.*u.*cos(v);z=4*u.A2;x=3*u.*sin(v);y=2*u.*cos(v);z=4*u.A2; surf(x,y,z);shading interp;light('position',[1,0,1]);10. t=0:pi/100:2*pi; y=sin(t);comet(t,y) 第4章一、思考题5.(1)A=eye(3);(2)C=100+(200-100)*rand(5,6);( 3) D=1+sqrt*randn(1,500);( 4) E=ones(size(A));( 5) A=A+30*eye(size(A));( 6) B=diag(diag(A))二、实验题1.P=pascal(5);H=hilb(5); Dp=det(P);Dh=det(H); Kp=cond(P);Kh=cond(H);P矩阵的性能更好，因为Kp较小2.A=[1,-1,2,3;0,9,3,3;7,-5,0,2;23,6,8,3] B=[3,pi/2,45;32,-76,sqrt(37);5,72,;exp(2),0,97] A1=diag(A);B1=diag(B);A2=triu(A);B2=triu(B); A3=tril(A);B3=tril(B); rA=rank(A);rB=rank(B);nA=norm(A);nb=norm(B); cA=cond(A);cB=cond(B);3.A=[31,1,0;-4,-1,0;4,-8,-2] ；[V,D]=eig(A);4.A=diag([-1,-1,-1,-1],-1)+diag([-1,-1,-1,-1],1)+diag([2,2,2,2,2])b=[1,0,0,0,0]';x1=inv(A)*b; x2=A\b; [L,U]=lu(A); x3=U\(L\b); [Q,R]=qr(a); [Q,R]=qr(A); x4=R\(Q\b) R=chol(A); x5=R\(R'\b) 5.B=sparse(A); x1=inv(B)*b; x2=B\b; [L,U]=lu(B); x3=U\(L\b); 第5章一、思考题3.A=randn(10,5); mean(A) std(A) max(max(A)) min(min(A)) sum(A,2) sum(sum(A)) sort(A,1) sort(A,2,'descend') 二、实验题1.A=rand(1,30000); mean(A) std(A) max(A) min(A) size(find(A>)/size(A)2.h=[466,715,950,1422,1635]; w=[,,,,];hh=[500,900,1500]; ww=interp1(h,w,hh,'spline')3.x=linspace(1,10,50); y=log(x);第6章一、思考题2.fx=i nlin e('1./(1+x.A 2)');[I,n]=quad(fx,-100000,100000,1e-3); [I,n]=quadl(fx,-100000,100000,1e-3); x=-100000::100000; y=1./(1+x.*x);f=polyfit(x,y,5); yy=polyval(f,x); plot(x,y,'r-',x,yy,'g.') 4. N=64; T=5;t=linspace(0,T,N); x=3*exp(-t); % dt=t(2)-t(1); f=1/dt; X=fft(x); F=X(1:N/2+1); f=f*(0:N/2)/N;plot(f,abs(F),'-*') % %% 求各采样点样本值 x% % %采样点数 采样时间终点给岀N 个采样时间ti(l=1:N) 采样周期采样频率 (Hz)计算 x 的快速傅立叶变换 X% F(k)=X(k)(k=1:N/2+1)% 使频率轴 f 从零开始 % 绘制振幅 - 频率图xlabel('Frequency');ylabel('|F(k)|')5.(1)p1=[1 2 0 0 7];p2=[1 -2];p3=[1 0 0 5 1];p12=conv(p1,p2);p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; roots(p)(2)A=[-1,4,3;2,1,5;0,5,6];Px=polyval(p,A) Pxm=polyvalm(p,A)6.(1) z=fzero('3*x-sin(x)+1',0)(2)建立函数文件 function F=myfun(X)x=X(1);y=X(2); F(1)=x*x+y*y-9;F(2)=x+y-1; 在命令窗口中输入以下命令： x=fsolve(@myfun,[3,0]',optimset('Display','of f'))trapz(x,y);3.(1)fx=inline('-2*y+2*x*x+2*x');[t,y]=ode23(fx,[0,],1)(2)fx=inline('y-exp(x)*cos(x)');[t,y]=ode23(fx,[0,3],1)二、实验题1.for x=1:3fx=[x,xA2,xA3;1,2*x,3*x;0,2,6*x]; diff(fx)end2.(1 ) x=0::1;y=x.A10+10.Ax+1./log10(x);dy=diff(y)/;(2)x=0::1;y=log(1+x);dy=diff(y,2)/;plot(x(1:99),dy)3.(1 ) fx=inline( 'x.A2.*sqrt(2*x.*x+3)');quad(fx,1,5)(2)fx=inline( 'x./sin(x).A2' ); quad(fx,pi/4,pi/3)(3)fx=inline( 'abs(cos(x+y))' ); dblquad(fx,0,pi,0,pi)(4)syms x y;fx=x*y;int(int(fx,yA2,y+2),-1,2)x的积分区间为【0, 2】时fx=inline( 'x.*y' );dblquad(fx,0,2,-1,2)4.x=::;y=[,,,,,,];trapz(x,y)5.(1)yp=i nlin e( '-+si n( 10*x))*y' );[t,y]=ode23(yp,[0,5],1);(2)令x1y, x2y ,x3 y''，则可写出原方程的状态方程形式: x1x2X2 X3cos 1x3cost 5 X3 X2 X1(t 1)2 3 sin t0 1 0 X1 0=>> x20 0 1 X2 01 / 5cos2t X3 12X3 cost3 sint (t 1)2建立函数文件fun cti on y=ztfu n( t,x)b=[0;0;cos(t)];y=[0,1,0;0,0,1;-1/(3+si n( t)),-1,5*cos(2*t)/(t+1)A2]*x+b; 解微分方程组[t,y]=ode23(@ztfu n,[0,5],[1;0;2]);6.建立函数文件fun cti on yy=ztfu n( t,y)yy=[ y( 2)*y(3);-y(1)* y(3) ;*y(1)*y(2)];解微分方程组[t,y]=ode23(@ztfu n,[0,5],[0;1;1])第7章一、思考题3.(1 )数值积分fx=i nlin e('exp(x).*(1+exp(x)).A2'); quad(fx,0,log(2)) 符号积分f=sym('exp(x)*(1+exp(x))A2');v=in t(f,0,log (2));eval(v)(2 )略二、实验题1.A=sym('[1,2,3;x,y, z; 3,2,1]')rank(A)inv(A)det(A)2.(1)y=sym('sqrt(x+sqrt(x+sqrt(x)))');y1=diff(y)y2=diff(y,'x',2)(2)syms x y;fxy=si n( x A2*y)*exp(-x A2-y);diff(diff(fxy,x),y)3.(1)syms xin t(1/(1+xA4))(2)syms x tin t((-2*x*x+1)/(2*x*x-3*x+1)A2,x,cos(t),exp(2*t))4.syms n xsymsum(1/(2* n+1)/(2*x+1)A(2* n+1), n,0,i nf)symsum(1/(2* n+1)/(2*x+1)A(2* n+1), n, 0,5)5.(1)syms xtaylor((exp(x)+exp(-x))/2,5,0)(2)syms a xtaylor(exp(-5*x)*si n(3*x+pi/3),5,a)6.(1)x=solve(sym('xA3+a*x+1=0'))(2)[x y]=solve(sym('sqrt(xA2+yA2)-100=0,3*x+5*y-8=0'))y' y17.方程转化为：’，严y1' y 1 一符号解[y1,y11]=dsolve(,Dy=y1,Dy1+y=1-t A2/pi,,,y(-2)=5,y1(-2)=5',,t,)数值解编写函数文件fun cti on yy=ztfu n( t,y)yy=[y(2);1-tA2/pi-y(1)];在命令窗口输入以下命令[t,y]=ode45(@ztfu n,[-2,7],[-5;5]);t=li nspace(-2,7,49)y2=y8.[x,y]=dsolve('Dx=3*x+4*y,Dy=-4*x+3*y','x(0)=0,y(0)=1')第9章二、实验题1.(1 )新建一个Blank GUI。
matlab练习题及答案详解(附程序)
Matlab练习题及答案详解一、基础题1、下表为1)2) 把任意两点距离的表中，自己到自己的距离，转变成无穷大clcclearclose alldata=xlsread('ti1.xls');%从excel里导入数据x=data(1,:);%将data里第一行的所有列赋值给xy=data(2,:);%将data里第二行的所有列赋值给xn=length(x);%表x的长度dis=zeros(n,n);%对距离表进行初始化for i=1:nfor j=1:ndis(i,j)=sqrt((x(i)-x(j))^2+(y(i)-y(j))^2);%平面坐标距离公式endenddis(dis==0)=inf;%将距离表中为0的数值，变成无穷大redis=dis;2、按要求步骤，操作下表要求：1) 对每列进行[0,1]区间化'(min())/(max min())=--；x x x x2) 把区间化后的表的右边3列，连接在左边3列下边，构成16行3列的表；3) 把16行3列进行转置，得到3行16列的表。
然后对列进行操作，把3行16列的表变成一列，后转置成一行，得到最终的结果。
clcclearclose allx=load('ti2.txt');%从txt里导入数据big=max(x);small=min(x);%算出每列的最大最小值[m,n]=size(x);%表x的行和列的大小newx1=zeros(m,n);%对newx1进行初始化，大小和初始x一样大for i=1:nnewx1(:,i)=(x(:,i)-small(i))./(big(i)-small(i));endnewx2=zeros(2*m,n/2);%对最新的表进行初始化大小为，行为newx1的2倍，列为一半newx2(1:m,1:n/2)=newx1(1:m,1:n/2);%把左边3列不操作的值，直接赋值给newx2上边newx2(m+1:end,1:n/2)=newx1(1:m,n/2+1:end);%把右边的3列，赋值给newx2下边[p,q]=size(newx2);%表newx2的行和列的大小 newx3=zeros(p*q,1);%对newx3进行初始化 for j=1:qnewx3((j-1)*p+1:j*p,1)=newx2(:,q);%对newx3进行操作 end% newx3=reshape(newx2,[],1); renewx=newx3';%最终的结果3、数值运算1)用matlab 求下列式子极限(a) lim x → (b) 0x →2)用matlab 求下列函数的导数(a)22sin (1)y x =+ (b) arccos()(,)x f x y ye =3)用matlab 求下列式子的定积分(a) 4⎰(b) 312-⎰⎰clc clear %===求极限 %====3.1.a=== syms xy=(x^(1/2)-8)/(x^(1/3)-4);re1a=limit(y,x,64)%====3.1.b===syms xy=((x^2-2*x+4)^(1/2)-2)/x;re1b=limit(y,x,0)%===求导数%====3.2.a===syms xf=(sin(x^2+1))^2;re2a=diff(f,x)%对x求导%====3.2.b===syms x yf=y*exp(acos(x));re2bx=diff(f,x)%对x求偏导re2by=diff(f,y)%对y求偏导%===求定积分===%====3.3.a===syms xre3a=int((x+2)/(2*x+1)^(1/2),x,0,4)%一重积分%====3.3.b===syms x yre3b=int(int(y/(x^2-1),x,-2,-sqrt(2)),y,1,3)%二重积分二、提高题1、画一个正五边形，边长自定。
matlab基础与应用教程课后答案
matlab基础与应用教程课后答案matlab基础与应用教程课后答案【篇一：matlab教程基本应用练习题及解答】txt>要求：将每题的答案（命令行和运行结果、图片或m文件的文件名及具体内容）直接拷贝插入到各题的下方：（1）若为命令行，要求将提示符“”一起拷入，并在右侧用“％”注明命令行的每条命令的作用；（2）若为多个运行结果，拷入后要求解释每个结果具体对应题目中的哪个要求，也在右侧用“％”注明；（3）如果为m 文件，除了将文件名和此文件的具体内容全部拷入外，再将所有原始m文件和本练习题电子版放在一个以“专业班级＋本人姓名＋学号”命名的文件夹内一起上传。
ans =1 0 00 1 00 0 1ans =0 0 00 0 0ans =1 1 11 1 11 1 11 1 120+40*rand(1,10) %生成10个在区间[20,60]上均匀分布的随机数。
ans =44.617351.677556.872549.528327.050636.228257.418856.6 76236 .410855.7460二．1）计算向量（2，4，6，8）的最大值，最小值，平均值，中值，排序，总和值； max([2,4,6,8])%最大值ans =8min([2,4,6,8])% 最小值ans =2mean([2,4,6,8])% 平均值ans =5median([2,4,6,8])% 中值ans =5sort([2,4,6,8])% 排序ans =2 4 6 8sum([2,4,6,8])% 总和值ans =202）在行向量（2，4，6，8）和（1，3，5，7）之间实施加减乘除及幂运算； a=[2 4 6 8];b=[1 3 5 7];a+b%加ans =3 7 11 15a-b%减ans =a.*b%乘ans =2 12 30 56a./b%除ans =2.0000 1.3333 1.2000 1.1429a.^b%幂ans =2 64 7776 20971523）在向量（1，3，5）与标量2之间实施加减乘除及幂运算。
MATLAB基础与应用第二版课后习题答案
通信电路仿真上机试题班级：姓名：学号：第一章4.gcd函数用于求两个数的最大公约数。
现拥有help命令查看该函数的用法，然后利用该函数15和35的最大约数。
程序: >> help gcdGCD Greatest common divisor.G = GCD(A,B) is the greatest common divisor of correspondingelements of A and B. The arrays A and B must contain non-negativeintegers and must be the same size (or either can be scalar).GCD(0,0) is 0 by convention; all other GCDs are positive integers.[G,C,D] = GCD(A,B) also returns C and D so that G = A.*C + B.*D.These are useful for solving Diophantine equations and computingHermite transformations.See also LCM.结果：>> g=gcd(15,35)g =56.以致三角形的三边a=9.6，b=13.7，c=19.4，求三角形的面积。
提示：利用海伦公式area=sqrt(s*(s-a)*(s-b)*(s-c))计算，其中s=(a+b+c)/2。
程序：clearclca=9.6,b=13.7,c=19.4s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c))结果：a = 9.6000 b =13.7000 c = 19.4000 s = 21.3500 area = 61.1739第二章5.计算下列分段函数0 x<=5F（x）= (x-3)/4 5<x<=102*x x>10程序：clearclcx=input('请输入一个数,x=');if x<=5y=0;elseif x>5&x<=10y=(x-3)/4;else x>10y=2*x;endy结果：请输入一个数,x=11y =228.已知S=1+2+2^2+2^3+…+2^63，求S 的值。
(完整版)matlab经典习题及解答
第1章 MATLAB 概论1.1 与其他计算机语言相比拟，MATLAB 语言突出的特点是什么？MATLAB 具有功能强大、使用方便、输入简捷、库函数丰富、开放性强等特点。
1.2 MATLAB 系统由那些局部组成？MATLAB 系统主要由开发环境、MATLAB 数学函数库、MATLAB 语言、图形功能和应用程序接口五个局部组成。
1.4 MATLAB 操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？在MATLAB 操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口成为独立窗口的Undock 按钮，点击Undock 按钮就可以使该窗口脱离桌面成为独立窗口，在独立窗口的view 菜单中选择Dock ……菜单项就可以将独立的窗口重新防止的桌面上。
1.5 如何启动M 文件编辑/调试器？在操作桌面上选择“建立新文件〞或“翻开文件〞操作时，M 文件编辑/调试器将被启动。
在命令窗口中键入edit 命令时也可以启动M 文件编辑/调试器。
1.6 存储在工作空间中的数组能编辑吗？如何操作？存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名翻开数组编辑器，再选中要修改的数据单元，输入修改内容即可。
1.7 命令历史窗口除了可以观察前面键入的命令外，还有什么用途？命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M 文件中。
1.8 如何设置当前目录和搜索路径，在当前目录上的文件和在搜索路径上的文件有什么区别？当前目录可以在当前目录浏览器窗口左上方的输入栏中设置，搜索路径可以通过选择操作桌面的file 菜单中的Set Path 菜单项来完成。
在没有特别说明的情况下，只有当前目录和搜索路径上的函数和文件能够被MATLAB 运行和调用，如果在当前目录上有与搜索路径上相同文件名的文件时那么优先执行当前目录上的文件，如果没有特别说明，数据文件将存储在当前目录上。
MATLAB语言基础与应用(第二版)第1章 习题答案
第1章习题与答案1.1 MA TLAB桌面主要有哪些窗口构成？这些窗口主要功能是什么？请参考1.3节1.2计算下列表达式(1) 3+6 (2) sin(1+i)(3) (1+2i)×(2-i) (4) 2×4+3解答：(1) >> 3+6ans = 9(2) >> sin(1+i)ans = 1.2985 + 0.6350i(3) >> (1+2*i)*(2-i)ans = 4.0000 + 3.0000i(4) >> 2*4+3ans = 111.3借助“help”函数了解“meshgrid”函数的意义。
解答：>> help meshgridmeshgrid Cartesian grid in 2-D/3-D space[X,Y] = meshgrid(xgv,ygv) replicates the grid vectors xgv and ygv toproduce the coordinates of a rectangular grid (X, Y). The grid vectorxgv is replicated numel(ygv) times to form the columns of X. The gridvector ygv is replicated numel(xgv) times to form the rows of Y.[X,Y,Z] = meshgrid(xgv,ygv,zgv) replicates the grid vectors xgv, ygv, zgvto produce the coordinates of a 3D rectangular grid (X, Y, Z). The gridvectors xgv,ygv,zgv form the columns of X, rows of Y, and pages of Zrespectively. (X,Y,Z) are of size numel(ygv)-by-numel(xgv)-by(numel(zgv).[X,Y] = meshgrid(gv) is equivalent to [X,Y] = meshgrid(gv,gv).[X,Y,Z] = meshgrid(gv) is equivalent to [X,Y,Z] = meshgrid(gv,gv,gv).The coordinate arrays are typically used for the evaluation of functionsof two or three variables and for surface and volumetric plots.meshgrid and NDGRID are similar, though meshgrid is restricted to 2-Dand 3-D while NDGRID supports 1-D to N-D. In 2-D and 3-D the coordinates output by each function are the same, the difference is the shape of theoutput arrays. For grid vectors xgv, ygv and zgv of length M, N and Prespectively, NDGRID(xgv, ygv) will output arrays of size M-by-N whilemeshgrid(xgv, ygv) outputs arrays of size N-by-M. Similarly,NDGRID(xgv, ygv, zgv) will output arrays of size M-by-N-by-P whilemeshgrid(xgv, ygv, zgv) outputs arrays of size N-by-M-by-P.Example: Evaluate the function x*exp(-x^2-y^2)over the range -2 < x < 2, -4 < y < 4,[X,Y] = meshgrid(-2:.2:2, -4:.4:4);Z = X .* exp(-X.^2 - Y.^2);surf(X,Y,Z)Class support for inputs xgv,ygv,zgv:float: double, singleinteger: uint8, int8, uint16, int16, uint32, int32, uint64, int64 See also surf, slice, ndgrid.Overloaded methods:codistributed/meshgridgpuArray/meshgridReference page in Help browserdoc meshgrid1.4通过帮助浏览器窗口了解函数sin和cos。
MATLAB程序设计和应用课后习题答案解析
西安科技大学MATLAB程序设计专业：信息与计算科学班级：1001班学号：1008060129姓名：刘仲能2012年6月27日实验一2.已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=723302131B 求下列表达式的值：（1）A+6*B 和A-B+I （其中I 为单位矩阵） （2）A*B 和A.*B （3）A^3和A.^3 （4）A/B 及B\A（5）[A,B]和[A([1,3],:);B^2]3.设有矩阵A 和B ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=25242322212019181716151413121110987654321A ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=11134079423096171603B （1） 求它们的乘积C 。
（2） 将矩阵C 的右下角3×2子矩阵赋给D 。
（3） 查看MATLAB 工作空间的使用情况(1) (2)（3）4.完成下列操作（1）求[100,999]之间能被21整除的数的个数。
（2）建立一个字符串向量，删除其中的大写字母。
(1)(2)实验二3.建立一个5×5矩阵，求它的行列式值、迹、秩和范数。
运行截图：A 矩阵的行列式值、迹、秩分别如下：范数如下：4.已知 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=5881252018629A 求A 的特征值及特征向量，并分析其数学意义。
运行截图：5.下面是一个线性方程组：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.06/15/14/15/14/13/14/13/12/1321x x x （1） 求方程的解； （2） 将方程右边向量元素改为0.53，在求解，并比较的变化和解的相对变化；（3） 计算系数矩阵A 的条件数并分析结论。
（2） 变大，其解中，相对未变化前的的解：x1变大，x2变小，x3变大。
（3）由于A 矩阵的条件数很大，故当线性方程组中的b 变大时，x 也将发生很大的变化，即数值稳定性较差。
matlab基本理解练习知识题(带答案解析)
Matlab 基础练习题常量、变量、表达式1、 MATLAB 中，下面哪些变量名是合法的？（） （A ）_num （B ）num_ （C ）num-（D ）-num2、 在MATLAB 中，要给出一个复数z 的模，应该使用（）函数。
（A ）mod(z)（B ）abs(z)（C ）double(z)（D ）angle(z)3、 下面属于MATLAB 的预定义特殊变量的是？（）（A ）eps（B ）none （C ）zero （D ）exp4、 判断：在MATLAB 的内存工作区中，存放一个英文字符 'a' 需要占用1个字节，存放一个中文字符‘啊’需要占用2个字节。
（ 错，都是2个字节）5、 判断：MATLAB 中，i 和j （对 ）6、 判断：MATLAB 中，pi 代表圆周率，它等于3.14。
（ 错，后面还有很多位小数 ）7、 在MATLAB 中，若想计算的51)3.0sin(21+=πy 值，那么应该在MATLAB 的指令窗中输入的MATLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。
8、 在MATLAB 中，a = 1，b = i ，则a 占_8__个字节，b 占_16_个字节，c 占________字节。
9、 在MATLAB 中，inf 的含义是__无穷大__，nan 的含义是__非数（结果不定）___。
数组1、在MATLAB中，X是一个一维数值数组，现在要把数组X中的所有元素按原来次序的逆序排列输出，应该使用下面的（）指令。
（A）X[end:1] （B）X[end:-1:1] （C）X (end:-1:1)（D）X(end:1)2、在MATLAB中，A是一个字二维数组，要获取A的行数和列数，应该使用的MATLAB的命令是（）。
（A）class(A) （B）sizeof(A) （C）size(A)（D）isa(A)3、在MATLAB中，用指令x=1:9生成数组x。
MATLAB习题问题详解
MATLAB习题问题详解习题二1.如何理解“矩阵是MATLAB最基本的数据对象”？答：因为向量可以看成是仅有一行或一列的矩阵，单个数据（标量）可以看成是仅含一个元素的矩阵，故向量和单个数据都可以作为矩阵的特例来处理。
因此，矩阵是MA TLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵，问：(1)A*B和A.*B的值是否相等？答：不相等。
(2) A./B和B.\A的值是否相等？答：相等。
(3)A/B和B\A的值是否相等？答：不相等。
(4)A/B和B\A所代表的数学含义是什么？答：A/B等效于A的逆左乘B矩阵，即inv(A)*B，而B/A等效于A矩阵的逆右乘B矩阵，即B*inv(A)。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答：B=A(2:5,1:2:5);(2)删除矩阵A的第7号元素。
答：A(7)=[](3)将矩阵A的每个元素值加30。
答：A=A+30;(4)求矩阵A的大小和维数。
答：size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答：t(find(t==0))=eps;矩阵。
(6)将含有12个元素的向量x转换成34答：reshape(x,3,4);(7)求一个字符串的ASCII码。
答：abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符。
答：char(49);4.下列命令执行后，L1、L2、L3、L4的值分别是多少？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答：L1的值为(0, 0, 0, 0, 1, 0, 0, 0, 0)L2的值为(1, 1, 1, 1, 1, 0, 0, 0, 0)L3的值为(0, 0, 0, 1, 1, 1, 0, 0, 0) L4的值为(4, 5, 6)5.已知23100.7780414565532503269.5454 3.14A --??=-?? 完成下列操作： (1)取出A 的前3行构成矩阵B ，前两列构成矩阵C ，右下角32?子矩阵构成矩阵D ，B 与C 的乘积构成矩阵E 。
MATLAB语言入门习题讲解(精编文档).doc
【最新整理，下载后即可编辑】<MATLAB 语言入门>习题讲解 1. 求下列联立方程的解81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y x程序A=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10];B=[4;-3;9;-8];X=A\B解：X =-1.4841-0.68160.5337-1.24292. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=81272956313841A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=793183262345B 求C1=AB’;C2=A’B;C3=A.*B,并求它们的逆阵。
程序 A=[1,4,8,13;-3,6,-5,-9;2,-7,-12,-8];B=[5,4,3,-2;6,-2,3,-8;-1,3,-9,7];C1= A*B',C2 = A'*B, C3 = A.*Binv(C1),inv(C2),inv(C3)3. a. 列出2×2阶的单位矩阵I, 4×4阶魔方矩阵M 和4×2阶的全幺矩阵A,全零矩阵Bb. 将这些矩阵拼接为6×6阶的矩阵C:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=M B A I C ' c. 求出C 的第2,4,6行,组成3×6阶的矩阵C1,及第2,4,6,裂,组成6×3阶的矩阵C2,d. 求D=C1C2及D1=C2C1.程序 >>I=eye(2),A=ones(4,2),B=zeros(4,2),M=magic(4),C=[I,A';B,M]>> C1=C([2,4,6,],:),C2=C(:,[2,4,6,])>> D=C1*C2, D1=C2*C14．设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点，画出以x 为横坐标，y 为纵坐标的曲线 解：程序x=linspace(0,2*pi,101)y=cos(x).*(0.5+3*sin(x)./(1+x.^2));plot(x,y),grid5．求代数方程3x 5+4x 4+7x 3+2x 2+9x+12=0的所有根。
MATLAB课后习题分解
第一部分 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e=+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.52. 已知：1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：(1) A+6*B 和A-B+I （其中I 为单位矩阵） (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2]3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量，删除其中的大写字母。
第二部分 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
2. 产生5阶希尔伯特矩阵H 和5阶帕斯卡矩阵P ，且求其行列式的值Hh 和Hp 以及它们的条件数Th 和Tp ，判断哪个矩阵性能更好。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作业一4、写出完成下列操作的命令。
（1）将矩阵A第2~5行中第1,3,5列元素赋给矩阵B。
>> M=[0:1:48];>> A=reshape(M,7,7)A =0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 476 13 20 27 34 41 48>> B=A(2:5,1:2:5)B =1 15 292 16 303 17 314 18 32（2）删除矩阵A的第七行元素。
>> A(7,:)=[]A =0 7 14 21 28 35 421 8 15 22 29 36 432 9 16 23 30 37 443 10 17 24 31 38 454 11 18 25 32 39 465 12 19 26 33 40 47 (3)将矩阵A的每个元素值加30。
>> A=A+30A =30 37 44 51 58 65 7231 38 45 52 59 66 7332 39 46 53 60 67 7433 40 47 54 61 68 7534 41 48 55 62 69 7635 42 49 56 63 70 77(4求矩阵A的大小和维素。
sizeA = size(A)dA = ndims(A)sizeA =6 7dA =2（5）将向量t的0元素用机器零来代替。
>> t=[1 2 3 4 0 5];t =1 2 3 4 0 5>> find(t==0)ans =5>> t(5)=epst =1.00002.00003.00004.0000 0.00005.0000（6）将含有12个元素的向量x转换成3*4矩阵。
>> x=[0:11]x =0 1 2 3 4 5 6 7 8 9 10 11 >> y=reshape(x,3,4)y =0 3 6 91 4 7 102 5 8 11（7）求一个字符串的ASCII。
>> abs('a')ans =97（8）求一个ASCII所对应的字符。
>> char(99)ans =c5、已知A[97 67 34 10-78 75 65 532 5 -23 -590 = -12 54 7]写出完成下列操作的命令。
（1）取出A的前3列构成矩阵B，前两列构成矩阵C，右下角3*2子矩阵构成矩阵D，B与C的乘积构成矩阵E。
>> B=A(1:3,:)B =97 67 34 10-78 75 65 532 5 -23 -59>> C=A(:,1:2)C =97 67-78 7532 50 -12>> D=A(2:4,3:4)D =65 5-23 -5954 7>> E=B*CE =5271 11574-11336 6641978 3112（2）输出【50,100】围的全部元素。
>> find(A>=50 & A<=100)ans =1561012>> output = [A(1) A(5) A(6) A(10) A(12)]output =97 67 75 65 54二、实验题>> x = -74*pi/180;y=-27*pi/180;sin((x*x+y*y))/(sqrt(tan((abs(x+y))))+pi) ans =0.1987 - 0.1434i>> a = -3.0:0.1:3.0,exp(-0.3.*a).*sin(a+0.3)>> x=[2 4;-0.45 5];0.5*log(x+sqrt(1+x.*x))ans =0.7218 1.0474-0.2180 1.1562>> A = [3 54 2;34 -45 7;87 90 15],B = [1 -2 67;2 8 74;9 3 0]>> A*BA.*Bans =129 432 41977 -407 -1052402 591 12489ans =3 -108 13468 -360 518783 270 0>> A^3A.^3>> A/BB\A>> [A,B][A([1,3],:);B^2]>> a=1+2i,b=3+4i,c=exp(pi/6*i)c+a*b/(a+b)作业二1、从键盘输入一个4位整数，按如下规则加密后输出。
加密规则：每位数字都加上7，然后用和除以10的余数取代该数字；然后将第1位数和第3位数交换，第2位数和第4位数交换。
M 文件名为：Untitled1.m程序：x=input('输入一个四位整数：');y=[fix(x/1000),mod(fix(x/100),10),mod(fix(x/10),10),mod(x,10)]z=mod((y+7),10)x=z(3)*1000+z(4)*100+z(1)*10+z(2)结果：输入一个四位整数：1234y =1 2 3 4z =8 9 0 1x =1892、硅谷公司员工的工资计算方法如下。
（1）工作时数超过120h者，超过部分加发15%。
（2）工作时数低于60h者，扣发700元。
（3）其余按每小时84元计发。
试编程按输入的工号和该号员工的工时数，计算应发工资。
程序：gonghao=input('输入工号');hour=input('输入工时');every=84;if hour>120gongzi=every*120+1.15* every *(hour-120);elseif hour<60gongzi=every*hour-700;elsegongzi=devery*hour;endformat bank;display([gonghao,gongzi])（1）结果：输入工号12输入工时130ans =12.00 11046.00（2）结果：输入工号12输入工时56ans =12.00 4004.00（3）结果：输入工号12输入工时80ans =12.00 6720.003、 根据n 2222211116321++++= π，求π的近似值。
当n 分别取100、1000、10000时，结果是多少？要求：分别用循环结构和向量运算（使用sun 函数）来实现。
（1）程序：（循环结构）：n=input('input n:');s=0;for i=1:ns=s+1/i^2;pai= sqrt(s*6);enddisplay(pai)input n:100pai =3.1321（2）程序：（向量结构）：n=input('input n:');i=1:n;pai= sqrt(sum(1./i.^2)*6);display(pai);结果：input n:100pai =3.13214、 根据12151311-++++=n y ，求： （1） y ﹤3时的最大n 值；（2） 与（1）的n 值对应的y 值。
y=0;k=0;while y<3k=k+1;y=y+1/(2*k-1);enddisplay([k-1,y-1/(2*k-1)])结果：ans =56.00 2.995、 考虑一下迭代公式：x x nn b a +=+1 其中，a 、b 为正的常数。
（1） 编写程序求迭代的结果，迭代的终止条件为|x x n n -+1|≤105-，迭代初值0.10=x ，迭代次数不超过500次。
程序：x0=1.0;a=input('a=');b=input('b=');x= a/(b+x0); m=1;while abs(x-x0)>1e-5 & m<500x0=x;x=a/(b+x0);m=m+1;enddisplay([m,x]);display([(-b+sqrt(b^2+4*a))/2,(-b-sqrt(b^2+4*a))/2]);结果：a=5b=5ans =7.0000 0.8541 ans =0.8541 -5.8541（2）如果迭代过程收敛于r，那么r的准确值是24 2ab b++-，当（a，b）的值取（1，1）、（8,3）、（10,0.1）时，分别对迭代结果和准确值进行比较。
a=1b=1ans =13.0000 0.6180ans =0.6180 -1.6180a=8b=3ans =13.0000 1.7016ans =1.7016 -4.7016a=10b=0.1ans =424.0000 3.1127 ans =3.1127 -3.21276、已知)20()30()40(f f f y +=（1） 当)5(10)(2++=n l n n f n 时，y 的值是多少？ 程序：该题使用了function 的调用。
函数文件f.m function b=f(n); b=n+10*log(n^2+5); 结果：y=f(40)/(f(30)+f(20)) y = 0.6390（2） 当)1(433221)(+⨯++⨯+⨯+⨯=n n n f 时，y 的值是多少？ 程序：函数文件fun.m function f=fun(n) f=sum([1:n].*([1:n]+1));结果：y=fun(40)/(fun(30)+fun(20)) y =1.7662作业三1、绘制下列曲线。
（1）!33x x y -= （2）exy 2221-=π（3）64222=+yx（4）⎩⎨⎧==tt y tt x cos sin解：（1）程序：x=-5:0.001:5;y=x-x.^3/(3*2*1);plot(x,y);(2)程序：x=-10:0.01:10;y= exp(-x.*x/2)/(2*pi); >> plot(x,y); （3） 程序：f='x.^2+2*y.^2-64';ezplot(f,[-10,10,-10,10]); ezplot('x.^2+2*y.^2-64',[-10,10,-10,10]); （4）程序：t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t); >> plot(x,y);已知⎩⎨⎧==-=(t)sin(3t)sin y (3t)cos(t)sin 5.02x x y 和，π≤≤t 0，完成下列操作：（1） 在同一坐标系下用不同的颜色和线型绘制两条曲线，给曲线添加文字说明；解：程序：x1=linspace(0,1,100);>> y1=2*x1-0.5;>> t=linspace(0,pi,100);>> x=sin(3*t).*cos(t);>> y=sin(3*t).*sin(t);>> plot(x1,y1,'k:',x,y,'bp');>> text(0.5,1,'y=2x-0.5');>> text(-0.5,0.5,'x=sin(3t)cos(t)');>> text(-0.5,0.4,'x=sin(3t)sin(t)');（2）以子图形式，分别用条形图和散点图绘制两条曲线，并为各子图添加函数标题。