福建省莆田市第六中学2021-2022高一数学上学期期中试题(B卷)(含解析)
福建省2022-学年高一数学上学期期中试题(B)

2021-2021 学年高一上期数学期中考试卷 考试时长:120 分钟,总分值:150, ,使用时间:11.18 一、选择题:本大题有 12 小题,每题 5 分,共 60 分,在每题给出的四个选项中,只有一项 符合题目要求.
1.设集合
,
,那么
〔〕
A.
B.
C.
【答案】B
【解析】
,
D. ,根据集合的补集的概念得到
A. 0,1 B. 1,2 C. 2,3 D. 3,
6、一空间几何体的三视图如下图,那么该几何体的体积为 〔〕 A. 1 B. 3 C. 6 D. 2 7、函数 f(x)=1+与在同一坐标系中的图象大致是( )
8. 如图是水平放置的平面图形的斜二测直观图,其原来平面 图形面积是〔 〕 A. 2 B. 4 C. 6 D. 8
,为奇函数,故排除 ;
对于 .
,由于定义域为
,不关于原点对称,故函数不具有奇偶性,故排
除;
对于 .
,由
,为偶函数,当
时,
,是增函数,
故 正确; 应选:D. 【点睛】此题考查函数的性质和运用,考查函数的奇偶性和单调性及运用,注意定义的运用, 以及函数的定义域,属于根底题和易错题.
5、函数
的零点所在区间是
A.
B.
C.
D.
【答案】C 【解析】 【分析】 计算各区间端点的函数值,根据零点的存在性定理判断.
【详解】
在
上为增函数,
且
,
,
,
,
的零点所在区间为
.
应选:C. 【点睛】此题考查了函数零点的存在性定理,对数运算,属于根底题. 6、一空间几何体的三视图如以下图所示,那么该几何体的体积为〔 〕
2020-2021学年福建省莆田市高一(上)期中考试数学试卷人教A版(2019)

2020-2021学年福建省莆田市高一(上)期中考试数学试卷一、选择题1. 设集合A={1,2,3},B={x|x2=1},则A∪B=( )A.⌀B.{1,2,3}C.{1}D.{−1,1,2,3}2. 命题“∃x0∈R,x2+4x+5>0”的否定是( )A.∃x0∈R,x2+4x+5>0B.∃x0∈R,x2+4x+5≤0C.∀x∈R,x2+4x+5>0D.∀x∈R,x2+4x+5≤03. 设x∈R,则“x>2”是“x2>4”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4. 函数f(x)=2x−1,x∈{−1, 1},则f(x)的值域为( )A.[−3, 1)B.(−3, 1]C.[−3, 1]D.{−3, 1}5. 下列函数中,既是偶函数又在(0, +∞)单调递增的函数是()A.y=x3B.y=|x|+1C.y=−x2+1D.y=2−|x|6. 已知函数f(x)={2x, x≤0,−(12)x,x>0,则f(f(2))=( )A.−4B.−12C.−8 D.127. 已知α∈{−3, −2, 13, 2},若幂函数f(x)=xα为奇函数,且在(0, +∞)上单调递减,则α的值为( ) A.−3 B.−2 C.13D.28. 已知y=f(x)是奇函数,若g(x)=f(x)+2,且g(1)=1,则g(−1)=( )A.1B.2C.3D.4二、多选题已知集合A={1, 16, 4x},B={1, x2},若B⊆A,则x可能取值有( )A.0B.−4C.1D.4以下说法正确的有( )A.实数x>y>0是1x<1y成立的充要条件B.不等式ab≤(a+b2)2对a,b∈R恒成立C.命题“∃x∈R,x2+x+1≥0”的否定是“∀x∈R,x2+x+1<0"D.若1x+1y=1,则x+y的最小值是4已知a,b,c为实数,且a>b>0,则下列不等式正确的是( )A.1a<1bB.ac2>bc2C.ba<abD.a2>ab>b2已知f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称,当0≤x≤1时,f(x)=x,关于函数g(x)=|f(x)|+f(|x|),下列说法正确的是( )A.g(x)为偶函数B.g(x)在(−1,0)上单调递增C.方程g(x)=0在[0,4]上恰有三个实根D.g(x)的最大值为2三、填空题已知f(2x+1)=3x−5,f(3)=________.已知函数f(x)=1−m5x+1是奇函数,则实数m的值为________.若函数y=f(x)的定义域是[0, 4],则函数g(x)=√x−1的定义域是________. 设a>0,b>0,称2aba+b为a,b的调和平均数.如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆.过点C作AB的垂线交半圆于D.连接OD,AD,BD.过点C作OD的垂线,垂足为E.则图中线段OD的长度是a,b的算术平均数,线段________的长度是a,b的几何平均数,线段________的长度是a,b的调和平均数.四、解答题已知函数f(x)=√4−x√x+3的定义域为集合A.(1)求集合A;(2)若集合B={x∈N|0<x<3},求A∩B并写出它的所有子集.已知命题p:∀x∈[1, 2],x2−a≥0,命题q:∃x∈R,x2+2ax+2−a=0.若命题p与q都是真命题,求实数a的取值范围.已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)现已画出函数f(x)在y轴左侧的图像,如图所示,请补出完整函数f(x)的图像,并根据图像写出函数f(x)的增区间;(2)写出函数f(x)的解析式和值域.已知函数f(x)=x+mx,且此函数图象过点(1, 5).(1)求f(x)的解析式;(2)讨论函数f(x)在[2, +∞)上的单调性?并证明你的结论.(3)求函数f(x)在区间[2, 4]上的最小值和最大值.如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=4米.(1)要使矩形AMPN的面积大于50平方米,则DN的长应在什么范围?(2)当AN的长为多少米时,矩形花坛AMPN的面积最小?并求出最小值.定义在非零实数集上的函数f(x)对任意非零实数x,y满足:f(xy)=f(x)+f(y),且当0<x<1时,f(x)<0.(1)求f(−1)及f(1)的值;(2)求证:f(x)是偶函数;)≤0.(3)解不等式:f(2)+f(x2−12参考答案与试题解析2020-2021学年福建省莆田市高一(上)期中考试数学试卷一、选择题1.【答案】D【考点】并集及其运算【解析】本题主要通过并集的基本概念,结合一元二次方差进行求解即可【解答】解:∵A={1,2,3},B={−1,1},∴A∪B={−1,1,2,3}.故选D.2.【答案】D【考点】命题的否定全称命题与特称命题【解析】根据命题的否定规则,将量词否定,结论否定,即可得到结论.【解答】解:将量词否定,结论否定,可得命题“∃x0∈R,x2+4x+5>0”的否定是:“∀x∈R,x2+4x+5≤0”.故选D.3.【答案】A【考点】一元二次不等式的解法必要条件、充分条件与充要条件的判断【解析】本题主要考查充分性与必要性的说明,结合一元二次方程进行求解即可【解答】解:由“x>2”可以推出“x2>4”,但由“x2>4”可以推出“x>2”或“x<−2”,则“x>2”是“x2>4”的充分不必要条件.故选A.4.【答案】D【考点】函数的值域及其求法元素与集合关系的判断【解析】根据函数的定义域可知该函数定义域中只含2个元素,分别代入解析式,从而可求出该函数的值域.【解答】解:f(−1)=−2−1=−3,f(1)=2−1=1.所以该函数的值域为{−3, 1}.故选D.5.【答案】B【考点】函数奇偶性的判断函数单调性的判断与证明【解析】根据奇函数、偶函数的定义,偶函数图象的对称性,以及二次函数、一次函数的单调性即可判断每个选项函数的奇偶性和在(0, +∞)上的单调性,从而便可找出正确选项.【解答】解:A,y=x3是奇函数,故此选项错误;B,y=|x|+1为偶函数,当x>0时,y=x+1为增函数,故此选项正确;C,二次函数y=−x2+1在(0, +∞)上单调递减,故此选项错误;D,指数函数y=2−|x|为偶函数,当x>0时,y=2−x为减函数,故此选项错误.故选B.6.【答案】C【考点】分段函数的应用 函数的求值【解析】本题主要是通过分段函数代入具体的函数值进行求解即可 【解答】解:∵f (2)=−(12)2=−14 ,且−14<0, ∴f (−14)=2−14=−8,∴f(f (2))=−8. 故选C . 7.【答案】 A【考点】幂函数的单调性、奇偶性及其应用 【解析】利用幂函数的性质求解. 【解答】解:∵ 幂函数f(x)=x α为奇函数,且在(0, +∞)上单调递减, ∴ α为奇数,且α<0, 根据选项可得,α=−3. 故选A . 8.【答案】 C【考点】函数奇偶性的性质 函数的求值【解析】利用函数的奇偶性,利用条件先求出f(1)的值,然后求g(−1)的值. 【解答】解:因为g(x)=f(x)+2,所以g(1)=f(1)+2=1, 所以f(1)=−1.因为y =f(x)是奇函数,所以f(−1)=−f(1)=1. 所以g(−1)=f(−1)+2=1+2=3. 故选C .二、多选题 【答案】 A,B【考点】集合的包含关系判断及应用 集合的确定性、互异性、无序性【解析】根据集合的包含关系与集合元素的互异性进行判断. 【解答】解:∵ A ={1, 16, 4x},B ={1, x 2},若B ⊆A ,则x 2=16或x 2=4x ,则x =−4或0或4. 又当x =4时,4x =16,A 集合出现重复元素, 因此x =0或−4. 故选AB . 【答案】 B,C【考点】必要条件、充分条件与充要条件的判断 命题的否定 基本不等式【解析】本题主要考查命题的真假判断,主要结合不等式的性质以及基本不等式和命题的否定进行考查 【解答】解:A ,当x <0,y >0时,1x<1y 显然成立,故选项A 错误;B ,当ab >0时,由基本不等式易得成立, 当ab <0时,(a+b 2)2≥0,得不等式成立,当ab =0时,易得不等式也成立,故选项B 正确; C ,命题“∃x ∈R ,x 2+x +1≥0”的否定是 “∀x ∈R ,x 2+x +1<0”,故选项C 正确; D ,x +y =(x +y ) (1x +1y ) =2+xy +yx ≥2+2√xy ⋅y x =4,当且仅当yx=xy ,且x >0,y >0时,等号成立,如当x=−1,y=12时,符合题意,但x+y=−1+12=−12<4,故选项D错误.故选BC.【答案】A,C,D【考点】不等式的基本性质【解析】本题主要运用作差法以及代特殊值法进行不等式的判断大小.【解答】解:A,∵a>b>0,∴1a <1b,故选项A正确;B,当c=0时,很明显ac2>bc2不成立,故选项B错误;C,∵a>b>0,∴0<ba <1<ab,故选项C正确;D,a2−ab=a(a−b),∵a>b>0,∴a−b>0,∴a2−ab=a(a−b)>0,∴a2>ab.ab−b2=b(a−b)>0,∴ab>b2,∴a2>ab>b2,故选项D正确.故选ACD.【答案】A,D【考点】函数奇偶性的判断函数单调性的判断与证明函数的最值及其几何意义【解析】此题暂无解析【解答】解:A,g(−x)=|f(−x)|+f(|−x|)=|−f(x)|+f(|x|)=g(x),∴g(x)为偶函数,故选项A正确;B,x∈(−1,0),则−x∈(0,1),∴f(−x)=−x,|x|∈(0,1),∴f(|x|)=|x|,∴g(x)=|f(x)|+f(|x|)=|−f(−x)|+|x|=|x|+|x|=2|x|=−2x,∴g(x)在(−1,0)上单调递减,故选项B错误;C,因为f(x)的图象关于直线x=1对称. 又f(x)是奇函数,所以f(x)是周期为4的函数,其部分图象如下图所示:所以当x≥0时,g(x)={2f(x),x∈[4k,2+4k],0,x∈(2+4k,4+4k],k∈N.g(x)在[0,4]上有无数个零点,故C错误;D,当x≥0时,易知g(x)的最大值为2,由偶函数的对称性可知,当x<0时,g(x)的最大值也为2,所以g(x)在整个定义域上的最大值为2,故D正确.故选AD.三、填空题【答案】−2【考点】函数的求值【解析】关于本题考查的函数的值,需要了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能得出正确答案.【解答】解:f(2x+1)=3x−5,f(3)=f(2×1+1)=3×1−5=−2.故答案为:−2.【答案】2【考点】函数奇偶性的性质【解析】根据函数的解析式,可求出函数的定义域,进而根据定义在R上的奇函数,图象必过原点,构造方程,解方程可得m的值.【解答】解:∵函数f(x)=1−m5x+1的定义域为R,且函数f(x)=1−m5x+1为奇函数,∴ f(0)=1−m 50+1=1−m 2=0, 解得m =2. 故答案为:2. 【答案】 (1, 2] 【考点】函数的定义域及其求法 【解析】由函数y =f(x)的定义域,列出不等式组,从而求出函数g(x)的定义域. 【解答】解:由函数y =f(x)的定义域是[0, 4], 在函数g(x)=√x−1中,令{0≤2x ≤4,x −1>0,解得1<x ≤2.所以函数g(x)的定义域是(1, 2]. 故答案为:(1, 2]. 【答案】 CD ,DE 【考点】 平均值不等式 【解析】在直角三角形中,由DC 为高,根据射影定理可得CD 2=AC ⋅CB ,变形两边开方,得到CD 长度为a ,b 的几何平均数;根据a ,b 与OC 之间的关系,表示出OC 的长度,根据直角三角形OCE 和直角三角形CDE 之间边的关系得到CE 的长,得到OE 进而ED ,得到结果. 【解答】解:在Rt △ADB 中DC 为高,由相似三角形的性质易得CD 2=AC ⋅CB , ∴ CD =√ab ,即CD 长度为a ,b 的几何平均数, 将OC =a −a+b 2=a−b 2,CD =√ab ,OD =a+b 2代入OD ⋅CE =OC ⋅CD ,可得CE =a−ba+b √ab ,故OE =√OC 2−CE 2=(a−b)22(a+b),∴ ED =OD −OE =2ab a+b,∴ DE 的长度为a ,b 的调和平均数. 故答案为:CD ;DE . 四、解答题 【答案】解:(1)∵ 函数f(x)=√4−x √x+3,∴ 函数的定义域为:{4−x ≥0,x +3>0,解得−3<x ≤4,∴ 集合A ={x|−3<x ≤4}.(2)∵ 集合B ={x ∈N|0<x <3}={1, 2}, 集合A ={x|−3<x ≤4}, ∴ A ∩B ={1, 2},∴ A ∩B 的所有子集为:⌀,{1},{2},{1, 2}. 【考点】函数的定义域及其求法 交集及其运算 子集与真子集【解析】(1)根据函数解析式有意义,列出不等式组,即可求出集合A . (2)先求出集合A ,再求出A ∩B ,从而写出A ∩B 的所有子集. 【解答】解:(1)∵ 函数f(x)=√4−x √x+3,∴ 函数的定义域为:{4−x ≥0,x +3>0,解得−3<x ≤4,∴ 集合A ={x|−3<x ≤4}.(2)∵ 集合B ={x ∈N|0<x <3}={1, 2}, 集合A ={x|−3<x ≤4}, ∴ A ∩B ={1, 2},∴ A ∩B 的所有子集为:⌀,{1},{2},{1, 2}.【答案】解:根据题意,命题p:∀x∈[1, 2],x2−a≥0,若命题p为真,必有a≤(x2)min=1,即a≤1;对于命题q,∃x∈R,x2+2ax+2−a=0,若命题q为真,即方程x2+2ax+2−a=0有解,则有Δ=4a2−4(2−a)≥0,解可得:a≥1或a≤−2.若命题p与q都是真命题,即{a≤1,a≥1或a≤−2,则有a≤−2或a=1.故a的取值范围为{a|a≤−2或a=1}.【考点】复合命题及其真假判断一元二次不等式的解法【解析】根据题意,求出命题p和命题q为真命题时a的取值范围,求出其交集即可得答案.【解答】解:根据题意,命题p:∀x∈[1, 2],x2−a≥0,若命题p为真,必有a≤(x2)min=1,即a≤1;对于命题q,∃x∈R,x2+2ax+2−a=0,若命题q为真,即方程x2+2ax+2−a=0有解,则有Δ=4a2−4(2−a)≥0,解可得:a≥1或a≤−2.若命题p与q都是真命题,即{a≤1,a≥1或a≤−2,则有a≤−2或a=1.故a的取值范围为{a|a≤−2或a=1}.【答案】解:(1)函数图像如图所示:f(x)的递增区间是(−1, 0),(1, +∞).(2)∵x≤0时,f(x)=x2+2x, 令x>0, 则−x<0,故f(−x)=x2−2x,∵函数f(x)为偶函数,∴f(x)=f(−x),∴当x>0时,f(x)=x2−2x.∴f(x)={x2+2x,x≤0,x2−2x,x>0,值域为:{y|y≥−1}.【考点】函数的单调性及单调区间函数图象的作法函数解析式的求解及常用方法函数的值域及其求法【解析】(1)根据函数f(x)是定义在R上的偶函数,图象关于y轴对称,从而得到函数f(x)在y 轴右侧的图象,再根据图象得到增区间;(2)根据函数图象可得函数的解析式,和值域;【解答】解:(1)函数图像如图所示:f(x)的递增区间是(−1, 0),(1, +∞).(2)∵x≤0时,f(x)=x2+2x,令x>0, 则−x<0,故f(−x)=x2−2x,∵函数f(x)为偶函数,∴f(x)=f(−x),∴当x>0时,f(x)=x2−2x.∴f(x)={x2+2x,x≤0,x2−2x,x>0,值域为:{y|y≥−1}.【答案】解:(1)∵函数图象过点(1, 5).得1+m=5,解得m=4,∴f(x)=x+4x.(2)函数f(x)在[2, +∞)上的单调递增,证明如下:∀x1,x2∈[2,+∞),且x1<x2,f(x1)−f(x2)=x1+4x1−x2−4x2=(x1−x2)+4(x2−x1)x1x2=(x1−x2)(x1x2−4)x1x2,∵x1,x2∈[2,+∞)且x1<x2,∴x1−x2<0,x1x2>4,x1x2>0,∴f(x1)−f(x2)<0,即f(x1)<f(x2),∴f(x)在[2,+∞)上单调递增.(3)由f(x)在[2, +∞)上单调递增,可知函数f(x)在区间[2, 4]上也单调递增,当x=2时,函数取得最小值4,当x=4时,函数取得最大值5.【考点】函数解析式的求解及常用方法函数的单调性及单调区间函数的最值及其几何意义【解析】(1)将点(1, 5)代入f(x)=x+mx求m,再求f(x)的解析式;(2)求f(x)的导数f′(x)≥0,利用导数判断在[2, +∞)上的单调性;(3)区间[2, 4]⊆[2, +∞),函数f(x)在区间[2, 4]也单调递增,利用单调性求最值.【解答】解:(1)∵函数图象过点(1, 5).得1+m=5,解得m=4,∴f(x)=x+4x.(2)函数f(x)在[2, +∞)上的单调递增,证明如下:∀x1,x2∈[2,+∞),且x1<x2,f(x1)−f(x2)=x1+4x1−x2−4x2=(x1−x2)+4(x2−x1)x1x2=(x1−x2)(x1x2−4)x1x2,∵x1,x2∈[2,+∞)且x1<x2,∴x1−x2<0,x1x2>4,x1x2>0,∴f(x1)−f(x2)<0,即f(x1)<f(x2),∴f(x)在[2,+∞)上单调递增.(3)由f(x)在[2, +∞)上单调递增,可知函数f(x)在区间[2, 4]上也单调递增,当x=2时,函数取得最小值4,当x=4时,函数取得最大值5.【答案】解:(1)设DN的长为x(x>0)米,则AN=x+4米.∵DNAN=DCAM,∴AM=3(x+4)x,∴S AMPN=AN⋅AM=3(x+4)2x,由矩形AMPN的面积大于50得:3(x+4)2x>50,又x>0,得:3x2−26x+48>0,解得:0<x<83或x>6,即DN长的取值范围为:(0,83)∪(6,+∞).(2)由(1)得,矩形花坛AMPN的面积为:y=3(x+4)2x=3x2+24x+48x=3x+48x+24≥2√3x⋅48x+24=48,当且仅当3x=48x,即x=4时,矩形花坛AMPN的面积取得最小值48,故DN的长为4米时,矩形AMPN的面积最小,最小值为48平方米.【考点】一元二次不等式的应用基本不等式在最值问题中的应用【解析】此题暂无解析【解答】解:(1)设DN的长为x(x>0)米,则AN=x+4米.∵DN AN=DC AM, ∴ AM =3(x+4)x, ∴ S AMPN =AN ⋅AM =3(x+4)2x,由矩形AMPN 的面积大于50得:3(x+4)2x>50,又x >0,得: 3x 2−26x +48>0, 解得: 0<x <83或x >6,即DN 长的取值范围为: (0,83)∪(6,+∞). (2)由(1)得,矩形花坛AMPN 的面积为: y =3(x +4)2x =3x 2+24x +48x =3x +48x +24≥2√3x ⋅48x+24=48,当且仅当3x =48x,即x =4时,矩形花坛AMPN 的面积取得最小值48,故DN 的长为4米时,矩形AMPN 的面积最小,最小值为48平方米. 【答案】解:(1)在f(xy)=f(x)+f(y)中,令x =y =1, 则f(1)=f(1)+f(1), ∴ f(1)=0, 再令x =y =−1,则f(1)=f(−1)+f(−1), ∴ f(−1)=0.(2)在f(xy)=f(x)+f(y)中,令y =−1, 则f(−x)=f(x)+f(−1)=f(x), ∴ f(−x)=f(x), ∴ f(x)为偶函数.(3)任取x 1,x 2∈(0, +∞),且x 1<x 2, ∴ 0<x 1x 2<1,∴ f(x1x 2)<0,∴ f(x 1)=f(x 2⋅x 1x 2)=f(x 2)+f(x1x 2)<f(x 2),∴ f(x)在(0, +∞)是增函数, ∴ f(x)在(−∞, 0)是减函数,∵ f(2)+f(x 2−12)=f(2x 2−1)≤0=f(1)=f(−1),∴ {2x 2−1<0,2x 2−1≥−1,或{2x 2−1>0,2x 2−1≤1,解得−√22<x <√22或−1≤x <−√22或√22<x ≤1, ∴ 不等式的解集为[−1, −√22)∪(−√22, √22)∪(√22, 1]. 【考点】抽象函数及其应用 函数的求值 函数奇偶性的判断 不等式的概念与应用【解析】(1)分别令x =y =1,x =y =−1,求出f(1)和f(−1)的值; (2)令x =x ,y =−1,即可求出f(−x)=f(x),f(x)为偶函数(3)先判断函数的单调性,在根据单调性得到关于x 的不等式组,解得即可. 【解答】解:(1)在f(xy)=f(x)+f(y)中,令x =y =1, 则f(1)=f(1)+f(1), ∴ f(1)=0, 再令x =y =−1,则f(1)=f(−1)+f(−1), ∴ f(−1)=0.(2)在f(xy)=f(x)+f(y)中,令y =−1, 则f(−x)=f(x)+f(−1)=f(x), ∴ f(−x)=f(x), ∴ f(x)为偶函数.(3)任取x 1,x 2∈(0, +∞),且x 1<x 2, ∴ 0<x 1x 2<1,∴ f(x1x 2)<0,∴ f(x 1)=f(x 2⋅x 1x 2)=f(x 2)+f(x1x 2)<f(x 2),∴ f(x)在(0, +∞)是增函数, ∴ f(x)在(−∞, 0)是减函数,∵ f(2)+f(x 2−12)=f(2x 2−1)≤0=f(1)=f(−1),第21页 共22页 ◎ 第22页 共22页∴ {2x 2−1<0,2x 2−1≥−1,或{2x 2−1>0,2x 2−1≤1,解得−√22<x <√22或−1≤x <−√22或√22<x ≤1,∴ 不等式的解集为[−1, −√22)∪(−√22, √22)∪(√22, 1].。
2021-2022学年福建省泉州市晋江市第一中学高一上学期期中质量检测数学试题(解析版)

2021-2022学年福建省泉州市晋江市第一中学高一上学期期中质量检测数学试题一、单选题1.设集合{1,2,3},{2,3,4}A B ==,则A B ⋃=A .{}123,4,, B .{}123,, C .{}234,, D .{}134,, 【答案】A【详解】由题意{1,2,3,4}A B ⋃=,故选A.点睛:集合的基本运算的关注点:(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图.2.已知命题2:R,210p x x x ∀∈-+≥,则p ⌝为( ) A .2R,210x x x ∃∈-+≥ B .2R,210x x x ∃∈-+< C .2R,210x x x ∀∈-+< D .2R,210x x x ∀∈-+≤ 【答案】B【分析】根据全称命题的否定为特称命题,可选出答案.【详解】由题意可知,命题2:R,210p x x x ∀∈-+≥的否定为:2,210x R x x ∃∈-+<, 故选:B.3.函数1()2x f x a -=+(0a >且1a ≠)的图像必经过定点是( ) A .()1,2 B .()1,3C .()0,2D .()0,1【答案】B【分析】利用01a =,求解指数型函数图像过的定点. 【详解】10x -=时,有1x =,则0(1)2123f a =+=+=,∴函数1()2x f x a -=+(0a >且1a ≠)的图像必经过定点是()1,3. 故选:B4.下列函数中,既是偶函数又在区间(,0)-∞上单调递增的是( ) A .2yxB .y x =C .ln y x =D .e x y -=【答案】A【分析】判断单调性和奇偶性得到A 正确,根据单调性排除BD ,根据奇偶性排除C ,得到答案. 【详解】对选项A :函数定义域为()(),00,∞-+∞,()2y f x x -==,2fx x f x ,函数为偶函数,当0x <时,函数单调递增,满足;对选项B :当0x <时,y x =-,函数单调递减,排除;对选项C :ln y x =的定义域为()0,∞+,是非奇非偶函数,排除; 对选项D :当0x <时,e x y -=单调递减,排除. 故选:A.5.已知函数()2log 030x x x f x x >⎧=⎨≤⎩,,,则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是( ) A .9- B .9C .19-D .19【答案】D【分析】根据题意,直接计算即可得答案. 【详解】解:由题知,211log 244f ⎛⎫==- ⎪⎝⎭,()2112349f f f -⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭.故选:D6.设3log 2a =,5log 2b =,2log πc =,则( ) A .a c b >> B .b c a >> C .c b a >> D .c a b >>【答案】D【详解】因为321log 2log 3a ==,521log 2log 5b ==,而22log 3log 21c =>=,2log 51>, 所以01a <<,01b <<, 又22log 5log 31>>, 所以2211log 5log 3<,即01b a <<<, 所以有c a b >>. 故选D .7.函数()()2ln 23f x x x =--的单调递增区间是( )A .().1-∞-B .(),1∞-C .()1,+∞D .()3,+∞【答案】D【解析】先由2230x x -->求出函数的定义域,再利用复合函数的单调性即可求解. 【详解】由2230x x -->可得()()310x x -+>,解得:3x >或1x <-,所以函数()()2ln 23f x x x =--的定义域为()(),13,-∞-+∞,因为()()2ln 23f x x x =--是由ln y t =和223t x x =--复合而成,因为ln y t =在定义域内单调递增,223t x x =--对称轴为1x =,开口向上,所以223t x x =--在(),1-∞-单调递减,在()3,+∞单调递增, 根据复合函数同增异减可得:()()2ln 23f x x x =--在(),1-∞-单调递减,在()3,+∞单调递增,所以函数()()2ln 23f x x x =--的单调递增区间是()3,+∞,故选:D【点睛】关键点点睛:本题解题的关键点是先计算函数的定义域,外层函数单调递增,只需求二次函数在定义域内的增区间即可.8.定义:区间[]()x x x x <1212,的长度为21x x -,已知函数2x y =的定义域为[]a b ,,值域为[]12,,记区间[]a b ,的最大长度为m ,最小长度为.n 则方程()ln m x n -+=20的实根个数( )A .1B .2C .0D .3【答案】B【分析】作出函数2xy =的图象,从而结合图象可得m ,n 的值;进而方程()ln m x n -+=20的根的个数转化为函数y m =与()ln y x n =+的图象交点的个数,分别作出函数的图象即可求解.【详解】由题意可知,作函数2xy =的图象,如图所示函数2xy =的定义域为[]a b ,,值域为[]12,, 可知区间[]a b ,的最大长度为2m =,最小长度为1n =,所以()ln m x n -+=20,即()ln x +=14方程()ln x -+=2210的根的个数转化为函数4y =与()ln y x =+1的图象交点的个数作函数4y =与()ln y x =+1的图象,如图所示由图可知,函数4y =与()ln y x =+1的图象有2个交点,所以方程()ln m x n -+=20的实根个数为2.故选:B .二、多选题9.下列说法正确的是( )A .命题“x ∀∈R ,21x >-”的否定是“x ∃∈R ,21x <-”B .命题“(3,)x ∃∈-+∞,29x ≤”的否定是“(3,)x ∀∈-+∞,29x >”C .“22x y >”是“x y >”的必要而不充分条件D .“0m <”是“关于x 的方程220x x m -+=有一正一负根”的充要条件 【答案】BD【解析】A.根据全称命题的否定的书写规则来判断;B. 根据特称命题的否定的书写规则来判断;C.根据充分性和必要性的概念判断;D. 根据充分性和必要性的概念判断. 【详解】解:A.命题“x ∀∈R ,21x >-”的否定是“x ∃∈R ,21x ≤-”,故错误; B.命题“(3,)x ∃∈-+∞,29x ≤”的否定是“(3,)x ∀∈-+∞,29x >”,正确;C.22x y x y >⇔>,x y >不能推出x y >,x y >也不能推出x y >,所以“22x y >”是“x y >”的既不充分也不必要条件,故错误;D.关于x 的方程220x x m -+=有一正一负根44000m m m ->⎧⇔⇔<⎨<⎩,所以“0m <”是“关于x 的方程220x x m -+=有一正一负根”的充要条件,正确,故选:BD.【点睛】本题考查全称命题,特称命题否定的写法,以及充分性,必要性的判断,是基础题. 10.下列各组函数表示的是同一个函数的是( )A .()f x x =与()g x =B .()f x =()g x x =C .2()lg f x x =与()2lg g x x =D .()xf x x=与0()g x x =【答案】AD【分析】根据两个函数定义域相同,对应关系也相同,判断它们是同一个函数即可得出结果.【详解】对于A 选项,()f x x =,定义域为R ,()||g x x ==,定义域为R ,两函数定义域相同, 对应关系相同,是同一个函数,所以A 选项正确;对于B 选项,()f x ==-(,0]-∞,()g x x =(,0]-∞, 两函数对应关系不同,不是同一个函数,所以B 选项错误;对于C 选项,2()lg f x x =,定义域(,0)(0,)-∞+∞,()2lg g x x =,定义域为(0,)+∞, 两函数定义域不同,不是同一个函数,所以C 选项错误;对于D 选项,()1xf x x==,定义域(,0)(0,)-∞+∞,0()1g x x ==,定义域(,0)(0,)-∞+∞, 两函数定义域相同,对应关系相同,是同一个函数,所以D 选项正确, 故选:AD11.若0m n >>,则下列结论一定成立( )A .1155m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B .lg()0m n ->C .1m n -π>D .11m mn n+>+ 【答案】AC【分析】利用指数函数单调性可以判定A 和C 选项,对数函数性质可判定B 选项, D 选项可代入特殊值法判断.【详解】若0m n >>,则0m n ->,根据指数函数单调性性质,直接得1155m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,01m n ππ->=,所以A 和C 选项正确,由对数函数性质,当01m n <-<时, lg()0m n -<,当1m n ->时,lg()0m n ->,所以B 选项错误,取特殊值3m =,12n =,1813m n +=+, 6mn =,所以11m m n n+<+,即D 选项错误, 故选:AC12.—般地,若函数()f x 的定义域为[],a b ,值域为[],ka kb ,则称[],a b 为()f x 的“k 倍跟随区间”;特别地,若函数()f x 的定义域为[],a b ,值域也为[],a b ,则称[],a b 为()f x 的“跟随区间”.下列结论正确的是A .若[]1,b 为()222f x x x =-+的跟随区间,则3b =B .函数()32f x x=-不存在跟随区间C .若函数()f x m =,则1,04m ⎛⎤∈- ⎥⎝⎦D .二次函数()212f x x x =-+存在“3倍跟随区间”【答案】BCD【解析】根据“k 倍跟随区间”的定义,分析函数在区间内的最值与取值范围逐个判断即可.【详解】对A, 若[]1,b 为()222f x x x =-+的跟随区间,因为()222f x x x =-+在区间[]1,b 为增函数,故其值域为21,22b b ⎡⎤-+⎣⎦,根据题意有222b b b -+=,解得1b =或2b =,因为1b >故2b =.故A 错误.对B,由题,因为函数()32f x x =-在区间(),0∞-与()0,+∞上均为增函数,故若()32f x x=-存在跟随区间[],a b则有3232aabb⎧=-⎪⎪⎨⎪=-⎪⎩,即,a b为32xx-=的两根.即2230x x-+=,无解.故不存在.故B正确.对C, 若函数()f x m=[],a b,因为()f x m=,故由跟随区间的定义可知b ma ba m⎧=⎪-=⎨=⎪⎩a b<即()()()11a b a b a b-=+-+=-,因为a b<,1=.易得01≤<.所以(1a m m==-,令t=20t t m--=,同理t=20t t m--=,即20t t m--=在区间[]0,1上有两根不相等的实数根.故140mm+>⎧⎨-≥⎩,解得1,04m⎛⎤∈- ⎥⎝⎦,故C正确.对D,若()212f x x x=-+存在“3倍跟随区间”,则可设定义域为[],a b,值域为[]3,3a b.当1a b<≤时,易得()212f x x x=-+在区间上单调递增,此时易得,a b为方程2132x x x-+=的两根,求解得0x=或4x=-.故存在定义域[]4,0-,使得值域为[]12,0-.故D正确.故选:BCD【点睛】本题主要考查了函数新定义的问题,需要根据题意结合函数的性质分析函数的单调性与取最大值时的自变量值,并根据函数的解析式列式求解.属于难题.三、填空题13.已知方程2410x x-+=的两根为12,x x,则2212x x+=_______.【答案】14【分析】根据韦达定理,得到1212,x x x x+⋅,将数值代入到()2212121222x x x x x x++⋅=-中即可求得.【详解】解:由题知2410x x-+=的两根为12,x x,由韦达定理可知:121241x xx x+=⎧⎨⋅=⎩,()2221212122x x x x x x ∴+=+-⋅162=-14=.故答案为:1414.函数()()ln 2f x x =-________. 【答案】{}12x x -≤<【解析】根据对数的真数大于零,偶次根式被开方数非负可得出关于x 的不等式组,即可解得函数()y f x =的定义域.【详解】由题意可得2010x x ->⎧⎨+≥⎩,解得12x -≤<.因此,函数()y f x =的定义域为{}12x x -≤<. 故答案为:{}12x x -≤<.【点睛】本题考查函数定义域的求解,一般要根据求函数定义域的基本原则建立不等式组求解,考查计算能力,属于基础题. 15.设函数()21221xx f x e x--=++,若()()24f ax f x ≥+恒成立,则实数a 的取值范围是_______. 【答案】[]4,4-【解析】首先判断函数的奇偶性和单调性,根据函数性质,不等式等价于()()()()2244f ax f x f ax f x ≥+⇒≥+,再根据函数的单调性得24ax x ≤+,再利用参变分离的方法,转化为函数的最值,求a 的取值范围.【详解】由函数的解析式可知函数的定义域为R ,且满足()()f x f x -=,所以函数是偶函数,当0x >时,()()22112224222x x x x f x e e x x ---++-=+=+++, ()12412x f x e x -∴=+-+ ()0x >, 1x y e -=是单调递减函数,()24102y x x =->+也是减函数, 所以函数()12412xf x e x-=+-+ ()0x >是单调递减函数 ()()()()2244f ax f x f ax f x ≥+⇒≥+,即24ax x ≤+,当0x =时,不等式成立,当0x ≠时,244x a x x x +≤=+,即min4a x x ⎛⎫≤+ ⎪ ⎪⎝⎭, 4424x x x x+≥⋅=,当2x =±时,等号成立, 即444a a ≤⇔-≤≤, 综上可知a 的取值范围是[]4,4-. 故答案为:[]4,4-【点睛】本题考查指数函数,函数的奇偶性和函数的单调性,解抽象不等式,属于中档题型. 方法点睛:本题涉及利用函数的奇偶性和单调性,解抽象不等式,一般包含以下方法: 1.奇函数和单调性解抽象不等式,首先确定函数的给定区间上的单调性,将不等式转化为()()12f x f x <的形式,再根据单调性去掉“f ”,再解不等式;2.偶函数和单调性解抽象不等式,首先确定函数在()0,∞+的单调性,根据()()()f x f x f x -==,将不等式转化为()()12f x f x <的形式,再根据单调性去掉“f ”,解不等式.四、双空题16.图①是某公交车线路的收支差额(票价总收入减去运营成本)与乘客量x 的函数图象.目前这条线路亏损,为了扭亏,有关部门提出了两种扭亏为赢的建议,如图②和图③,根据图象分别说明这两种建议,图②的建议是______;图③的建议是_____.【答案】 增加票价,运营成本不变 票价不变,降低运营成本【解析】由图①可以看出,直线的斜率的实际意义是票价,在y 轴上的截距的相反数表示运营成本,根据图②③中的斜率截距变化即可得出.【详解】由图①可以看出,直线的斜率的实际意义是票价,在y 轴上的截距的相反数表示运营成本, 图②中,直线的斜率增加,在y 轴上的截距不变,即表示增加票价,运营成本不变,图③中,直线斜率不变,直线的截距增加,即表示票价不变,降低运营成本. 故答案为:增加票价,运营成本不变;票价不变,降低运营成本.五、解答题17.计算下列各式的值.21513236231.538a a a-⎛⎫⋅÷+⨯ ⎪⎝⎭;(2)421lg log8log3log100++⋅【答案】(1)π(2)0【分析】(1)根据根式的定义与分数指数幂的运算法则计算.(2)根据对数的运算法则、换底公式计算.【详解】(1)原式223115323633222aπ-+-⎡⎤⎛⎫⎛⎫=-++⨯⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦22332122ππ-⎛⎫⎛⎫=-++⨯=⎪ ⎪⎝⎭⎝⎭.(2)原式()2323221lg10log2log3log22-⎛⎫⎪⎝=+⋅⎭+223312lg10log2log3log222⎛⎫=-++⋅ ⎪⎝⎭312022=-++=18.已知0,0x y>>,且141x y+=.(1)求x y+的最小值;(2)若26xy m m>+恒成立,求实数m的取值范围.【答案】(1)9(2)()8,2-【分析】(1)根据系数“1”的妙用,结合基本不等式即可得到结果;(2)根据题意结合基本不等式可得16xy≥,然后求解关于m的不等式,即可得到结果. 【详解】(1)因为0,0x y>>,所以()144559x yx y x yx y y x⎛⎫+=++=++≥+⎪⎝⎭当且仅当4x y y x=,即3,6x y ==时取等号, 所以x y +的最小值为9(2)因为0,0x y >>,所以141x y =+≥, 所以16xy ≥,当且仅当2,8x y ==时等号成立,因为26xy m m >+恒成立,所以2166m m >+,解得82m -<<所以实数m 的取值范围为()8,2-19.已知幂函数()93m f x x -=()*m N ∈的图像关于原点对称,且在R 上函数值随x 的增大而增大.(1)求()f x 的解析式;(2)求满足()()1340f a f a ++-<的a 的取值范围.【答案】(1)()3f x x =;(2)3,4⎛⎫-∞ ⎪⎝⎭ 【分析】(1)根据幂函数()f x 图像关于原点对称和在R 上递增,求得m 的值.(2)利用幂函数()f x 的奇偶性和单调性列不等式,解不等式求得a 的取值范围.【详解】(1)由题可知,函数在R 上单调递增,∴930m ->,解得3m <.又*m N ∈,∴1,2m =.又函数图像关于原点对称,∴93m -为奇数,故2m =.∴()3f x x =.(2)∵()()1340f a f a ++-<,∴()()134f a f a +<--.∵()f x 为奇函数,∴()()143f a f a +<-.又函数在R 上单调递增,∴143a a +<-.∴34a <. ∴a 的取值范围是3,4⎛⎫-∞ ⎪⎝⎭. 【点睛】本小题主要考查幂函数解析式的求法,考查幂函数的单调性和奇偶性,属于基础题. 20.已知()f x 是二次函数,()0f x >的解集是{35}x x -<<且()015f =.(1)求函数()f x 的解析式;(2)当[1,4]x ∈-时,函数()f x 的最值;(3)令()()()12g x m x f x =--.若函数()g x 在区间[]0,2上不是单调函数,求实数m 的取值范围.【答案】(1)()2215f x x x =-++;(2)()f x 的最大值为16,最小值为7;(3)13,22⎛⎫- ⎪⎝⎭. 【分析】(1)由()015f c ==,再转化()0f x >的解集是{35}x x -<<为3,5-是对应方程的两个根,结合韦达定理,可得12a b =-⎧⎨=⎩,即得解; (2)()2215f x x x =-++为开口向下的二次函数,对称轴为1x =,根据二次函数性质即得解;(3)转化为()()22115g x x m x =-+-的对称轴在给定区间的开区间内,即21022m +<<,求解即可 【详解】(1)设()()20f x ax bx c a =++≠.∵()015f =∴15c =又()0f x >的解集是{35}x x -<<∴3,5-是方程2150ax bx ++=的两个根 ∴351535b a c a a ⎧-+=-⎪⎪⎨⎪-⨯==⎪⎩,解得12a b =-⎧⎨=⎩ ∴()2215f x x x =-++.(2)由于()2215f x x x =-++为开口向下的二次函数,对称轴为1x =根据二次函数性质,当[1,4]x ∈-当1x =时,取得最大值,即max ()(1)16f x f ==,由于4比1-离对称轴远,故当4x =时,取得最小值,即min ()(4)7f x f ==(3)∵()()()12g x m x f x =--∴()()22115g x x m x =-+-.∵函数()g x 在区间[]0,2上不是单调函数 ∴21022m +<<,解之得:1322m -<<. ∴实数m 的取值范围是13,22⎛⎫- ⎪⎝⎭ 21.地铁给市民出行带来很多便利.已知某条线路通车后,地铁的发车时间间隔t (单位:分钟)满足220t ≤≤,N t ∈.经测算,地铁载客量与发车时间间隔t 相关,当1020t ≤≤时地铁为满载状态,载客量为1200人,当210t ≤<时,载客量会减少,减少的人数与(10)t -的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为()p t .(1)求()p t 的表达式,并求当发车时间间隔为6分钟时,地铁的载客量(2)若该线路每分钟的净收益为6()3360360p t Q t-=-(元),问当发车时间隔为多少时,该线路每分钟的净收益最大? 【答案】(1)210200200,210(),10401200,1020t t t p t t ⎧-++<=⎨⎩, (2)当发车时间间隔为6t =分钟时,该线路每分钟的净收益最大,最大为120元.【分析】(1)由题意知21200(10),210()1200,1020k t t p t t ⎧--<=⎨⎩,t N ∈,(k 为常数),再由p (2)560=求得k ,则()p t 可求,进一步求得p (6)得答案;(2)由6()3360360p t Q t -=-,可得2120010(10)5606[60],2103840360,1020t t t Q t t⎧----<⎪⎪=⎨⎪-⎪⎩,分段求最值得答案. 【详解】(1)由题意知21200(10),210()1200,1020k t t p t t ⎧--<=⎨⎩,t N ∈,(k 为常数), p (2)21200(102)560k =--=,10k ∴=,22120010(10),21010200200,210()1200,10201200,1020t t t t t p t t t ⎧⎧--<-++<∴==⎨⎨⎩⎩, p ∴(6)2120010(106)1040=--=;(2)由6()3360360p t Q t-=-,可得 2120010(10)5606[60],2103840360,1020t t t Q t t⎧----<⎪⎪=⎨⎪-⎪⎩, 当210t <时,366[14010()]6(1401012)120Q t t=-+-⨯=, 当且仅当6t =时等号成立;当1020t 时,7200336036038436024Q t -=--=,当10t =时等号成立, ∴当发车时间间隔为6t =分钟时,该线路每分钟的净收益最大,最大为120元.答:当发车时间间隔为6t =分钟时,该线路每分钟的净收益最大,最大为120元.【点睛】方法点睛:在用基本不等式求最值时,应具备三个条件:一正二定三相等.①一正:关系式中,各项均为正数;②二定:关系式中,含变量的各项的和或积必须有一个为定值;③三相等:含变量的各项均相等,取得最值.22.已知函数()()1e ,ln 1x f x g x x -==+.(1)判断函数()()()ln F x f x g x ⎡⎤⎦+⎣=在其定义域上的单调性(不需要证明)﹔ (2)对任意的1,e a ⎛⎫∈+∞ ⎪⎝⎭,都有()()f b a g a b =,若存在a 的两个取值()1212,a a a a ≠,使得2(b c c -=为常数),求12a a ⋅的值.【答案】(1)()F x 在()0,∞+上单调递增(2)212e a a =【分析】(1)求出函数式,然后根据单调性的性质判断;(2)已知等式交叉相乘后取对数变形利用(1)中函数的单调性得出ln 1b a =+,代入2b c -=,利用12,a a 是此方程的两个解,得出培训五日关系,完成证明.【详解】(1)由已知()1ln 1ln F x x x x x =-++=+,由于y x =和ln y x =在(0,)+∞上都是增函数, 因此()F x 在定义域内是增函数;(2)由()()f b a g a b=,即ln 10a +>,化简为()1e ln 1b b a a -=+. 因为1,a e ⎛⎫∈+∞ ⎪⎝⎭,所以ln 10a +>,又由题可知0a >,所以0b >. 所以两边取对数得()()1ln e ln ln 1b b a a -=+⎡⎤⎣⎦,即()1ln lne ln ln ln 1b b a a -+=++, 即()ln 1ln ln ln 1b b a a +-=++,即()()ln ln 1ln ln 1b b a a +=+++,即()()ln 1F b F a =+,由(1)知()ln F x x x =+为()0,∞+上的增函数,所以ln 1b a =+. 又因为2ln 1b a c -=-=,即存在()1212,a a a a ≠使ln 1a c -=成立,不妨设12a a <,即12ln 1ln 1a a c -=-=,即12ln 1ln 1a a -+=-,即12ln 2a a =,所以212e a a =.。
福建省福州市2021-2022学年高一上学期期中考试数学试题含解析

福州2021-2022学年第一学期期中考数学试卷(答案在最后)一、选择题(共8小题)1.已知全集{}1,2,3,4,5,6U =,集合{}2,3,5A =,集合{}1,3,4,6B =,则集合U A B ⋂=()ðA.{}3 B.{}2,5 C.{}1,4,6 D.{}2,3,5【答案】B 【解析】【详解】{}2,3,5A =,{}2,5U B =ð,则{}2,5U A B ⋂=()ð,故选B.考点:本题主要考查集合的交集与补集运算.2.命题“2,10x Q x x ∀∈++>”的否定为()A.2,10x Q x x ∃∈++>B.2,10x Q x x ∀∈++≤C.2,10x Q x x ∃∈++≤D.2,10x Q x x ∃∉++≤【答案】C 【解析】【分析】由全称命题的否定为特称命题即可求解.【详解】解:因为全称命题的否定为特称命题,所以命题“2,10x Q x x ∀∈++>”的否定为“2,10x Q x x ∃∈++≤”,故选:C.3.下列函数中既是奇函数,又是增函数的是()A.1()f x x=-B.()3xf x = C.3()log f x x= D.()f x =【答案】AD 【解析】【分析】由幂函数、指数函数、对数函数的奇偶性与单调性即可求解.【详解】解:对A :1()f x x=-是奇函数,且是增函数,符合题意;对B :()3x f x =不具有奇偶性,是增函数,不符合题意;对C :3()log f x x =不具有奇偶性,是增函数,不符合题意;对D :13()f x x==是奇函数,且是增函数,符合题意;故选:AD.4.设()f x 为奇函数,且当0x ≥时,()1x f x e -=-,则当0x <时,()f x =()A.e 1x -- B.e 1x -+ C.e 1x --- D.1x e -+【答案】D 【解析】【分析】首先设0x <,得到0x ->,再代入()1x f x e -=-,利用函数的奇偶性求解即可.【详解】设0x <,则0x ->,因为函数()f x 为奇函数,且当0x ≥时,()1x f x e -=-,()()1x f x e f x -=-=-,即:()1x f x e =-+.故选:D5.某高校为加强学科建设,制定了第“十四五”(2021-2025)规划,计划逐年加大科研经费投入,已知该校计划2021年全年投入科研资金20万元,2025年全年投入科研资金28万元,则第“十四五”期间,投入科研资金的年均增长率约为()A.141.41- B.151.41- C. 1.4log 51- D.1.4log 41-【答案】A 【解析】【分析】设年增长率为x ,由题意可得()420128x +=,从而即可求解.【详解】解:设年增长率为x ,由题意可得()420128x +=,即()4281 1.420x +==,所以141 1.4x +=,解得141.41x =-,所以投入科研资金的年均增长率约为141.41-,故选:A.6.函数2()21x xf x x =-+的图象大致为()A. B.C. D.【答案】A 【解析】【分析】根据奇偶函数的定义证明()f x 是偶函数,可排除B 、C ;再由()20f >可排除D.【详解】由题意知,函数()f x 的定义域为R ,()221x x f x x =-+2=21xxx x⋅-+,则()f x -22=2121x x xxx x x x---⋅+⋅-=++,所以()()f x f x =-,即函数()f x 为偶函数,故可排除B 和C ;当2x =时,()605f x =>,故可排除D.故选:A7.冈珀茨模型()tb y k a=⋅是由冈珀茨(Gompertz )提出,可作为动物种群数量变化的模型,并用于描述种群的消亡规律.已知某珍稀物种t 年后的种群数量y 近视满足冈珀茨模型:0.1251.40tey k e -=⋅(当0=t 时,表示2020年初的种群数量),若()m m N*∈年后,该物种的种群数量将不足2020年初种群数量的一半,则m 的最小值为()(ln 20.7)≈A.9 B.7 C.8D.6【答案】D 【解析】【分析】由已知模型列出不等式后,取对数变形求解.【详解】由已知0.12501.4 1.40012me e k ek e -⋅≤⋅,显然00k >,0.1251.4 1.412me ee -≤,两边取自然对数有:0.1251.4 1.4ln 20.7m e -≤-≈,0.12512m e -≤,所以0.125ln 20.7m -≤-≈-, 5.6m ≥.m 的最小值为6.故选:D .8.设34c =,4log 3b =,5log 4a =,则a ,b ,c 的大小关系为()A.b c a >>B.b a c >>C.a b c>> D.c b a>>【答案】C 【解析】【分析】对于a ,b 的比较,构造函数,通过研究函数的单调性来进行比较,对于a ,c 或b ,c 的比较通过作差法来进行比较【详解】444444log 33l 8164og og 0l b c ---=>=,故b c>;555444log 43lo 2561250g log a c --=->=,故a c >;4ln 3log 3ln 4b ==,5ln 4log 4ln 5a ==令()()ln ln 1xf x x =+,(0x >),则()()()()()()()()()()2221ln 1ln ln 1ln 11ln 1ln 1ln 11ln 11ln 1x xx x x x x x x x x f x x x x x x x x ⎛⎫++++- ⎪++-⎝⎭+'===+++++因为0x >,所以111x +>,1ln 10x ⎛⎫+> ⎪⎝⎭,()ln 10x +>,故()0f x '>恒成立,()()ln ln 1xf x x =+在0x >上单调递增,所以()()43f f >,故a b>综上:a b c >>故选:C二、多选题(共4小题)9.下列结论正确的是()A.lg(25)lg 2lg 5+=⋅B.1= C.1383272-⎛⎫=⎪⎝⎭D.24log 3log 6=【答案】BC 【解析】【分析】AD 选项应用对数运算法则进行计算,B 选项利用根式化简法则进行求解;C 选项,利用指数运算法则进行计算【详解】lg(25)lg 2lg 5+=⋅错误,正确的应该是lg(25)lg 2lg 5⨯=+,故A错误;,B 选项正确;1131338223==27332---⎡⎤⎛⎫⎛⎫⎛⎫=⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,C 选项正确;4221log 6=log 6=log 2D 选项错误.故选:BC10.下列四个命题中,真命题是()A.22a b ac bc >⇒> B.22||a b a b >⇒> C.11a b a b>⇒< D.22||a b a b>⇒>【答案】BD 【解析】【分析】利用不等式的性质分别对选项进行验证,即可得到答案.【详解】对于A 选项,当0c =时,22=ac bc ,故A 错误;已知||0b ≥,即||0a b >≥,左右两边同时平方即可得到22a b >,故B 正确.;当,a b 同号时,11a b a b>⇒<,当,a b 异号时,11a b a b>⇒>,故C 错误;22||||||a b a b a b >⇒>⇒>,故D 正确.故选:BD.11.下列命题中真命题的是()A.“1x >”是“21x >”的充分不必要条件B.若(1)f x +是偶函数,则()f x 的图像关于直线1x =-轴对称C.若(2)()f x f x +=--,则()f x 的图像关于点(1,0)-中心对称D.[1,1]x ∃∈-,使得方程21ax =有解的充要条件是1a ≥【答案】AD 【解析】【分析】解不等式21x >,再根据充分条件和必要条件的定义即可判断A ;根据偶函数的图像的特征及函数()f x 与函数(1)f x +图像的关系即可判断B ;由(2)()f x f x +=--,可得()()()111f x f x f x +=---=--+⎡⎤⎣⎦,再根据函数()f x 与函数(1)f x +图像的关系即可判断C ;根据方程21ax =有解,求得a 的范围,再根据充分条件和必要条件的定义即可判断D.【详解】解:对于A ,由21x >,得1x >或1x <-,所以“1x >”是“21x >”的充分不必要条件,故A 正确;对于B ,若(1)f x +是偶函数,则(1)f x +的图像关于y 轴对称,()f x 的图像是由函数(1)f x +向右平移1个单位得到的,所以函数()f x 的图像关于直线1x =轴对称,故B 错误;对于C ,若(2)()f x f x +=--,所以()()()111f x f x f x +=---=--+⎡⎤⎣⎦,令1m x =+,则()()f m f m =--,所以函数()f m 关于原点对称,又()f x 是由函数()f m 向右平移1个单位得到的,所以函数()f x 的图像关于点(1,0)中心对称,故C 错误;对于D ,[1,1]x ∃∈-,使得方程21ax =有解,当0x =时,01=不成立,舍去,当0x ≠时,即[)(]1,00,1x ∈- ,则211a x=≥,所以1a ≥,综上所述1a ≥,所以[1,1]x ∃∈-,使得方程21ax =有解的充要条件是1a ≥,故D 正确.故选:AD.12.已知函数()2xf x e x =+-的零点为1x ,函数()ln 2g x x x =+-的零点为2x ,则()A.122x x +=B.122x x > C.122x x e e e+> D.122x x <【答案】ACD 【解析】【分析】依题意可得112x e x =-,22ln 2x x =-,根据反函数的性质可得122x x +=,再利用基本不等式判断C ,利用零点存在性定理得到1102x <<、21x <<函数的单调性判断B 、D ;【详解】解:函数()2x f x e x =+-的零点为1x ,函数()ln 2g x x x =+-的零点为2x ,可得112x e x =-,22ln 2x x =-,即有1221ln 4()x e x x x +=-+,由x y e =的反函数ln y x =关于直线y x =对称,x y e =与直线2y x =-的交点为11(,2)x x -,ln y x =与直线2y x =-的交点为22(,2)x x -,可得122x x =-,即122x x +=,故A 正确;由基本不等式得,122x x e e e += ,而12x x ≠,∴等号不成立,故122x x e e e +>,故C 正确;因为()010f =-<,11221112 2.2520222f e ⎛⎫=+->+-= ⎪⎝⎭,所以1102x <<所以()12111220232x x x x x =----<=,所以122x x <,故B 错误;又()1ln1121g =+-=-,11221122 2.252022g e ==+->+-=,所以21x <<则()1222222ln x x x x x x -==,因为ln y x x =在(上单调递增,所以1222ln 2x x x x =<=,故D 正确;故选:ACD三、填空题(共4小题)13.函数()f x =___________,值域为___________.【答案】①.(,3]-∞②.[0,)+∞【解析】【分析】由真数大于0和被开方数大于等于0,可得不等式组,解不等式组,即可得定义域,根据对数函数的值域可知()f x 的值域.【详解】由题意得:()40,4,3lg 40,3,x x x x x -><⎧⎧⇒⇒≤⎨⎨-≥≤⎩⎩,∴函数的定义域为(],3-∞,(,3]x ∈-∞ ,lg(4)0x ∴-≥,0≥∴,即()f x =的值域为[0,)+∞.故答案为:(],3-∞;[0,)+∞14.已知函数()22x x f x a -=⋅-是偶函数,则=a ___________.【答案】-1【解析】【分析】根据奇偶函数的性质可得()()f x f x =-,列出方程,进而解出a 的值.【详解】因为函数()22x x f x a -=⋅-是偶函数,所以()()f x f x =-,又()22x x f x a --=⋅-,所以22x x a -⋅-=22x x a -⋅-,即(1)(22)0x x a -+-=,所以1a =-.故答案为:-115.已知a R ∈,函数2()log f x a x =.若2t ∀≥,使得(2)()1f t f t +-≤,则实数a 的最大值是___________.【答案】1【解析】【分析】化简(2)()1f t f t +-≤,得到212log a t t≤+在2t ∀≥上恒成立,故求出212log t t+在2t ≥的最小值1,让1a ≤即可【详解】(2)()1f t f t +-≤,即2222log (2)log log 1t a t a t a t++-=≤,因为2t ≥,所以22222log log 1log 10t t t +⎛⎫=+>= ⎪⎝⎭,所以212log a t t≤+恒成立,其中2222log log 1t y t t +⎛⎫==+ ⎪⎝⎭在2t ≥时单调递减,故22222log log 12t t ++≤≤,所以2112log t t≥+,所以1a ≤,故实数a 的最大值是1故答案为:116.已知函数()f x 满足21,0()lg ,0x x f x x x ⎧-≤⎪=⎨>⎪⎩,若方程22[()]4()20f x mf x m -++=有四个不相等的实数根,则实数m 的取值范围为___________.【答案】3m >或13m <<【解析】【分析】令()t f x =,则方程22[()]4()20f x mf x m -++=转化为22420t mt m -++=,作出函数()f x 的图象,由题意,原问题等价于22420t mt m -++=有两个大于1的不等实数根,根据一元二次方程根的分布列出不等式组求解即可得答案.【详解】解:令()t f x =,则方程22[()]4()20f x mf x m -++=转化为22420t mt m -++=,作出函数()f x的图象如下图所示,由题意,方程22[()]4()20f x mf x m -++=有四个不相等的实数根,即22420t mt m -++=有两个大于1的不等实数根,令22()42h t t mt m =-++,则()()22224420412(1)1420m m m h m m ⎧∆=--+>⎪⎪-->⎨⎪=-++>⎪⎩解得3m >或13m <<,则实数m 的取值范围为3m >或13m <<,故答案为:3m >或13m <<.四、解答题(共6小题)17.已知全集U =R ,集合{}{}2log 21,3327xA x x aB x =-≥=<<.(1)当3a =时,求A B ;(2)在①B A ⊆;②A B ⋂≠∅;③()U A B A ⋃=ð中任选一个条件,求实数a 的取值范围.【答案】(1)5|32x x ⎧⎫≤<⎨⎬⎩⎭(2)答案见解析【解析】【分析】(1)首先解指数不等式、对数不等式及绝对值不等式求出集合A 、B ,再根据交集的定义计算可得;(2)根据所选条件,得到不等式组,即可求出参数的取值范围;【小问1详解】解:由3327x <<,即13333x <<,解得13x <<,即{}{}|3327|13xB x x x =<<=<<,由21l g 2o x a -≥,即22log log 22x a -≥,所以22x a -≥,即22x a -≥或22x a -≤-,解得12a x ≥+或12a x ≤-,即{}2log 21A x x a =-≥{|12a x x =≥+或1}2a x ≤-当3a =时5{|2A x x =≥或1}2x ≤所以5|32⎧⎫=≤<⎨⎬⎩⎭A B x x 【小问2详解】解:由(1)可知{|12a A x x =≥+或1}2ax ≤-,{}|13B x x =<<;若选①,B A ⊆,则112a +≤或132-≥a,解得0a ≤或8a ≥,即(][),08,a ∈-∞⋃+∞;若选②,若A B =∅ ,则132112a a ⎧+≥⎪⎪⎨⎪-≤⎪⎩,解得4a =,所以4a ≠时A B ⋂≠∅;若选③,因为{}|13B x x =<<,所以{|1U B x x =≤ð或3}x ≥,因为()U A B A ⋃=ð,所以()U B A ⊆ð,所以132112aa ⎧+≤⎪⎪⎨⎪-≥⎪⎩,解得4a =;18.设函数2()2(2)1f x mx m x =+++.(1)若()f x 在[1,)+∞单调递增,求实数m 的取值范围;(2)解关于x 的不等式()0f x ≤.【答案】(1)0m ≥(2)当2m ≤-时,11,,2m ⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭ ;当20m -<<时,11,,2m ⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭;当0m =时,1,2⎛⎤-∞- ⎥⎝⎦;当02m <<时,11,2m ⎡⎤--⎢⎥⎣⎦;当2m ≥时,11,2m ⎡⎤--⎢⎥⎣⎦.【解析】【分析】(1)根据m 是否为0分类讨论,不等于0时根据二次函数的性质列式求解即可;(2)根据m 与0的大小分类讨论求解即可.【小问1详解】当实数0m =,()21f x x =+,()f x 在[1,)+∞单调递增,符合题意.当实数0m ≠,根据二次函数的性质,函数()f x 的对称轴为24m m+-,要使得()f x 在[1,)+∞单调递增,则2140m m m +⎧-≤⎪⎨⎪>⎩,解得0m >综上述,0m ≥.【小问2详解】当实数0m =,()21f x x =+,()0f x ≤时,12x ≤-.当实数0m >,()()2()2(2)11210f x mx m x mx x =+++=++≤如果112m -<-,即02m <<时,()0f x ≤得112x m -≤≤-,如果112m -≥-,2m >时,()0f x ≤得112x m-≤≤-.当实数0m <,此时1102m ->>-,()()()1210f x mx x =++≤,()()()1210f x mx x =--+≥解得12x ≤-或1x m ≥-综上述,()0f x ≤的解集为:当0m <时,11,,2m ⎛⎤⎡⎫-∞--+∞ ⎪⎥⎢⎝⎦⎣⎭;当0m =时,1,2⎛⎤-∞- ⎥⎝⎦;当02m <<时,11,2m ⎡⎤--⎢⎥⎣⎦;当2m ≥时,11,2m ⎡⎤--⎢⎣⎦.19.已知函数2()4mx n f x x +=+是定义在[2,2]-上的奇函数,且1(1)5f =.(1)求m ,n 的值,判断函数()f x 的单调性并用定义加以证明;(2)求使()2(1)10f a f a -+-<成立的实数a 的取值范围.【答案】(1)1,0==m n ,增函数,证明见解析(2)11a -≤<【解析】【分析】(1)因为函数()f x 为定义在[2,2]-上的奇函数,所以(0)0f =,又1(1)5f =,由此可得m ,n 的值,再由单调性定义判断函数的单调性;(2)()2(1)10f a f a -+-<,即()2(1)1f a f a -<-,根据定义域及单调性列出不等式组,从而可得出答案.【小问1详解】解:因为函数2()4mx nf x x +=+是定义在[2,2]-上的奇函数,所以()00f =,即04n=,解得0n =,又因1(1)55m f ==,所以1m =,所以1,0==m n ,2()4xf x x =+,经检验符合题意,在[2,2]-上任取1x ,2x ,且12x x <,则1212121222221212()(4)()()44(4)(4)x x x x x x f x f x x x x x ---=-=++++,因为1222x x -< ,所以120x x -<,1240x x ->,所以12())0(f x f x -<,即12()()f x f x <,所以函数()f x 在[2,2]-单调递增;【小问2详解】解:因为()2(1)10f a f a -+-<,所以()2(1)1f a f a -<--,即()2(1)1f a f a -<-,因为函数()f x 在[2,2]-单调递增,所以2211212212a a a a ⎧-<-⎪-≤-≤⎨⎪-≤-≤⎩,解得11a -≤<.20.已知函数44()32log ,()log f x x h x x =-=.(1)当[1,16]x ∈时,求函数()[()1]()g x f x h x =+⋅的值域;(2)如果对任意的[1,16]x ∈,不等式()2()f x f m h x ⋅>⋅恒成立,求实数m 的取值范围.【答案】(1)[0,2](2)3m <-【解析】【分析】(1)设4log t x =,把函数转化为二次函数,利用二次函数性质可得值域;(2)设4log t x =换元,分类0=t 时不等式成立,在(0,2]t ∈时,分离参数后应用函数单调性求得最小值得结论.【小问1详解】设4log t x =,由[1,16]x ∈得[0,2]t ∈,22()(321)242(1)2g x t t t t t =-+=-+=--+,所以1t =时,max ()2g x =,2t =或0时,min ()0g x =,所以所求值域为[0,2];【小问2详解】设4log t x =,又[1,16]x ∈,所以[0,2]t ∈,不等式()2()f xf m h x ⋅>⋅为2444(32log )(32log log x m x -->,即(34)(3)t t mt -->,0=t ,不等式显然成立,(]0,2t ∈时,不等式化为(34)(3)9415t t m t t t--<=+-,9415153t t +-≥-=-,当且仅当32t =时,等号成立,所以3m <-.综上,3m <-.21.已知福州地铁2号线路通车后,地铁的发车时间间隔t (单位:分钟)满足220t ≤≤,经市场调研测算,地铁的载客量与发车的时间间隔t 相关,当1020t ≤≤时,地铁为满载状态,载客量为400人;当210t ≤<时,载量会减少,减少的人数与()210t -成正比,且发车时间间隔为2分钟时的载客量为272人,记地铁的载客量为()p t .(1)求()p t 的表达式,并求发车时间间隔为6分钟时地铁的载客量;(2)若该线路每分钟的净收益为()123000150p t Q t-=-(元).问:当地铁发车时间间隔多少时,该线路每分钟的净收益最大?【答案】(1)()()2400210,210400,1020t t p t t ⎧--≤<⎪=⎨≤≤⎪⎩,发车时间间隔为6分钟时地铁的载客量为368人.(2)当地铁发车时间间隔为5分钟时,该线路每分钟的净收益最大.【解析】【分析】(1)当210t ≤<时,设()()240010p t k t =--,由()2272p =可求出k 的值,结合已知条件可得出函数()p t 的函数解析式,进而可求得()6p 的值;(2)分210t ≤<、1020t ≤≤两种情况讨论,求出Q 关于t 的函数解析式,利用基本不等式以及函数的单调性可求得Q 的最大值及其对应的t 值,即可得出结论.【小问1详解】解:当210t ≤<时,设()()240010p t k t =--,则()240064272p k =-=,解得2k =.由题意可得()()2400210,210400,1020t t p t t ⎧--≤<⎪=⎨≤≤⎪⎩.所以,发车时间间隔为6分钟时地铁的载客量为()2640024368p =-⨯=(人).【小问2详解】解:当210t ≤<时,()21230004802460060015015033024p t t t Q t t t t ---⎛⎫=-=-=-+ ⎪⎝⎭33090≤-(元),当且仅当5t =时,等号成立;当1020t ≤≤时,()1230001800150150p t Q tt-=-=-,此时函数1800150Q t =-单调递减,则18001503010Q ≤-=,当且仅当10t =时,等号成立.综上所述,当地铁发车时间间隔为6分钟时,该线路每分钟的净收益最大.22.对定义在[0,1]上,并且同时满足以下两个条件的函数()f x 称为G 函数.①对任意的[0,1]x ∈,总有()0f x ≥;②当11120,0,1x x x x ≥≥+≤时,总有()()()1212f x x f x f x +≥+成立.已知函数2()g x x =与()21x h x a =⋅-是定义在[0,1]上的函数.(1)试问函数()g x 是否为G 函数?并说明理由;(2)若函数()h x 是G 函数,(i )求实数a 的值;(ii )讨论关于x 的方程()21()()xg h x m m R --=∈解的个数情况.【答案】(1)是,理由见解析;(2)(i )1;(ii )详见解析.【解析】【分析】(1)根据G 函数的定义求解;(2)(i )根据函数()h x 是G 函数,由[0,1]x ∈,总有021x a ⋅-≥成立,求得1a ≥再由②当11120,0,1x x x x ≥≥+≤时,总有()121221222x x x x a a +≥⋅-+-成立,由()()12111221x x a -≤--,对11120,0,1x x x x ≥≥+≤时成立,求得1a ≤求解;(ii )将方程()21()()xg h x m m R --=∈,转化为()()22121x xm ---=,令[]210,1xt =-∈,转化为221124m t t t ⎛⎫=-=-- ⎪⎝⎭求解.【小问1详解】解:函数()g x 是为G 函数,理由如下:①对任意的[0,1]x ∈,总有2()0g x x =≥;②当12120,0,1x x x x ≥≥+≤时,()()()()222212122121212122x x x x x x g g x x x x x g x ==+++⋅=++≥+,所以函数()g x 是为G 函数,【小问2详解】(i )因为函数()h x 是G 函数,则①[0,1]x ∈,总有021x a ⋅-≥成立,即12xa ⎛⎫≥ ⎪⎝⎭,对[0,1]x ∈成立,所以1a ≥②当11120,0,1x x x x ≥≥+≤时,总有()121221222x x x x a a +≥⋅-+-成立,即()()12111221x x a -≤--,对11120,0,1x x x x ≥≥+≤时成立因为11120,0,1x x x x ≥≥+≤,所以12211,21100x x ≤≤--≤≤,因为12,x x 不同时为1,所以()()120211211xx <---≤,当120x x ==时,等号成立,所以1a ≤,综上:1a =,(ii )方程()21()()xg h x m m R --=∈,即为()()22121x xm ---=,令[]210,1xt =-∈,则方程为221124m t t t ⎛⎫=-=-- ⎪⎝⎭,当14m <-或0m >时,方程无解;当14m=-时,方程一个解;当104m-<≤时,方程有两个解.。
福建省莆田第六中学2021-2022高一语文上学期期中试题

福建省莆田第六中学2021-2022高一语文上学期期中试题注意:本试卷语文基础知识90分,作文60分,总共150分,考试用时150分钟。
请把答案填写在答题卡上,考试结束后,将答题卡交回。
一、基础积累(共38分)1.下列各句中,加点的成语使用恰当的一项是()(2分)A.机场附近山顶的大量无线发射台严重影响飞行安全,目前虽有一些已搬下山,但这对实现机场净空不过是九牛一毛....。
B.抗洪救灾形势严峻,各级领导都坚守岗位,没有擅离职守,久假不归....现象,确保了人民群众生命财产的安全。
C.在全省经济发展座谈会上,李教授的讲话直击时弊,同时又颇具前瞻性,对于当前经济工作而言,可谓空谷足音....。
D.他最近的状态一直不佳,接连几次考试都不理想,屡试不爽....,心情糟透了。
2.下列各句中,加点的成语使用恰当的一项是()(2分)A.今年有四到六成的作品流拍,成交总额同比减少一半,这说明以往超过底价数十倍成交的火爆场面已成明日黄花....。
B.沉迷网络使小明学习成绩急剧下降,幸亏父母及时发现,并不断求全责备....,他才戒掉了网瘾。
C.一名惯偷在车站行窃后正要逃跑,两位守候多时的反扒队员突然拦住他的去路,二人上下..其手..地将他摁倒,结果人赃俱获。
D.历史如同一条长河,从源头连绵不断地流去,每一个阶段都具有特立独行....的标志。
3.下列各句中,加点的成语使用恰当的一项是()(2分)A.这种首饰的款式非常新颖、时尚,一经推出,不少爱美的女士慷慨解囊....抢购。
B.这位专家的回答让我有一种醍醐灌顶....的感觉,实在没想到这个困扰我两年的问题他却理解得那么轻松。
C.随着出版业的市场化和多元化,类型多样、题材丰富的作品大量涌现,其中也有一些作品粗制滥造,令人不忍卒读....。
D.发展低碳经济首当其冲....的是要坚持节约资源、保护环境的基本国策,协调资源利用和环境保护的关系,实现可持续发展。
4、下列句中加点词语古今意义相近的一项是()(2分)A.诸郎中..之往来..执兵行李B.为之奈何....人不敢与忤视C.樊将军以穷困.....来归丹若舍郑以为东道主D.微夫人..之力不及此而伤长者..之意5、下列加点词的意义和用法相同的一组是()(2分)A. 若舍郑以.为东道主焉用亡郑以.陪邻B. 夫晋,何厌之.有使杞子、庞孙、杨孙戍之.C. 以其无礼于晋佚之狐言于郑伯曰D.为.之奈何何辞为.6、下列对各句划横线词的活用现象进行分类,正确的一项是()(2分)①此亡秦之续.耳②吾得兄.事之③沛公今事有急.④共其乏困..⑤沛公旦日从.百余骑来见项王⑥又前.而为歌曰⑦越国以鄙.远⑧函.封之⑨邻之厚.,君之薄也⑩刑.人如恐不胜A.① \②⑧ \③⑨\④\⑤⑦\⑥⑩⑩ B.①\②⑧\③④\⑤\⑦\⑥⑩\⑨C.① \②\③④\⑤⑦\⑥⑧\⑨\⑩ D.①⑧\②\③⑤\④\⑥\⑦⑨\⑩7、下面句子按句式归类正确的一项是()(2分)①不者,若属皆且为所虏②夫晋,何厌之有③欲呼张良与俱去④以其无礼于晋⑤毋从俱死也⑥ 私见张良,具告以事⑦是寡人之过也⑧沛公安在⑨燕国见陵之耻除矣⑩此臣日夜切齿拊心也A. ①③⑤/②④⑧/⑥⑦/⑨⑩B. ①⑨/②⑧/③⑤/ ④⑥/⑦⑩C. ①/②⑧/④⑥/⑦⑨⑩/③⑤D. ①③⑤/②④/⑥⑦⑨/⑧ ⑩8.对下列加点词的解释全都正确的一项是()(2分)A.晋军.函陵(驻军)因人之力而敝.之(损害)以乱易.整,不武(替代)B.今行而无信.(相信)秦王必说.见臣(通“悦”,喜欢,高兴)进兵北略.地(掠夺、夺取)C.愿大王少.假借之(稍微)轲既取图奉之,发.图(发放)乃引.其匕首提秦王(举起)D.旦日飨.士卒(犒劳)料大王士卒足以当.项王乎(抵挡)道.芷阳间行(道路)9.下列解说中不正确的一项是( ) (2分)A.古代爵位共有五等:公、候、伯、子、男。
福建省莆田市第二十五中学2021-2022高一数学上学期期中试题(含解析).doc

福建省莆田市第二十五中学2021-2022高一数学上学期期中试题(含解析)第I 卷(选择题)一、单选题1.设集合{}0,1,2,3,4,5A =,{}2,4,6B =,则集合A B =( )A. {}2,4,6B. {}0,1,2,3,4,5,6C. {}2,4D.{}0,1,2,3,4,5【答案】B 【解析】 【分析】由并集定义直接求得结果. 【详解】由并集定义可知:{}0,1,2,3,4,5,6A B =本题正确选项:B【点睛】本题考查集合运算中的并集运算,属于基础题. 2.计算log 416+129等于( ) A.73B. 5C.133D. 7【答案】B 【解析】 【分析】利用指数与对数运算性质即可得出. 【详解】log 416+129=2+3=5.【点睛】本题考查指数与对数运算性质,属于基础题.3.若()20x x f x x x ⎧≥=⎨-<⎩,,,则()()2f f -=( )A. 5B. 4C. 3D. 2【答案】B 【解析】根据函数解析式,由内到外逐步代入,即可求出函数值.【详解】因为()20x x f x x x ⎧≥=⎨-<⎩,,,所以(2)(2)2-=--=f ,所以()()22(2)24-===f f f .故选B【点睛】本题主要考查由分段函数求函数值的问题,根据函数解析式,直接代入计算即可,属于常考题型.4.下列函数中与函数y x =相等的是()A. y =B. 2x y x=C. yD. y x =【答案】C 【解析】 【分析】对于选项A,D 对应的函数与函数y x =的对应法则不同, 对于选项B 对应的函数与函数y x =的定义域不同,对于选项C 对应的函数与函数y x =的定义域、对应法则相同,得解. 【详解】解:对于选项A,y y x =,即A 不符合题意,对于选项B ,2x y x=等价于0)y x x =≠,(,即B 不符合题意,对于选项C,y =等价于y x =,即C 符合题意,对于选项D ,y x =,显然不符合题意,即D 不符合题意, 故选C.【点睛】本题考查了同一函数的判断、函数的对应法则及定义域,属基础题. 5.已知全集{}0,1,2,3,4,5A =,{}2,4,6B =,则A B =( )A. {}2,4,6B. {}0,1,2,3,4,5,6C. {}2,4D.{}0,1,2,3,4,5【解析】 【分析】根据并集定义即可求解.【详解】{}0,1,2,3,4,5A =,{}2,4,6B =,A B ={}0,1,2,3,4,5,6.故选:B.【点睛】本题考查集合间的运算,属于基础题.6.已知某函数的图像如图所示,则该函数的值域为 ( )A .()0,+∞B. (],1-∞-C. [)()1,00,-⋃+∞ D. (](),10,-∞-⋃+∞【答案】D 【解析】 【分析】根据函数的图象,确定函数的值域. 【详解】由图象可知,当x >0时,y >0, 当x ≤0时,y ≤﹣1, 综上:y >0或y ≤﹣1.故该函数的值域为(﹣∞,﹣1]∪(0,+∞). 故选D .【点睛】本题主要考查函数的值域的求法,利用图象即可判断函数的值域,比较基础. 7.函数1()2x f x a +=+(0a >且1a ≠)的图象恒过定点()A. (0,3)B. (1,3)C. (-1,2)D. (-1,3)【答案】D 【解析】令x +1=0,即x =﹣1时,y =a 0+2=3,故可得函数y =a x +1+2(a >0,且a ≠1)的图象必经过定点.【详解】令x +1=0,即x =﹣1时,y =a 0+2=3∴函数y =a x +1+2(a >0,且a ≠1)的图象必经过点(﹣1,3) 故选D .【点睛】本题考查函数过特殊点,解题的关键是掌握指数函数的性质,属于基础题. 8.已知4230.2,0.3,0.4a b c ===,则( ) A. b a c <<B. a c b <<C. c a b <<D.a b c <<【答案】B 【解析】 【分析】算出,,a b c 后可得它们的大小.【详解】∵40.20.0016a ==,20.30.09b ==,30.40.064c ==, ∴b c a >>, 故选B .【点睛】本题考查指数幂的大小比较,属于容易题. 9.下列函数中,在定义域内既是减函数又是奇函数的是 A. 1y x =-+B. 1y x=C. 3y x =-D.12xy ⎛⎫= ⎪⎝⎭【答案】C 【解析】 【分析】根据函数的奇偶性排除选项A,D,再根据函数的增减性排除C 得解. 【详解】由于选项A 和D 不是奇函数,都是非奇非偶函数,所以排除A,D. 对于选项B,函数1y x=在定义域不是减函数,在,0)0+-∞∞(和(,)上是减函数,所以排除B.对于选项C,3y x =-,在定义域内是减函数,又是奇函数. 故选C【点睛】本题主要考查函数的奇偶性和增减性,意在考查学生对这些知识的理解掌握水平,属于基础题.10.已知2(1)22f x x x +=-+,则(1)f =( )A. 2B. 1C. 0D. 2-【答案】A 【解析】 【分析】直接代入x=0求解函数值即可. 【详解】f (x +1)=x 2﹣2x +2,令x=0, ∴f (0+1)=f (1)=02﹣0+2=2. ∴f (1)=2. 故选A .【点睛】本题考查函数值的求法,考查计算能力.11.有以下四个结论:①lg(lg 10)=0;②ln(ln e)=0;③若10=lg x , 则x =100;④若e =ln x , 则x =e 2.其中正确的是( ) A. ①③ B. ②④ C. ①② D. ③④【答案】C 【解析】 【分析】通过底数与真数相同得对数是1,真数为1的对数为0判断出①②对;通过对数式与指数式间的转化判断出③④错.【详解】对于①∵lg (lg10)=lg1=0,故①对 对于②∵ln (lne )=ln1=0∴②对 对于③,∵10=lgx∴x=1010∴③错 对于④,∵e=lnx∴x=e e ∴④错 故选C .【点睛】本题考查两个特殊的对数值:底数与真数相同得对数是1,1的对数为0、考查对数式与指数式间的互化,属于基础题.12.已知()f x 是定义在R 上的奇函数,若(2)()f x f x +=-,(1)3f =,则(2018)(2019)f f +的值为( ) A. -3 B. 0C. 3D. 6【答案】A 【解析】 【分析】根据函数为奇函数,结合题中条件,求出函数()f x 的周期,即可求出结果. 【详解】∵()f x 为奇函数,∴()()f x f x -=-.又(2)()f x f x +=-,所以(2)()f x f x +=-,因此(4)(2)()f x f x f x +=-+=, ∴函数()f x 是周期为4的周期函数,所以(45042)(45043)(2)(3)(2018)(2019)f f f f f f ⨯++⨯+=++=. 又(2)(0)0f f ==,(3)(1)(1)3f f f =-=-=-, 因此(2018)(2019)3f f +=-. 故选A.【点睛】本题主要考查函数奇偶性与周期性的应用,灵活运用函数奇偶性与周期性即可,属于常考题型.第II 卷(非选择题)二、填空题13.集合{1,2}A =,则A 集合的子集的个数为________个. 【答案】4 【解析】 【分析】集合A 有两个元素,故子集个数有4个【详解】由已知,集合A 的子集个数为224=,答案:4 【点睛】集合的元素有n 个,那么子集个数有2n 个.14.若函数()()213f x kx k x =+-+是偶函数,则k 等于____.【答案】1 【解析】 【分析】利用偶函数的定义可得实数k 的值.【详解】由于函数()()213f x kx k x =+-+是偶函数,所以()()f x f x =-即()()221313kx k x kx k x +-+=--+,所以()210k x -=恒成立,所以1k =.【点睛】含参数的奇函数、偶函数中参数的确定,可以利用代数式恒成立或取特殊值来求其值,后者注意检验.15.已知()f x 为奇函数,()()9g x f x =+,(2)3g -=,则(2)g =________. 【答案】15 【解析】 【分析】将等式中的x 用2-代替,利用奇函数的定义及(2)3g -=,求出(2)g 的值. 【详解】因为(2)(2)9(2)93(2)6g f f f -=-+=-+=⇒=, 因为(2)(2)96915g f =+=+=,故填:15.点睛】本题考查奇函数的定义:对于定义域中的任意x 都有()()f x f x -=-.16.已知函数22,1()log (1),1x a x f x x x ⎧+≤=⎨->⎩,若[(1)]2f f =,则实数a 的值是_______.【解析】 【分析】先计算出(1)f 的值,然后再根据[(1)]2f f =,求出实数a 的值. 【详解】(1)4(4)2f f =∴=,即log 32a a =⇒=【点睛】本题考查了分段函数的性质,考查了已知复合函数的值求参数问题,考查了数学运算能力. 三、解答题17.设U =R ,{}|56A x x =-<≤,{|6B x x =≤-或}22x >,求: (1)AB ;(2)()()U U C A C B ⋂【答案】(1){}16x x <≤;(2){}65x x -<≤- 【解析】 【分析】求解出集合B ;(1)根据交集定义直接求得结果;(2)根据补集定义分别求得,A B 的补集,根据交集定义求得结果.【详解】由题意得:{6B x x =≤-或}1x > (1){}16A B x x ⋂=<≤ (2){5U C A x x =≤-或}6x >,{}61U C B x x =-<≤()(){}65U U C A C B x x ∴⋂=-<≤-【点睛】本题考查集合运算中的交集运算和补集运算,属于基础题. 18.求下列各式的值: (1)12-20.5312+22-(0.01)54-⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭;(2)33416(log 4log 8)(log 3log 3)++. 【答案】(1)1615(2)154【解析】 【分析】(1)根据指数幂的运算法则,即可求解;(2)由对数的运算法则及换底公式,即可得到结论. 【详解】解:(1)原式=12-20.5312+22(0.01)54-⎛⎫⎛⎫⨯- ⎪ ⎪⎝⎭⎝⎭112221311+[()]()42100-=⨯-1211+4310=⨯- 1615=; (2)原式=()()332232113152log 23log 2log 3log 35log 2log 32444⎛⎫⎛⎫+⋅+=⋅=⎪ ⎪⎝⎭⎝⎭【点睛】本题考查指数幂和对数的运算,熟记运算公式是解题的关键,属于基础题.19.函数()f x 是定义在R 上的奇函数,当0x >时,2()1f x x x =-+.(1)计算()0f ,()1f -; (2)当0x <时,求()f x 的解析式.【答案】(1)f (0)=0,f (-1)=-1;(2)2()1f x x x =--- 【解析】 【分析】(1)根据已知条件,得到f (-x )=-f (x ),进而得到f (0),同时利用对称性得到f (-1)的值. (2)令0x <则0,x ->则2()1f x x x -=++,结合性质得到结论.【详解】(1)()()()0000f f f =-⇒=,()21(1)(111)1f f -=-=--+=-(2)令0x <则0,x ->则2()1f x x x -=++,又函数f (x )是奇函数()()f x f x -=-所以()21f x x x =---【点睛】本题主要是考查函数奇偶性和函数的解析式的运用.解决该试题的关键是利用奇函数的对称性得到x <0的解析式,进而分析得到特殊的函数值.属于基础题. 20.已知集合2{40}A x x =-<,{012}B x x =≤-≤. (1)求AB ;(2)若{11}C x m x m =-≤≤+,A C ⋂≠∅,求实数m 的取值范围. 【答案】(1){}23A B x x ⋃=-<≤;(2)33m -<< 【解析】【分析】(1)可以求出集合{|22}A x x =-<<,{|13}B x x =,然后进行并集的运算即可;(2)根据A C ⋂≠∅即可得出212m -<+或212m --<,从而解出m 的范围即可. 【详解】(1){|22}A x x =-<<,{|13}B x x =, {|23}A B x x ∴⋃=-<;(2){|11}C x m x m =-+,且A C ⋂≠∅,212m ∴-<+或212m --<,解得33m -<<,∴实数m 的取值范围为()3,3-.【点睛】本题考查了描述法的定义,交集、并集的定义及运算,空集的定义,考查了计算能力,属于基础题. 21.已知函数2()(0,1,0)x f x a a a x -=>≠≥且的图像经过点(3,0.5),(1)求a 值; (2)求函数2()(0)x f x a x -=≥的值域;【答案】(1)12a =(2)0,4]( 【解析】 【分析】(1)将点()3,0.5代入函数解析,即可求出a 值; (2)由(1)可知12a =,可知函数()f x 在[0,+∞)上单调递减,根据函数的单调性即可求出函数的值域. 【详解】(1)函数()2x f x a-=的图像经过点()3,0.5320.5a -∴=12a ∴=(2)由(1)可知()()2102x f x x -⎛⎫=≥ ⎪⎝⎭1012<< ()f x ∴在[0,+∞)上单调递减,则()f x 在0x =时有最大值()()21042maxf x f f -⎛⎫∴=== ⎪⎝⎭ 又()0f x >∴函数()f x 的值域为0,4](【点睛】本题主要考查指数函数的单调性判断,并利用函数的单调性求函数的值域,属于基础题.22.设函数()1m f x x =+,且(1)2f = (1)求m 的值;(2)试判断()f x 在(0,)+∞上的单调性,并用定义加以证明;(3)若[]2,5x ∈求值域;【答案】(1)m=1;(2)单调递减,证明见解析;(3)63[,]52.【解析】【分析】(1)由由f (1)2=即可解得;(2)利用减函数的定义可以判断、证明;(3)利用函数的 单调性求函数的值域.【详解】(1)由f (1)2=,得12m +=,1m =.(2)()f x 在(0,)+∞上单调递减.证明:由(1)知,1()1f x x =+, 设120x x <<,则2112121211()()(1)(1)x x f x f x x x x x --=+-+=. 因为120x x <<,所以210x x ->,120x x >,所以12())0(f x f x ->,即12()()f x f x >,所以函数()f x 在(0,)+∞上单调递减.(3)由于函数()f x 在(0,)+∞上单调递减. 所以max min 1316()(2)1,()(5)12255f x f f x f ==+===+=所以函数的值域为63 [,] 52.【点睛】本题考查函数的单调性及其应用,定义证明函数单调性的常用方法,意在考查学生对这些知识的理解掌握水平,属于基础题.。
福建省莆田第一中学2021届高三上学期期中考试数学试题 含答案
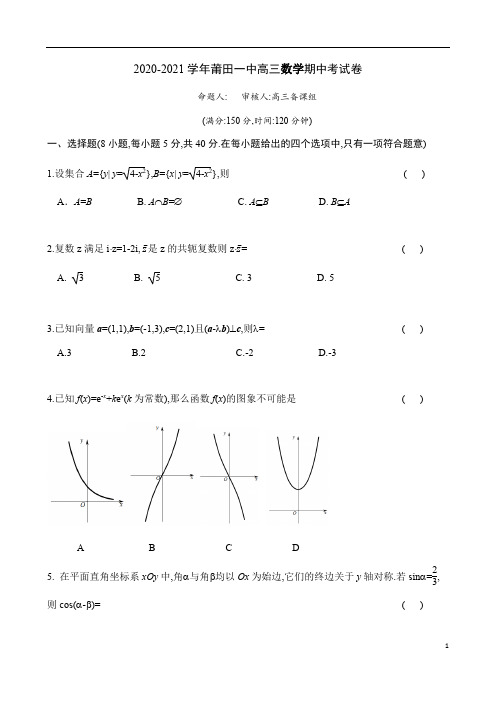
2020-2021学年莆田一中高三数学期中考试卷命题人: 审核人:高三备课组(满分:150分,时间:120分钟)一、选择题(8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题意)1.设集合A={y| y=4-x2},B={x| y=4-x2},则( ) A.A=B B. A⋂B=∅ C. A⊆B D. B⊆A2.复数z满足i⋅z=1-2i, z̅是z的共轭复数则z⋅z̅=( )A. 3B. 5C. 3D. 53.已知向量a=(1,1),b=(-1,3),c=(2,1)且(a-λb)⊥c,则λ=( )A.3B.2C.-2D.-34.已知f(x)=e-x+k e x(k为常数),那么函数f(x)的图象不可能是( )A B C D5. 在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sinα=2 3,则cos(α-β)=( )A.19B.459C.-19D.-4596. 把物体放在冷空气中冷却,如果物体原来的温度为θ1︒C,空气温度为θ0︒C,那么t 分钟后物体的温度θ(单位︒C)可由公式:θ=θ0+(θ1-θ0)e -kt 求得,其中k 是一个随着物体与空气的接触状况而定的正常数.现有100︒C 的物体,放在20︒C 的空气中冷却,4分钟后物体的温度是60︒C ,则再经过m 分钟后物体的温度变为40︒C(假设空气温度保持不变),则m = ( ) A.2 B.4 C.6 D.87.已知P 是椭圆C :x 2a 2+y 2b 2=1(a >b >0)上的点,F 1,F 2分别是C 的左,右焦点,O 是坐标原点, 若|OP →+OF 2→|=2|OF 1→|且∠F 1PF 2=60︒,则椭圆的离心率为 ( )A. 12B.32C. 3-12D. 338.集合论中著名的“康托三分集”是数学理性思维的产物,具有典型的分形特征,其具体操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段(13,23),记为第一次操作;再将剩余的两个区间[0,13],[23,1]分别均分为三段,并各自去掉中间的区间段,记为第二次操作;⋅⋅⋅;如此这样,每次在上一次操作的基础上将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段,操作的过程不断进行下去,以至无穷,剩下的区间集合即是“康托三分集”。
2024届福建省莆田市第六联盟校中考三模数学试题含解析

2024届福建省莆田市第六联盟校中考三模数学试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=1.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为()A.(﹣91255,)B.(﹣12955,)C.(﹣161255,)D.(﹣121655,)2.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有()A.1个B.2个C.3个D.4个3.已知直线m∥n,将一块含30°角的直角三角板ABC,按如图所示方式放置,其中A、B两点分别落在直线m、n 上,若∠1=25°,则∠2的度数是()A.25°B.30°C.35°D.55°4.函数y=ax+b与y=bx+a的图象在同一坐标系内的大致位置是()A.B.C.D.5.由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是()A.3 B.4 C.5 D.66.如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体()A.主视图不变,左视图不变B.左视图改变,俯视图改变C.主视图改变,俯视图改变D.俯视图不变,左视图改变7.下列运算正确的是()A.2a﹣a=1 B.2a+b=2ab C.(a4)3=a7D.(﹣a)2•(﹣a)3=﹣a58.如图,三棱柱ABC﹣A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为()A .3B .23C .22D .49.如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为( )A .9πB .10πC .11πD .12π 10.二次函数2y ax bx c =++()0a ≠的图象如图所示,则下列各式中错误的是( )A .abc >0B .a+b+c >0C .a+c >bD .2a+b=0二、填空题(共7小题,每小题3分,满分21分)11.已知点P (2,3)在一次函数y =2x -m 的图象上,则m =_______.12.分解因式:21a -=________.13.因式分解:2xy 2xy x ++=______.14.(11·湖州)如图,已知A 、B 是反比例函数(k >0,x <0)图象上的两 点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→” 所示路线)匀速运动,终点为C .过P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M 、N .设四边形OMPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为15.如图,菱形ABCD 的边8AB =,60B ∠=︒,P 是AB 上一点,3BP =,Q 是CD 边上一动点,将梯形APDQ沿直线PQ折叠,A的对应点为A',当CA'的长度最小时,CQ的长为__________.16.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于____度.17.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=▲ °.三、解答题(共7小题,满分69分)18.(10分)如图,AB是⊙O的直径,弧CD⊥AB,垂足为H,P为弧AD上一点,连接PA、PB,PB交CD于E.(1)如图(1)连接PC、CB,求证:∠BCP=∠PED;(2)如图(2)过点P作⊙O的切线交CD的延长线于点E,过点A向PF引垂线,垂足为G,求证:∠APG=12∠F;(3)如图(3)在图(2)的条件下,连接PH,若PH=PF,3PF=5PG,BE=25,求⊙O的直径AB.19.(5分)绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图:设销售员的月销售额为x (单位:万元)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省莆田市第六中学2021-2022高一数学上学期期中试题(B 卷)(含解析)(时间120分钟,满分150分)一、选择题:在每小题给出的四个选项中,只有一项是正确(每小题5分,共60分). 1.下列函数中,在其定义域内既是奇函数又是减函数的是( ) A. y x = B. 1y x=C. 3y x =-D. 1()2xy =【答案】C 【解析】试题分析:A 中函数不是减函数;B 中函数在定义域内不是减函数;C 中函数既是奇函数又是减函数;D 中函数不是奇函数 考点:函数奇偶性单调性2.已知集合2{|log ,1}A y y x x ==≥,集合1{|,1}3xB y y x ⎛⎫==≤ ⎪⎝⎭,则A B =( ) A. 1{|}3y y >B. 1{|}3y y ≥C. {|0}y y >D.{|0}y y ≥【答案】B 【解析】 【分析】分别计算得到{|0}A y y =≥,1{|}3B y y =≥,再计算AB 得到答案.【详解】2{|log ,1}{|0}A y y x x y y ==≥=≥;11{|,1}{|}33xB y y x y y ⎛⎫==≤=≥ ⎪⎝⎭ 1{|}3A B y y =≥故选:B【点睛】本题考查了交集的计算,属于简单题. 3.函数f (x )=2x e x +-的零点所在的一个区间是 A. (-2,-1)B. (-1,0)C. (0,1)D. (1,2)【答案】C 【解析】 试题分析:()()()()2102220,1120,0020,1120f e f e f e f e ---=--<-=--<=+-=+-()()100f f ∴<,所以零点在区间(0,1)上考点:零点存性定理4.下列函数中,与函数y x =为相同函数的是( )A. 2x y x =B. y =C. ln xy e =D.2log 2x y =【答案】C 【解析】 【分析】分别判断函数的定义域和表达式,与函数y x =作比较判断得到答案. 【详解】y x =定义域为RA. 2x y x=定义域为()(),00,-∞⋃+∞,不相同;B. y x == ,表达式不相同;C. ln xy e x ==,定义域为R ,是相同函数; D. 2log 2xy =定义域为()0,∞+,不相同;故选:C【点睛】本题考查了相同函数的判断,确定定义域和表达式是解题的关键.5.已知函数2()3f x ax bx a b =+++是定义域为[1,2]a a -的偶函数,则+a b 的值为( ) A. 0 B.13C. 1D. -1【答案】B 【解析】函数()23f x ax bx a b =+++是定义域为[]1,2a a -的偶函数,故1120,.3a a a -+==函数是偶函数,故奇次项系数为0.即0b=,此时13a b+=.故答案为B.6.三个数20.6a=,2log0.6b=,0.62c=之间的大小关系是()A. a c b<< B. b a c<<C. a b c<< D. b c a<<【答案】B【解析】试题分析:2log10b<=,001,21a c<=,所以b a c<<.考点:比较大小.7.函数()1xxay ax=>的图形大致形状是()A. B. C. D.【答案】C【解析】【分析】按x的正负分类讨论,结合指数函数图象确定结论.【详解】由题意,0,0xxa xya x⎧>=⎨-<⎩,∵1a>,∴只有C符合.故选:C.【点睛】本题考查由函数解析式选择函数图象,考查指数函数图象,这类问题可先化简函数式,然后结合基本初等函数的图象与性质确定结论.8.已知函数(2)1,(1)()log,(1)aa x xf xx x--≤⎧=⎨>⎩, 若()f x在(,)-∞+∞上单调递增,则实数a的取值范围为( ) A. (1,2) B. (2,3)C. (2,3]D. (2,)+∞【答案】C 【解析】 【分析】根据()f x 在R 上递增列不等式组,解不等式组求得a 的取值范围.【详解】由于()f x 在R 上递增,所以()201211log 1a a a a ⎧->⎪>⎨⎪-⨯-≤⎩,解得23a <≤.故选:C.【点睛】本小题主要考查分段函数的单调性,考查一次函数、对数函数的单调性,属于基础题.9.设25a b m ==,且112a b+=,则m = ( )B. 10C. 20D. 100【答案】A 【解析】 【分析】将指数式化为对数值,然后利用对数运算公式化简112a b+=,由此求得m 的值. 【详解】由25a b m==得25log ,log a m b m==,所以11log 2log 5log 102m m m a b+=+==,210,m m == A. 【点睛】本小题主要考查指数式和对数式互化,考查对数运算,属于基础题.10.某商场对顾客实行购物优惠活动规定,一次购物付款总额........: (1)如果标价总额....不超过200元,则不给予优惠; (2)如果标价总额....超过200元但不超过500元,则按标价总额....给予9折优惠; (3)如果标价总额....超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( ) A. 550元 B. 560元 C. 570元 D. 580元【答案】C 【解析】 【分析】先判断第一次购物不超过200,第二次不超过500,计算得到共购物650元,再计算得到答案. 【详解】若第一次购物超过200,则付款大于2000.9180⨯=,故第一次购物不超过200元; 若第二次购物超过500,则付款大于5000.9450⨯=,故第二次购物不超过500元; 第二次购物4230.9470÷= 合计470180650+= 付款为()5000.96505000.8450120570⨯+-⨯=+= 故选:C【点睛】本题考查了分段函数的应用,意在考查学生的计算能力和应用能力.11.()f x 是定义在()2,2- 上单调递减的奇函数,当()()2230f a f a -+-< 时,a 的取值范围是 ( ) A. ()0,4 B. 50,2⎛⎫ ⎪⎝⎭C. 15,22⎛⎫⎪⎝⎭D. 51,2⎛⎫⎪⎝⎭【答案】D 【解析】由函数是奇函数可得()()223f a f a -<--,即()()223f a f a -<-+;由函数是单调递减函数可得2235222122232a a a a a ->-+⎧⎪-<-<⇒<<⎨⎪-<-<⎩,应选答案D .12.用{}min ,,a b c 表示a ,b ,c 三个数中的最小值.设{}()min ,2,10,(0)xf x e x x x =+-≥,则()f x 的最大值为( ) A. 4 B. 5 C. 6 D. 7【答案】C 【解析】【分析】化简得到函数()()()104()24xx xf x x t xe x t⎧->⎪=+≤≤⎨⎪≤<⎩,画出函数图像得到答案.【详解】{}()()()104()min,2,1024xxx xf x e x x x t xe x t⎧->⎪=+-=+≤≤⎨⎪≤<⎩其中t为2xe x=+的大于零的根.画出函数图像知:当()max()46f x f==故选:C【点睛】本题考查了函数的新定义问题,分段函数最值,画出函数图像是解题的关键.二、填空题(共5小题,每小题5分,共20分)13.已知集合{}220A x x x=-->,则RA=_____【答案】{}12x x-≤≤【解析】【分析】通过求解不等式,得到集合A,然后求解补集即可.【详解】解不等式220x x-->得12x x-或,所以{}|12A x x x=-或,所以可以求得{}|12RC A x x=-≤≤故答案为{}|12x x-≤≤【点睛】本题考查不等式的解法,补集的运算,是基本知识的考查. 14.函数y 的定义域是________________________. 【答案】(3,4], 【解析】 【分析】直接利用函数定义域的定义得到不等式0.530log (3)0x x ->⎧⎨-≥⎩计算得到答案.【详解】函数y =的定义域满足:0.530log (3)0x x ->⎧⎨-≥⎩ 解得34x <≤故答案为:(3,4]【点睛】本题考查了函数的定义域,意在考查学生的计算能力.15.已知函数()y f x =与xy e =的图象关于直线y x =对称,则2(28)f x x --的单调递增区间为___________________.【答案】(4)+∞,, 【解析】 【分析】先计算得到()ln f x x =,根据复合函数的单调性得到22801x x x ⎧-->⎨≥⎩计算得到答案.【详解】函数()y f x =与xy e =的图象关于直线y x =对称,则()ln f x x =根据复合函数单调性得到2(28)f x x --的单调递增区间满足22801x x x ⎧-->⎨≥⎩解得4x >故答案为:(4)+∞,【点睛】本题考查了复合函数的单调性,忽略掉定义域是容易发生的错误.16.当生物死亡后,其体内原有的碳14的含量大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.2021年7月6日,第43届世界遗产大会宣布,中国良渚古城遗址成功申遗,获准列入世界遗产名录.目前中国世界遗产总数已达55处,位居世界第一.今年暑期,某中学的“考古学”兴趣小组对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测,检测出碳14的残留量约为初始量的54%.利用参考数据:lg 20.30,lg30.48==,请你推断上述所提取的草茎遗存物距今大约有_______________________年(精确到1年). 【答案】4966. 【解析】 【分析】根据题意得到方程5730154%2t⎛⎫= ⎪⎝⎭,计算得到答案.【详解】设时间为t ,根据题意知:573011543lg 3lg 2254%lg lg 57304966257302100lg 2t t t +-⎛⎫=∴=∴=⨯= ⎪-⎝⎭故答案为:4966【点睛】本题考查了指数函数的应用,意在考查学生的计算能力和应用能力.三、解答题(本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或或演算步骤)17.(1)计算:()2lg 25lg 2lg50lg 2⋅++; (2)已知()xxf x a a-=+(0a >且1a ≠),若132f ⎛⎫=⎪⎝⎭,求(0)(1)f f +的值. 【答案】(1)2(2)(0)(1)9f f += 【解析】 【分析】(1)直接利用对数的计算法则得到答案. (2)先计算(0)2f =,再得到11223a a -+=,计算211122(1)2f a a a a --⎛⎫=+=+- ⎪⎝⎭得到答案.【详解】(1)()2252?502lg lg lg lg ++()22(215)25lg lg lg lg +++=251()225lg lg lg lg +++=11225()()2252lg lg lg lg +=++==(2)()x x f x a a -=+,(0)2f ∴=,又132f ⎛⎫=⎪⎝⎭,即11223a a -+=,∴211122(1)2927f a a a a --⎛⎫=+=+-=-= ⎪⎝⎭则(0)(1)9f f +=【点睛】本题考查了对数的计算,函数值的计算,意在考查学生的计算能力.18.已知函数23()log (4)f x x x m =-+的图象过点(0)1,. (1)求实数m 的值,并求()f x 的定义域和值域; (2)解不等式()1f x ≤.【答案】(1)3m =,定义域为(,1)(3,)-∞+∞,()f x 的值域为R (2){|01x x ≤<或34}x <≤【解析】 【分析】(1)将(0)1,代入函数解得3m =,再计算2430x x -+>得到定义域,最后计算值域得到答案.(2)根据题意得到233log (43)log 3x x -+≤得到不等式2243040x x x x ⎧-+>⎨-≤⎩计算得到答案.【详解】(1)由题意得3(0)1log 1f m =∴=,所以3m =, 所以23()log (43)f x x x =-+,由2430x x -+>得1x <或3x >, 则()f x 的定义域为(,1)(3,)-∞+∞,因为243(0,)x x -+∈+∞,所以()f x 的值域为R .(2)不等式233()1log (43)log 3f x x x ≤∴-+≤,所以20433x x <-+≤∴2243040x x x x ⎧-+>⎨-≤⎩ 解得01x ≤<或34x <≤所以不等式()1f x ≤的解集为{|01x x ≤<或34}x <≤【点睛】本题考查了对数型函数的定义域,值域,解不等式,意在考查学生的计算能力. 19.对于函数2()21xf x a =-+()a R ∈.(1)定义法证明:函数()f x 为减函数; (2)是否存在实数a 使函数()f x 为奇函数?【答案】(1)详见解析(2)存在实数1a =使函数()f x 为奇函数 【解析】 【分析】(1)设任意12,x x R ∈且12x x <,计算()21121222()0(21)(21)x x x x f x f x --=>++得到证明. (2)根据()()f x f x -=-化简得到22222222122121x x xx x a ⋅⋅+=+==+++计算得到答案. 【详解】(1)函数2()21xf x a =-+的定义域为R ,设任意12,x x R ∈且12x x <, 则()121211()2121x x f x f x a a ⎛⎫⎛⎫-=--- ⎪ ⎪++⎝⎭⎝⎭21121211222121(21)(21)x x x x x x -=-=++++, 由12x x <,得12022x x <<,则21220x x ->,1210x +>,2210x +>,()12()0f x f x ∴->,即()12()f x f x >()f x ∴为R 上减函数;(2)若函数()f x 为奇函数,则()()f x f x -=-,222121x x a a -⎛⎫-=-- ⎪++⎝⎭,2221221x x x a a ⋅-=-+++,22222222122121x x xx x a ⋅⋅+=+==+++,即1a =, 所以存在实数1a =使函数()f x 奇函数.【点睛】本题考查了定义法证明函数的单调性,根据函数的奇偶性求参数,意在考查学生对于函数性质的综合应用.20.设02x ≤≤,求函数4325xxy =-⋅+最值及相应的x 的值.【答案】2log 31x =-时,min 114y =; 2x =时,max 9y =. 【解析】 【分析】()22325x x y =-⋅+,设214,x t t =≤≤得到2311()24f t t ⎛⎫=-+ ⎪⎝⎭根据二次函数的单调性得到答案.【详解】()2432543252325x x x x x x y =-⋅+=-⋅+=-⋅+, 设2,02,14x t x t =≤≤∴≤≤,且235y t t =-+, 由于22311()3524f t t t t ⎛⎫=-+=-+ ⎪⎝⎭, 则()f t 在31,2⎡⎤⎢⎥⎣⎦上为减函数,在3,42⎡⎤⎢⎥⎣⎦上为增函数, ∴当32t =,则322x =,即2log 31x =-时,min 114y = 又(1)3,(4)9f f ==,即(1)(4)f f <,∴当4t =,则24x =,即2x =时,max 9y =.【点睛】本题考查了函数的最值,换元2x t =可以简化运算,是解题的关键.21.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.(1)分别写出两类产品收益与投资额的函数关系式;(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?【答案】(1)()18f x x =()0x ≥,()g x =()0x ≥;(2)债券类产品投资16万元时,收益最大,为3万元【解析】【分析】 (1)由题意,得到()1f x k x =,()g x k =,代入求得12,k k 的值,即可得到函数的解析式;(2)设债券类产品投资x 万元,可得股票类产品投资()20x -万元,求得总的理财收益的解析式,利用换元法和二次函数的性质,即可求解.【详解】(1)设投资债券类产品的收益()f x 与投资额x 的函数关系式为()()10f x k x x =≥, 投资股票类产品的收益()g x 与投资额x 的函数关系式为()g x k =()0x ≥,可知()110.125f k ==,()210.5g k ==,所以()18f x x =()0x ≥,()g x =()0x ≥. (2)设债券类产品投资x 万元,则股票类产品投资()20x -万元,总的理财收益()()208x y f x g x =+-=+()020x ≤≤.令t =220x t =-,0t ≤≤, 故()()22220111420238288t y t t t t -=+=---=--+, 所以,当2t =时,即债券类产品投资16万元时,收益最大,为3万元.【点睛】本题主要考查了函数的实际应用问题,其中解答中认真审题,列出函数的解析式,熟练应用函数的图象与性质求解是解答的关键,着重考查了分析问题和解答问题的能力,属于中档试题.22.已知函数1()log 1amx f x x -=+(0,1,1)a a m >≠≠-,是定义在(1,1)-上的奇函数. (1)求实数m 的值;(2)判断函数()f x 在(1,1)-上的单调性.【答案】(1)1m =(2)答案不唯一,具体见解析【解析】【分析】(1)利用奇函数()()0f x f x 得到22211m x x -=-,计算得到答案. (2)设12111x t x x -==-+++,利用定义法证明为减函数,再讨论1a >和01a <<,利用复合函数单调性得到答案.【详解】(1)因为()f x 是在(1,1)-上的奇函数,所以()()f x f x -=-,即()()0f x f x , 所以1111log log 0log 01111a a a mx mx mx mx x x x x -+-++=∴⋅=+-++-+,则11111mxmxx x -+⋅=+-+,即22211m x x -=-对定义域中的x 都成立,所以21m =,又1m ≠-,所以1m =;(2)所以1()log 1a x f x x -=+设1(1)221111x x t x x x --++===-++++,设1211x x -<<<,则211212122()2211(1)(1)x x t t x x x x --=-=++++1211x x -<<<∴210x x ->,12(1)(1)0x x ++>∴12t t >.当1a >时,12log log a a t t >,即12()()f x f x >.∴当1a >时,()f x 在(1,1)-上是减函数.当01a <<时,12log log a a t t <,即12()()f x f x <.∴当01a <<时,()f x 在(1,1)-上是增函数.【点睛】本题考查了函数的奇偶性,单调性,分类讨论是常用的方法,需要熟练掌握.。
