测量光电管的伏安特性曲线

光电效应实验报告

一、引言当光束照射到金属表面时，会有电子从金属表面逸出，这种现象被称之为“光电效应”。

对于光电效应的研究，使人们进一步认识到光的波粒二象性的本质，促进了光的量子理论的建立和近代物理学的发展。

现在观点效应以及基于其理论所制成的各种光学器件已经广泛用于我们的生产生活、科研、国防军事等领域。

所以在本实验中，我们利用光电效应测试仪对爱因斯坦的方程进行验证，并且测出普朗克常量，了解并用实验证实光电效应的各种实验规律，加深对光的粒子性的认识。

二、实验原理1. 光电效应就是在光的照射下，某些物质内部的电子背光激发出来形成电流的现象；量子性则是源于电磁波的发射和吸收不连续而是一份一份地进行，每一份能量称之为一个能量子，等于普朗克常数乘以辐射电磁波的频率，即E=h*f （f表示光子的频率）。

2. 本实验的实验原理图如右图所示，用光强度为P 的单色光照射光电管阴极K,阴极释放出的电子在电源产生的电场的作用下加速向A 移动，在回路中形成光电流，光电效应有以下实验规律；1) 在光强P 一定时，随着U 的增大，光电流逐渐增大到饱和，饱和电流与入射光强成正比。

2) 在光电管两端加反向电压是，光电流变小，在理想状态下，光电流减小到零时说明电子无法打到A,此时eUo=1/2mv^2。

3) 改变入射光频率f 时，截止电压Uo 也随之改变，Uo 与f 成线性关系，并且存在一个截止频率fo,只有当f>fo 时,光电效应才可能发生，对应波长称之为截止波长（红限），截止频率还与fo 有关。

4) 爱因斯坦的光电效应方程：hf=1/2m(Vm)^2+W,其中W 为电子脱离金属所需要的功，即逸出功，与2)中方程联立得：Uo=hf/e – W/e 。

光电效应原理图3.光阑：光具组件中光学元件的边缘、框架或特别设置的带孔屏障称为光阑，光学系统中能够限制成像大小或成像空间范围的元件。

简单地说光阑就是控制光束通过多少的设备。

主要用于调节通过的光束的强弱和照明范围。

用示波器显示发光二极管的伏安特性曲线

用示波器显示发光二极管的伏安特性曲线实验目的：用示波器的X-Y方式显示发光二极管的伏安特性曲线（温度）仪器与用具：示波器、发光二极管、开关、电流表、电压表、稳压电源、变阻器、标准电阻预习报告：一：实验原理：发光二极管的正向电流与电压、反向电流与电压之间的关系可用I～V特性曲线表示，如图给出了发光管的伏安特性曲线及其符号。

从图中可以看出，给二极管两端加以正向电压，二极管表现为一个低阻值的非线性电阻，当正向电压较小时，正向电流几乎为零，只有当正向电压超过死区电压（一般硅管约为0.5V，锗管约为0.1V）时，正向电流才明显增大，当正向管压降达到导通时（一般硅管约为0.6～0.7V，锗管约为0.2～0.3V），管子才处在正向导通状态。

迅速增大的电流值有一最大限度，这个最大限度称为二极管的最大正向电流。

给二极管两端加以反向电压，二极管表现为一个高阻值电阻。

当反向电压较小时，反向电流很小，当反向电压超过反向击穿电压（一般在几十伏以上）后，反向电流会突然增大，二极管处于击穿状态。

如右图，在a、b端接上交流电压（其最大输出电压的有效值一般为6～8V左右，并能随时调节）若接上直流电压，屏幕上只显示正向特征曲线。

在Ａ、Ｂ之间测出的是近似加在待测元件R0的电压，在Ｃ、Ｂ间的是电阻R的电压，这个电压正比于R0的电流强度。

因而将二极管的电压U加到示波器的“X轴输入”端，将二极管的电流转化为电压后加到示波器的“Y轴输入”端，从而在示波器屏上得到伏安特性曲线图象。

我们希望显示图形从原点往右是X轴正向往上是Y轴的正向，在Y轴加正向电压时，光点往上走，和习惯相同，但对X轴取向，不同示波器有不同情况，连接电路时，根据图形显示情况，可以改变电路的连接方式，使二极管正确的显示。

为了正确的显示波形，示波器的Y轴输入和X轴输入要有公共端。

在测二极管伏安特性时，有时受实验室现有仪器设备本身结构的限制，可能示波器Y轴信号被短路，因此在实际电路设计中，取B点作为接地点。

光电效应讲义

实验三光电效应【实验目的】1. 加深对光的量子性的认识。

2. 验证爱因斯坦方程，测定普朗克常数。

3. 测定光电管的伏安特性曲线。

【实验原理】当一定频率的光照射到某些金属表面上时，可以使电子从金属表面逸出，这种现象称为光电效应．所产生的电子，称为光电子。

光电效应是光的经典电磁理论所不能解释的。

1905年爱因斯坦依照普朗克的量子假设，提出了光子的概念。

他认为光是一种微粒 — 光子；频率为ν 的光子具有能量h ν，h 为普朗克常数，目前国际公认值为h =(6．6260755±0．0000040)×10-34J ·s 。

当金属中的电子吸收一个频率为ν 的光子时，便获得这光子的全部能量h ν，如果这能量大于电子摆脱金属表面的约束所需要的逸出功W ，电子就会从金属中逸出．按照能量守恒原理有：W v m h m +=221ν (3.1)上式称为爱因斯坦方程，其中m 和v m 是光电子的质量和最大速度，221m v m 是光电子逸出表面后所具有的最大动能．它说明光子能量h ν小于W 时，电子不能逸出金属表面，因而没有光电效应产生；产生光电效应的入射光最低频率ν0=W ／h ，称为光电效应的极限频率(又称红限)。

不同的金属材料有不同的逸出功，因而ν0也是不同的。

用光电管进行光电效应实验，测量普朗克常数的实验原理如图3.1所示。

图中K 为图3.1光电效应实验原理图光电管的阴极，A 为阳极，微安表用于测量微小的光电流，电压表用于测量光电管两极间的电压，E 为电源，R 提供的分压可以改变光电管两极间的电势差。

当单色光入射到光电管的阴极K 上时，如有光电子逸出，则当阳极A 加正电势，K 加负电势时，光电子就被加速；而当K 加正电势，A 加负电势时，光电子就被减速。

当A 、K 之间所加电压U 足够大时，光电流达到饱和值I m ,当U ≤-U 0，并满足方程eU 0 =221m v m (3.2)时，光电流将为零，此时的U 0称为截止电压。

光电效应实验教案

光电效应实验实验目的：1．了解光电效应的基本规律； 2．测量光电管的伏安特性曲线；2．验证爱因斯坦方程，并测定普朗克常数。

实验原理：1．光电效应的实验规律金属在光的照射下释放出电子的现象叫做光电效应。

根据爱因斯坦的“光量子概念”，每一个电子具有能量E h ν=，当光照射到金属上时，其能量被电子吸收，一部分消耗于电子的逸出功W ，另一部分转换为电子逸出金属表面后的动能。

由能量守恒定律可得：212mv h W νν=- （1）（称为爱因斯坦光电方程）光电方程圆满解释了光电效应基本实验事实：（1）仅当光频高于某一阈值时，才能从金属表面打出光电子；（2）单个光电子的动能随光频提高而增大，与入射光强无关；（3）单位时间内产生光电子的数目仅与入射光强有关，与光频无关；（4）光电效应是瞬时完成的，电子吸收光能几乎不需要积累时间。

在理想光电管中，令光电子在反向电场中前进，当剩余的动能刚好被耗尽时，电子所经历的电势差U v 叫做遏止电势差，显然eU v =221νmv ，代入（1）式可得 h WU e eνν=- （2）（2）式表明，遏止电势差U v 是入射光频ν的一次函数，h/e 就是一次曲线的斜率。

爱因斯坦方程预见了实验测算普朗克常数的可行方案。

除了求出h 的量值以外，还可通过（2）式了解光电管的特性。

令ν=0，可得理想阴极的逸出电势等于曲线的纵轴截距，U 0=-W /e ；令U v =0，可得理想阴极的截止频率等于曲线的横轴截距，ν0=W /h 。

实际光电管的情况比较复杂，只能把两个截距U 0、ν0看作整体光电管的宏观参量。

2．验证爱因斯坦方程，求普朗克常数图1是研究光电效应的简化电路。

一束单色光照射真空光电管的阴极K ，设光频ν＞ν0，有光电子产生且有剩余动能。

只要外电路闭合，即使电源分压U =0，光电子也能到达阳极A图1实验原理图形成光电流I A，I A的量值由μA表读出。

仪器简介：本实验使用PC—Ⅱ型普朗克常数测定仪，它包括下列4部分：（1）光源：GGQ—50W高压汞灯，在320.3~872.0nm范围内有若干种单色光供选用。

光电管特性实验报告

一、实验目的1. 了解光电管的基本结构和工作原理。

2. 研究光电管的伏安特性，分析不同电压对光电流的影响。

3. 探究光电管的截止电压与入射光频率的关系。

4. 验证光电效应方程，并测定普朗克常量。

二、实验原理光电效应是指当光照射到金属表面时，金属表面会发射出电子的现象。

光电效应的实验原理如图1所示。

入射光照射到光电管阴极K上，产生的光电子在电场的作用下向阳极A迁移形成光电流。

改变外加电压，测量出光电流I的大小，即可得出光电管的伏安特性曲线。

光电效应的基本实验事实如下：1. 对应于某一频率，光电效应的I-U关系如图2所示。

从图中可见，对一定的频率，有一电压U0，当时，电流为零，这个相对于阴极的负值的阳极电压U0，被称为截止电压。

2. 当U>U0后，I迅速增加，然后趋于饱和，饱和光电流IM的大小与入射光的强度P成正比。

3. 对于不同频率的光，其截止电压的值不同，如图3所示。

4. 截止电压U0与频率v的关系如图4所示，与v成正比。

当入射光频率低于某极限值（随不同金属而异）时，不论光的强度如何，照射时间多长，都没有光电流产生。

5. 光电效应是瞬时效应。

即使入射光的强度非常微弱，只要频率大于v0，在开始照射后立即有光电子产生，所经过的时间至多为10^-9秒的数量级。

根据爱因斯坦的光量子理论，光子能量E与频率v的关系为E=hv，其中h为普朗克常量。

光电效应方程为E=hf=φ+KEmax，其中φ为金属的逸出功，KEmax为光电子的最大动能。

当光电子的最大动能KEmax为0时，对应的截止电压U0为U0=φ/hv。

三、实验仪器与材料1. 光电管2. 汞灯3. 光栅单色仪4. 电压表5. 微电流计6. 滑线变阻器7. 电阻箱8. 信号发生器9. 数据采集器10. 计算机及实验软件四、实验步骤1. 将光电管接入电路，调节滑线变阻器，使电压表显示为零。

2. 调节汞灯，使光栅单色仪的出射光垂直照射到光电管阴极上。

3. 调节电压表，使电压逐渐增加，同时观察微电流计的读数。

光电效应和普朗克常数的测定(1)要点

光电效应和普朗克常数的测定一、实验内容：1.通过实验加深对光的量子性了解；2.通过光电效应实验，测定普朗克常数；3.测量光电管的伏安特性曲线。

二、实验仪器：汞灯、干涉滤光片（365nm，405nm，436nm，546nm，577nm）、光电管、光电效应测试仪，示波器三、实验原理：1.光电效应图1所示的是研究光电效应的一种简单的实验装置。

在光电管的阴极K和阳极A之间加上直流电压U，当用单色光照射阴极K时，阴极上就会有光电子逸出，即为光电效应。

图1 光电效应实验装置图2 截止电压与入射光频率的关系图爱因斯坦方程： W mv h m +=221υ （1）其中m 和v m 是光电子的质量和最大速度，W 为金属的逸出功，221m mv 是光电子逸出表面后所具有的最大动能。

截至电压与最大动能的关系：2210eU m mv = （2）光电子的最大出动能与入射光光强无关。

当入射光频率υ逐渐增大时，截至电压U 0将随之线性增加。

由（1）式和（2）式可知e W e h U -=υ0 （3）对于每一种金属，只有当入射光频率υ大于一定的红限频率υ0时，才会产生光电效应。

光电效应是瞬时发生的。

实验发现，只要入射光频率0υυ>，无论光多么弱，从光照射阴极到光电子逸出这段时间不超过10-9s 。

2.普朗克常数测定根据（3）式可知，测量不同频率的光截止电压，寻求频率v 与截止电压U 0的线性关系h/e ，见图2，从而求得普朗克常数h 。

四、实验步骤：1．测量准备（1）将测试仪及汞灯电源打开，预热20分钟。

——汞灯及光电管的暗箱用遮光罩罩住（2）调整光电管与汞灯的距离，约为40厘米。

并保持不变。

（3）用专用电缆将光电管暗箱电压输入端与测试仪电压输出端连接起来。

（4）将“电流量程”选择开关置于所选档位（截止电压测试为10-13，伏安特性测试为10-10）。

（5）调零：将光电管暗箱电流输出端k 与测试仪微电流输入端断开，调节电压，使电流表指示为000.0。

二极管伏安特性曲线测量方法

二极管伏安特性曲线测量方法电路中有各种电学元件，如碳膜电阻、线绕电阻、晶体二极管和三极管、光敏和热敏元件等。

人们常需要了解它们的伏安特性，以便正确的选用它们。

通常以电压为横坐标，电流为纵坐标作出元件的电压—电流关系曲线，叫做该元件的伏安特性曲线。

如果元件的伏安特性曲线是一条直线，说明通过元件的电流与元件两端的电压成正比，则称该元件为线性元件（例如碳膜电阻）；如果元件的伏安特性曲线不是直线，则称其为非线性元件（例如晶体二极管、三极管）。

本实验通过测量二极管的伏安特性曲线，了解二极管的单向导电性的实质。

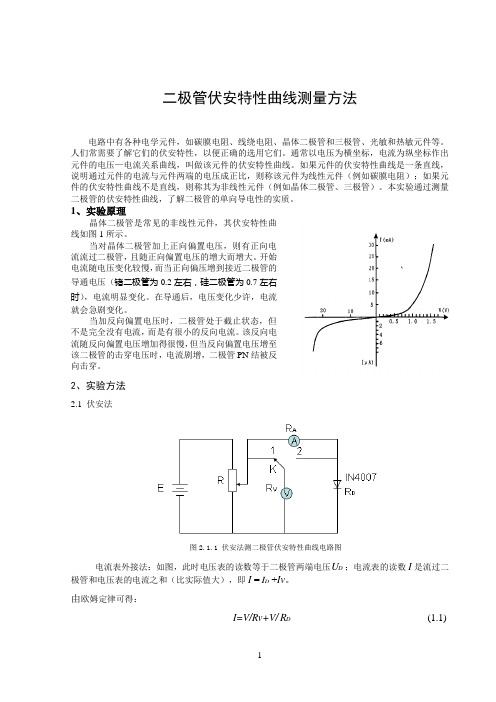
1、实验原理晶体二极管是常见的非线性元件，其伏安特性曲线如图1所示。

当对晶体二极管加上正向偏置电压，则有正向电流流过二极管，且随正向偏置电压的增大而增大。

开始电流随电压变化较慢，而当正向偏压增到接近二极管的导通电压（锗二极管为0.2左右，硅二极管为0.7左右时），电流明显变化。

在导通后，电压变化少许，电流就会急剧变化。

当加反向偏置电压时，二极管处于截止状态，但不是完全没有电流，而是有很小的反向电流。

该反向电流随反向偏置电压增加得很慢，但当反向偏置电压增至该二极管的击穿电压时，电流剧增，二极管PN 结被反向击穿。

2、实验方法2.1 伏安法图2.1.1 伏安法测二极管伏安特性曲线电路图电流表外接法：如图，此时电压表的读数等于二极管两端电压D U ；电流表的读数I 是流过二极管和电压表的电流之和（比实际值大），即I =D I +Iv 。

由欧姆定律可得：I=V/Rv+V/D R(1.1)用V 、I 所作伏安特性曲线电流是电压表和二极管的电流之和，显然不是二极管的伏安特性曲线，所用此方法测量存在理论误差。

在测量低电压时，二极管内阻较大，误差较大，随着测量点电压升高，二极管内阻变小，误差也相对减小；在测量二极管正向伏安曲线时，由于二极管正向内阻相对较小，用此方法误差相对较小。

表2.1.1 电流表外接法测二极管正向伏安特性曲线测量数据此次测量用作标纸绘图绘出伏安曲线电流表内接法：如图，这时电流表的读数I 为通过二极管D 的电流，电压表读数是电流表和二极管电压之和，U =D U +A U 。