matlab操作界面及基本命令简介
实验MATLAB介绍及其基础操作
实验一MATLAB介绍及其基础操作0800210402 冯晓霏1.实验目的:<1 )熟悉MATLAB软件的集成开发环境,学习常用窗口的功能和使用方法。
<2 )掌握帮助的使用方法以及搜索路径的添加方法。
<3 )掌握基本的MATLAB函数操作及其使用。
<4 )掌握简单的计算及其绘图操作。
<5 )了解M文件的编写和运行方法。
2.实验原理<1 )MATLAB 简介MATLAB是美国MathWorks公司开发的高性能的科学与工程计算软件。
经过几十年的扩充和完善,MATLAB已经发展成为集科学计算、可视化和编程于一体的高性能的科学计算语言和软件开发环境。
MATLAB的主要特点包括强大的矩阵计算能力、方便的绘图功能及仿真能力。
另外,MATLAB还附带了大量的专用工具箱,用于解决各种特定领域的问题。
通过学习软件的基本操作及其编程方法,体会和逐步掌握它在矩阵运算、信号处理等方面的功能及其具体应用。
通过本课程实验的学习,要求学生初步掌握MATLAB的使用方法,初步掌握M文件的编写和运行方法,初步将MATLAB运用于信号分析和系统分析中。
循序渐进地培养学生运用所学知识分析和解决问题的能力。
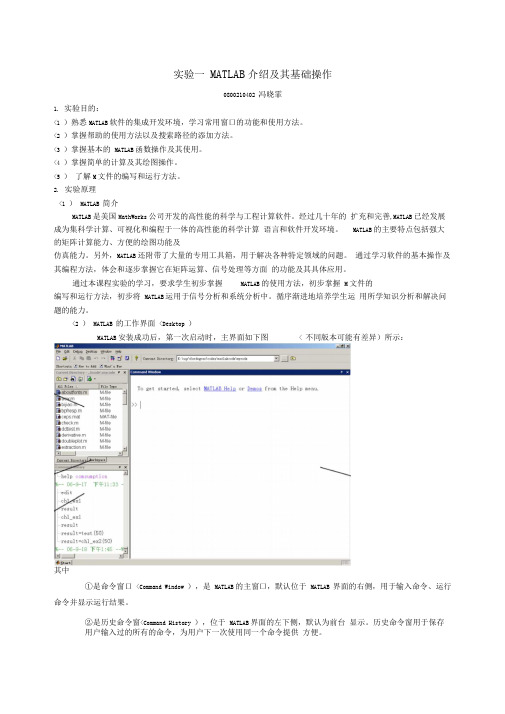
<2 )MATLAB 的工作界面<Desktop )MATLAB安装成功后,第一次启动时,主界面如下图< 不同版本可能有差异)所示:其中①是命令窗口<Command Window ),是MATLAB的主窗口,默认位于MATLAB 界面的右侧,用于输入命令、运行命令并显示运行结果。
②是历史命令窗<Command History ),位于MATLAB界面的左下侧,默认为前台显示。
历史命令窗用于保存用户输入过的所有的命令,为用户下一次使用同一个命令提供方便。
③是当前目录浏览器<Current Directory ),位于MATLAB界面的左上侧,默认为前台显示。
该窗口用于显示当前目录和目录中的所有文件。
MATLAB及其操作简述

第一章MATLAB及其操作简述§1.1 MATLAB简介MATLAB是由美国Math Works公司推出的软件产品。
MATLAB是“Matric Laboratory”的缩写,意及“矩阵实验室”。
MATLAB是一完整的并可扩展的计算机环境,是一种进行科学和工程计算的交互式程序语言。
它的基本数据单元是不需要指定维数的矩阵,它可直接用于表达数学的算式和技术概念,而普通的高级语言只能对一个个具体的数据单元进行操作。
因此,解决同样的数值计算问题,使用MATLAB要比使用Basic、Fortran和C语言等提高效率许多倍。
许多人赞誉它为万能的数学“演算纸”。
MATLAB采用开放式的环境,你可以读到它的算法,并能改变当前的函数或增添你自己编写的函数。
在欧美的大学和研究机构中,MATLAB是一种非常流行的计算机语言,许多重要的学术刊物上发表的论文均是用MATLAB来分析计算以及绘制出各种图形。
它还是一种有利的教学工具,它在大学的线性代数课程以及其它领域的高一级课程的教学中,已成为标准的教学工具。
最初的MATLAB是用FORTRAN编写的,在DOS环境下运行。
新版的MATLAB 是C语言编写的高度集成系统。
它在几乎所有流行的计算机机种,诸如PC、MACINTOSH、SUN、VAX上都有相应的MATLAB版本。
新版的MATLAB增强了图形处理功能,并在WINDOWS环境下运行。
现今,MATLAB的发展已大大超出了“矩阵实验室”的范围,在许多国际一流专家学者的支持下,Maths Works公司还为MATLAB配备了涉及到自动控制、信息处理、计算机仿真等种类繁多的工具箱(Tool Box),这些工具箱有数理统计、信号处理、系统辨识、最优化、稳健等等。
近年来一些新兴的学科方向,Maths Works公司也很快地开发了相应的工具箱,例如:神经网络、模糊逻辑等。
§1.2 MATLAB操作说明一.启动MATLAB启动MATLAB有两种方法:1.在WINDOWS下,点D:\matlab\bin\matlab.exe进入MATLAB环境2.在DOS下,键入matlab,这一命令会自动执行WINDOWS,并启动MATLAB 以上两种操作的结果都会出现一个MATLAB的命令窗口。
matlab仿真语言基本命令

matlab仿真语言基本命令MATLAB(Matrix Laboratory)是一种用于数值计算、数据分析和可视化的高级编程语言和环境。
以下是一些MATLAB仿真中常用的基本命令:1. 基本操作:•clear: 清除工作区变量。
•clc: 清除命令窗口。
•close all: 关闭所有图形窗口。
•help 或doc: 获取帮助文档。
2. 变量和赋值:• a = 5;: 将值5赋给变量a。
• b = [1, 2, 3];: 创建一个包含元素1、2、3的数组b。
• c = rand(3, 3);: 创建一个3x3的随机矩阵c。
3. 矩阵和数组操作:• A = [1, 2; 3, 4];: 创建一个2x2的矩阵A。
• B = eye(3);: 创建一个3x3的单位矩阵B。
• C = A * B;: 矩阵乘法。
• D = A .* B;: 元素相乘。
4. 绘图:•plot(x, y): 绘制二维图。
•surf(X, Y, Z): 绘制三维曲面图。
•imshow(image): 显示图像。
5. 控制流程:•if、else、elseif: 条件语句。
•for i = 1:5, disp(i); end: for循环。
•while condition, disp('Looping'); end: while循环。
6. 函数:•function result = myFunction(arg1, arg2): 定义函数。
•result = myFunction(2, 3);: 调用函数。
7. 文件和目录操作:•cd: 改变当前工作目录。
•ls 或dir: 列出当前目录的内容。
•save filename.mat variable: 将变量保存到.mat文件中。
•load filename.mat: 从.mat文件加载变量。
8. 统计和数学函数:•mean, std, min, max: 计算均值、标准差、最小值、最大值等。
MATLAB基础知识

一、1、数学建模基础知识及常用命令一、界面窗口介绍:1 命令窗口(command window),窗口中输入命令,回车实现计算或绘图功能。
2 工作空间窗口(work space)运行matlab命令时所产生的变量都被加入到工作空间,该窗口可以显示命令窗口中已输入的变量的名称,数值等。
3 命令历史窗口(command history)显示所有执行过的命令,选定某个命令时可以双击或按F9执行。
4 当前目录窗口(Current folder)显示当下目录下的文件信息。
二、常用运算1、算术运算符加+ 减- 乘* 左除/ 右除\ 乘方^注意:在普通的数值运算中,左除为我们常用的除法形式,左除右除结果比较像逆运算,如1/2 和1\2结果互为倒数,但在矩阵的运算中,结果完全不一样,类似于左乘和右乘结果一般会不一样。
运算的优先级:从左到右,幂运算最高优先级,乘除法具有相同次优先级,加减法具有相同的低优先级,括号可以用来改变优先次序。
大家可以进行几个普通计算(练习10分钟)1、325+47⨯÷2、4 59+986-2.7+55-1033.5+20⨯()29()2、数据显示格式默认情况下,matlab显示小数点后4位小数,可以利用format命令改变显示格式(一般写在要改变的数值的命令前):format short 小数点后4位format long 小数点后15位format bank 小数点后2位(以上为三个常用的)format rat 最接近的有理数如以 为例:>> pi= 3.1416>> format long>> pi>> format rat>> pians =355/113>> format bank>> pians =3.14>> format short>> pians =3.1416三、matlab变量1、变量赋值形式变量=表达式(数值)或表达式(数值)其中,“=”为赋值符号,将右边表达式的值赋给左边变量(上面左的含义),当不指定输出变量时,matlab将表达式的值赋给临时变量ans(右的含义)。
Matlab基本功能及使用方法

Matlab基本功能及使用方法Matlab是一种专业的计算机软件,广泛应用于科学计算、数据分析和工程模拟等领域。
它具有强大的数学计算功能和灵活的编程接口,使得科学家、工程师和研究人员能够快速、高效地处理和分析数据。
本文将介绍Matlab的基本功能及使用方法,帮助读者快速上手并掌握Matlab的基本操作和应用技巧。
1. Matlab的界面和基本操作Matlab的界面分为工作区、命令窗口、编辑器和图形界面等几个部分。
在工作区可以查看和管理当前变量,命令窗口可以输入和执行Matlab命令,编辑器则用于编写和运行Matlab脚本或函数。
同时Matlab还提供了丰富的工具箱,包括统计工具箱、优化工具箱、图像处理工具箱等,可以根据需要加载并使用。
2. Matlab的基本数据类型和运算Matlab支持常见的数据类型,如标量、向量、矩阵和多维数组等。
可以使用Matlab进行基本的数学运算,包括加减乘除、幂运算和三角函数等。
Matlab还提供了丰富的数学函数和操作符,使得数学计算变得更加简单和高效。
3. 数据的导入和导出Matlab可以方便地导入和导出各种数据格式,如文本文件、Excel文件、图像文件和音频文件等。
可以使用Matlab提供的函数读取和处理数据,也可以将计算结果和图表保存为文件,方便后续的使用和分享。
4. 数据的可视化Matlab具有强大的数据可视化功能,可以绘制各种类型的图表和图形,如折线图、散点图、柱状图和3D图等。
可以使用Matlab提供的函数设置图表的样式和属性,如线条颜色、坐标轴范围和图例等。
通过数据可视化,可以更直观地理解和展示数据,揭示数据背后的规律和趋势。
5. 图像处理和信号处理Matlab在图像处理和信号处理方面有着广泛的应用。
可以使用Matlab提供的函数读取和处理图像,如图像的滤波、边缘检测和图像增强等。
同时,Matlab还提供了丰富的信号处理函数和工具箱,如离散傅里叶变换、数字滤波器设计和信号重构等,可以对信号进行分析和处理,实现各种信号处理算法和方法。
MATLAB操作命令大全

MATLAB操作命令大全1.基本操作:- clear: 清除工作区中的所有变量。
- clc: 清除命令窗口的内容。
- close all: 关闭所有图形窗口。
- help function-name: 显示与函数相关的帮助文档。
- who: 显示当前工作区中的所有变量。
- save file-name: 保存当前工作区中的所有变量到指定的文件。
- load file-name: 从文件中加载变量到当前工作区。
2.变量操作:-=:赋值操作符,将右边的值赋给左边的变量。
-+:加法操作符。
--:减法操作符。
-*:乘法操作符。
-/:除法操作符。
-^:幂运算操作符。
- sqrt(x): 计算 x 的平方根。
- abs(x): 计算 x 的绝对值。
- max(x): 返回 x 中的最大值。
- min(x): 返回 x 中的最小值。
- sum(x): 计算 x 中所有元素的和。
3.数组操作:- zeros(m, n): 创建一个 m 行 n 列的全零数组。
- ones(m, n): 创建一个 m 行 n 列的全一数组。
- eye(n): 创建一个 n 行 n 列的单位矩阵。
- size(x): 返回 x 的维度。
- length(x): 返回 x 的长度。
- reshape(x, m, n): 将 x 重新排列为一个 m 行 n 列矩阵。
- transpose(x): 将 x 的行和列互换。
4.控制流程:- if-else: 条件语句,根据条件执行不同的代码块。
- for loop: 循环语句,执行指定次数的代码块。
- while loop: 循环语句,根据条件反复执行代码块。
- break: 在循环中使用,用来跳出当前循环。
- continue: 在循环中使用,用来跳过当前循环的剩余部分。
5.统计分析:- mean(x): 计算 x 的平均值。
- median(x): 计算 x 的中位数。
- std(x): 计算 x 的标准差。
MATLAB图形界面的使用方法

MATLAB图形界面的使用方法MATLAB(全称Matrix Laboratory)是一种用于科学计算和数据可视化的强大的数学软件工具。
它不仅具备强大的数值计算和分析能力,还集成了一套友好的图形界面,使得使用者可以直观地进行数据处理和可视化。
本文将介绍MATLAB图形界面的使用方法,帮助读者更好地掌握这个工具。
一、MATLAB的基本界面介绍在启动MATLAB后,会看到它的主界面,这个界面一般分为几个区域,如图1所示。
【插入图1:MATLAB主界面示意图】图1:MATLAB主界面示意图1. 菜单栏:位于主界面的上方,提供了各种操作和功能的选项,包括文件操作、编辑、运行、调试等等。
2. 工具栏:位于菜单栏下方,提供了一些常用的快捷按钮,如新建、打开、保存等。
3. 编辑器区域:位于主界面的左侧,用于编写和编辑MATLAB代码。
在这个区域,可以编写自己的函数、脚本或命令。
4. 工作区:位于主界面的右上角,用于显示当前MATLAB的工作空间。
在这个区域,可以查看已经定义的变量、函数等。
5. 命令窗口:位于主界面的右下角,是与MATLAB交互的主要途径。
我们可以在命令窗口中直接输入MATLAB命令,然后按回车键执行。
6. 图形窗口:位于主界面的中下方,用于显示MATLAB生成的图形和图像。
在这个窗口中,我们可以进行数据的可视化呈现。
二、图像的绘制MATLAB提供了丰富的绘图函数,可以绘制各种图形,如线图、柱状图、散点图等等。
下面以绘制折线图为例,介绍MATLAB的图形绘制方法。
1. 准备数据在绘制图形之前,首先需要准备好要绘制的数据。
可以通过直接输入数据,或者从文件中读取数据。
数据一般以矩阵或向量的形式存储,例如:x = 1:10;y = [3, 5, 6, 9, 11, 14, 18, 20, 23, 25];2. 绘制图形在命令窗口中输入以下代码,即可生成折线图:plot(x, y);xlabel('X轴');ylabel('Y轴');title('折线图');上述代码中,plot函数用于绘制折线图,x和y分别表示横轴和纵轴上的数据。
实验一_MATLAB_软件环境及基本操作

实验⼀_MATLAB_软件环境及基本操作实验⼀ MATLAB 软件环境及基本操作⼀、实验⽬的熟悉 MATLAB 软件的⼯作环境,练习 MATLAB 命令窗⼝的基本操作。
⼆、实验内容1、命令窗⼝(Command Window )运⾏⼊门(1)最简单的计算器使⽤法【例 1】求[12 + 2×(7- 4)]÷32的算术运算结果。
1)⽤键盘在 MATLAB 命令窗⼝中命令提⽰符>>后输⼊以下内容:(12+2*(7-4))/3^22)在上述表达式输⼊完成后,按【Enter 】键,执⾏命令。
3)MA TLAB 命令窗⼝中将显⽰以下结果:ans =【例 2】简单矩阵的输⼊步骤。
123A=4567891)在键盘上输⼊下列内容A = [1,2,3; 4,5,6; 7,8,9]2)按【Enter 】键执⾏命令。
3)在命令执⾏后,MATLAB 命令窗⼝中将显⽰以下结果:A =1 2 34 5 67 8 9【例 3】矩阵的分⾏输⼊A=[1 2 34 5 67 8 9](显⽰结果同例2)【例 4】命令的续⾏输⼊。
…是续⾏符号,表明下⼀⾏是本⾏的接续。
S = 1 – 1/2 + 1/3 –1/4 + 1/5 – 1/6 ... + 1/7 – 1/8S =0.6345 (2)复数和复数矩阵【例1】复数z1 = 3+ 4i,z2 =1+ 2i,z3 = 2eπi/6表达,及计算123z z zz(1)直⾓坐标表⽰法z1= 3 + 4iz1 =3.0000 +4.0000i(2)采⽤运算符构成的直⾓坐标表⽰法和极坐标表⽰法>> z2 = 1 + 2 * i %运算符构成的直⾓坐标表⽰法。
z2 =1.0000 +2.0000i>> z3=2*exp(i*pi/6) %运算符构成的极坐标表⽰法z3 =1.7321 + 1.0000i>> z=z1*z2/z3z =0.3349 + 5.5801i【例-2】复数矩阵的⽣成及运算>> A=[1,3;2,4]-[5,8;6,9]*iB=[1+5i,2+6i;3+8*i,4+9*i]C=A*BA =1.0000 - 5.0000i 3.0000 - 8.0000i2.0000 - 6.0000i 4.0000 - 9.0000iB =1.0000 + 5.0000i2.0000 + 6.0000i3.0000 + 8.0000i4.0000 + 9.0000iC =1.0e+002 * 0.9900 1.1600 - 0.0900i1.1600 + 0.0900i 1.3700【例3】求上例复数矩阵C 的实部、虚部、模和相⾓。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 路径编辑命令 路径编辑命令: path :显示所有matlab命令路径 addpath: eg:addpath c:/windows rmpath :清除子目录 • 显示格式设定命令 显示格式设定命令 命令: format:数据格式显示控制命令,默认 状态相当于format short eg:format long type、more:在命令窗口中显示原程序, type显示全部清单,more显 示一屏
MATLAB (shuzu2)
3、数组的方向
前面例子中的数组都是一行数列,是行方向分布的 前面例子中的数组都是一行数列,是行方向分布的. 称之为行向量 数组也可以是列向量 列向量, 称之为行向量. 数组也可以是列向量,它的数组操作和运 行向量 算与行向量是一样的,唯一的区别是结果以列形式显示 算与行向量是一样的,唯一的区别是结果以列形式显示. 产生列向量有两种方法: 产生列向量有两种方法: 直接产生 转置产生 例 例 c=[1;2;3;4] ; ; ; b=[1 2 3 4]; c=b’
• 操作系统命令 操作系统命令: cd:进入某目录,e.g.:cd c:/windows pwd:显示当前工作目录名称 dir:显示目录 delete:删除文件 mkdir:建立目录 web :打开浏览器 e.g.: web
联机帮助系统
• • • • help 命令或函数名 help菜单选项 lookfor 关键词 what 目录名:查询指定目录下各类文件 的性质,并分类显示, e.g.:what general • ver 工具箱:工具箱版本信息
Matlab语言程序设计基础
●
MATLAB作为线性系统的一种分析和仿真
工具,是理工科大学生应该掌握的技术工具,它 工程、 作为一种编程语言和可视化工具,可解决工程 工程 科学计算和数学学科 科学计算 数学学科中许多问题。 数学学科 ● MATLAB建立在向量 数组 矩阵 向量、数组 矩阵的基础 向量 数组和矩阵 上,使用方便,人机界面直观,输出结果可视 化。 ● 矩阵是MATLAB的核心 矩阵
安装及目录简介
• 安装(略) • 目录:
操作界面简介
• 菜单 • 工具栏 • 窗口
基本命令
• Matlab编辑命令 编辑命令:↑、↓、→、← 编辑命令 • 工作空间管理命令 工作空间管理命令: 命令 who、whos:显示当前工作变量情况 clear:删除当前工作变量 clc:命令窗口清屏 which:显示某个文件所在目录 quit、exit:退出matlab workspace:打开工作空间浏览器
MATLAB (matrix1)
2、矩阵中元素的操作 、
的第r行 (1)矩阵 的第 行:A(r,:) )矩阵A的第 ( ,:) 的第r列 (:,r) (2)矩阵 的第 列:A(:, ) )矩阵A的第 (:, 的每一列, 拉伸为一个列向量: (:) (3)依次提取矩阵 的每一列,将A拉伸为一个列向量:A(:) )依次提取矩阵A的每一列 拉伸为一个列向量 的第i 列构成新矩阵:A(i1:i2, j1:j2) (4)取矩阵 的第 1~i2行、第j1~j2列构成新矩阵 )取矩阵A的第 的第i 构成新矩阵:A(i2:-1:i1,:) (5)以逆序提取矩阵 的第 1~i2行,构成新矩阵 )以逆序提取矩阵A的第 : 的第j 构成新矩阵:A(:, j2:-1:j1 ) (6)以逆序提取矩阵 的第 1~j2列,构成新矩阵 )以逆序提取矩阵A的第 : 的第i 构成新矩阵:A(i1:i2,: ] ,:)=[ (7)删除 的第 1~i2行,构成新矩阵 )删除A的第 的第j 构成新矩阵:A(:, (8)删除 的第 1~j2列,构成新矩阵 :, j1:j2)=[ ] )删除A的第 拼接成新矩阵: (9)将矩阵 和B拼接成新矩阵:[A B];[A;B] )将矩阵A和 拼接成新矩阵 ; ; MATLAB (matrix2)
M文件建立方法:1. 在Matlab中,点:File->New->M-file 文件建立方法: 文件建立方法 中 2. 在编辑窗口中输入程序内容 3. 点:File->Save,存盘,M文件名必须 ,存盘, 文件名必须 与函数名一致。 与函数名一致。 Matlab的应用程序也以 文件保存。 的应用程序也以M文件保存 的应用程序也以 文件保存。
一、变 量 与 函 数 二、数 三、 矩 组 阵
四、 MATLAB编程 编程 五、 实 验 作 业
一、变 量 与 函 数
1、变量 、 命名规则: 命名规则 (1)变量名必须以字母打头,后可以跟 任意字母、数字或下划线; (2)变量名区分大小写; (3)变量名必须是不含空格的单个词.
特殊变量表
特殊变量 ans pi eps flops inf NaN i,j realmin realmax 取 值 用于结果的缺省变量名 圆周率 机器的浮点运算误差限 浮点运算数 无穷大,如 1/0 不定量,如 0/0 i=j= − 1 最小可用正实数 最大可用正实数
二、数
组
1、创建简单的数组 、 x=[a b c d e f ] 创建包含指定元素的行向量
MATLAB (shuzu1)
x=first:last : 创建从first开始,加1计数,到last结束的行向量 开始, 计数, 创建从 开始 计数 结束的行向量 x=first:increment:last : : 创建从first开始,加increment计数,last结束 开始, 计数, 创建从 开始 计数 结束 的行向量 x=linspace(first,last,n) , , ) 创建从first开始,到last结束,有n个元素的行向量 x=logspace(first,last,n) , , ) 创建从first开始,到last结束,有n个元素的对数分隔 的行向量.
(2)数组 数组运算 )数组-数组运算 当两个数组有相同维数时, 当两个数组有相同维数时,加、减、乘、除、 幂运算可按元素对元素方式进行的, 元素对元素方式进行的 幂运算可按元素对元素方式进行的,不同大小或维 数的数组是不能进行运算的. 数的数组是不能进行运算的
设:a=[a1,a2,…,an], b=[b1,b2,…,bn] 则:a+b= [a1+b1,a2+b2,…,an+bn] a.*b= [a1*b1,a2*b2,…,an*bn] a./b= [a1/b1,a2/b2,…,an/bn] a.\b=[b1/a1,b2/a2,…,bn/an] a.^b=[a1^b1,a2^b2,…,an^bn]
特殊矩阵
a=[ ] 产生一个空矩阵, 产生一个空矩阵,当对一项操作无结果 时,返回空矩阵,空矩阵的大小为零 返回空矩阵, b=zeros(m,n) , c=ones(m,n) , 产生一个m行 产生一个 行、n列的零矩阵 列的零矩阵 产生一个m行 产生一个 行、n列的元素 列的元素 全为1的矩阵 全为 的矩阵 d=eye(m,n) , 产生一个m行 产生一个 行、n列的单位矩阵 列的单位矩阵
2、 数组元素的访问 、
访问一个元素: x(i)表示访问数组 的第 个元素 表示访问数组x的第 个元素. (1)访问一个元素 访问一个元素 表示访问数组 的第i个元素 (2)访问一块元素 访问一块元素: x(a :b :c)表示访问数组 的从第 表示访问数组x的从第 访问一块元素 表示访问数组 a个元素开始,以步长为 到第 个元素(但不超过 ), 个元素开始, 到第c个元素 ),b 个元素开始 以步长为b到第 个元素(但不超过c), 可以为负数, 缺损时为 缺损时为1. 可以为负数,b缺损时为 (3)直接使用元素编址序号 x([a b c d]) 表示提 直接使用元素编址序号: 直接使用元素编址序号 取数组x的第 的第a、 、 、 个元素构成一个新的数组 取数组 的第 、b、c、d个元素构成一个新的数组 [x(a) x(b) x(c) x(d)].
5
MATLAB (shuzu4)
是一个向量时, 不能写成x^5, 注:如当x是一个向量时,求 x 时,不能写成 如当 是一个向量时 , 必须写成x.^5 必须写成 返回
三、 矩
阵
1、矩阵的建立 、 逗号或空格用于分隔某一行的元素,分号用于区分不 逗号或空格用于分隔某一行的元素,分号用于区分不 用于分隔某一行的元素 同的行. 除了分号,在输开始 一新行. 输入矩阵时,严格要求所有行有相同的列 一新行 输入矩阵时,严格要求所有行有相同的列. 例 m=[1 2 3 4 ;5 6 7 8;9 10 11 12] ; p=[1 1 1 1 2222 3 3 3 3]
3、数学函数 、
函 数 名 称 函 数 名 称 sin(x) cos(x) tan(x) abs(x) min(x) sqrt(x) log(x) sign(x) 正弦函数 余弦函数 正切函数 绝对值 最小值 开平方 自然对数 符号函数 asin(x) acos(x) atan(x) max(x) sum(x) exp(x) log10 ( x) fix(x) 反正弦函数 反余弦函数 反正切函数 最大值 元素的总和 以 e 为底的指数 以 10 为底的对数 取整
例:定义函数 f(x1,x2)=100(x2-x12)2+(1-x1)2 1.建立 文件:fun.m 建立M文件 建立 文件: function f=fun(x) f=100*(x(2)-x(1)^2)^2+(1-x(1))^2 2. 可以直接使用函数fun.m 可以直接使用函数fun.m
