分子模拟教程
分子模拟的第三章

构象个数: 构象个数: 36×36×36×36×36×36×36×4=313,456,656,384 × × × × × × ×
15
小分子构象分析方法
Conformational Analysis (small molecules)
1. 格点搜索方法 即在构象空间中以小的间隔变量进行逐点搜索,如果变量足够小,则有 即在构象空间中以小的间隔变量进行逐点搜索,如果变量足够小 则有 可能搜索到全部的可能性。此方法的优越性: 在自由度为10—20的分子构 可能搜索到全部的可能性。此方法的优越性 在自由度为 的分子构 象分析。 象分析。 步骤: 步骤: A 固定键长、键角 固定键长、 B 确定分子中所有旋转键 C 设定步长 D 极小化(优化) 极小化(优化) 格点搜索的一个主要缺点是产生和优化的结构数随可旋转键的数以一个连 乘形式增长。 乘形式增长。 构象数为248832。 69hr(设1s优化一个构象) 优化一个构象) 如N=5, , ,构象数为 。 ( 优化一个构象 构象数为36million。 415天 如N=7, , ,构象数为 。 天 N为旋转键的数。 为旋转键的数。 为旋转键的数
系统搜索方法 Systematic Scanning
– 搜索树方法 / 深度优先搜索
0 n-H
7
8
9
10
11
12
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
13
小分子构象分析方法
Conformational Analysis (small molecules)
14
小分子构象分析方法
Conformational Analysis (small molecules)
用“分子模拟”(MP)软件计算聚丙烯酸甲酯的构象能量-高分子物理-实验2-02
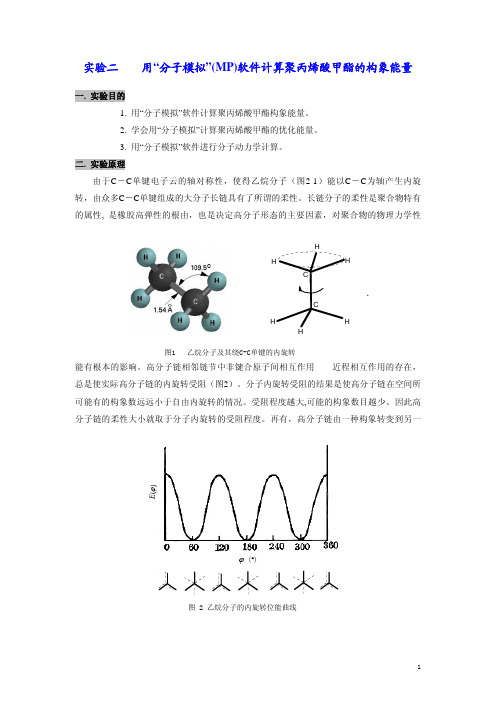
实验二 用“分子模拟”(MP)软件计算聚丙烯酸甲酯的构象能量一. 实验目的1. 用“分子模拟”软件计算聚丙烯酸甲酯构象能量。
2. 学会用“分子模拟”计算聚丙烯酸甲酯的优化能量。
3. 用“分子模拟”软件进行分子动力学计算。
二. 实验原理由于C -C 单键电子云的轴对称性,使得乙烷分子(图2-1)能以C -C 为轴产生内旋转,由众多C -C 单键组成的大分子长链具有了所谓的柔性。
长链分子的柔性是聚合物特有的属性, 是橡胶高弹性的根由,也是决定高分子形态的主要因素,对聚合物的物理力学性能有根本的影响。
高分子链相邻链节中非键合原子间相互作用——近程相互作用的存在,总是使实际高分子链的内旋转受阻(图2)。
分子内旋转受阻的结果是使高分子链在空间所可能有的构象数远远小于自由内旋转的情况。
受阻程度越大,可能的构象数目越少。
因此高分子链的柔性大小就取于分子内旋转的受阻程度。
再有,高分子链由一种构象转变到另一图1 乙烷分子及其绕C-C单键的内旋转H E (ϕ)ϕ (°)图 2 乙烷分子的内旋转位能曲线种构象时,各原子基团间的排布发生相应的变化,其间相互作用能也随之改变(图3)。
大多数柔性大分子可以在一系列不同的构象态之间变化。
因此比较柔性分子的重要任务之一就是进行构象态的比较。
尽管大部分的构象态是那些具有低能量的构象态,但是并不是说只有低能量的构象态才能参加分子间的相互作用。
“分子模拟”是用计算机以原子水平的分子模型来模拟分子的结构与行为,进而模拟分子体系的各种物理和化学性质。
分子模拟法不但可以模拟分子的静态结构,也可以模拟分子的动态行为(如分子链的弯曲运动,分子间氢键的缔合作用与解缔行为,分子在表面的吸附行为以及分子的扩散等)。
该方法不仅能通过分子力学计算得到静态分子的构象能量,还可以通过分子动态学来进行分子动态的计算,将分子几何以及相应的能量计算出来,并由此得到逼近真实分子体系的知识。
图 3 1,2二氯乙烷绕C -C 键内旋转势能随旋转角的变化,反式时旋转角为0度。
《分子模拟教程》PPT课件_OK

17
GEMC 的配分函数
对于原子系统,位型(构型)的配分函数
Q(N,V1,V2 ,T )
N
V N1 1
(V
V1 ) N N1
复杂流体如:胶体悬浮液、高分子溶液、 表面活性剂溶胶等。
❖ 超临界过程研究中的应用
37
❖ 在多相催化研究中的应用:
➢ 对催化剂进行表征 ➢ 表面吸附与脱附过程及表面性质的模拟 ➢ 催化剂表面反应机理的模拟
38
5.3 介观层次材料的计算机模拟
结构是多层次、多尺度的,并且不仅要研究平衡结构, 还要研究结构随时间的演变。所谓结构,就是粒子在空 间有规律的分布。(胡英院士)
N
exp[U (s N )]
14
Metropolis GCMC algorithm
产生巨正则系综的马尔可夫链的过程涉及到典型的、 三种不同的随机移动:
❖ Attempt to move a particle (just like canonical MC)
❖ Attempt to create a particle ❖ Attempt to delete a particle
19
各种随机移动的概率:
Pmove (m n) min{1, exp[Unm / kT]}
Pvolume (m n) min{1,
change
(V1n ) N1 (V - Vቤተ መጻሕፍቲ ባይዱn ) N-N1 (V1m ) N1 (V - V1m ) N-N1
exp[Unm / kT]}
分子模拟实验--Expt-3

(a) 画出三个共线的H原子, 沿X轴放置 (b) 改变两个HH的距离{0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2}, 计算共 7 × 7 = 49 个能量. (c) 采用Gamess, MP2/DZV计算, 具体设置见下页
实验三 — 能量计算和模拟
步骤3: 分子构象搜索 利用扫描一个或两个二面角, 寻找分子的不同构象.
乙醇构象
(a) 选择一个二面角
实验三 — 能量计算和模拟
步骤3: 分子构象搜索
乙醇构象
(b) 选中二面角的旋转 轴, 扫描这个二面角
实验三 — 能量计算和模拟
步骤3: 分子构象搜索 MM2力场扫描
乙醇构象
实验三 — 能量计算和模拟
步骤3: 分子构象搜索 扫描两个二面角
乙醇构象 构象I 构象II
过渡态
实验三 — 能量计算和模拟
步骤3: 分子构象搜索
成环的分子不能扫描!
问题3-5. 计算乙烷的构象, 并确 定其内转动的势垒高度.
实验三 — 能量计算和模拟
步骤4: H—H — H共线势能面的创建
分子的解离能量曲线实验三能量计算和模拟一般双原子分子的解离势能曲线可以用morse函数较好地拟合平衡解离能平衡键长势参数步骤1
实验三 — 能量计算和模拟
要求: 1. 掌握计算分子能量的不同方法 2. 掌握分子相互作用能的分析方法 3. 掌握分子构象的分析方法 4. 了解势能面的作用
实验三 — 能量计算和模拟
问题3-2. 为什么H2的解离曲线不趋向于零? 试分析可 能的原因.
分子模拟的原理与方法

分子模拟的原理与方法分子模拟是一种计算化学的方法,用于研究分子的结构、动力学和热力学性质。
它基于牛顿力学和量子力学的基本原理,通过计算机模拟分子的行为,从而获得有关分子结构和特性的信息。
分子模拟涉及多个学科领域,如计算机科学、物理学、化学和生物学。
本文将重点介绍分子模拟的原理和方法。
1. 分子模拟的原理分子模拟的基本原理是在牛顿力学或量子力学的框架下,构建分子的数学模型,并计算分子在特定条件下的行为。
牛顿力学基于牛顿第二定律,即力等于质量乘以加速度,在此基础上,分子的运动可以通过定量计算来模拟。
量子力学则基于薛定谔方程,以波函数为基础,对分子的运动和结构进行计算。
在分子模拟中,不同的方法选择不同的力场模型,最常用的是分子力场(Molecular Mechanics,MM)和分子轨道(Molecular Orbital,MO)。
分子力场主要考虑原子之间的相互作用,通过选择不同的力场参数可以描述分子的力学和热学性质。
分子轨道则利用量子化学的理论,通过求解薛定谔方程得到分子的能量和电子结构。
2. 分子模拟的方法分子模拟的方法多种多样,常用的方法有分子动力学(Molecular Dynamics,MD)、蒙特卡罗(Monte Carlo,MC)、量子化学计算等。
以下将分别介绍这些方法的基本原理和应用。
2.1 分子动力学分子动力学是模拟分子在一定温度、压力和体积(或密度)条件下运动规律的方法。
它基于牛顿运动定律和正则系综,通过求解拉格朗日方程和哈密顿方程,描述分子在力场作用下的运动轨迹。
分子动力学计算的结果包括分子的构型和动力学性质,如振动频率、热容和热膨胀系数等。
分子动力学的应用范围广泛,包括分子材料、生物分子、纳米颗粒和表面反应等领域。
例如,分子动力学可以用于预测有机分子的溶解度、材料的导电性能、蛋白质的稳定性和反应等。
分子动力学模拟通常需要大量的计算资源和时间,但也可以通过采用并行计算和GPU加速等方式提高计算效率。
分子模拟教程

rx L / 2
rx rx L
o
y
rx L / 2 rx rx L
采用数学 函数:
x
r r L ANINT( )
L
-L/2
L/2
r
r/L>0, ANINT(r/L) = AINT(r/L+0.5)
r/L0, ANINT(r/L) = AINT(r/L-0.5)yຫໍສະໝຸດ rx 0 rx rx L
采用数学 函数:
r r L Dble[ FLOOR( )]
L
r
o
L x
FLOOR(r/L): 返回不超过r/L的最大整数
FLOOR (4.8) has the value 4.
FLOOR (-5.6) has the value -6.
周期性边界条件的算法:
原子水平的模拟 计算机实验 检验理论、筛选实验 科学研究中的第三种方法
分子模拟中涉及的几个基本概念:
模拟计算盒子或模拟胞腔
Simulation box (cell)
装有一定数目流体分子的研 究对象,它是我们要研究的 宏观体系的缩微模型。
立方形胞腔
周期性边界条件(Periodic boundary condition, PBC)
缺点:
分子间力仍然在截断处不连续
。
截断势能函数的形式: ③ 位移-力截断势能函数(Shifted-Force Potential):
dU (r ) U (r ) U (rc ) U sf (r ) dr 0
优点:
r rc
(r rc ) r rc r rc
分子动力学模拟教学教材

分子动力学模拟分子动力学模拟分子动力学是一门结合物理,数学和化学的综合技术。
分子动力学是一套分子模拟方法,该方法主要是依靠牛顿力学来模拟分子体系的运动,以在由分子体系的不同状态构成的系统中抽取样本,从而计算体系的构型积分,并以构型积分的结果为基础进一步计算体系的热力学量和其他宏观性质。
这门技术的发展进程是:1980年:恒压条件下的动力学方法(Andersenの方法、Parrinello-Rahman法)1983年:非平衡态动力学方法(Gillan and Dixon)1984年:恒温条件下的动力学方法(能势‐フーバーの方法)1985年:第一原理分子动力学法(→カー・パリネロ法)1991年:巨正则系综的分子动力学方法(Cagin and Pettit).最新的巨正则系综,即为组成系综的系统与一温度为T、化学势为μ的很大的热源、粒子源相接触,此时系统不仅同热源有能量交换,而且可以同粒子源有粒子的交换,最后达到平衡,这种系综称巨正则系综。
进行分子动力学模拟的第一步是确定起始构型,一个能量较低的起始构型是进行分子模拟的基础,一般分子的其实构型主要是来自实验数据或量子化学计算。
在确定起始构型之后要赋予构成分子的各个原子速度,这一速度是根据玻尔兹曼分布随机生成,由于速度的分布符合玻尔兹曼统计,因此在这个阶段,体系的温度是恒定的。
另外,在随机生成各个原子的运动速度之后须进行调整,使得体系总体在各个方向上的动量之和为零,即保证体系没有平动位移。
由上一步确定的分子组建平衡相,在构建平衡相的时候会对构型、温度等参数加以监控。
进入生产相之后体系中的分子和分子中的原子开始根据初始速度运动,可以想象其间会发生吸引、排斥乃至碰撞,这时就根据牛顿力学和预先给定的粒子间相互作用势来对各个例子的运动轨迹进行计算,在这个过程中,体系总能量不变,但分子内部势能和动能不断相互转化,从而体系的温度也不断变化,在整个过程中,体系会遍历势能面上的各个点,计算的样本正是在这个过程中抽取的。
《分子模拟方法》课件

加速研发进程
分子模拟可以大大缩短药 物研发、材料合成等领域 的实验周期,降低研发成 本。
揭示微观机制
通过模拟,可以揭示分子 间的相互作用机制和反应 过程,有助于深入理解物 质的性质和行为。
分子模拟的发展历程
经典力学模拟
基于牛顿力学,适用于 较大分子体系,但精度
较低。
量子力学模拟
适用于小分子体系,精 度高,但计算量大,需
详细描述
利用分子模拟方法,模拟小分子药物与生物大分子(如蛋白质、核酸等)的相 互作用过程,探究药物的作用机制和药效,为新药研发提供理论支持。
高分子材料的模拟研究
总结词
研究高分子材料的结构和性能,优化 材料的设计和制备。
详细描述
通过模拟高分子材料的结构和性能, 探究高分子材料的物理和化学性质, 优化材料的设计和制备过程,为新材 料的研发提供理论指导。
分子动力学方法需要较高的计算资源和 精度,但可以获得较为准确的结果,因 此在计算化学、生物学、材料科学等领
域得到广泛应用。
介观模拟的原理
介观模拟是一种介于微观和宏观之间的模拟方 法,通过模拟一定数量的粒子的相互作用和演 化来研究介观尺度的结构和性质。
介观模拟方法通常采用格子波尔兹曼方法、粒 子流体动力学等方法,适用于模拟流体、表面 、界面等介观尺度的问题。
分子模拟基于量子力学、经典力 学、蒙特卡洛等理论,通过建立 数学模型来描述分子间的相互作
用和运动。
分子模拟可以用于药物研发、材 料科学、环境科学等领域,为实 验研究和工业应用提供重要支持
。
分子模拟的重要性
01
02
03
预测分子性质
通过模拟,可以预测分子 的性质,如稳定性、溶解 度、光谱等,为实验设计 和优化提供指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机分子模拟的发展历史: 计算机分子模拟的发展历史:
1. 蒙特卡罗方法(MC) 蒙特卡罗方法(MC)
1953 Metropolis, Ulam, Rosenbluth and Tell Los Alamos National Lab Monte Carlo simulation of hard sphere.
气体分子运动论 其它
主要的学习参考书籍: 主要的学习参考书籍:
1. Computer Simulation of Liquids. --- M. P. Allen and D.J. Tildesley, Oxford University (1987) 2. The Art of Molecular Dynamics Simulation. --- D. C. Rapaport, Cambridge University (1995) 3. Understanding Molecular Simulation: From Algorithms to Applications. ---- D. Frenkel and B. Smit, Academic (1996)
模拟算法(途径) 模拟算法(途径) 计算机硬件(工具) 计算机硬件(工具)
HPCx
计算机分子模拟的特点: 计算机分子模拟的特点:
1. 原子水平的模拟 2. 计算机实验 3. 检验理论、筛选实验 检验理论、 4. 科学研究中的第三种方法
2. MC方法简介 方法简介
利用马尔可夫链方法产生感兴趣的系综微观态。 利用马尔可夫链方法产生感兴趣的系综微观态 。 对这些微观态进行系综平均来获得热力学性质。 对这些微观态进行系综平均来获得热力学性质 。 只对系统中粒子的位置抽样, 不包含动能部分, 只对系统中粒子的位置抽样 , 不包含动能部分 , 提供的是系统的超额性质。 提供的是系统的超额性质。
GEMC 的配分函数
对于原子系统,位型(构型) 对于原子系统,位型(构型)的配分函数
V1N1 (V − V1 ) N − N1 Q( N ,V1 ,V2 , T ) = ∑ 3 N N1!( N − N1 )! N1 =0 λ
N N ds2 − N1 ∫ ds1N1 exp[−U (s1N1 / k BT )] ∫
3.4 经典分子动力学的分类: 经典分子动力学的分类:
NVE分子动力学 NVE分子动力学 恒温分子动力学 恒压分子动力学 恒温恒压分子动力学
其它分子动力学
粗粒化分子动力学(Coarse-grained molecular 粗粒化分子动力学(CoarseDynamics, CGMD) 耗散粒子动力学 (Dissipative Particle Dynamics,DPD) Dynamics,
1) 在某t时刻,体系内的粒子i 在某t时刻,体系内的粒子i具有位置 ri(t), 速度 vi(t). 从ri(t), 计算力fi(t). 利用质量mi, 获得ai(t). 计算力f 利用质量m 获得a 利用r 利用ri(t), vi(t), ai(t) 来计算出下一时刻 (t+dt) 时 的位置r 速度v 的位置ri(t+dt), 速度vi(t+dt). (t+dt),从第一步开始循环重复, 利用r 利用ri(t+dt), vi(t+dt),从第一步开始循环重复, 直到我们所需要的模拟时间长度为止。 直到我们所需要的模拟时间长度为止。
但是: 但是:
系综选择关系到热力学量的涨落大小; 系综选择关系到热力学量的涨落大小; 系综选择决定于物理现象的特点和关键物理量的计 算方便与否。 算方便与否。
3. MD方法简介 方法简介
概念: 概念:
从系统中各粒子间的相互作用解每个粒子的 牛顿运动方程: 牛顿运动方程: (F=ma) 。 =ma
3.1 MD 的一般算法: 的一般算法:
2. 分子动力学方法(MD) 分子动力学方法(MD)
1957 Alder and Wainwrigth Livermore Lab Molecular dynamics simulation of hard spheres.
计算机分子模拟的发展历史( 计算机分子模拟的发展历史(续) 分子模拟的发展历史
计算机分子模拟 (Molecular Simulation)
计算机分子模拟的部分应用领域: 计算机分子模拟的部分应用领域:
• 生物、制药: 生物、制药: • 力学、物理学: 力学、物理学: • 化学、化工: 化学、化工: • 微电子、微机械: 微电子、微机械: 大分子性质、药物设计 大分子性质、 应力与裂纹扩展、团簇研究 应力与裂纹扩展、 溶液理论、吸附、界面化学 溶液理论、吸附、 半导体工艺、微加工、 半导体工艺、微加工、 超薄膜润滑: 超薄膜润滑: • 地质、矿产: 地质、矿产: 地核动力学、熔融盐结构 地核动力学、 及其性质
particles N Volume V Temperature T Initial state r{N}
正则系综的配分函数
对于原子系统,位型(构型)的配分函数: 对于原子系统,位型(构型)的配分函数:
1 Q( N ,V , T ) = ⋅ ⋅ ⋅ ∫ exp[−U (r ) / k B T ]dr 3 N N! N !λ3 N ∫
< A(r, p) >τ =< A(r, p) &g算法: 解经典牛顿运动方程的算法:
数值积分 有限差分法 泰勒展开 Verlet算法: Verlet算法: 算法 优点:精确,时间可逆; 优点:精确,时间可逆; 缺点:速度有较大误差,轨迹与速度无关, 缺点:速度有较大误差,轨迹与速度无关,无法与热 浴耦联 Leapfrog形式 Leapfrog形式 优点:轨迹与速度有关, 优点:轨迹与速度有关,可与热浴耦联 缺点:速度近似; Verlet算子多花时间 缺点:速度近似;比Verlet算子多花时间 预测-校正格式 预测-
2) 3)
4)
< A(r , p ) >=
1
τ
∫ 0 A(r (t ), p (t ))dt
τ
3.2 各态遍历假说: 各态遍历假说:
一个力学体系在长时间的运动中, 一个力学体系在长时间的运动中 , 它的代 表点可以无限接近能量曲面上的任何点, 表点可以无限接近能量曲面上的任何点,系 综平均等于长时间的时间平均。 综平均等于长时间的时间平均。
exp(µN / k B T )V N PµVT ( s N , N ) ∝ exp[−U ( s N )] λ3 N N !
Metropolis GCMC algorithm
产生巨正则系综的马尔可夫链的过程涉及到典型的、 产生巨正则系综的马尔可夫链的过程涉及到典型的、 三种不同的随机移动: 三种不同的随机移动:
2. 什么是计算机分子模拟方法? 什么是计算机分子模拟方法?
分子模拟的定义: 分子模拟的定义:
从统计力学基本原理出发,将一定数量的分子输入 从统计力学基本原理出发, 计算机内进行分子微观结构的测定和宏观性质的计算。 计算机内进行分子微观结构的测定和宏观性质的计算。
按照获得微观态的方法不同,分子模拟分为: 按照获得微观态的方法不同,分子模拟分为:
分类: 分类:
正则系综 (Canonical MC) (NVT) MC, 巨正则系综 (Grand Canonical MC,GCMC) (µVT) Gibbs系综 Gibbs系综 (Gibbs Ensemble MC, GEMC) MC,
2.1 正则系综 正则系综MC (Canonical MC Simulation
Nλ = min{1, exp[−( µ + δU nm ) / kT ] } V
3
Pdelete
Pcreate
V = min{1, 3 exp[( µ − δU nm ) / kT ] } λ ( N + 1)
2.3 Gibbs Ensemble MC (GEMC)
特点: 特点:
尤其适用于研究纯流体或混合物的相平衡问题; 尤其适用于研究纯流体或混合物的相平衡问题; 此方法不能用于涉及到非常稠密流体的相平衡问题; 此方法不能用于涉及到非常稠密流体的相平衡问题; 此方法能同时获得共存相的各自密度及其组成; 此方法能同时获得共存相的各自密度及其组成; 此方法避免了共存相界面的问题。 此方法避免了共存相界面的问题。
掌握分子模拟方法的必备知识: 掌握分子模拟方法的必备知识:
编程技能 (Fortran or C/C++) 统计物理学(统计力学) 统计物理学(统计力学):
统计物理学基础; 统计物理学基础; 系综原理; 系综原理; 非平衡统计力学基础; 涨落理论 非平衡统计力学基础;
分子热力学 :
分子间相互作用理论; 分布函数理论 分子间相互作用理论;
巨正则系综配分函数
对于原子系统,位型(构型)的配分函数: 对于原子系统,位型(构型)的配分函数:
V N exp( Nµ / kT ) Ξ( µ , V , T ) = ∑ ⋅ ⋅ ⋅ ∫ exp[−U (s)/ kT ]dS 3 N ∫ N!λ3 N N =0
∞
其中, s 为标度坐标,r = V1/3 。 其中, 为标度坐标, 概率密度为: 概率密度为:
N1 (V - V1 ) Pparticle (m → n) = min{1, exp[−δU nm / kT ] } (N - N1 + 1)V1 change
总结与讨论
系综的等效性
采用什么系综来求体系的热力学量是无关紧要的, 采用什么系综来求体系的热力学量是无关紧要的, 其结果实际上都是一样的,这称为不同系综的热力 其结果实际上都是一样的, 学等同性。 学等同性。
