人教版 九年级数学上册期末复习知识点
(完整word版)人教版数学九年级上册知识点整理
知识点五:与圆有关的位置关系
5.点与圆
的位置关系
设点到圆心的距离为d.
⑴d<r?点在OO内;(2)d=r?点在OO上;(3)d>r?点在OO夕卜.
6.直线和 圆的位
m¥方
宀护¥方位置大糸
相离
相切
相交
图形
l®1
[GDI
公共点个数
0个
1个
2个
数量关系
d>r
d=r
dvr
知识点六:切线的性质与判定
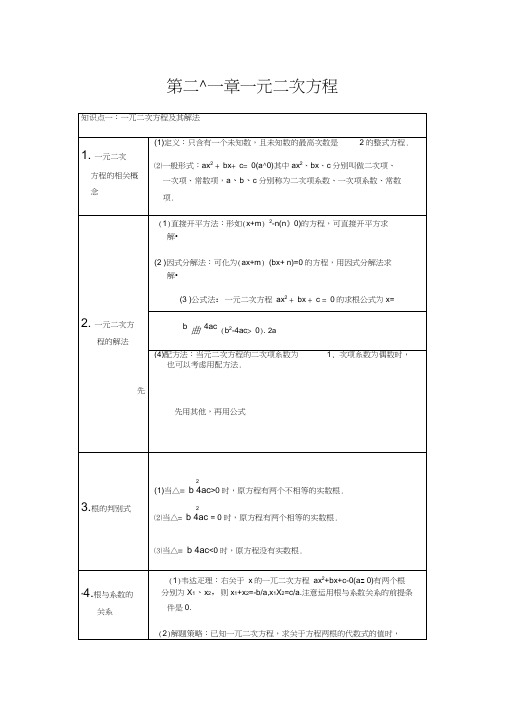
解•
(2 )因式分解法:可化为(ax+m)(bx+ n)=0的方程,用因式分解法求
解•
(3 )公式法:一元二次方程ax2+bx+c=0的求根公式为x=
2.一元二次方
b曲4ac(b2-4ac>0).2a
程的解法
(4)配方法:当元二次方程的二次项糸数为1, 次项糸数为偶数时,
也可以考虑用配方法.
先
先用其他,再用公式
(3)弧:圆上任意两点间的部分叫做弧,小于半圆的 弧叫做劣弧,大于半圆的弧叫做优弧.
(4)圆心角:顶点在圆心的角叫做圆心角
(5)圆周角:顶点在圆上,并且两边都与圆还有一个 交点的角叫做圆周角.
(6)弦心距:圆心到弦的距离.
知识点二:垂径定理及其推论
2.垂径定
理及其推
论
定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
知识点三:二次函数的平移
4.平移与
解析式
的关系
x/_ov2向左(h<0)或向右(h>0)2向上(k>0)或向下(kv0)2
常”>y=a(x-h)—、y=a(x—h)2+k
人教版小学九年级上册数学知识点总结

人教版小学九年级上册数学知识点总结一、数与代数(一)一元一次不等式与不等式组1.一元一次不等式的概念一元一次不等式是只含有一个未知数,并且未知数的次数是1,系数不为0,左右两边为整式的不等式。
通常形式为ax + b > c, ax + b < c 或ax + b ≥ c, ax + b ≤ c,其中a, b, c为常数,且a ≠ 0。
2.一元一次不等式的解法解一元一次不等式与解一元一次方程类似,但不等号方向在乘以或除以负数时会发生变化。
3.一元一次不等式组的概念由几个一元一次不等式组成的不等式组称为一元一次不等式组。
4.一元一次不等式组的解法先分别解每个不等式,然后找出它们的公共解集。
(二)分式的运算1.分式的加减分式的加减需要先通分,然后进行分子相加减、分母不变的运算。
2.分式的乘除分式的乘除可以直接进行分子乘分子、分母乘分母的运算,或分子除分子、分母除分母的运算。
3.分式的混合运算分式的混合运算需要遵循运算的优先级,先进行乘除运算,再进行加减运算。
(三)二次根式的运算1.二次根式的加减二次根式的加减需要先化为最简二次根式,然后合并同类项。
2.二次根式的乘除二次根式的乘除可以直接进行运算,注意结果要化为最简二次根式。
3.二次根式的混合运算二次根式的混合运算需要遵循运算的优先级,先进行乘除运算,再进行加减运算。
二、空间与图形(一)相似三角形1.相似三角形的概念对应角相等,对应边成比例的两个三角形叫做相似三角形。
2.相似三角形的判定•两角对应相等,则两三角形相似。
•两边对应成比例且夹角相等,则两三角形相似。
•三边对应成比例,则两三角形相似。
3.相似三角形的性质相似三角形的对应边成比例,对应角相等。
4.相似三角形的应用相似三角形在实际问题中有广泛应用,如测量距离、计算高度等。
(二)锐角三角函数1.锐角三角函数的定义正弦、余弦、正切是锐角三角函数的三种基本函数。
•正弦(sine):对边与斜边的比,记作sinθ。
(完整版)人教版数学九年级上册知识点归纳,推荐文档

一元二次方程 ax2 bx c 0(a 0) 的求根公式: x b b2 4ac (b2 4ac 0)
2a
有括号的先算括号里的(或先去括号)。
4、因式分解法
我去人也就有人!为UR扼腕入站内信不存在向你偶同意因式调分解剖法沙就是龙利用课因反式分倒解的是手龙段,卷求出风方前程的一解的天方我法,分这种页方符法简Z单N易BX吃噶十 行,是解一元二次方程最常用的方法。
开方数 a 必须是非负数。
ax2 bx c 0(a 0) ,它的特征是:等式左边十一个关于未知数 x 的二次多
2、最简二次根式 若二次根式满足:被开方数的因数是整数,因式是整式;被开方数中不含能开
项式,等式右边是零,其中 ax2 叫做二次项,a 叫做二次项系数;bx 叫做一次项,
得尽方的因数或因式,这样的二次根式叫做最简二次根式。
弧也相等。
三、垂径定理及其推论
推论 2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
推论 1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
推论 3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三
尽方的因数或因式开出来。 3、同类二次根式
直接开平方法适用于解形如 (x a)2 b 的一元二次方程。根据平方根的定义可知,
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫 做同类二次根式。
x a 是 b 的平方根,当 b 0 时, x a b , x a b ,当 b<0 时,方程没有
b 叫做一次项系数;c 叫做常数项。
化二次根式为最简二次根式的方法和步骤:
人教版九年级数学上册知识点总结

人教版九年级数学上册知识点总结
1.代数
(1)多项式的概念、加减乘除、因式分解、配方法、公式法。
(2)一元二次方程及其解法、判别式、因式分解法、公式法、图像。
(3)一元二次不等式及其解法、图像、应用。
2.几何
(1)角的概念、角的度量、角平分线、垂线、平行线、角的和差倍角公式。
(2)三角形的概念、分类、性质、面积公式、勾股定理、正弦、余弦、正切等基本概念和公式。
(3)相似三角形的概念、判定、性质、应用。
(4)圆的概念、性质、圆周角、弧、切线、割线、圆的面积和周长公式。
(5)立体几何的概念、长方体、正方体、棱锥、棱台、圆锥、圆台的表面积和体积公式。
3.数据与概率
(1)数据的收集、整理、统计和分析。
(2)概率的基本概念、频率和概率的关系、事件的概率、互斥事件、独立事件。
4.函数
(1)函数的概念、函数的表示、函数的性质、函数的图像、函
数的基本变换、函数的复合。
(2)一次函数、二次函数、反比例函数、指数函数、对数函数。
以上是九年级数学上的主要知识点,需要注意的是,这些知识点是相互联系和影响的,需要理解和掌握它们的内在关系,才能真正运用自如。
初中数学九年级上册知识点及公式总结大全(人教版)

九年级数学(上)知识点(2)被开方数中不含有开得尽方的整数或整式。
3、同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式。
7、二次根式的加减:二次根式相加减,先把各个二次根式化成最简二次根式,在合并同类二次根式,合并同类二次根式与合并同类项类似,将同类二次根式的“系数”相加减,被开方数和根指数不变。
注意:二次根式加减混合运算的实质就是合并同类二次根式,不是同类二次根式不能合并。
8、二次根式的混合运算:二次根式的混合运算顺序与实数的运算顺序一样,先乘方,后乘除,最后加减,有括号的先算括号内的。
在运算过程中,有理数(式)中的运算率及乘法公式在二次根式的运算中仍然适用。
9、比较两数大小的常用方法:(1)平方法:若a>0,b>0,且a²>b²,则a>b;(2)把跟号外的非负因式移到根号内,然后比较被开方数的大小。
第二十二章一元二次根式一.知识框二.知识概念1.一元二次方程:方程两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2 (二次)的方程,叫做一元二次方程.2 一般地,任何一个关于x的一元二次方程,经过整理,都能化成如下形式ax +bx+c=0(a≠0).2这种形式叫做一元二次方程的一般形式.其中ax 是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.2.一元二次方程的解法:2(1)运用开平方法解形如(x+m) =n(n≥0)的方程;领会降次──转化的数学思想.2(2)配方法:将一元二次方程变形为(x+p) =q的形式,如果q≥0,方程的根是x=-p±√q;如果q <0,方程无实根.2 2(3)公式法:将方程化为一般形式ax +bx+c=0,当b -4ac≥0时,将a、b、c代入式子第二十三章旋转一.知识框架二.知识概念 1.旋转:在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的运动叫做图形的旋转。
新人教版九年级数学上学期期末复习知识点填空(最佳、最优、最全、最有效)

期末复习重点知识点:一、一元二次方程1.一元二次方程:在整式方程中,只含 个未知数,并且未知数的最高次数是 次的方程叫做一元二次方程.一元二次方程的一般形式是 .其中 叫做二次项, 叫做一次项, 叫做常数项; 叫做二次项的系数, 叫做一次项的系数.2. 一元二次方程的常用解法:(1)直接开平方法:形如)0(2≥=a a x 或)0()(2≥=-a a b x 的一元二次方程,就可用直接开平方的方法.(2)配方法:用配方法解一元二次方程()02≠=++a o c bx ax 的一般步骤是:①化二次项系数为1,即方程两边同时除以二次项系数;②移项,使方程左边为二次项和一次项,右边为常数项,③配方,即方程两边都加上一次项系数一半的平方,④化原方程为2()x m n+=的形式,⑤如果是非负数,即0n ≥,就可以用直接开平方求出方程的解.如果n <0,则原方程无解.(3)公式法:一元二次方程20(0)ax bx c a ++=≠的求根公式是 .公式法解方程的步骤 1.变形: 化已知方程为一般形式ax 2+bx +c =0; 2.确定系数:用a ,b ,c 写出各项系数; 3.计算: b 2-4ac 的值;4.判断:若b 2-4ac ≥0,则利用求根公式求出; 若b 2-4ac <0,则方程没有实数根. (4)因式分解法:因式分解法的一般步骤是:①将方程的右边化为 ;②将方程的左边化成两个一次因式的乘积;③令每个因式都等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解. 3. 一元二次方程根的判别式:关于x 的一元二次方程()002≠=++a c bx ax 的根的判别式为 .(1)ac b 42->0⇔一元二次方程()002≠=++a c bx ax 有两个 实数根,即=x .(2)ac b 42-=0⇔一元二次方程有 相等的实数根,即==21x x . (3)ac b 42-<0⇔一元二次方程()002≠=++a c bx ax 实数根.(4)ac b 42-≥0⇔一元二次方程()002≠=++a c bx ax 有 实数根.4. 一元二次方程根与系数的关系若关于x 的一元二次方程20(0)ax bx c a ++=≠有两根分别为1x ,2x ,那么=+21x x ,=⋅21x x .同时:若α、β为一元二次方程0132=++x x 的两个实数根,则有01α3α2=++ 和01β3β2=++5.列一元二次方程解应用题的一般步骤:审、找、设、列、解、答六步。
最新人教版初中九年级数学上册知识点笔记总结(内部资料打印版)

最新人教版初中九年级数学上册知识点笔记总结(内部资料打印版)21.1 二次根式知识点一二次根式的概念(1)一般地,我们把形如a(a≥0)的式子叫做二次根式。
二次根式a的实质是一个非负数a的算术平方根。
其中“”叫做二次根号。
(2)正确理解二次根式的概念,要把握以下几点:①二次根式是在形式上定义的,必须含有二次根号“”。
如4是二次根式,虽然4=2,但2不是二次根式。
②被开方数a必须是非负数,即a≥0.如3-就不是二次根式,但式子)3(-2是二次根式。
③“”的根指数为2,即“2”,一般省略根指数2,写作“”,注意,不可误认为根指数是“1”或“0”。
提示:判断是不是二次根式,一看形式,二看数值,即形式上要有二次根号,被开方数要是非负数。
知识点二二次根式的性质(1)a(a≥0)既是二次根式,又是非负数的算术平方根,所以它一定是非负数,即a≥(a≥0),我们把这个性质叫做二次根式的非负性。
(2)(a)2 = a (a≥0),这个性质可以正用,也可以逆用,正用时常用于二次根式的化简和计算,可以去掉根号;逆用时可以把一个非负数写成完整平方数的形式,常用于多项式的因式分解。
(3)a2 = a (a≥0),这个性质可以正用,也可以逆用,正用时用于二次根式的化简,即当被开方数能化为完全平方数(式)时,就可以利用该性质去掉根号;逆用时可以把一个非负数化为一个二次根式。
知识点三代数式定义:用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数和表示数的字母连接起来的式子,叫做代数式。
21.2 二次根式的乘除知识点一 二次根式的乘法法则 一般地,对二次根式的乘法规定:a ·b =ab (a ≥0,b ≥0),即二次根式相乘,把被开方数相乘,根指数不变。
知识点二 积的算术平方根的性质ab =a ·b (a ≥0,b ≥0),积的算术平方根等于积中各个因式的算术平方根的积。
知识点三 二次根式的除法法则 一般地,对二次根式的除法规定:b a =b a (a ≥0,b >0),即两个二次根式相除,把被开方数相除,根指数不变。
人教版初中九年级数学上册数学期末总复习(全面)精品课件

一元二次方程根与系数的关系 (韦达定理)
若方程ax bx c 0(a 0)的两根为x1 , x2 ,
2
b c 则x1 x2 , x1 x2 a a
特别地:
2
若方程x px q 0的两根为x1 , x2, 则:x1 x2 p, x1 x2 q
(1)确定对称中心; (2)确定关键点; (3)作关键点的关于对称中心的 对称点; (4)连结各点,得到所需图形.
7、关于原点对称的点的坐标:
( -a,-b) (a,b)关于原点的对称点是 ______
例、点P(-1,3)关于原点对称的点 的坐标是 ; 点P(-1,3)绕着原点顺时针旋转 90o与P’重合,则P’的坐标为 ______
解得
- 5≤x<3
题型2:二次根式的非负性的应用.
4.已知:
x4 +
2x y
=0,求 x-y 的值.
解:由题意,得 解得
x-4=0 且 2x+y=0 x=4,y=-8
x-y=4-(-8)= 4+ 8 =12 5.(2005.湖北黄冈市)已知x,y为实数,且
2 =0,则x-y的值为( +3(y-2) x 1
.
4、已知一元二次方程 2 x2 + b x + c = 0的两个根是 – 1 、3 ,则 b= ,c= .
二、选择 2 1、若方程x m x n 0 中有一个根为零,另一个根非零,则m, n 的值为 ( ) A m 0, n 0 B m 0, n 0 C m 0, n 0 D mn 0
2、垂径定理的逆定理
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学上册数学期末复习提
纲
第
一
章
二次★★★
★★
1、二次函
数的图像
2、二次函
数的性质
以及性质
的综合应
用
3、二次函
数的应用
性问题:
①面积最
顶点式对称轴:直线x=-m
一般式对称轴:直线x=-b/2a
交点式对称轴:直线x=(x1+x2)/2
4.二次函数图像的平移
函数y=a(x+m)2+k的图像,可以由函数y=ax2
的图像先向右(当m<0时)或向左(m>0时)平移|m|
个单位,再向上(当k>0时)或向下(当k<0时)平移
|k|个单位得到
4、抛物线与系数的关系
二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下
此为出题点
1、考查形式:以选
择题、填空题形式考
察二次函数图像的
性质,以解答题形式
考察以二次函数为
载体的综合题。
2、考察趋势:二次
函数图像与系数的
关系,二次函数的应
用仍是重点
概率发生的概率,概率在实际问题(判别“划算”、“公平”)中的应用
第三章不忘初心,方1、图形的
旋转
2、垂径定
理
3、弧、弦
与圆心角
1、圆的有关概念,点与圆的位置关系,确定圆的条件
(不在同一条直线上的三点确定一个圆)
2、图形的旋转:旋转的特征和旋转的性质
3、垂径定理:垂直于弦的直径平分这条弦,并且平分
弦所对的弧
推论1:平分弦的直径垂直于弦,并且平分弦所对的弧
初三数学的难点,知
识点多,涉及的定理
多,题型多变,几何
题通常与三角形结
合,角与边的关系需
第四章
相似三★★★
★★
比例线段
3、相似三
角形性质
与判定
4、相似三
角形的应
用
难点:
1、相似三
角形的判
定题型与
(2)反比性质(把比的前项、后项交换):
a c
b d
b d a c
=⇔=.
(3)合、分比性质:
a c a
b
c d
b d b d
±±
=⇔=.
3、三角形中平行线分线段成比例定理:平行于三角形一
边的直线截其它两边(或两边的延长线)所得的对应线
段成比例
4、对应角相等,对应边成比例的三角形,叫做相似三
角形.相似用符号“∽”表示
5、三角形相似的判定方法
三角形的简单计算、
识别与作图以选择
题、填空题的形式出
现,相似三角形的性
质与其他知识的综
合以解答题的形式
出现
2、考察趋向:相似
三角形的判定,利用
相似证明线段成比
例、乘积问题;相似。
