解析几何三角形面积问题答案
解析几何三角形面积问题

解析几何三角形面积问题1、已知两定点12(1,0),(1,0)F F -,满足124PF PF +=u u u r u u u u r的动点P 的轨迹是曲线C .(Ⅰ) 求曲线C 的标准方程;(Ⅱ)直线:l y x b =-+与曲线C 交于,A B 两点, 求AOB ∆面积的最大值.2、已知椭圆(2222:1>>0)y x C a b a b+=的离心率为22,且椭圆上一点到两个焦点的距离之和为22.斜率为()0≠k k 的直线l 过椭圆的上焦点且与椭圆相交于P Q ,两点,线段PQ 的垂直平分线与y 轴相交于点(0)M m ,. (1)求椭圆的标准方程;(2)求m 的取值范围.(3)试用m 表示MPQ ∆的面积S ,并求面积S 的最大值.3、(2012潍坊期末)如图,椭圆G 的中心在坐标原点,其中一个焦点为圆F :0222=-+x y x 的圆心,右顶点是圆F 与x 轴的一个交点.已知椭圆G 与直线l :01-=-my x 相交于A 、B 两点.(I)求椭圆的方程;(Ⅱ)求∆AOB 面积的最大值.4、直线l 与椭圆22221(0)y x a b a b +=>>交于11(,)A x y ,22(,)B x y 两点,已知m ),(11by ax =,n ),(22by ax =,若n m ⊥且椭圆的离心率32e =,又椭圆经过点,1)2,O 为坐标原点. (1)求椭圆的方程;(2)若直线l 过椭圆的焦点(0,)F c (c 为半焦距),求直线l 的斜率k 的值; (3)试问:AOB ∆的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.5、已知椭圆的焦点坐标为1F (-1,0),2F (1,0),过2F 垂直于长轴的直线交椭圆于P 、Q两点,且|PQ |=3,(1) 求椭圆的方程;(2) 过2F 的直线l 与椭圆交于不同的两点M 、N ,则△1F MN 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.6、椭圆E 的中心在坐标原点O ,焦点在x 轴上,离心率为12,点P(1,32),A,B 在椭圆E 上,且→PA+→PB=m →OP (m ∈R)(1) 求椭圆E 的方程及直线AB 的斜率;求证:当△PAB 的面积取得最大值时,原点O 是△PAB 的重心7、已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为63,短轴一个端点到右焦点的距离为3.(1)求椭圆C 的方程;(2)设直线l 与椭圆C 交于A 、B 两点,坐标原点O 到直线l 的距离为32,求△AOB 面积的最大值.8、已知A (23-,0),B (23,0)为平面内两定点,动点P 满足|PA |+|PB |=2. (I )求动点P 的轨迹方程; (II )设直线)0)(23(>+=k x k y l :与(I )中点P 的轨迹交于M 、N 两点.求△BMN 的最大面积及此时直线l 的方程.9、平面直角坐标系内已知两点A (-1,0)、B (1,0),若将动点P (x ,y )的横坐标保持不变,纵坐倍后得到点Q (x y ),且满足AQ uuu r ·BQ uuu r=1.(Ⅰ)求动点P 所在曲线C 的方程;(Ⅱ)过点B 作斜率为的直线l 交曲线C 于M 、N 两点,且OM u u u u r +ON uuu r +OH u u u r =0r ,试求△MNH 的面积.10、在平面直角坐标系内已知两点(1,0)A -、(1,0)B ,若将动点(,)P x y 的横坐标保持不变,()Q x,且满足1AQ BQ⋅=u u u r u u u r.(Ⅰ)求动点P所在曲线C的方程;(Ⅱ)过点B作斜率为的直线l交曲线C于M、N两点,且0OM ON OH++=u u u u r u u u r u u u r r,又点H关于原点O的对称点为点G,试问M、G、N、H四点是否共圆?若共圆,求出圆心坐标和半径;若不共圆,请说明理由.11、[2011·湖南卷] 如图,椭圆1C:22221x ya b+=(0)a b>>,x轴被曲线2C:2y x b=-截得的线段长等于1C的长半轴长.(Ⅰ)求1C、2C的方程;(Ⅱ)设2C与y轴的交点为M,过坐标原点O的直线l与2C相交于点A、B,直线,MA MB 分别与1C相交与,D E.(i)证明:MD ME⊥;(ii)记,MAB MDE∆∆的面积分别是12,S S.问:是否存在直线l,使得121732SS=?请说明理由.12、设椭圆C1:22221(0)x ya ba b+=>>的左.右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图,若抛物线C2:21y x=-与y轴的交点为B,且经过F1,F2点。
文科数学高考二轮复习专题篇平面解析几何4由向量形式的三角形面积公式得到的坐标式三角形面积公式及其应

由向量形式的三角形面积公式获得的坐标式三角形面积公式及其应用高考题1(2010 年高考辽宁卷理科第8 题 )平面上 O, A, B 三点不共线,设 OA a,OB b ,则 OAB 的面积等于()22(a b ) 222(a b) 2 C. 122( a b) 2 D.122(a b )2A. a bB. a b a b a b22答案: C.这道高考题的结论就是向量形式的三角形面积公式:定理 1若三点 O, A, B 不共线,则 S OAB122(OA OB )2 . OA OB21122证明S OAB OA OB 1 c o 2s AOB OA OB(OA OB )2 .22由此结论,还可证得定理 2若三点 O, A, B 不共线,且点O是坐标原点,点 A, B 的坐标分别是(x1 , y1 ), ( x2 , y2 ) ,则S OAB 1x1 y2x2 y1 . 2证法 1由定理1,得S OAB12y122y22( x1 x2y1 y2 ) 21x1 y2 x2 y1(x1)( x2)22证法 2可得直线 AB 的方程是( y1y2 ) x (x1x2 ) y ( x1 y2x2 y1 ) 0因此坐标原点 O 到直线AB的距离是x1y2x2 y1,从而可得AOB 的面积是ABS OAB 1AB x1y2x2 y11x1 y2x2 y1 .AB22下边用定理 2 来简解 10 道高考题 .高考题2(2014 年高考四川卷理科第10 题 )已知 F 为抛物线 y2= x 的焦点,点 A,B 在该抛物线上且位于x 轴的双侧,→→OA· OB=2(此中 O 为坐标原点 ),则△ABO 与△ AFO 面积之和的最小值是 ()172A . 2B . 3 C.8 D.10解 B.得 F 1,0,可不如设 A(x1 , y1 ), B(x2 , y2 )( y10y2 ) . 4由OA OB x1x2y1 y222y1 y2 2 ,可得 y1 y222,得y1 y2,因此由定理SABO 1x1 y2x2 y11y1y2y2y11y1 y2y1y2y1 y2y1y222222因此SABOSAFOy 1 y 21 1 y 19 y 1 y 2 2 9y 1 y 2 32 4 8 8(可适当且仅当 y 14, y 29时取等号 )38因此选 B.高考题 3 (2011 年高考四川卷文科第12 题 )在会合1,2,3,4,5 中任取一个偶数 a 和一个奇数 b 构成以原点为起点的向量 (a, b) . 从全部获得的以原点为起点的向量中任取两个向量为邻边作平行四边形, 记全部作为平行四边形的个数为 n ,此中面积等于 2 的平行四边形的个数 m ,则m( )n2141A.B.C.D.155153解B.所 有满足题意 的 向 量 有 6个1 (2,1),2 (2,3),3 (2,5),4( 4,1), 5 ( 4,3), 6 (4,5) ,以此中的两个向量为邻边的平行四边形有 nC 62 15 个.设i(x 1 , y 1 ), j ( x 2 , y 2 ) ,得 x 1 , x 2(2,4); y 1 , y 2 (1,3,5) ,由定理 2 得,以i ,j为邻边的平行四边形的面积是S1x 1 y 2 x 2 y 1 2 ,可得这样的向量i ,j有3对:2(2,3), (4,5); (2,1), (4,3); (2,1), ( 4,1) .因此m3 1 . n15 5高考题 4 (2011 年高考四川卷理科第12 题 ) 在会合 {1,2,3,4,5} 中任取一个偶数 a 和一个奇数 b 构成以原点为起点的向量 (a, b) . 从全部获得的以原点为起点的向量中任取两个向量为邻边作平行四边形 .记全部作成的平行四边形的个数为 n ,此中面积不超出 4 的平行四边形的个数为 m ,则m()4 n1 22A.B.C.D.153 5 3解 基本领件是由向量(2,1), (2,3), (2,5), (4,1), (4,5), ( 4,3) 中任取两个向量为邻边作平行四边形,得 nC 26 15 .由定理 2 可得:构成面积为 2 的平行四边形的向量有3 对: (2,3), (4,5); (2,1), (4,3); (2,1),(4,1) .构成面积为 4 的平行四边形的向量有2 对: (2,3), (2,5); (2,1), (2,3) .构成面积为 6 的平行四边形的向量有 2 对: (2,3), (4,3); (2,1), (4,5) .构成面积为 8 的平行四边形的向量有 3 对: (2,1), (2,5); (4,1), (4,3);( 4,3),( 4,5) .构成面积为 10 的平行四边形的向量有 2 对: (2,3), (4,1); (2,5), ( 4,5) .构成面积为 14 的平行四边形的向量有 1 对: (2,5), (4,3) .构成面积为 16 的平行四边形的向量有 1 对: (4,1),( 4,5) .构成面积为 18 的平行四边形的向量有 1 对: (2,5), (4,1) .知足条件的事件有 m3 2 5个,因此m5 1 .n15 3高考题 5 (2009 年高考陕西卷文科、理科第21 题)已知双曲线C 的方程为y 2 x 2 1( a 0, b0) ,离心率 e52 5 a 2b 2 2,极点到渐近线的距离为.5(1)求双曲线 C 的方程;(2)如图 1 所示, P 是双曲线 C 上一点,A, B 两点在双曲线 C 的两条渐近线上,且分别位于第一、二象限 .若 APPB,1,2 ,求AOB 面积的取值范围 .3图 1解(1)( 过程略 ) y2x 21.4(2)可设 A(t ,2t), B( s,2s), s 0,t 0 ,由定理 2 及题设可得 S AOB 2st .由 APt2 s2t 2 s PB ,可得 P,,把它代入双曲线 C 的方程,化简得11(1 )24 st ,因此SAOB1 111223可得AOB 面积的取值范围是82,.3高考题 6 (2007 年高考陕西卷理科第 21 题即文科第 22 题)已知椭圆C : x2y 2 1(a b0) 的离心率是6,短轴的一个端点与右焦点的距离是3 .a 2b 23(1)求椭圆 C 的方程;(2)设直线 l 与椭圆 C 交于 A, B 两点,坐标原点O 到直线 l 的距离为3,求 AOB 面积2的最大值 .解(1)( 过程略 ) x 2y 21.3(2)设 A( x 1 , y 1 ), B(x 2 , y 2 ) ,由定理 2 及题设得2SAOBx 1 y 2 x 2 y 1由椭圆的参数方程知,可设 x 1 3 cos , y 1sin , x 23 cos , y 2 sin ,得2S AOB x 1 y 2 x 2 y 1 3 sin()从而可得,当且仅当点A, B 是椭圆 C 的两个极点且AOB时AOB 的面积取到最2大值,且最大值是3.2高考题 7(2010 年高考重庆卷理科第20 题 )已知以原点 O 为中心, F ( 5,0) 为右焦点的双曲线 C 的离心率 e5 .2(1)求双曲线 C 的标准方程及其渐近线方程;(2) 如图2 所示,已知过点M (x 1, y 1 ) 的直线l 1 : x 1 x 4y 1 y4 与过点 N ( x 2 , y 2 ) ( 此中x 2x 1 )的直线l 2 : x 2 x4 y 2 y4 的交点E 在双曲线C上,直线MN 与两条渐近线分别交于G 、 H两点,求OGH的面积.图 2解(1)( 过程略 )双曲线C的标准方程为x2y21,其渐近线方程为x 2 y0 .4(2)由“两点确立向来线”可得直线MN 的方程为: x E x 4 y E y 4 .分别解方程组x E x 4 y E y 4x E x 4 y E y 4,得x 2 y0,x 2y0G4,2, H4,2.x Ex E 2 y E x E2y E 2 y E x E2y E由于点 E 在双曲线C上,因此x E2 4 y E2 4 .由定理2,得S OGH 188882 2x E2 4 y E2x E2 4 y E2x E2 4 y E24注下边将指出图 2 的错误:由于点 E 对于 x 轴的对称点 E ( x E ,y E ) 也在双曲线 C 上,而双曲线C在点 E处的切线方程为xEx( y E ) y1即 x E x 4 y E y 4 也即直线 MN ,因此直线 MN 与双曲线 C 应该相4切,而不是相离 .高考题 8 (2011年高考山东卷理科第22题 )已知动直线x2y2交于l 与椭圆 C :132P(x1, y1 )、 Q (x2 , y2 ) 两不一样点,且OPQ 的面积 S6OPQ,此中 O 为坐标原点.22x2222(1)证明:x1和 y1y2均为定值;(2)设线段PQ的中点为M,求OM PQ 的最大值;(3)椭圆C上能否存在三点D、 E、 G ,使得 S ODE S ODG S OEG6?若存在,判2断 DEG 的形状;若不存在,请说明原因.解(1) 可设P(3cos , 2 sin )、 Q( 3cos , 2 sin ) ,由定理2,得SOPQ6sin()6 22SOPQ6sin()6, sin ()1,cos() 0 22k( k Z)2因此x12x223(cos2cos2) 3(sin 2cos2) 3, y12y223.(2)在 (1)的解答中:当k为奇数时,得P( 3 sin,2cos )、 Q ( 3cos , 2 sin),M3(sin cos),2(sin cos),因此 OM PQ125sin 2 2.222当k为偶数时,得P( 3 sin,2cos )、Q ( 3cos , 2 sin),M3(cos sin),2(cos sin),因此 OM PQ125sin 2 2.222因此 OM PQ 的最大值是5. 2(3)可设D(3cos ,2 sin )、 E(3cos ,2 sin)、G(3cos , 2 sin) ,由(1)的解答知k,l,m(k, l , m Z )2322把这三式相加,得0( k l m)(k l m Z ),这不行能!因此椭圆 C 上不存2在三点 D、 E、G ,使得 S ODE SODGSOEG6.2高考题 9(2013 年高考山东卷文科第22 题 )在平面直角坐标系xOy 中,已知椭圆C的中心在原点 O ,焦点在 x 轴上,短轴长为2,离心率为2 .2(1)求椭圆 C 的方程;(2) A, B 为椭圆 C 上知足AOB 的面积为6的随意两点, E 为线段 AB 的中点,射线4OE 交椭圆 C 与点 P ,设 OPtOE ,务实数 t 的值 .解 (1)( 过程略 )x 2y 2 1 .22 (2)当直线 OE 的斜率不存在时,可求得t 2或3 .3当直线 OE 的斜率存在时,可设A( 2 cos ,sin ), B( 2 cos ,sin ) ,由定理 2 得SOAB2 sin()6 )3, cos( 1 , cos1 3 2, sin()2或.42222可得E2 coscos, sin2 cos2, 所以直线22OE : yx tan ,求得 P2 cos, sin,因此2222y P12 或2t3y E cos32总之, t2或23.31高考题 10 (2008 年高考海南、宁夏卷理科第21 题 )设函数 f (x)ax(a ,b Z ) ,x b曲线 yf ( x) 在点 (2, f (2)) 处的切线方程为 y 3 .(1)求 f ( x) 的分析式 .(2)证明:函数 y f ( x) 的图象是一此中心对称图形,并求其对称中心;(3)证明:曲线 yf (x) 上任一点的切线与直线x 1 和直线 yx 所围三角形的面积为定值,并求出此定值.答案: (1) y x1.(2)略 .(3)2.x 1高考题 11(2008 年高考海南、宁夏卷文科第21 题 )设函数f (x)bf ( x) ax,曲线 yx在点 (2, f (2)) 处的切线方程为7x 4 y120.(1)求f ( x)的分析式;(2)证明:曲线y f (x) 上任一点处的切线与直线x 0和直线 y x 所围成的三角形面积为定值,并求此定值.答案: (1)y x 3.(2)6. x下边给出这两道高考题结论的推行.定理 3(1) 双曲线x2y 21( a0,b0)上任一点的切线与两条渐近线a 2b2b bS ab ;yx, y x 围成三角形的面积是a ab(2) 曲线y ax0)上任一点的切线与两条渐近线x 0, y ax 围成三角形的面(bx积是 S b ;(3) 曲线y ax c b(b0) 上任一点的切线与两条渐近线x d0, y ax cdx围成三角形的面积是S b .证明(1) 如图 3 所示,可求得过双曲线上任一点(,)(222222) 的切P x0y0 b x0 a y0 a b线方程是b2x0x a2 y0 y a2 b2,还可求得它与两条渐近线y bx, ybx 的交点分别为a aMa2 b,ab2a2b,ab22 可立得欲证建立 .bx0ay0, Nbx0bx0,再由定理bx0ay0ay0ay0图 3(2)由y axb b.因此过该曲线上任一点P x0 , ax0b(b 0) ,得 y ax 2的切x x0线方程是yb b( x x0 ) ax 0a2x0x0从而可求得它与两条渐近线x0, y ax 的交点分别为M0, 2b, N (2 x0 ,2ax0 ) ,再由x0定理 2 可立得欲证建立 .(3)因为y ax cba( x d )b所以曲线xc ad ,b d x dy ax c0) 是由曲线y ax b0) 沿向量 ( d , c ad ) 平移后获得的,(b(bx d x 因此由结论 (2) 立得结论 (3) 建立 .(4)。
解析几何-吕林根-课后习题解答一到五
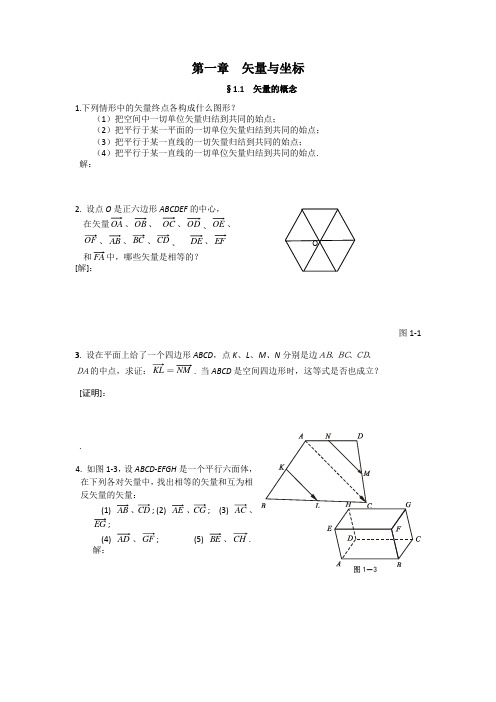
第一章矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点.解:2. 设点O是正六边形ABCDEF的中心,在矢量OA、OB、OC、OD、OE、OF、AB、BC、CD、DE、EF和FA中,哪些矢量是相等的?[解]:图1-13. 设在平面上给了一个四边形ABCD,点K、L、M、N分别是边AB、BC、CD、DA的中点,求证:KL=NM. 当ABCD是空间四边形时,这等式是否也成立?[证明]:.4. 如图1-3,设ABCD-EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB、CD; (2) AE、CG; (3) AC、EG;(4) AD、GF; (5) BE、CH.解:§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件? (1=+ (2+=+ (3-=+ (4+=- (5= 解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解:2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF . 解:3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 解:4 在四边形ABCD中,→→→+=baAB2,→→→--=baBC4,→→→--=baCD35,证明ABCD为梯形.解:6. 设L、M、N分别是ΔABC的三边BC、CA、AB的中点,证明:三中线矢量AL, BM, CN可以构成一个三角形.7. 设L、M、N是△ABC的三边的中点,O是任意一点,证明OBOA++OC=OL+OM+ON.解:8. 如图1-5,设M是平行四边形ABCD的中心,O是任意一点,证明OA+OB+OC+OD=4OM.解:9在平行六面体ABCDEFGH(参看第一节第4题图)中,证明→→→→=++AGAHAFAC2.证明:.10.用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分.解12. 设点O 是平面上正多边形A 1A 2…A n 的中心,证明: 1OA +2OA +…+n OA =0.解,13.在12题的条件下,设P 是任意点,证明 证明:§1.4 矢量的线性关系与矢量的分解1.在平行四边形ABCD 中,(1)设对角线,,b BD a AZ ==求.,,,DA CD BC AB 解(2)设边BC 和CD 的中点M 和N ,且q AN P AM ==,求CD BC ,。
解析几何s三角形oab的面积

解析几何s三角形oab的面积要解析三角形OAB的面积,我们可以使用以下方法:
1. 使用三角形的高和底边,首先,我们可以计算出三角形OAB 的底边OA的长度和高AB的长度。
然后,我们可以使用面积公式
S=1/2底边高来计算三角形的面积。
2. 使用三角形的两边和夹角,如果我们知道三角形OAB的两边OA和OB的长度以及它们之间的夹角,我们可以使用面积公式S=1/2边1边2sin(夹角)来计算三角形的面积。
3. 使用海伦公式,如果我们知道三角形OAB的三条边的长度,我们可以使用海伦公式来计算三角形的面积。
海伦公式为
S=√[p(p-a)(p-b)(p-c)],其中p是半周长,a、b和c分别是三角形的三条边的长度。
以上是几种常见的方法,你可以根据你手头的具体信息选择合适的方法来计算三角形OAB的面积。
希望这些方法能够帮助你解决问题。
过定点与坐标轴围成的三角形面积最小问题

过定点与坐标轴围成的三角形面积最小问题1.引言在平面解析几何中,经常会遇到求解围成的三角形面积的问题。
本文将围绕着过定点与坐标轴围成的三角形面积最小问题展开讨论。
我们将从基本原理开始,逐步推导出解决该问题的方法。
2.问题描述给定一个坐标轴上的一点P(x,y),以及坐标轴上的两个端点A(0,0)和B(a,0),其中a为正实数。
我们的目标是找到通过点P的直线与坐标轴围成的三角形A BC,使得该三角形的面积最小。
3.解决方法为了解决这个问题,我们可以按照以下步骤进行推导。
3.1建立坐标轴表示首先,我们可以将问题抽象为在坐标系中求解面积最小的三角形。
我们以P点在坐标系的位置为起点,建立坐标轴表示。
3.2确定点B的坐标由于点B在坐标轴上,且横坐标为a,纵坐标为0,我们可以确定B的坐标为B(a,0)。
3.3确定点C的坐标为了求得面积最小的三角形A BC,我们需要确定点C在坐标系中的位置。
由于P点在过点C的直线上,我们可以假设点C的坐标为C(c,0),其中c为正实数。
3.4确定三角形面积根据解析几何的面积公式,我们可以计算出三角形AB C的面积S为:S=0.5*|x*0-0*c+a*c-x*0|经过计算化简,可以得到:S=0.5*a*c3.5最小化面积为了使三角形AB C的面积最小,我们需要找到使S最小的c值。
由于c为正实数,所以我们可以对S进行求导,然后令导数为0,解得最小值。
3.6求解最小面积对S=0.5*a*c求导,并令导数为0,我们可以得到c的值:0.5*a*c'=0解得c'=0,即c为任意的正实数。
这说明无论c取多少,都不会改变S的最小值。
3.7结论根据上述推导,我们可以得出结论:过定点与坐标轴围成的三角形面积最小的条件是无论c取多少,c为任意的正实数。
4.总结通过以上推导,我们解决了过定点与坐标轴围成的三角形面积最小问题。
我们发现,无论点C在坐标系中的位置如何,三角形A BC的面积都不会改变。
解析几何面积公式

解析几何面积公式
1.解析几何法:由众多三角形的面积公式得出的结果:
(r是三角形内切圆半径)(R是三角形外接圆半径)
其中:
2.向量叉积法:任意两边向量的叉积的绝对值的1/2即为三角形的面积。
Code:
double TriangleArea(V l1,V l2){
return fabs((l1.end-l1.start)^(l2.end-l2.start))/2;}
多边形面积的计算。
现在讨论简单多边形,不考虑自交多边形,计算时采用剖分思想,将其转化为求多个三角形面积的子问题集合。
有三种转化方法:
1.将多边形内的一点与多边形顶点连线,可将多边形划分成多个三角形,分别求出每个三角形的面积,累加起来即为多边形的面积。
如图,J为多边形内一点。
2.采用三角剖分的方法,取多边形的一个顶点作为剖分出的三角形顶点,三角形的其他点作为多边形上相邻的点,
由于叉乘有正有负,所以正好可以抵消掉多余的面积部分。
面积的计算公式为:如图,以A点为剖分顶点。
解析几何教程习题答案

第一章 向量代数习题1.11. 试证向量加法的结合律,即对任意向量,,a b c 成立()().a b c a b c ++=++证明:作向量,,AB a BC b CD c ===(如下图),则 ()(),a b c AB BC CD AC CD AD ++=++=+=()(),a b c AB BC CD AB BD AD ++=++=+=故()().a b c a b c ++=++2. 设,,a b c 两两不共线,试证顺次将它们的终点与始点相连而成一个三角形的充要条件是0.a b c ++=证明:必要性,设,,a b c 的终点与始点相连而成一个三角形ABC ∆,则0.a b c AB BC CA AC CA AA ++=++=+== 充分性,作向量,,AB a BC b CD c ===,由于ABCabcABCDabca b +b c +0,a b c AB BC CD AC CD AD =++=++=+=所以点A 与D 重合,即三向量,,a b c 的终点与始点相连构成一个三角形。
3. 试证三角形的三中线可以构成一个三角形。
证明:设三角形ABC ∆三边,,AB BC CA 的中点分别是,,D E F (如下图),并且记,,a AB b BC c CA ===,则根据书中例 1.1.1,三条中线表示的向量分别是111(),(),(),222CD c b AE a c BF b a =-=-=- 所以,111()()()0,222CD AE BF c b a c b a ++=-+-+-=故由上题结论得三角形的三中线,,CD AE BF 可以构成一个三角形。
4. 用向量法证明梯形两腰中点连线平行于上、下底且等于它们长度和的一半。
证明:如下图,梯形ABCD 两腰,BC AD 中点分别为,E F ,记向量,AB a FA b ==,则,DF b =而向量DC 与AB 共线且同向,所以存在实数0,λ>使得.DC AB λ=现在,FB b a =+,FC b a λ=-+由于E 是BC 的中点,所以1111()()(1)(1).2222FE FB FC b a a b a AB λλλ=+=++-=+=+且A BabcE FD C111(1)()().222FE AB AB AB AB DC λλ=+=+=+ 故梯形两腰中点连线平行于上、下底且等于它们长度和的一半。
已知顶点坐标三角形面积

已知顶点坐标三角形面积
在解析几何中,如果给定了三角形三个顶点的坐标,我们可以通过下面的公式计算三角形的面积:
设三个顶点坐标分别为(x1,y1)、(x2,y2)、(x3,y3),则三角形面积S可以通过以下公式计算:
S = 1/2 * |x1(y2-y3) + x2(y3-y1) + x3(y1-y2)|
其中|...|表示取绝对值。
这个公式实际上是利用了向量外积的性质。
我们可以将三角形的两个边向量进行外积,所得向量的模长就等于这两个边向量所围成的平行四边形的面积。
由于三角形面积是平行四边形面积的一半,所以最终的公式就是上面这个形式。
需要注意的是,在使用该公式时,我们输入的顶点坐标必须按照逆时针或顺时针的顺序给出,否则将得到负值。
通过这个公式,我们可以快速而准确地计算出任意三角形的面积,只要知道它的三个顶点坐标即可。
这在计算机辅助设计、图形学等领域有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析几何三角形面积问题答案1、解: (Ⅰ)由题意知,曲线C 是以12,F F 为焦点的椭圆.∴2,1,a c ==23b ∴= 故曲线C 的方程为:22143xy+=. 3分(Ⅱ)设直线l 与椭圆22143xy+=交点1122(,),(,)A x y B x y ,联立方程223412y x b x y =-+⎧⎨+=⎩得22784120x bx b -+-= 4分 因为248(7)0b ∆=->,解得27b <,且212128412,77b b x x x x -+==5分点O 到直线l的距离d =6分AB == 9分∴12AO B S ∆=⋅= 10分≤当且仅当227b b =-即2772b =<时取到最大值.∴A O B ∆. 12分2、解:(1)依题意可得⎪⎩⎪⎨⎧-=-+=+,12,12c a c a 解得.1,2==c a从而.1,22222=-==c a b a 所求椭圆方程为.1222=+x y…………………4分(2)直线l 的方程为.1+=kx y由⎪⎩⎪⎨⎧=++=,12,122x y kx y 可得().012222=-++kx x k 该方程的判别式△=()22288244kkk +=++>0恒成立.设()(),,,,2211y x Q y x P 则.21,22221221+-=+-=+k x x k k x x ………………5分可得().24222121+=++=+k x x k y y设线段PQ 中点为N ,则点N 的坐标为.22,222⎪⎭⎫⎝⎛++-k k k………………6分线段PQ 的垂直平分线方程为.212222⎪⎭⎫ ⎝⎛++-+=k k x k k y 令0=x ,由题意.212+=k m ………………………………………………7分又0≠k ,所以0<m <.21…………………………………………………8分(3)点M ()m ,0到直线1:+=kx y l 的距离221111km km d +-=+-=()212212212411x x x x k x x kPQ -+⋅+=-+=242212222++⎪⎭⎫ ⎝⎛+-⋅+=k k k k =2881222++⋅+k k k于是28811121212222++⋅+⋅+-⋅=⋅⋅=∆k k k k m PQ d S MPQ.2882122++⋅-=k k m由,212+=k m 可得.212-=mk代入上式,得(),123m m S MPQ -=∆即()(0123m m S -=<m <⎪⎭⎫21.…………………………………………11分 设()(),13m m m f -=则()()().4112m m m f --='而()m f '>0⇔0<m <()m f ',41<041⇔<m <,21所以()m f 在⎪⎭⎫ ⎝⎛41,0上单调递增,在⎪⎭⎫ ⎝⎛21,41上单调递减. 所以当41=m 时,()m f 有最大值.2562741=⎪⎭⎫⎝⎛f ……………………13分 所以当41=m 时,△MPQ 的面积S 有最大值.1663…………………14分3、解:(Ⅰ)设椭圆方程为22221(0)x y a b ab+=>>.圆F 的标准方程为22(1)1x y -+=,圆心为(1,0)F ,圆与x 轴的交点为(0,0)和(2,0).………………………2分由题意2a =,半焦距1c =.∴222413b a c =-=-=.∴椭圆方程为22143xy+=.………………………………4分(Ⅱ)设1122(,),(,)A x y B x y 由2214310x yx m y ⎧+=⎪⎨⎪--=⎩得22(34)690m y m y ++-=. ∴12122269,3434m y y y y m m --+==++.……………………………6分122||34y y m -==+.1221||||234AO B S O F y y m =-=+ .…………………………8分t =,则221,1,t m t ≥=-∴2631A OB t S t =+22222226(31)(6)6(13)(31)(31)AO B t t t S t t +--'==++.……………………10分∵1t ≥,∴0AO B S '<.∴A O B S 在[1,)t ∈+∞上是减函数, ∴当1t =时,A O B S 取得最大值,最大值为32.………………………12分4、解:(1)∵2221314c e a a ab ⎧===⎪⎪⎨⎪+=⎪⎩ …………………2分 ∴2,1a b == ∴椭圆的方程为2214yx += ………………4分(2)依题意,设l的方程为y kx =+由2222(4)1014y kx k x y x ⎧=+⎪⇒++-=⎨+=⎪⎩ 显然0∆>1212221,44x x x x k k --+==++ ………………5分由已知=⋅n m 0得:22121212124(a x x b y y x x kx kx +=+++21212(4)()3k x x x x =++++221(k 4)()30k 4k 4=+-++=++ ……………7分解得k =……………………8分 (3)①当直线A B 斜率不存在时,即2121,x x y y ==-,由已知=⋅n m 0,得22221111404x y y x -=⇒=又11(,)A x y 在椭圆上,所以22111141||,||42x x x y +=⇒==1121111||||||2||122S x y y x y =-== ,三角形的面积为定值.………9分②当直线A B 斜率存在时:设A B 的方程为y kx t =+22222(4)24014y kx t k x ktx t y x =+⎧⎪⇒+++-=⎨+=⎪⎩ 必须0∆> 即222244(4)(4)0k t k t -+-> 得到12224kt x x k -+=+,212244t x x k -=+ ………………10分∵n m ⊥,∴12121212404()()0x x y y x x kx t kx t +=⇔+++= 代入整理得:2224t k -= …………………11分1|||2S AB t ==…………12分2||142||t k t ===+所以三角形的面积为定值. …………………14分 5、解:(1) 设椭圆方程为2222x y ab+=1(a>b >0),由焦点坐标可得c =1………1分由PQ |=3,可得22b a=3,……………………………………………2分解得a =2,b故椭圆方程为2243x y+=1……………………………………………4分(2) 设M 11(,)x y ,N 22(,)x y ,不妨1y >0, 2y <0,设△1F MN 的内切圆的径R ,则△1F MN 的周长=4a =8,112F MN S =(MN +1F M +1F N )R =4R因此1F MN S 最大,R 就最大,………………………………………6分1212121()2AMN S F F y y y y =-=-,由题知,直线l 的斜率不为零,可设直线l 的方程为x =my +1,由221143x my x y =+⎧⎪⎨+=⎪⎩得22(34)m y ++6my -9=0,………………………8分得1y =,2y =,则12AMN S =AB (12y y -)=12y y -,……………9分令则t ≥1,则212121313AMN t S t t t===++,………………………10分令f (t )=3t +1t,则f ′(t ) =3-21t,当t ≥1时,f ′(t )≥0,f (t)在[1,+∞)上单调递增,有f (t )≥f (1)=4, AMN S ≤123=3,即当t =1,m =0时,AMN S ≤123=3, AMN S =4R ,∴max R =34,这时所求内切圆面积的最大值为916π.故直线l :x =1,△AMN 内切圆面积的最大值为916π………………12分6、解:(1)由2221ab e -==41及149122=+ba解得a 2=4,b 2=3,椭圆方程为13422=+yx;…………………………………………………………2分设A (x 1,y 1)、B (x 2,y 2), 由OP m PB PA =+得(x 1+x 2-2,y 1+y 2-3)=m (1,23),即⎪⎩⎪⎨⎧+=++=+m y y mx x 23322121又1342121=+y x ,1342222=+y x ,两式相减得212332434*********-=++⨯-=++⨯-=--=mm y y x x x x y y k AB ; ………………………6分(2)设AB 的方程为 y =t x +-21,代入椭圆方程得:x 2-tx +t 2-3=0,△=3(4-t 2),|AB |=224215)4(3411tt -⨯=-⨯+,点P 到直线AB 的距离为d =5|24|t -,S △PAB=24|2|23tt --=t)(2t)-3(2213+ (-2<t <2). ……………….10分令f (t ) =3(2-t )3(2+t ),则f ’(t )=-12(2-t )2(t +1),由f ’(t )=0得t =-1或2(舍),当-2<t <-1时,f ’(t )>0,当-1<t <2时f ’(t )<0,所以当t =-1时,f (t )有最大值81, 即△PAB 的面积的最大值是29;根据韦达定理得 x 1+x 2=t =-1,而x 1+x 2=2+m ,所以2+m =-1,得m =-3, 于是x 1+x 2+1=3+m =0,y 1+y 2+23=3+23m +23=0,因此△PAB 的重心坐标为(0,0).……………………………………………………13分 7、解:(1)设椭圆的半焦距为c ,依题意⎪⎩⎪⎨⎧==336a a c ∴b =1.∴所求椭圆方程为x 23+y 2=1.(2)设A (x 1,y 1),B (x 2,y 2), ①当AB ⊥x 轴时,|AB |=3,②当AB 与x 轴不垂直时,设直线AB 的方程为y =kx +m .由已知|m |1+k2=32, 得m 2=34(k 2+1),把y =kx +m 代入椭圆方程,整理得(3k 2+1)x 2+6kmx +3m 2-3=0∴x 1+x 2=-6km 3k 2+1,x 1x 2=3(m 2-1)3k 2+1.∴|AB |2=(1+k 2)(x 2-x 1)2=(1+k 2)⎣⎡⎦⎤36k 2m 2(3k 2+1)2-12(m 2-1)3k 2+1=12(k 2+1)(3k 2+1-m 2)(3k 2+1)2=3(k 2+1)(9k 2+1)(3k 2+1)2=3+12k 29k 4+6k 2+1=3+129k 2+1k2+6(k ≠0)≤3+122×3+6=4. 当且仅当9k 2=1k 2,即k =±33时等号成立|AB |=2.当k =0时,|AB |=3,综上所述,|AB |max =2.∴当|AB |最大时,△AOB 面积取最大值,S =12×|AB |max ×32=32.8、解:(1)∵|PA |+|PB |=2>3=|AB |, ∴点P 的轨迹是以A ,B 为焦点,长轴长2a =2的椭圆.………………………………2分∴a =1, .21,2322=-==ca b c ………………………………4分设P (x ,y ),∴点P 的轨迹方程为14122=+yx . ………………………………6分(2)将)23(+=x k y l :代入1422=+yx ,消去x ,整理为.0413)14(22=--+y ky k…………………………………7分设),(),(2211y x N y x M ,,则21221214)(2321y y y y y y AB S BMN -+=-⋅=∆ ………………………………8分=.2131131)1()3(13411322222222≤+++=+++⋅=++⋅kk kk k k kk kk k ………………10分 当且仅当kk kk 311322+=+,即22=k 时,△BMN 的最大面积为.21此时直线l 的方程是4622+=x y . …………………………………………12分9、解:(Ⅰ)设点P 的坐标为(x ,y ),则点Q 的坐标为(x).依据题意,有A Q=(x), B Q=(x). ……2分∵A Q ·B Q =1,∴x 2-1+2 y 2=1.∴动点P 所在曲线C 的方程是22x + y 2=1 …4分(Ⅱ)因直线l 过点B ,且斜率为k2,故有l ∶y=-2(x -1).……5分联立方程组22121)2x y y x ⎧+=⎪⎪⎨⎪=--⎪⎩,消去y ,得2x 2-2x -1=0. ………7分设M (x 1,y 1)、N (x 2,y 2),可得12121,12x x x x +=⎧⎪⎨=-⎪⎩,于是121212x x y y +=⎧⎪⎨+=⎪⎩. …………8分又O M +O N +O H =0 ,得O H =(- x 1- x 2,- y 1- y 2),即H (-1,2)………9分∴|MN=……………………10分又l+2y,则H 到直线l 的距离为d|2(⨯--=故所求驻MNH 三角形的面积为S=124⨯= ………………12分10、解(Ⅰ)设点P 的坐标为(,)x y ,则点Q的坐标为()x ,依据题意,有(),().AQ x BQ x =+=-…………………1分221,12 1.AQ BQ x y ⋅=∴-+=∴动点P 所在曲线C 的方程是221.2xy +=………………3分(Ⅱ)因直线l 过点B,且斜率为2k =-,故有:1).2l y x =--………5分联立方程组22121)2x y y x ⎧+=⎪⎪⎨⎪=--⎪⎩,消去y ,得22210.x x --=………………6分设11(,)M x y 、22(,)N x y ,可得1212112x x x x +=⎧⎪⎨=-⎪⎩,于是121212x x y y +=⎧⎪⎨+=⎪⎩.………………………7分又0OM ON OH ++=,得1212(,),O H x x y y =----即(1,2H --而点G 与点H 关于原点对称,于是,可得点2G ……………………………8分若线段M N 、G H 的中垂线分别为1l 和2l,2G H k =121:),:.42l y x l y -=-= (9)分联立方程组1)42y x y ⎧-=-⎪⎨⎪=⎩,解得1l 和2l的交点为11(,88O -………………………10分因此,可算得1||8O H =1||8O M =所以M 、G 、N 、H四点共圆,且圆心坐标为11(,88O8…12分11、【解析】(I)由题意知2c e a==,从而2a b =,又a =,解得2,1a b ==。
