Ch4 固体中弹性波-05 声波在流体-固体界面上的反射和折射
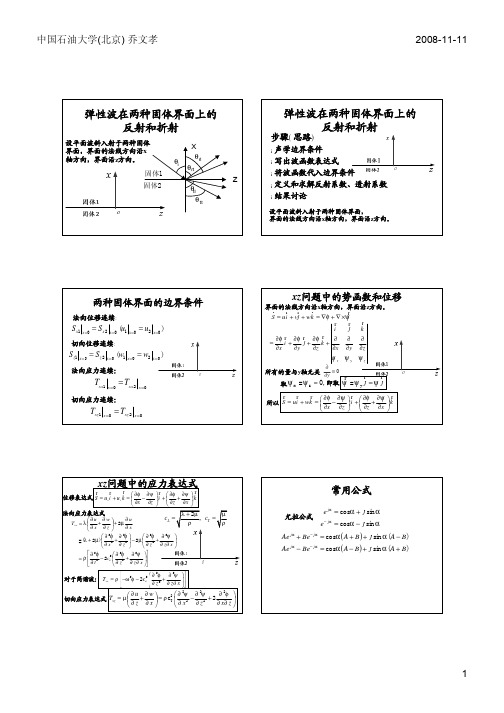
Ch4 固体中弹性波-06 声波在两种固体界面上的反射和折射
P波
ψ = ψ i exp( jk tx x ) + ψ r exp(− jk tx x ) S波
势函数具有的公共因子 exp j (ω t − k z z ) (界面波矢分量相等,在以下均略去不写,求导时仍考虑)
= jk lx [φ i exp ( jk lx x ) − φ r exp (− jk lx x )]
−2µ k z ktx cos ( ktx x )(ψ i −ψ r ) + j sin ( ktx x )(ψ i +ψ r )
任意一层中的Txz的表达式
∂ ψ ∂ ψ ∂ φ Txz = µ ∂x 2 − ∂z 2 + 2 ∂z∂x
2 2 2
介质中位移和应力的矩阵表达式
r ∂φ ∂ψ r ∂φ ∂ψ r r r − + 所以 S = ui + wk = i + k ∂x ∂z ∂z ∂x
x =0
r r r ∂φ ∂ψ r ∂φ ∂ψ r 位移表达式 S = u x i + u z k = ∂x − ∂z i + ∂z + ∂x k
ux φi u z = a ( x ) φi 4×4 Txx ψi Txz ψ i + φr − φr +ψ r −ψ r
= 2µk z klx [φi exp( jk lx x ) − φr exp(− jk lx x )] − µk [ψ i exp( jk tx x ) + ψ r exp(− jktx x )] + µk z2 [ψ i exp( jktx x ) + ψ r exp(− jk tx x )]
地球物理测#(第二章)声波测井

地球物理测井—声波测井 注意
岩石的声学性质
在井下,纵波和横波都能在地层传播,而
横波不能在流体(气、液体)中传播,因为 泥浆中只能传播纵波。 它的切变模量=0
纵波可以在气体、液体和固体中传播。
地球物理测井—声波测井
2、岩石的声速特性
岩石的声学性质
声波在介质中的传播特性主要指声速、声幅和频率特性。
纵波速度
岩性不同 VP、VS的影响不同 弹性模量不同 VP、VS 不同
Vp增加
地球物理测井—声波测井
2、孔隙度的影响
声速测井(声时差测井)
流体的弹性模量和密度都不同于岩石骨架,相对讲,即使岩性相 同,其中的流体也不同。
孔隙度
传播速度
3、岩层的地质时代的影响
实际资料表明:厚度、岩性相同,岩层越老,则传播速度越快。
横波速度
E (1 ) Vp (1 )(1 2 ) E Vs 2 (1 )
σ—泊松比 ρ—介质密度
E—杨氏模量
地球物理测井—声波测井
纵横波比
岩石的声学性质
Vp
2(1 ) Vs (1 2 )
由于大多数岩石的泊松比等于0.25,所以岩石的纵横波速度比 为1.73。可见,岩石中传播的纵波比横波速度快。一般,岩石 的密度越大,传播速度越快,反之亦然。
A. 瑞利波(井壁泥浆的交界面上产生的波,与横波混在一起 不易区分。) 在弹性介质的自由表面上,可以形成类似于水波的面波,这 种波叫瑞利波(Rayleigh waves)如图所示,瑞利波具有以下特点: (1)产生在弹性介质的自由表面。 (2)质点运动轨迹为椭圆。 (3)质点运动方向相对于波的传播方向是倒卷的,波速约为横 波波速的80%~90%。
弹性波的传播和衰减

弹性波的传播和衰减弹性波是一种在固体和流体介质中传播的波动形式。
它具有传播距离远、能量传递快、频率范围广、信息传递高效等特点,在地震学、声学、材料科学等领域具有重要应用。
本文将探讨弹性波的传播机理和衰减规律。
一、弹性波的传播机理在固体和流体介质中传播的弹性波可以分为纵波和横波。
纵波是沿着波的传播方向产生压缩和膨胀的弹性变形波动;横波则是垂直于传播方向产生横向位移的弹性波动。
弹性波的传播过程中,需要考虑介质的密度、速度、弹性模量等因素。
在固体介质中,声波的传播速度与固体的弹性模量和密度有关。
例如,高弹性模量和低密度的固体,其声波传播速度较高。
在流体介质中,声波传播的速度与介质的压力和密度相关。
弹性波传播过程中,会遇到不同介质之间的界面。
当波传播到界面时,会发生反射和折射现象。
反射是指波遇到不连续介质界面时,一部分能量被反弹回来,另一部分能量继续传播;折射则是指波穿过界面时,会改变传播方向和传播速度。
二、弹性波的衰减规律弹性波在传播过程中会发生衰减,主要是由于介质的吸收、散射和径向扩散引起的。
各种因素之间的相互作用决定了波能量的逐渐耗散和减弱。
介质的吸收是导致弹性波衰减的主要因素之一。
当波传播过程中,介质的分子或原子会吸收波的能量并转化为内能,导致波的振幅逐渐减弱。
吸收程度与介质的特性以及波的频率有关,高频率波的吸收相对较强。
散射是另一个导致弹性波衰减的因素。
当波传播过程中,遇到介质的不均匀性或杂质等异质结构时,波会发生散射现象,波的能量会被散射到不同的方向,使得整体的振幅减小。
散射的强度与杂质的尺寸和分布有关,尺寸较大或分布较密集的杂质会引起更强的散射。
径向扩散是弹性波在固体介质中衰减的特殊现象。
当波在均匀固体中传播时,波的能量会随着距离的增加而扩散,导致波的振幅衰减。
径向扩散的强度与波长、传播介质的特性有关,波长较长或介质的吸收和散射性质较强时,径向扩散效应更加显著。
三、应用与展望弹性波在地震勘探、医学成像、无损检测等领域具有广泛应用。
超声波衰减

时,实验记录到两组波脉冲——快波组和
慢波组,其中快波组包括快速层中的纵波脉冲及其产生的三种头波,慢波组
包括慢速层中的纵波脉冲及其产生的两种头波。诸国桢先生也用动态光弹法
对声波在流体饱和多孔介质及其与流体、固体介质界面的反射与折射
【19】
进
行了实验观察。用阴影法
【20】
记录了低频超声脉冲受埋在沙中圆柱体、类圆
4.3应力作用下声场的实验观测...................................34
第五章井间地震管波的实验观测......................................38
5.1引言.......................................................38
速度慢,声速和只与介质的参数有关,不依赖于声波的频率。对于平面
波,由
c
c
s
c
cs
c >c
c
c
s
c
c
c
s
c
ϕ标志的波通常称为纵波,由ψ标志的波通常称为横波,后面我们所
要讨论的声波即为平面波。
ρ
2
2
λ+
c
c=
μ
(2-8)
2
ρ
μ
=
s
c
4第一章绪论
1.1引言
超声波具有频率高、波长短、绕射现象小,特别是方向性好、能够成为
第四章固体和液体中的声场及其分析..................................25
4.1横波速度测量...............................................25
超声在流体和一般各向异性固体界面上的反射

( . e at n f l t ncE g er gadIfr t nS i c , i ri f i c n eh o g f hn ,He i 3 0 7 1D p r met e r i n i ei n omai c ne Unv s yo e eadT cn l yo i oE co n n n o e e t c S n o C a f 02 ; e2
维普资讯
文 章 编 号 :0 03 3 (0 2 0 ~0 —0 00 10 .6 0 2 0 ) 1 20 1.5
超 声 在 流 体 和 一 般 各 向 异 性 固体 界 面 上 的 反 射 *
邵 继 红 吴 昆 裕 一,
( . 国科 学 技 术 大 学 电 子 工 程 与 信 息 科 学 系 , 肥 1中 合
n m e i ls lt n o h n r y r f t n a d r n mi in c e f in e o r i e o o e a i to i r sa d c mp s e u rc o u i f t e e e g e e i n ta s s o o fi e t a b a n d f r s m n s r pc y tl a o o i a o l c o c r o c n t
波 的入 射 面 ,z=0为 流 体 与 固体 之 间 的 界 面 ( 图 1。当声 波从 流体 向各 向异 性 固体 媒 质 斜 入 射 时 , ) 在各 向异性 固体 中一 般会 产 生 3种 折 射波 : 种 准 一
2 D p r n f t e t sa d P yi , a a n t ueo T c n l y Hu ia 3 0 C ia . e at t h mai n h s me o Ma c s c Hu i n I s t t f eh oo , an n 2 2 0 , hn ) n i g 1
固体物理CH4-习题解答

第四章习题试解1. 一维单原子晶格,在简谐近似下,考虑每一原子与其余所有原子都有作用,求格波的色散关系.解:设原子质量为m ,周期为a ,第n 个原子偏离平衡位置的位移为μn ,第n-k 与n+k 个原子偏离平衡位置的位移分别为μn-k ,μn+k ,其与第n 个原子间的弹性恢复力系数为β-k ,βk .n-k n-1 n n+1 n+k显然:k k ββ-=第n 个原子受n-k 和n+k 原子的合力为:第n 个原子受所有原子的合力为:振动的运动学方程可写为:代入振动的格波形式的解()i qna t nq Ae ωμ-= 有2()[()][()]()()(2)i qna t i q n k a t i q n k a t i qna t k km i Ae Ae Ae Ae ωωωωωβ-+----=+-∑色散关系即为2.聚乙烯链…—CH =CH —CH =CH…的伸张振动,可以采用一维双原子链模型来描述,原胞两原子质量均为M,但每个原子与左右邻原子的力常熟分别为β1和β2,原子链的周期为a .证明振动频率为证:如图,任意两个A 原子〔或B 原子〕之间的距离为a,设双键距离b 2,单键距离b 1 …—CH =CH —CH =CH —CH =CH —CH =CH —CH =CH …2n-2 2n-1 2n 2n+1 2n+2 AB Ab2 b1只考虑近邻作用的A,B 两原子的运动方程为A :222121221()()n n n n n M μβμμβμμ+-=---B : 21122212212()()n n n n n M μβμμβμμ++++=---将格波解()2i qna t n Ae ωμ-= 和2[()]21i q na b t n Be ωμ+-+= 代入以上运动方程,有 化简得:1221212()()0iqb iqb M A e e B ββωββ-+--+=同理:1221212()()0iqb iqb e e A M B ββββω--+++-=化为以A 、B 为未知数的线性齐次方程组,它的有解条件是从而得到3.求一维单原子链的振动模式密度g<ω>,若格波的色散可以忽略,其g<ω>具有什么形式,比较这两者的g<ω>曲线.解:一维情况q 空间的密度约化为L/2π,L=Na 为单原子链的长度,其中a 为原子间距,N 为原子数目.则在dq 间隔内的振动模式数目为2L dq π.dω频率间隔内的振动模式数目为 等式右边的因子2来源于ω〔q 〕具有中心反演对称,q ﹥0和q ﹤0区间是完全等价的.从而有 对于一维单原子链,只计入最近邻原子之间的相互作用时,有其中ωm 为最大频率.代入g <ω>得考虑ω=cq 〔德拜近似〕由q →0〔德拜近似下〕, 有111()222m m q qa qa a q ωωω==⋅=⋅ 即12m c a ω=⋅ 则有:12m d a dq ωω=⋅ 121()12m m NaN g a ωππωω==⋅ 〔常数〕考虑ω=ω0〔爱因斯坦近似〕显然有()000g ωωωωω∞=⎧=⎨≠⎩ 4.金刚石〔碳原子量为12〕的杨氏模量为1012N·m -2,密度ρ=3.5g·cm -3.试估算它的德拜温度ΘD =? 解:德拜温度D D B k ωΘ=223231()4()(2)2j V V g c c c ωωπωππ==, 2233()2V g c ωωπ== 近似看作弹性介质时,1/2410/C m s ⎛⎫=⨯ ⎪⎝⎭杨氏模量密度 每摩尔原子数目为N=6.02×1023,摩尔质量m=12g,则摩尔体积代入,得ωm =57.97×1013最后得 ΘD =4427K5.试用德拜模型求晶体中各声频支格波的零点振动能. 解:根据量子理论,各简谐振动的零点能为12ω 德拜近似下2233()2V g C ωωπ= 总零点能为034232301()2331444m m m E g d VV d C C ωωωωωωωωππ===⎰⎰ 由自由度确定的21/3[6()]m NC V ωπ=代回上式中6.一根直径为3mm 的人造蓝宝石晶体的热导率,在30K 的温度达到一个锐的极大值,试估计此极大值.〔蓝宝石在T ﹤﹤ΘD =1000K 时,c V =10-1T 3J·m -3·K -1〕解:m D B k ωΘ=→ωm =1.31×1014λ与晶格常数10-10m 近似时约为2.09×103,近似作为平均声速代入 热导率35.643103c l υκυ==⨯ 7.Na 和Cl 的原子量分别为23和37.氯化钠立方晶胞边长为0.56nm,在[100]方向可以看做是一组平行的离子链.离子间距d=0.28nm.NaCl 晶体的杨氏模量为5×1010N·m -2,如果全反射的光频率与q=0的光频模频率相等,求对应的光波波长.解:当q=0时,光频支频率为杨氏模量10510a β=⨯,且90.2810a -=⨯m故201.7910β=⨯,再同两原子质量一同代入频率式则波长02c πλω==1.53×10-14m8.立方晶体有三个弹性模量C 11,C 12和C 44.铝的C 11=10.82×1010N·m -2,C 44=2.85×1010N·m -2,铝沿[100]方向传播的弹性波纵波速度l υ=,横波速度t υ=,Al 的密度ρ=2.70×103kg·m -3.求德拜模型中铝的振动模式密度g<ω>.解:由题条件知36.3310l υ=⨯,33.2510t υ=⨯若所考虑的晶体体积为V,则。
应用地球物理学原理第二章04弹性波的特征

03
弹性波在地壳中的传播
地壳的分层结构
地壳是地球最外层的硬壳,由 岩石和土壤组成,具有明显的 分层结构。
地球的地壳分为多个板块,板 块之间的相互作用可以产生地 震波。
地壳的分层结构对弹性波的传 播具有重要影响,不同层中的 波速和传播方向可能不同。
弹性波在不同介质中的传播
弹性波在固体、液体和气体中传播时具有不同的特征。
地下结构的不确定性可能导致弹性波传播模型的 误差,从而影响解释结果的准确性。
需要对地下结构进行详细调查和建模,以获得更 准确的弹性波传播特征。
数据处理与解释的复杂性
01
02
03
弹性波数据的处理涉及 多种算法和技术,如滤 波、反演、成像等,处
理过程较为复杂。
弹性波数据的解释需要 丰富的专业知识和经验 ,对解释人员的素质要
应用地球物理学原理第二章 04弹性波的特征
目录
• 弹性波的基本概念 • 弹性波的物理特性 • 弹性波在地壳中的传播 • 弹性波的应用 • 弹性波的局限性
01
弹性波的基本概念
弹性波的定义
弹性波
在弹性介质中传播的波动现象,由于介质的弹性性质,当 受到外力作用时,介质发生形变并产生恢复力,这种恢复 力会以波动的形式在介质中传播。
资源开发规划
通过分析地下岩层的弹性波特征,评 估资源的可开采性和开发风险,为资 源开发提供科学依据。
环境保护监测
利用弹性波技术监测环境变化,如土 壤污染、地下水污染等,为环境保护 提供技术支持。
05
弹性波的局限性
对地下结构的依赖性
弹性波的传播特性与地下结构密切相关,不同的 地下介质对弹性波的传播有显著影响。
弹性波的传播方式
弹性波可以通过反射、折射、散射等方式传播, 其传播路径和速度受到介质的不均匀性和边界条 件的影响。
6 声波测井(1)

质中以速度 V2 沿界面传播,在声波测井
中叫滑行波,对应的入射角为第一临界角。
sin i v1 v2
24
波型转换
vpi vpr
sin i sin r
vpt vst
sin pt sin st
vpi、vpr、vpt、vst 入射波、反射波速度; vpt、vst 折射纵波、横波速度;
i、r 入射角、反射角; pt、st 纵波折射角、横波折射角。
声系结构示意图
2、已知流体声速为1460m/s。地层密度为 2.32g/cm3,地层的拉梅系数λ为1.02×1010N/m2, 剪切模量为1.12×1010N/m2,求地层纵横波速度、速 度比、泊松比、第一临界角、第二临界角。
27
第二节 声波速度测井
声波速度测井简称声速测井,测量地层滑行波
的时差 (t 地层纵波速度的倒数,单位 或 s / m )。
声波通过波阻抗(即声速与介质体密度的乘 积)不同的两种介质分界面时,会发生反射和折 射,并遵循斯奈尔反射、折射定律。即入射波、 反射波、折射波在同一平面内沿不同方向传播 。 图5-1是声波的反射和折射示意图。
21
入射线 法线
αα Ⅰ
Ⅱ
β
O
反射线
Ⅰ
Ⅱ
折射线
法线 M ii
β 滑行波
临界入射
图5-1、声波在介质分界面上的反射及折射
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当入射角满足1c i 2c时,折射侧仅存在折射横波。
声波在流体/固体界面上的 反射和折射
Amplitude
c1Lc2T c2L
1.0 0.8 0.6 0.4 0.2
R f
1000.,1483 2700.,6260.,3080.
T p
fluid solid
0.0
0
5
(a)
1.0
0.8
T p
10
15
20
两种介质中的势函数表达式
媒质I中的声标势为,
e e j ( k 1 L c o six k 1 L s i n iz )
j ( k 1 L c o sr x k 1 L s i n r z )
1i
r
e k1L c1L,这里省略了公共时间因子 j t
P
i r
P
媒质II中声标势可以表示成
切向应力连续: tk 2 2 L s in 2tTtk 2 2 L c o s2tT 0
势函数的反射和折射系数的定义为
r
r i
,
t
t i
,t
t i
反射系数与折射系数
势函数的反射和折射系数为
rr i
z z2 2L Lc co os s2 22 2ttT T z z2 2T Ts siin n2 22 2ttT T z z1 1L L,
I
z
ej(k2LcostLxk2LsintLz)
2
t
k2L c2L
tT
tL
P
媒质II中的矢量声势(矢势)的y方向分量为
x
e j(k2Tco stTx k2TsintTz)
2
y
t k2T c2T
kx
S
k
媒质I中只有纵波,而媒质II中既有纵波,也有横波.
kz
k 2 kx2 kz2
流固界面边界条件的表达式
流体
z
固体
x y z 假设所有的量与y轴无关 0
tT tL
P
y
S
所以可以取 x
=z
0, 即取
r =yrj
r
j
x
所以 S ru irw k r x z ir z x k r
xz问题中的应力表达式
位移表达式 S ru irw k r x z ir z x k r
,
流体 固体
t 0 .
z
tT tL
P
S
x
结果讨论-临界角
P
P
当 c1Lc2T c2L时,
i r
I
z
固体侧的纵、横波折射角都大于入射角。
tT
tL
P
S
当入射角为1c
sin 1
c1L c2L
x
时纵波的折射角为90度
当入射角为 2c
sin
1
c1L c2T
时横波的折射角为90度
1c和2c 分别称为第一临界角和第二临界角。
=0
反射与折射定律
运用法向位移连续条件,可得
ik 1 Lc o siejk 1 Lsin izrk 1 Lc o srejk 1 Lsin rz
= tk2 Lc o stL ejk2Lsin tL ztk2 TsintT ejk2 Tsin tTz
上式应对所有的z都成立,因而式中指数因子部分必然应该恒等,即
声 压的三 维波函数
rrxiryjrzkr
kkxi kyjkzk
r
r
r
k cosi cosjcosk
Z
o
k (波矢量)
Y
k kx2ky2kz2 c0
X
、、为波矢量与x、y、z三个坐标轴的夹角。
对于p沿任p意A方ej向传t播krgr的r平面p波Aejtkxxkyykzz
pejtkcosxkcosykcosz A
法向位移连续: u1 x0 u2 x0
P
P
1 xx0
x2 z2
x0
i r I
z
法向应力连续:Txx1x0 Txx2 x0
tT
tL
P
1 21x02 222cT 2 2 z 2 2z 2 2 x x= 0 x
S
切向应力连续:Txz2 x0 0
2 x22
22 z2
2z22xx=0
Incident Angle
0.6 0.4
1000.,1483 1700.0,1700.0,600.0
P i r
tT tL S
x
k
z kx
P
kz
k2
k
2 x
k
2 z
反射系数与折射系数
考虑了反射定律与折射定律后边界条件表示为:
法向位移连续: i rk 1 L c o s i t k 2 L c o s t L t k 2 T s i n t T
法向应力连续: 1 2tcos2tTtsin2tTir
声波在流体/固体界面上的 反射和折射
P
P
i r
流体
z
固体
tT tL
P
S
x
xz问题中的势函数和位移
设平面波由流体斜入射于界面,界面的法线方向沿x轴方向,
界面r沿z方r 向。r S ui vj
r wk
r
rrr i jk
P
P
r r r
i r
i j k x y z x y z
2
法向应力表达式
cL , cT P
P
Txx
u x
w z
2
u x
i r
流体
z
=(
2)
2
x2
2
z2
2
2
z2
2 z x
固体
2
t2
2cT2
2
z2
2 z x
tT tL
P
S
x
对于简谐波:Txx22cT 22 z2z2x
0流体
切向应力表达式 T xz u z w x cT 2 2 x 2 2 z 22x 2 z
tt i
1 2 z2Lcos222 tz T2 Lc zo 2T s2 sin tT 22tTz1L,
tt i
1 2 z2Lcos222 tT z2 Ts zi2 n T2 sin tT 22tTz1L,
其中z1Lco 1s c1L i,z2Lco 2 sc2L tL,z2Tco 2 sc2T tT为法向声阻抗率
结果讨论
模式转换:当一种模式波入射于界面时,在折射波中 产生另外一种或若干种模式波的现象.(产生转换波 的现象)
反射系数和折射系数与入射角、两种介质的声阻抗
等因素有关.
、
当纵波垂直入射于界面时,不产生折射横波.
r
2c2L 2c2L
1c1L 1c1L
,
P
P
i r
t
1 2
2 2c2L 2c2L 1c1L
k 1 L s i n i k 1 L s i n r k 2 L s i n t L k 2 T s i n t T 波矢的界面分量相等
从此导得反射定律 i r
P
与折射定律
sin i sin tL
k 2 L c1L k1L c2L
,
I
sin i k 2T c1L . sin tT k1L c2T
