Ch4 固体中弹性波-06 声波在两种固体界面上的反射和折射
Ch4 固体中弹性波-06 声波在两种固体界面上的反射和折射
P波
ψ = ψ i exp( jk tx x ) + ψ r exp(− jk tx x ) S波
势函数具有的公共因子 exp j (ω t − k z z ) (界面波矢分量相等,在以下均略去不写,求导时仍考虑)
= jk lx [φ i exp ( jk lx x ) − φ r exp (− jk lx x )]
−2µ k z ktx cos ( ktx x )(ψ i −ψ r ) + j sin ( ktx x )(ψ i +ψ r )
任意一层中的Txz的表达式
∂ ψ ∂ ψ ∂ φ Txz = µ ∂x 2 − ∂z 2 + 2 ∂z∂x
2 2 2
介质中位移和应力的矩阵表达式
r ∂φ ∂ψ r ∂φ ∂ψ r r r − + 所以 S = ui + wk = i + k ∂x ∂z ∂z ∂x
x =0
r r r ∂φ ∂ψ r ∂φ ∂ψ r 位移表达式 S = u x i + u z k = ∂x − ∂z i + ∂z + ∂x k
ux φi u z = a ( x ) φi 4×4 Txx ψi Txz ψ i + φr − φr +ψ r −ψ r
= 2µk z klx [φi exp( jk lx x ) − φr exp(− jk lx x )] − µk [ψ i exp( jk tx x ) + ψ r exp(− jktx x )] + µk z2 [ψ i exp( jktx x ) + ψ r exp(− jk tx x )]
物理选修3-4同步测控:第2章第2节波的反射和折射 含解

同步测控我夯基 我达标1.关于声波的传播,下列说法中正确的是( )A.声波能在空气、固体和液体中传播,但不能在真空中传播B.声波无论在哪种介质中传播,都只是纵波C.声波从空气传入液体或固体后,波长变短,波速变小D.从障碍物反射的声波到达人耳,比原声到人耳滞后小于0.1 s,则人能区分开解析:声波是机械波,在传播时必须有介质,所以在气体、液体和固体中均能传播,在真空中不能传播;声波在气体、液体中是纵波,在固体中既可以是纵波,也可以是横波.声波由空气进入液体、固体,有时波速变大,如钢铁;有时波速变小,如橡胶.因而有两种可能.回声比原声滞后0.1 s 人耳才能区分开,因而A 、D 正确.答案:AD2.下列现象中属于声波反射现象的是( )A.隔着墙能听到墙外的人讲话B.音响设备制作时要考虑混响效应C.夏日的雷声有时轰鸣不绝D.在水里的人能听到岸上的声音解析:声波的反射是指声波遇到障碍物时会返回到原介质中的现象,所以B 、C 对. 答案:BC3.如图2-2-9是一列机械波从一种介质进入另一种介质时发生的现象,已知波在介质Ⅰ中的波速为v 1,波在介质Ⅱ中的波速为v 2,则v 1∶v 2为( )图2-2-9A.1∶2B.2∶1C.3∶2D.2∶3解析:在折射现象中2121sin sin v v =θθ,所以45sin 60sin 21=v v =3∶2,故选C. 答案:C4.人们听不清对方说话时,除了让一只耳朵转向对方,还习惯性地把同侧的手附在耳旁,这样做是利用声波的提___________高耳的接收能力.解析:当用手附在耳旁时,手就可反射一部分声波进入人耳,以提高耳的接收能力.故应填“反射”.答案:反射5.教室中未搬入桌凳前说话常有嗡嗡的尾声,摆了桌凳坐满了学生后这种现象减轻到似乎听不到了,这是为什么?解析:当声音遇到障碍物时,除一部分被反射外,还有一部分进入障碍物中,发生折射现象,由于能量损失,反射回的声波能量减少,所以摆了桌凳坐满了学生后回声很弱了.答案:见解析6.一列波以60°入射角入射到两种介质的交界面,反射波刚好与折射波垂直,若入射波的波长为0.6 m,那么折射波的波长为___________,反射波的波长是___________.解析:画出规律图,如图所示,由几何知识可知折射角θ2=30°,由折射定律2121sin sin v v =θθ 因波的频率不变,由v=λf ,可得:2121sin sin λλθθ=,代入数据,得26.030sin 60sin λm = ,解得λ2=0.35 m反射波的波长与入射波波长相同,则λ3=λ1=0.6 m.答案:0.35 m 0.6 m7.分析下列现象产生的原因:(1)回声;(2)夏日的雷声轰鸣不绝;(3)在空房间里讲话感觉声音响.解析:(1)回声是声波的反射现象.原因是对着山崖或高墙说话,声波传到山崖或高墙时,会被反射回来继续传播.(2)夏日的雷声轰鸣不绝,原因是声波在云层界面多次反射.(3)在空房间里讲话感觉声音响,原因是声波在空房间里遇到墙壁、地面、天花板发生反射时,由于距离近,原声与回声几乎同时到达人耳,人耳只能分辨相差0.1 s 以上的声音,所以人在空房间里讲话感觉声音响.答案:见解析8.利用超声波可以探测鱼群的位置.在一只装有超声波发射和接收装置的渔船上,当它向选定的方向发射出频率为5.8×104 Hz 的超声波后,经过0.64 s 收到从鱼群反射回来的反射波,已知5.8×104 Hz 的超声波在水中的波长为2.5 cm,则这群鱼到渔船的距离为多少米?解析:由题意可知渔船是静止的,设渔船跟鱼相距x m,则x=vt/2又因为v=λ·f ,代入数据,得:v=2.5×10-2×5.8×104 m/s=1.45×103 m/s所以x=2vt =1.45×103×264.0m=464 m. 答案:464 m我综合 我发展9.一列波从一种介质进入另一种介质时,一定发生变化的是( )A.波的速度B.传播方向C.波的频率D.波的波长解析:波速与介质有关,频率与波源有关,所以波速一定变,频率一定不变,又因λ=v/f,所以波长一定变,故A 、D 对,C 错.若波是垂直进入另一种介质时,波的传播方向不变.若波以某一角度进入另一种介质时,则传播方向改变,故B 错.答案:AD10.甲、乙两人平行站在一堵墙前面,二人相距2a m,距墙均为3a m,当甲开了一枪后,乙在t s 后听到第一声枪响,则乙在什么时候才听到第二声枪响( )A.听不到B.甲开枪后3t sC.甲开枪后2t sD.甲开枪后273+s 解析:甲、乙与墙的位置如图所示,由声波的传播可知,乙听到的第一声枪响是声波由A 直接传到B 的,第二声枪响是声波经墙反射后传到B 的,所以⎪⎪⎩⎪⎪⎨⎧+==v BO AO t v AB t '其中AO=BO=AB=2a,解得:t′=2t.答案:C11.声波在空气中传播速度v 1=340 m/s,在钢铁中的传播速度v 2=4 900 m/s,一人用锤子敲击一下铁桥的一端而发出声音,经空气和桥传到另一端的时间差为2 s,则桥长为___________m,空气中和钢铁中声波的频率之比是___________,波长之比是___________.解析:设桥长为l m,经空气传播所用时间为t s,则经铁桥传播所用时间为(t-2) s,l=v 1t ①l=v 2(t-2)②由①②代入数据解得:l=731 m在不同介质中,频率不变,则f 1∶f 1=1∶1由λ=v/f,得λ1∶λ2=v 1∶v 2=340∶4 900=17∶245.答案:731 1∶1 17∶24512.如果旅游者走过一个山谷,他拍手以后经过0.5 s 听到右边山坡反射回来的声音,经过1.5 s 听到左边山坡反射回来的声音,则这个山谷的宽度大约是___________m.(v 声=340 m/s) 解析:设山谷的宽度为L,人站的位置与山谷的位置如图所示,由题意,得:L=v 声·(22t +21t )代入数据解得:L=340×(25.1+25.0)m=340 m. 答案:34013.一架飞机水平匀速地从某同学头顶飞过,当他听到飞机的发动机声从头顶正上方传来时,发现飞机在他前上方约与地面成60°角的方向上,据此可估算出此飞机的速度约为声速的___________倍.解析:画出情景示意图,如图所示,则tan60°=tv t v 飞声所以33=声飞v v . 答案:33 14.一个观察者在高处用望远镜注视在地上的木工以每秒2次的频率击钉子,他听到声音时恰好看到击锤动作,若观察者距木工680 m,当木工停止击钉后,他还能听到几次击钉声?(声波在空中传播速度为340 m/s)解析:题中木工击钉子产生的声波属于一种时间短暂的“脉冲波”,如图所示,设脉冲的间距为d ,由于声速是v=340 m/s ,木工击钉频率为f=2 Hz所以d=2340=f v m. 因此在680 m 距离内有n=170680=4个脉冲间隔,也就是说木工停止击钉后还能听到4次击钉声.答案:4次。
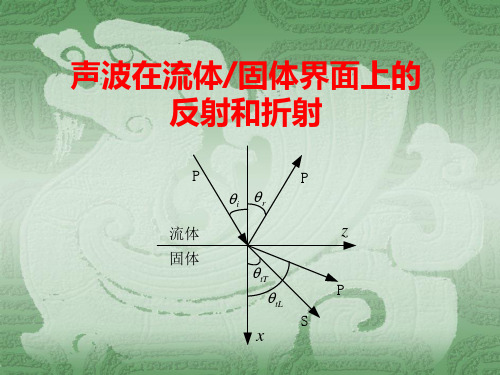
Ch4 固体中弹性波-05 声波在流体-固体界面上的反射和折射
k 1 L s i n i k 1 L s i n r k 2 L s i n t L k 2 T s i n t T 波矢的界面分量相等
从此导得反射定律 i r
P
与折射定律
sin i sin tL
k 2 L c1L k1L c2L
,
I
sin i k 2T c1L . sin tT k1L c2T
声 压的三 维波函数
rrxiryjrzkr
kkxi kyjkzk
r
r
r
k cosi cosjcosk
Z
o
k (波矢量)
Y
k kx2ky2kz2 c0
X
、、为波矢量与x、y、z三个坐标轴的夹角。
对于p沿任p意A方ej向传t播krgr的r平面p波Aejtkxxkyykzz
pejtkcosxkcosykcosz A
,
流体 固体
t 0 .
z
tT tL
P
S
x
结果讨论-临界角
P
P
当 c1Lc2T c2L时,
i r
I
z
固体侧的纵、横波折射角都大于入射角。
tT
tL
P
S
当入射角为1c
sin 1
c1L c2L
x
时纵波的折射角为90度
当入射角为 2c
sin
1
材料物理性能(山东联盟)智慧树知到期末考试章节课后题库2024年青岛科技大学

材料物理性能(山东联盟)智慧树知到期末考试答案章节题库2024年青岛科技大学1.反铁磁材料磁偶极子方向交替变化且具有相同的大小。
()答案:对2.二向色性是由于晶体具有折射率的各向异性。
()答案:错3.两种不同的材料相接触,两端温度不同,则产生塞贝克效应。
塞贝克效应是珀尔贴和汤姆逊效应的综合效应。
()答案:对4.光与物质相互作用时将经历受激吸收、自发辐射、受激辐射三个过程。
()答案:对5.非均匀介质中双折射现象使晶体有两个折射率:其一是遵循折射定律的寻常光折射率n0,而另一折射光的折射率不遵循折射定律,称为非寻常光折射率ne。
()答案:对6.材料的折射率将随着材料元素的离子半径的增大而增大。
()答案:错7.当激发除去后在10-8s内发出的光称为荧光,其发光是被激发的电子跳回价带时,同时发射光子。
()答案:对8.洛伦兹发现对各种导热材料而言,比值λ/σ与温度T成正比,该比例常数L为洛伦兹数,即魏德曼-弗朗兹定律。
()答案:对9.导体导电机制不同,同一影响因素却有不同的影响结果,如同是温度升高,金属电导率升高,而离子导体电导率下降。
()答案:错10.和熔点、内能相似,德拜温度也能反映原子间结合力的强弱。
()答案:对11.散射前后,光的波长(或光子能量)不发生变化的散射称为非弹性散射;光的波长(或光子能量)发生变化的散射称为弹性散射。
()答案:错12.某材料的能带结构是允带内的能级未被填满,则该材料属于半导体材料;允带内的能级被填满且禁带宽度较宽的属于绝缘材料。
()答案:错13.在晶体点阵完整性遭到破坏的地方,电子波受到散射,这是金属产生衍射的根本原因。
()答案:错14.某些材料在极高温度条件下,突然电阻为零的现象叫做超导电性。
()。
答案:错15.金属总的电阻包括基本电阻与溶质(杂质)浓度引起的电阻,后者与温度无关,又称为剩余电阻,可在常温条件下测得()。
答案:错16.金属和合金的热膨胀曲线发生偏离,可能是由于。
高一年级化学上册第一章知识点

高一年级化学上册第一章知识点1.高一年级化学上册第一章知识点篇一1、物理性质:无色、无味的气体,极难溶于水,密度小于空气,俗名:沼气、坑气2、分子结构:CH4:以碳原子为中心,四个氢原子为顶点的`正四面体(键角:109度28分)3、化学性质:①氧化反应:(产物气体如何检验?)甲烷与KMnO4不发生反应,所以不能使紫色KMnO4溶液褪色②取代反应:(三氯甲烷又叫氯仿,四氯甲烷又叫四氯化碳,二氯甲烷只有一种结构,说明甲烷是正四面体结构)4、同系物:结构相似,在分子组成上相差一个或若干个CH2原子团的物质(所有的烷烃都是同系物)5、同分异构体:化合物具有相同的分子式,但具有不同结构式(结构不同导致性质不同)烷烃的溶沸点比较:碳原子数不同时,碳原子数越多,溶沸点越高;碳原子数相同时,支链数越多熔沸点越低同分异构体书写:会写丁烷和戊烷的同分异构体2.高一年级化学上册第一章知识点篇二物质的量浓度概念的理解n(B)在公式c(B)=中V(B)(1)溶质是用物质的量表示而不是质量表示;体积表示溶液的体积,而不表示溶剂的体积,并且体积单位为L。
(2)带结晶水的物质溶于水后,溶质是不含结晶水的化合物,溶剂中的水包括结晶水。
(3)从一定物质的量浓度溶液中取出任意体积的溶液,物质的量浓度不变,但随溶液体积的变化溶质的物质的量不同。
(4)气体溶于一定体积的水中,溶液的体积不等于溶剂的.体积而应根据溶液密度和溶液质量求算。
(5)若浓溶液稀释或浓度差别较大的溶液混合,混合后溶液的总体积比原来的体积之和小。
3.高一年级化学上册第一章知识点篇三原子与分子的异同分子原子区别在化学反应中可再分,构成分子中的原子重新组合成新物质的分子在化学反应中不可再分,化学反应前后并没有变成其它原子相似点:(1)都是构成物质的基本粒子;(2)质量、体积都非常小,彼此间均有一定间隔,处于永恒的运动中;(3)同种分子(或原子)性质相同,不同种分子(或原子)性质不同;(4)都具有种类和数量的含义。
2020-2021学年新教材鲁科化学选修性必修2课时分层作业:2.4 分子间作用力 Word版含解析

课时分层作业(十)分子间作用力(建议用时:40分钟)[合格过关练]1.下列叙述与范德华力无关的是( )A.气体物质加压或降温时能凝结或凝固B.通常状况下氯化氢为气体C.氟、氯、溴、碘单质的熔、沸点依次升高D.氯化钠的熔点较高D [范德华力主要影响物质的熔、沸点等物理性质。
A项,气体物质加压时,范德华力增大,降温时,气体分子的平均动能减小,两种情况下,分子靠自身的动能不足以克服范德华力,从而聚集在一起形成液体甚至固体;B项,氯化氢分子之间的作用力是很弱的范德华力,因此通常状况下氯化氢为气体;C项,一般来说,组成和结构相似的物质,随着相对分子质量的增加,范德华力逐渐增强,物质的熔、沸点逐渐升高;D项,NaCl中存在的作用力是很强的离子键,所以NaCl 的熔点较高,与范德华力无关。
]2.范德华力的作用能为a kJ·mol-1,化学键的键能为b kJ·mol -1,则a、b的大小关系是( )A.a>b B.a<bC.a=b D.无法确定B [范德华力是分子间作用力,其强度较弱,化学键的键能比范德华力的作用能大得多.]3.干冰汽化时,下列所述内容发生变化的是( )A.分子内共价键B.分子间的作用力增大C.分子间的距离D.分子内共价键的键长[答案]C4.关于氢键,下列说法正确是( )A.所有含氢元素的化合物中都存在氢键,氢键比范德华力强B.H2O是一种非常稳定的化合物,是由水分子间形成氢键所致C.氢原子和非金属性很强的元素原子(F、O、N)形成的共价键,称为氢键D.分子间形成的氢键使相应物质的熔点和沸点升高,氢键也可存在于分子内D [在某些含N-H、O—H、F-H的化合物中形成氢键,所以含有氢元素的化合物中不一定有氢键,如甲烷分子间不能形成氢键,故A 错误;氢键只影响物质的物理性质,H2O是一种非常稳定的化合物,是因为H—O键的稳定性强,故B错误;氢键是一种特殊的分子间作用力,不属于化学键,故C错误;分子间氢键的存在使分子间作用力增强,能够显著提高物质的熔、沸点,氢键也可存在于分子内,如邻羟基苯甲醛分子()中的羟基与醛基之间存在氢键,故D正确。
固体物理CH4-习题解答
第四章习题试解1. 一维单原子晶格,在简谐近似下,考虑每一原子与其余所有原子都有作用,求格波的色散关系.解:设原子质量为m ,周期为a ,第n 个原子偏离平衡位置的位移为μn ,第n-k 与n+k 个原子偏离平衡位置的位移分别为μn-k ,μn+k ,其与第n 个原子间的弹性恢复力系数为β-k ,βk .n-k n-1 n n+1 n+k显然:k k ββ-=第n 个原子受n-k 和n+k 原子的合力为:第n 个原子受所有原子的合力为:振动的运动学方程可写为:代入振动的格波形式的解()i qna t nq Ae ωμ-= 有2()[()][()]()()(2)i qna t i q n k a t i q n k a t i qna t k km i Ae Ae Ae Ae ωωωωωβ-+----=+-∑色散关系即为2.聚乙烯链…—CH =CH —CH =CH…的伸张振动,可以采用一维双原子链模型来描述,原胞两原子质量均为M,但每个原子与左右邻原子的力常熟分别为β1和β2,原子链的周期为a .证明振动频率为证:如图,任意两个A 原子〔或B 原子〕之间的距离为a,设双键距离b 2,单键距离b 1 …—CH =CH —CH =CH —CH =CH —CH =CH —CH =CH …2n-2 2n-1 2n 2n+1 2n+2 AB Ab2 b1只考虑近邻作用的A,B 两原子的运动方程为A :222121221()()n n n n n M μβμμβμμ+-=---B : 21122212212()()n n n n n M μβμμβμμ++++=---将格波解()2i qna t n Ae ωμ-= 和2[()]21i q na b t n Be ωμ+-+= 代入以上运动方程,有 化简得:1221212()()0iqb iqb M A e e B ββωββ-+--+=同理:1221212()()0iqb iqb e e A M B ββββω--+++-=化为以A 、B 为未知数的线性齐次方程组,它的有解条件是从而得到3.求一维单原子链的振动模式密度g<ω>,若格波的色散可以忽略,其g<ω>具有什么形式,比较这两者的g<ω>曲线.解:一维情况q 空间的密度约化为L/2π,L=Na 为单原子链的长度,其中a 为原子间距,N 为原子数目.则在dq 间隔内的振动模式数目为2L dq π.dω频率间隔内的振动模式数目为 等式右边的因子2来源于ω〔q 〕具有中心反演对称,q ﹥0和q ﹤0区间是完全等价的.从而有 对于一维单原子链,只计入最近邻原子之间的相互作用时,有其中ωm 为最大频率.代入g <ω>得考虑ω=cq 〔德拜近似〕由q →0〔德拜近似下〕, 有111()222m m q qa qa a q ωωω==⋅=⋅ 即12m c a ω=⋅ 则有:12m d a dq ωω=⋅ 121()12m m NaN g a ωππωω==⋅ 〔常数〕考虑ω=ω0〔爱因斯坦近似〕显然有()000g ωωωωω∞=⎧=⎨≠⎩ 4.金刚石〔碳原子量为12〕的杨氏模量为1012N·m -2,密度ρ=3.5g·cm -3.试估算它的德拜温度ΘD =? 解:德拜温度D D B k ωΘ=223231()4()(2)2j V V g c c c ωωπωππ==, 2233()2V g c ωωπ== 近似看作弹性介质时,1/2410/C m s ⎛⎫=⨯ ⎪⎝⎭杨氏模量密度 每摩尔原子数目为N=6.02×1023,摩尔质量m=12g,则摩尔体积代入,得ωm =57.97×1013最后得 ΘD =4427K5.试用德拜模型求晶体中各声频支格波的零点振动能. 解:根据量子理论,各简谐振动的零点能为12ω 德拜近似下2233()2V g C ωωπ= 总零点能为034232301()2331444m m m E g d VV d C C ωωωωωωωωππ===⎰⎰ 由自由度确定的21/3[6()]m NC V ωπ=代回上式中6.一根直径为3mm 的人造蓝宝石晶体的热导率,在30K 的温度达到一个锐的极大值,试估计此极大值.〔蓝宝石在T ﹤﹤ΘD =1000K 时,c V =10-1T 3J·m -3·K -1〕解:m D B k ωΘ=→ωm =1.31×1014λ与晶格常数10-10m 近似时约为2.09×103,近似作为平均声速代入 热导率35.643103c l υκυ==⨯ 7.Na 和Cl 的原子量分别为23和37.氯化钠立方晶胞边长为0.56nm,在[100]方向可以看做是一组平行的离子链.离子间距d=0.28nm.NaCl 晶体的杨氏模量为5×1010N·m -2,如果全反射的光频率与q=0的光频模频率相等,求对应的光波波长.解:当q=0时,光频支频率为杨氏模量10510a β=⨯,且90.2810a -=⨯m故201.7910β=⨯,再同两原子质量一同代入频率式则波长02c πλω==1.53×10-14m8.立方晶体有三个弹性模量C 11,C 12和C 44.铝的C 11=10.82×1010N·m -2,C 44=2.85×1010N·m -2,铝沿[100]方向传播的弹性波纵波速度l υ=,横波速度t υ=,Al 的密度ρ=2.70×103kg·m -3.求德拜模型中铝的振动模式密度g<ω>.解:由题条件知36.3310l υ=⨯,33.2510t υ=⨯若所考虑的晶体体积为V,则。
2019-2020学年鲁科版物理选修3-4同步配套学案:第2章 第2节 波的反射和折射 Word版含答案
第2节波的反射和折射1.知道什么是波面、波线.知道它们之间的关系.2.了解惠更斯原理,知道用惠更斯原理描述波的方法.(重点)3.掌握波的反射定律,能进行较简单的应用.(重点+难点) 4.知道什么是波的折射,理解波的折射定律.(重点+难点)一、惠更斯原理1.波面和波线(1)波面:从波源发出的波,经过同一传播时间到达的各点所组成的面,如图所示.(2)波线:用来表示波的传播方向的线,波线与各个波面总是垂直的.2.波的分类(1)球面波:波面是球形的波.如空气中的声波.(2)平面波:波面是平面的波.如水波.3.惠更斯原理(1)内容:介质中波阵面上的每一个点,都可以看成一个新的波源,这些新波源发出子波,经过一定时间后,这些子波的包络面就构成下一时刻的波面.(2)包络面:某时刻与所有子波波面相切的曲面.(1)波面一定与波线垂直.()(2)波面一定是平面.()(3)波的传播方向与波面平行.()(4)用惠更斯原理能够解释波的衍射现象与障碍物大小的关系.()提示:(1)√(2)×(3)×(4)×二、波的反射1.定义:波遇到障碍物时会返回来继续传播的现象,如图所示.2.反射规律反射波的波长、频率和波速都与入射波相同.反射定律:反射波线、入射波线和法线在同一平面内,反射波线和入射波线分别位于法线两侧,反射角等于入射角.1.人们听不清对方说话时,除了让一只耳朵转向对方,还习惯性地把同侧的手附在耳旁,这样做是利用声波的什么特点提高耳朵的接收能力?提示:在耳廓原有形状、面积的基础上增加一个手的面积是为了增加波的反射来提高耳朵的接收能力. 三、波的折射1.折射现象:波在传播过程中,由一种介质进入另一种介质时传播方向发生偏折的现象,如图所示 .2.折射定律(1)内容:入射角的正弦跟折射角的正弦之比,等于波在第Ⅰ种介质中的波速与波在第Ⅱ种介质中的波速之比. (2)公式:sin i sin r =v 1v 2.2.波由一种介质进入另一种介质而发生折射时,其频率、波速与波长发生变化吗? 提示:频率由波源的振动频率决定,所以频率不变.波速由介质的性质决定,所以波速发生变化,由v =λf 知,波长也发生变化.对惠更斯原理的理解与应用1.球面波和平面波的比较球面波平面波区别波面形状球面平面形成点波源在均匀介质中向各个方向发出的波面波源在均匀介质中向波源面两侧发出的波波面与波源关系波面以点波源为球心波面与波源平行联系球面波传至距波源很远处时,在空间的某一小区域内的球形波面可看成平面波2.利用惠更斯原理解释波的传播如图甲所示,以O为球心的球面波在t时刻的波面为γ,按照惠更斯原理,γ面上每个点都是子波的波源.设各个方向的波速都是v,在Δt时间之后各子波的波面如图中虚线所示,虚线圆的半径是vΔt,γ′是这些子波波面的包络面,它就是原来球面波的波面在时间Δt后的新位置.可以看出,新的波面仍是一个球面,它与原来球面的半径之差为vΔt,表示波向前传播了vΔt的距离.与此类似,可以用惠更斯原理说明平面波的传播,如图乙所示.(多选)关于对惠更斯原理的理解,下列说法正确的是()A.同一波面上的各质点振动情况完全相同B.同一振源的不同波面上的质点的振动情况一定不同C.球面波的波面是以波源为中心的一个个球面D.无论怎样的波,波线始终和波面垂直[解题探究] (1)同一波面上各点到波源的距离是否相等?这些点的振动情况有什么特点? (2)平面波和球面波有什么区别?[解析] 按照惠更斯原理:波面是由振动情况完全相同的点构成的面,而不同波面上质点的振动情况可能相同,如相位相差2π整数倍的质点的振动情况相同,故A 对,B 错.由波面和波线的概念,不难判定C 、D 对. [答案] ACD1.(多选)下列说法中错误的是( )A .只有平面波的波面才与波线垂直B .只有球面波的波线与波面垂直C .任何波的波线都表示波的传播方向D .有些波的波面表示波的传播方向解析:选ABD.不管是平面波,不是球面波,其波面与波线均垂直,选项A 、B 错误.只有波线才表示波的传播方向,选项C 正确,选项D 错误.波的反射现象的应用1.回声测距(1)当声源不动时,声波遇到了障碍物会返回来继续传播,反射波与入射波在同一介质中传播速度相同,因此,入射波和反射波在传播距离一样的情况下,用的时间相等,设经时间t 听到回声,则声源距障碍物的距离为s =v 声·t2.(2)当声源以速度v 向静止的障碍物运动或障碍物以速度v 向静止的声源运动时,声源发声时障碍物到声源的距离为s =(v 声+v )·t2.(3)当声源以速度v 远离静止的障碍物或障碍物以速度v 远离声源时,声源发声时障碍物到声源的距离s =(v 声-v )·t2.2.超声波定位蝙蝠能发出超声波,超声波遇到障碍物或捕食目标时会被反射回来,蝙蝠就根据接收到的反射回来的超声波来确定障碍物或食物位置,从而确定飞行方向.另外海豚、雷达也是利用波的反射来定位和测速的.(1)反射波与入射波在同一种介质中的传播速度相同.(2)人耳能将原声和回声区分开的最小时间间隔为0.1 s.(3)雷达是利用波的反射来定位和测速的.某物体发出的声音在空气中的波长为1 m ,波速340 m/s ,在海水中的波长为4.5 m. (1)该波的频率为______Hz ,在海水中的波速为______m/s.(2)若物体在海面上发出的声音经0.5 s 听到回声,则海水深为多少? (3)若物体以5 m/s 的速度由海面向海底运动,则经过多长时间听到回声? [思路点拨] 解答本题时应注意在同一介质中,声波与其反射波的传播速度相同. [解析] (1)由f =v λ得:f =3401 Hz =340 Hz.因波的频率不变,则在海水中的波速为 v 海=λ海f =4.5×340 m/s =1 530 m/s.(2)入射声波和反射声波用时相同,则海水深为 s =v 海t 2=1 530×0.52m =382.5 m.(3)物体与声音运动的过程示意图如图所示设听到回声的时间为t , 则v 物t ′+v 海t ′=2s . 代入数据解得t ′≈0.498 s.[答案] (1)340 1 530 (2)382.5 m (3)0.498 s对折射定律的理解1.表达式:sin i sin r =v 1v 22.理解(1)折射的原因:波在两种介质中的传播速度不同.(2)由于波在一种介质中的波速是一定的,所以v 1v 2是一个只与两种介质的性质有关,与入射角、折射角无关的常数,叫做第二种介质相对第一种介质的折射率,所以n 21=v 1v 2.(3)当v 1>v 2时,i >r ,折射光线靠近法线;当v 1<v 2时,i <r ,折射光线远离法线;当垂直于界面入射(i =0°)时,r =0°,传播方向不变.3.几点说明(1)频率f 由波源决定,故无论是反射波的频率还是折射波的频率都与入射波的频率,即波源的振动频率相同.(2)波速v 由介质决定,因反射波与入射波在同一介质中传播,故波速不变;折射波与入射波在不同介质中传播,波速变化.(3)据v =λf 知,波长λ与v 及f 有关,即与介质和波源有关,反射波与入射波在同一介质中,波速相同,频率相同,故波长相同.折射波与入射波在不同介质中传播,v 不同,f 相同,故λ不同.如图所示,某列波以60°的入射角由甲介质射到乙介质的界面上同时产生反射和折射,若反射波的波线与折射波的波线的夹角为90°,此波在乙介质中的波速为1.2×105km/s.(1)该波的折射角为________. (2)该波在甲介质中的传播速度为多少? (3)该波在两种介质中的波长比为多少?[思路点拨] 由反射定律可得反射角的大小,由反射波与折射波垂直可得折射角的余角大小,从而求得折射角,由折射定律可得波速.由波速公式再变形可得波长. [解析] (1)由反射定律可得反射角为60°,由题图的几何关系可得折射角为r =30°. (2)由波的折射规律v 甲v 乙=sin i sin r,所以v 甲=sin i sin r v 乙=sin 60°sin 30°v 乙=3212×1.2×105 km/s≈2.08×105 km/s.(3)因波长λ=v f ,又因为波在两种介质中的频率相同,则λ甲λ乙=v 甲v 乙=2.08×1051.2×105=26∶15.[答案] (1)30° (2)2.08×105 km/s (3)26∶152.如图所示是声波从介质Ⅰ进入介质Ⅱ的折射情况,由图判断下面的说法正确的是( )A .若i >r ,则声波在介质Ⅰ中的传播速度小于声波在介质Ⅱ中的传播速度B .若i >r ,则Ⅰ可能是空气,Ⅱ可能是水C .若i >r ,则Ⅰ可能是钢铁,Ⅱ可能是空气D .在介质Ⅰ中的传播速度v 1与在介质Ⅱ中的传播速度v 2满足v 1v 2=sin rsin i解析:选C.根据折射规律v 1v 2=sin isin r ,知A 、D 项均错.若i >r ,则v 1>v 2,若Ⅰ是空气,则Ⅱ不可能是水,因为声波在空气中的传播速度比在水中的小,B 错,C 对.典型问题——波的反射和折射中各物理量的变化波向前传播在两介质的界面上同时发生了反射和折射现象,一些物理量相应发生了变化,比较如下:波现象比较项目波的反射波的折射传播方向 改变θ反=θ入改变θ折≠θ入频率f 不变 不变 波速v 不变 改变 波长λ不变改变 如图中1、2、3分别代表入射波、反射波、折射波的波线,则( )A .2与1的波长、频率相等,波速不等B .2与1的波速、频率相等,波长不等C.3与1的波速、频率、波长均相等D.3与1的频率相等,波速、波长均不等[解析]由于波的频率由波源决定,因此波在不同介质中传播时,频率保持不变.波在不同介质中传播时,波速发生变化,由v=λf可知波长也发生变化.由此可知只有D选项正确.[答案] D。
实验八超声波
实验八超声波实验超声波是频率在2⨯104Hz~1012Hz的声波。
超声广泛存在于自然界和日常生活中,如老鼠、海豚的叫声中含有超声成分,蝙蝠利用超声导航和觅食;金属片撞击和小孔漏气也能发出超声。
超声波测试把超声波作为一种信息载体,它已在海洋探查与开发、无损检测与评价、医学诊断等领域发挥着不可取代的独特作用。
例如,在海洋应用中,超声波可以用来探测鱼群或冰山、潜艇导航或传送信息、地形地貌测绘和地质勘探等。
在检测中,利用超声波检验固体材料内部的缺陷、材料尺寸测量、物理参数测量等。
在医学中,可以利用超声波进行人体内部器官的组织结构扫描(B超诊断)和血流速度的测量(彩超诊断)等。
【实验目的】1. 理解压电效应;了解超声波的产生和传播规律。
2. 认识超声脉冲波及其特点。
3. 理解超声波的发射、折射和波型转换。
【实验原理】1.压电效应某些固体物质,在压力(或拉力)的作用下产生变形,从而使物质本身极化,在物体相对的表面出现正、负束缚电荷,这一效应称为压电效应。
物质的压电效应与其内部的结构有关。
如石英晶体的化学成分是SiO2,它可以看成由+4价的Si离子和-2价O离子组成。
晶体内,两种离子形成有规律的六角形排列,如图1所示。
其中三个正原子组成一个向右的正三角形,正电中心在三角形的重心处。
类似,三个负原子对(六个负原子)组成一个向左的三角形,其负电中心也在这个三角形的重心处。
晶体不受力时,两个三角形重心重合,六角形单元是电中性的。
整个晶体由许多这样的六角形构成,也是电中性的。
图1 石英晶体的压电效应当晶体沿x方向受一拉力,或沿y方向受一压力,上述六角形沿x方向拉长,使得正、负电中心不重合。
尽管这是六角形单元仍然是电中性的,但是正负电中心不重合,产生电偶极矩p。
整个晶体中有许多这样的电偶极矩排列,使得晶体极化,左右表面出现束缚电荷。
当外力去掉,晶体恢复原来的形状,极化也消失。
(许多大学物理教材都有关于电极化理论的介绍)由于同样的原因,当晶体沿y方向受拉力,或沿x方向受压力,正原子三角形和负原子三角形都被压扁,也造成正、负电中心不重合。
高中物理 第2章 机械波 2_4 惠更斯原理 波的反射与折射教师用书 沪科版选修3-4
2.4 惠更斯原理 波的反射与折射[先填空]1.在均匀介质中,质点的振动会向各个方向匀速传播,形成球面波.2.波在介质中传播时,任一时刻介质振动步调相同的点的包络面叫做波面;最前面的波面又叫波前,垂直于波面并指向波传播方向的直线叫做波线.如图241所示.图2413.波面是平面的波叫做平面波.4.惠更斯原理的内容是:介质中波前上的各点,都可以看成是一个新的波源(子波源),并发出子波;其后,这些子波的包络面就是新的波面.[再判断]1.只有平面波的波面才与波线垂直.(×)2.任何波的波线与波面都相互垂直.(√)3.任何波的波线都表示波的传播方向.(√)[后思考]波面一定是平面吗?根据下图思考波线与波面的关系是怎样的.图242【提示】波面不一定是平面.波线与波面互相垂直,一定条件下由波面可确定波线,由波线可确定波面.[核心点击]1.惠更斯原理的实质:波面上的每一点(面源)都是一个次级球面波的子波源,子波的波速与频率等于初级波的波速和频率,此后每一时刻的子波波面的包络面就是该时刻总的波动的波面.其核心思想是介质中任一处的波动状态是由各处的波动决定的.2.惠更斯原理的局限性:光的直线传播、反射、折射等都能用此来进行较好的解释.但是,惠更斯原理是比较粗糙的,用它不能解释衍射现象与狭缝或障碍物大小的关系,而且由惠更斯原理推知有倒退波的存在,而倒退波显然是不存在的.1.关于对惠更斯原理的理解,下列说法正确的是( )A.同一波面上的各质点振动情况完全相同B.同一振源的不同波面上的质点的振动情况一定不同C.球面波的波面是以波源为中心的一个个球面D.无论怎样的波,波线始终和波面垂直E.波面可以表示波的传播方向【解析】按照惠更斯原理:波面是由振动情况完全相同的点构成的面,而不同波面上质点的振动情况可能相同,如相位相差2π整数倍的质点的振动情况相同,故A对,B错.由波面和波线的概念,不难判定C、D正确.只有波线才能表示波的传播方向,E错误.故正确答案为A、C、D.【答案】ACD2.下列叙述中正确的是( )A.空间点波源发出的球面波,其波面是一个球面,波线就是以波源为圆心的同心圆B.平面波的波线是一条直线,其波线相互平行C.根据惠更斯原理,波面各点都可看作一个子波源,子波前进的方向的包络面就是该时刻的波面D.利用惠更斯原理,只要知道t时刻波面的位置和波速,就可确定t+Δt时刻波面的位置E.不同波面上的质点振动情况一定不相同【解析】球面波的波线沿球面的半径方向,A错误.平面波的波线是一条直线,由于波线与波面垂直,故平面波的波线相互平行,B正确.由惠更斯原理可知,C正确.利用惠更斯原理,只要知道t时刻波面的位置和波速,就可确定另一时刻波面的位置,D正确.不同波面上质点的振动情况可能相同,如相位差相差2π整数倍的质点的振动情况相同,故E 错误.【答案】BCD利用惠更斯原理解释波的传播的一般步骤1.确定一列波某时刻一个波面的位置.2.在波面上取两点或多个点作为子波的波源.3.选一段时间Δt.4.根据波速确定Δt时间后子波波面的位置.5.确定子波在波前进方向上的包络面,即为新的波面.6.由新的波面可确定波线及其方向.[先填空]1.机械波的反射规律(1)波遇到障碍物时会返回来继续传播,如图243所示.图243(2)反射定律①入射角:入射波线与反射面法线的夹角,如图中的α.②反射角:反射波线与反射面法线的夹角,如图中的β.③反射定律:反射波线、入射波线和法线在同一平面内,反射波线和入射波线分别位于法线两侧,反射角等于入射角.2.机械波的折射规律 (1)折射现象波在传播过程中,由一种介质进入另一种介质时,传播方向发生偏折的现象,如图244所示.图244(2)折射规律 ①频率:频率不变. ②波速:发生改变. ③波长:发生改变. (3)折射定律①内容:入射角的正弦跟折射角的正弦之比,等于波在第Ⅰ种介质中的波速与波在第Ⅱ种介质中的波速之比.②公式:sin i sin r =v 1v 2.[再判断]1.反射波的频率、波速与入射波相同.(√)2.折射波的频率、波速与入射波相同.(×)3.发生波的折射时,折射角的大小一定和入射角成正比. (×) [后思考]人们听不清对方说话时,除了让一只耳朵转向对方,还习惯性地把同侧的手附在耳旁.你能说出其中的道理吗?【提示】 当用手附在耳旁时,手就可以反射一部分声波进入人耳,以提高耳的接收能力.[核心点击]1.回声测距(1)当声源不动时,声波遇到了静止障碍物会返回来继续传播,由于反射波与入射波在同一介质中传播速度相同,因此,入射波和反射波在传播距离一样的情况下,用的时间相等,设经过时间t 听到回声,则声源距障碍物的距离为s =v 声t2.(2)当声源以速度v 向静止的障碍物运动或障碍物以速度v 向静止的声源运动时,声源发声时障碍物到声源的距离为s =(v 声+v )t2.(3)当声源以速度v 远离静止的障碍物或障碍物以速度v 远离静止的声源时,声源发声时障碍物到声源的距离s =(v 声-v )t2.2.超声波定位蝙蝠、海豚能发出超声波,超声波遇到障碍物或捕食目标时会被反射回来.蝙蝠、海豚就是根据接收到反射回来的超声波来确定障碍物或食物的位置,从而确定飞行或游动方向.3.波的反射、折射现象中各量的变化(1)频率(f )由波源决定:故无论是反射波还是折射波都与入射波的频率相等,即波源的振动频率相同.(2)波速(v )由介质决定:故反射波与入射波在同一介质中传播,波速不变,折射波与入射波在不同介质中传播,波速变化.(3)据v =λf 知,波长λ与波速和频率有关.反射波与入射波,频率相同、波速相同,故波长相同,折射波与入射波在不同介质中传播,频率相同,波速不同,故波长不同.具体见下表所示.3.如图245所示为一束平面波从介质1进入另一种介质2的情形,则波从介质1进入介质2时波速将________(选填“增大”或“减小”),其入射角和折射角的正弦之比为________.图245【解析】 由公式sin i sin r =v 1v 2可知,当v 1>v 2时,i >r ,即折射角折向法线,折射角小于入射角;当v 1<v 2时,i <r ,即折射角折离法线,折射角大于入射角;sin i sin r =sin 30°sin 60°=1232=33. 【答案】 增大334.一列声波从空气中传入水中,已知水中声速较大,则声波频率________,波长________ 【解析】 由于波的频率由波源决定,因此波无论在空气中还是在水中频率都不变.又因波在水中速度较大,由公式v =λf 可得,波在水中的波长变大.【答案】 不变 变大5.某物体发出的声音在空气中的波长为1 m ,波速为340 m/s ,在海水中的波长为4.5 m. (1)该波的频率为________Hz ,在海水中的波速为________ m/s. (2)若物体在海面上发出的声音经过0.5 s 听到回声,则海水深为多少? (3)若物体以5 m/s 的速度由海面向海底运动,则经过多长时间听到回声?【解析】 (1)由f =v λ得f =3401Hz =340 Hz ,因波的频率不变,则在海水中的波速为v 海=λ′f =4.5×340 m/s=1 530 m/s.(2)入射声波和反射声波用时相同,则海水深为h =v 海t 2=1 530×0.52m =382.5 m.(3)物体与声音运动的过程示意图如图所示,设听到回声的时间为t ′,则v 物t ′+v 海t ′=2 h代入数据解得t ′=0.498 s.【答案】(1)340 1 530 (2)382.5 m (3)0.498 s回声测距的方法技巧利用回声测距是波的反射的一个重要应用,它的特点是声源正对障碍物,声源发出的声波与回声在同一条直线上传播.1.若是一般情况下的反射,反射波和入射波是遵从反射定律的,可用反射定律作图后再求解.2.利用回声测距时,要特别注意声源是否运动,若声源运动,声源发出的原声至障碍物再返回至声源的这段时间与声源的运动时间相同.3.解决波的反射问题,关键是根据物理情景规范作出几何图形,然后利用几何知识结合物理规律进行解题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u z Txx Txz x = 0+
ux u = z Txx Txz x =0−
势函数的反射系数和透射系数的计算
1.4 1.2
Tp
1.0
0.8
R&T
2332,5216,3146 1888,3406,1978 TS Rp RS
0.6
0.4
解此线性方程组可得P波入射时的反射系数和透射系数. 类似可得横波入射时反射系数、透射系数的计算公式。
0.2
0.0 0 10 20 30 40 50 60 70 80 90
Incident Angle
能流的反射系数和透射系数的计算
1.0
横波入射情况
S
θ rL
S
S P
0.8
Tp
θi
θrT
θi 固体 I 固体
ux φi u z = a ( x ) φi 4×4 Txx ψi Txz ψ i + φr − φr +ψ r −ψ r
= 2µk z klx [φi exp( jk lx x ) − φr exp(− jk lx x )] − µk [ψ i exp( jk tx x ) + ψ r exp(− jktx x )] + µk z2 [ψ i exp( jktx x ) + ψ r exp(− jk tx x )]
对于简谐波: Txx = ρ −ω 2φ − 2 cT2
∂ 2φ ∂ 2ψ + 2 ∂ z∂ x ∂ z
2 ∂ 2ψ ∂ 2φ ∂u ∂ w 2 ∂ ψ + 切向应力表达式 Txz = µ = ρ cT 2 − 2 + 2 ∂ x ∂ z ∂ x∂ z ∂z ∂x
+
1 + RP = [a ]4×3 1 − RP Rs
反射系数和透射系数的求解
根据边界条件, u x
RP 1 + RP Tp 1 − R = b a [ ]4×2 T 或 [u ]4× 4 Rs = [V ]4×1 可得 [ ]4×3 P Tp s Rs Ts
xz问题中的应力表达式
cL = λ + 2µ µ , cT = ρ ρ
常用公式
尤拉公式
法向应力表达式
∂u ∂u ∂w Txx = λ + + 2µ ∂x ∂ x ∂ z
e jα = cosα + j sin α e− jα = cosα − j sin α
∂ 2φ ∂ 2φ ∂ 2φ ∂ 2ψ =(λ + 2 µ ) 2 + 2 − 2 µ 2 + ∂ x ∂ z ∂ z ∂ z∂ x
下行波 上行波
P波
ψ = ψ i exp( jk tx x ) + ψ r exp(− jk tx x ) S波
势函数具有的公共因子 exp j (ω t − k z z ) (界面波矢分量相等,在以下均略去不写,求导时仍考虑)
= jk lx [φ i exp ( jk lx x ) − φ r exp (− jk lx x )]
中国石油大学(北京) 乔文孝
2008-11-11
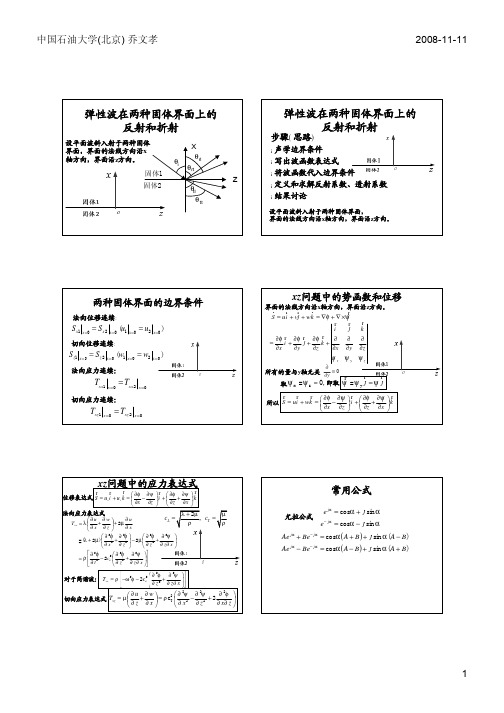
弹性波在两种固体界面上的 反射和折射
设平面波斜入射于两种固体 界面,界面的法线方向沿x 轴方向,界面沿 z方向。 固体1 固体2 θi X θ rl θrt Z θtl θ tt
步骤(思路)
弹性波在两种固体界面上的 反射和折射
¡声学边界条件 ¡写出波函数表达式 ¡将波函数代入边界条件 ¡定义和求解反射系数、透射系数 ¡结果讨论
= 2µ k z klx cos ( klx x )(φi − φr ) + j sin ( klx x )(φi + φr )
2 + µ ( k z2 − ktx ) cos ( ktx x )(ψ i +ψ r ) + j sin ( ktx x )(ψ i −ψ r )
2
2 2 = cos ( klx x )(φi + φr ) + j sin ( klx x )(φi − φr ) 2 µ k z − ( λ + 2 µ ) kl
[ [
] ]
+ jktx cos ( ktx x )(ψ i −ψ r ) + j sin ( ktx x )(ψ i +ψ r )
P波入射时入射侧的位移和应力的表达式
P波入射时透射侧的位移和应力的表达式
任意层 介质中位移和应力的矩阵表达式 ux φi + φr u z = a ( x ) φi − φr 4 × 4 Txx ψ i + ψ r Txz ψ i −ψ r 对于透射侧界面,令 φ r = 0,ψ r = 0, T p = φ i , Ts = ψ i 于是有 jklx ux u − jk z z = 2 µ k z2 − ( λ + 2 µ ) kl2 Txx 2 µ k z klx Txz x = 0 − T p Tp = b T [ ]4× 2 T s s 2 µ ( kz2 − ktx ) jk z jktx −2µ k z ktx
任意一层中的z方向位移
∂φ ∂ψ uz = + ∂z ∂x
任意一层中的Txx的表达式
∂ 2φ ∂ 2φ ∂ 2φ ∂ 2ψ Txx =(λ + 2µ ) 2 + 2 − 2µ 2 + ∂ ∂ x z ∂ z ∂ z∂ x
= (λ + 2 µ ) − kl2 (φi exp ( jklx x ) + φr exp (− jklx x )) − 2 µ − kz2 (φi exp ( jklx x ) + φr exp (− jklx x )) − 2 µ [k z ktx (ψ i exp ( jk tx x ) − ψ r exp (− jk tx x ))]
θrT
S
z
θ tT θ tL P
zHale Waihona Puke θ tT SR & T (Energe)
0.6
2332,5216,3146 1888,3406,1978
0.4
x
TS
S
x
0.2
Rp
0.0 0 10 20 30 40 50 60
RS
70 80 90
Incident Angle
SH波入射 正应力及法向位移为零 切向位移和切向应力连续 H-Horizontal 入射角接近于90度时的声波入射称之为声波掠入射; 掠入射时,SV波的偏振方向接近垂直于界面。 SV波入射 应力和位移连续 V-Vertical
设平面波斜入射于两种固体界面, 界面的法线方向沿 x轴方向,界面沿 z方向。
两种固体界面的边界条件
法向位移连续:
xz问题中的势函数和位移
界面的法线方向沿 x轴方向,界面沿 z方向。 r r r r r S = ui + vj + wk = ∇φ + ∇ ×ψ r r r i j k ∂φ r ∂φ r ∂φ r ∂ ∂ ∂ = i+ j+ k+ ∂x ∂y ∂z ∂x ∂y ∂z ψx ψy ψz 所有的量与 y轴无关 取 ψ x =ψ z = 0, 即取 ψ =ψ y j = ψ j
−2µ k z ktx cos ( ktx x )(ψ i −ψ r ) + j sin ( ktx x )(ψ i +ψ r )
任意一层中的Txz的表达式
∂ ψ ∂ ψ ∂ φ Txz = µ ∂x 2 − ∂z 2 + 2 ∂z∂x
2 2 2
介质中位移和应力的矩阵表达式
∂ ≡0 ∂y
S x1 x = 0 = S x 2 S z1 x =0 = S z 2
x =0
(u1 x =0 = u2
x =0
) )
切向位移连续:
x =0
( w1 x =0 = w2
x =0
法向应力连续:
Txx1 x =0 = Txx 2
切向应力连续:
x =0
r
r
r
Txz1 x =0 = Txz 2
r ∂φ ∂ψ r ∂φ ∂ψ r r r − + 所以 S = ui + wk = i + k ∂x ∂z ∂z ∂x
x =0
r r r ∂φ ∂ψ r ∂φ ∂ψ r 位移表达式 S = u x i + u z k = ∂x − ∂z i + ∂z + ∂x k
2 ∂ 2φ ∂ 2ψ 2∂ φ = ρ 2 − 2cT 2+ t z z∂ x ∂ ∂ ∂
Ae jα − Be− jα = cosα ( A − B ) + j sin α ( A + B)
Ae jα + Be− jα = cosα ( A + B ) + j sin α ( A − B)
若只有P波入射,ψ i=0,并设φ i=1, RP、 Rs分别为纵波和横波的反射系 数,于是入射侧界面(x=0)有, 0 jklx jk z ux 1 + RP u − jk 0 − jk z tx 1 − R z = P 2µ k z2 − ( λ + 2µ ) kl2 0 2 µ k z ktx Txx Rs 2 2 T 0 2 µ k k µ k − k ( ) xz x =0 z lx z tx
