化工工艺学 第三章 机械分离
第三章机械分离和固体流态化

第三章机械分离和固体流态化具有不同物理性质(如密度差别)的分散物质和连续介质所组成的物系称为非均相混合物或非均相物系。
颗粒相对于流体(静止或运动)运动的过程称为沉降分离。
流体相对于固体颗粒床层运动而实现固液分离的过程称为过滤。
工业上分离非均相混合物的目的是:1、回收有价值的分散物质。
2、净化分散介质以满足后继生产工业的要求。
3、环境保护和安全生产。
第一节颗粒及颗粒床层的特性;表单一的颗粒:1、球形颗粒体积:面积:;比表面积:2、非球形颗粒:体积当量直径形状系数(又称球形度):,任何非球形颗粒的形状系数皆小于1。
不同粒径范围内所含粒子的个数或质量,即粒径分布。
当使用某一号筛子时,通过筛孔的颗粒量称为筛过量,截留于筛面上的颗粒量则称为筛余量。
称取各号筛面上的颗粒筛余量即得筛分分析的基础数据。
颗粒的平均直径:最常用的是平均比表面积直径:由颗粒群堆积成的床层疏密程度可用空隙率来表示:床层的比表面积:壁面附近床层的空隙率总是大于床层内部的,较多的流体必然趋向近壁处流过,使床层截面上流体分布不均匀,这种现象称为壁效应。
第二节沉降过程沉降操作是指在某种力场中利用分散相和连续相之间的密度差异,使之发生相对运动而实现分离的操作过程。
实现沉降操作的作用力可以是重力,也可以是惯性离心力。
因此,沉降过程有重力沉降和离心沉降两种方式。
静止流体中颗粒的沉降过程可分为两个阶段,起初为加速段而后为等速段。
滞流区或斯托克斯定律区(10-4<Re t<1)阻力系数:。
滞流区(斯托克斯公式):颗粒的球形度愈小,对应于同一Re t值的阻力系数愈大,但值对的影响在滞流区内并不显著,随着Re t的增大,这种影响逐渐变大。
自由沉降速度的公式不适用于非常微细颗粒(如d<0.5 )的沉降计算,这是由于流体分子热运动使得颗粒发生布朗运动。
二、重力沉降设备(一)降尘室籍重力沉降从气流中分离出尘粒的设备称为降尘室。
理论上降尘室的生产能力()只与其沉降面积bl及颗粒沉降速度u t有关,而与降尘室高度H无关。
3第三章机械分离剖析

重力沉降 沉降分离 离心沉降 重力过滤 加压过滤 过滤分离 真空过滤 离心过滤
工业上分离混合物的目的是: ①作为生产的主要阶段。如从淀粉液制取淀粉,从牛奶制取奶油和脱脂奶,将 晶体与母液分离制取纯净晶体食品等。 ②提高制品纯度。如牛奶的除杂净化和啤酒的过滤净化除去微粒固体等。 ③回收有价值物质。如从含微粒固体的气溶胶中分离出奶粉。
100≤ Reb ≤ 420, 湍流, 形体阻力占绝对主导, 等式右边第一项可忽略; 【例题3-1】颗粒及床层特性公式应用;床层压降计算。
§3 机械分离及固体流态化
§ 3.3 沉降过程
3.3.1 重力沉降
阻力Fd
浮力Fb
一. 沉降速度
A. 球形颗粒的自由沉降 颗粒在流体中的受力
重力 Fg 浮力 Fb
§3.2.3 固定床流动阻力
3.2.3 固定床流动阻力——康采尼模型
固定床层颗粒间形成的可供流体通过的通道细小、曲折且相互交联, 非常 复杂, 流体流过这些通道的流动阻力(压降)很难计算, 必须作适当的假设, 并在此基础上建立数学模型——康采尼模型就是其中较成功的一个模型。
1. 平行细管模型 将床层内的复杂通道假设成为长度为L(床层 高度)、当量直径为deb 的平行细管,并且假定: 流体 L deb
1) 细管的全部流动空间等于床层的空隙体积; 2) 细管的侧表面积等于床层的表面积。
设床层体积为Vb,
细管的体积 床层的空隙体积 Vb
细管的侧表面积 床层的表面积 Vbab Vb (1 )a
细管的当量直径 d eb d eb 4细管截面积 4细管截面积 L 4细管体积 4 细管湿周长 细管湿周长 L 细管侧表面积 (1 )a
化工原理 第三章 机械分离与固体流态化

• 3.1 过 滤
• 3.2 沉
降
• 3.3 固体流态化
3.1 过
• • • • •
滤
3.1.1 概述 3.1.2 过滤基本方程 3.1.3 过滤常数的测定 3.1.4 滤饼洗涤 3.1.5 过滤设备及过滤计算
3.1.1 概 述
• 滤饼过滤其基本原理是在外力(重力、压力、离心 力)作用下,使悬浮液中的液体通过多孔性介质,而 固体颗粒被截留,从而使液、固两相得以分离,如图 3-1所示。
3.1.5 过滤设备及过滤计算
• 对叶滤机,洗涤速率则为:
2 LA d V d V d V KA w d L A d d V V w w e w e e 2
综合板框压滤机、叶滤机,洗涤速率可统一写成:
而过滤时间
V 2 2VV e
2 KA
将、w表达式代入式3-6得:
2 KA V Q 2 2 2 V 2 VV b V VV KA e e D
将上式对V求导数,得:
2 2 2 2 KA KA V bV d Q D 2 2 2 2 d VV 2 VV b V VV KA e e D
常用的助滤剂有:硅藻土、纤维粉末、活性炭、石棉等。
3.1.2 过滤基本方程
L u1 u u le
图3-3
流 体 在 滤 饼 中 流 动 的 简 化 模 型
• 将孔道视为长度均为le的一组平行细管,流体 在细管中的平均流速u1,同时考虑到滤饼较薄, 广义压力降可近似用压力降代替,则:
p1 2 u1 de 32le
化工原理 机械分离 过滤分离

40 1773 + 1267 = 1.51(h ) θC = θF + θ W + θR = + 60 3600 0.76 Q= = 0.5(m 3 / h ) 1.51
化工原理(上) 化工原理(
第三章 机械分离 —— 过滤分离过程
3.2 过 滤 一 过滤基本原理
1 过滤
滤 浆 滤 饼 过滤介质
滤 液
固液混合,外力驱动,多孔介质,颗粒截留, 固液混合,外力驱动,多孔介质,颗粒截留,液体通过
名词: 名词: 1过滤介质;滤浆;滤渣(饼);滤液 2过程推动力:重力;压力(差);离心力 3滤饼过滤与深层过滤 4操作目的:固体或清净的液体 5洗涤——回收滤饼中残存的滤液或除去其杂质
一个周期中全部面积经历过滤时间 一个周期中全部面积经历过滤时间 全部面积
θ F = φθ C = φ / n θ F = φθ C
部分面积,全部时间 →全部面积, 部分面积,全部时间—→全部面积,部分时间
φA
θC
A
(2)生产能力
Qh = 3600qA / θ c = 3600nqA 2 q + 2qqe = Kθ F = Kφ / n
模型简化
细管)当量直径 ③孔道(细管 当量直径 e: 孔道 细管 当量直径d
4 × 流通截面积 l 4 × 空隙体积 4 × 床层体积 × 空隙率 de = = = 润湿周边长 l 颗粒表面积 比表面积 × 颗粒体积 4 × 床层体积 × 空隙率 4ε = = 比表面积 × 床层体积 × (1 − 空隙率 ) a (1 − ε )
2.转筒过滤机 . (1)结构与工作原理 )
四 过滤计算
1.间歇过滤机的计算 卸渣、清理、装合 卸渣、清理、
《化工原理》第三章 机械分离与固体流态化3讲

3.3 固体流态化
一、固体流态化的几个阶段 二、流化床的两种形态 三、流化床的主要特性
浙江大学本科生课程 化工原理
第三章 机械分离与固体流态化
1/6
3.3 固体流态化
一、固体流态化的几个阶段
固定床阶段:此时流体的真实速度
流化床阶段:
u1
u
ut
u1
<
颗粒的沉降速度ut
此时颗粒悬浮于流体中,床层有一个明
pWA
(a)
(b)
(c)
流化床的类似于液体的特性
浙江大学本科生课程 化工原理
第三章 机械分离与固体流态化
(d) 5/6
恒定的压降 pA m s g m l g
p
固定床
流化床
带出开始
C
聚式流化床
B
A
A
0 起始流化速度
D(带出速度)
表观速度
流化床压力降与气速关系
ห้องสมุดไป่ตู้
浙江大学本科生课程 化工原理
第三章 机械分离与固体流态化
显的上界面,与沸腾水的表面相似
浮力
曳力 u1(真正速度)
重力
(a)固定床
(b)流化床
(c)气力输送
浙江大学本科生课程
化工原理 流态化过程的第几三个章阶机段械分离与固体流态化
u(表观速度)
2/6
3.3 固体流态化
颗粒输送阶段: u1 ut
浮力
曳力 u1(真正速度)
重力
u(表观速度)
(a)固定床
(b)流化床
6/6
流态化过程的几个阶段
(c)气力输送
浙江大学本科生课程 化工原理
第三章 机械分离与固体流态化
化工原理上册 第3章 流体相对颗粒(床层)的流动及机械分离
τm
AP
(a)
(b)
(c)
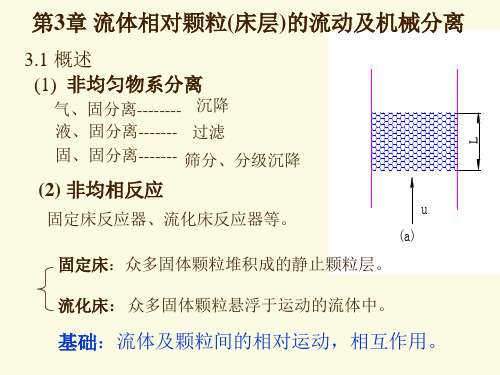
图3-5 物体的不同形状和位向对曳力的影响 (a)-平板平行于流向;(b)-平板垂直于流向;(c)-流线型物体
水平方向,颗粒所受曳力:
颗粒微元: dFD p cosdA w sindA
总曳力:FD p cosdA w sindA
A
A
Pcosa dA PdA
τwdA
aB
A VB
V
A a(1 ) (1 )
aB a
3.3 流体和颗粒的相对运动
流体和颗粒相对运动的情况:
① 颗粒静止,流体绕过颗粒流动; ② 流体静止,颗粒流动; ③ 颗粒和流体都运动,维持一定相对速度。
3.3.1 流体绕过颗粒的流动
(1) 曳力 阻力:颗粒对流体的作用力 曳力:流体对颗粒的作用力
② 非球形颗粒的曳力系数 计算方法: ◇ 近似用球形颗粒公式,ds→da 或 dv ◇ 实测ξ-Rep 关系(书P168 图3.3.2)
3.3.2 颗粒在流体中的流动
(1) 颗粒在力场中的受力分析
Fb
① 质量力 Fe mae Vs sae
②
浮力
Fb
m
s
ae
Vs ae
③
曳力
FD
AP
1 2
u 2
1
)3
( 6dV2 / a )1/3 ( 6dV2 )1/3
a
因此, dV
6
a
2)等比表面积当量直径 da 指:与非球形颗粒比表面积相等的球形颗粒的直径
a
as
d
2 s
6
d
3 s
6/ ds
da
因此,da 6 / a
南工大化工原理第三章颗粒流体力学基础与机械分离

过滤基本方程式
可压缩滤饼 压缩性指数 s= 0
~
r r0 (p)
1
s
不可压缩滤饼:s=0
过滤基本方程式
dq p d r0 (q qe )
1 s
过滤基本方程
令:
2(p) K r0
1 s
( 恒压过滤常数)
dq K d 2(q qe )
过滤设备
2
2 1 u 1.75 3 dm
欧根方程的误差约为±25%
Re’ ﹤20/6时 右第二项可略 Re’ ﹥1000/6时 右第一项可略
*** 颗粒床层简化模型常用的有一维、二维和三维模型, 这些模型都是将流体通过固定床层的流动进行了大量的 简化,因此所得到的数学模型只能在一定范围内反映事 物的规律。随着科学技术的发展,特别是数学理论的发 展,一些新的在更大程度上能反映流动规律的模型相继 问世。如流体流过一个颗粒表面,当流速较小时颗粒后 面的流体运动是定常的,当流速大到一定程度会发生边 界层分离现象,颗粒后面的流体运动变为湍流运动, 这就属于数学中的混沌现象, 由此建立的混沌模型就 比较复杂。又如固定床层中的颗粒通常看成球形,对于 非球形颗粒通常用平均半径来表示,当考虑颗粒的具体 的不规则形状时,就可能出现非整数维数,由此建立的 数学模型也就很复杂了。但在工程上使用最广、最成熟 的是一维模型。介绍床层的一维简化模型。
1.表格式:表1 石英砂的筛分数据
编号 筛号范围 平均粒径dp, 质量分数 mm x 9/10 10/12 12/14 14/16 16/20 20/24 24/28 1.816 1.524
筛上粒子的 d
筛孔尺寸 d, mm 1.651(10号) 1.397 (12号) 1.168 (14号) 0.991 (16号) 0.833 (20号) 0.701 (24号) 0.589 (28号)
第三章非均相机械分离

1.自由沉降速度
自由沉降:单个颗粒在流体中的沉降过程。
干扰沉降:若颗粒数量较多,相互间距离 较近,则颗粒沉降时相互间会干扰,称为 干扰沉降。
第三章 非均相机械分离
盐城工学院
3.3.2 颗粒在流体中的沉降过程
颗粒在流体中受到三个力的作用,如图3-3所示:
重力Fg 浮力Fb 曳力Fd
Fg=mg (重力),或FB=mac(离心力)
盐城工学院
1.混合物的分类
溶液:精馏、萃取 均相混合物
混合气体:吸收、吸附
混合物
非均相
含雾气体 气态非均相
含尘气体
混合物
悬浮液
液态非均相 乳浊液
泡沫液
第三章 非均相机械分离
3.3.1 概述
盐城工学院
分散相(分散物质):处于分散状态的物质
连续相(分散介质):处于连续状态的物质
2.非均相物系分离的目的 回收有价值的分散物质 净化分散介质 环境保护和安全生产
第三章 非均相机械分离
盐城工学院
第三章 非均相机械分离
➢3.1沉 降 ➢3.2过 滤
第三章 非均相机械分离
3.3 颗粒的沉降
• 3.3.1 概述
盐城工学院
• 3.3.2 颗粒在流体中的沉降过程
• 3.2.3 重力沉降设备
• 3.2.4 离心沉降设备
• 3.2.4 离心机
第三章 非均相机械分离
3.3.1 概述
设为层流,则:
1.86 105 Pa s
ut
d
2 p
(p
)g
18
(40106 )2 9.81 (2600 1.165)
18 1.86 105
0.12m s
校核: Re du 0.3 2 (正确) t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章机械分离本章学习指导1.本章学习目的通过本章学习能够利用流体力学原理实现非均相物系分离(包括沉降分离和过滤分离),掌握过程的基本原理、过程和设备的计算及分离设备的选型。
建立固体流态化的基本概念。
2.本章重点掌握的内容(1)沉降分离(包括重力沉降和离心沉降)的原理、过程计算和旋风分离器的选型。
(2)过滤操作的原理、过滤基本方程式推导的思路,恒压过滤的计算、过滤常数的测定。
(3)用数学模型法规划实验的研究方法。
本章应掌握的内容(1)颗粒及颗粒床层特性(2)悬浮液的沉降分离设备本章一般了解的内容(1)离心机的类型与应用场合(2)固体流态化现象(包括气力输送)3.本章学习中应注意的问题本章从理论上讨论颗粒与流体间相对运动问题,其中包括颗粒相对于流体的运动(沉降和流态化)、流体通过颗粒床层的流动(过滤),并借此实现非均相物系分离、固体流态化技术及固体颗粒的气力输送等工业过程。
学习过程中要能够将流体力学的基本原理用于处理绕流和流体通过颗粒床层流动等复杂工程问题,即注意学习对复杂的工程问题进行简化处理的思路和方法。
4.本章教学的学时数分配知识点3-1 授课学时数1 自学学时数2知识点3-2 授课学时数3 自学学时数6知识点3-3 授课学时数3 自学学时数6知识点3-4 授课学时数1 自学学时数2参考书籍(1)柴诚敬,张国亮.化工流体流动与传热.北京:化学工业出版社,2000(2)陈维枢主编.传递过程与单元操作.上册.浙江:浙江大学出版社,1993(3)陈敏恒等,化工原理(上册).北京:化学工业出版社,1999(4)机械工程手册编辑委员会.机械工程手册(第二版),通用设备卷.北京:机械工业出版社,1997(5)大连理工大学化工原理教研室.化工原理,上册.辽宁:大连理工大学出版社,1993 (6)时钧等.化学工程手册,上卷.2版.北京:化学工业出版社,1996(7)McCabe W. L. and Smith. J. C. Unit Operations of Chemical Engineering. 5th. ed. New York: McGraw Hill,1993(8)Foust A. S. and Wenzel. L.3.1本章概述一.混合物的分类自然界的大多数物质为混合物。
混合物分为两类:1.均相混合物若物系内各处组成均匀且不存在相界面,则称为均相混合物。
如溶液及混合气体属于此类。
均相混合物组分的分离采用传质分离方法。
2.非均相混合物由具有不同物理性质(如尺寸、密度差别)的分散物质(分散相)和连续介质(连续相)所组成的物系称为非均相物系或非均相混合物。
显然,非均相物系中存在相界面,且界面两侧物料的性质不同。
根据连续相状态的不同,非均相混合物又可分为两种类型:(1)气态非均相混合物,如含尘气体、含雾气体等;(2)液态非均相混合物,如悬浮液、乳浊液、泡沫液等。
对于非均相混合物,工业上一般采用机械分离方法将两相进行分离,即造成分散相和连续相之间的相对运动。
二.非均相混合物分离方法的分类根据相态和分散物质尺寸的大小,非均相混合物的分离方法如下表所示。
三.非均相混合物分离的目的(1)收集分散物质。
例如收取从气流干燥器或喷雾干燥器出来的气体以及从结晶器出来的晶浆中带有的固体颗粒,这些悬浮的颗粒作为产品必须回收;又如回收从催化反应器出来的气体中夹带的催化剂颗粒以循环使用。
再如某些金属冶炼过程中,有大量的金属化合物或冷凝的金属烟尘悬浮在烟道气中,收集这些烟尘不仅能提高该种金属的收率,而且是提炼其它金属的重要途径。
(2)净化分散介质。
某些催化反应,原料气中夹带有杂志会影响触媒的效能,必须在气体进反应器之前清除催化反应原料气中的杂质,以保证触媒的活性。
(3)环境保护与安全生产。
为了保护人类生态环境,消除工业污染,要求对排放的废气、废液中的有害物质加以处理,使其达到规定的排放标准;很多含碳物质与金属细粉及空气混合会形成爆炸物,必须除去这些物质以消除爆炸的隐患。
机械分离操作涉及到颗粒相对于流体以及流体相对于颗粒床层的流动。
同时,在许多单元操作和化学反应中经常采用的流态化技术同样涉及两相间的流动,它们都遵循流体力学的基本规律,因此本章还介绍流态化技术的基本概念。
3.2 颗粒及颗粒床层的特性颗粒与流体之间的相对运动特性与颗粒本身的特性密切相关,因而首先介绍颗粒的特性。
一. 单一颗粒的特性表述颗粒特性的主要参数为颗粒的形状、大小(体积)及表面积。
(一)球形颗粒不言而喻,球形颗粒的形状为球形,其尺寸由直径d来确定,其它有关参数均可表示为直径d的函数,诸如体积(3-1)表面积(3-2)比表面积(单位颗粒体积具有的表面积)(3-3)式中d――球形颗粒的直径,m;S――球形颗粒的表面积,m2;V――球形颗粒的体积,m3;a――颗粒的比表面积,m2/m3。
(二)非球形颗粒非球形颗粒必须有两个参数才能确定其特性,即球形度和当量直径。
1.球形度φS颗粒的球形度又称形状系数,它表示颗粒形状与球形的差异,定义为与该颗粒体积相等的球体的表面积除以颗粒的表面积,即φS=(3-4)式中φS――颗粒的球形度或形状系数,无因次;S――与该颗粒体积相等地球体的表面积,m2;S P――颗粒的表面积,m2。
由于同体积不同形状的颗粒中,球形颗粒的表面积最小,因此对非球形颗粒,总有φS ﹤1,颗粒的形状越接近球形,φS越接近1;对球形颗粒,φS=1。
2.颗粒的当量直径工程中,经常将非球形颗粒以某种“当量”的球形颗粒来代替,以使非球形颗粒的某种特性与球形颗粒等效,这一球粒的直径为当量直径。
当量直径表示非球形颗粒的大小。
根据不同方面的等效性,通常有两种表示方法;(1)等体积当量直径颗粒的等体积当量直径为与该颗粒体积相等的直径,即d=(3-5)e式中d e――颗粒的等体积当量直径,m;V P――颗粒的体积,m3。
(2)等比表面积当量直径即与非球形颗粒比表面积相等的直径为该颗粒的等比表面积当量直径。
根据此定义并结合式(3-3)得(3-6)式中――颗粒的等比表面积当量直径,m;依据式(3-5)和式(3-6)可以得出颗粒的等体积当量直径和等比表面积当量直径之间的关系:φs d e (3-7)所以说,非球形颗粒的等比表面积当量直径一定小于其等体积当量直径。
用上述的形状系数及当量直径便可表述非球形颗粒的特性,即(3-1a)(3-2a)(3-3a)工业中遇到的颗粒群可分为两类:若颗粒群是由大小不同的粒子组成的集合体,称为非均一性粒子或多分散性粒子;而将具有同一粒径的颗粒群称为单一性或单分散性粒子。
显然,多分散性粒子才需讨论其粒度分布和平均参数。
1.颗粒群的粒度分布不同粒径范围内所含粒子的个数或质量称为粒度分布。
颗粒粒度的测量方法有筛分法、显微镜法、沉降法、电感应法、激光衍射、动态光散射法等,这里介绍筛分法。
筛分是用单层或多层筛面将松散的物料按颗粒粒度分成两个或多个不同粒级产品的过程。
它是机械分离方法分离固-固混合物的操作。
筛分时,筛面上有筛孔,尺寸小于筛孔尺寸的物料通过筛孔,称为筛下产品,其质量称为筛过量;尺寸大于筛孔尺寸的物料被截留在筛面上,称为筛上产品,其质量称为筛余量。
若用n层筛面,可得n+1种产品。
筛分分析是在一套标准筛中进行的,标准筛的筛网为金属丝网,各国标准筛的规格不尽相同,常用的泰勒制是以每英寸边长的孔数为筛号,称为目。
例如100目的筛子表示每英寸筛网上有100个筛孔。
表3-2是泰勒标准筛的目数和对应孔径的节录。
用标准筛测粒度分布时,将一套标准筛按筛孔上大下小的顺序叠在一起,若从上向下筛子的序号分别为1、2...i-1及i ,相应筛孔的直径分别为d 1>、d 2...d i-1及d i >。
将称重后的颗粒样品放在最上面的筛子上,整套筛子用振荡器振动过筛,不同粒度的颗粒分别被截留于各号筛网面上。
第i 号筛网上的颗粒的尺寸应在d i-1>和d i >之间,分别称取各号筛网上的颗粒筛余量,即可得到样品的粒度分布数据。
目前各种筛制正向国际标准组织ISO 筛统一。
表3-2 泰勒标准筛2.粒群的平均直径停留在第i 层筛网上的颗粒的平均直径d pi >值可按d i-1>和d i >的算术平均值计算,即(3-8)根据各号筛网上截留的颗粒质量,可以计算出直径为d pi >的颗粒占全部样品的质量分率x i >,再根据实测的各层筛网上的颗粒质量分率,按下式可计算出颗粒群的平均直径为(3-9)式中――颗粒群的平均直径,m ; ――粒径段内颗粒的质量分率;>――被截留在第i 层筛网上的颗粒的平均直径,m 。
3.颗粒的密度单位体积内粒子的质量称为密度,其单位为kg/m 3。
若粒子的体积不包括颗粒之间空隙,则称为粒子的真密度,用ρS >表示;若粒子所占体积包括颗粒之间空隙,则称为堆积密度或表观密度,用ρb >表示。
设计颗粒贮存设备时,应以堆积密度为准。
三.颗粒床层的特性大量固体颗粒堆积在一起便形成颗粒床层。
静止的颗粒床层又称为固定床。
对流体通过床层流动产生重要影响的床层特性有如下几项:(一)床层的空隙率床层中颗粒之间的空隙体积与整个床层体积之比称为空隙率(或称空隙度),以ε表示,即式中ε-床层的空隙率,m3/m3;空隙率的大小与颗粒形状、粒度分布、颗粒直径与床层直径的比值、床层的填充方式等因素有关。
对颗粒形状和直径均一的非球形颗粒床层,其空隙率主要取决于颗粒的球形度和床层的填充方法。
非球形颗粒的球形度越小,则床层的空隙率越大。
由大小不均匀的颗粒所填充成的床层,小颗粒可以嵌入大颗粒之间的空隙中,因此床层空隙率比均匀颗粒填充的床层小。
粒度分布越不均匀,床层的空隙率就越小;颗粒表面愈光滑,床层的空隙率亦愈小。
因此,采用大小均匀的颗粒是提高固定床空隙率的一个方法。
空隙率在床层同一截面上的分布是不均匀的,在容器壁面附近,空隙率较大;而在床层中心处,空隙率较小。
器壁对空隙率的这种影响称为壁效应。
壁效应使得流体通过床层的速度不均匀,流动阻力较小的近壁处流速较床层内部大。
改善壁效应的方法通常是限制床层直径与颗粒直径之比不得小于某极限值。
若床层的直径比颗粒的直径大得多,则壁效应可忽略。
床层的空隙率可通过实验测定。
一般非均匀、非球形颗粒的乱堆床层的空隙率大致在0.47~0.7之间。
均匀的球体最松排列时的空隙率为0.48,最紧密排列时的空隙率为0.26。
(二)床层的自由截面积床层截面上未被颗粒占据的流体可以自由通过的面积,称为床层的自由截面积。
小颗粒乱堆床层可认为是各向同性的。
各向同性床层的重要特性之一是其自由截面积与床层截面积之比在数值上与床层空隙率相等。
同床层空隙率一样,由于壁效应的影响,壁面附近的自由截面积较大。
