2013年陕西省中考数学试题和答案
2013陕西中考数学试题及答案
2013陕西中考数学试题及答案2013年陕西省中考数学试题一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. -1B. 0C. 1D. 22. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是多少？A. 5B. 6C. 7D. 83. 以下哪个选项是二次方程 \( ax^2 + bx + c = 0 \) 的判别式？A. \( b^2 - 4ac \)B. \( b^2 + 4ac \)C. \( 4a^2 + b^2 \)D. \( a^2 - b^2 \)4. 一个圆的半径是5，那么它的面积是多少？A. 25B. 50C. 75D. 1005. 下列哪个是正比例函数？A. \( y = 3x^2 \)B. \( y = 2x \)C. \( y = x^2 \)D. \( y = x + 1 \)6. 一个数的平方根是4，这个数是多少？A. 16B. -16C. 8D. -87. 以下哪个选项是反比例函数？A. \( y = \frac{1}{x} \)B. \( y = x \)C. \( y = x^2 \)D. \( y = \frac{1}{x^2} \)8. 一个长方体的长、宽、高分别是10cm、8cm和6cm，那么它的体积是多少？A. 480B. 560C. 640D. 7209. 一个数的立方根是2，这个数是多少？A. 6B. 8C. 2D. 410. 以下哪个选项是指数函数？A. \( y = 2^x \)B. \( y = x^2 \)C. \( y = \log_2 x \)D. \( y = \sqrt{x} \)二、填空题（每题2分，共20分）11. 一个数的绝对值是5，这个数可以是________。
12. 一个数的相反数是-3，这个数是________。
13. 一个数的倒数是\( \frac{2}{3} \)，这个数是________。
2013陕西西安中考数学(含解析)
15．如果一个正比例函数的图象与反比例函数 y
( x2 x1 )( y2 y1 ) 的值为__________．
6 的图象交于 A( x1 , y1 ) 、 B( x2 , y2 ) 两点，那么 x
5 / 13
23． （本题满分 8 分） 如图，直线 l 与⊙ O 相切于点 D ．过圆心 O 作 EF∥l 交⊙ O 于 E 、 F 两点，点 A 是⊙ O 上一 点，连接 AE 、 AF ．并分别延长交直线 l 于 B 、 C 两点． （ 1 ）求证： ABC ACB 90 ； （ 2 ）当⊙ O 的半径 R 5 ， BD 12 时，求 tan ACB 的值．
3 8 3 5 AM 等于（ MD
） ．
2 3 4 5
B． D．
10．已知两点 A(5 , y1 ) 、 B(3 , y2 ) 均在抛物线 y ax2 bx c （ a 0 ）上，点 C ( x0 , y0 ) 是该抛物 线的顶点，若 y1 y2≥y0 ，则 x0 的取值范围是（ A． x0 5 C． 5 x0 1 B． x0 1 D． 2 x0 3 ） ．
） ．
1 x 0 4．不等式组 2 的解集为（ 1 2 x 3
） ．
1 2 1 2
A． x
1 2
B． x 1
C． 1 x
D． x
5． 我省某市五月份第二周连续七天的空气质量指数分别为：111 ，96 ，47 ，68 ，70 ，77 ，105 ． 则 这七天空气质量指数的平均数是（ A． 71.8 B． 77 ） ． C． 82 D． 95.7 ） ．
陕西省2013年中考数学试题(WORD版含答案)
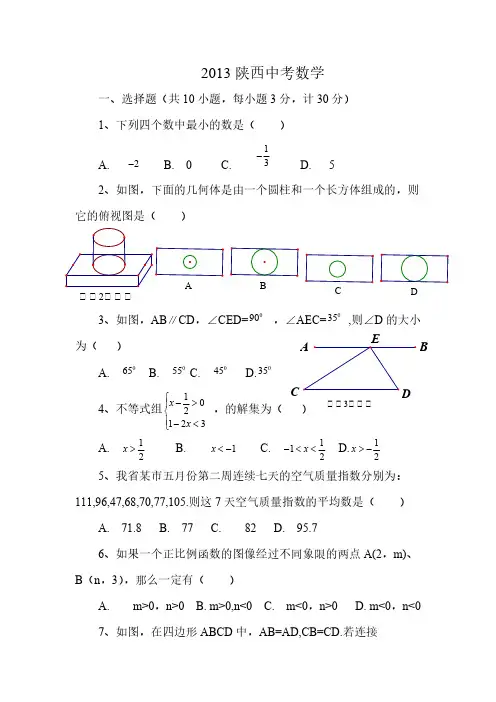
陕西省2013年中考数学试题第Ⅰ卷（选择题 共30分）A 卷一、选择题（共10小题，每小题3分，计30分.每小题只有一个选项是符合题意的） 1.下列四个数中最小的数是（ ） A .－2B.0C.31-D.5 2.如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是（ ）3.如图，AB ∥CD ，∠CED=90°，∠AEC=35°，则∠D 的大小为（ ） A.65° B.55° C.45° D.35°4.不等式组⎪⎩⎪⎨⎧--321021x x 的解集为（ ） A. x ＞21B. x ＜－1C. －＜x ＜21D. x ＞－215.我省某市五月份第二周连续七天的空气质量指数分别为：111，96，47，68，70，77，105.则这七天空气质量指数的平均数是（ ） A.71.8 B.77 C.82 D.95.7 6.如果一个正比例函数的图象经过不同．．象限的两点A （2，m ）、B （n ，3），那么一定有（ ） A. m ＞0，n ＞0 B. m ＞0，n ＜0 C. m ＜0，n ＞0 D. m ＜0，n ＜0 7.如图，在四边形ABCD 中，AB=AD ，CD=CB.若连接AC 、BD 相交于点O ，则图中全等三角形共有（ ） A.1对 B.2对 C.3对 D.4对8.x 与y 的对应值，可得P 的值为（ ）A.1 B .－1 C.3 D.－39.如图，在矩形ABCD 中，AD=2AB，点M 、N 分别在边AD、BC 上， 连接BM、DN.若四边形MBND 是菱形，则MDAM等于（） A.83 B.32 C.53 D.54 EDB CA （第2题图） （第3题图）A B C D O DBCA（第7题图） NM DBCA （第9题图）10.已知两点A （－5，1y ）、B （3，2y ）均在抛物线()02≠++=a c bx ax y 上，点C （0x ，0y ）是该抛物线的顶点，若1y ＞2y ≥0y ，则0x 的取值范围是（ ） A. 0x ＞－5 B. 0x ＞－1 C .－5＜0x ＜－1 D .－2＜0x ＜3 B 卷第Ⅱ卷（非选择题 共90分）二、填空题（共6小题，每小题3分，共18分） 11.计算：()()03132-+-= .12.一元二次方程032=-x x 的根是 .13.请从经以下两个小题中任选一个．．．．作答，若多选，则按所选的第一题计分. A.在平面直角坐标系中，线段AB 的两个端点的坐标分别为A （－2，1）、B （1，3，）将线段AB 经过平移后得到线段A ′B ′.若点A 的对应点为A ′（3，2），则点B 的对应点B ′的坐标是 . B.比较8cos31.（填“＞”、“=”若“＜”）14.如图，四边形ABCD 的对角线AC 、BD 相交于点O ，且BD 平分AC.若BD=8，AC=6，∠BOC=120°，则四边形ABCD 的面积为 .（结果保留根号） 15.如果一个正比例函数的图象与反比例函数xy 6=的图象交于A （1x ，1y ）、B （2x ，2y ）两点，那么（2x －1x ）（2y －1y ）的值为 .16.如图，AB 是⊙O 的一条弦，点C 是⊙O 上一动点，且∠ACB=30°，点E 、F 分别是AC 、BC 的中点，直线EF 与⊙O 交于G 、H 两点.若⊙O 的半径为7，则GE+FH 的最大值为 .三、解答题（共9小题，计72分.解答应写出过程） 17.（本题满分5分）解分式方程：12422=-+-x xx .OD B C AC （第14题图） （第16题图）18.（本题满分6分）如图，∠AOB=90°，OA=OB ，直线L 经过点O ，分别过A 、B 两点作AC ⊥L 交L 于点C ，BD ⊥L 交L 于点D. 求证：AC=OD19.（本题满分7分）我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度（程度分为：“A —了解很多”，B —“了解较多”，“C —了解较少”，“D —不了解”），对本市一所中学的学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅统计图.根据以上信息，解答下列问题：（1） 本次抽样调查了多少名学生？ （2） 补全两幅统计图；（3） 若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？lO D B C A（第18题图） 45%30%D B CA 了解程度DBC A （第19题图） 被调查学生对“节约教育”内容了解程度的统计图一天晚上，李明和张龙利用灯光下的影子长来测量一路灯D 的高度.如图，当李明走到点A 处时，张龙测得李明直立向高AM 与其影子长AE 正好相等；接着李明沿AC 方向继续向前走，走到点B 处时，李明直立时身高BN 的影子恰好是线段AB ，并测得AB=1.25m.已知李明直立时的身高为1.75m ，求路灯的高度CD 的长.（精确到0.1m ）21.（本题满分8分）“五一节”期间，申老师一家自架游去了离家170千米的某地.下面是他们离家的距离y （千米）与汽车行驶时间x （小时）之间的函数图象.（1） 求他们出发半小时时，离家多少千米？ （2） 求出AB 段图象的函数表达式；（3） 他们出发2小时时，离目的地还有多少千米？EAx/小时2.51.5O （第20题图） （第21题图）甲、乙两人用手指玩游戏，规则如下：ⅰ）每次游戏时，两人同时随机地各伸出一根手指：ⅱ）两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指，小拇指只胜大拇指，否则不分胜负.依据上述规则，当甲、乙两人同时随机地各伸出一根手指时. （1）求甲伸出小拇指取胜的概率； （2）求乙取胜的概率.23.（本题满分8分）如图，直线L 与⊙O 相切于点D.过圆心O 作EF ∥L 交⊙O 于E 、F 两点，点A 是⊙O 上一点，连接AE 、AF.并分别延长交直线L 于 B 、C 两点. （1） 求证：∠ABC+∠ACB=90°；（2） 当⊙O 的半径R=5，BD=12时，求tan ∠ABC 的值.24.（本题满分10分）在平面直角坐标系中，一个二次函数的图象经过A （1，0）、B （3，0）两点. （1） 写出这个二次函数图象的对称轴；（2） 设这个二次函数图象的顶点为D ，与y 轴交于点C ，它的对称轴与x 轴交于点E ，连接AC 、DE 和DB.当⊿AOC 与⊿DEB 相似时，求这个函数的表达式.lD（第23题图）（第24题图）问题探究（1） 请在图①中作出两条直线，使它们将圆面四等分；（2） 如图②，M 是正方形ABCD 内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M ），使它们将正方形ABCD 的面积四等分，并说明理由.问题解决（3）如图③，在四边形ABCD 中，AB ∥CD ，AB+CD=BC ，点P 是AD 的中点.如果AB=a ，CD=b ，且b ＞a ，那么在边BC 上是否存在一点Q ，使PQ 所在直线将四边形ABCD 的面积分成相等的两部分？若存在，求出BQ 的长；若不存在，说明理由.D BDB （第25题图） ① ② ③参考答案1.A；2.D；3.B；4.A；5.C；6.D；7.C；8.A；9.C；10.B11.-7；12.0，3；13.A：（6，4）B：＞；14.123；15.24；16.10.5；。
【VIP专享】2013陕西中考数学试题及答案word版
9、如图，在矩形 ABCD 中，
AD=2AB，点 M,N 分别在 AD、BC
上，连接 BM、DN.若四边形பைடு நூலகம்MBDN
是菱形，则 AM 等于（ ）
MD
A. 3 B. 2
8
3
2
3
C. 3 D. 4
5
10、已知两点 A 5，y1 B 3, y2 均在抛物线 y ax2 bx c(a 0)
上，点 C x0, y0 是该抛物线的顶点.若 y1 y2 y0 ，则 x0 的取值范围
为（ ）
A. 650 B. 550 C. 450 D. 350
4、不等式组
A. x 1
2
x
1 2
1 2x 3
B.
0
，的解集为（
x 1
5、我省某市五月份第二周连续七天的空气质量指数分别为：
111,96,47,68,70,77,105.则这 7 天空气质量指数的平均数是（ ）
A. 71.8 B. 77 C. 82 D. 95.7
B
3
D. 5
A
C
）
C. 1 x 1 D. x 1
2
C
图 图 3图 图 图
E
2
D
D
B
AC、BD 相交于点 O，则图中全等三角形共有（ ）
A. 1 对 B. 2 对 C. 3 对 D. 4 对 B
8、根据下表中一次函数的自变量 x 与函数 y 的对应值，可得 p 的值为（ ）
x
y
A. 1 B. 1 C. 3 D. 3
2013 陕西中考数学
一、选择题（共 10 小题，每小题 3 分，计 30 分）
1、下列四个数中最小的数是（ ）
2013年陕西省中考数学试卷-答案
3AO︒=sin602113+2BD AE BD CF=⨯⨯22为O的直径时，∵O的半径为14.连接OA，OBACB∠=260∠=ACB30=，∴OA OB故答案为11.5为O的直径时，【考点】垂径定理，三角形中位线定理，圆周角定理x=-【答案】3补全统计图，如图所示：【提示】（1）先运用待定系数法求出OA 的解析式，再将0.5x =代入，求出y 的值即可；（2）设AB 段图象的函数表达式为+y k x b ='，将A 、B 两点的坐标代入，运用待定系数法即可求解；【解析】解；（1）设A ，B ，C ，D ，E 分别表示大拇指、食指、中指、无名指、小拇指，列表如下：由表格可知，共有25种等可能的结果，甲伸出小拇指取胜只有一种可能，故1()25P=甲伸出小拇指获胜；（2）解：连接OD，则OD BD⊥，过E作EH BC⊥于H，11 / 11【提示】（1）画出互相垂直的两直径即可；（2）连接AC ，BD 交于O ，作直线OM ，分别交AD 于P ，交BC 于Q ，过O 作EF OM ⊥交DC 于F ，交AB 于E ，则直线EF 、OM 将正方形的面积四等份，根据三角形的面积公式和正方形的性质求出即可； （3）当BQ CD b ==时，PQ 将四边形ABCD 的面积二等份，连接BP 并延长交CD 的延长线于点E ， 证ABP DEP △≌△求出BP EP =，连接CP ，求出BPC EPC S S =△△，作PF CD ⊥，PG BC ⊥，由++BC AB CD DE CD CE ===，求出++ABP BPC CQP CPE DEP CQP S S SS S S -=-△△△△△，即可得出ABQP CDPQ S S =四边形四边形即可．【考点】四边形综合题．。
最新2013陕西省中考数学试题及答案优秀名师资料
2013陕西省中考数学试题及答案陕西省2013年中考数学试题第?卷(选择题共30分)A卷一、选择题(共10小题，每小题3分，计30分.每小题只有一个选项是符合题意的) 1.下列四个数中最小的数是( )1,A.,2B.0C.D.5 32.如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是( )A B C D (第2题图)3.如图，AB?CD，?CED=90?，?AEC=35?，则?D的大小为( ) A.65? B.55? C.45?D.35?,1Ex,,0,BA2,4.不等式组的解集为( ),x1,2,3,CD111(第3题图)A. xxxx ,B. ,,1C. ,,,D. ,, 2225.我省某市五月份第二周连续七天的空气质量指数分别为:111，96，47，68，70，77，105.则这七天空气质量指数的平均数是( )A.71.8B.77C.82D.95.7 6.如果一个正比例函数的图象经过不同象限的两点A(2，m)、B(n，3)，那么一定有( ) ((A. m,0，n,0B. m,0，n,0C. m,0，n,0D. m,0，n,0 7.如图，在四边形ABCD 中，AB=AD，CD=CB.若连接AC、BD相交于点O，则图中全等三角形共有( ) A.1对B.2对C.3对D.4对x8.根据下表中一次函数的自变量与的对应值，可得P的值为( ) yx 0 1 ,2y3 P 0 AA.1 B.,1 C.3 D.,3 AMD9.如图，在矩形ABCD中，AD=2AB，点M、N 分别在边AD、BC上，AMOBD连接BM、DN.若四边形MBND是菱形，则等于( ) CBNMDC2334(第7题图) (第9题图) A. B. C. D. 83552，，10.已知两点A(,5，)、B(3，)均在抛物线上，点C(，)是该y,ax，bx，ca,0yyyx1200抛物线的顶点，若,?，则的取值范围是( ) yyyx1200A. ,,5B. ,,1C.,5,,,1D.,2,,3 xxxx0000B卷第?卷(非选择题共90分)二、填空题(共6小题，每小题3分，共18分)03，，，，11.计算:= . ,2，3,1212.一元二次方程的根是 . x,3x,013.请从经以下两个小题中任选一个作答，若多选，则按所选的第一题计分. ((((A.在平面直角坐标系中，线段AB的两个端点的坐标分别为A(,2，1)、B(1，3，)将线段AB经过平移后得到线段A′B′.若点A的对应点为A′(3，2)，则点B 的对应点B′的坐标是 .B.比较8cos31? .(填“,”、“=”若“,”) 3514.如图，四边形ABCD的对角线AC、BD相交于点O，且BD平分AC.若BD=8，AC=6，?BOC=120?，则四边形ABCD的面积为 .(结果保留根号)6y15.如果一个正比例函数的图象与反比例函数的图象交于A(，)、B(，)两点，那么yyxx,1212x(,)(,)的值为 . yyxx212116.如图，AB是?O的一条弦，点C是?O上一动点，且?ACB=30?，点E、F分别是AC、BC的中点，直线EF与?O交于G、H两点.若?O的半径为7，则GE+FH的最大值为 .AD CO OF HGBECBA(第14题图) (第16题图)三、解答题(共9小题，计72分.解答应写出过程)17.(本题满分5分)x2，,1解分式方程:. 2xx,2,418.(本题满分6分)如图，?AOB=90?，OA=OB，直线L经过点O，分别过A、B两点作AC?L交L于点C，BD?L交L于点D. 求证:AC=ODlBDACO(第18题图)19.(本题满分7分)我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”，B—“了解较多”，“C—了解较少”，“D—不了解”)，对本市一所中学的学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅统计图.根据以上信息，解答下列问题:(1) 本次抽样调查了多少名学生,(2) 补全两幅统计图;(3) 若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名,被调查学生对“节约教育”内容了解程度的统计图人数6050 3640 C 3024 D45%20B 610A30% 0 了解程度DABC(第19题图)20.(本题满分8分)一天晚上，李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图，当李明走到点A处时，张龙测得李明直立向高AM与其影子长AE正好相等;接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m.已知李明直立时的身高为1.75m，求路灯的高度CD的长.(精确到0.1m)DNMEBCA(第20题图)21.(本题满分8分)“五一节”期间，申老师一家自架游去了离家170千米的某地.下面是他们离家的距离(千米)与汽车行y驶时间(小时)之间的函数图象. x(1) 求他们出发半小时时，离家多少千米,(2) 求出AB段图象的函数表达式;(3) 他们出发2小时时，离目的地还有多少千米,y/千米 B170A90O1.52.5x/小时(第21题图)22.(本题满分8分)甲、乙两人用手指玩游戏，规则如下:?)每次游戏时，两人同时随机地各伸出一根手指:?)两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指，小拇指只胜大拇指，否则不分胜负.依据上述规则，当甲、乙两人同时随机地各伸出一根手指时.(1)求甲伸出小拇指取胜的概率;(2)求乙取胜的概率.23.(本题满分8分)如图，直线L与?O相切于点D.过圆心O作EF?L交?O于E、F两点，点A是?O 上一点，连接AE、AF.并分别延长交直线L于 B、C两点.(1) 求证:?ABC+?ACB=90?;(2) 当?O的半径R=5，BD=12时，求tan?ABC的值.AEF Ol CBD(第23题图)24.(本题满分10分)在平面直角坐标系中，一个二次函数的图象经过A(1，0)、B(3，0)两点. (1) 写出这个二次函数图象的对称轴;(2) 设这个二次函数图象的顶点为D，与轴交于点C，它的对称轴与x轴交于点E，连接AC、DE和DB.y当?AOC与?DEB相似时，求这个函数的表达式.y4321x–4–3–2–11234O–1–2–3–4(第24题图)25.(本题满分12分)问题探究(1) 请在图?中作出两条直线，使它们将圆面四等分;(2) 如图?，M是正方形ABCD内一定点，请在图?中作出两条直线(要求其中一条直线必须过点M)，使它们将正方形ABCD的面积四等分，并说明理由.问题解决abba(3)如图?，在四边形ABCD中，AB?CD，AB+CD=BC，点P是AD的中点.如果AB=，CD=，且,，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分,若存在，求出BQ的长;若不存在，说明理由.AD MDP AB CBC?? ?(第25题图)参考答案1. A;2.D;3.B;4.A;5.C;6.D;7.C;8.A;9.C;10.B 11.-7;12.0，3;13.A:(6，4)B:,;14.12;15.24;16.10.5; 3。
2013年陕西省中考数学试卷
2013年陕西省中考数学试卷一、选择题(共10小题，每小题3分，共30分，每小题只有一个选项最符合题意的)1.(3分)下列四个数中最小的数是()A.-2 B.01C.-3 D.52.(3分)如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是()A. B.C. D.3.(3分)如图，AB ⎳CD ，∠CED =90°，∠AEC =35°，则∠D 的大小为()A ．65°B ．55°C ．45°D ．35°1-2>1-4.(3分)不等式组x 2< x 0的解集为(3)1A.x >2 B.x <-11C.-1<x <21D.x >-25.(3分)我省某市五月份第二周连续七天的空气质量指数分别为：111、96、47、68、70、77、105，则这七天空气质量指数的平均数是()A.71.8 B.77 C.82 D.95.76.(3分)如果一个正比例函数的图象经过不同象限的两点A (2,m )，B (n ,3)，那么一定有()A.m >0，n >0 B.m >0，n <0 C.m <0，n >0 D.m <0，n <07.(3分)如图，在四边形ABCD 中，AB =AD ，CB =CD ，若连接AC 、BD 相交于点O ，则图中全等三角形共有()A.1对B.2对C.3对D.4对8.(3分)根据表中一次函数的自变量x与函数y的对应值，可得p的值为()x201-y3p0C.33A.11 D.-B.-9.(3分)如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则AMMD等于()A.38B.23C.35D.4510.(3分)已知两点A(-5,y1)，B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上，点C(x0，y0)是该抛物线的顶点．若y1>y2≥y0，则x0的取值范围是()A.x0>-5B.x0>-1C.-5<x0<-1D.-2<x0<3二、填空题(共6小题，计18分)11.(3分)计算：(-2)3+(3-1)0= ．12.(3分)一元二次方程x2-3x=0的解是．13.(3分)请从以下两个小题中任选一个作答，若多选，则按所选的第一题计分．A、在平面直角坐标系中，线段AB的两个端点的坐标分别为A(-2,1)、B(1,3)，将线段AB通过平移后得到线段A′B′，若点A的对应点为A′(3,2)，则点B的对应点B′的坐标是．B、比较大小：8cos31°35(填“>”，“=”或“<”)14.(3分)如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，．)∠BOC=120°，则四边形ABCD的面积为(结果保留根号15.(3分)如果一个正比例函数的图象与反比例函数y=x6的图象交于A(x1，y1)，B(x2，y2)两点，那么(x2-x1)(y2-y1)的值为．16.(3分)如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为．三、解答题(共9小题，计72分，解答应写出过程)217.(5分)解分式方程：x 2x -4+x -2=1．18.(6分)如图，∠AOB =90°，OA =OB ，直线l 经过点O ，分别过A 、B 两点作AC ⊥l 交l 于点C ，BD ⊥l 交l 于点D ．求证：AC =OD ．19.(7分)我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”．某市教育局督导组为了调查学生对“节约教育”内容的了解程度(程度分为：“A --了解很多”、“B --了解较多”，“C --了解较少”，“D --不了解”)，对本市一所中学的学生进行了抽样调查．我们将这次调查的结果绘制了以下两幅统计图．根据以上信息，解答下列问题：(1)本次抽样调查了多少名学生？(2)补全两幅统计图；(3)若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？20.(8分)一天晚上，李明和张龙利用灯光下的影子长来测量一路灯CD的高度．如图，当李明走到点A处时，张龙测得李明直立时身高AM与影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m，已知李明直立时的身高为1.75m，求路灯的高CD的长．(结果精确到0.1m)．21.(8分)“五一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象．(1)求他们出发半小时时，离家多少千米？(2)求出AB段图象的函数表达式；(3)他们出发2小时时，离目的地还有多少千米？22.(8分)甲、乙两人用手指玩游戏，规则如下：①每次游戏时，两人同时随机地各伸出一根手指；②两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指、小拇指只胜大拇指，否则不分胜负．依据上述规则，当甲、乙两人同时随机地各伸出一根手指时，(1)求甲伸出小拇指取胜的概率；(2)求乙取胜的概率．23.(8分)如图，直线l与⊙O相切于点D，过圆心O作EF⎳l交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF，并分别延长交直线l于B、C两点．(1)求证：∠ABC+∠ACB=90°；(2)当⊙O的半径R=5，BD=12时，求tan∠ACB的值．24.(10分)在平面直角坐标系中，一个二次函数的图象经过点A(1,0)、B(3,0)两点．(1)写出这个二次函数图象的对称轴；(2)设这个二次函数图象的顶点为D，与y轴交于点C，它的对称轴与x轴交于点E，连接AC、DE和DB，当ΔAOC与ΔDEB相似时，求这个二次函数的表达式．[提示：如果一个二次函数的图象与x轴的交点为A(x1，0)、B(x2，0)，那么它的表达式可表示为y=a(x -x1)(x-x2)]．25.(12分)问题探究：(1)请在图①中作出两条直线，使它们将圆面四等分；(2)如图②，M是正方形ABCD内一定点，请在图②中作出两条直线(要求其中一条直线必须过点M)使它们将正方形ABCD的面积四等分，并说明理由．问题解决：(3)如图③，在四边形ABCD中，AB⎳CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b>a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．。
2013年陕西省中考数学试卷(含解析)
2013年陕西省中考数学试卷一、选择题1、下列四个数中最小的数是（ ）A ．-2B ．0C ．-D ．52、如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是（ ）A ．B ．C ．D ．3、如图，AB∥CD，∠CED=90°，∠AEC=35°，则∠D 的大小为（ ）A ．65°B ．55°C ．45°D ．35°4、不等式组的解集为（ ） A ．x ＞ B ．x ＜-1 C ．-1＜x ＜ D ．x ＞-5、我省某市五月份第二周连续七天的空气质量指数分别为：111、96、47、68、70、77、105，则这七天空气质量指数的平均数是（ ）A ．71.8B ．77C ．82D ．95.76、如果一个正比例函数的图象经过不同象限的两点A （2，m ），B （n ，3），那么一定有（ ）A．m＞0，n＞0B．m＞0，n＜0C．m＜0，n＞0D．m＜0，n＜0 7、如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（）A．1对B．2对C．3对D．4对8、根据表中一次函数的自变量x与函数y的对应值，可得p的值为（）A．1B．-1C．3D．-39、如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则等于（）A．B．C．D．10、已知两点A（-5，y1），B（3，y2）均在抛物线y=ax2+bx+c（a≠0）上，点C（x0，y）是该抛物线的顶点．若y1＞y2≥y，则x的取值范围是（）A．x0＞-5B．x＞-1C．-5＜x＜-1D．-2＜x＜3二、填空题11、计算：（-2）3+（-1）0= __________ ．12、一元二次方程x2-3x=0的根是__________ ．13、请从以下两个小题中任选一个作答，若多选，则按所选的第一题计分．A、在平面直角坐标系中，线段AB的两个端点的坐标分别为A（-2，1）、B（1，3），将线段AB通过平移后得到线段A′B′，若点A的对应点为A′（3，2），则点B的对应点B′的坐标是 __________ ．B、比较大小：8cos31°__________（填“＞”，“=”或“＜”）14、如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，∠BOC=120°，则四边形ABCD的面积为 __________ ．（结果保留根号）15、如果一个正比例函数的图象与反比例函数y=的图象交于A（x1，y1），B（x2，y2）两点，那么（x2-x1）（y2-y1）的值为 __________ ．16、如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH的最大值为__________ ．三、解答题17、解分式方程：+=1．18、如图，∠AOB=90°，OA=OB，直线l经过点O，分别过A、B两点作AC⊥l交l于点C，BD⊥l交l于点D．求证：AC=OD．19、我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”．某市教育局督导组为了调查学生对“节约教育”内容的了解程度（程度分为：“A--了解很多”、“B--了解较多”，“C--了解较少”，“D--不了解”），对本市一所中学的学生进行了抽样调查．我们将这次调查的结果绘制了以下两幅统计图．根据以上信息，解答下列问题：（1）本次抽样调查了多少名学生？（2）补全两幅统计图；（3）若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？20、一天晚上，李明和张龙利用灯光下的影子长来测量一路灯CD的高度．如图，当李明走到点A处时，张龙测得李明直立时身高AM与影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB=1.25m，已知李明直立时的身高为1.75m，求路灯的高CD的长．（结果精确到0.1m）．21、“五一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．（1）求他们出发半小时时，离家多少千米？（2）求出AB段图象的函数表达式；（3）他们出发2小时时，离目的地还有多少千米？22、甲、乙两人用手指玩游戏，规则如下：①每次游戏时，两人同时随机地各伸出一根手指；②两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指、小拇指只胜大拇指，否则不分胜负．依据上述规则，当甲、乙两人同时随机地各伸出一根手指时，（1）求甲伸出小拇指取胜的概率；（2）求乙取胜的概率．23、如图，直线l与⊙O相切于点D，过圆心O作EF∥l交⊙O于E、F两点，点A是⊙O 上一点，连接AE、AF，并分别延长交直线l于B、C两点．（1）求证：∠ABC+∠ACB=90°；（2）当⊙O的半径R=5，BD=12时，求tan∠ACB的值．24、在平面直角坐标系中，一个二次函数的图象经过点A（1，0）、B（3，0）两点．（1）写出这个二次函数图象的对称轴；（2）设这个二次函数图象的顶点为D，与y轴交于点C，它的对称轴与x轴交于点E，连接AC、DE和DB，当△AOC与△DEB相似时，求这个二次函数的表达式．[提示：如果一个二次函数的图象与x轴的交点为A（x1，0）、B（x2，0），那么它的表达式可表示为y=a（x-x1）（x-x2）]．25、问题探究：（1）请在图①中作出两条直线，使它们将圆面四等分；（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M）使它们将正方形ABCD的面积四等分，并说明理由．问题解决：（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．2013年陕西省中考数学试卷的答案和解析一、选择题1、答案：A试题分析：根据有理数的大小比较方法，找出最小的数即可．试题解析：∵-2＜-＜0＜5，∴四个数中最小的数是-2；故选A．2、答案：D试题分析：找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．试题解析：从上面看所得到的图形是一个长方形，中间有一个没有圆心的圆，与长方形的两边相切．故选：D．3、答案：B试题分析：根据平角等于180°求出∠BED，再根据两直线平行，内错角相等解答．试题解析：∵∠CED=90°，∠AEC=35°，∴∠BED=180°-∠CED-∠AEC=180°-90°-35°=55°，∵AB∥CD，∴∠D=∠BED=55°．故选B．4、答案：A试题分析：分别计算出两个不等式的解集，再根据大小小大中间找确定不等式组的解集即可．试题解析：，由①得：x＞，由②得：x＞-1，不等式组的解集为：x＞，故选：A．5、答案：C试题分析：根据平均数的计算公式列出算式，再进行计算即可．试题解析：根据题意得：（111+96+47+68+70+77+105）÷7=82；故选C．6、答案：D试题分析：根据正比例函数图象所在象限，可判断出m、n的正负．试题解析：A、m＞0，n＞0，A、B两点在同一象限，故A错误；B、m＞0，n＜0，A、B两点不在同一个正比例函数，故B错误；C、m＜0，n＞0，A、B两点不在同一个正比例函数，故C错误；D、m＜0，n＜0，A、B两点在同一个正比例函数的不同象限，故D正确．故选：D．7、答案：C试题分析：首先证明△ABC≌△ADC，根据全等三角形的性质可得∠BAC=∠DAC，∠BCA=∠DCA，再证明△ABO≌△ADO，△BOC≌△DOC．∵在△ABC和△ADC中，∴△ABC≌△ADC（SSS），∴∠BAC=∠DAC，∠BCA=∠DCA，∵在△ABO和△ADO中，∴△ABO≌△ADO（SAS），∵在△BOC和△DOC中，∴△BOC≌△DOC（SAS），故选：C．8、答案：A试题分析：设一次函数的解析式为y=kx+b（k≠0），再把x=-2，y=3；x=1时，y=0代入即可得出k、b 的值，故可得出一次函数的解析式，再把x=0代入即可求出p的值．试题解析：一次函数的解析式为y=kx+b（k≠0），∵x=-2时y=3；x=1时y=0，∴，解得，∴一次函数的解析式为y=-x+1，∴当x=0时，y=1，即p=1．故选A．9、答案：C试题分析：首先由菱形的四条边都相等与矩形的四个角是直角，即可得到直角△ABM中三边的关系．试题解析：∵四边形MBND是菱形，∴MD=MB．∵四边形ABCD是矩形，∴∠A=90°．设AB=x，AM=y，则MB=2x-y，（x、y均为正数）．在Rt△ABM中，AB2+AM2=BM2，即x2+y2=（2x-y）2，解得x=y，∴MD=MB=2x-y=y，∴==．故选：C．10、答案：B试题分析：先判断出抛物线开口方向上，进而求出对称轴即可求解．试题解析：∵点C（x0，y）是抛物线的顶点，y1＞y2≥y，∴抛物线有最小值，函数图象开口向上，∴a＞0；∴25a-5b+c＞9a+3b+c，∴＜1，∴-＞-1，∴x＞-1∴x0的取值范围是x＞-1．故选：B．二、填空题11、答案：试题分析：先分别根据有理数乘方的法则及0指数幂的计算法则计算出各数，再根据实数混合运算的法则进行计算即可．试题解析：原式=-8+1=-7．故答案为：-7．12、答案：试题分析：首先利用提取公因式法分解因式，由此即可求出方程的解．试题解析：x2-3x=0，x（x-3）=0，∴x1=0，x2=3．故答案为：x1=0，x2=3．13、答案：试题分析：（1）比较A（-2，1）与A′（3，2）的横坐标、纵坐标，可知平移后横坐标加5，纵坐标加1，由于点A、B平移规律相同，坐标变化也相同，即可得B′的坐标；（2）8cos31°很接近4，再比较即可．试题解析：（1）由于图形平移过程中，对应点的平移规律相同，由点A到点A′可知，点的横坐标加5，纵坐标加1，故点B′的坐标为（1+5，3+1），即（6，4）；（2）∵8cos31°≈4，∴4＞．故答案为：（6，4）；＞．14、答案：试题分析：如图，过点A作AE⊥BD于点E，过点C作CF⊥BD于点F．则通过解直角△AEO和直角△CFO求得AE=CF=，所以易求四边形ABCD的面积．试题解析：如图，过点A作AE⊥BD于点E，过点C作CF⊥BD于点F．∵BD平分AC，AC=6，∴AO=CO=3．∵∠BOC=120°，∴∠AOE=60°，∴AE=AO•sin60°=．同理求得CF=，∴S四边形ABCD =S△ABD+S△CBD=BD•AE+BD•CF=2×××8=12．故答案是：12．15、答案：试题分析：正比例函数与反比例函数y=的两交点坐标关于原点对称，依此可得x1=-x2，y1=-y2，将（x2-x 1）（y2-y1）展开，依此关系即可求解．试题解析：∵正比例函数的图象与反比例函数y=的图象交于A（x1，y1），B（x2，y2）两点，关于原点对称，依此可得x1=-x2，y1=-y 2，∴（x2-x1）（y2-y1）=x2y2-x2y1-x1y2+x1y1=x2y2+x2y2+x1y1+x1y1=6×4=24．故答案为：24．16、答案：试题分析：由点E、F分别是AC、BC的中点，根据三角形中位线定理得出EF=AB=3.5为定值，则GE+FH=GH-EF=GH-3.5，所以当GH取最大值时，GE+FH有最大值．而直径是圆中最长的弦，故当GH为⊙O的直径时，GE+FH有最大值14-3.5=10.5．试题解析：当GH为⊙O的直径时，GE+FH有最大值．当GH为直径时，E点与O点重合，∴AC也是直径，AC=14．∵∠ABC是直径上的圆周角，∴∠ABC=90°，∵∠C=30°，∴AB=AC=7．∵点E、F分别为AC、BC的中点，∴EF=AB=3.5，∴GE+FH=GH-EF=14-3.5=10.5．故答案为：10.5．三、解答题17、答案：试题分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．试题解析：去分母得：2+x（x+2）=x2-4，解得：x=-3，经检验x=-3是分式方程的解．18、答案：试题分析：根据同角的余角相等求出∠A=∠BOD，然后利用“角角边”证明△AOC和△OBD全等，根据全等三角形对应边相等证明即可．证明：∵∠AOB=90°，∴∠AOC+∠BOD=90°，∵AC⊥l，BD⊥l，∴∠ACO=∠BDO=90°，∴∠A+∠AOC=90°，∴∠A=∠BOD，在△AOC和△OBD中，，∴△AOC≌△OBD（AAS），∴AC=OD．19、答案：试题分析：（1）由等级A的人数除以所占的百分比，即可求出调查的学生人数；（2）根据总人数减去A、C、D等级的人数求出等级B的人数，补全条形统计图；由C的人数除以总人数求出C的百分比，进而求出D的百分比，补全扇形统计图即可；（3）由1800乘以B的百分比，即可求出对“节约教育”内容“了解较多”的人数．试题解析：（1）抽样调查的学生人数为36÷30%=120（名）；（2）B的人数为120×45%=54（名），C的百分比为×100%=20%，D的百分比为×100%=5%；补全统计图，如图所示：（3）对“节约教育”内容“了解较多”的有1800×45%=810（名）．20、答案：试题分析：根据AM⊥EC，CD⊥EC，BN⊥EC，EA=MA得到MA∥CD∥BN，从而得到△ABN∽△ACD，利用相似三角形对应边的比相等列出比例式求解即可．试题解析：设CD长为x米，∵AM⊥EC，CD⊥EC，BN⊥EC，EA=MA∴MA∥CD∥BN∴EC=CD=x∴△ABN∽△ACD，∴即解得：x=6.125≈6.1．经检验，x=6.125是原方程的解，∴路灯高CD约为6.1米．21、答案：试题分析：（1）先运用待定系数法求出OA的解析式，再将x=0.5代入，求出y的值即可；（2）设AB段图象的函数表达式为y=k′x+b，将A、B两点的坐标代入，运用待定系数法即可求解；（3）先将x=2代入AB段图象的函数表达式，求出对应的y 值，再用170减去y即可求解．试题解析：（1）设OA段图象的函数表达式为y=kx．∵当x=1.5时，y=90，∴1.5k=90，∴k=60．∴y=60x（0≤x≤1.5），∴当x=0.5时，y=60×0.5=30．故他们出发半小时时，离家30千米；（2）设AB段图象的函数表达式为y=k′x+b．∵A（1.5，90），B（2.5，170）在AB上，∴，解得，∴y=80x-30（1.5≤x≤2.5）；（3）∵当x=2时，y=80×2-30=130，∴170-130=40．故他们出发2小时，离目的地还有40千米．22、答案：试题分析：（1）首先根据题意画出表格，由表格求得所有等可能的结果，即可求出甲伸出小拇指取胜的概率；（2）由（1）中所求即可得出乙取胜的概率；试题解析：解；（1）设A，B，C，D，E分别表示大拇指、食指、中指、无名指、小拇指，列表如下：出小拇指获胜）=，；（2）又上表可知，乙取胜有5种可能，故P（乙获胜）==．23、答案：试题分析：（1）由题意可知EF是圆的直径，所以∠EAF=90°，即∠ABC+∠ACB=90°；（2）连接OD，则OD⊥BD，过E作EH⊥BC于H，则四边形EODH是正方形，易求tan∠BEH==，再证明∠ACB=∠BEH即可．试题解析：（1）证明：∵EF是圆的直径，∴∠EAF=90°，∴∠ABC+∠ACB=90°；（2）连接OD，则OD⊥BD，过E作EH⊥BC于H，∴EH∥OD，又∵EO∥HD，∴四边形OEHD是矩形，又∵OE=OD，∴四边形EODH是正方形，∴EH=HD=OD=5，又∵BD=12，∴BH=7，在Rt△BEH中，tan∠BEH==，∵∠ABC+∠BEH=90°，∠ABC+∠ACB=90°，∴∠ACB=∠BEH，∴tan∠ACB=．24、答案：试题分析：（1）根据二次函数对称性得出对称轴即可；（2）首先求出C，D点坐标，进而得出CO的长，利用当△AOC与△DEB 相似时，根据①假设∠OCA=∠EBD，②假设∠OCA=∠EDB，分别求出即可．试题解析：解；（1）∵二次函数的图象经过点A（1，0）、B（3，0）两点，∴二次函数图象的对称轴为直线x=2；（2）设二次函数的表达式为：y=a（x-1）（x-3）（a≠0），当x=0时，y=3a，当x=2时，y=-a，∴点C坐标为：（0，3a），顶点D坐标为：（2，-a），∴OC=|3a|，又∵A（1，0），E（2，0），∴AO=1，EB=1，DE=|-a|=|a|，当△AOC与△DEB相似时，①假设∠OCA=∠EBD，可得=，即=，∴a=或a=-，②假设∠OCA=∠EDB，可得=，∴=，此方程无解，综上所述，所得二次函数的表达式为：y=x2-x+或y=-x2+x-．25、答案：试题分析：（1）画出互相垂直的两直径即可；（2）连接AC、BD交于O，作直线OM，分别交AD于P，交BC于Q，过O作EF⊥OM交DC于F，交AB于E，则直线EF、OM将正方形的面积四等份，根据三角形的面积公式和正方形的性质求出即可；（3）当BQ=CD=b时，PQ将四边形ABCD的面积二等份，连接BP并延长交CD的延长线于点E，证△ABP≌△DEP求出BP=EP，连接CP，求出S△BPC =S△EPC，作PF⊥CD，PG⊥BC，由BC=AB+CD=DE+CD=CE，求出S△BPC -S△CQP+S△ABP=S△CPE-S△DEP+S△CQP，即可得出S四边形ABQP=S四边形CDPQ即可．试题解析：（1）如图1所示，（2）连接AC、BD交于O，作直线OM，分别交AD于P，交BC于Q，过O作EF⊥OM交DC于F，交AB于E，则直线EF、OM将正方形的面积四等份，理由是：∵点O是正方形ABCD的对称中心，∴AP=CQ，EB=DF，在△AOP和△EOB中∵∠AOP=90°-∠AOE，∠BOE=90°-∠AOE，∴∠AOP=∠BOE，∵OA=OB，∠OAP=∠EBO=45°，∴△AOP≌△EOB，∴AP=BE=DF=CQ，设O到正方形ABCD一边的距离是d，则（AP+AE）d=（BE+BQ）d=（CQ+CF）d=（PD+DF）d，∴S四边形AEOP =S四边形BEOQ=S四边形CQOF=S四边形DPOF，直线EF、OM将正方形ABCD面积四等份；（3）存在，当BQ=CD=b时，PQ将四边形ABCD的面积二等份，理由是：如图③，连接BP并延长交CD的延长线于点E，∵AB∥CD，∴∠A=∠EDP，∵在△ABP和△DEP 中∴△ABP≌△DEP（ASA ），∴BP=EP，连接CP ，∵△BPC 的边BP 和△EPC 的边EP 上的高相等，又∵BP=EP，∴S △BPC =S △EPC ，作PF⊥CD，PG⊥BC，则BC=AB+CD=DE+CD=CE ，由三角形面积公式得：PF=PG ，在CB 上截取CQ=DE=AB=a ，则S △CQP =S △DEP =S △ABP ∴S △BPC -S △CQP +S △ABP =S △CPE -S △DEP +S △CQP 即：S 四边形ABQP =S 四边形CDPQ ，∵BC=AB+CD=a+b，∴BQ=b，∴当BQ=b 时，直线PQ 将四边形ABCD 的面积分成相等的两部分．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2013年陕西中考数学试卷一、选择题（共10小题，每小题3分，计30分） 1 下列四个数中最小的数是（ ）A.2-B.0C.31-D.5 2 如图，下面几何体是由一个圆柱和一个长方体组成的，则它的俯视图是（ ）AB C D3 如图，AB//CD ，∠CED=90°，∠AEC=35°，则∠D 的大小是（ ） Ａ．65° B.55° C.45° D.35°4 不等式组⎪⎩⎪⎨⎧<->-321021x x 的解集为（ ） A.21>x B.1-<x C.211<<-x D.21->x 5 我省某市五月份第二周连续七天的空气质量指数分别为：111，96，47，68，70，77，105.则这七天空气质量指数的平均数是（ ）A.71.8B.77 C .82 D.95.76 如果一个正比例函数的图象经过不同象限的两点,3)B()A(2,n m 、，那么一定用（ ）A.0,0>>n mB.0,0<>n mC.0,0><n mD.0,0<<n m 7 如图，在四边形ABCD 中，AB=AD,CB=CD,若连接AC ，BD 相交于点O ，则图中全等三角形共有（ ）A.1对B.2对C.3对D.4对8 根据下表中一次函数的自变量x 与函数y 的对应值，可得p 的值为（ ）x -2 0 1 y 3 p 0 A.1 B.-1 C.3 D.-39.如图，在矩形ABCD 中，AD=2AB,点M 、N 分别在AD 、BC 上，连接BM 、DN.若四边形MBND 是菱形，则MDAM等于（ ） A.83 B.32 C.53 D.54 10 已知两点),5(1y A -、),3(1y B 均在抛物线)0(2≠++=a c bx ax y 上，点),(00y x C 是该抛物线的顶点，若021y y y ≥>，则0x 的取值范围是（ ）E DB CAA 50->xB 10->xC 150-<<-xD 320<<-x 第Ⅱ卷（非选择题 共90分）二、填空题（共6小题，每小题3分，计18分）11.计算：=-+-03)13()2( .12.一元二次方程032=-x x 的根是 .13.请从以下两个小题中任选一个．．．．作答，若多选，则按所选的第一题计分． A 在平面直角坐标系中，线段AB 的两个端点的坐标分别为)3,1()1,2(B A 、-，将线段AB 经过平移后得到线段B A ''.若点A 的对应点(3,2)A '，则点B 的对应点B '的坐标为是 . B 比较大小：︒31cos 835（填“>”、“=”或“<”）.14.如图，四边形ABCD 的对角线AC 、BD 相交于点O,且BD 平分AC.若BD=8，AC=6，∠BOC=120°，则四边形ABCD 的面积为 .(结果保留号)第14题图 第16题图15.如果一个正比例函数的图象与反比例函数xy 6=的图象交于),(),(2211y x B y x A 、两点，那么))((1212y y x x --的值为 .16.如图，AB 是⊙O 的一条弦，点C 是⊙O 上一动点，且∠ACB=30°，点E 、F 分别是AC 、BC 的中点，直线EF 与⊙O 交于G 、H 两点，若⊙O 的半径为7，则CE+FH 的最大值为 . 三、解答题（共9小题，计72分．解答应写过程） 17．（本题满分5分）解分式方程:12422=-+-x xx 18．（本题满分6分）如图，∠AOB=90°，OA=OB,直线l 经过点O ，分别过A 、B 两点作AC ⊥l 交l 于点C ，BD ⊥l 交l 于点D 。
求证：AC=OD 19．（本题满分7分）我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度（程度分为：“A—了解很多”，“B—了解较多”，“C—了解较少”，“D—不了解”），对本市一所中学的学生进行了抽样调查。
我们将这次调查的结果绘制了以下两幅统计图。
根据以上信息，解答下列问题: (1) 本次抽样调查了多少名学生？ (2) 补全两幅统计图;(3) 若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”有多少名？20. （本题满分8分）一天晚上，李明和张龙利用灯光下影子的长来测量一路灯D 高度，如图，当李明走到点A 处时，张龙测得李明直立时身高AM 与其影子长AE 正好相等；接着李明沿AC 方向继续向前走，走到点B 处时，李明直立时身高BN 的影子是线段AB ，并测得AB=1.25m,已知李明直立时的身高为1.75m.求路灯的高CD 的长.（结果精确到0.1m ）21. （本题满分8分）了解程度人数624060504030201036D B CA N ME D B C A“五一节”期间，申老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y （千米）与汽车行驶时间x （小时）之间的函数图象.(1) 求他们出发半小时时，离家多少千米？(2) 求出AB 段图象的函数表达式；(3) 他们出发2小时时，离目的地还有多少千米？22. （本题满分8分）甲、乙两人用手指玩游戏。
规则如下：ⅰ）每次游戏时，两人同时随机地各伸出一根手指；ⅱ）两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小指、小指只胜大拇指，否则不分胜负.依据上述规则，当甲、乙两人同时随机地各伸出一根手指时，（1）求甲伸出小拇指取胜的概率 （2）求乙取胜的概率23. （本题满分8分）如图，直线l 与⊙O 相切于点D ，过圆心O 作EF//l 交⊙O 于E 、F 两点，点A 是⊙O 上一点，连接AE 、AF ，并分别延长交直线l 于B 、C 两点，（1）求证：∠ABC+∠ABC=90°（2）当⊙O 的半径5 R ，BD=12时，求tan ∠ACB 的值。
24. （本题满分10分）在平面直角坐标系中，一个二次函数的图象经过)0,3()3,1(B A 、两点。
（1）写出这个二次函数图象的对称轴；（2）设这个二次函数图象的顶点为D ，与y 轴交于点C ，它的对称轴与x 轴交于点E ，连接AC 、DE 和DB ，当AOC ∆与DEB ∆相似时，求这个二次函数的表达式。
25. （本题满分12分） 问题探究（1）请在图①中，作出两条直线，使它们将圆面四等分；（2）如图②，M 是正方形ABCD 内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M ），使它们将正方形ABCD 的面积四等分，并说明理由。
问题解决（3）如图③，在四边形ABCD 中，AB//CD,AB ＋CD=BC ，点P 是AD 的中点，如果AB=a ,CD=b ,且a b >，那么在边BC 上是否存在一点Q,使PQ 所在的直线将四边形ABCD 的面积分成相等的两部分？若存在，求出BQ 的长；若不存在，说明理由。
图① 图② 图③xy –1–2–3–41234–1–2–3–41234O参考答案一、选择题：ADBAC DCADB 二、填空题 11：7 12：0，3 13题：A ：（6，4），B ：> 14:312 15: 24 16: 10.5 三、简答题 17、解：2222(2)4(2)2243(4)3x x x x x x x x ++=-++=-=-=-分分经检验，是原分式方程的根.（5分）18、证明： 00009090.(1),,90.90..(3),.(5).(6)AOB AOC BOD AC l BD l ACO BDO A AOC A BOD OA OB AOC OBD AC OD ∠=∴∠+∠=⊥⊥∴∠=∠=∴∠+∠=∴∠=∠=∴≅∴=，分分又分分19、解：（1）抽样调查的学生人数为：36÷30%=120（名）…（2分） （2）B 的人数：120×45%=54（名）C 的百分比：24100%=20%120⨯， D 的百分比：6100%=5%.120⨯ 补全两幅统计图如图所示。
………………………………（5分）（略）（1） 对“节约教育”内容“了解较多”的学生人数为： 1800×45%=810（名）………………………（7分） 20、解：.CD xm 设长为,,,,//,//....(5)AM EC CD EC BN EC EA MA MA CD BN CD EC CD x ABN ACD BN ABCD AC⊥⊥⊥=∴∴==∴∴=分即1.75 1.25.1.75x x =-解之，得 6.125 6.1.x =≈∴路灯高CD 约为6.1m .………………………（8分） 21、解：设OA 段图像的函数表达式为.y kx = ∵当x =1.5时，y =90； ∴1.5k =90. ∴k =60.∴60,(0 1.5)y x x =≤≤ ∴当x =0.5时，y =60×0.5=30.∴行驶半小时时，他们离家30千米，………（3分）（2）设AB 段图像的函数表达式为',y k x b =+ ………………（4分）∴A(1.5，90)，B(2.5，170)在AB 上，∴90 1.5'170 2.5'.k b k b =+⎧⎨=+⎩解之，得'80,30.k b ==-8030.(1.5 2.5)y x x ∴=-≤≤ ………………………………（6分）（3）当x =2时，y =80×2-30=130.∴170-130=40.∴他们出发2小时后，离目的地还有40千米。
…………（8分）22、解：设A,B,C,D,E 分别表示大拇指，食指，中指，无名指，小拇指，列表如下：乙甲ABCDEA AA AB AC AD AE B BA BB BC BD BE C CA CB CC CD CE D DA DB DC DD DE EEAEBECEDEE由表格可知，共有25种等可能的结果。
（1）由上表可知，甲伸出小拇指取胜有1种可能。
∴P （甲伸出小拇指取胜）=125………………………………（3分）（2）由上表可知，乙取胜有5种可能。
∴P(乙取胜)=51=255……………………………………………（8分） 23、（1）证明：∵EF 是⊙O 的直径， ∴∠EAF=090 ，∴∠ABC+∠ACB=090.…………………（3分）(2)解：连接OD,则OD ⊥BD 。