微分几何曲面论曲面的概念
微分几何 2-1曲面的概念
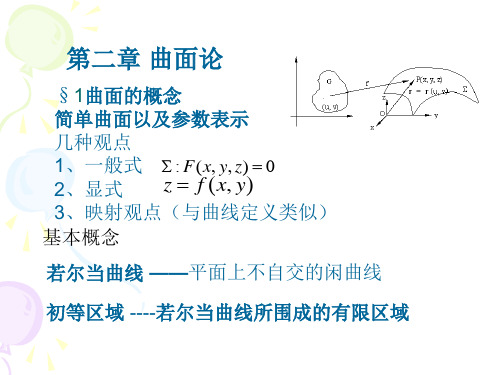
微分方程: A(u, v)du2 +2B(u, v)dudv + C(u, v)dv 2 =0
当 [B(u, v)]2 A(u,v) C(u,v) >0时
表示曲面上的两族曲线——曲线网。
当 A C 0时,方程变为
dudv 0
它表示的曲线网就是曲面上的曲纹坐标网
谢谢观看! 2020
v (1,2)
1 3,1,2
14
, ,2
|
4 2 (1,2)
过点(1,2)的切平面方程是
[R r(1,2)] n(1,2) 0.
即 3x+y-2z-4=0.
3. 曲面上的曲线族和曲线网
曲面 r r(u,v)S上的曲线用方程 u(t),v v(t)
或 r r[ut , vt ] rt
ru (u ,v ) r(v u ,v ) 0
此时U内两坐标曲线构成的网为曲面的正规坐标网 命题1:曲面在正则点的邻域中总可以有形如
z = z(x, y)的表示 因为 ru (u ,v ) r(v u ,v ) 0,至少有一分量不为零
假设 ( (xu, ,yv) ) 0, 一对单值连续函数
则有隐函数存在定理有唯一
u和v称曲面上的点的曲纹坐标曲面上的点的曲纹坐标uu常数或常数或v常数在曲面上的常数在曲面上的象称为曲面的曲面的坐标曲坐标曲u常数而常数而vv变动的曲线叫变动的曲线叫vv线v常数而常数而uu变动的曲线叫变动的曲线叫uu成的网称为曲面上的成的网称为曲面上的曲纹坐标网曲纹坐标网曲纹坐标网曲纹坐标网坐标曲线坐标曲线曲线z常数即它是垂直于轴的平面和原柱面的交线它们都是圆
u ( u x,y),v (v x,y)
代入则有z = z(x, y)
微分几何的曲线与曲面

微分几何的曲线与曲面微分几何是数学中的一个分支,它研究的是曲线与曲面以及其在空间中的性质和变形。
曲线与曲面是微分几何的基本概念,它们在几何学、物理学和工程学等领域中都具有重要的应用价值。
一、曲线曲线是空间中一条连续的轨迹,可以用参数方程或者向量值函数表示。
对于参数方程,通常使用参数t来表示曲线上的点的位置,而向量值函数则将参数t映射到空间中的点。
在微分几何中,我们通常关注曲线的切向量、弧长、曲率和挠率等性质。
曲线的切向量表示曲线在某一点处的方向,它的大小与曲线在该点的速率有关。
弧长表示曲线上两点之间的距离,它是曲线长度的度量。
曲率是衡量曲线的弯曲程度的量,它描述了曲线在某点附近的几何性质。
挠率则刻画了曲线弯曲的方向。
二、曲面曲面是空间中的一个二维对象,它可以用参数方程、隐函数方程或者显函数方程表示。
参数方程和向量值函数类似,将两个参数u和v 映射到空间中的点。
隐函数方程将曲面表示为一个方程,其中的变量与坐标之间存在一定的关系。
显函数方程则直接给出了曲面的形式。
曲面的法向量、切平面、曲率和高斯曲率等性质是微分几何中研究的重点。
曲面的法向量垂直于曲面上每一点的切平面,它的方向和切平面的变化率有关。
切平面是通过曲面上一点并与该点的切向量垂直的平面。
曲率是衡量曲面的弯曲程度的量,它描述了曲面在某点附近的几何性质。
高斯曲率是刻画曲面弯曲方向的指标,它可以判断曲面上某点处的性质。
三、微分几何的应用微分几何在几何学、物理学和工程学等领域中都有广泛的应用。
在几何学中,微分几何可以研究曲线和曲面的性质,进而推导出一些几何定理和结论。
在物理学中,微分几何可以描述空间中物体的运动轨迹和性质,以及引力场等物理现象。
在工程学中,微分几何可以应用于地图绘制、计算机图形学和机械设计等领域,用来分析和描述实际问题的几何性质。
总结微分几何研究曲线与曲面在空间中的性质和变形,涉及到曲线的切向量、弧长、曲率和挠率,以及曲面的法向量、切平面、曲率和高斯曲率等概念。
微分几何与曲面的性质与变换

微分几何与曲面的性质与变换微分几何是数学中的一个分支,主要研究曲线和曲面的性质以及它们在空间中的变换。
通过微分几何的研究,我们能够深入了解曲面的形态、曲率以及它们的变换规律。
本文将重点探讨微分几何与曲面的性质与变换。
1. 曲面的定义与性质曲面是由平面来包裹而成的几何对象。
在微分几何中,我们主要关注的是二维曲面,即可以用二维投影来表示的曲面。
曲面可以通过参数方程来定义,例如常见的球面、圆柱面和锥面等。
曲面上的点可以由参数方程中的参数表示。
曲面的性质包括曲面的形状、曲率和法线等。
曲面的形状可以通过曲面的方程或参数方程来描述,例如曲面的曲率半径描述了曲面在某一点的局部弯曲程度。
曲面上每一点都有一个法线向量,它垂直于曲面,在计算曲面的性质时,法线的方向和长度起着重要的作用。
2. 第一基本形式微分几何中引入了第一基本形式的概念,用来刻画曲面上的测量性质。
第一基本形式是曲面上的度量,它由曲面的内部点之间的距离关系推导而来。
第一基本形式包含了曲面上的切线、曲率和曲面间的距离等信息。
通过第一基本形式,我们可以计算曲面上的曲率、曲面上两点之间的距离以及曲面上的长度等。
3. 曲面的变换微分几何中,曲面的变换是一个重要的研究对象。
曲面的变换包括刚体变换和仿射变换。
刚体变换是指在平移、旋转和缩放等约束下,可以保持曲面的形状和曲面上的相对距离不变。
仿射变换是指将曲面映射到另一个曲面,保持曲面上所有的直线和比例关系不变。
曲面的变换对于研究曲面的性质和形态有重要的意义。
通过变换,我们可以将一个曲面变形为另一个曲面,从而研究曲面的不同形态和性质。
变换还可以用于曲面的拓扑研究,通过变换可以判断两个曲面是否同胚,即是否存在一一对应的关系。
在计算机图形学和计算机视觉等领域中,曲面的变换是一个重要的研究内容。
通过曲面的变换,我们可以实现曲面的形变、变形以及场景中不同曲面之间的相互作用等效果。
微分几何与曲面的性质与变换之间有着密切的联系。
微分几何与曲面的性质与变换

微分几何与曲面的性质与变换微分几何是研究曲线、曲面及其在高维空间中性质的一门学科。
曲面是微分几何研究的重要对象之一,掌握曲面的性质和变换是理解微分几何的关键。
本文将介绍微分几何的基本概念、曲面的性质以及曲面的变换。
一、微分几何的基本概念微分几何是微积分的一个分支,它以微积分的方法研究曲线、曲面以及更高维空间中的几何性质。
微分几何的基本概念包括曲线的参数化表示、切向量、曲率、曲面的参数化表示等。
在微分几何中,曲线通常被表示为参数形式。
例如,给定参数t,曲线可以表示为r(t)=(x(t), y(t), z(t)),其中x(t),y(t),z(t)分别是曲线在x、y、z轴上的坐标函数。
切向量是曲线上某一点处切线的方向向量,它可以表示为曲线的导数向量。
曲率描述了曲线在某一点处的弯曲程度,它可以通过曲线的切向量的导数来计算。
曲面的参数化表示类似于曲线的参数化表示,只不过坐标函数变成了两个参数的函数。
二、曲面的性质曲面是三维空间中的一个二维对象,它有许多独特的性质。
曲面的性质包括曲率、法向量、第一和第二基本形式等。
曲率是描述曲面在某一点处曲率的一个度量。
曲率可以通过曲面的法向量和曲面上的切平面相互之间的关系来定义。
曲面的法向量是与曲面上的每个点处的切平面垂直的一个向量。
第一基本形式描述了曲面上切向量的内积,它刻画了曲面的局部几何性质。
第二基本形式描述了曲面上法向量的内积,它刻画了曲面的弯曲性质。
三、曲面的变换曲面的变换在微分几何中是一个重要的研究内容。
曲面的变换可以通过变换函数对曲面的坐标进行操作来实现。
常见的曲面变换包括平移、旋转、放缩等。
平移是将曲面沿着某一方向移动一定距离,旋转是将曲面绕着某一轴旋转一定角度,放缩是改变曲面的尺寸。
这些变换操作可以通过矩阵乘法来表示,从而方便实现对曲面坐标的变换。
此外,曲面的变换还可以通过曲面之间的映射来实现。
例如,曲面之间的正则映射可以将一个曲面映射到另一个曲面上,保持曲面上的点之间的距离关系不变。
微分几何中的曲率与曲面性质

微分几何中的曲率与曲面性质微分几何是研究曲线和曲面的一种数学分支,其中曲率是一个重要的概念。
曲率描述了曲线或曲面在某一点上的弯曲程度,也反映了曲线或曲面的性质。
在本文中,我们将探讨微分几何中的曲率与曲面性质的关系。
1. 曲率的定义与计算曲率描述了曲线或曲面在某一点上的弯曲程度,是微分几何中的基本概念之一。
对于曲线来说,我们可以通过曲率半径来表示曲率。
曲率半径是曲线上某一点处的切线与曲线的凸包之间的最短距离,它的倒数即为曲率。
对于曲面而言,曲率有两个主要方向:主曲率和法曲率。
主曲率是曲面上某一点上曲线在曲面上的投影的曲率,法曲率是曲面上某一点处法线方向上的曲率。
曲面的平均曲率是主曲率的平均值,而曲面的高斯曲率则是主曲率的乘积。
2. 曲率与曲面性质的关系曲面的曲率与其性质之间存在着密切的关系。
下面我们将探讨几个重要的曲率与曲面性质的关联。
2.1. 曲率与曲面的形状曲率可以反映曲面的形状。
例如,当曲面的高斯曲率为正时,曲面呈现凸状;当高斯曲率为负时,曲面呈现凹状。
而平均曲率则可以用来描述曲面的光滑程度,平均曲率越小,曲面越光滑。
2.2. 曲率与曲面的局部性质曲率还可以反映曲面在某一点上的局部性质。
例如,在曲面上的最大和最小主曲率之间的差异可以反映曲面的弯曲程度。
当最大和最小主曲率的差异较大时,曲面呈现出较大的弯曲;当曲率差异较小时,曲面则较为平坦。
2.3. 曲率与曲面的拓扑性质曲率还与曲面的拓扑性质有关。
根据微分几何的基本定理,高斯曲率与曲面的欧拉特征数相关。
欧拉特征数是用来描述曲面的拓扑结构的一个数值,它与曲面的几何特征密切相关。
3. 曲率在实际应用中的意义曲率在实际应用中有着广泛的应用价值。
例如,在计算机图形学中,曲线和曲面的曲率可以用来实现真实感渲染,提高图像的真实度。
在机器人技术中,曲率可以用来进行路径规划和运动控制,提高机器人的灵活性和精确度。
此外,曲率还在物理学、工程学和生物学等领域中发挥着重要作用。
曲面论的概念

曲面论的概念曲面论是微分几何学的一个分支,研究的对象是曲面及其在空间中的性质和变化。
曲面是三维空间中的一个二维物体,可以用参数方程或隐函数方程来描述。
曲面论的核心思想是通过微分几何工具来研究曲面的几何性质和变化规律。
首先,我们来看曲面的定义。
对于一个三维空间中的点P,如果存在一个邻域使得这个邻域内的点可以由两个独立的参数u和v来唯一确定,则这个邻域就构成了一个曲面。
曲面可以用参数方程表示为:\[\begin{cases}x = x(u,v) \\y = y(u,v) \\z = z(u,v)\end{cases}\]或者用隐函数方程表示为F(x,y,z)=0。
曲面论主要研究的内容可以分为以下几个方面:1. 曲面的基本性质:曲面论研究曲面的局部性质,例如曲面上的切向量、法向量、曲率等。
曲面上每一点都有一个与之相切的平面,称为切平面。
曲面的法向量是垂直于切平面的向量,它可以用曲面的参数方程来表示。
2. 第一基本形式:第一基本形式是曲面的内禀度量,描述了曲面上切向量的内积。
它反映了曲面的长度、角度、曲线弯曲等性质。
第一基本形式可以通过曲面的参数方程来计算。
3. 第二基本形式:第二基本形式是曲面对于切平面的曲率性质。
它与曲面的法向量和曲面的法向量的导数相关。
第二基本形式可以用曲面的方程来计算。
4. 高斯曲率和平均曲率:高斯曲率和平均曲率是曲面论中的重要概念。
高斯曲率是曲面上局部形状的量度,描述了曲面的弯曲程度。
平均曲率反映了曲面在某一点的整体弯曲情况。
5. 曲面的变化:曲面论还研究了曲面的变化规律,包括曲面的平移、旋转、放缩等。
这些变化可以通过微分几何的方法来描述和研究。
应用方面,曲面论在计算机图形学、计算机辅助设计、物理学、生物学等领域都有广泛的应用。
在计算机图形学中,曲面论可以用来构造和渲染三维模型。
在计算机辅助设计中,曲面论可以用来建立和分析复杂曲面形状。
在物理学中,曲面论可以用来描述空间中的电磁场、引力场等。
微分几何--第二章1曲面的概念1.3曲面上的曲线族和曲线网

A(u, v)du B(u, v)dv 0
表示曲面上的一簇曲线——曲线族. 设 A 0 ,则有 du B(u, v) 解之得
(2.14)
dv A(u, v) u (v, c)
F (u, v)
其中,c为待定常数; 每一个c对应曲面上一条曲线,所以(2.14)表示一族曲线。 特别地, 当B = 0或 A = 0 时,有 d u = 0或 d v = 0 , 此时为坐标曲线(P60) u = c 或 v = c。 此时(2.14)表示坐标曲线的方程。
2、二阶微分方程
A(u, v)du2 2B(u, v)dudv C(u, v)dv2 0
若 [ B(u, v)]2 A(u, v)C (u, v) 0
方程表示曲面上的两簇曲线 —— 曲线网。 设
du 2 du A 0 , 则 A( ) 2 B( ) C 0 dv dv 得 du B B 2 AC F1 (u, v)或F2 (u, v) dv A
消去 t ,可得曲面上曲线的方程为
u (v) ,或 v (u) ,或 f (u, v) 0
1、一阶线性微分方程
A(u, v)du B(u, v)dv 0
表示曲面上的一簇曲线——曲线族.
消去 t ,可得曲面上曲线的方程为
u (v) ,或 v (u) ,或 f (u, v) 0
分别解这两个一阶微分方程,可得两簇曲线,它们构成曲 面上的曲线网。
特别有 A C 0 时, dudv 0 , 它们表示坐标曲线,从而构成曲纹坐标网(P60)。
微分几何
主讲人:郭路军
第二章 曲面论
1、曲面的概念(简单曲面、光滑曲面、切平面和法线)
曲面论知识点总结

曲面论知识点总结曲面是三维空间中的一个特殊的几何概念,它在数学中有着重要的地位。
曲面理论研究曲面的性质、形状以及与其他几何概念之间的关系,广泛应用于物理学、计算机图形学、工程等领域。
本文将就曲面的定义、参数化、曲面的性质等知识点进行总结。
一、曲面的定义曲面是三维空间中的一种二维对象,可以用各种数学方法描述,常见的方法有参数方程和隐式方程。
常见的曲面包括球面、圆柱面、圆锥面等。
曲面的定义可以用数学语言描述为:在三维空间中,一般点(x, y, z)可以用参数形式描述为:P(u, v) = (x(u, v), y(u, v), z(u, v)),其中u和v分别表示曲面上的两个参数。
根据参数的不同取值,曲面上的点可以覆盖整个曲面。
二、曲面的参数化曲面的参数化是指用参数的方法来描述曲面上的点。
参数化的目的是将曲面上的点与参数空间中的点建立起一一对应的关系,以方便对曲面上的点进行计算和研究。
不同的曲面可以采取不同的参数化方法,一般来说,可以采用自然参数化、球坐标参数化等方法来描述曲面。
例如,球面可以用球坐标参数化描述为:P(u, v) = (r * sinu * cosv, r * sinu * sinv, r * cosu),其中u和v分别表示极角和方位角,r表示球的半径。
通过参数化,我们可以方便地对球面上的点进行计算和研究。
三、曲面的性质曲面有许多重要的性质,包括曲率、法线、切平面等。
这些性质可以帮助我们更好地理解曲面的形状和结构,从而在实际问题中应用。
以下就曲面的性质进行详细介绍:1. 曲率:曲率是描述曲面弯曲程度的重要概念,可以分为高斯曲率、平均曲率等多种类型。
曲率的计算可以通过偏微分方程或直接计算曲面上某点的曲率向量而得到。
2. 法线:曲面上的每一点都有一个与曲面垂直的法线,它可以用来描述曲面的方向。
法线在计算机图形学中有着重要的应用,可以用来进行阴影计算、光照计算等。
3. 切平面:曲面上的每一点都有一个切平面,它与曲面在该点的切线垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲面论
§1 曲面的概念
1.简单曲面及其参数表示;
主要内容 2.光滑曲面 曲面的切平面和法线; 3.曲面上的曲线族和曲线网.
1.1 简单曲面及其参数表示
1.简单曲面
定义1(约当曲线)平面上不自交的闭曲线称为约当曲线.
注
(约当定理)约当曲线分平面为两部分,
并 且 每 一 部 分 都 以 此 曲线 为 边 界 ,
r (u0 , v0 ) [ru(u0 , v0 ) rv (u0 , v0 )]
X x(u0 , v0 )
Y y(u0 , v0 )
Z z(u0 , v0 )
yu (u0 , v0 ) zu (u0 , v0 ) zu (u0 , v0 ) xu (u0 , v0 ) xu (u0 , v0 ) yu (u0 , v0 )
3.曲纹坐标网
v坐标直线
v
G
f
z
.
(u0 , v0 )
v坐标曲线 P(u0 , v0 )S
O
u u坐标直线 O
y u坐标曲线
x
设u坐曲标面直( S线)的的方方程程为为 rvr(vu0,,v ),
则 过 曲面(S)上点P(u0 , v0
r r (u, v0 ) {x(u,v0 ), y(u,v0
证:设总点 的存P参(在u数0(,u表 v00,)v示为0 .)的正一常个点邻,则域ruU(,u0在,v0此)邻rv (域u0内 ,vr0u)r0v,
0,y即ຫໍສະໝຸດ urvu yv
z z
u z
,
u z
v v
x x
u x
,
u x
v v
y
u y
0,
(u, v)U .
v
x y
不 妨 设 u x
v坐标曲线族 P(u0 , v0 )S
O
u u坐标直线族 O
x
u坐标曲线族的方程为v 常数;
v坐标曲线族的方程为u 常数.
y
u坐标曲线族
u坐标曲线族与v坐标曲线族形成的曲线网
叫做曲纹坐标网(或参数曲线网)
例1(带缝的圆柱面)
z
v(t)
f
O
2 u( )
o
t R
y
x
参数方程:x Rcos , y Rsin , z t
v( )
2
R
f
O θ
y
O
2 u()
x
2
参数方程:x Rcos cos, y Rcos sin, z Rsin
(其中 ,0 2 )
2
2
其坐标曲线为:
曲线( 常数) : 纬 圆.
曲线( 常数) : 经 线.
例3(带缝的旋转曲面)
将xoz面上的曲线(C):x (t), z (t),( t )
u y
0,
v v ( u0 ,v0 )
由反函数存在定理可知,总 存 在(u0 , v0 )的 一 个 邻 域V, 在 此 邻 域V内 ,方 程 组()有 唯 一 一 对 连 续 可 微 的反 函 数
u u( x, y)
v
v(
x,
y)
将其代入z z(u,v)得:z z[u( x, y), v( x, y)] z( x, y)
注 (1)切方向的表示法:
v
Gf
.
(u, v)
z
C P (u,v) S
O
u
O
y
切方向//
dr dt
ru
du dt
rv
x
dv dt
//dr
rudu
rv dv ,
切方向//dr
dv(ru
du dv
rv
),
切方向//
ru
du dv
rv
,
切方向常用du : dv表示,也 用dr或(d )表 示.
则 称 点P(u0 , v0 )为 曲 面 上 的 正 常 点 , 否 则, 称 为 奇 点.
注
正 常点的几 何意义:
rv (u0 , v0 )
ru(u0,v0 ) rv (u0,v0 ) 0 表 示 经 过 点(u0 , v0 )的
z S P
u -曲 线 和v -曲 线 不 相 切.
O
y
v -曲线 ru (u0 , v0 )
若 函 数 组()满 足 下 列 条 件 :
(i) 函 数 组()至 少 有 一 阶 连 续 偏 微 商;
u v
(ii)
Jocbi行列式(u, v) (u, v )
u u
u v
0,
v v (iii) 函数组()给出了G到G的一宗一一对应.
则称函数 组()为曲面(S)的一个参 数变换.
注
G
v
(u., v)
(u0 , v0 )为 正 常 点 , 0, 因为曲面是光滑
的,ru
在(u0 , v0 )的 一 个 邻 域U,
,
rv
连
续,
于 是 点P(u0 , v0 )在 邻 域U所 对 应 的 正 则 曲 面 片 上,
其上的曲纹坐标网是正规网.
命题1曲面在正常点的邻域中总可以用形如
z z(x, y)或y y(x, z)或x x( y, z)
或u u(t), v v(t)
曲线(C )的曲纹坐标方程
或u u(v)或v v(u) 或f (u, v) 0
曲 线(C )在 点P(u0 , v0 )的 切 向 量 为
r t0
du
ru (u0 , v0 ) dt
t0
dv
rv (u0 , v0 ) dt
t0
定义7(切方向) 与曲线(C )在点P的切向量平行的方向
rv
P(u0 , v0 )ru S
X x(u0 , v0 ) Y y(u0 , v0 ) Z z(u0 , v0 )
xu (u0 , v0 )
yu (u0 , v0 )
zu (u0 , v0 ) 0
xv (u0 , v0 )
yv (u0 , v0 )
zv (u0 , v0 )
法
线 方 程:
f
g
简单曲面
2.简单曲面的参数表示
v
G
.
(u, v)
f
z
P(xu, vy), z) S
r r (u, v)
O
u
O
y
r
r (u,
v)
{
x(u,
v),
y(u,
v),
x
z(u,
v)},(
S
)的
向
量
式
参
数
表
示
x x(u,v), y y(u,v), z z(u,v), (S)的坐标式参数表示
u, v叫做曲面的参数或曲纹坐标. 曲面上的点P( x, y, z)也可直接写作P(u, v).
注 (2)切空间
v
Gf
.
(u0 , v0 )
rv
z
TP
(C )
P(u0
,v ru
0
)
S
O
u
O
y
任给一个向量V
x ru(u0 , v0 )
rv
(u0,v0 ),
则 在曲 面S上 必 定 能 找 到 过 点P(u0 , v0 )的 曲 线:
r r (u0 (t t0 ), v0 (t t0 )),
此曲线在点P(u0,v0 )的切向量就是V .
TP {ru
称 , rv
为 曲面S在点P处的 切空 }是 切 空 间TP的 一 组 基.
间
,
3.曲面的参数变换及曲面的正侧
定义10
给
定曲
面( S
)
:
r
r (u,
v),
(u,
v
)
G
及 函 数 组uv
u(u,v ) v(u , v )
()
(u , v ) G
叫做曲面在该点的切方向 (或方向).
命题2 曲面在一点处的所有切方向都在过该点的
定义8
坐标曲线的切向量ru , rv所决定的平面上. (切平面) 曲 面 在 一 点 处 的 坐 标 曲线 的 切 向
量ru
,
rv
所 决 定 的 平 面 上 叫 做 曲面 在 该 点 的 切 平 面.
定义9 (法方向、法线)曲 面 在 正 常 点 处 垂 直 于切 平 面 的
方 向 称 为 曲 面 的 法 方 向. 过 该 点 平 行 于 法 方 向 的直 线 叫 做 曲 面 在 该 点 的
法 法
单
线 向 位.量 法N向量rnu
rvr, u
rv
.
P
S
ru rv
切(1)平若面曲和面S法:线r 方r(程u, v),
切 平面方程:
(R r (u0 , v0 ), ru(u0 , v0 ), rv (u0 , v0 )) 0
x
u -曲线
定义6(正规曲线网) 曲面上两族曲线构成的曲线网,
如 果 任 意 两 条 异 族 曲 线不 相 切 ,则 称 该 曲 线 网 为
正规曲线网.
注 (1)正则曲面上的曲纹坐标网是正规网. (2)曲面的正常点总在一正则曲面片上,
因而其上的曲纹坐标网是正规网.
事 实 上 ,如 果 点P 从 则 在r而此u(ru邻 u0,v域 r0u)连内 rr续 vu(.u0r,v总v0 )存0,
z ,q x
z , y
曲面在点( x, y)处的切平面方程为:
Xx Yy Zz
1
0
p 0
0
1
q
即Z z p( X x) q(Y y).
