工程与材料力学第11章-弯曲应力
合集下载
工程力学第17讲 弯曲应力:正应力 惯性矩(完整)

第 11 章 弯曲应力
本章主要研究:
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yCb 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
2
§1 引 言
弯曲应力与对称弯曲 本章内容
本章主要研究:
单辉祖:工程力学
对称弯曲正应力 对称弯曲切应力 梁的强度分析与设计 非对称弯曲应力
1
§1 §2 §3 §4 §5 §6 §7
引言 对称弯曲正应力 惯性矩与平行轴定理 对称弯曲切应力 梁的强度条件 梁的合理强度设计 双对称截面梁的非对称弯曲
单辉祖:工程力学
Ai yCi AyC
yC
i 1
n
A y
i 1
n
i Ci
21
A
A1 yC 1 A2 yCb 2 2
bd db
0.045 m
3. 惯性矩计算
I z I z1 I z 2
2
bd 3 d 3.0210 -6 m4 I z1 bd yC 12 2
d b3 b I z2 db d yC 5.8210 -6 m4 12 2
I z I z 1 I z 2 8.8410 6 m 4
2
4. 最大弯曲正应力
M B yC 30.5 MPa Iz M ( b d yC ) s c,max B 64.5 MPa Iz
dA 0 (b) F x 0 , s A M z 0, A ysdA M (c)
10
物理方面:
s ( y ) E ( y )
单辉祖:工程力学
s E
y
(a)
sdA 0 A
(b)
A ysdA M
yC y dA A 0 A
(c)
(a)(b)
A ydA 0
2
§1 引 言
弯曲应力与对称弯曲 本章内容
材料力学C11_交变应力

M 70 50 M
对称循环,r=-1 ②查图表求各影响系数,计算构件持久限。 求K:
D r 1.4 ; 0.15 ; b 600MPa 查图 d d 求 :查图得 0.79
r=7.5
K 1.4
求 :表面精车, =0.94 0 1 0.79 0.94 1 250 69.8MPa 1 1
第11章 交变应力
11.1 交变应力与疲劳失效 11.2 交变应力的循环特征、应力幅和平均应力 11.3 持久极限 11.4 影响持久极限的因素 11.5* 对称循环下构件的疲劳强度计算 11.6* 持久极限曲线 11.7* 不对称循环下构件的疲劳强度计算 11.8* 弯扭组合交变应力的强度计算 11.9* 变幅交变应力 11.10 提高构件疲劳强度的措施 11.* 习题**
2 max min 应力幅(~ Amplitude): a 2 min 循环特征、 r max /应力比(~ ratio):
5特征量仅2个独立,如m+a 或max+r
不稳定
max m min max m min a
t t
a
对称循环(symmetric reversed
加工方法 磨 削 车 削 粗 车 未加工的表面 轴表面粗糙度 Ra/m 0.4~0.2 3.2~0.8 1.25~6.3
b/MPa
400 1 0.95 0.85 0.75 800 1 0.90 0.80 0.65 1200 1 0.80 0.65 0.45
下降明显
b高者
表面越差,下降越多 b越高,影响越显著
m, ra
K
1
a rm m
a rm
对称循环,r=-1 ②查图表求各影响系数,计算构件持久限。 求K:
D r 1.4 ; 0.15 ; b 600MPa 查图 d d 求 :查图得 0.79
r=7.5
K 1.4
求 :表面精车, =0.94 0 1 0.79 0.94 1 250 69.8MPa 1 1
第11章 交变应力
11.1 交变应力与疲劳失效 11.2 交变应力的循环特征、应力幅和平均应力 11.3 持久极限 11.4 影响持久极限的因素 11.5* 对称循环下构件的疲劳强度计算 11.6* 持久极限曲线 11.7* 不对称循环下构件的疲劳强度计算 11.8* 弯扭组合交变应力的强度计算 11.9* 变幅交变应力 11.10 提高构件疲劳强度的措施 11.* 习题**
2 max min 应力幅(~ Amplitude): a 2 min 循环特征、 r max /应力比(~ ratio):
5特征量仅2个独立,如m+a 或max+r
不稳定
max m min max m min a
t t
a
对称循环(symmetric reversed
加工方法 磨 削 车 削 粗 车 未加工的表面 轴表面粗糙度 Ra/m 0.4~0.2 3.2~0.8 1.25~6.3
b/MPa
400 1 0.95 0.85 0.75 800 1 0.90 0.80 0.65 1200 1 0.80 0.65 0.45
下降明显
b高者
表面越差,下降越多 b越高,影响越显著
m, ra
K
1
a rm m
a rm
材料力学——弯曲应力

公式推导
线应变的变化规律 与纤维到中性层的距离成正比。
从横截面上看: 点离开中性轴越远,该点的线应变越大。
2、物理关系
当σ<σP时 虎克定律
E
E
y
y
弯曲正应力的分布规律 a、与点到中性轴的距离成正比; 沿截面高度 线性分布; b、沿截面宽度 均匀分布; c、正弯矩作用下, 上压下拉; d、危险点的位置, 离开中性轴最远处.
M max ymax IZ
x
67.5 103 90 103 5.832 105
104.17MPa
6、已知E=200GPa,C 截面的曲率半径ρ q=60KN/m A FAY B 1m C 3m FBY
M C 60kN m
I z 5.832 105 m 4
M EI
4 103 88 103 46.1MPa 6 7.64 10
9KN
4KN
C截面应力计算
A FA
M 1m
C 1m
B
1m FB
C截面应力分布 应用公式
t ,max
My Iz
2.5KNm
2.5 103 88 103 28.8MPa 6 7.64 10
Fb Fa
C截面: max M C Fb3 62.5 160 32 46.4MPa d W 3
zC
2
0.13
32
(5)结论 轮轴满足强度条件
一简支梁受力如图所示。已知 [ ] 12MPa ,空心圆截面 的内外径之比 一倍,比值不变,则载荷 q 可增加到多大? q=0.5KN/m A B
反映了截面的几何形状、尺寸对强度的影响
最大弯曲正应力计算公式
材料力学弯曲剪应力
F* N2
自由边 t1 t1
A* F* dx
N1
u
但是,如果从长为dx的梁段 中用铅垂的纵截面在翼缘上截取如 图所示包含翼缘自由边在内的分离 体就会发现,由于横力弯曲情况下 梁的相邻横截面上的弯矩不相等, 故所示分离体前后两个同样大小的 部分横截面上弯曲正应力构成的合 力FN*1 FN*2
和 不相等,因而铅垂的纵截
Iz S*
z ,max
d
75103 N 47.73 102m 12.5 103m
12.6 106 Pa 12.6 MPa
例题 4-13
2. 求ta ta
其中:
FS
,max
S
* za
Izd
S
* za
166
mm
21
mm
560 mm 2
21
mm 2
940 103 mm3
于是有:
ta
FS
S
* z
Izb
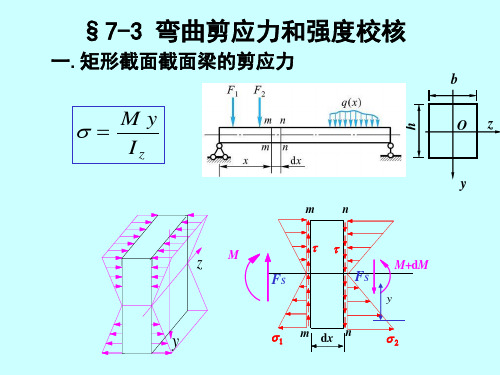
§5.7 梁的切应力
3.切应力分布规律
t
FS
S
* z
FS ( h 2 y 2 )
I zb 2I z 4
6FS bh3
h 2 4
y2
S* z
A*
y* C
b
h
y
y
h 2
y
2
2
b 2
h2 4
y2
Iz
bh3 12
b
F
S
h y
t
y
z
t max
t
t max
3 2
FS bh
规律变化的。
思考题: 试通过分析说明,图a中
所示上、下翼缘左半部分 和右半部分横截面上与腹 板横截面上的切应力指向 是正确的,即它们构成了 “切应力流”。
第11章材料力学弯曲应力练习题

mpa132804012301010118图示简支粱由no28工字钢制成在集度为q的均布载荷作用下测得横截面c底边的纵向正应变30104试计算梁内的最大弯曲正应力已知钢的弹性模量e200gpaa1m
11—5(a) 试计算图示截面对水平形心轴z的惯性矩。
解: (1)确定形心轴位置
yC A2 C 60 Wz 4Wz
可得:
60 4Wz q 240Wz 2 a
1 2 qa 4
3、计算梁内最大弯曲正应力; 由弯矩图得:
M max 9 qa 2 32
1 2 qa 4
所以梁内最大弯曲正应力:
max
M max 9 240Wz 67.5MPa Wz 32Wz
FN 12103 2、计算应力; N MPa A 5 (40 x)
M
M 6 103 x MPa W 1 5 (40 x) 2 6
3、根据强度条件;
N M
12 103 6 103 x 100 5 (40 x) 1 5 (40 x) 2 6
2、计算最大弯曲正应力; 最大弯矩在固定端。;
M max 7.5 103 103 6 max 176MPa 2 Wz 40 80
3、计算固定端k点处弯曲正应力;
M max yk 7.5 103 103 3012 k 132MPa 3 Iz 40 80
结论:
c=146.9mm
3
A截面的强度足够。
11—17 外伸梁承受载荷F作用,已知载荷F=20 kN,许用应力[σ]=160 MPa,许用切应力[τ] =90 MPa,试选择工字钢型号。
解: 1、绘制剪力图、弯矩图;
11—5(a) 试计算图示截面对水平形心轴z的惯性矩。
解: (1)确定形心轴位置
yC A2 C 60 Wz 4Wz
可得:
60 4Wz q 240Wz 2 a
1 2 qa 4
3、计算梁内最大弯曲正应力; 由弯矩图得:
M max 9 qa 2 32
1 2 qa 4
所以梁内最大弯曲正应力:
max
M max 9 240Wz 67.5MPa Wz 32Wz
FN 12103 2、计算应力; N MPa A 5 (40 x)
M
M 6 103 x MPa W 1 5 (40 x) 2 6
3、根据强度条件;
N M
12 103 6 103 x 100 5 (40 x) 1 5 (40 x) 2 6
2、计算最大弯曲正应力; 最大弯矩在固定端。;
M max 7.5 103 103 6 max 176MPa 2 Wz 40 80
3、计算固定端k点处弯曲正应力;
M max yk 7.5 103 103 3012 k 132MPa 3 Iz 40 80
结论:
c=146.9mm
3
A截面的强度足够。
11—17 外伸梁承受载荷F作用,已知载荷F=20 kN,许用应力[σ]=160 MPa,许用切应力[τ] =90 MPa,试选择工字钢型号。
解: 1、绘制剪力图、弯矩图;
材料力学 第11章 组合变形习题集

横截面m-m上任一点C(y,z)处由 弯矩Mz和My引起的正应力分别为
M z y M cos y M y z M sin z
Iz
Iz
Iy
Iy
38
C点的正应力
' ''
M
cos
Iz
y
sin
Iy
z
悬臂梁固定端截面A的弯矩Mz和My 均达到最大值,故该截
面是危险截面。设yo、zo为中性轴上任一点的坐标,并令σ
算 圆轴表面上与轴线成30°方位上的正应变。
32
解: (1)由内力图知,所有截面均为危险截面,危险点为靠近
轴表面的各点,应力状态如图。计算危险点的主应力。轴力
引起的正应力
FN 4F
A πd 2
扭矩引起的切应力
T M 8F
Wp Wp 5πd 2
危险点处的主应力为
1
2
(
)2
( )2
它在y、z两轴上的截距分别为
y* z* h / 2
该截面惯性半径的平方为
iy2
Iy A
h2 12
iz2
Iz A
b2 12
28
中性轴①对应的核心边界上点1的坐标为
ey1
iz2 y*
0
ez1
iy2 z*
h 6
按上述方法可求得与它们对应的截面核
心边界上的点2、3、4,其坐标依次为:
ey2
b 6
ez2 0
车臂的直径d。
18
解:两个缆车臂各承担缆车重量的一半,如 图。则缆车臂竖直段轴力为FN=W/2=3kN 弯矩为M=Wb/2=540N·m 危险截面发生在缆车臂竖直段左侧,由强度条件
第11章 深受弯构件

a)正截面弯曲破坏
b)斜截面弯曲破坏 图11-1 简支深梁的弯曲破坏
c)拉杆拱受力图式
§11-1深受弯构件
(2)剪切破坏 ( 较高) 1) 斜压破坏
2) 劈裂破坏
(a)斜压破坏
(b)劈裂破坏
(3)局部受压和锚固破坏
§11-1深受弯构件
二、短梁的受力性能
(1)弯曲破坏 适筋梁破坏 少筋梁破坏 超筋梁破坏 (2)剪切破坏 斜压破坏 (m<1) 剪压破坏 (m=1~2.5) 斜拉破坏 (m>2.5) (3)局部受压和锚固破坏
第11章 深受弯构件
深受弯构件
基本概念和应用
浅梁(普通受弯构件)
P
P h
l / h >5 l / h≤5
l 深受弯构件
l / h≤2
(简支梁)
l / h ≤ 2.5 (连续梁) 2 <l / h ≤ 5 (简支梁) 2.5 <l / h ≤ 5(连续梁)
深梁
深受弯构件
短梁
深受弯构件
基本概念和应用
图11-8 撑杆计算高度 a)盖梁立面示意图 b)盖梁侧面示意图
0Td fsd As
(11-10)
3.抗剪承载力计算
可按一般钢筋混凝土受弯构件计算。
§11-2 深受弯构件的计算
图11-3 柱式墩台示意图 a)正面图 b)侧面图
§11-2 深受弯构件的计算
一、深受弯构件(短梁)的计算
1. 深受弯构件的正截面抗弯承载力计算
fsd As C
0Md Mu fsd As z
l z (0.75 0.05 )( h0 0.5 x) h
深受弯构件
基本概念和应用
深受弯构件
弯曲应力-材料力学

弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
另外,根据不同的弯曲形式和受力情 况,还可以采用其他计算公式来求解 弯曲应力,如均布载荷下的简支梁、 集中载荷下的悬臂梁等。
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
弯曲应力可能导致材料发生弯曲变形,影响结构的稳定性和精度。
弯曲应力对材料刚度的影响
弯曲应力对材料的刚度有影响,材料的刚度随着弯曲应力的增大而 减小。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
弯曲应力
材料的韧性和强度都会影响其弯曲应力的大小和分布。韧性好的材料能够更好地分散和 吸收弯曲应力,而高强度的材料则能够承受更大的弯曲应力而不发生断裂。
材料韧性、强度与弯曲应力的关系
韧性
是指材料在受到外力作用时吸收能量的能力。韧性好的材料能够吸收更多的能量,从而 减少因弯曲应力而产生的脆性断裂。
强度
剪切应力的分布
剪切应力在材料截面的边缘最大,向中性轴方向 逐渐减小。
3
剪切应力和弯曲应力的关系
剪切应力和弯曲应力共同作用,影响梁的承载能 力和稳定性,在设计时需要考虑两者的相互作用。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 惯性矩计算
Iz = Iz1 + Iz2
I z1
=
bδ 3 12
+ bδ
yC
−δ2
2
= 3.02×10-6
m4
I
z
2
= δb 3 12
+δb δ
+
b 2
−
yC
2
= 5.82×10-6
m4
I z = I z1 + I z2 =8.84×10−6 m4
4. 最大弯曲正应力
σ
t,max
本章主要内容
l 对称弯曲正应力 l 对称弯曲切应力 l 弯曲强度计算与合理强度设计 l 双对称截面梁非对称弯曲
应力与强度 l 弯拉(压)组合应力与强度
§2 对称弯曲正应力
r 弯曲试验与假设 r 对称弯曲正应力公式 r 例题
r 弯曲试验与假设
弯 曲 试 验
试验现象 (纯弯与正弯矩作用)
u 横线为直线, 仍与纵线正交 v 靠顶部纵线缩短, 靠底部纵
90kN 2. C 截面上K点正应力
x
σK
=
M C ⋅ yK IZ
=
60 ×103 × (180 − 30) ×10−3 2
5.832 ×10−5
= 61.7 ×106 Pa = 61.7MPa (压应力)
q=60kN/m
A
1m
FAY
C
l = 3m
3. C 截面最大正应力
120
C 截面弯矩
B
x
180
第 11 章 弯曲应力
本章主要研究:
l 对称弯曲正应力 l 对称弯曲切应力 l 梁的强度分析与设计 l 非对称弯曲应力 l 弯拉(压)组合问题
§1 引言 §2 对称弯曲正应力 §3 惯性矩与平行轴定理 §4 对称弯曲切应力 §5 梁的强度条件 §6 梁的合理强度设计 §7 双对称截面梁的非对称弯曲 §8 弯拉(压)组合
§1 引 言
r 弯曲应力与对称弯曲 r 本章内容
r 弯曲应力与对称弯曲
弯曲应力 l 弯曲正应力 梁弯曲时横截面上的σ l 弯曲切应力 梁弯曲时横截面上的τ
对称弯曲
对称截面梁,在纵向对称面承受横向外力时的受力与 变形形式-对称弯曲
r 弯曲应力与对称弯曲
梁的纵向对称面: 梁的横截面竖向对称轴与梁的轴线组成的平面。
=
bh2 6
空心矩形截面
IZ
=
b0h03 12
−
bh3 12
WZ
=
( b0h03 12
−
bh3 12
) /(h0
/
2)
r 平行轴定理
平行轴定理
建立 Iz 与 Iz0 的关系
Iz = ∫A y2dA Iz = ∫A( y0 + a)2dA
Iz = ∫A y02dA + 2a∫A y0dA + Aa2
z 3.全梁上最大正应力
FBY
y
FS 90kN
(+ ) (− )
(+)
M ql2 / 8 = 67.5kN⋅ m
解:1. 求支反力
FAy = 90kN FBy = 90kN
M C = 90×1− 60×1× 0.5 = 60kN ⋅ m
x
IZ
=
bh3 12
=
0.12× 0.183 12
= 5.832 ×10−5 m4
=
M B yC Iz
= 30.5
MPa
σ
c,max
=
M
B
(
b+δ Iz
−
yC
)
=
64.5
MPa
例 3-3 已知:钢带厚 δ = 2mm, 宽 b = 6mm, D=1400mm, E=200GPa。试计算:带内的 σmax 与 M
解:1. 问题分析 已知钢带的变形(轴线曲率 半径),求钢带应力与内力
r 静矩与惯性矩
静矩
∫ Sz =
ydA = AyC
A
[L]3
-截面对z轴的静矩
n
n
∑ Sz = Sz i = ∑ Ai yCi
i =1
i =1
n
∫ ∑ Sy =
zdA=
A
AzC
S y = Ai zCi
i =1
惯性矩
Iz = ∫A y2dA [L]4
-截面对 z 轴的惯性矩
n
Iz = ∑ Izi
i=1
∫σdA = 0 (b) A
∫ yσdA = M (c) A
(a)→(b)
∫ ydA=0 A
∫ ydA
yC =
A
A
=0
中性轴通过横截面形心
(a)→(c)
∫E y2dA= M
ρA
∫ Iz = y2dA-截面对z轴的惯性矩 A
1= M ρ EI z
(d)
EIZ-弯曲刚度
(d)→(a)
σ ( y)= My Iz
中性轴与形心轴
中性轴-横截面受拉与受压区的分界线 形心轴-通过横截面形心的坐标轴
截面弯曲刚度与抗弯截面系数 弯曲刚度EI-代表梁截面抵抗弯曲变形的能力 抗弯截面系数Wz-代表梁截面几何性质对弯曲强度 的影响
r 例题
例 2-1 梁用№18 工字钢制成,Me=20 kN•m, E=200 GPa。 试计算:最大弯曲正应力σmax ,梁轴曲率半径 ρ
w 正应力公式: σ ( y) = My
Iz
σ
max
=
M Wz
(Wz - 抗弯截面系数)
x 应用条件: σ max ≤σ p , 对称弯曲 , 纯弯与非纯弯
一些易混淆的概念
对称弯曲与纯弯曲 对称弯曲-对称截面梁,在纵向对称面承受横向外 力时的受力与变形形式 纯 弯 曲-梁或梁段各横截面的剪力为零弯矩为常 数的受力状态
∫ I z0 = A y02dA
∫A y0dA = 0
I z = I z0 + Aa2
同理得: I y = I y0 + Ab2
Cy0z0-形心直角坐标系 Oyz -任意直角坐标系
二者平行
例
q=60kN/m
A
1m
FAY
C
l = 3m
120
1.C 截面上K点正应力
180
B
K
x
30 2.C 截面上最大正应力
τ
max
=
3 2
FS A
截面翘曲与非纯弯推广
切应力非均布 → 切应变非均布 → 截面翘曲 l 当FS=常数时, ab = a'b' ,弯曲 σ 仍保持线性分布 l 当梁上作用横向分布载荷时,只要 l > 5h,纯弯σ
线伸长 Ž 纵线伸长区,截面宽度减小
纵线缩短区, 截面宽度增大
弯曲假设
u 横截面变形后保持平面,仍与纵线正交-弯曲平 面假设
v 各纵向“纤维”处于单向受力状态-单向受力假设
推论 u 梁内存在一长度不变的过渡层-中性层 中性层与横截面的交线-中性轴
v 中性轴⊥截面纵向对称轴 w 横截面间绕中性轴相对转动
=
2 5.832 ×10−5
= 104.17 ×106 Pa = 104.17MPa
M ql2 / 8 = 67.5kN⋅ m
r 例题
例 3-2 已知:F=15 kN, l=400 mm, b=120mm, δ=20mm 试计算:截面 B-B 的最大拉应力σt,max与压应力σc,max
解:1. 弯矩计算
解:1. 工字钢(GB 706-1988) 一种规范化、系列化的工字形截面的标准钢材 №18 工字钢:
I z = 1.66 × 10−5 m4 Wz = 1.85 × 10−4 m3
I z = 1.66 × 10−5 m4 Wz = 1.85 × 10−4 m3
Me=20 kN•m,E=200 GPa,求 σmax 与 ρ
σ
max
=
Mymax Iz
Wz
=
Iz ymax
-抗弯截面系数
σ
max
=M Wz
总结
假设 平面假设,单向受力假设
综合考虑三方面
ε
(
y)=
y ρ
结论
σ ( y)= Eε ( y)
∫ ∫ σdA=0 yσdA= M
A
A
u 中性轴位置:中性轴过截面形心
v 中性层曲率:1 = M
ρ EI z
(I z -惯性矩) (EI z - 截面弯曲刚度)
u 应力~变形关系:
σ =E y ρ
∴
σ max
=
E
ymax ρ
v 内力~变形关系:
1= M ρ EIz
∴
M
=
EI z ρ
带厚 δ=2 mm, 宽 b= 6mm, D = 1400mm,
E = 200GPa,求 σmax 与 M
2. 应力计算
σ max
=
E
ymax ρ
ρ = D + δ = 0.701 m 22
σ ( y)= Eε ( y)
σ
(
y)=
E
y ρ
(a)
r 对称弯曲正应力公式
应力的分布图: M
σ = E ε = Ey ρ
z 中性轴 M
x
Z
σmax
y
σmax
y
中性轴的位置?
中性层的曲率
1 =? ρ
1 ρ 为梁弯曲变形后的曲率
M Z 静力方面:
y
由横截面上的弯矩和正应力
zAσdA x 的关系→正应力的计算公式。
2. 应力计算
