深入理解计算机系统习题答案
计算机操作系统习题及答案(5)

计算机操作系统习题及答案(5)
计算机操作系统习题及答案(5)
1:进程管理
1.1 进程与线程的区别是什么?
答案:进程是操作系统中执行的一个程序,它包含了程序代码、数据以及其运行状态的描述信息。
线程是进程中的一个执行单元,
它可以与同一进程中的其他线程共享资源。
1.2 进程调度算法有哪些?
答案:常见的进程调度算法有先来先服务(FCFS)、最短作业
优先(SJF)、优先级调度、轮转调度等。
2:存储管理
2.1 什么是虚拟内存?
答案:虚拟内存是一种将物理内存和磁盘空间组合起来使用的
技术。
它允许进程访问超过物理内存大小的地址空间,将不常用的
数据存储在磁盘上,并且能够在需要时将其换入内存。
2.2 页面置换算法有哪些?
答案:常见的页面置换算法有先进先出(FIFO)、最近未使用(LRU)、时钟置换算法等。
3:文件系统
3.1 什么是文件系统?
答案:文件系统是操作系统中用于管理存储设备上文件的一种
机制。
它定义了文件和目录的层次结构以及文件的访问方式。
3.2 文件系统的常见组织方式有哪些?
答案:常见的文件系统组织方式有单层目录结构、多层目录结
构和索引节点结构。
附件:无
法律名词及注释:
1:版权法:保护创造者对其作品的独立性和权益的法律制度。
2:著作权:在法律上规定的对创作原创性个人和集体作品的
特殊权利。
3:商标法:保护商标所有人对其商标的专有权的法律制度。
深入理解计算机系统(5.1)------优化程序性能

深⼊理解计算机系统(5.1)------优化程序性能 你能获得的对程序最⼤的加速⽐就是当你第⼀次让它⼯作起来的时候。
在讲解如何优化程序性能之前,我们⾸先要明确写程序最主要的⽬标就是使它在所有可能的情况下都能正常⼯作,⼀个运⾏的很快的程序但是却是错误的结果是没有任何⽤处的,所以我们在进⾏程序性能优化之前,⾸先要保证程序能正常运⾏,且结果是我们需要的。
⽽且在很多情况下,让程序跑的更快是我们必须要解决的问题。
⽐如⼀个程序要实时处理视频帧或者⽹络包,那么⼀个运⾏的很慢的程序就不能解决此问题。
再⽐如⼀个计算任务计算量⾮常⼤,需要数⽇或者数周,如果我们哪怕只是让它运⾏的快20%也会产⽣重⼤影响。
1、编写⾼效程序的切⼊点 ①、选择⼀组合适的算法和数据结构。
②、编写出编译器能够有效优化以转换成⾼效可执⾏的源代码。
③、多线程并⾏处理运算。
对于第⼀点,程序=数据结构+算法,选择合适的数据结构和算法⽆疑对于提⾼程序的运⾏效率有很⼤的影响。
第⼆点对于编程者则需要理解编译器的优化能⼒以及局限性,编写程序看上去只是⼀点⼩⼩的改动,可能都会引起编译器优化⽅式很⼤的变化;第三点技术主要这对运算量特别⼤的运算,我们将⼀个⼤的任务分成多个⼩任务,这些任务⼜可以在多核和多处理器的某种组合上并⾏的计算,这⾥我们也需要知道,即使是利⽤并⾏性,每个并⾏的线程都要以最⾼性能的⽅式执⾏。
2、编译器的优化能⼒和局限性 正确性,正确性,正确性这个要着重提醒,所以编译器必须很⼩⼼的对程序使⽤安全的优化。
限制编译器只进⾏安全的优化,会消除⼀些造成错误的运⾏结果,但是这也意味着程序员必须花费更⼤的⼒⽓写出程序使编译器能够将之转换为有效机器代码。
对于下⾯两个程序:void add1(int *xp,int *yp){*xp += *yp;*xp += *yp;}void add2(int *xp,int *yp){*xp += 2* *yp;} 对上上⾯两个函数add1和add2,它们都是将存储在由指针 yp 指⽰的位置处的值两次加到指针 xp 指⽰的位置处的值。
深入理解计算机系统配套练习卷终审稿)

深入理解计算机系统配套练习卷文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-《深入》题目李永伟第一章题目我们通常所说的“字节”由_____个二进制位构成。
A 2B 4C 6D 8微型计算机硬件系统中最核心的部位是__。
A 主板B. CPUC 内存处理器D I/O设备CPU中有一个程序计数器(又称指令计数器)。
它用于存储__。
A.保存将要提取的下一条指令的地址B.保存当前CPU所要访问的内存单元地址C.暂时存放ALU运算结果的信息D.保存当前正在执行的一条指令下列叙述中,正确的是A.CPU能直接读取硬盘上的数据B.CPU能直接存取内存储器C.CPU由存储器、运算器和控制器组成D.CPU主要用来存储程序和数据“32位微型计算机”中的32指的是()。
A.微机型号B.内存容量C.运算速度D.机器字长第二章题目求下列算是得值,结果用十六进制表示:0x503c + 64 =______A. 0x507cB.0x507bC. 0x506cD.0x506b将十进制数167用十六进制表示的结果是______A.0XB7B.0XA7C.0XB6D.0XA6位级运算:0x69 & 0x55 的结果是_______A.0X40B.0X41C.0X42D.0X43逻辑运算!!0x41的结果用十六进制表示为_____A.0X00B.0X41C.0X14D.0X01位移运算:对参数则x>>4(算术右移)的结果是______A.[01010000]B.[00001001]C.D.截断:假设一个4位数值(用十六进制数字0~F表示)截断到一个3位数值(用十六进制0~7表示),[1011]截断后的补码值是___A.-3B.3C.5D.-5浮点表示:数字5用浮点表示时的小数字段frac的解释为描述小数值f,则f=______A.1/2B.1/4C.1/8D.1/162.4.2 _25-8数字5用浮点表示,则指数部分E=_____A.1B.2C.3D.4数字5用浮点表示,则指数部分位表示为___A .2^ (K-1)+1B. 2^K+1C. 2^ (K-1)D. 2^K浮点运算:(3.14+1e10)-1e10 在计算机中的运算结果为A .3.14B .0C .1e10D .0.0第三章题目计算Imm(E b ,E i ,s)这种寻址模式所表示的有效地址:A .Imm + R[E b ]+R[E s ] *sB. Imm + R[E b ]+R[Es]C. Imm + R[E b ]D. Imm +R[E s ]下面这种寻址方式属于_____M[R[E b ]]A. 立即数寻址B. 寄存器寻址C. 绝对寻址D. 间接寻址假设初始值:%dh=CD,则执行下面一条指令后,%eax的值为多少?MOVB %DH ,%ALA. %eax= 987654CDB. %eax= CD765432C %eax= FFFFFFCDD. %eax= 000000CD假设初始值:%dh=CD,则执行下面一条指令后,%eax的值为多少?MOVSBL %DH ,%ALA. %eax= 987654CDB. %eax= CD765432C %eax= FFFFFFCDD. %eax= 000000CD假设初始值:%dh=CD,则执行下面一条指令后,%eax的值为多少?MOVZBL %DH ,%ALA. %eax= 987654CDB. %eax= CD765432C %eax= FFFFFFCDD. %eax= 000000CD假设寄存器%eax的值为x,%ecx的值为y,则指明下面汇编指令存储在寄存器%edx中的值Leal (%eax ,%ecx),%edxA. xB yC x + yD x –y假设寄存器%eax的值为x,%ecx的值为y,则指明下面汇编指令存储在寄存器%edx中的值Leal 9(%eax ,%ecx , 2),%edxA. x +y +2B 9*(x + y + 2)C 9 + x + y +2D 9 + x + 2y条件码CF表示______A 零标志B 符号标志C 溢出标志D进位标志条件码OF表示______A 零标志B 符号标志C 溢出标志D进位标志在奔腾4上运行,当分支行为模式非常容易预测时,我们的代码需要大约16个时钟周期,而当模式是随机时,大约需要31个时钟周期,则预测错误处罚大约是多少?A. 25B. 30C. 35D. 40第五章题目指针xp指向x,指针yp指向y,下面是一个交换两个值得过程:Viod swap (int *xp ,int *yp){*xp = *xp + *yp //x+y*yp = *xp - *yp //x+y-y=x*xp = *xp - *yp //x+y-x=y}考虑,当xp=yp时,xp处的值是多少A . xB. yC . 0D.不确定考虑下面函数:int min( int x , int y ) { return x < y x : y;}int max( int x , int y ){ return x < y y : x; }viod incr (int *xp ,int v) { *xp += v;}int square( int x ) { return x *x; }下面一个片段调用这些函数:for( i = min(x,y) ;i< max(x,y); incr(&i,1))t +=square(i) ;假设x等于10,y等于100.指出该片段中4个函数 min (),max(),incr(),square()每个被调用的次数一次为A.91 1 90 90B.1 91 90 90C.1 1 90 90D.90 1 90 90考虑下面函数:int min( int x , int y ) { return x < y x : y;}int max( int x , int y ){ return x < y y : x; }viod incr (int *xp ,int v) { *xp += v;}int square( int x ) { return x *x; }下面一个片段调用这些函数:for( i = max(x,y) -1;i >= min(x,y); incr(&i,-1))t +=square(i) ;假设x等于10,y等于100.指出该片段中4个函数 min (),max(),incr(),square()每个被调用的次数一次为A.91 1 90 90B.1 91 90 90C.1 1 90 90D.90 1 90 90考虑下面函数:int min( int x , int y ) { return x < y x : y;}int max( int x , int y ){ return x < y y : x; }viod incr (int *xp ,int v) { *xp += v;}int square( int x ) { return x *x; }下面一个片段调用这些函数:Int low = min(x,y);Int high = max(x,y);For(i= low;i<high;incr(&i,1)t +=square(i);假设x等于10,y等于100.指出该片段中4个函数 min (),max(),incr(),square()每个被调用的次数依次为A.91 1 90 90B.1 91 90 90C.1 1 90 90D.90 1 90 90假设某个函数有多个变种,这些变种保持函数的行为,又具有不同的性能特性,对于其中的三个变种,我们发现运行时间(以时钟周期为单位)可以用下面的函数近似的估计版本1:60+35n版本2:136+4n版本3:157+1.25n问题是当n=2时,哪个版本最快?A.1B.2C.3D.无法比较假设某个函数有多个变种,这些变种保持函数的行为,又具有不同的性能特性,对于其中的三个变种,我们发现运行时间(以时钟周期为单位)可以用下面的函数近似的估计版本1:60+35n版本2:136+4n版本3:157+1.25n问题是当n=5时,哪个版本最快?A.1B.2C.3D.无法比较假设某个函数有多个变种,这些变种保持函数的行为,又具有不同的性能特性,对于其中的三个变种,我们发现运行时间(以时钟周期为单位)可以用下面的函数近似的估计版本1:60+35n版本2:136+4n版本3:157+1.25n问题是当n=10时,哪个版本最快?A.1B.2C.3D.无法比较下面有一个函数:double poly( double a[] ,double x, int degree){long int i;double result = a[0];double xpwr =x;for(i=1 ; i<=degree; i++){result += a[i] *xpwr;xpwr =x *xpwr;}return result;}当degree=n,这段代码共执行多少次加法和多少次乘法?A.n nB.2n nC.n 2nD.2n 2n一名司机运送一车货物从A地到B地,总距离为2500公里。
深入理解计算机系统(3.1)------汇编语言和机器语言

深⼊理解计算机系统(3.1)------汇编语⾔和机器语⾔ 《深⼊理解计算机系统》第三章——程序的机器级表⽰。
作者⾸先讲解了汇编代码和机器代码的关系,阐述了汇编承上启下的作⽤;接着从机器语⾔IA32着⼿,分别讲述了如何存储数据、如何访问数据、如何完成运算以及如何进⾏跳转。
通过这些步骤,⼜告诉了我们分⽀语句、循环语句是怎么完成的,函数调⽤、栈帧结构以及递归过程。
最后能通过编译器产⽣的汇编代码表⽰,我们要了解编译器和它的优化能⼒,知道编译器能为我们完成哪些⼯作。
⽽这篇博客我们将讲解汇编和机器代码的关系。
⾸先下⾯⼀张图是C语⾔、汇编语⾔以及翻译过的机器语⾔,⼤家可以先有个⼤概的眼熟。
上图引⽤⾄:1、机器语⾔ 这系列博客第⼀篇我们就详细讲解了程序的编译,⼀个C语⾔程序是经过编译器变成汇编程序,然后通过汇编器变成机器代码,最后被计算机执⾏。
计算机是不能直接识别我们所编写的C程序或者Java程序的。
它只能识别机器语⾔,⽽机器语⾔是⽤⼆进制代码表⽰的计算机能直接识别和执⾏的⼀种机器指指令系统令的集合。
早期计算机就是指可以执⾏机器指令,进⾏运算的机器。
在我们常⽤的PC机中,有⼀个芯⽚,就是我们常说的CPU(Central Processing Unit,中央处理单元)可以完成前⾯所说的计算机的功能,但是每⼀种这样的微处理器(CPU)由于硬件设计和内部结构的不同,就需要⽤不同的电平脉冲来控制,使它⼯作。
所以每⼀种微处理器都有⾃⼰的机器指令集,也就是机器语⾔。
早期的程序设计均使⽤机器语⾔。
程序员们将⽤0, 1数字编成的程序代码打在纸带或卡⽚上,1打孔,0不打孔,再将程序通过纸带机或卡⽚机输⼊计算机,进⾏运算。
⽤机器语⾔编写程序,编程⼈员要⾸先熟记所⽤计算机的全部指令代码和代码的涵义。
⼿编程序时,程序员得⾃⼰处理每条指令和每⼀数据的存储分配和输⼊输出,还得记住编程过程中每步所使⽤的⼯作单元处在何种状态。
这是⼀件⼗分繁琐的⼯作。
《深入理解计算机系统》第三版第三章家庭作业答案

《深⼊理解计算机系统》第三版第三章家庭作业答案简述相信⼤部分⼈在做这些题的时候,因为书中没有给答案,⽽去⽹上找参考答案,⽐如那些⾼阅读量的博客和git 。
当然,我也是这样,但他们的答案中还是有好多错误,⽐如3.59他们⼏乎都没讲清楚提⽰中的公式怎么来的,3.60中对移位操作中对%cl 的读取,等等。
希望读者们在阅读这些⽂章时,要带着⾃⼰的思想和疑问去理解,⽽不是⼀味地觉得答案就肯定是对的,当然,本⽂有任何错误,也欢迎各位指出。
3.58long decode2(long x,long y,long z){y = y - z;x = x * y;y <<= 63;y >>= 63;return y ^ x;}y 先左移63位,再右移63位,如果之前y 是奇数,那么y 的⼆进制全是1;y 是偶数,那么y 的⼆进制全是0.3.59⾸先讲解⼀下,提⽰⾥的公式x =264∗x h +x l x =264∗xh +xl ,之所以可以这么写是因为符号拓展,以4位⼆进制int 为例:1111的补码数,为-1.将其进⾏符号拓展后为1111 1111,其值也为-1,但这⾥可以将1111 1111写为⾼位1111的补码数 * 2424 + 低位1111的⽆符号数:即-1 * 2424 + 15 = -1.原理:%rdx 和%rax 的⼆进制连起来表⽰这个数,既然连起来了,符号位就跑到了%rdx 的最⾼位了,除符号位权值为负外,其余位的权值均为正。
所以,⾼位寄存器%rdx 当做补码数,低位寄存器%rax 当做⽆符号数。
因为符号位现在在⾼位寄存器那⼉呢,所以⾼位寄存器当做补码数了;⽽低位寄存器的每⼀位的权值现在都是正的了,所以低位寄存器要当做⽆符号数。
所以x l xl 为T 2U (x )T2U(x)即x 的⼆进制表⽰作为⽆符号数。
x l xl 与x x 有相同的位级表⽰。
x h xh ,当原数符号位为1,64位⼆进制位上全为1,其值为-1;当原数符号位为0时,64位⼆进制位上全为0,其值为0。
深入理解计算机系统(第二版)家庭作业问题详解

int saturating_add(int x, int y){int w = sizeof(int)<<3;int t = x + y;int ans = x + y;x>>=(w-1);y>>=(w-1);t>>=(w-1);int pos_ovf = ~x&~y&t;int neg_ovf = x&y&~t;int novf = ~(pos_ovf|neg_ovf);return(pos_ovf & INT_MAX) | (novf & ans) | (neg_ovf & INT_MIN); }2.74对于有符号整数相减,溢出的规则可以总结为:t = a-b;如果a, b 同号,则肯定不会溢出。
如果a>=0 && b<0,则只有当t<=0时才算溢出。
如果a<0 && b>=0,则只有当t>=0时才算溢出。
不过,上述t肯定不会等于0,因为当a,b不同号时:1) a!=b,因此a-b不会等于0。
2) a-b <= abs(a) + abs(b) <= abs(TMax) + abs(TMin)=(2^w - 1)所以,a,b异号,t,b同号即可判定为溢出。
int tsub_ovf(int x, int y){int w = sizeof(int)<<3;int t = x - y;x>>=(w-1);y>>=(w-1);t>>=(w-1);return(x != y) && (y == t);}顺便整理一下汇编中CF,OF的设定规则(个人总结,如有不对之处,欢迎指正)。
t = a + b;CF: (unsigned t) < (unsigned a) 进位标志OF: (a<0 == b<0) && (t<0 != a<0)t = a - b;CF: (a<0 && b>=0) || ((a<0 == b<0) && t<0) 退位标志OF: (a<0 != b<0) && (b<0 == t<0)汇编中,无符号和有符号运算对条件码(标志位)的设定应该是相同的,但是对于无符号比较和有符号比较,其返回值是根据不同的标志位进行的。
深入理解计算机系统(第三版)第二章家庭作业答案
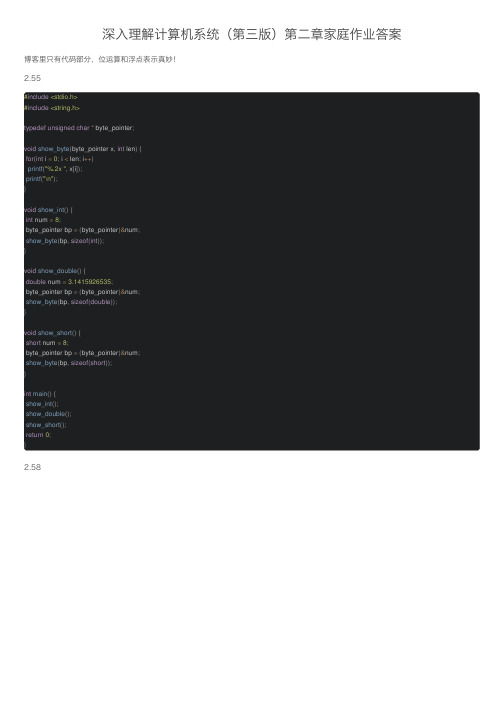
深⼊理解计算机系统(第三版)第⼆章家庭作业答案博客⾥只有代码部分,位运算和浮点表⽰真妙!2.55#include <stdio.h>#include <string.h>typedef unsigned char* byte_pointer;void show_byte(byte_pointer x,int len){for(int i =0; i < len; i++)printf("%.2x ", x[i]);printf("\n");}void show_int(){int num =8;byte_pointer bp =(byte_pointer)#show_byte(bp,sizeof(int));}void show_double(){double num =3.1415926535;byte_pointer bp =(byte_pointer)#show_byte(bp,sizeof(double));}void show_short(){short num =8;byte_pointer bp =(byte_pointer)#show_byte(bp,sizeof(short));}int main(){show_int();show_double();show_short();return0;}2.58#include <iostream>using namespace std;typedef unsigned char* byte_point;int is_little_endian(){int32_t num =1;byte_point bp =(byte_point)# printf("%s\n", bp);cout <<*bp << endl;printf("%d\n", num);if(*bp)return1;elsereturn0;}int main(){printf("%d\n",is_little_endian());}2.59typedef unsigned char* byte_point;void show_byte(int x,int len){byte_point bp =(byte_point)&x;for(int i =0; i < len; i++)printf("%.2x ", bp[i]);printf("\n");}byte_point change(int x,int y){byte_point bx =byte_point(&x);byte_point by =byte_point(&y);byte_point bz =(byte_point)malloc(sizeof(int));for(int i =0; i <sizeof(int); i++){if(i ==0)*bz =*bx;else*(bz + i)=*(by + i);}return bz;}int main(){int x =0x89abcdef;int y =0x76543210;printf("%d %d\n", x, y);byte_point z =change(x, y);show_byte(x,sizeof(int));show_byte(y,sizeof(int));for(int i =0; i <sizeof(int); i++)printf("%.2x ", z[i]);// show_byte(z, sizeof(int));return0;}2.60#include <stdio.h>unsigned replace_byte(unsigned x,int i,unsigned char b){ int move = i <<3;return(x &~(0xFF<< move)| b << move);}int main(){int x =0x12345678;printf("0x%.8X\n",replace_byte(x,2,0xAB));printf("0x%.8X\n",replace_byte(x,0,0xAB));return0;}2.61int main(){int move =(sizeof(int)-1)<<3;//全为1输出1,否则输出0int x =0x0;int y =0xffffffff;printf("%d %d\n",!(x ^~0x0),!(y ^~0x0));printf("%d %d\n",!(~x),!(~y));//全为0输出1printf("%d %d\n",!(x ^0),!(y ^0));printf("%d %d\n",!x,!y);//最低有效字节全为1输出1printf("%d %d\n",!(~(x &0xff)<< move),!(~(y &0xff)<< move)); //最⾼有效字节全为0输出1printf("%d %d\n",!(x >> move),!(y >> move));printf("%d\n", y >> move);return0;}2.62#include <stdio.h>bool int_shifts_are_arithmetic(){int x =0x80000000;return(x >>30)&8;}int main(){printf("%d",int_shifts_are_arithmetic());return0;}2.63signed srl(unsigned x,int k){unsigned xsra =(int)x >> k;int obj =~(((1<< k)-1)<<((sizeof(int)<<3)- k)); return xsra & obj;}signed sra(int x,int k){int xsrl =(unsigned) x >> k;int sum =sizeof(int)<<3;int judge =1<<(sum -1- k);judge &= xsrl;int obj =~(judge -1);return xsrl | obj;}int main(){printf("%.8x\n",srl(0x81001100,4));printf("%.8x\n",sra(0x81001100,4));return0;}2.64#include <stdio.h>int any_odd_one(unsigned x){unsigned obj =0x55555555;return!!(x & obj);}int main(){unsigned x =0x00000001;printf("%d\n",any_odd_one(x));return0;}2.65#include <iostream>int odd_ones(unsigned x){int w =sizeof(int)<<3;x ^= x >>16;x ^= x >>8;x ^= x >>4;x ^= x >>2;x ^= x >>1;return x &1;}int main(){int a =0xffff0000;int b =0x00000103;printf("%d %d",odd_ones(a),odd_ones(b)); return0;}2.66int leftmost_one(int x){int w =sizeof(int)<<3;x |= x >>1;x |= x >>2;x |= x >>4;x |= x >>8;x |= x >>16;return x &((~x)>>1|0x80000000);}int main(){int a =0xff000000;int b =0x00000040;printf("%.8x %.8x\n",leftmost_one(a),leftmost_one(b)); return0;}2.67#include <stdio.h>int bad_int_size_is_32(){int set_msb =1<<31;int beyond_msb = set_msb <<1;return set_msb &&!beyond_msb;}int bad_int_size_is_32_in16(){int set_msb =1<<15;set_msb <<=15;set_msb <<=1;int beyond_msb = set_msb <<1;return set_msb &&!beyond_msb;}int main(){printf("%d\n",bad_int_size_is_32());printf("%d\n",bad_int_size_is_32_in16());return0;}2.68#include <stdio.h>int lower_one_mask(int x){int w =sizeof(int)<<3;return(unsigned)-1>>(w - x);}int main(){int a =6;int b =17;printf("%.8x\n",lower_one_mask(a));printf("%.8x\n",lower_one_mask(b));return0;}2.69unsigned rotate_left(unsigned x,int n){ int w =sizeof(int)<<3;unsigned ans = x;ans <<= n;ans |= x >>(w - n);return ans;}int main(){int a =0x12345678;int x1 =0;int x2 =20;printf("0x%.8x\n",rotate_left(a, x1)); printf("0x%.8x\n",rotate_left(a, x2)); return0;}2.70#include <stdio.h>#include <limits.h>int fits_bits(int x,int n){int w =sizeof(int)<<3;int obj = x <<(w - n)>>(w - n); return obj == x;}int main(){int x =0x00000011;int n =1;printf("%d\n",fits_bits(x, n));printf("%d\n",fits_bits(INT_MAX,32)); printf("%d\n",fits_bits(0,0));return0;}2.71#include <stdio.h>typedef unsigned packed_t;int xbyte(packed_t word,int bytenum){ int w = bytenum +1<<3;return(int)word <<(32- w)>>(3<<3); }int main(){int word =0xf1f2f380;printf("%.8x\n",xbyte(word,0));printf("%.8x\n",xbyte(word,1));printf("%.8x\n",xbyte(word,2));printf("%.8x\n",xbyte(word,3)); return0;}2.72void copy_int(int val;void*buf,int maxbytes){if(maxbytes <0)return;if(maxbytes >=sizeof(val))memcpy(buf,(void*)&val,sizeof(val));}2.73#include <stdio.h>#include <limits.h>int saturating_add(int x,int y){int w =sizeof(int)<<3;int is_diff_sign =(x ^ y)>>(w -1);int is_overflow =((x + y)^ x)>>(w -1);int judge = x >>(w -1);// printf("%d %d %d\n", is_diff_sign, is_overflow, judge);// printf("%d\n", is_diff_sign & (x + y));int a =(is_diff_sign &(x + y));int b =((~is_diff_sign &((~is_overflow &(x + y))+(is_overflow &(judge & INT_MIN +~judge & INT_MAX)))));int c=((is_diff_sign &(x + y))+(~is_diff_sign &((~is_overflow &(x + y))+(is_overflow &((judge & INT_MIN)+(~judge & INT_MAX)))))); //printf("%d %d %d\n", a, b, c);return c;}int main(){printf("%d\n",saturating_add(1,100));printf("%d\n",saturating_add(1000,-10));printf("%d\n",saturating_add(INT_MAX,12321));printf("%d\n",saturating_add(INT_MIN,-1));return0;}2.74#include <stdio.h>#include <limits.h>int tsub_ok(int x,int y){y =-y;int w =sizeof(int)<<3;int same =(x ^ y)>>(w -1);int overflow =((x + y)^ x)>>(w -1);return same ||!overflow;}int main(){printf("%d\n",tsub_ok(INT_MIN,1));printf("%d\n",tsub_ok(-1,100));printf("%d\n",tsub_ok(-23,INT_MAX));return0;}2.75#include <inttypes.h>int signed_high_prod(int x,int y){int64_t high_prod =(int64_t)x * y;return high_prod >>32;}unsigned unsigned_high_prod(unsigned x,unsigned y){int w =sizeof(int)<<3;int bit_x = x >>(w -1);int bit_y = y >>(w -1);int sig_high =signed_high_prod(x, y);return sig_high + x * bit_y + y * bit_x;}unsigned unsigned_high_prod_two(unsigned x,unsigned y){ uint64_t high_prod =(uint64_t)x * y;return high_prod >>32;}int main(){unsigned x =0xffffffff;unsigned y =0x12345678;printf("%.8x\n",unsigned_high_prod(x, y));printf("%.8x\n",unsigned_high_prod_two(x, y));return0;}2.76#include <stdio.h>#include <stdlib.h>#include <string.h>#include <assert.h>void*calloc(size_t nmemb, size_t size){if(!nmemb ||!size)return NULL;// return (int*)malloc(sizeof(int) * size);size_t size_sum = nmemb * size;if(nmemb == size_sum / size){void*ptr =malloc(size_sum);memset(ptr,0, size_sum);return ptr;}elsereturn NULL;}int main(){void*p =calloc(123,1);if(p ==NULL){printf("P = NULL\n");}elsefree(p);return0;}2.77int mul1(int x){return(x <<4)+ x;}int mul2(int x){return x -(x <<3);}int mul3(int x){return(x <<6)-(x <<2);}int mul4(int x){return(x <<4)-(x <<7);}int main(){int x =10;printf("%d\n",mul1(x));//*17printf("%d\n",mul2(x));//*-7printf("%d\n",mul3(x));//*60printf("%d\n",mul4(x));//*-112return0;}2.78#include <stdio.h>#include <limits.h>int divide_power2(int x,int k){int w =sizeof(int)<<3;int sign = x >>(w -1);int bias =(1<< k)-1;return(~sign &(x >> k))+(sign &(x + bias)>> k); }int main(){printf("%d\n",divide_power2(51,1));printf("%d\n",divide_power2(-51,1));return0;}2.79#include <stdio.h>#include <limits.h>int mul3div4(int x){int w =sizeof(int)<<3;x =(x <<1)+ x;int sign = x >>(w -1);int bias =(1<<2)-1;return(~sign &(x >>2))+(sign &((x + bias)>>2)); }int main(){printf("%d\n",mul3div4(3));printf("%d\n",mul3div4(4));return0;}2.80#include <stdio.h>#include <limits.h>int threefourths(int x){int w =sizeof(int)<<3;int sign = x >>(w -1);int bias =(1<<2)-1;x =(~sign &(x >>2))+(sign &(x + bias)>>2);return(x <<1)+ x;}int main(){printf("%d\n",threefourths(4));printf("%d\n",threefourths(5));printf("%d\n",threefourths(-5));return0;}2.81#include <stdio.h>int A(int k){return(-1)<< k;}int B(int k,int j){return~A(k)<< j;}int main(){printf("%.8x\n",A(4));printf("%.8x\n",B(8,4));return0;}2.82#include <stdio.h>#include <stdlib.h>/*A错。
深入理解计算机系统LAB2

实验二报告一、实验内容根据实验文件里的提示,补充15段代码,熟悉对整型和浮点型数的操作,并成功调试运行。
二、实验程序解释1.bitAnd要求只运用~和|符号实现and的功能。
a and b=not(not a or not b),根据德摩根律易得结果。
int bitAnd(int x, int y) {return ~(~x|~y);}2.getByte得到x的第n个字节的值,规定其中x的最低位为第0个字节,最高位为第3个字节。
如果是第0个字节,将x右移0个字节再利用掩码0xFF将高位的三个字节置为0。
如果是求第1个字节,将x右移1个字节,同理利用掩码。
可以知道,将x右移n个字节也就是n*8位、即(n<<3)位。
接下来清除前三个高位字节,保留最低字节的信息,与0xFF进行&运算。
int getByte(int x, int n) {int t;t=x>>(n<<3);t=t&0xFF;return t;}3.LogicalShift逻辑右移是将移动后补充的高位置0,而算数右移时补充的和符号位相同。
对于字x,需要进行逻辑右移n位。
将x用sxxxxxxx表示,s为符号位,算术右移n-1位的结果为ss…sxx..(有n个s)。
想要得到的结果是00…xxx..(n个0),所以如果能得到s’s’…s’111..(n个s’)的话,按位与就能得到结果。
首先提取符号位t,1左移31位得到100..00,与x进行按位与操作得到s000..0,接着算术右移n位,得到ss..s00..00(n+1个s),再左移1位,得到s..s0..0(n个s),取反得到s’s’..s’111..1。
这样就能得到逻辑右移n位的结果了。
注意,在得到s’s’…111的过程中,不能直接将s00.. 0右移n-1位,考虑特殊情况,n为0时,右移-1位是不正确的。
int logicalShift(int x, int n) {int t=(1<<31)&x;t=~((t>>n)<<1);t=(x>>n)&t;return t;}4.bitCount要求计算32位二进制数x中1个个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2
10 11 12 13 14
CHAPTER 1. SOLUTIONS TO HOMEWORK PROBLEMS
void show_double(double x) { show_bytes((byte_pointer) &x, sizeof(double)); } code/data/show-ans.c
Homework Problems. These are found at the end of each chapter. They vary in complexity from simple drills to multi-week labs and are designed for instructors to give as assignments or to use as recitation examples.
Problem 2.40 Solution: This exercise should be a straightforward variation on the existing code.
code/data/show-ans.c
1 2 3 4 5 6 7 8 9
void show_short(short int x) { show_bytes((byte_pointer) &x, sizeof(short int)); } void show_long(long int x) { show_bytes((byte_pointer) &x, sizeof(long)); }
code/data/show-ans.c
1 2 3 4 5 6 7 8
int is_little_endian(void) { /* MSB = 0, LSB = 1 */ int x = 1; /* Return MSB when big-endian, LSB when little-endian */ return (int) (* (char *) &x); } code/data/show-ans.c
Problem 2.41 Solution: There are many ways to solve this problem. The basic idea is to create some multibyte datum with different values for the most and least-significant bytes. We then read byte 0 and determine which byte it is. In the following solution is to create an int with value 1. We then access its first byte and convert it to an int. This byte will equal 0 on a big-endian machine and 1 on a little-endian machine.
Problem 2.42 Solution: This is a simple exercise in masking and bit manipulation. It is important to mention that ˜0xFF is a way to generate a mask that selects all but the least significant byte that works for any word size. (x & 0xFF) | (y & ˜0xFF) Problem 2.43 Solution: These exercises require thinking about the logical operation ! in a nontraditional way. Normally we think of it as logical negation. More generally, it detects whether there is any nonzero bit in a word. A. !!x B. !!˜x C. !!(x & 0xFF) D. !!(˜x & 0xFF) Problem 2.44 Solution:
Computer Systems: A Programmer’s Perspective Instructor’s Solution Manual 1
Randal E. Bryant David R. O’Hallaron December 4, 2003
1
Copyright c 2003, R. E. Bryant, D. R. O’Hallaron. All rights reserved.
This document gives the solutions to the homework problems.
1.1 Chapter 1: A Tour of Computer Systems 1.2 Chapter 2: Representing and Manipulating Information
2
பைடு நூலகம்
Chapter 1
Solutions to Homework Problems
The text uses two different kinds of exercises:
Practice Problems. These are problems that are incorporated directly into the text, with explanatory solutions at the end of each chapter. Our intention is that students will work on these problems as they read the book. Each one highlights some particular concept.
