成都实验外国语学校2017年高中自主招生数学 真卷
成都外国语学校2017年高中自主招生数学真卷(一)

成都外国语学校2017年高中自主招生数学真卷(一)(考试时间:120分钟 满分:150分)A 卷(共100分)一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、如图,是一个单心圆曲隧道的截面,如果路面AB 宽为10米,净高CD 为7米,那么所在半径OA 为 ( ) A 、5米 B 、377 C 、375D 、7米第1题图 第2题图 第3题图2、在正方形网络中,∠AOB 如图放置,则cos ∠AOB 的值为 ( ) A 、55 B 、255 C 、12D 、2 3、如图是一个立方体的表面展开图,已知立方体的每一个面上都有一个实数,且相对两数互为倒数,那么代数式b ca-的值等于 ( ) A 、34- B 、14- C 、1 D 、344、把多项式2212xy x y -+-分解因式的结果是 ( ) A 、(1)(1)x y x y +--+ B 、(1)(1)x y x y --+- C 、(1)(1)x y x y ---+ D 、(1)(1)x y x y +-++5、在一个地球仪的赤道上用铁丝打一个箍,现将地球仪的半径增大1米,需增加m 米的铁丝,假设地球赤道上也有一个铁箍,同样地球半径增大1米,则需要增加n 米的铁丝,则m 与n 的大小关系是 ( ) A 、m>n B 、m<n C 、m=n D 、不能确定6、已知一组数据7,6,x ,9,11的平均数是9,那么x 等于 ( ) A 、3 B 、10 C 、12 D 、97、如图,在矩形ABCD 中, AB=2,BC=1,动点P 从点B 出发,沿路线B →C →D 做匀速运动,那么△APB 的面积S 与点P 运动的路程之间的函数图像大致是 ( )第7题图A B C D8、点P 在第一象限内,P 到x 轴的距离是4,到y 轴的距离是3,点P 的坐标是 ( ) A 、(—4,3) B 、(—3,—4) C 、(—3,4) D 、(3,4)9、若α、β是方程2220070x x +-=的两实数根,则23ααβ++的值是 ( )A 、2007B 、2005C 、—2007D 、401010、如图,在ABC 中,AB=10,AC=8,BC=6,经过点C 且与边AB 相切的动圆CA 、CB 分别相交于P 、Q ,则线段PQ 长度的最小值是 ( ) A 、4.75 B 、4.8 C 、5 D 、42第10题图二、填空题(本大题共5小题,每小题4分,共20分。
成都外国语学校2017年初升高直升考试试卷(学生版)无水印

第 2 页 共 8 页(By AC)
三、解答题:(本大题共六小题,共54 分)
15、(本小题满分12 分,每小题6 分)
(1)计算:
32
(2)已知
x x2
22
200 17
1
1 3
,求3x3
8x2
1 tan160 2xx26 1
16、(本小题满分6 分)当m 为何值时,关于x 的方程
m x2 x
x 2x
成都外国语学校2017 年初升高直升考试
(数学试题)
一、选择题(每小题3 分,共45 分)
A 卷(共 100 分)
1、下列各数 (
A.1 个
3.14, 2 , 3 1,cos30 中,无理数的个数)是
B. 2 个
C.3 个
D. 4 个
2、下列各式正确的是( )
A. m m2 m3 m5
B.
2x
2
1 4x2
所以点 P(-1,2)到直线 y=3x+7 的距离为 d
k+x071+0ky
+b
2
3 ( 1) 2 2
1+k 2
10
10 5
.
根据以上材料,解答下列问题: (1)求点 P(1,-1)到直线 y=x-1 的距离;
(2)已知⊙Q 的圆心 Q 坐标为(0,5),半径 r 为 2,判断⊙Q 与直线 y 3x+9 的位置关系并说明理由;
第 4 页 共 8 页(By AC)
19、(本小题满分10 分)如图,已知双曲线y
k x
经过点D(6,1),点C 是双曲线第三象限上的动点,过C
作 CA⊥x 轴,过D 作 DB⊥y 轴,垂足分别为A,B,连接AB,BC,且 BCD 的面积为12.
成都外国语学校初升高直升考试试卷学生版无水印.doc

成都外国语学校2017 年初升高直升考试( 数学试题 )A 卷(共100分)一、选择题(每小题 3 分,共45 分)1、下列各数,,31,中,无理数的个数是()3.14 2 cos30A.1 个B. 2 个C.3 个D. 4 个2、下列各式正确的是()2 3 5B. 2 x 2 1A. m m m m 4x2C. m2 3m6 D . 4m 1 4m 1 1 16m23、从一个边长为3cm 的大立方体挖去一个边长为1cm 的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是()4、已知一组数据从小到大依次为- 1,0,4,x,6,15,其中位数为5,则其众数为()A. 4B. 5C. 5.5D. 65、函数 y 2x 3 0中自变量x 的取值范围是()x2 x 31A. x 1 且x 3 B.x 3且x 1,x 3C.x 3且x 1D. x且2 23 x 16 a的圆桌布平铺在对角线长为a的正方形桌面上, 若四周下垂的最大长度相等, 则桌、如图 , 用一块直径为布下垂的最大长度x 为( )A. 2 1 aB. 2 1C.22 a D. 2 2a 2a4第 1 页共8页(By AC)7、适合下列条件的ABC (A, B , C 所对的边分别是a, b, c )中,① A BC ;② A 2 B 3 C ;③ a : b : c 13:12 :5 ;④ sin2 A sin2 B sin2C.直角三角形的个数为 ( )A 1个B 2个C 3D 4个. . . 个.8、下列说法正确的个数是()①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③平分弦的直径垂直于弦;④经过半径外端且垂直于半径的直线是圆的切线;A. 1 个B. 2 个C. 3 个D. 4 个9、如图 , 王华晚上由路灯 A 下的 B 处走到 C 处时 , 测得影子 CD 的长为 1 米 , 继续往前走 3 米到达 E 处时, 测得影子 EF 的长为 2 米, 已知王华的身高是 1. 5 米, 那么路灯 A 的高度 AB 等于 ( )A 4 5米B.6米C.7 2米D.8米.. .10 ABCD中,E为AD中点,AF丄BE交BE于G,交CD于F,连CG延长交AD于H. 下列结、在正方形论:① CG= CB; ②HE1 ; ③EG 1;④以 AB 为直径的圆与CH 相切于点 G,其中正确的有()个 . BC 4 GF 3A. 1 个B. 2 个C. 3 个D. 4 个第 9 题第 10 题第 13 题第 14 题二、填空题(本大题共 4 小题,每小题 4 分,共 16 分)11、 H 7N9 禽流感是一种传染性极强的新亚型流感,其中的一种球形病毒的直径约120nm,已知1nm 1 109m,则这种病毒直径用科学记数法表示为 ______ m.12、现有三张分别标有数字1、 2、6 的卡片 , 它们除了数字外完全相同, 把卡片背面朝上洗匀, 从中任意抽取一张 , 将上面的数字记为a( 不放回 ), 再从中任意抽取一张 , 将上面的数字记为b, 这样的数字 a, b 能使关于 x的一元二次方程 x2 2 a 3 x b2 9 0 有两个正根的概率为 ___.13、如图 , 小阳发现电线杆AB 的影子落在土坡的坡面 CD 和地面 BC 上 , 量得 CD = 8 米,BC=20 米,CD 与地面成 30°角,且此时测得 1 米杆的影长为 2 米,则电线杆的高度为 ___米。
成都实验外国语学校2017年高中自主招生数学真卷

成都实验外国语学校2017年高中自主招生数学真卷一、选择题1、下列计算正确的是 ( )A.46222-=-y yB.532=+C.326x x x ∙=D.y x yx y x +=--22 2、在数轴上已知点A 表示3-,把点A 向右平移2个单位到达点B ,设点B 表示的数为n ,则()211++-n n 的值是 ( )A.n 3B.1+nC.2D.33、如图,有甲、乙、丙三种地砖,其中甲、乙是正方形,边长分别为a 、b ,丙是长方形,长为a ,宽为b (其中b a >).如果要用它们拼成若干个边长为()b a 3+的正方形,那么应取甲、乙、丙三种地砖块数的比是 ()A.1:4:4B.1:3:2C.1:2:2D.无法确定4、如图,在一笔直的海岸线l 上有A 、B 两个观测站,km 2=AB ,从A 测得船C 在北偏东︒45的方向,从B 测得船C 在北偏东︒5.22的方向,则船C 离海岸线l 的距离(即CD 的长)为 ( )A.km 4B.()22+kmC.km 22D.()24-km5、端午节到了,妈妈去超市买了1个豆沙粽,2个鲜花粽,3个腊肉粽,粽子从外观看都一样,小明从中拿走2个粽子,其中一个是鲜花粽,一个是腊肉粽第4题图的概率是 ( ) A.31 B.65 C.52 D.158 6、由多个相同的小正方体堆成的一个物体,它的主视图、侧视图、俯视图都是同一个图(如图所示),那么堆成该物体至少需要的小正方体个数为 ( )A.12B.15C.19D.27第8题图7、如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中折扇无重叠),则梅花图案中五角星的五个锐角的度数均是 ( )A.︒46B.︒48C.︒52D.︒578、在平面直角坐标系中,矩形OABC 如图所示.点A 在x 轴的正半轴上,点C 在y 轴正半轴上,且6=OA ,4=OC ,D 为OC 的中点,点E 、F 在线段OA 上,点E 在点F 左侧,3=EF .当四边形BDEF 的周长最小时,点E 的坐标是 ( ) A.⎪⎭⎫ ⎝⎛0,21 B.()0,1 C.⎪⎭⎫ ⎝⎛023, D.()0,2 9、如图所示,在正方形ABCD 的对角线BD 上取一点E ,使得︒=∠15BAE ,连接AE 、CE ,延长CE 到F ,连接BF ,使得BF BC =.若1=AB ,有下列结论:①CE AE =;②点F 到BC 的距离为22;③EF EC BE =+;④8241+=∆AED S .则其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个10、如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B 两点,OP 交⊙O 于点C ,连接BO 并延长交⊙O 于点D ,交PA 的延长线于点E ,连接AD 、BC .下列结论:①PO AD //;②PCB ADE ∆∆~;③EAED EAD =∠tan ;④OP AD BD ∙=22.其中一定正确的是( ) A.①③④ B.②④ C.①②③ D.①②③④第10题图二、填空题11、分解因式:=+-363a a .12、a 是不为1的数,我们把a -11称为a 的差倒数,如:2的差倒数为1-2-11=;-1的差倒数是()211--11=;已知211-=a ,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是4a 的差倒数……依次类推,则=2015a .13、已知012=-+a a ,则=+-44a a .14、在矩形ABCD 中,15=AD ,点E 在边DC 上,连接AE ,ADE ∆沿直线AE翻折后点D 落到点F ,过点F 作AD FG ⊥,垂足为点G ,如图,如果GD AD 3=,那么=DE .15、(1)若40<<x ,化简()5122--+x x 的结果是 .(2)观察分析,寻找规律:0,3,6,3,32,15…那么第10个数应该是 .16、对于任意实数m 、n ,定义一种新运算m ※3+--=n m mn n ,等式的右边是通常的加减和乘法运算,例如:3※10353535=+--⨯=.请根据上述定义解决问题:若2<a ※7<x ,且解集中有两个整数解,则a 的取值范围是 .17、如图,在AOB Rt ∆中,23==OB OA ,⊙O 的半径为1,点P 是AB 边上的动点,过点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线PQ 的最小值为 .18、(1)方程052=-+m x x 的一个根是2,则=m .另一个根是 .(2)设a 、b 是方程020102=-+x x 的两个实数根,则b a a ++22的值 为 .19、如图,点A 为直线x y -=上一点,过A 作OA 的垂线交双曲线xk y =(0<x )于点B ,若1222=-AB OA ,则k 的值是 .20、已知a 、b 、m 均为正整数,若存在整数k 使得km b a =-,则称a 、b 关于m同余,记作b a ≡(mod m ).若a 、b 、c 、d 、m 均为正整数,则以下结论正确的是 .(填写出所有正确的序号)①27≡(mod 5);②若b a ≡(mod 2),c b ≡(mod 2),则c a ≡(mod 2); ③若b a ≡(mod m ),d c ≡(mod m ),则bd ac ≡(mod m ); ④若bd ac ≡(mod m ),则b a ≡(mod m ),d c ≡(mod m ).三、解答题21、化简:⎪⎪⎭⎫ ⎝⎛-+b a b a 4422÷ab a a b 24222+-22、谋生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶6元的价格出售,如果当天卖不完,剩余的只有倒掉,店主记录了30天的日需求量(单位:瓶),整理得下表:(1)求这30天内日需求量的众数.(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数.(3)以30天记录的各需求量的频率作为各需求发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.23、如图,ABC ∆和DEF ∆是两个全等的等腰直角三角形,︒=∠=∠90EDF BAC ,DEF ∆的顶点E 与ABC ∆的斜边BC 的中点重合.将DEF ∆绕点E 旋转,旋转过程中,线段DE 与线段AB 相交于点P ,线段EF 与射线CA 相交于点Q .(1)如图①,当点Q 在线段AC 上,且AQ AP =时,求证:CQE BPE ∆≅∆.(2)如图②,当点Q 在线段CA 的延长线上是,求证:CQE BPE ∆∆~;并求当a BP =,a CQ 29=时,P 、Q 两点间的距离(用含a 的代数式表示).24、已知一次函数()2--=k x y 的图象与反比例函数x k y 2=的图象在第一、三象限交于A 、C 两点,并且过点(1-a ,k ),2=∆AO C S ,其中a 、k 为常数,求a 的值.25、如图,AB 是⊙O 的直径,C 、G 是⊙O 上的两点,且CG AC =,过点C 的直线BG CD ⊥于点D ,交BA 的延长线于点E ,连接BC ,交OD 于点F .(1)求证:CD 是⊙O 的切线.(2)连接AD ,若32=FD OF ,3=CD ,求AD 的长.26、如图,已知二次函数的图象M 经过A (1-,0),B (4,0),C (2,6-)三点.(1)求该二次函数的解析式.(2)点G 是线段AC 上的动点(点G 与线段AC 的端点不重合),若ABG ∆与ABC ∆相似,求点G 的坐标.(3)设图象M 的对称轴为l ,点D (m ,n )(21<<-m )是图象M 上一动点,当ACD ∆的面积为827时,点D 关于l 的对称点为E ,能否在图象M 和l 上分别找到点P 、Q ,使得以点D 、E 、P 、Q 为顶点的四边形为平行四边形? 若能,求出点P 的坐标;若不能,请说明理由.。
成都实验外国语学校2017年高中自主招生数学真卷

成都实验外国语学校2017年⾼中⾃主招⽣数学真卷成都实验外国语学校2017年⾼中⾃主招⽣数学真卷(直升卷)⼀、选择题1、根据调查,某市2016年的房价为9000元/平⽅⽶,预计2018年的房价将达到11000元/平⽅⽶,求这两年的平均增长率,设年平均增长率为x ,根据题意,所列⽅程为() A.()1100019000=+x B.()11000190002 =+xC.()1100019000=-xD.()11000190002=-x2、关于x 的⽅程()()012132=+++-a x a ax 有两个不相等的实数根1x ,2x ,且a x x x x -=+-12211,则a 的值是()A.1B.-1C.-1或1D.23、⼀个⼏何体由若⼲个⼩⽴⽅块搭成,它的主视图、左视图、俯视图分别如下,则搭建这个⼏何体的⼩⽴⽅块的个数是()A.4B.5C.6D.74、如图,ABC ?中,BC AB ⊥,3=AB ,4=BC ,D 为ABC ?的内⼼,则ABD ?的⾯积是() A.43 B.23 C.25D.2 5、对于任意的11≤≤-x ,032>-+a ax 恒成⽴,则a 的取值范围为()A.1>a 或0=aB.3>aC.03=>a a 或D.31<6、⼀个平⾯封闭图形内(含边界)任意两点距离的最⼤值称为该图形的“直径”,封闭图形的周长与直径之⽐称为图形的“周率”,下⾯四个图形:正三⾓形、正⽅形、正六边形、圆的周率分别记为1a ,2a ,3a ,4a ,则下列关系正确的是()A.324a a a >>B.214a a a >>C.321a a a >>D.432a a a >>7、ABO ?的顶点坐标分别为()4,1A ,()1,2B ,()0,0O ,若将ABO ?绕点O 按逆时针⽅向旋转?90得到'''O B A ?,那么线段''B A 的中点坐标为()A.??? ??-23,25B.??? ??-23,2C.()2,2-D.??-2,258、如图,在四边形ABCD 中,BC AB ⊥,3=AB ,4=BC ,5=CD ,25=AD ,则BD 等于()A.35B.59C.65D.89、如图,三⾓形ABC 中,AC AB =,D 、E 分别为AB 、AC 上的点,DM 平分BDE ∠,EN 平分DEC ∠,若?=∠110DMN ,则=∠DEA () A.?40 B.?50 C.?60 D.?7010、将函数b x y +=3(b 为常数)的图象位于x 轴下⽅的部分沿x 轴翻折⾄其上⽅后,所得的折线是函数b x y +=3(b 为常数)的图象,若该图象在直线3=y 下⽅的点的横坐标x 满⾜30<A.6-bB.6-≤b 或3-≥bC.36-<<-bD.36-≤≤-b11、⼆次函数c bx ax y ++=2(0≠a )经过坐标原点,当1-=x 时,12≤≤-y ;当2=x 时,40≤≤y ;则当1=x 时,y 的取值范围是()A.3134-≤≤-yB.334≤≤-yC.231≤≤-yD.331≤≤-y12、已知a ,b 为有理数,m 、n 分别表⽰75-的整数部分与⼩数部分,且12=+bn amn ,则=+b a 2() A.1 B.23 C.2 D.25⼆、填空题13、已知实数x 、y ,满⾜()y y x --=+111,则=-20172017y x .14、关于x 的⽅程()02=+-b m x a 的解释11=x ,22-=x (a 、m 、b 均为常数,0≠a ),则⽅程()022=++-b m x a 的解是 .15、若321=+a a ,则=-aa 1. 16、若点()11,y x A ,()22,y x B 在反⽐例函数xy 4=的图象上,且021<x x="" ,以线段ab="" 为直径的圆的⾯积为s="" ,则s="" 的最⼩值为="" .="" 17、已知a="" 是⽅程012="-+x" 的⼀个根,则<="" p="" bdsfid="216">。
成都实验外国语学校2017年高中自主招生数学真卷

成都实验外国语学校2017年高中自主招生数学真卷一、选择题1、下列计算正确的是()A.46222-=-yy B.532=+ C.326xxx•= D.yxyxyx+=--222、在数轴上已知点A表示3-,把点A向右平移2个单位到达点B,设点B表示的数为n,则()211++-nn的值是()A.n3B.1+n C.2 D.33、如图,有甲、乙、丙三种地砖,其中甲、乙是正方形,边长分别为a、b,丙是长方形,长为a,宽为b(其中ba>).如果要用它们拼成若干个边长为()ba3+的正方形,那么应取甲、乙、丙三种地砖块数的比是()A.1:4:4B.1:3:2C.1:2:2D.无法确定4、如图,在一笔直的海岸线l上有A、B两个观测站,km2=AB,从A测得船C在北偏东︒45的方向,从B测得船C在北偏东︒5.22的方向,则船C离海岸线l的距离(即CD的长)为()A.km4 B.()22+km C.km22 D.()24-km5、端午节到了,妈妈去超市买了1个豆沙粽,2个鲜花粽,3个腊肉粽,粽子从外观看都一第4题图样,小明从中拿走2个粽子,其中一个是鲜花粽,一个是腊肉粽的概率是 ( )A.31B.65C.52D.158 6、由多个相同的小正方体堆成的一个物体,它的主视图、侧视图、俯视图都是同一个图(如图所示),那么堆成该物体至少需要的小正方体个数为 ( ) A.12 B.15 C.19 D.27第8题图7、如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中折扇无重叠),则梅花图案中五角星的五个锐角的度数均是 ( ) A.︒46 B.︒48 C.︒52 D.︒578、在平面直角坐标系中,矩形OABC 如图所示.点A 在x 轴的正半轴上,点C 在y 轴正半轴上,且6=OA ,4=OC ,D 为OC 的中点,点E 、F 在线段OA 上,点E 在点F 左侧,3=EF .当四边形BDEF 的周长最小时,点E 的坐标是 ( )A.⎪⎭⎫ ⎝⎛0,21B.()0,1C.⎪⎭⎫⎝⎛023,D.()0,2 9、如图所示,在正方形ABCD 的对角线BD 上取一点E ,使得︒=∠15BAE ,连接AE 、CE ,延长CE 到F ,连接BF ,使得BF BC =.若1=AB ,有下列结论:①CE AE =;②点F 到BC 的距离为22;③EF EC BE =+;④8241+=∆AED S .则其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个10、如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B 两点,OP 交⊙O 于点C ,连接BO并延长交⊙O 于点D ,交PA 的延长线于点E ,连接AD 、BC .下列结论:①PO AD //;②PCB ADE ∆∆~;③EAEDEAD =∠tan ;④OP AD BD •=22.其中一定正确的是( ) A.①③④ B.②④ C.①②③ D.①②③④第10题图二、填空题11、分解因式:=+-363a a . 12、a 是不为1的数,我们把a -11称为a 的差倒数,如:2的差倒数为1-2-11=;-1的差倒数是()211--11=;已知211-=a ,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是4a 的差倒数……依次类推,则=2015a .13、已知012=-+a a ,则=+-44a a .14、在矩形ABCD 中,15=AD ,点E 在边DC 上,连接AE ,ADE ∆沿直线AE 翻折后点D 落到点F ,过点F 作AD FG ⊥,垂足为点G ,如图,如果GD AD 3=,那么=DE . 15、(1)若40<<x ,化简()5122--+x x 的结果是 .(2)观察分析,寻找规律:0,3,6,3,32,15…那么第10个数应该是 . 16、对于任意实数m 、n ,定义一种新运算m ※3+--=n m mn n ,等式的右边是通常的加减和乘法运算,例如:3※10353535=+--⨯=.请根据上述定义解决问题: 若2<a ※7<x ,且解集中有两个整数解,则a 的取值范围是 .17、如图,在AOB Rt ∆中,23==OB OA ,⊙O 的半径为1,点P 是AB 边上的动点,过点P是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线PQ 的最小值为 .18、(1)方程052=-+m x x 的一个根是2,则=m .另一个根 是 .(2)设a 、b 是方程020102=-+x x 的两个实数根,则b a a ++22的值 为 .19、如图,点A 为直线x y -=上一点,过A 作OA 的垂线交双曲线xky =(0<x )于点B ,若1222=-AB OA ,则k 的值是 .20、已知a 、b 、m 均为正整数,若存在整数k 使得km b a =-,则称a 、b 关于m 同余,记作b a ≡(mod m ).若a 、b 、c 、d 、m 均为正整数,则以下结论正确的是 .(填写出所有正确的序号) ①27≡(mod 5);②若b a ≡(mod 2),c b ≡(mod 2),则c a ≡(mod 2); ③若b a ≡(mod m ),d c ≡(mod m ),则bd ac ≡(mod m ); ④若bd ac ≡(mod m ),则b a ≡(mod m ),d c ≡(mod m ).三、解答题21、化简:⎪⎪⎭⎫ ⎝⎛-+b a b a 4422÷ab a a b 24222+-22、谋生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶,然后以每瓶6元的价格出售,如果当天卖不完,剩余的只有倒掉,店主记录了30天的日需求量(单位:瓶),整理得下表:(1)求这30天内日需求量的众数.(2)假设鲜奶店在这30天内每天购进28瓶,求这30天的日利润(单位:元)的平均数. (3)以30天记录的各需求量的频率作为各需求发生的概率.若鲜奶店每天购进28瓶,求在这记录的30天内日利润不低于81元的概率.23、如图,ABC ∆和DEF ∆是两个全等的等腰直角三角形,︒=∠=∠90EDF BAC ,DEF ∆的顶点E 与ABC ∆的斜边BC 的中点重合.将DEF ∆绕点E 旋转,旋转过程中,线段DE 与线段AB 相交于点P ,线段EF 与射线CA 相交于点Q .(1)如图①,当点Q 在线段AC 上,且AQ AP =时,求证:CQE BPE ∆≅∆.(2)如图②,当点Q 在线段CA 的延长线上是,求证:CQE BPE ∆∆~;并求当a BP =,a CQ 29=时,P 、Q 两点间的距离(用含a 的代数式表示).24、已知一次函数()2--=k x y 的图象与反比例函数xky 2=的图象在第一、三象限交于A 、C 两点,并且过点(1-a ,k ),2=∆AOC S ,其中a 、k 为常数,求a 的值.25、如图,AB 是⊙O 的直径,C 、G 是⊙O 上的两点,且CG AC =,过点C 的直线BGCD ⊥于点D ,交BA 的延长线于点E ,连接BC ,交OD 于点F . (1)求证:CD 是⊙O 的切线. (2)连接AD ,若32=FD OF ,3=CD ,求AD 的长.26、如图,已知二次函数的图象M 经过A (1-,0),B (4,0),C (2,6-)三点. (1)求该二次函数的解析式.(2)点G 是线段AC 上的动点(点G 与线段AC 的端点不重合),若ABG ∆与ABC ∆相似,求点G 的坐标.(3)设图象M 的对称轴为l ,点D (m ,n )(21<<-m )是图象M 上一动点,当ACD∆的面积为827时,点D 关于l 的对称点为E ,能否在图象M 和l 上分别找到点P 、Q ,使得以点D 、E 、P 、Q 为顶点的四边形为平行四边形? 若能,求出点P 的坐标;若不能,请说明理由.答案: 一、选择题 1、D 2、C 3、A 4、B 5、C 6、B 7、B 8、B 9、B 10、A二、填空题 11、2)1(3-a 12、32 13、7 14、5315、(1)43-x (2)33 16、54<≤a 17、2218、(1)14,-7 (2)200919、-620、①②三、解答题。
成都外国语学习2017年高中自主招生数学真卷2
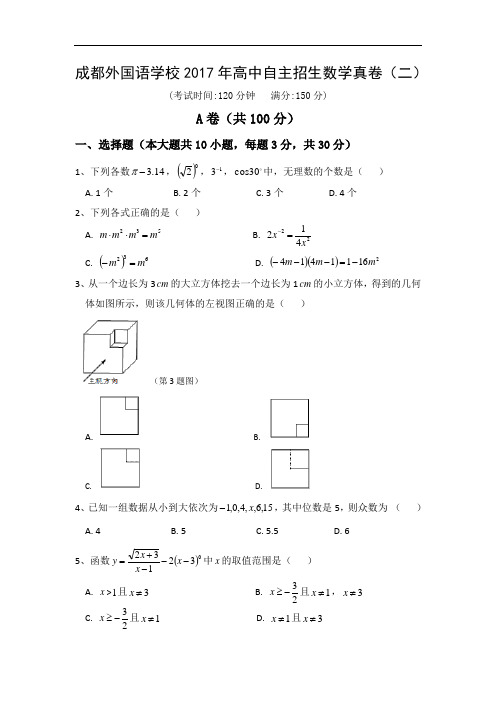
① ∠ A ∠ B ∠ C ;② ∠ A 2 ∠ B 3 ∠ C ;③ a : b : c 13:12: 5 ;
④ sin2 A sin2 B sin2 C .直角三角形的个数为( )
A. 1 个
B. 2 个
C. 3 个
D. 4 个
8、 下列说法中,正确的个数是( )
①过一点有且只有一条直线与已知直线平行
背面朝上洗匀,从中任意抽取一张,将上面的数字记为 a (不放回),再从 中任意抽取一张,将上面的数字记为 b ,这样的数字 a 、 b 能使关于 x 的一
元二次方程 x2 2a 3x b2 9 0 有两个正根的概率为________
13、如图,小阳发现电线杆 AB 的影子落在土坡的坡面 CD 和地面 BC 上,量得
x2 x 2 x 1 x 2
17、(本题满分 8 分)
已知点 P0 x0, y0 和直线 y kx b ,则点 P 到直线 y kx b 的距离 d 可用公式
d kx0 y0 b 计算. 1 k2
例如:求点 P1,2到直线 y 3x 7 的距离.
解:因为直线 y 3x 7 ,其中 k 3, b 7 .
成都外国语学校 2017 年高中自主招生数学真卷(二)
(考试时间:120 分钟 满分:150 分)
A 卷(共 100 分)
一、选择题(本大题共 10 小题,每题 3 分,共 30 分)
1、下列各数 3.14 , 2 0 , 31, cos30 中,无理数的个数是( )
A. 1 个
B. 2 个
2、下列各式正确的是( )
1.5 米,那么路灯 A 的高度 AB 等于( )
A. 4.5 米
B. 6 米
C. 7.2 米
9成都外国语学校招生数学试题真卷 (2017年) A3

2017年小学数学毕 业 试 题 (满分:100分时间:60 分钟) 一、判断题(每小题1分,共4分) 1. (最简分数)一个分数,如果分母中含有2和5以外的质因数,这个分数就不能化为有限小数。
( )2. (倍数和约数)一个数的最大约数就是它的最小倍数。
( )3. (平行四边形)正方形是平行四边形。
4. (百分数的应用)六年级学生体育锻炼有100人达标,5二、选择题(每小题1分,共5分,1. (角的认识)右图中共有角( )。
A.4个B.5个C.10个D.122.(分数的性质)比85大而比87小的分数有( )。
A.1个 B.2个 C.无数个 D.3. (对称轴)等边三角形的对称轴有( )。
A.1条B.2条C.3条D.4. (立方的意义)3a 表示( )。
A. a 的3倍B.3个a 相乘C.3个a 相加D.a 与35. (比例的应用)A.成正比例 B.成反比例 C.不成比例 D.三、填空题(每题2分,共28分) 1. (数的写法)十九亿五千八百万零四百写作 ,四舍五人到亿位记作2. (名数互化)4.25小时= 小时 分;2吨50千克= 吨。
3. (和倍问题)甲、乙两数的和是323.2角形)在直角三角形中, 直角和其中一个锐角的角度比是5:3数中最大的合数作分母,最小的质数作分子,这个分数是 ,它的分数单位是6. (统计图)一个养禽专业户去年养鸡、鸭、鹅分别是1200只、500 示养鸡只数的扇形圆心角是 度。
7. (乘法原理)有0、1、2、4、7有 个。
8. (找规律)找规律填数:1、3、7、15、 、63、 .....9.(组合图形求面积)图中三个圆的周长都是25.12厘米,圆心恰好在直角梯形 的三个顶点处,则圆与梯形重叠部分的面积是 平方厘米。
(π取3.14)10.(长方体体积)一个长方体的棱长之和是96厘米。
长、宽、高的比是5:4:3,它的体积是。
11.(正方体表面积)一个正方体的棱长扩大10倍,它的表面积扩大 倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都实验外国语学校
2017年高中自主招生数学真卷(直升卷)
一、选择题
1、根据调查,某市2016年的房价为9000元/平方米,预计2018年的房价将达到11000元/
平方米,求这两年的平均增长率,设年平均增长率为x ,根据题意,所列方程为 ( ) A.()1100019000=+x B.()11000190002
=+x
C.()1100019000=-x
D.()11000190002
=-x
2、关于x 的方程()()012132=+++-a x a ax 有两个不相等的实数根1x ,2x ,且a x x x x -=+-12211,
则a 的值是 ( )
A.1
B.-1
C.-1或1
D.2
3、一个几何体由若干个小立方块搭成,它的主视图、左视图、俯视图分别如下,则搭建这个
几何体的小立方块的个数是 ( )
A.4
B.5
C.6
D.7
4、如图,ABC ∆中,BC AB ⊥,3=AB ,4=BC ,D 为ABC ∆的内心,
则ABD ∆的面积是 ( ) A.43 B.23 C.25
D.2 5、对于任意的11≤≤-x ,032>-+a ax 恒成立,则a 的取值范围为 ( )
A.1>a 或0=a
B.3>a
C.03=>a a 或
D.31<<a
6、一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形
的周长与直径之比称为图形的“周率”,下面四个图形:正三角形、正方形、正六边形、圆的周率分别记为1a ,2a ,3a ,4a ,则下列关系正确的是 ( )
A.324a a a >>
B.214a a a >>
C.321a a a >>
D.432a a a >>
7、ABO ∆的顶点坐标分别为()4,1A ,()1,2B ,()0,0O ,若将ABO ∆绕点O 按逆时针方向旋转︒90得
到'''O B A ∆,那么线段''B A 的中点坐标为 ( )
A.⎪⎭⎫ ⎝⎛-23,25
B.⎪⎭⎫ ⎝⎛-23,2
C.()2,2-
D.⎪⎭
⎫
⎝⎛-2,25
8、如图,在四边形ABCD 中,BC AB ⊥,3=AB ,4=BC ,5=CD ,25=AD ,则BD 等于 ( )
A.35
B.59
C.65
D.8
9、如图,三角形ABC 中,AC AB =,D 、E 分别为AB 、AC 上的点,DM 平分BDE ∠,EN 平分DEC ∠,若︒=∠110DMN ,则=∠DEA ( ) A.︒40 B.︒50 C.︒60 D.︒70
10、将函数b x y +=3(b 为常数)的图象位于x 轴下方的部分沿x 轴翻折至其上方后,所得
的折线是函数b x y +=3(b 为常数)的图象,若该图象在直线3=y 下方的点的横坐标x 满足30<<x ,则b 的取值范围为 ( )
A.6-<b 或3->b
B.6-≤b 或3-≥b
C.36-<<-b
D.36-≤≤-b
11、二次函数c bx ax y ++=2(0≠a )经过坐标原点,当1-=x 时,12≤≤-y ;当2=x 时,
40≤≤y ;则当1=x 时,y 的取值范围是 ( )
A.3134-≤≤-y
B.334≤≤-y
C.231≤≤-y
D.33
1
≤≤-y
12、已知a ,b 为有理数,m 、n 分别表示75-的整数部分与小数部分,且12=+bn amn ,
则=+b a 2( ) A.1 B.
23 C.2 D.2
5
二、填空题
13、已知实数x 、y ,满足()y y x --=+111,则=-20172017y x .
14、关于x 的方程()02
=+-b m x a 的解释11=x ,22-=x (a 、m 、b 均为常数,0≠a ),则
方程()022
=++-b m x a 的解是 .
15、若321=+
a a ,则=-a
a 1
. 16、若点()11,y x A ,()22,y x B 在反比例函数x
y 4
=
的图象上,且021<x x ,以线段AB 为直径的圆的面积为S ,则S 的最小值为 . 17、已知a 是方程012=-+x x 的一个根,则
=---a
a a 221
12 . 18、若a x x ≥-++32对任意实数x 都成立,则a 的取值范围是 .
19、水平相当的甲、乙二人进行乒乓球比赛,赛制为五局三胜制,则甲以3:1战胜乙的概率
是 . 20、给定函数1
1
3--=
x x y ,下列说法正确的有 . (1)不等式0>y 的解为31
<x 或1>x ;
(2)无论t 为何值,方程t y =一定有解;
(3)若点()11,y x ,()22,y x 在该函数图象上且21x x <,则21y y <; (4)经过原点的直线和该函数的图象一定有交点; (5)该函数图象既是中心对称图形,又是轴对称图形.
三、解答题
21、(1)计算:()1
5232160tan 4327232-⎪⎭⎫ ⎝⎛-++︒--++-π
(2)先化简,再求值:423252+-÷
⎪⎭
⎫ ⎝⎛
+--x x x x ,其中32-=x .
(3)解关于x 的不等式组:()⎪⎩⎪
⎨⎧->-+-≤--1312423x x x x
(4)01
4233241=-+-----x x x x .
(5)解关于x 的方程:()0112=--+x a ax (a 为参数).
22、为解决交通拥堵问题,公交公司新开通了一条555路公交汽车线路,为了解555路公交
汽车的运营情况,公交公司统计了某天555路公共汽车每个运行班次的载客量,并按载客量的多少分成A、B、C、D四组,得到如下统计图:
(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天555路公共汽车平均每班的载客量.
23、已知某函数的图象只在第二、第四象限,过图象上任意一点P向x轴作垂线,垂足为A,
∆的面积为3.
AOP
(1)求该函数的解析式;
(2)若P点横坐标为2,将点P沿x轴方向平移3个单位,再沿y轴平移n(0
n)个单位
>得到点'P,使点'P恰好在该函数的图象上,求n的值和点P沿y轴平移的方向.
24、如图,圆O 的半径为R ,其内接锐角三角形ABC 中,角A 、B 、C 所对的边分别为a 、
b 、
c . (1)求证:
R C
c
B b A a 2sin sin sin ===; (2)在AB
C ∆中,︒=∠45B ,︒=∠60C ,2=AC ,利用(1)的结论求BC 长和A sin 的值.
25、如图,四边形ABCD 内接于圆O ,BD AC ⊥,求证:点O 到四边形ABCD 各边的距离之
和等于四边形ABCD 周长的一半.
26、过点F ()1,0的直线与二次函数2
4
1x y =的图象交于A ()11,y x ,B ()22,y x 两点. (1)求证:21y y 为定值; (2)设P 为二次函数2
4
1x y =
的图象上的动点,求证:点P 到点F 的距离等于点P 到定直线1:-=y l 的距离;
(3)求证:定直线1:-=y l 是以线段AB 为直径的圆的切线. 答案: 一、选择题 1、B 2、B 3、B 4、B 5、B 6、B 7、A 8、C 9、A 10、D 11、C 12、D
二、填空题 13、-2
14、11-=x 或42-=x
15、22±
16、π8 17、1 18、5≤a
19、16
3
20、(1)(4)(5)。
