九年级 数学 第六讲 二次函数与面积问题
九年级数学二次函数综合--面积问题课件

例题:如图,已知抛物线y=-x2-2x+3经过点A(-3,0)、点B(1,0)、点C (0,3),直线y=x+3经过点A(-3,0)、点C(0,3). (1)P为抛物线在第二象限内的一点,直线PQ⊥x轴,交AC于点Q,若 PQ=2,求P坐标。 (2)P为抛物线在第二象限内的一点,直线PQ⊥x轴,交AC于点Q,请问线 段PQ是否存在最大值,若存在,求出最大值;若不存在,请说明理由。
二次函数综合 ---面积类
二次函数综合 ---面积类
1. 中考考查频率 自2012年以来几乎每年必考 12年,13年, 14年(线段最值),15年,16年(四边形面积最值),18年, 19年
2. 中考难易程度 压轴解答 7:2:1中的 2
3. 本节学习目标 铅锤法解决线段,面积定值,最值问题
知识储备1:竖直线段的表示
知识储备2:面积的表示
(3)P为抛物线在第二象限内的一点,若△PAC面积为3, 求点P的坐标。
(4)P为抛物线在第二象限内的一点,请问△PAC面积是否存在 最大值,若存在,请求出最大值;若不存在,请说明理由
巩固练习:
思维导图:
作业布置:
二次函数与面积问题

二次函数与面积问题一、引言二次函数是高中数学中的重要内容之一,它在实际生活中有许多应用。
其中之一就是与面积问题相关联。
本文将详细讨论二次函数与面积问题的关系,并分析实际应用。
首先,我们将介绍二次函数的基本概念和公式,然后探讨如何利用二次函数解决面积问题。
二、二次函数基本概念2.1 二次函数的定义二次函数是指具有形如f(x)=ax2+bx+c的函数,其中a、b、c为实数且a≠0。
二次函数的图像通常为一个抛物线。
2.2 二次函数的图像与性质二次函数的图像可分为三种情况:开口向上、开口向下和与x轴相切。
其开口的方向由二次项的系数a决定。
二次函数还具有顶点坐标、对称轴和零点等性质,这些性质对于解决面积问题非常关键。
2.3 二次函数的标准形式和一般形式二次函数可通过变换转化为标准形式或一般形式。
标准形式为f(x)=a(x−ℎ)2+ k,其中(ℎ,k)为顶点坐标。
一般形式为f(x)=ax2+bx+c。
三、二次函数与面积问题3.1 二次函数与矩形面积问题矩形是我们生活中常见的图形之一。
假设一个矩形的长度为x,宽度为y,则它的面积A可以表示为A=xy。
现在,我们希望找到一个长度固定的矩形,使得它的面积最大。
我们可以建立一个二次函数来解决这个问题。
首先,根据矩形的面积公式A=xy,我们可以将y表示为x的函数:y=Ax。
然后,我们将该函数进行变形,得到一个二次函数的标准形式。
将x的取值范围限定为正实数,我们可以排除矩形不存在的情况。
通过对二次函数的顶点坐标求解,我们可以找到使得面积最大的矩形。
3.2 二次函数与三角形面积问题二次函数与三角形面积问题也有密切的联系。
考虑一个等腰三角形,已知其底边长为x,高为y。
我们希望找到一个底边固定的三角形,使得它的面积最大。
根据三角形的面积公式A=12xy,我们可以得到y=2Ax。
类似地,我们将其转化为二次函数的形式,并求解顶点坐标,从而找到最大面积的三角形。
3.3 二次函数与其他面积问题除了矩形和三角形,二次函数还可以应用于其他形状的面积问题,如圆形、梯形等。
二次函数中的面积问题
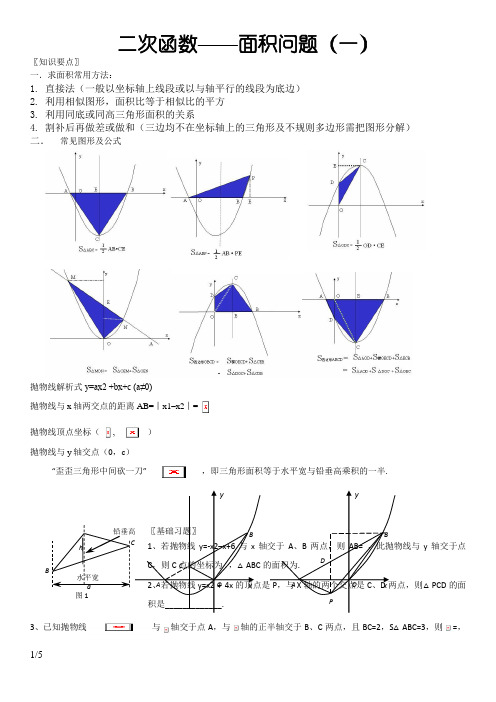
二次函数——面积问题(一)〖知识要点〗一.求面积常用方法:1. 直接法(一般以坐标轴上线段或以与轴平行的线段为底边)2. 利用相似图形,面积比等于相似比的平方3. 利用同底或同高三角形面积的关系4. 割补后再做差或做和(三边均不在坐标轴上的三角形及不规则多边形需把图形分解) 二. 常见图形及公式抛物线解析式y=ax2 +bx+c (a≠0)抛物线与x 轴两交点的距离AB=︱x1–x2︱=抛物线顶点坐标(-, ) 抛物线与y 轴交点(0,c )“歪歪三角形中间砍一刀”,即三角形面积等于水平宽与铅垂高乘积的一半. 〖基础习题〗 1、若抛物线y=-x2–x+6与x 轴交于A 、B 两点,则AB= ,此抛物线与y 轴交于点C ,则C 点的坐标为 ,△ABC 的面积为.2、若抛物线y=x2 + 4x 的顶点是P ,与X 轴的两个交点是C 、D 两点,则△PCD 的面积是_____________.3、已知抛物线与轴交于点A ,与轴的正半轴交于B 、C 两点,且BC=2,S △ABC=3,则=,B C 铅垂高水平宽ha图1 C BA O y x DB A O y x P=.〖典型例题〗● 面积最大问题1、二次函数的图像与轴交于点A (-1,0)、B (3,0),与轴交于点C ,∠ACB=90°.(1)求二次函数的解析式;(2)P 为抛物线X 轴上方一点,若使得△PAB 面积最大,求P 坐标(3)P 为抛物线X 轴上方一点,若使得四边形PABC 面积最大,求P 坐标(4) P 为抛物线上一点,若使得,求P 点坐标。
● 同高情况下,面积比=底边之比2.已知:如图,直线y=﹣x+3与x 轴、y 轴分别交于B 、C ,抛物线y=﹣x2+bx+c 经过点B 、C ,点A 是抛物线与x 轴的另一个交点.(1)求B 、C 两点的坐标和抛物线的解析式;(2)若点P 在直线BC 上,且,求点P 的坐标.3.已知:m 、n 是方程x2﹣6x+5=0的两个实数根,且m <n ,抛物线y=﹣x2+bx+c 的图象经过点A (m ,0)、B (0,n ).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x 轴的另一交点为C ,抛物线的顶点为D ,试求出点C 、D 的坐标和△BCD 的面积;(注:抛物线y=ax2+bx+c (a≠0)的顶点坐标为(3)P 是线段OC 上的一点,过点P 作PH ⊥x 轴,与抛物线交于H 点,若直线BC 把△PCH 分成面积之比为2:3的两部分,请求出P 点的坐标. yx B A C O三角形面积等于水平宽与铅垂高乘积的一半4.阅读材料:如图,过△ABC的三个顶点分别作出水平垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可以得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图,抛物线顶点坐标为点C(1,4)交x轴于点A,交y轴于点B(0,3)(1)求抛物线解析式和线段AB的长度;(2)点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;(3)在第一象限内抛物线上求一点P,使S△PAB=S△CAB.法一:同底情况下,面积相等转化成平行线法二:同底情况下,面积相等转化成铅垂高相等变式一:如图2,点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.变式二:抛物线上是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明点动+面积5.如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC.(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.形动+面积6.如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.(1)试求抛物线的解析式;(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?。
二次函数与三角形面积问题

二次函数与三角形面积问题二次函数与三角形面积问题的关系是通过求解二次函数图像与x轴交点来得到三角形的面积。
具体而言,如果给定二次函数的表达式,我们可以求解方程f(x) = 0的解,这些解就是二次函数图像与x轴交点的横坐标。
通过这些横坐标,我们可以确定三角形的底边的长度。
同时,我们可以求解二次函数的最值来确定三角形的高,进而计算出三角形的面积。
首先,让我们来回顾一下二次函数的定义和性质。
二次函数的一般形式为f(x) = ax^2 + bx + c,其中a、b和c是实数且a不等于零。
二次函数的图像是一个抛物线,它的开口方向由a的正负号决定,当a 大于零时开口向上,当a小于零时开口向下。
二次函数的顶点是抛物线的最值点,当a大于零时顶点是最小值点,当a小于零时顶点是最大值点。
现在,让我们将二次函数与三角形面积问题联系起来。
假设我们有一个给定的二次函数f(x) = ax^2 + bx + c,我们希望求解该二次函数图像与x轴交点的横坐标,并计算出通过这些交点确定的三角形的面积。
首先,我们需要求解方程f(x) = 0,也就是求解ax^2 + bx + c = 0。
这可以通过使用求根公式来进行计算。
根据求根公式,对于一个二次方程ax^2 + bx + c = 0,它的解为x = (-b ± √(b^2 - 4ac)) / (2a)。
根据这个公式,我们可以求解出具体的x值。
假设我们求解得到了两个根,x1和x2。
接下来,我们可以通过计算这两个根之间的距离来确定三角形的底边的长度。
根据数学知识,我们知道两个点(x1, 0)和(x2, 0)之间的距离等于|x2 - x1|。
因此,通过计算|x2 - x1|,我们可以得到底边的长度。
接下来,我们需要确定三角形的高。
为了做到这一点,我们需要找到二次函数的顶点。
二次函数的顶点的横坐标可以通过使用公式x = -b / (2a)来计算。
通过计算出的顶点横坐标,我们可以计算出顶点在x轴上的纵坐标。
二次函数的应用课件面积问题(共10张PPT)

请同学们完成这个 问题的解答
你会解吗?
例6:用6m长的铝合金型材料做一个形状如图所示的矩形窗框。窗框 的长、宽各为多少时,它的透光面积最大?最大透光面积是多少?
解:设矩形的宽为x米,矩形的透光面积为y米。由题 意得:
y=x· 6-3x 2
(0<x<2)
即:y=- 3 x2+3x
2
配方,得:
的距离)能否通过此隧道? 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1
米为数轴的单位长度,建立平面直角坐标系,
A CB
)
(6)y=- x2-4x+1
值范围; 例6:用6m长的铝合金型材料做一个形状如图所示的矩形窗框。
该店想通过降低售价、增加销售量的办法来提高利润。
O x
(2) 有一辆宽2.8米,高3米的 y=x·
(0<x<2)
∴当x=5,y最大值=50
农用货车(货物最高处与地面AB y随着x的增大而减小。
(4)y=100-5x2 将这个函数关系式配方,得:
y=- 3 (x-1)2+ 3
2
2
∴它的顶点坐标是(1,1.5)
∴当x=1,y最大值=1.5
因为x=1时,满足0<x<2,这时
6-3x 2
=1.5
答:当矩形窗框的宽为5m时,长为1.5m时,它的透光
面积最大,最大面积为1.5m2。
1.求下列函数的最大值或最小值:
(1)y=x2-3x+4
(2)y=1-2x-x2
物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角
《二次函数与图形面积问题》PPT课件 人教版九年级数学

即当AC、BD的长均为5时,四边形ABCD的面积最大.
2.用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(如 图所示),墙长为18m,这个矩形的长,宽各为多少时, 菜园的面积最大,最大面积是多少?
解:设矩形的长为x m,面积为y m2,则矩形的宽为15- 2xm.
y
x
15
x
2
=
1 2
x2
15x.
二次函数与图 形面积问题
R·九年级上册
复习导入
用你认为最简单的方法求出顶点坐标,说
出开口方向,对称轴及最值.
(1)y=x2-4x-5
开口方向 对称轴 顶点坐标 最小值
向上 x=2 (2,-9) -9
(2)y=-x2+x+ 1 4
向上
x=1 4
(1 ,1) 22 1
2
探究新知
知识点 利用二次函数解决最大(小)面积问题
2
2
x2
5x
A
B
所以当
x= -
2
5 (-
1
=5 )
时,S取最大值,S最大值
1 52 2
5 5=
25 2
2
当AC,BD的长均为5时,四边形ABCD的面积最大.
6. 一块三角形材料如图所示,∠A=30°,∠C=90°,
AB=12. 用这块材料剪出一个矩形CDEF,其中,点D,
E,F分别在BC,AB,AC上,要使剪出的矩形CDEF的
D
GC
则AH=a-x,HE = a - x2 + x2 ,
H
S正方形EFGH [ (a - x)2 x2 ]2 =2 x2 2ax + a2
当x=
a 2
二次函数动点与面积问题

二次函数动点与面积问题二次函数动点与面积问题在高中数学的二次函数学习中,常常会碰到一类问题,即如何确定二次函数图像与坐标系的位置关系。
在这类问题中,最常见的方法就是利用动点法和面积法来解决问题。
动点法主要用于确定二次函数的顶点和对称轴的位置,而面积法则则主要用于确定二次函数与坐标轴之间的相互位置关系,下面我们来详细讨论一下这两种方法的具体应用。
一、二次函数的顶点和对称轴的确定考虑如何确定一个二次函数的顶点和对称轴,最常见的方法就是采用动点法。
动点法的基本思想就是将二次函数拆分成一元二次函数 f(x) = ax^2+bx+c,并通过对f(x) 的导数求零点来确定顶点的位置。
具体来说,我们可以通过以下步骤来进行顶点和对称轴的确定:第一步,分离 y = ax^2+bx+c 函数中的常数项:y - c = ax^2+bx ----->f(x) = ax^2+bx第二步,求解导数f’(x) = 2ax+b 的根(也就是切线的斜率),令其等于0,解出 x = -b/2a,这个值就是二次函数的对称轴的位置;第三步,将求得的对称轴的位置带入一元二次函数f(x) = ax^2+bx+c 中,即可求出二次函数的顶点位置,也就是 (x, y) = (-b/2a, f(-b/2a)+c)。
可以说,这个动点法是二次函数解题中的一个基本应用,学习二次函数的选手一定要掌握。
二、二次函数与坐标轴的相对位置的确定二次函数的另一个常见问题是如何确定它与坐标轴之间的相对位置关系。
为此,我们可以采用面积法,基本思想是利用图形所围成的面积,从而确定二次函数与坐标轴之间的相对位置。
具体来说,我们可以通过以下步骤来确定二次函数与坐标轴之间的相对位置:第一步,确定二次函数的顶点位置和二次函数的开口方向(向上还是向下);第二步,利用顶点和坐标轴的交点,将整个坐标系分成不同的部分;第三步,分别计算出不同部分围成的面积,具体的计算方式以二次函数与 x 轴的相对位置情况为准,例如:情形1:当二次函数与 x 轴没有任何交点时,可以直接计算出二次函数的面积,此时,图形所围成的面积就是函数的定积分的绝对值:S = ∫_{x1}^{x2}|f(x)|dx情形2:当二次函数与 x 轴只有一个交点时,此时,图形所围成的面积就是上下两个三角形的面积之和:S = [f(x)-0] × (x-x1)÷2 + [0-f(x)] × (x2-x)÷2情形3:当二次函数与 x 轴有两个交点时,此时,图形所围成的面积就是上下两个三角形面积和与中间小矩形部分的面积之和:S = [f(x)-0] × (x-x1)÷2 + [0-g(x)] × (x2-x)÷2 + g(x)×(x2-x1)其中,g(x)就是与原函数相对称的一条直线的函数表达式。
二次函数与几何综合-面积问题(解析版)

专项11 二次函数与几何综合-面积问题【方法1直接法】一般以坐标轴上线段或以与轴平行的线段为底边【方法2 铅锤法】铅锤高水平宽⨯=21S 【方法3 其他面积方法】如图1,同底等高三角形的面积相等.平行线间的距离处处相等.如图2,同底三角形的面积比等于高的比.如图3,同高三角形的面积比等于底的比.如图1 如图2 如图3【方法4 利用相似性质】利用相似图形,面积比等于相似比的平方。
【方法1 铅锤法求面积】【典例1】(聊城)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),点B(4,0),与y轴交于点C(0,8),连接BC.又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E.(1)求抛物线的表达式;(2)作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.【答案】(1)y=﹣x2+2x+8 (2)【解答】解:(1)将点A、B、C的坐标代入二次函数表达式得:,解得:,故抛物线的表达式为:y=﹣x2+2x+8;(2)在Rt△PFD中,∠PFD=∠COB=90°,∵l∥y轴,∴∠PDF=∠OCB,∴Rt△PFD∽Rt△BCO,∴,∴S△PDF=•S△BOC,而S△BOC=OB•OC==16,BC==4,∴S△PDF=•S△BOC=PD2,即当PD取得最大值时,S△PDF最大,将B、C坐标代入一次函数表达式并解得:直线BC的表达式为:y=﹣2x+8,设点P(m,﹣m2+2m+8),则点D(m,﹣2m+8),则PD=﹣m2+2m+8+2m﹣8=﹣(m﹣2)2+4,当m=2时,PD的最大值为4,故当PD=4时,∴S△PDF=PD2=【变式1-1】(娄底)如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,且过点D(2,﹣3).点P、Q是抛物线y=ax2+bx+c上的动点.(1)求抛物线的解析式;(2)当点P在直线OD下方时,求△POD面积的最大值.【答案】(1):y=x2﹣2x﹣3 (2)①﹣m2+m+3 ②【解答】解:(1)函数的表达式为:y=a(x+1)(x﹣3),将点D坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)设点P(m,m2﹣2m﹣3),①当点P在第三象限时,设直线PD与y轴交于点G,设点P(m,m2﹣2m﹣3),将点P、D的坐标代入一次函数表达式:y=sx+t并解得:直线PD的表达式为:y=mx﹣3﹣2m,则OG=3+2m,S△POD=×OG(x D﹣x P)=(3+2m)(2﹣m)=﹣m2+m+3,②当点P在第四象限时,设PD交y轴于点M,同理可得:S△POD=×OM(x D﹣x P)=﹣m2+m+3,综上,S△POD=﹣m2+m+3,∵﹣1<0,故S△POD有最大值,当m=时,其最大值为;【变式1-2】(2021秋•龙江县校级期末)综合与探究如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式,连接BC,并求出直线BC的解析式;(2)请在抛物线的对称轴上找一点P,使AP+PC的值最小,此时点P的坐标是(,);(3)点Q在第一象限的抛物线上,连接CQ,BQ,求出△BCQ面积的最大值.(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.【解答】解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,解得,∴y=﹣x2+3x+4;在y=﹣x2+3x+4中,令x=0,则y=4,∴C(0,4),设BC的解析式为y=kx+b,∵B(4,0),C(0,4),∴,∴,∴直线BC的解析式为y=﹣x+4;(2)如图1中,由题意A,B关于抛物线的对称轴直线x=对称,连接BC交直线x=于点P,连接P A,此时P A+PC的值最小,最小值为线段BC的长==4,∵直线BC的解析式为y=﹣x+4,∴x=时,y=﹣+4=,∴此时P(,).故答案为:(,);(3)设Q(m,﹣m2+3m+4)过Q作QD⊥x轴,交BC于点D,则D(m,﹣m+4),∴QD=(﹣m2+3m+4)﹣(﹣m+4)=﹣m2+4m,∵B(4,0),∴OB=4,,当m=2时,S△BCQ取最大值,最大值为8,∴△BCQ面积的最大值为8;【变式1-2】(2022春•南岸区月考)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x 轴交于A(﹣1,0),B(3,0),交y轴于点C,且OC=3.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;【解答】解:(1)∵OC=3,∴C(0,﹣3),将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,得,解得,∴y=x2﹣2x﹣3;(2)∵S四边形PCAB=S△ABC+S△PBC,∴当S△PBC面积最大时,S四边形PCAB的面积最大,设BC的直线解析式y=kx+b,∴,解得,∴y=x﹣3,过点P作PQ⊥x轴交BC于点Q,设P(t,t2﹣2t﹣3),则Q(t,t﹣3),∴当PQ最大时,S△PBC面积最大,∴PQ=t﹣3﹣t2+2t+3=﹣t2+3t=﹣(t﹣)2+,当t=时,PQ取最大值,∴P(,﹣),∵A(﹣1,0),B(3,0),C(0,3),∴AB=4,∴S四边形PCAB=S△ABC+S△PBC=×4×3+××3=;【方法2 其他方法】【典例2】(深圳)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB =OC.(1)求抛物线的解析式及其对称轴;(2)点P为抛物线上一点,连接CP,直线CP把四边形CBP A的面积分为3:5两部分,求点P的坐标.【答案】(1)y=﹣x2+2x+3 ;x=1(2)P的坐标为(4,﹣5)或(8,﹣45)【解答】解:(1)∵OB=OC,∴点B(3,0),则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,故﹣3a=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+3…①,函数的对称轴为:x=1;(2)如图,设直线CP交x轴于点E,直线CP把四边形CBP A的面积分为3:5两部分,又∵S△PCB:S△PCA=EB×(y C﹣y P):AE×(y C﹣y P)=BE:AE,则BE:AE=3:5或5:3,则AE=或,即:点E的坐标为(,0)或(,0),将点E的坐标代入直线CP的表达式:y=kx+3,解得:k=﹣6或﹣2,故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②联立①②并解得:x=4或8(不合题意值已舍去),故点P的坐标为(4,﹣5)或(8,﹣45).【变式2-1】(2021秋•合川区)如图,抛物线y=ax2+bx+6(a≠0)与x轴交于A(﹣1,0),B(6,0),与y轴交于点C,点P为第一象限内抛物线上一动点,过点P作x轴的垂线,交直线BC于点D,交x轴于点E,连接PB.(1)求该抛物线的解析式;(2)当△PBD与△BDE的面积之比为1:2时,求点P的坐标;【答案】(1)y=﹣x2+5x+6 (2)P(,)【解答】解:(1)∵抛物线y=ax2+bx+6(a≠0)与x轴交于A(﹣1,0),B(6,0),∴,∴,∴抛物线的解析式为y=﹣x2+5x+6;(2)∵抛物线y=﹣x2+5x+6过点C,∴C(0,6),设直线BC的解析式为y=kx+n,∴,∴,∴直线BC的解析式为y=﹣x+6,设P(m,﹣m2+5m+6),则D(m,﹣m+6),∴PE=﹣m2+5m+6,DE=﹣m+6,∵△PBD与△BDE的面积之比为1:2,∴PD:DE=1:2,∴PE:DE=3:2,∴3(﹣m+6)=2(﹣m2+5m+6),解得,m2=6(舍去),∴P(,);【典例3】(淮安)如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5,0),点D的坐标为(1,3).(1)求该二次函数的表达式;(2)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的?若存在,求出点G的坐标;若不存在,请说明理由.【答案】(1)y=﹣(x﹣1)2+3(2)G的坐标为(0,)或(﹣15,﹣45).【解答】解:(1)依题意,设二次函数的解析式为y=a(x﹣1)2+3将点B代入得0=a(5﹣1)2+3,得a=﹣∴二次函数的表达式为:y=﹣(x﹣1)2+3(2)存在点G,当点G在x轴的上方时,设直线DG交x轴于P,设P(t,0),作AE⊥DG于E,BF⊥DG于F.由题意:AE:BF=3:5,∵BF∥AE,∴AP:BP=AE:BF=3:5,∴(﹣3﹣t):(5﹣t)=3:5,解得t=﹣15,∴直线DG的解析式为y=x+,由,解得或,∴G(0,).当点G在x轴下方时,如图2所示,∵AO:OB=3:5∴当点G在DO的延长线上时,存在点G使得S△ADG:S△BDG=3:5,此时,DG的直线经过原点,设直线DG的解析式为y=kx,将点D代入得k=3,故y=3x,则有整理得,(x﹣1)(x+15)=0,得x1=1(舍去),x2=﹣15当x=﹣15时,y=﹣45,故点G为(﹣15,﹣45).综上所述,点G的坐标为(0,)或(﹣15,﹣45).【变式3】(2021秋•南阳)如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x 轴相交于A,B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标.(2)已知a=1,C为抛物线与y轴的交点.①求抛物线的解析式.②若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.【答案】(1)点B的坐标为(1,0)(2)①y=x2+2x﹣3②点P的坐标为(4,21)或(﹣4,5)【解答】解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2,将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3,∴抛物线的解析式为y=x2+2x﹣3;②∵抛物线的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3,设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×OC×|x|=4××OC×OB,即×3×|x|=4××3×1,∴|x|=4,解得x=±4,当x=4时,x2+2x﹣3=16+8﹣3=21,当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5,∴点P的坐标为(4,21)或(﹣4,5);1.(2021秋•日喀则市月考)如图,二次函数y=﹣x2+4x+5的图象与x轴交于A,B两点,与y轴交于点C,M为抛物线的顶点.(1)求M点的坐标;(2)求△MBC的面积;【解答】解:(1)y=﹣x2+4x+5=﹣(x﹣2)2+9,∴M(2,9);(2)令y=0,得﹣x2+4x+5=0,解得x=﹣1或x=5,∴A(﹣1,0),B(5,0),令x=0,得y=﹣x2+4x+5=5,∴C(0,5),过点M作ME⊥y轴于点E,∴S△MBC=S四边形MBOE﹣S△MCE﹣S△BOC==15;2.(2022•东方二模)如图,抛物线y=x2+bx+c经过B(3,0)、C(0,﹣3)两点,与x 轴的另一个交点为A,顶点为D.(1)求该抛物线的解析式;(2)点E为该抛物线上一动点(与点B、C不重合),当点E在直线BC的下方运动时,求△CBE的面积的最大值;【解答】解:(1)将B(3,0),C(0,﹣3)代入y=x2+bx+c得:,解得,∴抛物线的解析式为y=x2﹣2x﹣3;(2)连接CE、BE,经过点E作x轴的垂线FE,交直线BC于点F,设直线BC的解析式为y=kx+m,将B,C两点的坐标代入得:,解得:,∴直线BC的解解析式为y=x﹣3,设点F(x,x﹣3),点E(x,x2﹣2x﹣3),∴EF=(x﹣3﹣x2+2x+3)=﹣x2+3x,∴S△CBE=S△CEF+S△BEF=EF•OB=(﹣x2+3x)=﹣(x﹣)2+,∵a=﹣<0,且0<x<3,∴当x=时,S△CBE有最大值,最大值是,此时E点坐标为(,﹣);3.(2022•广东)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B 两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.(1)求该抛物线的解析式;(2)求△CPQ面积的最大值,并求此时P点坐标.【解答】(1)∵抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,∴B(﹣3,0),∴,解得,∴抛物线的解析式为y=x2+2x﹣3;(2)过Q作QE⊥x轴于E,过C作CF⊥x轴于F,设P(m,0),则P A=1﹣m,∵y=x2+2x﹣3=(x+1)2﹣4,∴C(﹣1,﹣4),∴CF=4,∵PQ∥BC,∴△PQA∽△BCA,∴,即,∴QE=1﹣m,∴S△CPQ=S△PCA﹣S△PQA=P A•CF﹣P A•QE=(1﹣m)×4﹣(1﹣m)(1﹣m)=﹣(m+1)2+2,∵﹣3≤m≤1,∴当m=﹣1时S△CPQ有最大值2,∴△CPQ面积的最大值为2,此时P点坐标为(﹣1,0).4.(2022春•青秀区校级期末)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c,与y 轴交于点A,与x轴交于点E、B.且点A(0,5),B(5,0),抛物线的对称轴与AB 交于点M.(1)求二次函数的解析式;(2)若点P是直线AB上方抛物线上的一动点,连接PB,PM,求△PMB面积的最大值;【解答】解:(1)∵点A(0,5),B(5,0)在抛物线y=﹣x2+bx+c上,∴,∴,∴二次函数的解析式为y=﹣x2+4x+5;(2)如图,∵A(0,5),B(5,0),∴直线AB的解析式为y=﹣x+5,∵点M是抛物线的对称轴与直线AB的交点,∴M(2,3),由(1)知,二次函数的解析式为y=﹣x2+4x+5,过点P作PH∥y轴交AB于H,设P(m,﹣m2+4m+5)(0<m<5),∴H(m,﹣m+5),∴PH=﹣m2+4m+5﹣(﹣m+5)=﹣m2+5m,∴S△PMB=PH(x B﹣x M)=(﹣m2+5m)(5﹣2)=﹣(x﹣)2+,∴当x=时,S△PMB最大=,即△PMB面积的最大值为;5.(2022春•南岸区月考)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A (﹣1,0),B(3,0),交y轴于点C,且OC=3.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB 的面积的最大值,以及此时点P的坐标;【解答】解:(1)∵OC=3,∴C(0,﹣3),将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,得,解得,∴y=x2﹣2x﹣3;(2)∵S四边形PCAB=S△ABC+S△PBC,∴当S△PBC面积最大时,S四边形PCAB的面积最大,设BC的直线解析式y=kx+b,∴,解得,∴y=x﹣3,过点P作PQ⊥x轴交BC于点Q,设P(t,t2﹣2t﹣3),则Q(t,t﹣3),∴当PQ最大时,S△PBC面积最大,∴PQ=t﹣3﹣t2+2t+3=﹣t2+3t=﹣(t﹣)2+,当t=时,PQ取最大值,∴P(,﹣),∵A(﹣1,0),B(3,0),C(0,3),∴AB=4,∴S四边形PCAB=S△ABC+S△PBC=×4×3+××3=;6.(2022•兴宁区校级模拟)如图,抛物线y=﹣x2+bx+c过点A、B,抛物线的对称轴交x 轴于点D,直线y=﹣x+3与x轴交于点B,与y轴交于点C,且.(1)求抛物线的解析式;(2)点M(t,0)是x轴上的一个动点,点N是抛物线对称轴上的一个动点,当DN=2t,△MNB的面积为时,求出点M与点N的坐标;【解答】解:(1)对于直线y=﹣x+3,令y=0,即﹣x+3=0,解得:x=3,令x=0,得y=3,∴B(3,0),C(0,3),∵A为x轴负半轴上一点,且OA=OB,∴A(﹣1,0).将点A、B的坐标分别代入y=﹣x2+bx+c中,得,解得,∴抛物线的解析式为y=﹣x2+2x+3;(2)由(1)知:A(﹣1,0),B(3,0),D(1,0),∴BM=|3﹣t|,∵S△MNB=BM•DN=,即•|3﹣t|•2t=,当t<3时,•(3﹣t)•2t=,化简得:4t2﹣12t+15=0,∵Δ=(﹣12)2﹣4×4×15=﹣96<0,∴方程无解;当t>3时,•(t﹣3)•2t=,解得t1=,t2=(舍),∴DN=2t=3+2,∴点M的坐标为(,0),点N的坐标为(1,3+2);7.(2022•烟台)如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.(1)求抛物线的表达式;(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S 的最大值及此时D点的坐标;【解答】解:(1)当x=0时,y=4,∴C(0,4),当y=0时,x+4=0,∴x=﹣3,∴A(﹣3,0),∵对称轴为直线x=﹣1,∴B(1,0),∴设抛物线的表达式:y=a(x﹣1)•(x+3),∴4=﹣3a,∴a=﹣,∴抛物线的表达式为:y=﹣(x﹣1)•(x+3)=﹣x2﹣x+4;(2)如图1,作DF⊥AB于F,交AC于E,∴D(m,﹣﹣m+4),E(m,m+4),∴DE=﹣﹣m+4﹣(m+4)=﹣m2﹣4m,∴S△ADC=OA=•(﹣m2﹣4m)=﹣2m2﹣6m,∵S△ABC===8,∴S=﹣2m2﹣6m+8=﹣2(m+)2+,∴当m=﹣时,S最大=,当m=﹣时,y=﹣=5,∴D(﹣,5);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六讲 二次函数与面积问题
一、【知识梳理】
1、二次函数与面积问题的分析中研究思路为:
(1)分析图形的成因 (2)识别图形的形状 (3)找出图形的计算方法 注意:
(1)取三角形的底边时一般以坐标轴上线段或以与轴平行的线段为底边. (2)三边均不在坐标轴上的三角形及不规则多边形需把图形分解.(即采用 割或补 的方法把它分解成易于求出面积的图形) (3)在求图形的面积时常常使用到以下公式:
抛物线与x 轴两交点的距离AB=︱x 1–x 2︱=a
∆
抛物线顶点坐标(-a
b 2, a
b a
c 442
-)
抛物线与y 轴交点(0,c ) 二、【二次函数常见图形】
【例1】 若抛物线y=-x 2–x+6与x 轴交于A 、B 两点,则AB= ,此抛物
线 与y 轴交于点C ,则C 点的坐标为 △ABC 的面积为 .
【例2】 已知抛物线y=x 2–4x+1, 与x 轴交于A 、B 两点,在抛物线上有一点N,使△ABN 的面积为43,求点N 的坐标.
【例
3
】
已知二次函数y=-2
1x 2+x+4的图象与x 轴的交点从右向左为A 、B 两点,与 y
轴交点为C ,顶点为D ,求四边形ABCD 的面积.
图2
【例4】 已知直线3y kx =-与x 轴交于点()40A ,,与y 轴交于点C ,抛物线
23
4
y x mx n =-++经过点A 和点C ,
动点P 在x 轴上以每秒1个长度单位的速度由抛物线与x 轴的另一个交点B 向点A 运动,点Q 由点C 沿线段CA 向点A 运动且速度是点P 运动速度的2倍.
(1)求此抛物线的解析式和直线的解析式;
(2)如果点P 和点Q 同时出发,运动时间为t (秒),试问当t 为何值时,PQA △是直角三角形;
(3)在直线CA 上方的抛物线上是否存在一点D ,使得ACD △的面积最大,若存在,求出点D 坐标;若不存在,请说明理由.
【例5】 已知抛物线2y x bx c =++交x 轴于A (1,0)、B (3,0)两点,交y 轴于点C ,其顶点为D .
(1)求b 、c 的值并写出抛物线的对称轴;
(2)连接BC ,过点O 作直线OE ⊥BC 交抛物线的对称轴于点E . 求证:四边形ODBE 是等腰梯形;
(3)抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE
的面积的1
3
?若存在,求点Q 的坐标;若不存在,请说明理由.
1、已知抛物线y=2x2+3mx+2m与y轴交于点N,顶点为C,且△OCN的面积为16/27,求此
抛物线的解析式.
2、已知一次函数y=kx+m的图象与二次函数y=a x
2 +bx+c相交于A(-2,-1),B(6,
3)两点,且二次函数图象与y轴的负半轴交于C点,若△ABC的面积为12,求一次函
数及二次函数解析式.
3、如图,过A(8,0)、B(0,x
y3
交于点C.平行于y
轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;
l分别交线段BC、OC于点D、E,以DE为边向左侧作等边△DEF,设△DEF与△BCO重
叠部分的面积为S(平方单位),直线l的运动时间为t(秒).
(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线l与x轴交于点P,是否存在这样的点P,
使得以P、O、F为顶点的三角形为等腰三角形,若存
在,请直接写出点P的坐标;若不存在,请说明理由.
与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E
作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若
能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积
的最大值.。
